1 Introduction

An optimization problem is a problem of finding the best solution from all feasible solutions. Every optimization problem has a unique global optimal solution, where the output is optimized. Global search and optimization algorithm (GSOA) has been designed to solve the optimization problems as it plays the role to find the global optimal solution for a given optimization problem. Swarm-based algorithms, categorized under the group of global search and optimization algorithm, are commonly developed by imitating the behavior of creatures in nature. They have been widely involved in different fields of application, such as knapsack problem solving, text document clustering analysis (Abualigah et al. 2018a, b; Karol and Mangat 2013) and maximum power point tracking (MPPT). There exists another option of mathematical optimization problem, named multi-criteria optimization which involves more than one objective function to be optimized simultaneously. Multi-criteria optimization is an area of multiple criteria decision making. Although it is not implicated in this paper, the works of the literature (Amin et al. 2018a, b; Fahmi et al. 2018; Shakeel et al. 2018) are reviewed to study the respective employed methods in solving multi-criteria optimization problems.

The relatively popular swarm-based algorithms include ant colony optimization algorithm (ACO) (Colomi et al. 1991; Dorigo et al. 1999), particle swarm optimization (PSO) algorithm (Bai 2010; Eberhrt and Kennedy 1995), artificial bee colony (ABC) algorithm (Basturk and Karaboga 2007; Karaboga 2005; Karaboga and Basturk 2008) and many more. The artificial fish swarm algorithm (AFSA) is one of the most recent swarm-based algorithms [originally proposed by Li et al. (2002)].

Naturally, fish swarm lives in an environment with greater food density. AFSA imitates the preying behavior process of fish swarm in the real environment. In this algorithm, each artificial fish (AF) is trained to take action according to the real-time situation. Each AF learns to perform four kinds of basic behaviors: follow, swarm, prey and random behaviors. Prey behavior is the foundation of the algorithm’s convergence, swarm behavior enhances the stability and global convergence of the algorithm, follow behavior speeds-up the algorithm’s convergence and the random behavior balances the contradiction of the other three behaviors. Input parameters given to each AF are visual, as the perception, and step, as the moving step length. AFs will gather the information and take a move using visual and step. These behaviors of AFs tend to influence each other’s fitness as well.

The beneficial advantages of AFSA over other swarm-based algorithms are as follows: parallelism, simplification, strong global search ability, fast convergence and less sensitive to the requirements of the objective functions (Wang et al. 2016). With these advantages, AFSA has been successfully applied in a wide range of optimization problems.

Although many improvements and modifications have been proposed regularly on fish swarm algorithm, they mostly focused on balancing the process of exploration and exploitation, but not appointed for detailed navigation to guide toward accurate and precise direction. The fact is that the existing fish swarm algorithms have reached neither the real optimal solution nor an extremely good convergence rate.

In this paper, an improved algorithm, named normative fish swarm algorithm (NFSA), is proposed. NFSA hybridizes the characteristics of AFSA optimized by PSO with extended memory (PSOEM-FSA) (Duan et al. 2016) with the normative knowledge that was implemented in the cultural artificial fish swarm algorithm (CAFSA) (Wu et al. 2011). The normative knowledge is employed to prepare the complementary guidelines to be merged with the behavioral patterns of PSOEM-FSA. The generated guidelines lead the artificial fishes (AFs) to cite an extremely accurate and precise direction when they perform the modified search behaviors. The exchanging and sharing of information are employed in the population. NFSA further enhances the adaptive parameters to further balance the contradiction between the global search and local search abilities. The aim of the proposed algorithm is to obtain better performance in terms of best optimal solution and convergence rate by solving the presented optimization benchmark functions. The specific contributions are as follows:

  1. i.

    Present a comprehensive survey on the optimization methods to solve the optimization benchmark functions with a focus to achieve better best optimal solution and convergence rate.

  2. ii.

    Introduce a normative communication behavior that was inspired by the behavioral pattern in PSOEM-FSA. Normative communication behavior is mainly employed to enhance the global search ability with a focus to provide detailed navigation to the candidates.

  3. iii.

    Introduce a normative memory behavior that has similar characteristics with normative communication behavior. Just that, normative communication behavior emphasizes the global search action, while normative memory behavior emphasizes the delicate local search.

  4. iv.

    Improve the adaptive parameters, mainly on the perceptions of visual/step and visualmin/stepmin along the iterative process, to solve the imbalance problem occurred in manipulating the process of exploration and exploitation.

  5. v.

    Introduce the parallelism in executing the behaviors of the proposed algorithm to make sure that every behavior is utilized in any given situation.

The proposed algorithm is simulated on ten nonlinear benchmark functions. Out of the ten benchmark functions, seven of them are the multimodal optimization functions while the other three are the unimodal optimization functions. Without a doubt, multimodal functions are much more difficult to be solved due to the higher possibility of candidate solutions being trapped inside the local optima. The parameters of NFSA are adopted from the literature (Mao et al. 2017). For the purpose of validation, a fair comparison with other comparative algorithms published in the literature (Mao et al. 2017) is employed. The results obtained by the proposed algorithm include the best optimum on each benchmark function, the means of the statistical data and the standard deviations. Collected results reveal that the NFSA is highly robust and precise due to the relatively superior standard deviations. NFSA outperforms other comparative algorithms on almost all the datasets. The convergence characteristic of NFSA was examined by comparing it with comparative algorithms. The convergence rate of NFSA was found to be extremely outstanding. It can be deduced that the respective contributions solve their problems in either way of global or local search.

This paper is outlined as follows. Section 2 reviews the works of the literature, Sect. 3 lays out the proposed algorithm, Sect. 4 explains the experimental settings, Sect. 5 analyzes the computational results, and Sect. 6 describes the conclusion of this research.

2 Literature review

2.1 Standard artificial fish swarm algorithm (AFSA)

Recently, there have been plenty of researches done on AFSA, in various ways of modification and a variety of application. The works of Zhang et al. (2018); Zhou et al. (2018); and Zhu et al. (2018) have been cited to prove that AFSA tends to maintain its popularity in 2018.

Artificial fish swarm algorithm (AFSA) was inspired by the characteristic of fish swarm’s behavior in searching for a maximum food density. Let the environment where AF lives in is the problem space given by [L, U] (Azizi 2014). Suppose that the state vector of the artificial fish swarm is X = (X1, X2…Xn), where X1, X2…Xn is the position of the population (Huang and Chen 2013) and n is the total number of artificial fishes (AFs) involved. The food concentration is determined by the object function Y = f(X), where Y represents the fitness value at position X. Each AF has been given a perception, in term of visual to gather the information in order to seek for a better food solution and determine the current situation of other companions. step represents the maximum step size of an artificial fish (AF) (Huang and Chen 2013) to approach a certain targeted position. The other necessary parameters include crowding factor , try_number and iteration number t. In AFSA, each AF has been taught to perform different behaviors (i.e., follow, swarm, prey and random) according to its current situation.

Figure 1 shows the process flow of standard AFSA for a count of iteration. The entire behaviors of an AF have been mentioned, with the conditions stated. The pseudo code of AFSA is given in Sumathi et al. (2016).

figure a
Fig. 1
figure 1

Flowchart of AFSA

Full size image

2.1.1 Follow behavior

The current position of i-th artificial fish (AF) is Xi, and the food concentration at this position is Yi (Zhang et al. 2014). The total number of neighbor companions which fulfills the condition

$$ d_{ij} < visual $$

is denoted as nf value, where dij is the distance between the i-th AF and the j-th neighbor companion. As long as “nf > 0,” there is at least one neighbor companion located within its perceived visual and follow behavior is ready to be executed. Among the neighbor companions, the one with the best fitness Ymin is referred to and its position is denoted as Xmin. If \( \frac{{\varvec{Y}_{ \hbox{min} } }}{{n_{f} }} < \delta \varvec{Y}_{i} \), it indicates that the food density at Xmin is greater than at Xi. In this case, the i-th AF will chase the reliable companion using the following expression (Li et al. 2002):

$$ \varvec{X}_{i}^{t + 1} = \varvec{X}_{i}^{t} + \frac{{\varvec{X}_{\hbox{min} } - \varvec{X}_{i}^{t} }}{{|\varvec{X}_{\hbox{min} } - \varvec{X}_{i}^{t} |}}rand \times step $$
(1)

where \( \varvec{X}_{i}^{t} \) represents the position vector of i-th individual at the t-th iterative process.

2.1.2 Swarm behavior

Similar to follow behavior, the total number of neighbor companions which fulfills the condition

$$ d_{i \, j} < visual $$

is denoted as nf. If “nf > 0,” swarm behavior is ready to be executed. By including all neighbor companions, the center position of the swarm is calculated and denoted as XC, which yield a center fitness value YC. If \( \frac{{\varvec{Y}_{C} }}{{n_{f} }} < \delta \varvec{Y}_{i} \), it indicates the food density at XC is greater than at Xi. In this case, i-th AF will follow the expression to swarm together (Li et al. 2002):

$$ \varvec{X}_{i}^{t + 1} = \varvec{X}_{i}^{t} + \frac{{\varvec{X}_{C} - \varvec{X}_{i}^{t} }}{{|\varvec{X}_{C} - \varvec{X}_{i}^{t} |}}rand \times step $$
(2)

2.1.3 Prey behavior

Without consulting to any information from companions, AF performs a random preying behavior. Random position Xj is selected within its perceived visual given by (Li and Qian 2003).

$$ \varvec{X}_{j} = \varvec{X}_{i}^{t} + rand[ - 1,1] \times visual $$
(3)

If Yj< Yi, it indicates a greater food density at Xj, and AF will move toward the selected position. The expression is given below (Li et al. 2002).

$$ \varvec{X}_{i}^{t + 1} = \varvec{X}_{i}^{t} + \frac{{\varvec{X}_{j} - \varvec{X}_{i}^{t} }}{{|\varvec{X}_{j} - \varvec{X}_{i}^{t} |}}rand \times step $$
(4)

In case of Xj fail to yield a better food solution, it performs again the preying behavior as long as the try_number does not reach its limit.

2.1.4 Random behavior

In general, random behavior is conducted after frustration in other behaviors. AF abides the expression to move a random step (Li et al. 2002):

$$ \varvec{X}_{i}^{t + 1} = \varvec{X}_{i}^{t} + rand \times step $$
(5)

2.2 AFSA optimized by PSO with extended memory (PSOEM-FSA)

Generally, PSOEM (Duang et al. 2011) upgraded PSO (Eberhrt and Kennedy 1995) with the extension of memory, which employed the information at previous iterations. The expressions of PSOEM are denoted as (Duan et al. 2016):

$$ \varvec{X}_{t + 1} = \varvec{X}_{t} + \varvec{v}_{t + 1} $$
(6)

and

$$ \begin{aligned} \varvec{v}_{t + 1} & = \omega \varvec{v}_{t} + \alpha_{t}^{l} \left[ {\xi_{t} \left( {\varvec{\rho}_{t}^{l} - \varvec{X}_{t} } \right) + \xi_{t - 1} \left( {\varvec{\rho}_{t - 1}^{l} - \varvec{X}_{t - 1} } \right)} \right] \\ & \quad + \,\alpha_{t}^{g} \left[ {\xi_{t} \left( {\varvec{\rho}_{t}^{g} - \varvec{X}_{t} } \right) + \xi_{t - 1} \left( {\varvec{\rho}_{t - 1}^{g} - \varvec{X}_{t - 1} } \right)} \right] \\ \end{aligned} $$
(7)

where t denotes the index of iteration; \( \varvec{v}_{t} \) represents the speed of the particle at the t-th iterative process, and hence, \( \varvec{v}_{t + 1} \) represents its updated speed vector; \( \varvec{X}_{t} \) represents the position of the particle at the t-th iterative process, \( \varvec{X}_{t + 1} \) represents the updated position of the particle; \( \varvec{\rho}_{t}^{l} \) represents the current individual extreme value point of the particle at the t-th iterative process; \( \varvec{\rho}_{t - 1}^{l} \) represents extreme value point of the particle at the (t − 1)-th iterative process; \( \varvec{\rho}_{t}^{g} \) represents the current global extreme value point of the population at the t-th iterative process; \( \varvec{\rho}_{t - 1}^{g} \) represents the global extreme value point of the population at the (t − 1)-th iterative process; \( \alpha_{t}^{l} \) and \( \alpha_{t}^{g} \) are the acceleration factors; \( \omega \) is known as the inertia weight; \( \xi_{t} \) is called current effective factor; \( \xi_{t - 1} \) is called the effective factor of extended memory; \( \mathop \sum \nolimits \xi = \xi_{t} + \xi_{t - 1} = 1. \)

Integrating the behaviors of the standard AFSA (Li et al. 2002) into PSOEM produced PSOEM-FSA. From the statements of PSOEM-FSA in the literature (Duan et al. 2016), \( \varvec{\rho}_{t}^{g} \) and \( \varvec{\rho}_{t}^{l} \) were extracted and combined exclusively with the fish swarm behavior. Hence, the communication behavioral pattern and memory behavioral pattern were introduced, respectively.

The updated speed vector of communication behavior in PSOEM-FSA is expressed as follows (Duan et al. 2016):

$$ \varvec{v}_{t + 1} = \omega \varvec{v}_{t} + rand[0,1] \times step\left[ {\left( {\frac{{\xi_{t} \left( {\varvec{X}_{\text{gbest}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{\text{gbest}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)}}{{\left| {\xi_{t} \left( {\varvec{X}_{\text{gbest}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{\text{gbest}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)} \right|}}} \right)} \right] $$
(8)

where \( \varvec{v}_{t} \) represents the speed of the individual at the t-th iterative process; hence, \( \varvec{v}_{t + 1} \) represents its updated speed vector; \( \varvec{X}_{\text{gbest}}^{t} \) represents the current global extreme value point of the population at the t-th iterative process; \( \varvec{X}_{\text{gbest}}^{t - 1} \) represents the global extreme value point of the population at the (t − 1)-th iterative process; \( \varvec{X}_{i}^{t} \) represents the current position vector of i-th individual at the t-th iterative process.

Communication behavioral pattern trains the artificial fishes (AFs) to swim while referring to the current and previous global optimal positions (i.e., \( \varvec{X}_{\text{gbest}}^{t} \) and \( \varvec{X}_{\text{gbest}}^{t - 1} \)) of the entire communities. This helps to strengthen the ability in exchanging and sharing information between the individuals in the search process and further reduces the blindness of the fish in the search process (Duan et al. 2016).

On the other side, the updated speed vector of memory behavior is expressed as follows (Duan et al. 2016):

$$ \varvec{v}_{t + 1} = \omega \varvec{v}_{t} + rand[0,1] \times step\left[ {\left( {\frac{{\xi_{t} \left( {\varvec{X}_{\text{lbest}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{\text{lbest}}^{t - 1} - \varvec{X} _{i}^{t - 1} } \right)}}{{\left| {\xi_{t} \left( {\varvec{X}_{\text{lbest}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{\text{lbest}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)} \right|}}} \right)} \right] $$
(9)

where \( \varvec{X}_{\text{lbest}}^{t} \) represents the current individual extreme value point of the particle at the t-th iterative process; \( \varvec{X}_{\text{lbest}}^{t - 1} \) represents the global extreme value point of the population at the (t − 1)-th iterative process.

Memory behavioral pattern trains the AFs to swim while referring to its own optimal positions (i.e., \( \varvec{X}_{\text{lbest}}^{t} \) and \( \varvec{X}_{\text{lbest}}^{t - 1} \)). It definitely helps to reduce the blindness of the fish in the search process (Duan et al. 2016).

Communication behavioral pattern [Eq. (8)] mainly strengthens the global search ability, while memory behavioral pattern [Eq. (9)] mainly strengthens the local search ability. The implication of (t − 1)-th iterative information indicates the extended memory used.

2.3 Normative knowledge in cultural artificial fish swarm algorithm (CAFSA)

CAFSA involves the implementation of normative knowledge, which describes the feasible solution space of an optimization problem (Wu et al. 2011). Normative knowledge is a set of promising variable range that provides standards for individual behaviors and guidelines within which individual adjustments can be made (Reynolds and Peng 2004). It is a set of information for each variable and is given by:

$$ N = \varvec{I},\varvec{U},\varvec{L},\varvec{D} $$
(10)

where U, L and D are N-dimensional vectors and Ik denotes the closed interval for variable k∈ (1, 2 … N), which is expressed as (Reynolds and Peng 2004):

$$ I_{k} = \left[ {\varvec{l}_{k} ,\varvec{u}_{k} } \right] = \{ \varvec{X}|\varvec{l}_{k} \le \varvec{X} \le \varvec{u}_{k} \} $$
(11)

where \( \varvec{l}_{k} \) and \( \varvec{u}_{k} \) are the lower and upper bounds of feasible space, respectively, for k-th variable. \( \varvec{l}_{k} \) and \( \varvec{u}_{k} \) are initialized with lower and upper bounds of the population (Wu et al. 2011) and are updated based on the following expressions (Wu et al. 2011):

$$ \begin{aligned} \varvec{l}_{k}^{t + 1} & = \left\{ {\begin{array}{*{20}l} {\varvec{X}_{i,k} ,} \hfill & {\quad \varvec{X}_{i,k} < \varvec{l}_{k}^{t} \;{\text{or}}\; f\left( {\varvec{X}_{i}^{t} } \right) < \varvec{L}_{k}^{t} } \hfill \\ {\varvec{l}_{k}^{t} ,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \varvec{u}_{k}^{t + 1} & = \left\{ {\begin{array}{*{20}l} {\varvec{X}_{j,k} , } \hfill & {\quad \varvec{X}_{j,k} \ge \varvec{u}_{k}^{t} \;{\text{or}}\; f\left( {\varvec{X}_{j}^{t} } \right) < \varvec{U}_{k}^{t} } \hfill \\ {\varvec{u}_{k}^{t} ,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(12)

where X represents the state (position) vector of the population, i-th individual affects the lower bound for variable k, j-th individual affects the upper bound for variable k, \( \varvec{L}_{k}^{t} \) and \( \varvec{U}_{k}^{t} \) are the values of the fitness function associated with the bounds \( \varvec{l}_{k}^{t} \) and \( \varvec{u}_{k}^{t} \), respectively, at the t-th iteration (Wu et al. 2011). The fitness functions \( \varvec{L}_{j}^{t} \) and \( \varvec{U}_{j}^{t} \) are updated as follows (Wu et al. 2011):

$$ \begin{aligned} \varvec{L}_{k}^{t + 1} & = \left\{ {\begin{array}{*{20}l} {f\left( {\varvec{X}_{i}^{t} } \right),} \hfill & {\quad \varvec{X}_{i,k} < \varvec{l}_{k}^{t} \; {\text{or}} \;f\left( {\varvec{X}_{i}^{t} } \right) < \varvec{L}_{k}^{t} } \hfill \\ {\varvec{L}_{k}^{t} ,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \varvec{U}_{k}^{t + 1} & = \left\{ {\begin{array}{*{20}l} {f\left( {\varvec{X}_{j}^{t} } \right),} \hfill & {\quad \varvec{X}_{j,k} \ge \varvec{u}_{k}^{t} \; {\text{or}} \;f\left( {\varvec{X}_{j}^{t} } \right) < \varvec{U}_{k}^{t} } \hfill \\ {\varvec{U}_{k}^{t} ,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(13)

Generally, the normative knowledge leads an AF to “jump” into a satisfactory range if it is not there yet (Reynolds and Peng 2004). In the normative knowledge, the parameters selected by the acceptance function are used to calculate the current acceptable interval for each parameter in the belief space. The idea is to be conservative when narrowing the interval and be progressive when widening the interval (Chung and Reynolds 1996). In CAFSA, normative knowledge is mainly used to adjust the current visual and step range to provide a suitable perception at every iterative process.

3 Proposed algorithm

In this section, a new normative fish swarm algorithm (NFSA) is proposed to combine the strengths of PSOEM-FSA (Duan et al. 2016) and normative knowledge. Transformed normative knowledge is used to find the complementary guidelines to be merged into the communication behavior and memory behavior to produce the newly proposed features referred to as normative communication behavior and normative memory behavior, respectively. In addition, NFSA improves the technique in adapting parameters, mainly on visual/visualmin and step/stepmin along the iterative process. The improvements are ordinarily based on AFSA, PSOEM-FSA and CAFSA. The pseudo code of NFSA is given below.

figure b

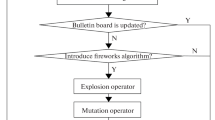
Figure 2 shows the flowchart of the proposed NFSA algorithm. It involves the following stages:

Fig. 2
figure 2

Flowchart of NFSA

Full size image
Step 1:

Random initialization of artificial fishes (AFs) population, the position of the fishes, the optimal locations of each fish’s memory and the global optimal position parameters.

Step 2:

Execute the four association behavior models which run in parallel:

  1. (a)

    Follow or prey behavior.

  2. (b)

    Swarm or prey behavior.

  3. (c)

    Normative communication or prey behavior.

  4. (d)

    Normative memory or prey behavior.

Each behavior model yields distinct updated location and solution. The possible number of executions per iteration is decided by the given number of tries.

Step 3:

Apply greedy selection to select the optimal association behavior and update the current location of AFs.

Step 4:

Update the current global, local optima and current global, local extreme points in the bulletin board.

Step 5:

If the global optimal value is not upgraded for tlimit times, gradient decline the visualmin and stepmin, otherwise go to Step 6.

Step 6:

Adapt the visual and step parameters.

Step 7:

If the maximum iteration number is reached, the optimization process ends; otherwise, go back to Step 2.

The following sub-sections explain the structure of the newly designed features in NFSA. Sect. 3.1 explains normative communication behavior, Sect. 3.2 explains normative memory behavior, Sect. 3.3 describes the improved adaptive parameters and Sect. 3.4 depicts the structure of a bulletin board in NFSA.

3.1 Normative communication behavior (AF_NORM_COMM)

The global and local searches in PSOEM-FSA employed extended memory. AF tends to refer to the current and previous guidelines to decide on an accurate direction. Yet, some insufficiencies have been found in Eq. (8), regarding the communication behavior. Since the search direction is totally dependent upon the global extreme points \( \varvec{X}_{\text{gbest}}^{t} \) and \( \varvec{X}_{\text{gbest}}^{t - 1} \), it causes a lack of flexibility in the global search action. Hence, further improvements are proposed to enhance the communication behavioral pattern [Eq. (8)].

In the original communication behavioral pattern, the current location of AFs is updated by substituting the updated speed vector from Eq. (8) into Eq. (6). The connection of speed vector is removed and the current location of AFs will be updated using only position vector features. In addition to that, the reconnaissance is executed around the current and previous global extreme points \( \varvec{X}_{\text{gbest}}^{t} \) and \( \varvec{X}_{\text{gbest}}^{t - 1} \) to find the complementary guidelines (i.e., \( \varvec{X}_{\text{cg}}^{t} \) and \( \varvec{X}_{\text{cg}}^{t - 1} \)) other than global optima. This helps AFs to cite an even more accurate direction and further reduces the blindness of AFs. Let the reconnaissance radius is set to be a variable range of feasible space [lj, uj] based on the theorem of normative knowledge. To accommodate the enhanced behavioral pattern, some transformations are made regarding the variation of feasible space [lj, uj]. Yet, the idea is still the same, to be conservative when narrowing the search interval and be progressive when widening the search interval. \( \varvec{l}_{j} \) and \( \varvec{u}_{j} \) are initialized with initial lower and upper bounds, \( \varvec{l}_{j}^{{{\text{initial}}, t = 1}} \) and \( \varvec{u}_{j}^{{{\text{initial}}, t = 1}} \) respectively. Parameters \( \varvec{l}_{j} \) and \( \varvec{u}_{j} \) are updated as follows:

$$ \begin{aligned} \varvec{l}_{k}^{t + 1} & = \left\{ {\begin{array}{*{20}l} {\arg \hbox{min} \left( {\varvec{X}_{k}^{t + 1} } \right),} \hfill & {\quad \arg \hbox{min} \left( {\varvec{X}_{k}^{t + 1} } \right) < \varvec{l}_{k}^{t} } \hfill \\ {\varvec{l}_{k}^{t} + |\Delta X_{\hbox{min} ,k} |,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \varvec{u}_{k}^{t + 1} & = \left\{ {\begin{array}{*{20}l} {\arg \hbox{max} \left( {\varvec{X}_{k}^{t + 1} } \right),} \hfill & {\quad \arg \hbox{max} \left( {\varvec{X}_{k}^{t + 1} } \right) > \varvec{u}_{k}^{t} } \hfill \\ {\varvec{u}_{k}^{t} - |\Delta \varvec{X}_{\hbox{max} ,k} |,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(14)

where k denotes the variable of dimension, k∈ (1, 2… N); t denotes the index of iteration; \( \varvec{X}_{k}^{t + 1} \) represents the position vector of the population for k-th dimension at the (t + 1)-th iterative process; \( \varvec{l}_{k}^{t + 1} \) is the lower bound for k-th dimension at the (t + 1)-th iterative process; \( \varvec{u}_{k}^{t + 1} \) is the upper bound for k-th dimension at the (t + 1)-th iterative process; \( \Delta \varvec{X}_{\hbox{min} ,k} = \arg \hbox{min} (\varvec{X}_{k}^{t + 1} ) - \varvec{l}_{k}^{t} \); \( \Delta \varvec{X}_{\hbox{max} ,k} = \arg \hbox{max} \left( {\varvec{X}_{k}^{t + 1} } \right) - \varvec{u}_{k}^{t} \).

Hence, the reconnaissance radius and the selective method of the complementary guidelines, \( \varvec{X}_{\text{cg}}^{t} \) and \( \varvec{X}_{\text{cg}}^{t - 1} \), are expressed as follows:

$$ {\text{radius}}^{t} = {\text{distance}}[\varvec{l}^{t} ,\varvec{u}^{t} ] $$
(15)

and

$$ \begin{aligned} \varvec{X}_{\text{cg}}^{t} & = \varvec{X}_{\text{gbest}}^{t} + rand\left[ { - 1,1} \right] \times {\text{radius}}^{t} \\ \varvec{X}_{\text{cg}}^{t} & = \left\{ {\begin{array}{*{20}l} {\varvec{X}_{\text{cg}}^{t} , } \hfill & {\quad f\left( {\varvec{X}_{\text{cg}}^{t} } \right) < f\left( {\varvec{X}_{\text{gbest}}^{t} } \right)} \hfill \\ {\varvec{X}_{\text{gbest}}^{t} ,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(16)

and

$$ \begin{aligned} \varvec{X}_{\text{cg}}^{t - 1} & = \varvec{X}_{\text{gbest}}^{t - 1} + rand\left[ { - 1,1} \right] \times {\text{radius}}^{t} \\ \varvec{X}_{\text{cg}}^{t - 1} & = \left\{ {\begin{array}{*{20}l} {\varvec{X}_{\text{cg}}^{t - 1} ,} \hfill & {\quad f\left( {\varvec{X}_{\text{cg}}^{t - 1} } \right) < f\left( {\varvec{X}_{\text{gbest}}^{t - 1} } \right)} \hfill \\ {\varvec{X}_{\text{gbest}}^{t - 1} , } \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(17)

where t denotes the index of iteration; \( \varvec{X}_{\text{cg}}^{t} \) and \( \varvec{X}_{\text{cg}}^{t - 1} \) are the selected guidelines within the reconnaissance radius from \( \varvec{X}_{\text{gbest}}^{t} \) and \( \varvec{X}_{\text{gbest}}^{t - 1} \), respectively; \( \varvec{X}_{\text{gbest}}^{t} \) represents the current global extreme value point of the population at the t-th iterative process; \( \varvec{X}_{\text{gbest}}^{t - 1} \) represents the global extreme value point of the population at the (t − 1)-th iterative process; \( \varvec{X}_{i}^{t} \) represents the current position vector of i-th individual at the t-th iterative process.

As for normative communication behavioral pattern, the updated position vector \( \varvec{X}_{i}^{t + 1} \) can be presented as follows:

$$ \begin{aligned} \varvec{X}_{i}^{t + 1} & = \varvec{X}_{i}^{t} + rand\left[ {0,1} \right] \\ & \quad \times \,step\left[ {\beta_{1} \left( {\frac{{\xi_{t} \left( {\varvec{X}_{\text{cg}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{\text{cg}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)}}{{\left| {\xi_{t} \left( {\varvec{X}_{\text{cg}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {X_{\text{cg}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)} \right|}}} \right)} \right. \\ & \left. {\quad + \,\beta_{2} \left( {\frac{{\xi_{t} \left( {\varvec{X}_{\text{gbest}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{\text{gbest}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)}}{{\left| {\xi_{t} \left( {\varvec{X}_{\text{gbest}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{\text{gbest}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)} \right|}}} \right)} \right] \\ \end{aligned} $$
(18)

where \( \beta_{1} \) and \( \beta_{2} \) are known as the speed factors; \( \xi_{t} \) is denoted as the current effective factors; \( \xi_{t - 1} \) is denoted as the effective factor of extended memory; \( \mathop \sum \nolimits \beta = \beta_{1} + \beta_{2} = 1 \); \( \mathop \sum \nolimits \xi = \xi_{t} + \xi_{t - 1} = 1 \).

3.2 Normative memory behavior (AF_NORM_MEMORY)

Normative memory behavior is quite similar to normative communication behavior. Just that, normative communication behavior emphasizes the global search action, while normative memory behavior emphasizes the delicate local search. Some weaknesses have been found in Eq. (9) as well. Similar to the communication behavior, the search direction in memory behavior is totally dependent upon the local extreme point \( \varvec{X}_{\text{lbest}}^{t} \) and \( \varvec{X}_{\text{lbest}}^{t - 1} \). This leads to a lack of flexibility in the local search action. Hence, this work further improves the memory behavioral pattern [i.e., Eq. (9)].

In the original memory behavioral pattern, the current location of AFs is updated by substituting the updated speed vector from Eq. (9) into Eq. (6). The connection of speed vector is proposed to be removed and the inertia weight \( \omega \) is erased. The reconnaissance is executed around the current and previous local extreme points \( \varvec{X}_{\text{lbest}}^{t} \) and \( \varvec{X}_{\text{lbest}}^{t} \), respectively, to find the complementary guidelines other than individuals’ own optima. This helps the artificial fishes (AFs) to cite an even more precise direction and further increase the local search’s efficiency. Let the reconnaissance radius be a variable range of feasible space [lj, uj] and is expressed the same as Eq. (15). \( \varvec{l}_{j} \) and \( \varvec{u}_{j} \) are initialized with initial lower and upper bounds, \( \varvec{l}_{j}^{{{\text{initial}}, t = 1}} \) and \( \varvec{u}_{j}^{{{\text{initial}}, t = 1}} \), respectively. Parameters \( \varvec{l}_{j} \) and \( \varvec{u}_{j} \) are updated based on Eq. (14).

Hence, the selective method of new guidelines, \( \varvec{X}_{\text{cl}}^{t} \) and \( \varvec{X}_{\text{cl}}^{t - 1} \), are expressed as follows:

$$ \begin{aligned} \varvec{X}_{\text{cl}}^{t} & = \varvec{X}_{\text{lbest}}^{t} + rand\left[ { - 1,1} \right] \times {\text{radius}}^{t} \\ \varvec{X}_{\text{cl}}^{t} & = \left\{ {\begin{array}{*{20}l} {\varvec{X}_{\text{cl}}^{t} , } \hfill & {\quad f\left( {\varvec{X}_{\text{cl}}^{t} } \right) < f\left( {\varvec{X}_{\text{lbest}}^{t} } \right)} \hfill \\ {\varvec{X}_{\text{lbest}}^{t} ,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(19)

and

$$ \begin{aligned} \varvec{X}_{\text{cl}}^{t - 1} & = \varvec{X}_{\text{lbest}}^{t - 1} + rand\left[ { - 1,1} \right] \times {\text{radius}}^{t} \\ \varvec{X}_{\text{cl}}^{t - 1} & = \left\{ {\begin{array}{*{20}l} {\varvec{X}_{\text{cl}}^{t - 1} ,} \hfill & {\quad f\left( {\varvec{X}_{\text{cl}}^{t - 1} } \right) < f\left( {\varvec{X}_{\text{lbest}}^{t - 1} } \right)} \hfill \\ {\varvec{X}_{\text{lbest}}^{t - 1} , } \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$
(20)

where \( \varvec{X}_{\text{cl}}^{t} \) and \( \varvec{X}_{\text{cl}}^{t - 1} \) are the new selected guidelines in normative memory behavior; \( \varvec{X}_{\text{lbest}}^{t} \) represents the current individual extreme value point of the particle at the t-th iterative process; \( \varvec{X}_{\text{lbest}}^{t - 1} \) represents the individual extreme value point of the population at the (t − 1)-th iterative process

As for normative memory behavioral pattern, the updated position vector \( \varvec{X}_{i}^{t + 1} \) can be presented as follows:

$$ \begin{aligned} \varvec{X}_{i}^{t + 1} & = \varvec{X}_{i}^{t} + rand\left[ {0,1} \right] \\ & \quad \times \,step\left[ {\beta_{1} \left( {\frac{{\xi_{t} \left( {\varvec{X}_{{i,{\text{cl}}}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{{i,{\text{cl}}}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)}}{{\left| {\xi_{t} \left( {\varvec{X}_{{i,{\text{cl}}}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{{i,{\text{cl}}}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)} \right|}}} \right)} \right. \\ & \quad \left. { + \,\beta_{2} \left( {\frac{{\xi_{t} \left( {\varvec{X}_{{i,{\text{lbest}}}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{{i,{\text{lbest}}}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)}}{{\left| {\xi_{t} \left( {\varvec{X}_{{i,{\text{lbest}}}}^{t} - \varvec{X}_{i}^{t} } \right) + \xi_{t - 1} \left( {\varvec{X}_{{i,{\text{lbest}}}}^{t - 1} - \varvec{X}_{i}^{t - 1} } \right)} \right|}}} \right)} \right] \\ \end{aligned} $$
(21)

where \( \varvec{X}_{\text{cl}}^{t} \) and \( \varvec{X}_{{i,{\text{cl}}}}^{t - 1} \) are the new selected guidelines of i-th individual; \( \varvec{X}_{{i,{\text{lbest}}}}^{t} \) represents the current individual extreme value point of i-th individual at the t-th iterative process; \( \varvec{X}_{{i,{\text{lbest}}}}^{t - 1} \) represents the individual extreme value point of i-th individual at the (t − 1)-th iterative process; \( \varvec{X}_{i}^{t} \) represents the current position vector of i-th individual at the t-th iterative process.

3.3 Improved adaptive parameters

In the standard AFSA, visual and step remain unchanged throughout the iterative processes. If the given initial parameters of visual and step are large, artificial fish swarm move faster toward the global optima, due to greater visual search for the larger environment and hence move with bigger step (Azizi 2014). This way, artificial fish are more capable of escaping from local optima traps (Azizi 2014). However, at the same time, it reduces the accuracy of global search optimization as large visual and step are proficient in approaching the global optimal region, but not in performing the accurate local search. On the other hand, by using small visual and step, it is capable to carry on with an improved local search but has to compromise the convergence speed to reach the global optima.

To balance the contradiction between the global search ability and local search ability of AFSA, the adaptive method utilized in the literature (Li and Qian 2003) is reviewed. In the early stage, relatively large visual and step are adopted to enhance the global search ability and convergence speed of the algorithm (Zhang et al. 2014). Along the iterations, these parameters are decreased based on the following equations:

$$ \left\{ {\begin{array}{*{20}l} {visual^{t + 1} = visual^{t} - visual^{t} *\lambda + visual_{\hbox{min} } } \\ {step^{t + 1} = step^{t} - step^{t} *\lambda + step_{\hbox{min} } } \\ {\lambda = \exp \left( { - \frac{\sigma }{{\sqrt[4]{{(t_{\hbox{max} } )^{3} }}}}*\left( {t_{\hbox{max} } - t} \right)} \right)} \\ \end{array} } \right. $$
(22)

where \( visual_{\hbox{min} } \) is the minimum visual value; \( step_{\hbox{min} } \) is the minimum step value; \( t \in \left( {1,2 \ldots t_{\hbox{max} } } \right) \); \( 0.5 < \sigma < 1 \) at any stage. Hence, at the later stage, it improves the local search of the algorithm.

From the expression in Eq. (22), it can be obviously deduced that the visual and step are gradually decreasing along the iterations and eventually drop to the value approximately equals to visualmin and stepmin, respectively. Without a doubt, visualmin and stepmin play the role to limit the iterative variation of visual and step, respectively. Without the presence of visualmin and stepmin, visual and step will definitely drop to an approximately zero value at a later stage. If this happens, AFs will definitely lose the ability to perform any further local search, as they fail to perform any significant move.

Yet, it is still problematic to decide the values of visualmin and stepmin. If large visualmin and stepmin are set, it may affect the accuracy of local search, but small visualmin and stepmin may consume more time to reach the exact optimum. Hence, the visualmin and stepmin are proposed to be gradient declined under a certain condition, where the optimum remains the same without upgrading after a given limitation of iterations tlimit. The declinations of both parameters are presented as follows:

$$ visual_{\hbox{min} }^{t + 1} = \frac{{visual_{\hbox{min} }^{t} }}{{0.5 \times \sqrt[3]{{t_{\hbox{max} } }}}} $$
(23)

and

$$ step_{\hbox{min} }^{t + 1} = \frac{{step_{\hbox{min} }^{t} }}{{\sqrt[3]{{t_{\hbox{max} } }}}} $$
(24)

where \( t \in \left( {1,2 \ldots t_{\hbox{max} } } \right) \) is the index number of iteration.

3.4 Bulletin board

Bulletin board is a terminal for collecting data and sharing among all the users. Generated n AFs are the users of the bulletin board. It basically records the global optima \( \varvec{Y}_{\text{gbest}} \), together with its global extreme position vector \( \varvec{X}_{\text{gbest}} \) and the local optima \( \varvec{Y}_{\text{lbest}} \), together with its local extreme position vector \( \varvec{X}_{\text{lbest}} \). The data are updated along the iterations, as long as they found a better optimal solution. In other words, if \( \varvec{Y}_{i}^{t + 1} = \arg \hbox{min} [\varvec{Y}^{t + 1} ] < \varvec{Y}_{\text{gbest}}^{t} \) at the t-th iterative process, \( \varvec{Y}_{\text{gbest}}^{t + 1} \) and \( \varvec{X}_{\text{gbest}}^{t + 1} \) are replaced by \( \varvec{Y}_{i}^{t + 1} \) and \( \varvec{X}_{i}^{t + 1} \) respectively, where i∈ (1, 2… n).

4 Experimental setting

Although the algorithm is made to be user dependent, for the purpose of validation and a fair comparison with other works, the employed parameters are adopted from the literature (Mao et al. 2017). The parameter settings for NFSA are displayed in Table 1.

Table 1 Parameter settings for NFSA
Full size table

Ten optimization benchmark functions are used to evaluate the performance of NFSA. Evaluations have been carried out using maximum iteration numbers, tmax = 1000. The proposed algorithm is proposed to run 10 times independently on each benchmark function, in order to ensure that the best optimal solution, mean and standard deviation (SD) of each function are obtained.

The representation of the employed benchmark functions are as follows:

  1. 1.

    f1 = \( f_{\text{Ackley}} \left( x \right) \)

  2. 2.

    f2 = \( f_{\text{Alipine}} \left( x \right) \)

  3. 3.

    f3 = \( f_{\text{Griewank}} \left( x \right) \)

  4. 4.

    f4 = \( f_{\text{Levy}} \left( x \right) \)

  5. 5.

    f5 = \( f_{\text{Quadric}} \left( x \right) \)

  6. 6.

    f6 = \( f_{\text{Rastrigin}} \left( x \right) \)

  7. 7.

    f7 =  \( f_{\text{Rosenbrock}} \left( x \right) \)

  8. 8.

    f8 = \( f_{\text{Elliptic}} \left( x \right) \)

  9. 9.

    f9 = \( f_{\text{Sphere}} \left( x \right) \)

  10. 10.

    f10 = .\( f_{\text{SumPower}} \left( x \right) \)

5 Computational results and discussion

5.1 Assessment of NFSA

The evaluation of NFSA mainly tests the contributions of proposed normative communication behavior, normative memory behavior and improved adaption of parameters. Table 2 displays the best optimum, mean and standard deviation (SD) obtained by NFSA on each benchmark function in the case of N  = 10. It has to be noted that the closer the data values with reference to its global minimum, the better the performance of NFSA on a specific function. Table 2 shows the relatively superior results from NFSA on every benchmark function, especially Rastrigin function (f6) which obtained the real global minimum. The fact that the proposed NFSA tends to reach the real global minimum on certain benchmark functions, and shows the relatively superior results on all the benchmark functions, certifies the contributions of newly proposed features in NFSA. The relatively small standard deviations (SD) reveal that NFSA is highly robust and precise.

Table 2 Performance evaluation of NFSA
Full size table

5.2 Comparison of NFSA with related algorithms

The results of the performance of PSOEM-FSA (Duan et al. 2016), CIAFSA (Mao et al. 2017) and AFSA (Li et al. 2002) on f1–10 are adopted from the literature (Mao et al. 2017). As observed from Table 3, data obtained by NFSA (with references to Table 2) were compared with these related algorithms, using the same maximum number of iterations tmax in the case of dimension N  = 10.

Table 3 NFSA performance comparison with related algorithms on benchmark functions
Full size table

As explained, PSOEM-FSA is actually the predecessor of CIAFSA. Hence, both algorithms exhibit the same characteristics of communication behavior and memory behavior which is the origin of the proposed features in NFSA—normative communication behavior and normative memory behavior. CIAFSA is proposed after PSOEM-FSA, with the additional feature of improved adaptive visual and step. They are comparatively suited to be used to test the contributions of normative communication behavior and normative memory behavior.

Some insightful conclusions can be drawn from Table 3. The bold and highlighted data represent the best results on each function among different algorithms. Apart from Griewank function (f3), the proposed NFSA has clearly outperformed PSOEM-FSA, CIAFSA, and AFSA. Especially on Ackey, Alipine, Levy, Rastrigin, Rosenbrock, Elliptic, Sphere and SumPower functions (f1, f2, f4, f6, f7, f8, f9, f10), NFSA achieved relatively superior best optima and means over other algorithms, affirming that NFSA tends to approach closer to the respective global minimum. The relatively smaller standard deviations (SD) also prove that NFSA is way more precise than other comparative algorithms.

Figures 3 and 4 display the convergence characteristics of NFSA and other related algorithms on f1–f10. The convergence rate of the algorithm is tightly related and influenced by visual and step variations. Due to the improved technique of adaption of visual and step in NFSA, the convergence rates become more superior to other related algorithms on most tested benchmark functions. The truth is that NFSA tends to strike closer to the global minimum, as shown in Table 2, Figs. 3 and 4.

Fig. 3
figure 3

Convergence characteristics of NFSA in comparison with af1 to ff6 benchmark functions

Full size image
Fig. 4
figure 4

Convergence characteristics of NFSA in comparison with af7 to df10 benchmark functions

Full size image

5.3 Statistical test

Student t test is a statistical test which is widely used to compare the means of two groups of samples. It is, therefore, to evaluate whether the means of the two sets of data are statistically significantly different from each other. The t test can be commonly distributed into three types:

  • The one-sample t test used to compare the mean of a population with a theoretical value.

  • The unpaired two-sample t test used to compare the mean of two independent samples.

  • The paired t test used to compare the means between two related groups of samples.

Using the mean (\( \tilde{x} \)), standard deviation (SD) and the number of population (n) for each sample from Tables 1 and 3, the independent two-sample t test is performed. Assuming all the conditions for inference are met and using the significant level of 0.05, it is reasonable to assume that two populations have the same standard deviation as the sample standard deviations of the algorithms are reasonably close. An alternative procedure known as the pooled t procedure will be used.

Considering the t test between NFSA and CIAFSA on Ackley benchmark function (f1) as an example, the datasets are summarized in Table 4.

Table 4 Summarized data as taken from Tables 1 and 3
Full size table

denotes the population means. The hypothesis difference between the population means is set to 0. The null hypothesis is then constructed as follows:

$$ {\text{H}}_{0} :\mu_{\text{NFSA}} = \mu_{\text{CIAFSA}} $$
(25)

The alternate hypothesis is written as follows:

$$ {\text{H}}_{a} :\mu_{\text{NFSA}} < \mu_{\text{CIAFSA}} $$
(26)

Based on the sample data in Table 4, our t statistic is equal to:

$$ \begin{aligned} t & = \frac{{\tilde{x}_{\text{NFSA}} - \tilde{x}_{\text{CIAFSA}} }}{{s_{p} \sqrt {\frac{1}{{n_{\text{NFSA}} }} + \frac{1}{{n_{\text{CIAFSA}} }}} }} \\ & = \frac{{3.73 \times 10^{ - 15} - 3.56 \times 10^{ - 04} }}{{2.79307 \times 10^{ - 04} \sqrt {\frac{1}{50} + \frac{1}{50}} }} = - \,6.373 \\ \end{aligned} $$

where \( s_{p} \) is calculated by using the following expression:

$$ \begin{aligned} s_{p} & = \sqrt {\frac{{\left( {n_{\text{NFSA}} - 1} \right)\left( {{\text{SD}}_{\text{NFSA}} } \right)^{2} + \left( {n_{\text{CIAFSA}} - 1} \right)\left( {{\text{SD}}_{\text{CIAFSA}} } \right)^{2} }}{{n_{\text{NFSA}} + n_{\text{CIAFSA}} - 2}}} \\ & = \sqrt {\frac{{\left( {50 - 1} \right)\left( {1.50 \times 10^{ - 15} } \right)^{2} + (50 - 1)\left( {3.95 \times 10^{ - 04} } \right)^{2} }}{50 + 50 - 2}} \\ & = 2.79307 \times 10^{ - 04} \\ \end{aligned} $$

Next step is to obtain the p value. p value is the probability of obtaining the observed difference between the samples if the null hypothesis were true. The elements used to achieve the p value are the t statistic and degree of freedom df, where df is expressed as follows:

$$ df = n_{\text{NFSA}} + n_{\text{CIAFSA}} - 2 = 50 + 50 - 2 = 98 $$

The easiest way to determine the p value is by referring to the p value table or using the p value from t score calculator. The one-tailed (left-tailed) hypothesis is employed. The obtained p value is \( < 0.0001 \). The area of the reddish region in Fig. 5 indicates the p value.

Fig. 5
figure 5

The normalized t distribution sample

Full size image

Assuming the null hypothesis is true, and the p value that is rather a low probability which is below the significant level of 0.05, the null hypothesis should be rejected. Since the null hypothesis is rejected, the alternative hypothesis is suggested, where the estimated population mean of NFSA is superior to CIAFSA (\( \mu_{\text{NFSA}} < \mu_{\text{CIAFSA}} \)).

Some insightful conclusions can be drawn from Table 5. The “rejected” null hypotheses H0 in Table 5 demonstrate convincingly that the population means of NFSA are predicted to be superior in comparison with respective comparative algorithms on specific benchmark function, according to the statement of alternative hypothesis Ha in Eq. (26). Most results display the “rejected” state for the null hypotheses, except on the Griewank function (f3), where the null hypotheses are “accepted” in the t test between NFSA and CIAFSA, and between NFSA and AFSA, indicating the failures of NFSA to overcome CIAFSA and AFSA on Griewank function (f3) in terms of the population means. Yet, based on the overall results in Table 5, it can be deduced that overall, the population of NFSA are fitter in comparison with the population of other comparative algorithms.

Table 5 Results obtained after performing two-sample t test between NFSA and respective comparative algorithms
Full size table

6 Conclusion

Although many optimization algorithms have been introduced, no matter what kind of solutions they are, none of them could claim that they have perfectly solved the respective optimization problems. Somehow it has become a challenging topic for many researchers.

This work had successfully developed the proposed normative fish swarm algorithm (NFSA) for optimization. Numerical simulation experiments were performed to compare its performance with the predecessors of the proposed algorithm: PSOEM-FSA and CIAFSA. The experimental results showed that NFSA outperformed its predecessors and standard AFSA in terms of convergence speed and global optimum achievement. The real global optima were achieved for most of the benchmark functions used, confirming the contributions attained through the modifications done on existing optimization algorithms. The results bring researchers one step closer toward more efficient solution for solving optimization problems.

Other optimization problems can be solved in the future to ensure the capability of the proposed algorithm in this domain. Moreover, other powerful local search strategies can be employed to further improve the exploitation capability of fish swarm algorithm.