1 Introduction

An automatic voltage regulator (AVR) is important equipment used in power system utilities. As its name implies, it is designed to automatically control, adjust or maintain a constant voltage level of a synchronous generator by adjusting its exciter voltage (Chatterjee and Mukherjee 2016). Thus, it is essential for enhancing stability and sustaining a nominal voltage level under off-nominal operating conditions, which has been regarded as one of the main control problems in an electric power system, since nominal voltage level is vital for any electrical devices connected to that power system (Chatterjee and Mukherjee 2016; Gozde and Taplamacioglu 2011). Deviation of the nominal voltage level from the rated one might give rise to a decline in the operating performance of these devices and fall in their life expectancy. Since the reactive power flow depends on the difference between infinite bus voltage and generator terminal voltage, this forms another application area of an AVR, such that it can adjust reactive power by regulating generator voltage. While providing accurate sharing of the reactive power among all the parallel-connected generators, this control also makes it feasible to effectively reduce real line losses, which are caused due to real and reactive power flow. Besides these properties, controlling of generator exciter by using of AVR is attracting attention because of its inherent cost advantage (Shayeghi et al. 2015).

In order to maintain the generator terminal voltage at a specified level, AVR system is implemented as a closed-loop control system, and numerous control methods such as optimal control, robust control, adaptive control, etc. have been dedicated in this area for achieving an AVR with stable and fast dynamic response. Therefore, increasing the AVR performance in terms of both time-domain and frequency-domain specifications is still a challenging control problem for constancy, stability and security of the electric power network, thus attracting attention by the researchers. In the past decades, despite the great advances made in process control techniques, proportional–integral–derivative (PID) controllers have continued to be widely implemented in many forms of industry control plants due to their excellent advantages such as simple structure, low implementation effort and robust performance within a wide range of operating conditions (Gaing 2004; Panda et al. 2012). They are the standard controllers used at the lowest level in process control configurations, also often used at higher levels in many other engineering areas (Hägglund 2012). It is a known fact that the majority of industrial control loops, e.g., more than 90%, are of PI/PID type (Zhu et al. 2009; Tepljakov et al. 2016). However, to have a PID controller that offers satisfactory performance in the event of a number of different operating circumstances, a simultaneous tuning progress of all the controller gains, i.e., proportional, integral and derivative gains must be established properly, which is still an ill-defined problem and often a difficult task for researchers and plant operators when dealing with classical tuning rules. Instead, the use of metaheuristics to solve such design problem in a better way has been captivating among the researches since 2000 where the PID gains are obtained automatically using a properly defined cost function. Given an example, in a robot trajectory control system, particle swarm optimization (PSO) is applied to tune the parameters of PID, fuzzy logic controller (FLC) and fractional order PID (FOPID) controller, the expansion of classical PID controller based upon fractional calculus requiring extra two non-integer parameters (Bingul and Karahan 2011). Simulation results are given to affirm that PSO-tuned FOPID controller performs better than other controllers while yielding an improved robustness to the considered changes in the system. In 2018, the same authors make use of artificial bee colony (ABC) and PSO algorithms to find out optimal parameters of PID and FOPID controllers installed in two different second-order systems (Bingul and Karahan 2018). Three different cost functions are also considered in the paper to visualize their influences over the control performance. From the reported results, it is initially captured that FOPID controller outperforms its classical counterpart under both normal and abnormal conditions. When comparing the algorithm performances, PSO is found to contribute improvement to the step response of the second-order system, whereas better performance is achieved with ABC algorithm on a time-delayed process at the cost of computational burden heavier than PSO.

Our literature survey dictates that studies employing evolutionary optimization algorithms to efficiently design a PID controlled-AVR system are widespread. For instance, in Gaing (2004), to gain the optimal PID parameters of an AVR system, a design method based on particle swarm optimization (PSO) algorithm is proposed along with a new cost function defined in time-domain. Obtained results are compared with genetic algorithm (GA), and it is inferred that the proposed method is superior to the GA in terms of searching for optimal controller parameters. In 2007, a hybrid method that gathers the properties of GA and bacterial foraging (BF) algorithm is adopted to design the PID controller optimally of an AVR (Kim et al. 2007). The results of applying GA-BF are found to be promising. At the same year, determination of off-line, nominal, optimal PID gains is achieved by craziness-based PSO (CRPSO) and also binary-coded GA (Mukherjee and Ghoshal 2007). Results show that CRPSO is more efficient than GA in terms of transient response performance and computational time. Two years after, the authors apply two new versions of PSO algorithm, which are based on velocity update relaxation (VURPSO) and novel position, velocity updating strategy and craziness (CRPSO) (Chatterjee et al. 2009). With these algorithms, search ability of the PSO algorithm is highly boosted, and therefore VURPSO is said to perform better in transient performance compared with CRPSO/GA. In Coelho (2009), the use of chaotic optimization approach is analyzed based on Lozi map, and it is shown that the tuning performance of proposed approach is encouraging when a suitable value for the parameter of step size λ is described, which regulates a balance between exploration and exploitation abilities. By employing the chaotic ant swarm (CAS) algorithm in Zhu et al. (2009), it is repeated to provide the optimal PID design for an AVR system. In the study, authors employ a new performance criterion to have small amount of overshoot, instead of using classical performance criteria, such as integrated absolute error (IAE), integral of squared error (ISE), integral of time multiplied absolute error (ITAE) and integral of time multiplied squared error (ITSE). According to the simulation results, CAS has the ability of finding better PID parameters, and thus, CAS-PID offers better solution and computational efficiency with respect to GA method. Later on, in 2011, an application of artificial bee colony (ABC) algorithm to obtain optimal AVR control is made in Gozde and Taplamacioglu (2011) where PSO and differential evolution (DE) algorithms are also used to assess the contribution of ABC algorithm to tuning performance for controller parameters. Considering the results concluded in a comparative manner, ABC is proved to make the system operate more optimally and robustly than the PSO and DE. Afterwards, a simplified version of PSO, also called many optimizing liaisons (MOL) algorithm, is suggested in Panda et al. (2012) with a purpose to have a high-performance AVR system, and comparative analysis results of the presented approach with the algorithms reported in Gozde and Taplamacioglu (2011) demonstrate that MOL optimized PID controller is suited better. More recently, in the year of 2014, for the same type of optimization problem, local unimodal sampling (LUS) optimization algorithm is adopted in Mohanty et al. (2014) as well as new cost functions that consider weighted sum of standard cost functions and transient response parameters such as overshoot and settling time. At the end of the study, it is shown that the proposed approach with modified cost function yields promising results concerning settling time, peak overshoot and stability margin relative to the algorithms used in Gozde and Taplamacioglu (2011). In 2016, biogeography-based optimization (BBO) algorithm is documented in order to improve the transient response of the system under consideration (Güvenç et al. 2016). Results of applying this algorithm to the optimization of PID design installed in an AVR show the excellence of the algorithm to have a superior search ability for controller parameters, which in turn leads to a better step response of incremental change in terminal voltage. The study given in Chatterjee and Mukherjee (2016) takes teaching–learning-based optimization (TLBO) algorithm as the optimization technique to solve the optimization problem of seeking the optimum set of PID gains. In the study, a first-order low pass filter is introduced in the derivative part of the PID controller to make the response profile smoother by eliminating step changes in the output. This filter has two important parameters, namely time constant and filter coefficient, which are to be optimized in the given study, in addition to three controller parameters. By comparing the TLBO-based results to the reported state-of-the-art literature (Gozde and Taplamacioglu 2011; Panda et al. 2012; Gaing 2004; Mohanty et al. 2014), it is stated that proposed approach has better unit step dynamic response than the other utilized optimization methods. Eventually, in 2018, stochastic fractal search (SFS) algorithm is applied to efficient design problem of PID controller for an AVR (Çelik 2018). A clear illustration of the superiority of SFS algorithm is exemplified in comparison with Gozde and Taplamacioglu (2011), Panda et al. (2012), Mohanty et al. (2014), Güvenç et al. (2016) and Razmjooy et al. (2016) under the same circumstances, and it is attested that the proposed algorithm is capable of attaining a more optimal ITSE value compared to other approaches. As a result of this outcome, dynamic response profile of the system is improved, in that the values of settling time, rise time and peak time are reduced.

Having the features of simple structure, robust performance against different problems, symbiotic organisms search (SOS) algorithm is a promising technique, recently introduced to solve numerical optimization and engineering design problems (Cheng and Prayogo 2014; Banerjee and Chattopadhyay 2017). The algorithm uses two parameters of maximum iteration number and population size only. No other algorithmic parameters are required; thus, it favorably eliminates the risk of deteriorated performance due to inappropriate parameter tuning. The efficacy of SOS over some competitive algorithms has been attested by encouraging results in the literature (Cheng and Prayogo 2014). However, SOS is not very good at exploiting a local area by itself as it is a global search algorithm intended to explore the search space. Thus, if merely SOS algorithm is employed, a possible better solution that is in the neighborhood of the current solution may be missed. To avoid such phenomenon and ensure a more localized search for improving the solution quality of the SOS algorithm, the authors of this article are encouraged to integrate simulated annealing (SA) into the SOS, which is abbreviated as hSOS-SA algorithm in the paper. In this sense, once the SOS does not improve the current solution any longer, SA is invoked subsequently to continue search in a narrowed region around the neighborhood of the best point found by the previous search with SOS. An important advantage of this hybrid algorithm is that it can increase the solution accuracy to a certain extent in a reasonable time that the SOS cannot on its own.

The use of classical integral-based cost functions like IAE, ISE, ITAE, ITSE or combined version of them is common among some of the researchers while others define their own, which may involve essential time-domain specifications such as steady-state error, maximum overshoot, settling time and rise time with suitable weighting factors. When performing optimization by one of the classical performance indices, e.g., by ITSE, fast response profile is often obtained at the cost of increased overshoot and oscillation as well as deterioration in the stability margin of the controlled system. Moreover, using a weighted composite cost function may lead to sluggish response, and also obtaining the desirable damping ratio cannot be guaranteed. These deficiencies of the earlier works encourage us to define a new cost function that takes into account not only transient response specifications, but also stability status of the system, which forms our main contribution. The other new idea involved in the paper is the introduction of a new hybrid algorithm termed as hSOS-SA which suggests the combination of the superior global search ability of SOS and the local search strength of SA in order to efficiently search for better PID parameters. The transient response performance of the hSOS-SA optimized AVR system is compared to those tuned by original SOS, TLBO (Chatterjee and Mukherjee 2016), ABC (Gozde and Taplamacioglu 2011), PSO (Gaing 2004), LUS (Mohanty et al. 2014) and BBO (Güvenç et al. 2016) algorithms for the same AVR system. Then, in order to examine the results from the stability point of view, root locus analysis and bode analysis are conducted to find out how much stable the obtained system is. Finally, robustness analysis of the AVR system tuned by hSOS-SA is performed against parameter uncertainties. Numerical results are promising and support the feasibility and contribution of our proposal for controlling the AVR system.

2 Structure of AVR system with PID control

2.1 PID controller

Classical PID controller or its attributes remain the popular choice in industry because of its simple and robust structure, ease of design and appropriate system output independent of the parameter variation with proper tuning of controller gains (Guha et al. 2017; Aström and Hägglund 2001). Design of a PID controller includes setting of only three parameters, i.e., proportional gain Kp, integral gain Ki and derivative gain Kd (Aström and Hägglund 2001). A PID controller is expressed by the following transfer function in the continuous s-domain where U(s) is the control signal produced by acting on the error signal E(s)

$$ G_{\text{PID}} \,\left( s \right) = \frac{U\left( s \right)}{E\left( s \right)} = P + I + D = K_{\text{p}} + \frac{{K_{\text{i}} }}{s} + K_{\text{d}} s. $$
(1)

2.2 Description and modeling of a practical AVR system

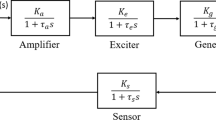
In a power station, regulating the exciter voltage of a synchronous generator to simply match the voltage drop or rise has a crucial impact upon power system stability and quality of electric power generated. Besides, it is important to provide reliability with high performance required to support the power industry on a worldwide scale. Thus, an AVR system is designed to fulfill these goals whose main duty in a power plant is to maintain the magnitude of generator voltage automatically within a specified limit (Shayeghi et al. 2015). As it offers a cost-friendly and simpler solution, there has been always great interest toward improving its performance. A simplified model of a practical AVR system is presented in Fig. 1, where four components, namely amplifier, excitation system, generator and sensor, are considered. As shown, as our aim is to control the terminal voltage of the alternator, it is continuously measured from the point the AVR is connected to the power utility. This signal, following the rectification and smoothening, is subtracted from the voltage setpoint in the comparator to obtain an error signal. After being amplified, the voltage error is forwarded to the excitation system which has the role to control the field winding voltage or current of the alternator through the exciter in order to compensate the voltage variation according to the error signal.

Fig. 1
figure 1

Simplified model of a practical AVR system

Full size image

In order to analyze dynamics of the system, an acceptable transfer function model of the AVR is required. Given the context of this article, our main motivation is not to propose a more realistic AVR model, but to instead improve the dynamic performance of the previously studied system using the model in Fig. 2 which is widespread in the literature (Chatterjee and Mukherjee 2016; Gozde and Taplamacioglu 2011; Shayeghi et al. 2015; Gaing 2004; Panda et al. 2012; Mukherjee and Ghoshal 2007; Chatterjee et al. 2009; Coelho 2009; Zhu et al. 2009; Mohanty et al. 2014; Güvenç et al. 2016; Çelik 2018; Razmjooy et al. 2016; Zamani et al. 2009). As such, each component is modeled linearly using a gain and a time constant avoiding any saturation or other nonlinear properties. Note that this model in Fig. 2 describes the ratio of the incremental change in terminal voltage \( \Delta V_{\text{t}} \left( s \right) \) to an incremental change in reference voltage input \( \Delta V_{\text{ref}} \left( s \right) \).

Fig. 2
figure 2

Overall transfer function model of AVR along with a PID controller

Full size image

The chosen parameter values for the AVR system in the present work are reported in Table 1, which are taken from the studies (Chatterjee and Mukherjee 2016; Gozde and Taplamacioglu 2011; Gaing 2004; Mohanty et al. 2014; Güvenç et al. 2016). The constants of Kg and Tg depend on load.

Table 1 Limits and chosen values of the parameters used in AVR system
Full size table

Eventually, by adopting the above model parameters, closed-loop transfer function of the studied system without a PID controller is given by Eq. 2

$$ G\left( s \right) = \frac{{\Delta V_{\text{t}} \left( s \right)}}{{\Delta V_{\text{ref}} \left( s \right)}} = \frac{0.1s + 10}{{0.0004s^{4} + 0.0454s^{3} + 0.555s^{2} + 1.51s + 11}} $$
(2)

where the transfer function has one zero and two real poles at Z = − 100 and at S1 = − 99.97 and S2 = − 12.49, respectively, and two complex poles at S3,4 = − 0.52 ± 4.66i. Obtained original step response of the output voltage change in this AVR system is displayed in Fig. 3.

Fig. 3
figure 3

Output voltage change in the AVR system without controller

Full size image

It may be concluded from this figure that the system is stable, but exhibiting high oscillatory behavior during transient condition with a percentage overshoot of 65.77% relative to the actual steady-state value of 0.9091 p.u., which leads to a remarkable error of 0.0909 p.u. Such a response in power systems is highly undesirable and must be dampened while allowing only a negligible deviation from the nominal value at steady state. Thus, for enhanced system response, a PID controller may be included in the system and design process of the studied hSOS-SA incorporated PID controller is discussed in detail in Sect. 4.

3 Proposed hSOS-SA

SOS is a relative new, powerful metaheuristic search algorithm derived from the idea to simulate the natural phenomena of interactive behavior seen among organisms living together in an ecosystem. SOS has consistent performance across different problems since it does not use specific algorithm parameters. It is based on three most common symbiotic connections found in natures such as mutualism phase, commensalism phase and parasitism phase (Banerjee and Chattopadhyay 2017). By adopting these connections, organisms adapt themselves to variations in their living spaces to survive and propagate in the ecosystem. In mutualism, each organism benefits from the other’s activity. Commensalism takes place when one organism gets benefits, while the other organism is neither significantly harmed nor helped, and parasitism takes place when an organism obtains benefits from a particular interaction at the cost of degrading the other (Yu et al. 2017).

SA, among the most popular iterative techniques, is a random local search algorithm developed in 1983 through the inspiration of a physical process known as simulated annealing (Kirkpatrick et al. 1983). The SA algorithm operates on the basis of the idea of neighborhood search and can produce satisfactory solutions for hard optimization problems (Hedar and Ismail 2012). After the algorithm is started with an initial temperature and a single feasible random solution, it employs two loops: the outer loop is responsible for updating the temperature and the inner loop successively applies random modifications to the current solution at current temperature for the iteration number of inner loop, where if a modification exhibits a good solution, it is automatically accepted. For a bad solution, there is still a chance to be accepted as the new solution with a probability according to the following acceptance function:

$$ r \le {\text{e}}^{{\left[ {f\left( {p_{\text{old}} } \right) - f\left( {p_{\text{new}} } \right)} \right]/{\text{T}}}} $$
(3)

where r is a uniform random number and T denotes the current temperature. pold and pnew are the current and candidate solution, respectively. When the inner loop is completed in this way searching for better neighboring solutions of the given solution, the outer loop conventionally decreases the temperature and reiterates the search process. The selection of neighboring solution and cooling schedule play an important role with regard to the SA’s search performance and that of initial temperature value. In the case, initial temperature is changed from too hot to very cold, the search will be guided from a randomized manner moving to nearly any neighborhood state to the search leading to a final solution probably very close to the starting solution (Tavares et al. 2011).

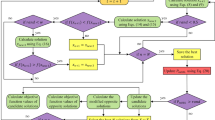
As mentioned earlier, since SOS is a global optimization technique, its exploitation performance around a promising region is weak and computationally inefficient. In order to intensify the search toward the most promising region of the search space to raise the chance of obtaining better solution, SA is contemplated in this study after the SOS does not any longer make progress around the global best solution. A detailed pseudocode of proposed hSOS-SA algorithm is given in Fig. 4, where eco_size defines the number of organisms in ecosystem and f is considered as cost function. The first while loop of hSOS-SA constitutes the portion of original SOS algorithm. When the SOS can no longer improve the current solution, that is, when it has converged, the algorithm is forwarded with the SA algorithm by setting the final best solution from the SOS as starting solution in SA. By keeping the initial SA temperature cool enough, the search process is intensified toward an encouraging point which helps the algorithm enhance its exploitation property over search space. As a result, by the integration of SA in pursuit of SOS, it is expected that the presented algorithm will provide more promising results than the original SOS in terms of solution quality.

Fig. 4
figure 4

Pseudocode of proposed hSOS-SA algorithm

Full size image

4 The hSOS-SA implementation for efficient PID design

In this section, for achieving enhanced step response of an AVR system, hSOS-SA implementation and definition of the new cost function will be discussed. The reason why we adopt hSOS-SA as the optimization technique is owing to our intention to search for better parameters of the PID controller installed in an AVR, so that the controlled system could have a better voltage response profile. For the self-tuning of a PID controller, it is usually mandatory to choose an appropriate performance measure to assess the performance of different controller parameters by considering the whole closed-loop response. As mentioned before, IAE, ISE, ITAE and ITSE are some performance indices that are often employed in control system design, each of which has its own advantages and disadvantages. For instance, a disadvantage of IAE and ISE is that their minimization can result in a response with relatively small overshoot but long settling time because ISE weights all errors equally independent of time (Gaing 2004). On the other hand, control systems subject to minimize ITAE settle a lot more quickly than IAE and ISE, but lead to a slow initial response. ITSE generally reduces the rise and settling time while with an overshoot and sustained oscillation. In addition, more importantly, all these performance criteria do not take into account the stability margin of the controlled system, e.g., minimizing one of these performance criteria may give rise to a plant being controlled with weak stability. As small overshoot, minimal settling time and improved stability are of the concerns of this study, a new cost function that enhances the control action over both time-domain and frequency-domain specifications is designed as in Eq. 4, where four terms are involved, the importance of which is determined by a weight factor αi

$$ J\left( O \right) = \alpha_{1} \int_{0}^{\text{t}_{\text{sim}}} {t \cdot e\left( t \right)^{2} \cdot {\text{d}}t + \alpha_{2} \cdot M_{\text{p}} + \alpha_{3} \cdot iscmplx + \alpha_{4} \cdot diffdamp} $$
(4)

where O represents each organism in the ecosystem by O = [Kp, Ki, Kd], Mp is the overshoot, and tsim is simulation time. The first term on the right side of Eq. 4 is the error and time-based ITSE formula, and its value is obtained directly from the step response profile in addition to that of Mp. In order to guarantee improved stability of the AVR, we also obtain the vector containing the poles of the resulting system and damping ratio of each pole. Recall that if the poles are real and lie in the left-half of the s-plane, they exhibit a damping ratio equal to 1, whereas it may be in the range 0 ≤ ξ < 1 when the poles form a complex conjugate pair. Thus, from the stability point of view, a system can be interpreted to be more stable to the extent that the respective damping ratios are 1 or closer to 1, since low damping ratio means weak stability. From this, iscmplx is added in Eq. 4 to give the number of complex poles, i.e., assuming a fifth order system with three real poles and two complex poles leads to iscmplx = 2. As for diffdamp, it provides the sum of the differences between the value of 1 and the damping ratios for the complex poles, which, in turn, aims to determine how much the damping ratios of complex poles are closer to 1. hSOS-SA will attempt to minimize J by performing a search for PID parameters that not only ensure good dynamic response with respect to ITSE and Mp, but also reduce the number of complex poles and try to bring the damping ratios of the complex poles closer to 1 for increased stability. In order to achieve the desired specification, selection of the weight factor is up to the user. Good results are attained when the selections are α1 = 7, α2 = 1, α3 = 0.1 and α4 = 0.2. An increase in αi will lead to some improvement in the corresponding objective while deteriorating other objectives. The flowchart of the proposed method is depicted in Fig. 5.

Fig. 5
figure 5

Flowchart of optimization of PID controller using the proposed algorithm

Full size image

As there are three controller parameters to be optimized, each organism is composed of three members, which are initiated at random in the range [0.2, 2] as real values. By feeding each organism into the AVR model, the system is simulated for a reasonable time tsim to get the response of output voltage change. After the ITSE, Mp, iscmplx and diffdamp are computed numerically from the resulting response, a fitness value based on the weighted sum of the computed values is assigned to each organism. This is followed by typical SOS phases to update organisms. If i is different from eco_size, then algorithm proceeds with another value of i. When these steps happen to have no more influence on the quality of solution Obest, then a transition from SOS to SA is realized by setting Obest as the starting solution in SA. The temperature value, which determines the acceptance of inferior neighboring solutions in SA, is initially set to be cool enough in order to intensify the search process in the neighborhood of Obest and is reduced geometrically with α = 0.982 along the process. By employing the standard SA steps where better trial solutions are accepted along with even worse trial ones with a probability function in Eq. 3, it is hoped that a more promising solution compared with Obest may be effectively found. When the temperature condition is not satisfied, the SA terminates, and the optimized PID parameters are used in the subsequent simulations.

5 Analysis and results

In order to assess the performance of AVR system tuned by the presented technique, an analysis of the output voltage change curve is made by using the state-of-the-art techniques in the literature such as TLBO (Chatterjee and Mukherjee 2016), ABC (Gozde and Taplamacioglu 2011), PSO (Gaing 2004), LUS (Mohanty et al. 2014) and BBO (Güvenç et al. 2016) as a benchmark for the same conditions. Both ecosystem size and maximum iteration number are set to 50 in SOS. Simulations were carried out in the MATLAB 8.5.0 (R2015a) environment on an Intel Core i5-3.30Ghz processor and 8 GB memory computer. The first operating scenario including a comparison of the optimized transient response profiles under nominal condition with Kg = 1 and Tg = 1 is depicted in Fig. 6, where circles indicate settling times. The comparison clearly shows that hSOS-SA tuned PID controller is able to create better transient and steady-state response characteristics such that after a minimal amount of overshoot, the terminal voltage follows its reference more strictly than the others. Such profile, with also comparably good settling time, is grossly desired for improved stability.

Fig. 6
figure 6

Comparison of the resulting step responses of voltage changing curves

Full size image

Controller signal U(s) for employing hSOS-SA and other benchmark techniques is shown in Fig. 7(a–f), respectively, for the first 50 ms. For the remaining interval (0.05–2.0 s), the zoomed view of them is given in a superimposed manner in Fig. 7g. As shown, controller signals have oscillations with varying magnitude and settling time in the initialization mode, which eventually settles to its required value. As we can see in Fig. 7g, our proposal indicated with black trace exhibits the best transient performance since it is driven to the reference value more quickly without no sustained oscillation, which is followed by the red trace based on LUS. Thus, by the application of this kind of control signal to the input of the AVR system, the desired level of system performance in time-domain can be achieved as well as in frequency-domain, as will be discussed later.

Fig. 7
figure 7

Controller signals employing, a hSOS-SA, b TLBO (Chatterjee and Mukherjee 2016), c ABC (Gozde and Taplamacioglu 2011), d PSO (Gaing 2004), e LUS (Mohanty et al. 2014), f BBO (Güvenç et al. 2016), g comparative zoomed view

Full size image

Optimized PID gains and their time-domain performance for hSOS-SA against previous approaches are tabulated in Table 2 in terms of maximum overshoot, settling time (5% band), rise time and steady-state error. In any of the following tables, results of interest signifying best solution are bolded. Since different cost functions are used, reporting the optimized values of them as comparing criterion is considered useless. From the comparative analysis, obtained results of maximum overshoot and steady-state error using hSOS-SA and SOS are similar and best among those offered by the other published studies. The closest competitor to hSOS-SA and SOS is LUS, and the worst performance for the settling time and rise time belongs to ABC and TLBO algorithms. It is worth mention that by the employment of hSOS-SA, Kp, Ki and Kd become slightly different from those in the case of SOS, which accordingly lead to a mild increase in settling time and rise time. However, such fine-tuning progress on the controller parameters will contribute to stability margin of the system in the following.

Table 2 Comparison of optimized PID gains and their corresponding performance
Full size table

Figure 8 presents the root locus and bode diagrams of the AVR system tuned by the hSOS-SA. From the root locus diagram, it is obvious that the control system is stable since all closed-loop poles are located at the left-half of the s-plane. Numerical results of closed-loop poles and their respective damping ratios are gathered in Table 3.

Fig. 8
figure 8

Stability diagrams of the hSOS-SA optimized system, a root locus plot, b bode plot

Full size image
Table 3 Results of stability analysis based on root locus stability criterion
Full size table

From Table 3, it is convenient to realize that the system governed with the SOS-PID controller has only one complex conjugate pole pair and it exhibits a better damping ratio with a value of 0.677 than the existing algorithms. When the results of hSOS-SA are investigated, it is clear that the value of damping ratio is further increased to 0.678. This outcome affirms our earlier claim and proves that the AVR system tuned by hSOS-SA algorithm operates with the highest stability margin.

For further investigating the stability-related results through another measure of stability criterion, frequency response of the system is also analyzed with the help of bode diagram. Computed results of peak gain, phase margin, delay margin and bandwidth are represented in Table 4. It is apparent that the proposed hSOS-SA, SOS and LUS are the pioneers that exhibit the best results in terms of minimum peak gain, maximum phase margin and maximum delay margin. Note that the bandwidth of the system is improved by the proposed hSOS-SA algorithm comparing to the original SOS and LUS. The maximum bandwidth pertains to BBO algorithm and the minimal to TLBO algorithm.

Table 4 Results of stability analysis based on bode stability criterion
Full size table

In order to study the robustness of the AVR system tuned by hSOS-SA algorithm, time constants of amplifier, exciter, generator and sensor are separately varied within the interval of ± 50% in steps of 25%. Resulting voltage change curves under parameter variations are displayed in Fig. 9.

Fig. 9
figure 9

Resulting voltage change curves ranging from + 50% to − 50% for a Ta, b Te, c Tg, d Ts

Full size image

Results of transient response analysis obtained from the responses in Fig. 9 are depicted in Table 5.

Table 5 Numerical results of transient response analysis under parameter uncertainties
Full size table

Besides, the range of total deviations along with maximum deviations in percentage is also provided in Table 6. When analyzing these results, it is seen that almost no deviation is observed by the variation of sensor time constant Ts. The average deviation for maximum overshoot is 4.2% that for settling time is 85.8% and that for rise time is 24.1%. All ranges of the total deviations from the nominal values are almost below 0.5.

Table 6 Range of total deviations and percentage of maximum deviations under parameter uncertainties
Full size table

Consequently, these results lead to an understanding of ours that proposed hSOS-SA tuned PID controller is robust and gives the desired control objective with an acceptable deviation in the presence of varying time constants in the specified interval.

6 Conclusion

The motivation behind this article comes from three objectives. The first one is related to the incorporation of recently introduced SOS algorithm for the first time to search for better gains of PID controller installed in an AVR system. The second one is the integration of SA after the SOS convergence in the hope of improving the system frequency response further. And the last one introduces a new cost function which involves both time-domain and frequency-domain specifications. In this regard, the trade-off between the time-domain performance specifications and those of frequency-domain is intended to ameliorate. Initially, the transient response performance of the system deploying the SOS is compared to those offered by five studies popular in the literature. Then, the SOS optimized controller gains are fine-tuned by invoking the SA subsequently. It has been demonstrated that both hSOS-SA and SOS exhibit the same overshoot and steady-state error which are lesser than other indicated optimization techniques as desired. On the other hand, the proposed hSOS-SA algorithm leads to a slight increase in settling time and rise time compared to SOS, but it allows to control the AVR system with the highest stability margin in comparison with SOS and other state-of-the-art approaches. From the robustness analysis made against parameter uncertainty, it may be noted that PID parameters tuned by hSOS-SA algorithm render acceptable performance; thus, they are not required to be reset for a broad range of variation in system parameters. As a result, we conclude that, thanks to the contribution of proposed hSOS-SA technique in cooperation with the newly defined cost function, most accurate (minimum oscillation) and most stable (minimum overshoot) unit step response of the AVR system is achieved along with the best steady-state performance (minimum steady-state error).