Geometric structure information based multi-objective function to increase fuzzy clustering performance with artificial and real-life data

Abstract

Grey wolf optimizer (GWO) is an efficient meta-heuristic algorithm that is inspired by the particular hunting behavior and leadership hierarchy of grey wolves in nature. In this paper, an efficient opposition-based grey wolf optimizer algorithm is proposed for solving the fuzzy clustering problem over artificial and real-life data. This work also tries to use the benefit of fuzzy properties which presents capability to handle overlapping clusters. However, centroid information and geometric structure information of clusters are the two important issues in fuzzy data clustering to improve the clustering performance. According to, in this paper, we derive two-objective functions, such as compactness and overlap–partition (OP) measures to handle above drawbacks. The centroid information issue is solved by compactness measure, and the OP measure is used to handle the geometric structure of clustering problem. Additionally, in the proposed clustering approach, the concept of opposition-based generation jumping and opposition-based population initialization is used with the standard GWO to enhance its computational speed and convergence profile. The efficiency of the proposed algorithm is shown for five artificial datasets and five real-life datasets of varying complexities. Experimental results show that the proposed method outperforms some existing methods with good clustering qualities.

1 Introduction

Clustering is an important method in data exploratory analysis to classify a group of objects into clusters, and it is used for many disciplines such as health informatics, pattern classification, image segmentation. For that reason, the vital objective of data clustering is to achieve an unsupervised classification of complex data where there is little or no prior knowledge of those data (Gan et al. 2007; Rui and Wunsch 2005). The most widely used algorithms to solve this problem are k-means (James 1967) and fuzzy c-means (FCM) (Bezdek et al. 1984). Both algorithms are centroid based and require a fixed number of clusters beforehand. Particularly, the aim of FCM is to minimize the generalized least-squares objective function, in which the degree of membership plays an important role to optimize the data partitioning problem. However, the drawbacks of both algorithms are well known: a correct number of clusters are required beforehand, and the algorithms are quite sensitive to centroid initialization (Hruschka et al. 2009; Gowthul Alam and Baulkani 2016). Most research papers have proposed solutions for such problems by running an algorithm repeatedly with different fixed values of k and with different initializations (Hruschka et al. 2009). However, this may not be feasible with large datasets and large k. Moreover, the algorithm running only with a limited number of k may be inefficient or not attractive since a solution depends on a limited set of initializations. This is known as the “number of clusters dependency” problem (Ripon et al. 2006).

From the above reasons, evolutionary algorithms (Vinu Sundararaj 2016) are shown to be alternative optimization methods using stochastic principles to evolve clustering solutions. In other words, they are based on probabilistic rules to search for a near-optimal solution from a global search space. Some evolutionary algorithms have been proposed in (Karaboga and Ozturk 2011; Izakian and Abraham 2011; Maulik and Bandyopadhyay 2000; Chang et al. 2009; Min and Siqing 2010; Cai et al. 2010; Handl and Knowles 2004; Bandyopadhyay and Saha 2008) to optimize the number of clusters in data partitioning problems. The approaches in Karaboga and Ozturk (2011) and Izakian and Abraham (2011) are based on swarm intelligence. In Karaboga and Ozturk (2011), simple artificial bee colony (ABC) algorithm which simulates the intelligent foraging behavior of honey bee swarms has been applied. In Izakian and Abraham (2011), the author have developed a hybrid algorithm which combines fuzzy c-means and particle swarm optimization (PSO) also known as FCM-FPSO. In Maulik and Bandyopadhyay (2000), and Chang et al. (2009), genetic algorithms (GAs) have been applied for the automatic determination of the number of clusters, where variable length strings have an important role in tackling the problem of the number of clusters. In Min and Siqing (2010), the k-means clustering has been enhanced by a GA, which considers the affect of isolated points. Additionally, the k-means based on GA has also been applied in Cai et al. (2010). The immune GA and dynamic chromosome coding have been proposed to improve the search and to increase the convergence.

Multi-objective evolutionary algorithms (MOEAs) have been shown to carry promising solutions for such problems with effective search performance over single-objective clustering algorithms (Handl and Knowles 2004). Two or more conflicting objective functions are organized in the evolutionary process. MOEAs for clustering have been proposed in Handl and Knowles (2004) and Saha and Bandyopadhyay (2010). In Handl and Knowles (2004), the algorithm called MOCK is based on PESA-II with locus-based chromosome encoding. It has shown to outperform single-objective clustering algorithms and ensemble techniques. However, it performs well for hyperspherical-shaped or well-separated clusters, but provides low performance on overlapping clusters (Saha and Bandyopadhyay 2010). Another drawback on the locus-based encoding is the length of the string, which increases with the size of the dataset. This imposes expensive computation when a large dataset is analyzed (Wikaisuksakul 2014).

To overcome this drawback, this paper develops a multi-objective evolutionary method to optimize data clustering with no necessity of the number of clusters. For that purpose, we use an iterative algorithm, named as opposition grey wolf optimizer. This work also tries to use the benefit of fuzzy properties which present capability to handle overlapping clusters. However, centroid information and geometric structure information of clusters are the two important issues in fuzzy data clustering to improve the clustering performance. According to, we develop two-objective functions, such as compactness and overlap–partition (OP) measures to handle above drawback. The centroid information issue is solved by compactness measure, and the OP measure is used to handle the geometric structure of cluster problem. Furthermore, the concept of opposition-based generation jumping and opposition-based population initialization is used with the standard GWO to enhance its computational speed and convergence profile.

• Our main contributions of the proposed approach are summarized as follows:

• We present a multi-objective GWO-based approach for fuzzy clustering problem which provides the capability to handle overlapping clusters.

• We derive a fitness function with two objectives, namely compactness and overlap–partition (OP).

• We present an efficient population initialization scheme, namely opposition-based learning (OBL) and generation jumping strategy to enhance the computational speed and convergence profile.

• We perform extensive simulation on the proposed algorithm, compare and analyze results with existing and related algorithms over artificial and real-life data.

The remainder of this paper is organized as follows: Sect. 2 reviews the related works on different evolutionary-based data clustering techniques. Section 3 provides the background information about FCM. In Sect. 4, the design of opposition grey wolf optimizer (OGWO) is explained. In Sect. 5, the detailed explanation of proposed clustering approach is presented. In Sect. 6, we present the experimental results. Finally, Sect. 7 concludes the work.

2 Review of related works

This section discusses the most relevant papers related to the meta-heuristic-based clustering methods. In recent years, some machine algorithms have been developed. Particularly, Jiao et al. (2012) have developed a semi-supervised clustering scheme with enhanced spectral embedding. Initially, they constructed a symmetry-favored k-NN graph, which was highly robust to noisy data points and capable of characterizing the underlying geometrical structures of datasets. After that, they formulated learning the enhanced spectral representation as a semi-definite-quadratic-linear program (SQLP) problem. Shang et al. (2016a) have introduced an algorithm namely self-representation-based dual-graph regularized feature selection clustering. Meanwhile, the local geometrical information of both data space and feature space was preserved simultaneously. Additionally, Shang et al. (2016b) have developed two spectral clustering methods, named global discriminative-based nonnegative and spectral clustering.

There are many particle swarm optimization (PSO)-based hard clustering methods, yet there are fewer proposals for fuzzy clustering with PSO. Saha and Bandyopadhyay (2010) have developed a multi-objective clustering technique based on a point symmetry-based distance which can automatically determine the proper number of clusters and the proper partitioning from a given dataset. Here assignment of points to different clusters was done based on the point symmetry-based distance rather than the Euclidean distance. Two cluster validity measures, one based on the point symmetry-based distance, Sym-index, and another based on the Euclidean distance, XB-index, are optimized simultaneously. Niu and Huang (2011) have developed a fuzzy c-means clustering algorithm based on an enhanced particle swarm optimization which avoids premature convergence. In addition, Szabo et al. (2011) presented an extension of the crisp data clustering algorithm named particle swarm clustering (PSC) particularly tailored to deal with fuzzy clusters. Ma et al. (2011) introduced a fuzzy clustering algorithm based on adaptive particle swarm optimization algorithm (APSO) in order to overcome the disadvantages of the FCM algorithm such as the sensitivity to initial values and the easy involvement in partial optimum, and enhance the abilities of APSO algorithm such as global search and escape from partial optimum.

A chaotic particle swarm fuzzy clustering (CPSFC) algorithm based on chaotic particle swarm (CPSO) and the gradient method was proposed by Li et al. (2012). These methods have made efforts to improve the quality of the clustering, but they do not consider that PSO parameters have a significant impact on the performance of the algorithm. According to this, Zhang et al. (2013) have developed a modified method to increase the convergence speed. They showed that the automatic adjustment of the parameters enables their PSO version (improved self-adaptive particle swarm optimization—IDPSO) to achieve a better performance in function optimization problems. On another hand, Pimentel and De Souza (2013) have developed a multivariate membership algorithm for FCM clustering which is different from one variable to another and from one cluster to another. To deal with more complex data types, such as interval data, Pimentel and Souza (2014) developed a multivariate FCM method with relevance weights for each variable that is different from one cluster to another. Shouwen et al. (2014) have proposed a hybrid clustering algorithm based on two improved versions of PSO (HPSOFCM), which combines the merits of both algorithms and showed that the proposed method is able to escape local optima. Armano and Mohammad Reza (2016) have developed a partitional clustering as a multi-objective optimization problem. The aim was to obtain well-separated, connected, and compact clusters, and for this purpose, two-objective functions have been defined based on the concepts of data connectivity and cohesion.

In addition, Mukhopadhyay (2014) have surveyed several multi-objective evolutionary algorithms (MOEAs) used for data mining problems. Additionally, Luo et al. (2016) have developed a multi-objective evolutionary algorithm based on sparse representation to construct the similarity matrix for spectral clustering. Li et al. (2017) have proposed a complex network clustering algorithm, called quantum-behaved discrete multi-objective particle swarm optimization (QDM-PSO). An evolutionary method has introduced by Amiri and Mahmoudi (2016) for data clustering problem using cuckoo optimization algorithm. Firstly, the algorithm generated a random solution equal to cuckoo population and with length dataset objects and with a cost function calculates the cost of each solution. Finally, fuzzy logic tried for the optimal solution. In addition, Jensi and Jiji (2016) have developed an improved krill herd algorithm (IKH) by making the krill the global search capability. The enhancement comprised of adding global search operator for exploration around the defined search region and thus the krill individuals move toward the global best solution. The proposed method was tested on a set of twenty-six well-known benchmark functions and was compared with thirteen popular optimization algorithms, including original KH algorithm.

Tizhoosh introduced the concept of opposition-based learning (OBL) in Tizhoosh (2005). Some of the OBL-based clustering algorithms have been developed in recent years. Bharti and Singh (2016) have developed a text clustering using a hybrid intelligent algorithm, which combines the binary particle swarm optimization (BPSO) with opposition-based learning, chaotic map, fitness-based dynamic inertia weight, and mutation. Here, an opposition-based initialization was used to start with a set of promising and well-diversified solutions to achieve a better final solution. In addition, Zhang et al. (2016) have developed a multi-objective evolutionary fuzzy clustering (MOEFC) algorithm to convert fuzzy clustering problems for image segmentation into multi-objective problems. Also, opposition-based learning was utilized to improve search capability of the proposed algorithm.

3 Background information about fuzzy c-means algorithm

The major processes of the FCM algorithm (Bezdek 1973) are the computation of membership degree and the update of cluster centers. The membership degree is employed to indicate the extent to which each data point belongs to each cluster, and this information is also used to update the values of cluster centers. Let $P=\left\{ {p_1 ,p_2 ,\ldots ,p_N } \right\}$be data points of N patterns, where each pattern $p_k$ is a vector of features in $R^{d}$ (d-dimensional space). C is the number of clusters. A distance from a data point $p_k$ to a cluster center $v_i$ is calculated using the squared Euclidean distance as follows:

$$\begin{aligned} d_{ik}^2 =\sum _{j=1}^d {\left( {p_{kj} -v_{ij} } \right) ^{2}} , \quad 1\le k\le N, 1\le i\le C \end{aligned}$$

(1)

where $d_{ik}^2$ indicates the squared Euclidean distance computed in d-dimensional space. After that, the distance is employed in the calculation of membership degree in equation (2).

$$\begin{aligned} u_{ik} =\frac{1}{\sum _{j=1}^C {\left( {\frac{d_{ik} }{d_{jk} }} \right) ^{2/{\left( {m-1} \right) }}} }, \quad 1\le k\le N, 1\le i\le C \end{aligned}$$

(2)

where $u_{ik}$ represents a degree of membership of $p_k$ in the $i^{th}$ cluster. $m>1$ is a parameter which controls a degree of fuzziness. This means that each data pattern has a degree of membership in every cluster.

After that, the values of the centroids are updated using Eq. (3). Lastly, the membership degree of each data point is computed once again using equation (2) taking the new centroid values.

$$\begin{aligned} v_i =\frac{\sum \nolimits _{k=1}^N {\left( {u_{ik} } \right) ^{m}} p_k }{\sum \nolimits _{k=1}^N {\left( {u_{ik} } \right) ^{m}} }, \quad 1\le i\le C \end{aligned}$$

(3)

4 Formulation for opposition grey wolf optimizer

Grey wolf optimization (GWO) is a trendy optimization technique that has been widely used in various applications. As a random search method, the performance of simple GWO greatly depends on its parameters; moreover, it often suffers from the problem of solutions being trapped in local optima so as to be premature convergence. In this paper, opposition-based learning (OBL) process is used to speed up the searching process of GWO.

4.1 Simple grey wolf optimization algorithm

Grey wolf optimization algorithm is developed by Seyedali et al. (2014), and it reflects the behavior of the grey wolf in searching and hunting for their prey (Seyedali et al. 2014). Grey wolves prefer to live in a group size of 5–12 members on average. The group is called pack. The leaders of the pack are a male and a female. There are four categories in a pack, alpha ($\alpha$), beta ($\beta$), delta ($\delta$) and omega ($\omega$).

Alpha is the first level and is mostly responsible for making decisions. The decisions of alpha are dictated to the pack. Alpha is not necessarily the strongest member of the pack, but they are best in terms of managing the group. This behavior of the pack shows that organization and discipline of a group are important than its strength. Beta is the second level of wolf and they help the alpha in decision making or in other activities. Beta can take charge of the pack in absence of the alpha. Beta wolf reinforces the alpha’s command throughout the pack and gives feedback to the alpha. Delta is the third level and this level includes scouts, sentinels, hunters, and caretakers. Scouts are responsible for watching the boundaries of the territory. They issue warning to the pack in case of any danger. Sentinels are responsible for the safety of the pack. Hunters help the alphas and betas when hunting the prey. The lowest ranking of the pack is omega. They are last wolves that are allowed to eat. The mathematical expression of GWO algorithm is explained clearly as below:

Step 1: Calculating$\alpha$, $\beta$, $\delta$and$\omega$

During every iteration, the first three best wolves (based upon the fitness) are considered as alpha$(\alpha )$, beta $\left( \beta \right)$, and delta$(\delta )$, who lead other wolves toward promising zones of the search space. Let the first best fitness solution (based upon the fitness) be $F_\alpha$, the second best fitness solution be $F_\beta$ and the third best fitness solution be $F_\delta$. The rest of grey wolves are assumed to be the omega$(\omega )$. In the GWO algorithm, the hunting (optimization) is guided by alpha$(\alpha )$, beta$\left( \beta \right)$, and delta$(\delta )$. The omega$(\omega )$ wolves follow these three wolves.

Step 2: Prey encircling strategy

The hunting is guided by $\alpha ,\beta ,\delta$ and $\omega$ follow these three candidates. In order to hunt a prey for the pack to hunt a prey is first encircling it.

$$\begin{aligned}&\vec {K}=|\vec {H}. \vec {F}_p (t)-\vec {F}(t)| \end{aligned}$$

(4)

$$\begin{aligned}&\vec {F}(t+1)=\vec {F}_p (t)-\vec {A}. \vec {K} \end{aligned}$$

(5)

where t represents current iteration; $\vec {F}_p$ and $\vec {F}$ are the location vectors of a prey and grey wolf, respectively. $\vec {A}$ and $\vec {H}$ are the coefficient vectors and these are illustrated as follows:

$$\begin{aligned} \vec {A}=2\vec {a}\vec {r}_1 -\vec {a} \hbox { and } \vec {H}=2\vec {r}_2 \end{aligned}$$

(6)

where $r_1$ and $r_2$ are the random vectors uniformly spanned in [0, 1], while $\vec {a}$ is the encircling efficient vector, where components are linearly decreased from 2 to 0 during each iteration, respectively. To see the effects of equations (5) and (6), a two-dimensional position vector and some of the possible neighbors are shown in Fig. 1. Different places around the best agent can be reached with respect to the current position by adjusting the value of $\vec {A}$ and $\vec {H}$ vectors. For example, $\left( {U^{*}-V,V^{*}} \right)$ can be attained by setting $\vec {A}=(1,0)$ and .

Fig. 1

2D position vectors and their possible next locations (Seyedali et al. 2014)

Step 3: Hunting group strategy

During the process of hunting, the first three best solutions achieved so far in terms of $\alpha ,\beta$, and $\delta$ are saved and remained, then the remaining wolves such as $\omega$ possess the ability to relocate their positions based on the first three best wolves. The positions of wolves are updated using Eqs. (7)–(9):

$$\begin{aligned}&\vec {K}_\alpha =|\vec {H}_1 . \vec {F}_\alpha -\vec {F}| ,\quad {\vec {K}_\beta =|\vec {H}_2 .\vec {F}_\beta -\vec {F}|,}\quad \nonumber \\&{\vec {K}_\delta =|\vec {H}_3 . \vec {F}_\delta -\vec {F}|} \end{aligned}$$

(7)

$$\begin{aligned}&\vec {F}_1 =\vec {F}_\alpha -\vec {A}_1 .(\vec {K}_\alpha ), \quad \vec {F}_2 =\vec {F}_\beta -\vec {A}_2 .(\vec {K}_\beta ), \quad \nonumber \\&\vec {F}_3 =\vec {F}_\delta -\vec {A}_3 .(\vec {K}_\delta ) \end{aligned}$$

(8)

$$\begin{aligned}&\vec {F}(t+1)=\frac{\vec {F}_1 +\vec {F}_2 +\vec {F}_3 }{3} \end{aligned}$$

(9)

where $\vec {F}_\alpha$, $\vec {F}_\beta$ and $\vec {F}_\delta$ specify the positions of the alpha, beta, and delta, respectively. Also, $\vec {H}_1 ,\vec {H}_2,\vec {H}_3$ and $\vec {A}_1,\vec {A}_2,\vec {A}_3$ are all random vectors. $\vec {F}$ is the position of current solution and t is the number of iteration.

Step 4: Attacking prey (exploitation) and search for prey (exploration)

Exploration and exploitation are performed using the adaptive values of a and A. The adaptive values of parameters a and A permit GWO to show smooth transition among exploration and exploitation. By declining A, half of the iterations are dedicated to exploration ($|A|\ge 1)$ and the other half are devoted to exploitation ($|A| <1$). From the above-described criterion, we obtain the knowledge that the $\vec {H}$ vector contains random values in [0, 2]. This module gives random weights for prey in order to stochastically emphasize ($H >1$) or deemphasize ($H <1$) the effect of prey in defining the distance in Eq. (4). This assists GWO to show a more random behavior during the course of optimization and favors exploration and local optima avoidance.

Step 5: Termination criteria

The algorithm discontinues its execution only if a maximum number of iterations are achieved, and the solution which is holding the best fitness value is selected and it is specified as the best result.

4.2 Opposition grey wolf optimizer

Opposition-based learning (OBL) scheme is developed by Tizhoosh (2005), which considers the current individual (solution) and its opposite individual simultaneously in order to obtain a better approximation at the same time for a current candidate solution.

In the OBL-based proposed system, two definitions, namely opposite point, opposite number and two steps, namely opposition-based population initialization and opposition-based generation jumping are clearly described below:

Definition 1

Opposite number: Let $m\in \left[ {p,q} \right]$ be the real number. The opposite number of $m(m^*)$ is described as follows:

$$\begin{aligned} m^{*}=p+q-m \end{aligned}$$

(10)

Likewise, this definition can be extended to higher dimensions (Tizhoosh 2006) as stated in Definition 2.

Definition 2

Opposite point: Let $M=m_1 ,m_2 ,m_3 ,\ldots ,m_d$ be a point in d-dimensional search space, where $m_1 ,m_2 ,m_3 ,\ldots ,m_d \in R$, R be the real number and $m_i \in \left[ {p_i ,q_i } \right] \forall _i \in \left\{ {1,2,\ldots ,d} \right\}$. The opposite point $\mathrm{OM}=( m_1^*,m_2^*,m_3^*,\ldots ,m_d^*)$ is completely defined by its components:

$$\begin{aligned} \mathrm{OM}=p_i +q_i -m_i \end{aligned}$$

(11)

Now, by using the opposite point definition, the opposition-based optimization is defined in the following section.

Opposition-based population initialization:

In our approach, the fittest individuals are chosen as follows: Let $M=\left( {m_1 ,m_2 ,m_3 ,\ldots ,m_d } \right)$ be a point in d-dimensional space (i.e., a candidate solution). Suppose $f=\left( {\bullet } \right)$ is a fitness function which is employed to measure the candidate’s fitness. In our approach, we build the fitness function depending on the two efficient measures like partition and compactness (detailed in Sect. 5.1). According to the definition of the opposite point, $\mathrm{OM}=\left( {m_1^*,m_2^*,m_3^*,\ldots ,m_d^*} \right)$ is the opposite of $M=\left( {m_1 ,m_2 ,m_3 ,\ldots ,m_d } \right)$. Now, if $f\left( {\mathrm{OM}\ge M} \right)$, then point M can be replaced with $\mathrm{OM}$; otherwise, we continue with M. Hence, the point and its opposite point are evaluated simultaneously in order to continue with the fitter one. The same approach is applied not only to the initial solution but also continued to each solution in the current population.

Opposition-based generation jumping:

If we apply a similar approach to the current population, the whole evolutionary process can be forced to jump to a new candidate solution which is more suitable than the current one. Based on a jumping rate ($J_{\mathrm{R}}$), after following the GWO operator, the new population is generated and opposite population is calculated. From this comparison, the fittest $N_{\mathrm{F}}$ individuals are selected. In each generation, search space is reduced to calculate the opposite points, i.e.

$$\begin{aligned} \mathrm{OM}_{i,j}= & {} \mathrm{Min}_j^\mathrm{gen} +\mathrm{Max}_j^\mathrm{gen} -M_{i,j} \quad \nonumber \\&i=1,2,\ldots ,N_F j=1,2,\ldots ,n \end{aligned}$$

(12)

where $\left[ {\mathrm{Min}_j^{\mathrm{gen}} +\mathrm{Max}_j^{\mathrm{gen}} } \right]$ is the current interval in the population which is becoming increasingly smaller than the corresponding initial range $\left[ {p_j ,q_j } \right]$.

The detailed explanation of opposition grey wolf optimizer is presented in algorithm 1.

5 Implementation of opposition grey wolf optimizer for solving multi-objective fuzzy clustering problem

In this study, a novel multi-objective clustering algorithm is proposed combining centroid and geometric structure information of clusters using an efficient opposition grey wolf optimizer algorithm. The usage of opposition grey wolf optimizer to solve the multi-objective clustering problem includes the identification of the optimal cluster to minimize the objective function and to provide better clustering accuracy. This section describes our proposed technique, which uses the evaluation of overlap–partition (OP) and compactness measure for the calculation of fitness that is used to find the best agent (solution) in opposition grey wolf optimizer algorithm.

Fig. 2

Two groups contain distance between centroids from Kim et al. (2004)

5.1 Derivation of fitness function

The fitness value of a solution symbolizes its level of quality on the basis of the objectives. In the proposed approach, our aim is to find the optimal clusters from the given databases. Here, we build the fitness function depending on the two efficient measures like partition and compactness.

The compactness index represents deviation between cluster centroid and data or between data within a cluster, and it must be kept small. The partition measures the isolation of clusters that is preferred to be large. If only partition or compactness is taken in a single-objective optimization, some drawbacks may degrade the performance of the optimization. In Capitaine and Frélicot (2008), its difficulty has been raised for conventional partition. Partition considering inter-distance measurement between cluster centroids cannot exactly identify geometric structures. As shown in Fig. 2, the distance from centroids A to B in the group 1 compared to the distance between C and D in the group 2 is equal.

These two groups have the same property of partition, but naturally, group 2 is illustrated to have more partition in terms of the conventional measure of inter-cluster distance. In addition, it can be observed that the measurement of centroid distance only can misjudge the partition of clusters because the overall shape is not considered. This leads to inadequate information about cluster structures.

In order to solve the above-mentioned problems, two objectives are optimized concurrently in the multi-objective optimization of OGWO-FCM. These objectives are based on the overlap–partition (OP) together with a compactness measure.

The first objective function of the compactness is prepared by Bezdek et al. (1984) as represented in Eq. (13):

$$\begin{aligned} J_n (U,V)= & {} \sum _{k=1}^N {\sum _{i=1}^C {\left( {u_{ik} } \right) ^{m}\left\| {p_{kj} -v_{ij} } \right\| ^{2}} } ,\nonumber \\&1\le k\le N, 1\le i\le C \end{aligned}$$

(13)

where C is the number of clusters, and N is the number of data points, $p_{kj}$ is the data point. $v_{ij}$ is the cluster center. $u_{ik}$ and m are characterized in accordance with equations (2)–(3). The sum of the squared error is calculated through the squared Euclidean distance from a pattern to each centroid with the weight $\left( {u_{ik} } \right) ^{m}$ appended. The main intention is to minimize $J_n$ to optimize compactness taking into account distance and degree of membership.

The second objective function of the overlap and partition measure (OP) is derived from a combination of overlapping and centroid partition problem. Figure 2 illustrates the details explanation of this problem. For the partition measure (Kim et al. 2004), the maximum degree of $\mathop {\max }\limits _{i=1,C} u_{ik}$ is obtained into account. Consequently, the overall overlap–partition (OP) measure for N patterns is characterized as follows:

$$\begin{aligned} OP=\frac{1}{N}\sum _{k=1}^N {\frac{O\bot \left( {u_k (p_k ),C} \right) }{\mathop {\max }\limits _{i=1,C} u_{ik} }} \end{aligned}$$

(14)

The OP is defined as the ratio of the overlap degree to partition. The small value of OP indicates a separation in which the clusters are overlapped to a lesser degree and are more separated from each other. Here, the OP measure is formulated based on an aggregation process of fuzzy membership degrees. It contains two components. The first component is the overlap measure developed by Capitaine and Frélicot (2008) and Capitaine and Frélicot (2011), which calculates an inter-cluster overlap through fuzzy degrees as illustrated in Eq. (15).

$$\begin{aligned} O\bot \left( {u_k (p_k ),C} \right) =\mathop \bot \limits _{h=2,C}^1 \left( {\mathop \bot \limits _{i=1,C}^h u_{ik} } \right) \end{aligned}$$

(15)

where a pattern $p_k$ has membership vector $u_k (p_k )=\left( {u_{1k} ,u_{2k} ,\ldots ,u_{ck} } \right)$. The ambiguity measurement of numerous membership values requires an aggregation operator (AO). Here the AO applied is based on triangular norms (t-norms) for l-order ambiguity measurement. In this aggregation, the standard t-norm and t-conorm are used.

With a single value $\mathop \bot \limits ^h u_{ik} \in \left[ {0,1} \right]$, the h-order fuzzy-OR operator (fOR-h) which is the combination of dual couple (Mascarilla et al. 2008) is combined with $u_k$, denoted by

$$\begin{aligned} \mathop \bot \limits _{i=1,C}^h u_{ik} =\mathop {\mathrm{T}}\limits _{A\in \rho _{h-1} } \left( {\mathop \bot \limits _{j\in C|A}^h u_j } \right) \end{aligned}$$

(16)

where $\rho$ indicates the power set of $C=\left\{ {1,2,\ldots ,c} \right\}$ and $\rho _{_h } =\left\{ {A\in \rho :\left| {A=h} \right| } \right\}$. Here, $\left| A \right|$ is the cardinality of the subset A.

Fitness computation:

We describe the intermediate steps for fitness computation with $J_n$ and OP as follows:

Step 1::

Initialize the parameters related to the FCM: given a number of clusters; $m=2$; threshold $\varepsilon$ and membership function $\left( {u_{ik} } \right)$.

Step 2::

Update the fuzzy membership function and cluster centroid using Eqs. (2) and (3).

Step 3: :

If the improvement in $J_n (U,V)$ is less than a certain threshold $\varepsilon$, then go to step 4; otherwise, go to step 2.

Step 4: :

Compute and store the overlap measure and partition measure for the fuzzy partition U obtained in step 3.

Step 5: :

Compute the overlap–partition OP using Eq. (14) for each cluster.

Step 6::

Find the minimum $OP^{(\min )}$ and report the value of cluster that minimizes OP as the best cluster.

5.2 Agent representation

The agent (solution) in the OGWO-FCM algorithm is represented by a string of real-coded values defining cluster centers in n-dimensional space. Figure 3 illustrates an example of an agent comprising four centers $\left[ {c_1 ,c_2 ,c_3 ,c_4 } \right]$ in two dimensions. For instance, a string representation can be $\left\{ {\left( {6.10,2.78} \right) ,\left( {4.88,3.39} \right) ,\left( {5.39,3.24} \right) ,\left( {6.87,3.07} \right) } \right\}$. The number of clusters is represented by the length of the string. Each individual in an initial population has different lengths varied over a range of 2 to $\sqrt{M}$.

Fig. 3

Solution representation: Cluster centers $\left\{ {C_1 ,C_2 ,C_3 ,C_4 } \right\}$ in two-dimensional features

Fig. 4

Omega wolves ($\omega )$ update process with a same length, b different length

5.3 Solution updation using GWO operators

After fitness computation, the first three best wolves are selected based on the basis of functions $J_n$ and OP (fitness) and save them as $\alpha ,\beta$ and $\delta$. The rest of the solutions $\omega$ have to be optimized in continuous search space according to the real-coding string representation of cluster centers using Eqs. (7)–(9). Since each solution in the population has different lengths, the solutions of four parents such as $\alpha ,\beta ,\delta$ and $\omega _i$ may have equal or different lengths, where $\omega _i$ is $i^{th}$ solution from the solution set $\omega$.

In case, string lengths are equal to $\alpha ,\beta ,\delta$ and $\omega _i$ can be considered as Fig. 4a. Let four parents $\alpha =\left\{ {a_1 ,a_2 ,a_3 ,a_4 } \right\} ,\beta =\left\{ {b_1 ,b_2 ,b_3 ,b_4 } \right\} ,\delta =\left\{ {c_1 ,c_2 ,c_3 ,c_4 } \right\}$ and $\omega _i =\left\{ {d_1 ,d_2 ,d_3 ,d_4 } \right\}$ denote parent solutions with four cluster centers, where each $a_j ,b_j ,c_j$ and $d_j$ is a vector of features. The four new children solutions are created. For this conversion process, the same values are directly copied from parents’ solutions. After that, the updation process is performed using Eqs. (7)–(9).

In case, strings lengths of four parents are different, an example of this operation is given in Fig. 4b. Let four parents $\alpha =\left\{ {a_1 ,a_2 ,a_3 ,a_4 ,a_5 ,a_6 } \right\} ,\beta =\left\{ {b_1 ,b_2 ,b_3 ,b_4 ,b_5 } \right\} ,\delta =\left\{ {c_1 ,c_2 ,c_3 ,c_4 ,c_5 } \right\}$ and $\omega _i =\left\{ {d_1 ,d_2 ,d_3 ,d_4 } \right\}$ indicate parent solutions with different cluster centers. To convert the equal length, the size of $\omega _i$ is chosen. The size of all the remaining parent solutions such as $\alpha$, $\beta$ and $\delta$ is converted into the size of $\omega _i$. The four new children solutions are then created. To do that, the centroids are randomly chosen with equal size of $\omega _i$ from the parent solutions. The calculation of the new values of children then follows the same procedures as in the case of equal length.

Fig. 5

Overall flow diagram of the proposed algorithm

5.4 The procedure of OGWO-FCM

As described in Fig. 5, at first, the random operator initializes N solutions based upon OBL process (detailed explanation in Sect. 4.2) for an initial population by randomly choosing cluster center points from M data patterns. The initial numbers of clusters are generated from a uniform distribution over the range 2 to $\sqrt{M}$. The assignment of membership degree and the update of center values are based on the FCM algorithm further described in Sect. 3. The values of fitness are then computed according to the two objectives. After that, the updating strategies are performed using GWO operators. The process runs and searches for non-dominated front solutions until it meets the termination criterion (e.g., the maximum number of generations). The non-dominated solutions are finally obtained. On each solution, each data point is assigned to a cluster corresponding to its maximum degree of membership. The best solution ($\alpha$) is then identified from these non-dominated solutions by the minimum value of MS. The overall process of the proposed clustering algorithm as follows:

Step 1::

Opposition-based population initialization: Cluster range size 2 to $\sqrt{M}$.

Step 2::

Compute the corresponding fitness function value for each solution using Eq. (13)–(16).

Step 3::

Select first three best wolves based upon their fitness values (described as Sect. 5.1) and save them as $\alpha ,\beta$ and $\delta$.

Step 4::

Update the position of rest of the population ($\omega$ wolves) using Eqs. (4)–(9).

Step 5::

Update membership degree and center values using FCM.

Step 6::

Update parameters a, A, H

Step 7::

Opposition-based generation jumping based upon the fitness.

Step 8::

The process runs and searches for non-dominated front solutions until it meets the termination criterion (e.g., the maximum number of generations).

Step 9::

Return the position of $\alpha$ as the best-approximated optimum from the non-dominated set (detailed in Sect. 5.4).

The detail explanations for each phase of the algorithm are presented in Fig. 4.

Fig. 6

AD_5_2 dataset ($K=5$): a true solution, b data clustering using OGWO-FCM ($\mathrm{MS}=0.30$)

5.5 Selection and evaluation of the optimal solution set

The OGWO-FCM algorithm produces a set of non-dominated solutions in the final generation, whose number varies according to the size of the population. By using the two objectives, all the solutions are considered to be equal in terms of fitness values compromised. A single solution must be selected out of this set in most real-world problems. As presented in Ripon et al. (2006), we arrange the selection method, where a semi-supervised method has been used.

Table 1 Information of datasets

In the whole dataset, the class label of 10% dataset is imagined to be known. The remaining 90% of the dataset has no class label information presented and OGWO-FCM executes on these unknown label samples called test datasets. Patterns are partitioned into their corresponding clusters after the clustering process in the multi-objective optimization has finished, excluding class labels of clusters have not been identified.

Afterward, the class labels are allocated as follows. In Saha and Bandyopadhyay (2010), the nearest center criterion-based class label allocation is described. In our OGWO-FCM, the class label allocation is done by the combination of the fuzzy degree of membership and the center-based criterion. Initially, based on the maximum degree of membership, each known label sample is mapped to a cluster. Secondly, by using the frequency of the samples, a frequency table is constructed that falls in their mapped clusters. Lastly, based upon the maximum frequency, the label of the cluster is selected from the known label of the samples. If frequencies between the partitions are equal, the cluster label is allocated by the label of the sample that has the maximum fuzzy degree with the corresponding cluster.

Fig. 7

AD_10_2 dataset ($K=10$): a true solution, b data clustering using OGWO-FCM ($\mathrm{MS}=0.14$)

Fig. 8

Square1 dataset ($K=4$): a true solution, b data clustering using OGWO-FCM ($\mathrm{MS}=0.20$)

Fig. 9

Square4 dataset ($K=4$): a true solution, b data clustering using OGWO-FCM ($\mathrm{MS}=0.48$)

Fig. 10

Sizes5 dataset ($K=4$): a true solution, b data clustering using OGWO-FCM ($\mathrm{MS}=0.20$)

According to Saha and Bandyopadhyay (2010), Minkowski score (MS) is calculated after the label allocation process to measure the amount of misclassification as denoted in Eq. (17). Let assume the true solution set S and the solution set to be measured T.

$$\begin{aligned} \mathrm{MS}(S,T)=\sqrt{\frac{m_{01} +m_{10} }{m_{11} +m_{10} }} \end{aligned}$$

(17)

From Eq. (17), the measure is derived by the number of point-pairs allocations of data items between S and T. $m_{11}$ represents the number of point pairs that are in the same class in both T and S. $m_{01}$ and $m_{10}$ represent the mismatched number of point pairs between the two sets. $m_{01}$ represents the number of point pairs that are in T only, and $m_{10}$ represents the number of point pairs that belong to S only. A lower score specifies a better solution. Once the scores of all non-dominated solutions have been computed, the solution with the minimum score is selected as the best (optimal) solution $\alpha$.

6 Simulation result and discussion

All simulations for solving multi-objective clustering problem using GWO are implemented using MATLAB on Windows 8 operating system and Intel® Core$^{\mathrm{TM}}$ i5-2330M CPU @ 2.30 GHz 8 GB RAM system configuration.

6.1 Dataset description

To evaluate our proposed system, the datasets have been utilized as similar (Saha and Bandyopadhyay 2010) in this study. There are two set of databases, real-life and artificial datasets. Ten datasets are used for the experiment: five of them are artificial data (AD_5_2, AD_10_2, Square1, Square4, and Sizes5) and five are real-life datasets (Iris, Breast Cancer, New thyroid, Wine and Liver Disorder). The detailed information of this ten dataset is given in Table 1.

• 1. AD_5_2: This dataset contains 250 two-dimensional data points distributed over five spherically shaped clusters. The clusters present in this dataset are highly overlapping, each consisting of 50 data points. This dataset is shown in Fig. 6a.

• 2. AD_10_2: This dataset contains 500 two-dimensional data points distributed over 10 different clusters. Some clusters are overlapping in nature. Each cluster consists of 50 data points. This dataset is shown in Fig. 7a.

• 3. Square1: This dataset consists of 1000 data points distributed over four squared clusters. This is shown in Fig. 8a.

• 4. Square4: This dataset contains 1000 data points distributed over four squared clusters. This is shown in Fig. 9a.

• 5. Sizes5: This dataset contains 1000 data points distributed over four clusters. The densities of these clusters are not uniform. This is illustrated in Fig. 10a.

• 6. Liver Disorders: These data has six attributes including five blood tests and a number of daily drinks. The data are divided into two sets which indicate whether an individual suffers from alcoholism.

• 7. Iris: This dataset contains 150 four-dimensional data points distributed over three clusters. Each cluster consists of 50 points. This dataset symbolizes different groups of irises characterized by four feature values. It has three classes, Virginica, Versicolor, and Setosa.

• 8. Breast Cancer: This Wisconsin breast cancer dataset contains 683 sample points. Each pattern has nine features corresponding to clump thickness, cell size uniformity, cell shape uniformity, marginal adhesion, single epithelial cell size, bare nuclei, bland chromatin, normal nucleoli and mitoses. There are two categories of the data: malignant and benign. The two classes are known to be linearly separable.

• 9. New thyroid: Five laboratory tests are employed to predict whether a patient’s thyroid belongs to the class euthyroidism, hypothyroidism or hyperthyroidism. There is a total of 215 instances and the number of attributes is five.

• 10. Wine: It is a Wine recognition data, which contains 178 instances having 13 features resulting from a chemical analysis of wines grown in the same region in Italy but derived from three different cultivars. The analysis determined the quantities of 13 constituents found in each of the three types of wines.

6.2 Experimental results

6.2.1 Parameter setting of opposition grey wolf optimizer

In opposition grey wolf optimizer-based clustering approach, ten datasets detailed in Sect. 6.1 have been applied with the parameter settings summarized in Table 2.

Table 2 Summary of parameter settings for the experiment

6.2.2 Results for multi-objective function optimization

In this section, visual results of the data partitioning obtained through OGWO-FCM with center markings and the true data partitioning. The high values of Minkowski score (MS) achieved in Figs. 6 and 9; it shows higher overlapped shape in AD_5_2 and Square4 datasets. The OGWO-FCM-based proposed approach achieves the well-separated structures of AD_10_2 is illustrated in Fig. 7. From Fig. 8 for Square1 dataset, we obtain unequally sized shape clusters compare with a true solution. Additionally, in Fig. 10, Sizes5 obtain similar results as Square1 dataset. It can be observed that the overlap–partition objective achieves well to identify overlapping clusters.

6.2.3 Results for optimal solution set selection

The final optimal solution set is obtained by OGWO-FCM on the real-life datasets, Iris, Breast Cancer, Wine, Newthyroid and Liver Disorders shown in Figs. 11, 12, 13, 14 and 15.

Fig. 11

Non-dominated solutions obtained by OGWO-FCM on the Iris dataset, where K varies along the Pareto front

Fig. 12

Non-dominated solutions obtained by OGWO-FCM on the Breast Cancer dataset, where K varies along the Pareto front

Fig. 13

Non-dominated solutions obtained by OGWO-FCM on the Wine dataset, where K varies along the Pareto front

Fig. 14

Non-dominated solutions obtained by OGWO-FCM on the Newthyroid dataset, where K varies along the Pareto front

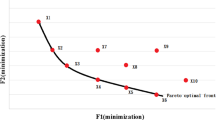
The obtained solutions are plotted in the two-objective space and clustered according to K, the number of clusters. OGWO-FCM gives solutions with a range of different numbers of clusters varying from 2 to 8 on Iris (in Fig. 11), 2 to 21 on Breast Cancer (in Fig. 12), 2 to 9 on Wine (in Fig. 13), 2 to 11 on Newthyroid (in Fig. 14) and 2 to 14 on Liver Disorders (in Fig. 15). Some numbers of K are removed. This can be supposed that the solutions with skipped numbers of K are dominated by better solutions according to a trade-off between their fitness values from the two objectives. All results of the Pareto-optimal front are accordingly revealed as the value of overlap–partition (OP) increases, whereas $J_{n}$ decreases with an increasing number of K. These solutions are approximately ordered by K increasing from left to right. This illustrates the conflict between the two objectives when a range of numbers of clusters is considered. To partition data for the appropriate number of clusters, a trade-off between the $J_{n}$ index and overlap–partition (OP) is needed. The preservation of diversity in the population is another key to maintaining solutions with different numbers of clusters. It illustrates that OGWO-FCM through the opposition grey wolf optimizer mechanism is capable to handle such preservation from the reasonable spread of the solutions.

Fig. 15

Non-dominated solutions obtained by OGWO-FCM on the Liver Disorders dataset, where K varies along the Pareto front

6.3 Comparative analysis

In this experiment, the parameters of the proposed opposition GWO-based clustering approach are as follows: maximum iteration $iter_{\max } =80$, jumping rate $J_r =0.3$, and population size are 50. The iteration of FA-FCM is 100, while PSO-FCM iterates 120 times for finish the convergence. Moreover, the GWO-FCM algorithm iterates 100 times for the convenience of comparison on convergence performance with the other two algorithms.

The fitness convergence characteristic obtained from GWO and opposition GWO is shown in Fig. 16. It is seen from Fig. 16 that fitness converges more quickly in case of opposition GWO than GWO algorithm. For the purpose of comparison, the opposition GWO-based fuzzy clustering algorithm is proposed and compared with other four multi-objective methods, VAMOSA (Saha and Bandyopadhyay 2010), FCM with firefly algorithm (FA), FCM with particle swarm optimization (PSO) and FCM with basic GWO algorithm (GWO-FCM).

However, GWO-FCM has high computational complexity with $O\left( {MN^{3}} \right)$, where M is the number objectives and N is the number of population size. Therefore, OGWO-FCM is achieved from the first version to reduce the complexity from $O\left( {MN^{3}} \right)$ to $O\left( {MN^{2}} \right)$. The OGWO-FCM uses a fast non-dominated sorting to search for a non-dominated front and opposition-based learning (OBL) to maintain diversity in population.

Fig. 16

Fitness convergence characteristic for opposition GWO (OGWO) and GWO

Table 3 Mean and Standard deviation of Minkowski score measured in the outputs of OGWO-FCM (over 50 independent runs) PSO-FCM, FA-FCM, VAMOSA (Saha and Bandyopadhyay 2010) and GWO-FCM

Fig. 17

Box plots representing the Minkowski scores results obtained by the proposed OGWO-FCM and three existing algorithms for AD_10_2 dataset (artificial) over 50 independent trails

Fig. 18

Box plots representing the Minkowski scores results obtained by the proposed OGWO-FCM and three existing algorithms for Iris dataset (real-life) over 50 independent trails

In our approach, the optimal cluster set is obtained from non-dominated solutions by the minimum value of MS. In order to achieve this, 50 independent trails have been performed and the decision-making process just selects the final clustering from the obtained non-dominated solutions (for each run). Lastly, the average value of Minkowski score corresponding to the selected clustering solutions over 50 independent runs has been calculated and considered as the performance measure of each algorithm. The results over 10 datasets are summarized in Table 3. Additionally, the box plots for two datasets (one from the artificial dataset, another from the real-life dataset) are shown in Figs. 17 and 18. Real-life datasets: It can be seen that GWO-FCM and FA-FCM have better performance than OGWO-FCM on only two datasets (Liver Disorders and New thyroid) in terms of Minkowski score (MS). It is worth noting that that elongated shape and spatially well-separated clusters, which occur in the Liver Disorders and New thyroid datasets. This is the reason why this algorithm shows a good performance on Liver Disorders and New thyroid datasets. However, OGWO-FCM has obtained the second best values of MS, beating the other algorithms on these datasets. But our OGWO-FCM-based method has achieved better performance than other four methods on Iris, Breast cancer, and Wine datasets. Particularly, from the box plot (Fig. 18), for Iris dataset, the average performance obtained by OGWO-FCM is best followed by PSO-FCM, FA-FCM, VAMOSA (Saha and Bandyopadhyay 2010) and GWO-FCM. Artificial datasets: From Table 3, it is worth noting that, the high values of MS are shown for PSO-FCM, FA-FCM, VAMOSA (Saha and Bandyopadhyay 2010) and GWO-FCM while dealing with different clustering problems. In contrast, the results obtained by OGWO-FCM highlight that this method shows a more robust behavior, in comparison with PSO-FCM, FA-FCM, VAMOSA (Saha and Bandyopadhyay 2010) and GWO-FCM. Particularly, from box plot (Fig. 17) the average performance achieved by OGWO-FCM is lower and spread is better compared to the counterpart algorithms for AD_ 5_ 2 dataset.

Table 4 Mean and Standard deviation of misclassification percentages of five clustering algorithms such as OGWO-FCM, PSO-FCM, FA-FCM, VAMOSA (Saha and Bandyopadhyay 2010) and GWO-FCM executed on 10 artificial and real-life datasets

Table 5 Comparison table of proposed approach against four other existing approaches in terms of Minkowski score (MS)

6.3.1 Comparison results with CEP measure

To evaluate further, we use the Clustering Error Percentage (CEP) measure, which is the percentage of misclassification over the test dataset. The CEP is calculated as follows: Initially, the test data set is clustered and the number of misclassification is counted. This is possible because, in the test dataset, we know the actual class label of each data instance. After that, this number is divided by a total number of instances in the test set, and finally, to achieve percentage it is multiplied by 100.

$$\begin{aligned} \mathrm{CEP}=\frac{\hbox {Number of misclustered instances }}{\hbox {Total size of test dataset}}\times 100 \end{aligned}$$

(18)

Table 4 illustrates that opposition GWO outperforms the PSO algorithm in all datasets and overcomes firefly algorithm (FA) in nine datasets. On another hand, in the case of one dataset (wine), opposition GWO and GWO get the same results. In addition, opposition GWO obtained acceptable results in comparison with GWO; just the case of the datasets Wine, Thyroid and AD_ 10_ 2, GWO obtains the better results. Furthermore, the average CEP for all datasets is 5.111 for opposition GWO, 6.513 for GWO, 7.547 for FA, and 9.267 for PSO algorithm. The proposed approach of opposition GWO-based clustering algorithm is ranked in the first place among five approaches.

6.3.2 Comparison results with MS measure

Table 5 shows that the valuation results with Minkowski score measure for ten datasets.

• 1. The MS value of the AD_ 10_ 2 dataset illustrates that OGWO-FCM achieves the best separation over other four algorithms.

• 2. For the AD_ 5_ 2 dataset, OGWO-FCM and VAMOSA (Saha and Bandyopadhyay 2010) provide the minimum MS value which demonstrates the best separation. Both OGWO-FCM and VAMOSA (Saha and Bandyopadhyay 2010) can detect the appropriate number of clusters, but PSO-FCM and FA-SVM fail to do so.

• 3. From the Square1 dataset, OGWO-FCM obtains the minimum MS value. OGWO-FCM and VAMOSA are able to determine the correct number of clusters, whereas OGWO-FCM overestimates and PSO-FCM underestimates the number of clusters.

• 4. Regarding the MS result from the Square4 dataset, all five approaches are able to determine the appropriate number of clusters.

• 5. For the Sizes5 dataset, OGWO-FCM presents the minimum MS value. All techniques except FA-FCM can determine the correct number of clusters. PSO-FCM provides the highest MS value, which means poor separation is obtained.

• 6. With respect to the first real-life data, the best result of separation the Iris dataset is obtained by OGWO-FCM with the minimum value of MS.

• 7. Regarding the Breast Cancer dataset, all five algorithms are able to find out the appropriate number of clusters, but the minimum value of MS is obtained by OGWO-FCM.

• 8. Regarding the Wine dataset, OGWO-FCM obtains the minimum MS value; however, all five algorithms are able to find out the appropriate number of clusters.

• 9. From the Newthyroid dataset, FA-FCM and GWO-FCM provide the minimum MS value. However, all five algorithms are able to find out the appropriate number of clusters.

• 10. The result from the Liver Disorders dataset demonstrates the best separation from VAMOSA which gains the minimum MS value. The MS value of VAMOSA (Saha and Bandyopadhyay 2010) is slightly better than that of OGWO-FCM and GWO-FCM. However, both GWO-FCM, OGWO-FCM and VAMOSA are able to detect the proper number of clusters.

Time complexity:

The OGWO-FCM has a worst-case $O\left( {GPNk_{\max } d} \right)$ time complexity, where G represents the number of generations, P is the population size, N is the size of data, $k_{\max }$ is maximum number of clusters and d is the data dimensions.

• 1. In an initial population, strings are created $k_{\max } d$ time and each string is created in d-dimensional features until the population size P is full. Therefore, this construction requires $O\left( {Pk_{\max } d} \right)$.

• 2. In FCM clustering for each individual, both procedures of membership assignment and updating of center values take $Nk_{\max } d$ time. This requires $O\left( {PNk_{\max } d} \right)$ for all individuals in the population.

• 3. The first fitness assignment of the overlap–partition objective needs $k_{\max } \log (k_{\max } )$ to sort membership degrees of all clusters. $Nk_{\max } \log (k_{\max } )$ time is executed for all data points. In another fitness assignment of $J_m$ index, $Nk_{\max } d$ is required to compute distance from data points to cluster centers. The overlap–partition and $J_m$ index take $O\left( {PNk_{\max } \log (k_{\max } )} \right)$ and $O\left( {PNk_{\max } d} \right)$, respectively.

• 4. OGWO operators executes $O\left( {Pk_{\max } d} \right)$ time each.

• 5. The non-dominated sorting in OGWO needs MP time for each solution to compare with every other solution to find if it is dominated. M is the number of objectives and a maximum number of the non-dominated solutions equal the population size P. The comparison for all population members therefore requires $O\left( {MP^{2}} \right)$ time, where $M=2$.

• 6) In the label assignment for each non-dominated solution, $Nk_{\max } d$ time is required to assign label for every data point. To select the best solution from P non-dominated solutions, this yields $O\left( {PNk_{\max } d} \right)$ time.

The computation is dominated by the operations of FCM and fitness assignment of $J_m$ index. This worst-case time complexity is $O\left( {PNk_{\max } d} \right)$ per generation. It therefore becomes $O\left( {GPNk_{\max } d} \right)$ for G number of generations.

7 Conclusion

In this paper, the OGWO-FCM approach has been proposed using multi-objective-based opposition grey wolf optimizer and fuzzy c-means clustering algorithms to solve the data clustering problem. An efficient opposition grey wolf optimizer was used to control the multi-objective optimization considering two criteria: compactness and overlap–partition (OP). The algorithm optimized simultaneously these two criteria to search the optimal clustering solutions. A string of real-coded values was encoded to represent cluster centers. Moreover, in the proposed clustering approach, the concept of opposition-based generation jumping and opposition-based population initialization was used with the standard GWO to enhance its computational speed and convergence profile. At last, the algorithm produced a set of optimal solutions. The final solution was chosen from this set by a semi-supervised method with the FCM concept for label assignment. The effectiveness of the proposed approach was evaluated for five real-life datasets and five artificial datasets of varying complexities. Its performance was compared with firefly algorithm (FA), particle swarm optimization (PSO) and basic grey wolf optimizer (GWO). These benefits of the proposed approach increase their attractiveness for use in real-world applications in comparison with other optimization-based fuzzy clustering approaches.

Additionally, the proposed system has a shortcoming regarding the performance of the opposition GWO; because GWO has some randomly choosing control elements such as $r_1 ,r_2$, the static controlling elements may lead to the local minima problems. This is an interesting issue and would be worth in a future research. The future scope is to implement a hybrid algorithm to resolve these inadequacies in future.