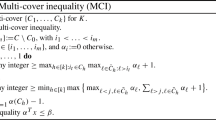Optimization algorithms for the disjunctively constrained knapsack problem

Abstract

This paper deals with the Knapsack Problem with conflicts, also known as the Disjunctively Constrained Knapsack Problem. The conflicts are represented by a graph whose vertices are the items such that adjacent items cannot be packed in the knapsack simultaneously. We consider a classical formulation for the problem, study the polytope associated with this formulation and investigate the facial aspect of its basic constraints. We then present new families of valid inequalities and describe necessary and sufficient conditions for these inequalities to be facet defining. We also devise separation routines for these inequalities. Using these results, we develop a Branch-and-Cut algorithm for the problem. An extensive computational study is also presented.

1 Introduction

In this paper, we consider a variant of the 0–1 Knapsack Problem, where some items are incompatible with others, and cannot then be packed simultaneously in the knapsack. We are given a knapsack of capacity c, a set $V=\{1,2,\ldots ,n\}$ of items, and a graph of conflicts between some items $G=(V,E)$. For each edge $(i,j) \in E$, items i and j are incompatible. With each item $i \in V$ is associated a nonnegative profit $p_i$ and a nonnegative weight $w_i$. The Disjunctively Constrained Knapsack Problem (DCKP) consists in determining a maximum-profit set of compatible items to be packed in the knapsack.

The DCKP is an NP-hard combinatorial optimization problem since it is a combination of two NP-hard combinatorial optimization problems. Indeed, when no conflicts between items exist (i.e., $E=\emptyset$), the problem reduces to a 0–1 Knapsack Problem (0–1 KP) which is known to be NP-hard Martello and Toth (1990). When the knapsack constraint is omitted, the problem is the maximum independent set which is known to be NP-hard as well Garey and Johnson (1979). For some special classes of conflict graphs, the problem becomes easier. For example, in Pferschy and Schauer (2009), Pferschy and Schauer present pseudo-polynomial algorithms to solve the DCKP for two special classes of graphs, namely graphs of bounded tree-width and chordal graphs.

The DCKP is relatively a recent variant of the Knapsack Problem that has been firstly introduced by Yamada et al. (2002). Yamada et al. (2002) present a heuristic method as well as an implicit enumeration algorithm together with an interval reduction method in order to solve the DCKP to optimality.

Later, more focus has been given to the problem. Heuristic and exact resolution approaches have been proposed. Senisuka et al. (2005) present an exact algorithm to solve the DCKP. The algorithm combines Lagrangian relaxation techniques with the pegging test for ordinary knapsacks which helps reducing significantly the problem size. The approach proves to be efficient in solving huge instances of the DCKP in a reasonable time of computation. In parallel, Hifi and Michrafy (2007) propose several versions of an exact algorithm for the DCKP, based on a reduction procedure combined with a Branch-and-Bound algorithm. A further exact approach has been proposed by Bettinelli et al. (2014) who present an efficient Branch-and-Bound algorithm using a combination of several upper bounding procedures as well as a variety of branching strategies.

Along with the exact methods and due to the difficulty of the problem, many heuristic methods have been proposed in the literature. These have, in general, provided good results in a reasonable amount of time. Different meta-heuristics have been, in this context, used to solve efficiently the DCKP. These include local branching algorithms Hifi et al. (2009); Akeb et al. (2011), a version of Scatter Search Hifi and Otmani (2011), a parallel large neighborhood search-based heuristic Hifi et al. (2014), and recently a guided neighborhood search Hifi et al. (2015).

In some cases, the DCKP appears as a subproblem of a more general one. Sadykov and Vanderbeck (2013) propose a Branch-and-Price algorithm to solve the Bin Packing Problem with conflicts and prove that the associated pricing subproblem is nothing but a DCKP. The authors propose a dynamic programming algorithm for the DCKP when the conflict graph is an interval graph. They develop a Depth-First-Search Branch-and-Bound approach when the conflict graph has no special structure.

To the best of our knowledge, our work constitutes the first contribution considering the polyhedral aspect of the DCKP. The only works presenting close polyhedral studies are those dealing with the 0–1 knapsack polyhedron (see Balas 1975; Balas and Zemel 1978; Weismantel 1997), and polyhedra related to some variants of the Knapsack Problem (see Atamtürk and Narayanan 2009; Boyd 1993; Farias Jr and Nemhauser 2003; Hanafi and Glover 2007; Zeng and Richard 2011), along with the ones dealing with the independent set polyhedron Nemhauser and Trotter (1974).

This paper is organized as follows. In the next section, we state the classical Integer Linear Programming (ILP) formulation used in the literature to model the DCKP and we define the associated polytope and study the facial aspect of the basic constraints. In Sect. 3, we describe some valid inequalities and give necessary conditions and sufficient conditions for these inequalities to be facet defining. In Sect. 4, we devise separation algorithms for these inequalities and describe our Branch-and-Cut algorithm. In Sect. 5, we present an extensive computational study. Some concluding remarks and indications for future work are given in Sect. 6.

2 Formulation and polyhedral analysis

A natural and compact Integer Linear Programming formulation for the DCKP makes use of a set of binary variables $x_i$ associated with items $i \in V$, taking value 1 if item i is packed in the knapsack, and 0 otherwise. The DCKP is equivalent to the following program:

$$\begin{aligned}&\max \sum _{i \in V}p_{i}x_{i} \end{aligned}$$

(1)

$$\begin{aligned}&\sum _{i \in V}w_{i}x_{i} \le c \end{aligned}$$

(2)

$$\begin{aligned}&x_i+x_j \le 1 \quad {\text { for all }}\; e=(i,j) \in E \end{aligned}$$

(3)

$$\begin{aligned}&0 \le x_{i} \le 1 \quad {\text { for all }}\; i \in V, \end{aligned}$$

(4)

$$\begin{aligned}&x_{i} \in \{0,1\} \quad {\text { for all }}\; i \in V, \end{aligned}$$

(5)

where (1) denotes the objective function, (2) represents the knapsack capacity constraint inequality, (3) are the disjunctive constraint inequalities, and (4) and (5) are the trivial and integrality constraints, respectively.

In the sequel, and w.l.o.g., we will assume that the set of edges E is composed of two subsets $E_d$ and $E_c$, i.e., $E= E_d \cup E_c$, where $E_d$ is the set of edges representing conflicts due to the disjunction constraints (3), and $E_c$ is the set of edges representing conflicts due to the capacity constraint (2). In other words, for all $e=(i,j) \in E_c$, $w_i + w_j > c$, that is i and j form a cover.

We will also assume that $w_i \le c$ for all $i \in V$, that is any single item induces a solution for the problem.

Denote by DCKP(G) the polytope associated with the DCKP, that is the convex hull of the incidence vectors of all its solutions, i.e.,

$$\begin{aligned} {\text {DCKP}}(G)=\hbox {conv} \Bigl \{ x \in \{ 0,1\}^n\, :\, x\; {\text {satisfies}}\; (2){-}(5) \Bigr \}. \end{aligned}$$

A solution $S \subseteq V$ of DCKP will be represented by the set of items retained to be packed in the knapsack and that are not in conflict. That is to say, the incidence vector of S, $x^S$ is such that $x^S_i=1$ if $i \in S$ and $x^S_i=0$ otherwise, satisfies the DCKP constraints.

We first state the following preliminary result.

Theorem 1

DCKP(G) is full dimensional.

Proof

Consider the solutions of DCKP $S_0,S_1, \dots , S_{n}$ defined as follows, $S_0=\emptyset$, $S_i=\{i\}$, for all $i \in V$. Clearly $x^{S_0}, x^{S_1}, \dots , x^{S_{n}}$ are $n+1$ affinely independent points of DCKP(G). Consequently, ${\text {dim}}({\text {DCKP}}(G))=n$. $\square$

Having established the dimension of DCKP(G), next, we will characterize when the trivial and disjunctive inequalities define facets.

Theorem 2

$x_k \ge 0$ defines a facet of DCKP(G).

Proof

Let $S_0=\emptyset$, and for all $i \in V \setminus \{k\}$, $S_i=\{i\}$. These constitute $n=\vert V \vert$ solutions of DCKP whose incidence vectors satisfy $x_k=0$ and are affinely independent. $\square$

Theorem 3

$x_k \le 1$ defines a facet of DCKP(G) if and only if for all $i \in V \setminus \{k\}$, $(i,k) \notin E$.

Proof

Assume that there is an item $i_0 \in V$ such that $(i_0,k) \in E$, i.e., $x_k+x_{i_0} \le 1$. Since this inequality dominates $x_k \le 1$, the latter cannot be facet defining.

Now, suppose that $(i,k) \notin E$ for all $i \in V \setminus \{k\}$. Consider the solutions $S_1, \dots , S_k, \dots ,S_n$ of DCKP defined by $S_k=\{k\}$, and for all $i \in V \setminus \{k\}$, $S_i=\{i,k\}$. These form n solutions of DCKP whose incidence vectors satisfy $x_k=1$ and are affinely independent. $\square$

Theorem 4

For $(k,m) \in E$, $x_k+x_m \le 1$ defines a facet of DCKP(G) if and only if for all $i \in V \setminus \{k,m\}$, i is not in conflict with at least one of the two items k and m.

Proof

Assume that there exists an item $i^* \in V$ in conflict with both k and m. In this case, we can pack in the knapsack at most one item among k, m and $i^*$. This implies that the inequality $x_k+x_m+x_{i^*} \le 1$ is satisfied by every solution of the problem. Since this inequality dominates $x_k+x_m \le 1$, the latter cannot define a facet.

Assume now that for all $i \in V \setminus \{k,m\}$, i is not in conflict with at least one of the items k and m. Let $U_{k,m}=\{ i \in V \setminus \{k,m\} : (i,k) \notin E$, and, $(i,m) \notin E\}$ be the set of items that are not in conflict neither with k nor with m. Let $U_k=\{ i \in V \setminus \{k,m\} : (i,k) \notin E$, and, $(i,m) \in E \}$ be the set of items that are not in conflict with k but in conflict with m, and $U_m=\{ i \in V \setminus \{k,m\} :(i,m) \notin E$, and, $(i,k) \in E\}$ the set of items that are not in conflict with m but in conflict with k.

Consider the solutions $S_k=\{k\}$, $S_m=\{m\}$, $S_i=\{k,i\}$ for all $i \in U_k \cup U_{k,m}$, $S_j=\{m,j\}$ for all $j \in U_m$. Clearly, these sets constitute a family of n solutions of the problem, whose incidence vectors satisfy the equation $x_k+x_m = 1$. Moreover, as illustrated in Fig. 1, these vectors are affinely independent.$\square$

Fig. 1

Solutions incidence matrix

Along with the basic constraints of the formulation, we have identified new families of valid inequalities for DCKP(G). These will be presented in the next section.

3 Valid inequalities

As mentioned previously, the DCKP can be seen as a combination of two classical problems, namely the knapsack and the independent set problems. Therefore, valid inequalities for these problems have helped us to determine families of valid inequalities for the DCKP.

3.1 Clique inequalities

Given a graph $G=(V,E)$, a clique of G is a subset of vertices $K \subset V$ such that every two distinct vertices are adjacent.

A clique is said to be maximal if it is not strictly contained in another clique.

If K is a clique of G, then all the vertices of K are pairwise in conflict. This implies that one can pack at most one element from K in the knapsack; therefore, the following inequality is valid for DCKP(G).

$$\begin{aligned} \sum \limits _{i \in K} x_i \le 1. \end{aligned}$$

(6)

Theorem 5

Inequality (6) defines a facet of DCKP(G) if and only if K is maximal.

Proof

If K is not maximal, then there is an element $j\in V\backslash K$ such that $K'=K\cup \{j\}$ is a clique. Therefore, $\sum \nolimits _{i\in K'} x_i=\sum \nolimits _{i\in K} x_i+x_j\le 1$ is valid for DCKP(G). Since this inequality dominates (6), the latter cannot define a facet.

Now suppose K is maximal. Then for every item $j\in V\backslash K$, there is an item $j'\in K$ such that $(j,j')\notin E$. Consider the sets $S_i=\{i\}$ for all $i \in K$, and $S_j=\{j,j'\}$ for all $j \in V \setminus K$, where $j' \in K$ is an item of K not adjacent to j. It is clear that these sets are solutions of the DCKP. Moreover, their incidence vectors satisfy (6) with equality and are affinely independent. $\square$

3.2 Cover inequalities

A cover for the DCKP is a set C of items such that $\sum \nolimits _{i\in C} w_i> c$. Clearly, a cover cannot be packed in the knapsack. Hence, the following inequalities are valid for the DCKP(G)

$$\begin{aligned} \sum \limits _{i\in C} x_i\le |C|-1 ~ ~~{\text {for all}} ~ C \in {\mathscr {C}} \end{aligned}$$

(7)

where ${\mathscr {C}}$ is the set of the covers of the DCKP instance. Inequalities (7) will be called cover inequalities.

A cover C is called minimal if

$$\begin{aligned} \sum \limits _{i\in C\backslash \{j\}} w_i\le c ~ ~~{\text {for all}} ~ j\in C. \end{aligned}$$

The following theorem characterizes the covers that may induce facets for DCKP(G). For this, note that if a cover is not minimal, then it contains a proper subset which is a cover. Moreover, this set may consist of two elements i, j such that $(i,j)\in E$, that is to say i and j are either in conflict or form a cover.

Theorem 6

A cover inequality (7), induced by a cover C, defines a facet for DCKP(G) if and only if

• (1) C is minimal,

• (2) for all $j\in V\backslash C$, $w_j < w_{j^*}=max\{w_j:j\in C\}$,

• (3) every item $j\in V\backslash C$ is not in conflict with more than one item of C, and if j is in conflict with item $j'$ of C, then $(C\backslash \{j'\})\cup \{j\}$ is not a cover.

Proof

Necessity

• (1) If C is not minimal, then a proper subset $\widetilde{C}$ of C is a cover. Hence,

  $$\begin{aligned} \sum \limits _{i\in \widetilde{C}} x_i\le |\widetilde{C}|-1 \end{aligned}$$

  (8)

  is valid for DCKP(G). By summing inequality (8) together with $x_i\le 1$ for all $i\in C\backslash \widetilde{C}$, we obtain (7). Since $C\backslash \widetilde{C}\ne \emptyset$, inequality (7) is a linear combination of valid inequalities and thus it cannot define a facet.

• (2) If there exists an item $j\in V\backslash C$ such that $w_j\ge w_{j^*}$, then the inequality

  $$\begin{aligned} \sum \limits _{i\in C} x_i +x_j\le |C|-1 \end{aligned}$$

  (9)

  is also valid for DCKP(G). In fact, item j cannot be packed with $|C|-1$ items of C. However, inequality (7) is redundant with respect to (9) and $x_j\ge 0$. It cannot, therefore, define a facet.

• (3) If an item j of $V\backslash C$ is in conflict with two items $i_1$, $i_2$ of C, then any solution of DCKP containing j cannot contain more than $|C|-2$ elements from C. Hence, its incidence vector cannot satisfy inequality (7) with equality. This implies that inequality (7) is equivalent to $x_j\ge 0$. Since (7) is not a positive multiple of $x_j\ge 0$, it cannot be facet defining. Also, if an item j of $V\setminus C$ is in conflict with an item $j'$ and $(C\setminus \{j'\})\cup \{j\}$ is a cover, then it follows, along the same way, that inequality (7) is equivalent to $x_j\ge 0$ and cannot hence define a facet.

Sufficiency

Suppose that Conditions $(1)--(3)$ are all satisfied. Let $ax\le \alpha$ denote inequality (7), and let us suppose there is a facet defining inequality $bx\le \beta$ of DCKP(G) such that $\{x\in$ DCKP(G) $~|~ ax=\alpha \}\subseteq \{x\in$ DCKP(G)$~|~bx=\beta \}$. We will show that $b=\rho a$.

By (1), it follows that any set $Q\subset C$ such that $|Q|=|C|-1$ is a solution of DCKP. Let $i,j\in C$, and consider the solutions

$$\begin{aligned} S_1=C\backslash \{i\},~ S_2=C\backslash \{j\}. \end{aligned}$$

As $ax^{S_1}=ax^{S_2}=\alpha$, we have that $bx^{S_1}=bx^{S_2}$. This yields $b_i=b_j$. As i and j are arbitrary in C, it follows that all the $b_i$’s are the same in C, and thus

$$\begin{aligned} b_i=\rho ~ {\text {for all}} ~ i\in C \quad {\text {for some}} ~ \rho \in {\mathbb {R}}. \end{aligned}$$

(10)

Now let $j\in V\backslash C$. By (2) we have that $w_j<w_{j^*}$, and by 3) j is in conflict with at most one element of C. Suppose, for instance, that j is in conflict with an element, say $j'$, of C. Consider the set $S=(C\backslash \{j'\})\cup \{j\}$. By 3), S is a solution of DCKP. Moreover, we have that $ax^S=\alpha$, and hence $bx^S=\beta$. As $S\backslash \{j\}=C\backslash \{j'\}$ is also a solution of the problem and $ax^{S\backslash \{j\}}=\alpha$, we have $bx^{S\backslash \{j\}}=\beta$. But this implies that $b_j=bx^S-bx^{S\backslash \{j\}}=0$. If j is not in conflict with any item of C, as by (2), $w_j < w_{j^*}$, $(C\backslash \{j^*\})\cup \{j\}$ is a solution of DCKP. And, similarly, it follows that $b_j=0$. Thus, we obtain that $b_j=0$ for all $j\in V\backslash C$. This together with (10) yields $b=\rho a$, and the proof is complete. $\square$

Balas (1975), Hammer et al. (1975) and Wolsey (1975) observed that when C is minimal the cover inequalities (7) are the strongest. Balas (1975) proposes a way to strengthen the cover inequalities. Let $w^*=\max \limits _{j \in C} w_j$, and consider the extension $E(C)=C \cup \{ j\in V \setminus C : w_j \ge w^* \}$. Then, a valid inequality for the DCKP(G) called the Extended Cover Inequality (ECI) is given by

$$\begin{aligned} \sum \limits _{j \in E(C)} x_j \le \vert C \vert -1. \end{aligned}$$

(11)

Balas (1975) and Wolsey (1975) also showed that, given a minimal cover C, there exists at least one facet defining Lifted Cover Inequality having the following form:

$$\begin{aligned} \sum \limits _{j \in C} x_j + \sum \limits _{j \in V \setminus C} \alpha _j x_j \le \vert C \vert -1, \end{aligned}$$

(12)

where $\alpha _j \ge 0$ for all $j \in V \setminus C$.

Inequalities (12) can be obtained by a sequential lifting from inequalities (11). This means that the lifting coefficients $\alpha _j, \, j \in V{\setminus }C$, are computed one by one in a given order. Suppose that $V{\setminus }C = \{j_1,\dots ,j_t \}$, and that $\alpha _{j_1},\dots ,\alpha _{j_{t-1}}$ are computed, that is to say the inequality $\sum \nolimits _{j \in C} x_j + \sum \nolimits _{i=1}^{t-1} \alpha _{j_i} x_{j_i} \le \vert C \vert -1$ is valid for KP. In order to determine coefficient $\alpha _{j_{t}}$, one can compute $\alpha _0 = \max \{ \sum \nolimits _{j \in C} x_j + \sum \nolimits _{i=1}^{t-1} \alpha _{j_i} x_{j_i} \, : x \, {\text {solution of KP}}, x_{j_{t}}=1 \}$, and set $\alpha _{j_{t}} = \vert C \vert -1-\alpha _0$. The coefficients $\alpha _{j_{i}}, \, i=1,\dots ,t$ depend on the order in which they are computed.

As it appears, the computation of each coefficient $\alpha _j$ requires the resolution of a KP. Zemel (1989) showed that given a fixed cover C and a fixed sequence of lifting, the lifting coefficients can be computed in O(n|C|).

Gu et al. (1998) referred to inequalities (12) as Simple Lifted Cover Inequality. This has been later generalized by Van Roy and Wolsey (1987) who derived the General Lifted Cover Inequality of the form

$$\begin{aligned} \sum \limits _{j \in C \setminus D} x_j + \sum \limits _{j \in V \setminus C} \alpha _j x_j + \sum \limits _{j \in D} \beta _j x_j \le \vert C \setminus D \vert + \sum \limits _{j \in D} \beta _j -1, \end{aligned}$$

(13)

where C is a cover, $D \subset C$, $\alpha _j \ge 0$ for all $j \in V{\setminus }C$, and $\beta _j \ge 0$ for all $j \in D$.

As for inequalities (12), inequalities (13) can be obtained from (11) by a sequential lifting. For more details on lifting techniques in combinatorial optimization, one can refer to Wolsey and Nemhauser (1999).

We will follow Gu et al. (1998) in referring to the computation of the lifting coefficients $\alpha$ and $\beta$ as up-lifting and down-lifting, respectively.

3.3 Odd-cycle and hypercycle inequalities

A cycle in a graph is a sequence $v_1, e_1, v_2, \ldots , v_k, e_k, v_1$ of nodes and edges such that $e_i=(v_i,v_{i+1})$, $i=1, \ldots , k-1$ and $e_k=(v_k,v_1)$. We will also denote a cycle C by its sequence of nodes and write $C=(v_1, \ldots , v_k)$. A cycle of k nodes is said of length k. A cycle is said to be even (odd) if its length is even (odd). A chord of a cycle is an edge joining two non-consecutive nodes of the cycle. A cycle is called simple if its nodes $v_1, \ldots , v_k$ are all different.

Odd cycles induce valid inequalities for the independent set problem and hence for the DCKP(G). Consider a cycle C of G where nodes are $1, \ldots , k$ with k odd. Then the inequalities

$$\begin{aligned} x_i+x_{i+1}\le 1, \quad {\text {for all}} \quad i=1, \ldots , k, \end{aligned}$$

where the indices are taken modulo k, are valid for DCKP(G). By summing these inequalities, dividing by 2 and rounding down the right-hand side, we obtain the inequality

$$\begin{aligned} \sum \limits _{i\in C} x_i\le \frac{k-1}{2}, \end{aligned}$$

(14)

which is valid for DCKP(G). Inequalities of type (14) are called Odd-Cycle Inequalities. Inequalities (14) may define facets for DCKP(G). A necessary condition for inequality (14) to be facet defining is that the cycle C does not contain a chord. If C contains a chord ($i_0 , j_0$), $i_0<j_0$, then one of the cycles $C_1=(1, \ldots i_0, j_0, \ldots , k)$ and $C_2=(i_0, \ldots , j_0)$, say $C_1$, is odd. It is not hard to see that (14) can be obtained as a linear combination of the odd-cycle inequality induced by $C_1$ and the disjunctive inequalities $x_{i_0+l}+x_{i_0+l+1}\le 1$, $l=1, \ldots , j_0-2$. Inequalities (14) can be strengthened by the so-called lifted odd-cycle inequalities to be facet defining for the independent set polytope Nemhauser and Trotter (1974) and the DCKP(G) as well.

In what follows, we are going to introduce a more general class of valid inequalities for the DCKP(G). For this, let us first give an example.

Consider the DCKP given by the system

$$\begin{aligned} (P_1)\left\{ \begin{array}{lll} &{} 5x_1+4x_2+3x_3+5x_4+2x_5\le 11, \\ &{} x_1+x_4\le 1, \\ &{} x_4+x_5\le 1. \\ \end{array} \right. \end{aligned}$$

Observe that $C_1=\{1,2,3\}$ and $C_2=\{2,3,4\}$ are covers. Thus, the following inequalities are valid for DCKP(G),

$$\begin{aligned} x_1+x_2+x_3\le & {} 2, \\ x_2+x_3+x_4\le & {} 2. \end{aligned}$$

By summing these inequalities together with $x_1+x_4\le 1$, we obtain the inequality $2(x_1+x_2+x_3+x_4)\le 5$. By dividing by 2 and rounding down the right-hand side, we obtain that

$$\begin{aligned} x_1+x_2+x_3+x_4\le 2 \end{aligned}$$

(15)

is valid for DCKP(G). Moreover, (15) defines a facet. In fact, it is easy to see that the sets $S_1=\{1,2\}$, $S_2=\{1,3\}$, $S_3=\{2,3\}$, $S_4=\{3,4\}$, $S_5=\{3,4,5\}$ are solutions of the problem. Moreover, their incidence vectors satisfy (15) with equality and are affinely independent.

In what follows, we are going to show this as a special case of a more general class of facets. This will be presented within the framework of hypergraphs. Given a finite set $V=\{v_1, \ldots , v_n\}$, a hypergraph H on V is a family ${\mathscr {E}}=\{E_1, E_2, \ldots , E_m\}$ of subsets of V such that

$$\begin{aligned}&E_i\ne \emptyset \quad {\text {for}} ~ i=1, \ldots , m, \\&\quad \bigcup \limits _{i=1}^m E_i=V. \end{aligned}$$

The elements $v_1, \ldots , v_n$ of V are called nodes, and the sets $E_1, \ldots , E_m$ are called hyperedges. A hypergraph $H=(V,{\mathscr {E}})$ is said to be simple if no hyperedge is strictly contained in another hyperedge, that is to say $E_i\not \subset E_j$ for all $E_i, E_j\in {\mathscr {E}}$. A graph without loops is a hypergraph where each hyperedge consists of exactly two nodes. Given a hypergraph $H=(V,{\mathscr {E}})$, a hypercycle is a sequence $(v_1, E_1, v_2, \ldots , v_k, E_k, v_1)$ with $\{v_i, v_{i+1}\} \subseteq E_i$, for $i=1, \ldots , k$, where the indices are modulo k. Note that the $E_i$’s may not be all different. Also note that the $E_i$’s may contain nodes different from $v_1, \ldots , v_k$. A cycle in a graph corresponds to the case where $|E_i|=2$ for $i=1, \ldots , k$. Now consider the DCKP along with the corresponding conflict graph $G=(V,E)$, and let us associate with it the hypergraph $H=(V,{\mathscr {E}})$ where ${\mathscr {E}}$ is the set of minimal covers of the problem together with the sets $\{i,j\}$ such that $(i,j)\in E$, i.e., i and j are in conflict. Also as a cover, which contains two items in conflict may be considered as a non-minimal cover, we will suppose w.l.o.g., that no hyperedge strictly contains an edge of E. In other words, the hyperedges will correspond to the covers C such that $C\backslash \{i\}$ is a solution of DCKP(G) for all $i\in C$. The hypergraph $H=(V,{\mathscr {E}})$, associated with problem $(P_1)$ above, is depicted in Fig. 2. Here $V=\{1, 2, 3, 4, 5\}$ and ${\mathscr {E}}$ contains the hyperedges $E_1=\{1, 2, 3\}$, $E_2=\{2, 3, 4\}$, $E_3=\{1, 4\}$, and $E_4=\{4, 5\}$.

Fig. 2

The hypergraph associated with $(P_1)$

Now consider a hypercycle of $H=(V,{\mathscr {E}})$ whose hyperedges are $E_1, \ldots , E_k$. Let $W=\bigcup \nolimits _{i=1}^k E_i$. Let $W'\subseteq W$ be a subset of W such that every node of $W'$ appears in exactly q hyperedges among $E_1, \ldots , E_k$. For every $j\in W\backslash W'$ let $\rho _j$ be the number of hyperedges, among $E_1, \ldots , E_k$, to which j belongs.

Suppose that $\rho _j<q$ for all $j\in W\backslash W'$ and $\sum \limits _{i=1}^k (|E_i|-1)+ \sum \limits _{j\in W\backslash W'} (q-\rho _j)$ is not a multiple of q. Now consider the following valid cover inequalities

$$\begin{aligned} \sum _{j\in E_i} x_j\le & {} |E_i|-1 \quad {\text {for all}}~ i=1, \ldots , k,\\ (q-\rho _j)x_j\le & {} q-\rho _j \quad {\text {for all}}~ j\in W\backslash W'. \end{aligned}$$

By summing these inequalities, we obtain the inequality

$$\begin{aligned} q\left( \sum \limits _{i\in W} x_i\right) \le \sum \limits _{i=1}^k (|E_i|-1)+\sum \limits _{j\in W\backslash W'} (q-\rho _j). \end{aligned}$$

As the right-hand side of the above inequality is not a multiple of q, by dividing by q and rounding down the right-hand side of the resulting inequality, we obtain the following valid inequality

$$\begin{aligned} \sum \limits _{i\in W} x_i\le \left\lfloor { \displaystyle \frac{\sum \limits _{i=1}^k |E_i|+\sum \limits _{j\in W\backslash W'} (q-\rho _j)-k}{q} } \right\rfloor . \end{aligned}$$

(16)

Since each node of $W'$ is in q $E_i$’s and each node j of $W\backslash W'$ is in $\rho _j$ $E_i$’s, we have that $\sum \nolimits _{i=1}^k |E_i|+\sum \nolimits _{j\in W\backslash W'} (q-\rho _j)=q|W|$.

Hence, inequality (16) can be written as

$$\begin{aligned} \sum \limits _{i\in W} x_i\le |W|- \left\lceil { \displaystyle \frac{k}{q} } \right\rceil . \end{aligned}$$

(17)

Inequalities of type (17) will be called Hypercycle Inequalities.

Remark 1

Any solution T of DCKP whose incidence vector satisfies (17) with equality is such that $|W\backslash T|=\left\lceil { \displaystyle \frac{k}{q}} \right\rceil$ and $W\backslash T$ covers ${\mathscr {E}}=\{E_1, \ldots , E_k\}$. Otherwise, one of the covers would be included in $W\cap T$, which is not possible.

In order to illustrate the hypercycle inequalities, consider the problem $(P_1)$ given above. Consider the hypercycle $(1,E_1,3,E_2,4,E_3,1)$ whose hyperedges are $E_1=\{1,2,3\}$, $E_2=\{2,3,4\}$, $E_3=\{1,4\}$. Observe that every node i of $E_1\cup E_2\cup E_3$ belongs to exactly two sets among $E_1$, $E_2$, $E_3$. So here $W=\{1,2,3,4\}$, $k=3$, $q=2$ and $W'=W$. The corresponding hypercycle inequality (16) is nothing but inequality (15).

Now suppose that in $(P_1)$, items 2 and 4 are also in conflict. Thus, $E_2=\{2,3,4\}$ is no more hyperedge of the associated hypergraph and must then be replaced by $E'_2=\{2,4\}$. Consider the hypercycle whose hyperedges are $E_1$, $E'_2$, $E_3$. Here we have $W=\{1,2,3,4\}$, $k=3$, $q=2$, $W'=\{1,2,4\}$, $\rho =1$. We still obtain inequality (15).

Observe that inequality (15) is an extended cover inequality obtained from cover $\{1,2,3\}$. However, the hypercycle inequalities may be different from the extended and lifted cover inequalities as shown in the following example. Consider the problem

$$\begin{aligned} (P_2)\,\left\{ \begin{array}{lll} &{} x_1+4x_2+3x_3+x_4+x_5+x_6+x_7\le 7, \\ &{} x_4+x_5\le 1, \\ &{} x_4+x_6\le 1, \\ &{} x_1+x_5\le 1, \\ &{} x_1+x_6\le 1. \\ \end{array} \right. \end{aligned}$$

Clearly, the sets $E_1=\{1,2,3\}$, $E_2=\{2,3,4\}$, $E_3=\{2,3,5\}$ are minimal covers for $(P_2)$. Consider the hypercycle in the related hypergraph, induced by the hyperedges $E_1$, $E_2$, $E_3$ together with $E_4=\{1,6\}$, $E_5=\{1,5\}$, $E_6=\{4,5\}$, $E_7=\{4,6\}$. Here we have $W=\{1,2,3,4,5,6\}$, $k=7$, $q=3$, $W'=\{1,2,3,6\}$, $\rho _4=1$, $\rho _6=2$. The corresponding hypercycle inequality is given by

$$\begin{aligned} x_1+x_2+x_3+x_4+x_5+x_6\le 3. \end{aligned}$$

This is different from an extended and a lifted cover inequality. Moreover, this inequality is facet defining for the associated DCKP(G).

As a further example, consider the DCKP whose constraints are

$$\begin{aligned} x_1+2x_2+3x_3+x_4\le & {} 5, \\ x_1+x_4\le & {} 1. \end{aligned}$$

By considering the hypercycle induced by the hyperedges $\{1,2,3\}$, $\{2,3,4\}$ and $\{1,4\}$ of the related hypergraph, we obtain the inequality

$$\begin{aligned} x_1+x_2+x_3+x_4\le 2. \end{aligned}$$

which is valid and facet defining for the associated polytope.

Let us remark that odd-cycle inequalities (14), obtained from the conflict graph G, are nothing but the hypercycle inequalities when the hyperedges are all edges of G.

We have the following result which gives necessary and sufficient conditions for a hypercycle inequality to be facet defining.

Theorem 7

A hypercycle inequality (17) defines a facet of DCKP(G) if and only if the following hold.

• (1) For every node $j\in V\backslash W$, there is a set $S\subset W$ of $\left\lceil { \displaystyle \frac{k}{q} } \right\rceil$ items which covers the hyperedges $E_1$, ..., $E_k$ and such that $(W\backslash S)\cup \{j\}$ is not a cover.

• (2) There are |W| sets $S_1$, ..., $S_{|W|}\subset W$ which cover $E_1$, ..., $E_k$ such that $|S_i|=\left\lceil { \displaystyle \frac{k}{q} } \right\rceil$, and $T_i=W\backslash S_i$ is not a cover for $i=1, \ldots , |W|$ and $x^{S_1}$, ..., $x^{S_{|W|}}$ are affinely independent. (Note that two items i, j such that $(i,j)\in E$ are considered as a cover and any set containing a cover is a cover).

• (3) k is not a multiple of q.

Proof

Necessity

• (1) Suppose that for some $j\in V\backslash W$, any set $S\subset W$ of $\left\lceil { \displaystyle \frac{k}{q} } \right\rceil$ items that covers $E_1, \ldots , E_k$ is such that $(W\backslash S)\cup \{j\}$ is a cover. By Remark 1, it then follows that j cannot belong to any solution of the problem whose incidence vector satisfies (17) with equality. This implies that (17) is equivalent to the inequality $x_j\ge 0$. Since (17) is not a positive multiple of $x_j\ge 0$ and DCKP(G) is full dimensional, this implies that (17) does not define a facet.

• (2) First of all, observe that the incidence vectors of subsets $S_1$, ..., $S_l$ of W with $|S_i|=\left\lceil { \displaystyle \frac{k}{q} } \right\rceil$ for $i=1, \ldots , l$ are affinely independent if and only if the incidence vectors of the sets $T_1$, ..., $T_l$ where $T_i=W\backslash S_i$, for $i=1, \ldots , l$, are affinely independent. Suppose that the statement does not hold. By Remark 1 and the observation above, it follows that there do not exist sufficiently many (|V|) solutions of the problem whose incidence vectors satisfy (17) with equality and are affinely independent. Hence, (17) cannot define a facet.

• (3) If k is a multiple of q, then clearly, (17) can be obtained as a linear combination of valid inequalities of DCKP(G) and cannot, thus, be facet defining.

Sufficiency:

Suppose that 1)-3) hold. Let us denote (17) by $ax\le \alpha$ and let $bx\le \beta$ be a facet defining inequality of DCKP(G) such that $\{x\in$ DCKP(G) $~|~ ax=\alpha \}\subseteq \{x\in$ DCKP(G)$~|~bx=\beta \}$. We will show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

By (2), it follows that the sets $T_i=W\backslash S_i$, $i=1, \ldots , |W|$, are solutions of the DCKP. Moreover, as $x^{S_1}$, ..., $x^{S_{|W|}}$ are affinely independent, it follows that $x^{T_1}$, ..., $x^{T_{|W|}}$ so are. Let A be the square matrix whose columns are $x^{T_1}$, ..., $x^{T_{|W|}}$. As these vectors are affinely independent and are so linearly independent since they do not contain the zero vector, we have that A is non-singular. Moreover, as $|T_i| = |W| - \lceil \frac{K}{q} \rceil$ for all $i=1,\ldots , |W|$ it follows that system

$$\begin{aligned} \lambda A=(\beta , \ldots , \beta ) \end{aligned}$$

has a unique solution given by $\lambda _i=\frac{\beta }{|W|-\left\lceil { \displaystyle \frac{k}{q} } \right\rceil },$ for all $i=1, \ldots , |W|.$

As $T_1, \ldots , T_{|W|}$ are such that $ax^{T_i}=\alpha$ for $i=1, \ldots , |W|$, and thus $bx^{T_i}=\beta$ for $i=1, \ldots , |W|$, it follows that $b_i=\frac{\beta }{|W|-\left\lceil { \displaystyle \frac{k}{q} } \right\rceil }=\rho$ for $i=1, \ldots , |W|$. Now let j be an element of $V\backslash W$. By 1) there is $S\subset W$ with $S=\left\lceil { \displaystyle \frac{k}{q} } \right\rceil$ which covers $E_1,\ldots ,E_k$ and such that $T=(W\backslash S)\cup \{j\}$ is not a cover. Thus, $T\backslash \{j\}$ and T are both solutions of DCKP. As $ax^{T\backslash \{j\}}=ax^T=\alpha$, and hence $bx^{T\backslash \{j\}}=bx^T=\beta$, it follows that $b_j=0$. Altogether we have that

$$\begin{aligned} b_i= & {} \rho \quad {\text {for all}} ~ i\in W, \\ b_i= & {} 0 \quad {\text {for all}} ~ i\in V\backslash W. \end{aligned}$$

Thus, $b=\rho a$, and the proof is complete. $\square$

In what follows, we characterize a special case in which inequality (17) may define a facet.

Theorem 8

Consider a hypercycle ($v_1, E_1, v_2, \ldots , v_k, E_k, v_1$) in H and suppose that $E_1, \ldots , E_k$ are distinct sets, and $v_1, \ldots , v_k$ are distinct nodes. Then inequality (17) defines a facet of DCKP(G) if the following hold.

• (1) Each node belongs to at most two sets among $E_1, \ldots , E_k$ (that is to say $q=2$).

• (2) k is odd.

• (3) For any set $S=\{v, v_{i+2}, \ldots , v_{i+2l}\}$ where $v\in E_i$ and l is such that $k=2l+1$, the set $W\backslash S$ does not contain a cover. Here the indices are taken modulo k.

• (4) For every $j\in V\backslash W$, there is a set S among those introduced in (3) such that $(W\backslash S)\cup \{j\}$ is not a cover.

Proof

First remark that from 1), it follows that any set $S\subset W$ of the form $\{v, v_{i+2}, \ldots , v_{i+2l}\}$, where $v \in E_i$, covers all the hyperedges $E_1, \ldots , E_k$. Moreover by 3), the complementary set $W\backslash S$ in W induces a solution of DCKP.

Now as before, let us denote (17) by $ax\le \alpha$ and let $bx\le \beta$ be facet defining inequality such that $\{x\in$ DCKP(G) $~ | ~ ax=\alpha \}\subseteq \{x\in$ DCKP(G)$~|~bx=\beta \}$. We will show that $b=\rho a$ for some $\rho \in {\mathbb {R}}$.

Consider the sets

$$\begin{aligned} W_1= & {} W\backslash S_1 ~ {\text {with}} ~ S_1=\{v_1, v_3, \ldots , v_k\}, \\ W_2= & {} W_1\backslash S_2 ~ {\text {with}} ~ S_2=\{v_2, v_3, \ldots , v_k\}. \end{aligned}$$

It is not hard to see that $W_1$ and $W_2$ are solutions of DCKP such that $ax^{W_1}=ax^{W_2}=\alpha$. Thus, $bx^{W_1}=bx^{W_2}=\beta$, implying that $b_{v_1}=b_{v_2}$. As nodes $v_1, \ldots , v_k$ play similar roles, by symmetry, it follows that

$$\begin{aligned} b_{v_i}=b_{v_j}=\rho ~ {\text {for all}}\quad i,j\in \{1, \ldots , k\}. \end{aligned}$$

(18)

Now let v be a node of $E_1$ different from $v_1$. We have that $W_3=(W_1\backslash \{v\})\cup \{v_1\}$ is also a solution of DCKP with $ax^{W_3}=\alpha$. Hence, $bx^{W_3}=\beta$. As $bx^{W_1}=\beta$, this yields $b_v=b_{v_1}$. Since v is arbitrary in $E_1$, it follows that $b_v=\rho$ for all $v\in E_1$. And by (18), we obtain that $b_v=\rho$ for all $v\in W$.

To complete the proof, using 4), we can show in a similar way as in Theorem 6. that $b_j=0$ for all $j\in V\backslash W$. Hence, $b=\rho a$. $\square$

Note that the solutions to the DCKP induce an independence system whose circuits are precisely the minimal covers (see Schrijver 2002 for basic notions on the independence systems). Euler et al. (1987) introduce a generalization of the odd-cycle inequalities to independence systems. These more general inequalities have a structure different from that of (17), and, in some cases, can be seen as a special case of (17).

In what follows, we present new families of valid inequalities that combine the knapsack and independent set problems structures.

3.4 Clique-cover inequalities

Proposition 1

Let C be a cover of V and $K \subset V$ a clique. Let $C^* \subset C$ such that $\vert C^* \vert =\vert K \vert$, and suppose that for all $i \in C^*$, there exists a unique item $j \in K$ that is in conflict with i. Then the following inequality

$$\begin{aligned} \sum \limits _{i \in K} x_i + \sum \limits _{j \in C^*} x_j \le \Bigl \lfloor \frac{\vert C \vert + \vert K \vert }{2} \Bigr \rfloor , \end{aligned}$$

(19)

is valid for the DCKP(G).

Proof

The inequality is obtained by a Chvátal-Gomory procedure. We have

$$\begin{aligned} \begin{aligned} x(K)&\le 1,&\\ x_i+x_j&\le 1,&\quad&{\text {for all}} \; i \in C^*, j \in K\\ x(C)&\le \vert C \vert -1,&\\ -x_l&\le 0,&\quad&{\text {for all}} \; l \in C \setminus C^* \end{aligned} \end{aligned}$$

Inequalities (19) are obtained by adding the previous inequalities, dividing by 2, and then rounding down the right-hand side. $\square$

3.5 Clique-cover partition inequalities

Proposition 2

Consider a clique $K \subset V$ and let $K_1, K_2,\dots ,K_r$ (r is even) be a partition of K, i.e., $\cup _{i} K_i=K$, and $K_i \cap K_j = \emptyset$ for all $i\ne j$. Consider a subset of items $T \in V$ such that for all $i=1,2, \dots ,r$, $T \cup K_i$ is a cover. Then the inequality

$$\begin{aligned} x(K)+ \frac{r}{2} x(T) \le \Bigl \lfloor \frac{r \vert T \vert + \vert K \vert - r + 1}{2} \Bigr \rfloor , \end{aligned}$$

(20)

is valid for the DCKP(G).

Proof

The inequality is obtained by a Chvátal-Gomory procedure. We have

$$\begin{aligned} x(K)&\le \; 1, \\ x(T)+ x(K_i)&\le \;\vert T \vert + \vert K_i \vert -1, \; {\text {for all}} \; i=1,2, \dots ,r. \end{aligned}$$

Inequalities (20) are obtained by adding the previous inequalities, dividing by 2, and then rounding down the right-hand side. $\square$

In the following section, we devise a Branch-and-Cut for the DCKP based on the polyhedral results given before.

4 Branch-and-cut algorithm

The Branch-and-Cut algorithm alternates a cutting plane phase and a branching phase. During the cutting plane phase, we add, if there exist, violated inequalities. This is known as the separation process. In our Branch-and-Cut algorithm, we devise separation routines for the valid inequalities (6), (11), (12), and (14). Depending on the class of valid inequalities, we devise heuristic or exact procedures of separation.

Moreover, taking advantage of the close relationship with the classical KP, we develop a greedy heuristic allowing us to have an initial feasible solution for the DCKP.

4.1 Initial solution and preprocessing

In order to have an initial lower bound, we generate a feasible solution for the DCKP using the greedy heuristic given in Algorithm 1. The idea of this heuristic is the following. We first start by sorting items $j\in \{1,\dots ,n\}$ in a decreasing order of $\frac{p_j}{w_j+|{\mathscr {V}}_j|}$, where ${\mathscr {V}}_j$ represents the set of items that are in conflict with item j. Note that the fraction used for sorting the items refers to the classical $\frac{p_j}{w_j}$ of the KP, but also includes the item’s degree in the conflict graph. That is to say, it is more interesting to begin with items having the less conflicts in order to pack more items in the knapsack during the subsequent iterations. Once the items are sorted, we put the first in the knapsack and automatically delete all its neighbors in the conflict graph. This process continues while the knapsack capacity is not violated.

4.2 Separation routines

Let $\bar{x} \in {\mathbb {R}}^n$ be the current fractional solution to be cut, that is the optimal solution of the linear relaxation of the ILP given by (1)–(5). Separating a valid inequality consists in finding one or more inequalities that are violated by $\bar{x}$, or show that such inequality does not exist.

In what follows, we describe separation routines for the valid inequalities (6), (11), (12), and (14).

4.2.1 Clique inequalities separation

Clique inequalities (6) represent an interesting family of valid inequalities that are easily generated. For this reason, we choose to generate a set of valid clique inequalities within the first linear relaxation of the Branch-and-Cut tree’s root node. We hence solve the linear relaxation of the ILP given by (21).

$$\begin{aligned} \left\{ \begin{array}{llll} \max &{} {\sum }_{i \in V}p_{i}x_{i}\\ &{} {\sum }_{i \in V}w_{i}x_{i} \le c \\ &{} {\sum }_{j \in K}x_{j} \le 1 &{} \quad &{} {\text {for all}}\; K \in {\mathcal {K}},\\ &{} x_i+x_j \le 1 &{} \quad &{} {\text {for all}}\; (i,j) \!\in \!E\,:\,\{ i,j\} \nsubseteq K,\,{\text {for all}}\; K \!\in \!{\mathcal {K}},\\ &{} x_{i} \in \{0,1\} &{}\quad &{} {\text {for all}}\; i \in V,\\ \end{array}\right. \end{aligned}$$

(21)

where ${\mathcal {K}}$ is a family of cliques.

Since identifying the whole set of cliques is NP-hard, we choose to generate a set of cliques ${\mathcal {K}}$ using a heuristic method. To this end, we used the greedy Algorithm 2.

Let ${\mathcal {K}}= \emptyset$ be the set of cliques that we are looking for, and consider $K=\emptyset$ that initially denotes an empty clique. For each item, say i, in V, we iterate the following. We first put i in K. Then, we add to K an item j in conflict with i such that $\vert {\mathscr {V}}_j \vert$ is maximum. After that, among all the other nodes, we add the one that is universal to items in K (i.e., that is to say adjacent to all the items of K), and with a maximum degree in G. The process is repeated until no more universal node can be added. At the end, if $|K| > 2$, we obtain a clique K that we add to the family of cliques ${\mathcal {K}}$.

Concerning now the separation phase, we decided to apply, with slight modifications, a simple greedy heuristic presented by Nemhauser and Sigismondi (1992) for the independent set problem. The idea of the heuristic is detailed in Algorithm 3 and can be described as follows. We choose a vertex, say j, of maximum weight regarding $\bar{x}$, and set $K= \{ j \}$. Then we iterate the following process. Determine, if it exists, a maximum-weight vertex according to $\bar{x}$, say t, from all the vertices that are universal to K (i.e., t is adjacent to every vertex in K). Add t to K and repeat the procedure until no more universal vertex can be found. If $\vert K \vert >2$ and $\bar{x}(K) > 1$, then the K-Clique inequality is violated. The whole process is then iterated for another initial vertex j until either we find a violated inequality or a maximum number of iterations is reached. In our algorithm, we generate, if possible, only one violated clique inequality per iteration.

4.2.2 Odd-cycle inequalities separation

The separation problem of the odd-cycle inequalities (14) can be solved exactly in polynomial time as it has been shown by Grötschel et al. (2012). The separation procedure is described in Mahjoub (2010). Consider the current fractional solution $\bar{x}$. Consider $e=(i,j) \in E$ and let $z_e=1 - \bar{x}_i - \bar{x}_j$. It is clear that, since $\bar{x}$ satisfies (3) and (4), $z_e \ge 0$ for all $e \in E$. Using this, inequalities (14) can be written as

$$\begin{aligned} \sum \limits _{e \in C} z_e \ge 1 \qquad {\text {for all}}\; \quad C\; {\text {odd cycle of}}\; G. \end{aligned}$$

(22)

As a consequence, separating inequalities (14) with respect to $\bar{x}$ reduces to separating inequalities (22) with respect to z, and this can be ensured as follows. Consider graph G and let $z_e$ be the weight of edge e for all $e \in E$. In order to separate inequalities (22), one has to look for a minimum-weight cycle in a graph with nonnegative weights. This problem can be solved in polynomial time. To this end, consider the bipartite graph $\widetilde{G}=(V' \cup V'',\widetilde{E})$ obtained from G in the following way : for each vertex $v \in V$, consider two vertices $v' \in V'$ and $v'' \in V''$, and for each edge (u, v) consider two edges $(u',v'') \in \widetilde{E}$ and $(u'',v') \in \widetilde{E}$ with the same weight $\tilde{z}_{u'v''}=\tilde{z}_{u''v'}=z_{uv}$. Obviously, looking for a minimum-weight odd cycle in G with respect to z going through a vertex v is nothing but determining a minimum-weight path in $\widetilde{G}$ with respect to $\tilde{z}$ between $v'$and $v''$. Since $\tilde{z} \ge 0$, this can be done in polynomial time, using for instance Dijkstra’s algorithm. At the end of this step, we have (if it exists) a minimum-weight cycle in G, say C. If $\sum \nolimits _{e \in C} z_e < 1$, then a violated odd-cycle inequality is detected.

4.2.3 Hypercycle inequalities separation

In what follows, we will describe a heuristic for separating the hypercycle inequalities. First, note that a hypercycle inequality (17) can also be written as

$$\begin{aligned} \sum \limits _{i\in W} (1-x_i)\ge \left\lceil { \displaystyle \frac{k}{q} } \right\rceil . \end{aligned}$$

The heuristic works as follows. First, we generate a set of minimal covers $\{E_1, \ldots , E_r\}$ where $|E_i|\ge 3$, for $i=1, \ldots , r$. Let $\mathscr {E'}=\{E_1, \ldots , E_r, E_{r+1}, \ldots , E_s\}$, where $E_{r+1}, \ldots , E_s$ are all the edges of the conflict graph G. Let $U=\bigcup \nolimits _{i=1}^s E_i$.

Then we construct a bipartite graph $\varGamma =(U \cup \mathscr {E'},F)$ whose nodes on the left are the nodes in U, and the nodes on the right correspond to the elements of $\mathscr {E'}$. The set F of edges in $\varGamma$ is defined as follows. We consider an edge between a node u of U and a set $E_i$ of $\mathscr {E'}$ if $u\in E_i$. We associate with each $E_i$ the weight $\sum \nolimits _{j\in E_i} (1-\bar{x}_j)$. We associate to the nodes of U the weight zero. Each path in $\varGamma$ between a node u and a set $E_k$, such that $u\in E_k$, is a hypercycle in the hypergraph $H=(V, {\mathscr {E}})$. Remark that since $\varGamma$ is bipartite each path alternates between the nodes of U and the sets of $\mathscr {E'}$. The heuristic will compute a minimum weight path between u and $E_h$ for all $E_h$, $h=1, \ldots , s$ and $u\in E_h$. Each computed path induces a hypercycle inequality for which we determine the corresponding q. If the weight of this path is $< \left\lceil { \displaystyle \frac{k}{q} } \right\rceil$, then the corresponding hypercycle inequality is violated by $\bar{x}$.

In our Branch-and-Cut algorithm, such inequalities were not quite efficient in the resolution. In fact, separating the hypercycle inequalities generally takes huge time, and in the majority of the cases we did not succeed to find a violated inequality. For this reason, we decided to not include them in the separation process.

4.2.4 Cover inequalities separation

We now turn our attention to the cover inequalities. The separation algorithm of the cover inequalities (7) is an NP-hard problem Klabjan et al. (1998), and it seems to be the same for the extended cover inequalities (11). Crowder et al. (1983) show that the separation problem associated with cover inequalities is equivalent to the following 0–1 knapsack-like problem:

$$\begin{aligned} \left\{ \begin{array}{cccc} \min \sum _{j \in V}(1-\bar{x}_{j})y_j\\ \qquad \sum _{j \in V}w_{j}y_{j} > c \\ \quad y_{j} \in \{0,1\} &{}\quad &{} \forall j \in V,\\ \end{array} \right. \end{aligned}$$

(23)

where $y_j$ is a binary variable taking 1 if j is to be inserted into the cover C, and 0 otherwise. A cover inequality is hence violated when the optimal solution of (23), say $y^*$, has an objective value less than 1. In this case, the cover $C= \{ j \in V : y^*_j=1 \}$ yields a violated cover inequality.

In order to speed up the separation, Crowder et al. (1983) proposed a heuristic method that runs in ${\mathscr {O}}(n\,log(n))$. This consists in inserting items into C in a non-decreasing order regarding $\frac{1-\bar{x}_j}{w_j}$ until a cover is obtained.

Now, concerning the extended cover inequalities (ECI) (11), Gabrel and Minoux (2002) proposed an exact separation which reduces to the resolution of a sequence of 0–1 knapsack-like problems. In our algorithm, we choose to separate these inequalities using a heuristic algorithm inspired from the ones proposed by Kaparis and Letchford (2010b). This heuristic is described in Algorithm 4. We first begin by sorting items in a non-decreasing order of $\frac{1-\bar{x}_j}{w_j}$ and store them in a list L. We also initialize the cover $C^*$ to the empty set and $w^*$ to the capacity of the knapsack c. We then remove an item from the head of the sorted list L. If its weight is larger than $w^*$, then we ignore it; otherwise, we insert it in $C^*$. If $C^*$ is a minimal cover, then we try to extend it to obtain a violated extended cover inequality. If the obtained extended cover inequality is not violated, we delete the heaviest items from $C^*$, form a new extended cover inequality induced by $C^*$, and check again whether this inequality is violated or not. The whole process is then iterated until either a violated ECI is found or the list L is totally explored.

Along with the extended cover inequalities, we also separate the Simple Lifted Cover inequalities (12). To this end, we devise the routine described in Algorithm 5.

We first begin by forming a cover C, then making the cover C minimal. We consider then two subsets of C, i.e., F and R, corresponding to the subsets of elements of C having $\bar{x}_j >0$ and $\bar{x}_j =0$, respectively. Steps 9 and 11 of the Algorithm  6 refer to the up-lifting phase for the two subsets F and R. This corresponds to calculating the $\alpha$ coefficients for inequalities (12) given in Algorithm 6. Note that in Algorithm 6, one has to solve a knapsack problem. In our case, we use a greedy heuristic to this end. We first begin by sorting items in a non-increasing order of $\frac{z_i}{w_i}$, where $z_i=1$ if item $i \in C$, and $z_i=\alpha _i$ otherwise. We then pack the sorted items in the knapsack while the corresponding capacity constraint is not violated.

For a deep description of the covers inequalities separations, the reader is referred to Kaparis and Letchford (2008, 2010a, b).

Using the previous polyhedral analysis and the devised separation algorithms, we propose a Branch-and-Cut algorithm to solve the DCKP. An experimental study is held on a set of problem instances. This will be presented in the next section.

5 Computational results

The Branch-and-Cut algorithm is implemented in C++ and tested on Bi-Xeon quad-core E5507 2.27GHz with 8Go of RAM, running under Linux. We use CPLEX 12.5 as a linear solver.

Problem instances are generated using David Pisinger’s instance generator (used in Pisinger (1999) and Martello et al. (1997), see http://www.diku.dk/~pisinger/codes.html) and following the generated instances by Hifi and Michrafy (2007) and Yamada et al. (2002). We tested two kind of instances: uncorrelated and strongly correlated. For the uncorrelated instances, items’ weights and profits are randomly generated from 1 to 100. Concerning the strongly correlated ones, items’ weights are randomly generated from 1 to 100, and each profit $p_i=w_i+10$ for $i=1,\dots ,n$. We tested three groups of instances containing 100–1000 items.

The knapsack capacity for each group of instances is calculated using the formula proposed by David Pisinger:

$$\begin{aligned} c= \frac{l \times \sum _{j \in V}w_j}{S+1}, \end{aligned}$$

where l and S are fixed parameters. We set S to 1000, and l to 5 and 10, respectively. Concerning the disjunctive aspect, conflicts between items are randomly generated and the density $\eta$ of the conflict graph G takes, as in Hifi and Michrafy (2007) and Yamada et al. (2002), the following values $\eta =0.005,\;0.007,\;0.009,\;0.010$, and 0.020. Moreover, we set a time limit to 10,800 s.

In order to evaluate the performance of our Branch-and-Cut algorithm, we compare our results to the results given by running Cplex on the original formulation for the DCKP, i.e., ILP (1)–(5), without taking into account the valid inequalities. Note that we also disable the valid inequalities generated by default by Cplex, in order to be able to compare it with the Branch-and-Cut. Recall that in our Branch-and-Cut algorithm we separated the valid inequalities (6), (14), (11) and (12). After testing different order of separation, we chose to separate the valid inequalities in the following order, which proved to be the most effective. We first separate the cliques (6), then the simple lifted cover inequalities (12), then the extended cover inequalities (11), and finally the odd cycles (14).

The results are reported in Tables 1, 2, 3 and 4. The three first columns of each table represent the instance main characteristics. Then the 8 following columns report results corresponding to the Branch-and-Cut algorithm. Finally, the remaining 4 columns give the results obtained by running Cplex.

Entries of the tables are the following
n	:	Number of items
m	:	Number of edges in G (disjunction constraints)
$\eta$	:	Conflict graph density
Nodes	:	Number of nodes in the Branch-and-Cut tree
Gap-final	:	Relative error between the best lower bound and the best upper bound
Gap-root	:	Relative error between the best lower bound and the upper bound at the root
ECI	:	Number of generated Extended Cover Inequalities
LCI	:	Number of generated Lifted Cover Inequalities
Cliques	:	Number of generated cliques inequalities
OddCycles	:	Number of generated odd-cycle inequalities
CPU	:	Total time of execution (in seconds)

The value of Gap-final is used to analyze the efficiency of the algorithm. When it is equal to 0, this means that the instance is solved to optimality. The value of Gap-root points the quality of the linear relaxation at the root node of the Branch-and-Cut tree before branching compared to the best lower bound obtained at the end. Note also that the number of disjunctive constraints, i.e. m, is linked to the conflict graph’s order and density through the following formula $m=\eta \frac{n(n-1)}{2}$.

In total, we tested the Branch-and-Cut algorithm and Cplex over 170 instances. These can be classified to easy, medium, and hard instances. The difficulty of an instance highly depends on the number of items n, the number of disjunctive constraints m, and parameter l which is directly impacting the value of the knapsack capacity (c.f., the capacity formula given above). The higher the values of n and m are, the harder the instance is. We also note that instances with capacities calculated with $l=10$ are a bit harder than those with $l=5$.

For the group of easy instances, our algorithm was able to solve to optimality the instances within a small amount of time. In fact, for 61 instances we reached optimality with less than 300 s. Medium instances took much more time to be solved to optimality (8 instances), and hard ones reached the time limit without having an optimal solution. Within the group of hard instances, we find some “soft” instances for which we obtained a final gap less than or equal to 10% (23 instances). Strongly hard ones reached, however, important and sometimes huge values of final gaps, showing hence the hardness of the tested instances.

Table 1 Uncorrelated instances with $l=5$

Table 2 Uncorrelated instances with $l=10$

Table 3 Strongly correlated instances with $l=5$

Table 4 Strongly correlated instances with $l=10$

Based on the results of the four tables, we can conclude that our Branch-and-Cut algorithm outperforms Cplex results for almost all the instances. In fact, applying the Branch-and-Cut algorithm, we have been able to reduce the gap values for all the instances. Our gaps at the root are always better than those of Cplex, which proves the efficiency of the generated valid inequalities to have a tightened linear relaxation. These valid inequalities were in fact extremely crucial in improving the resolution of hard instances. In fact, for instances with more than 600 items, our Branch-and-Cut algorithm provides acceptable values of gaps for which Cplex reached very huge values. Our algorithm was also able to solve to optimality instances that Cplex could not solve within the time limit. Consider Table 1 and take for instance the instance with $n=500$, and $\eta = 0.1$ that Cplex could not solve and got a final gap equal to 6.84%. The same instance has been solved to optimality by the Branch-and-Cut algorithm in around 4080 s. The same case happened for the instance with $n=300$ and $\eta = 0.2$ and the instance with $n=400$ and $\eta =0.07$ in Table 2. We also notice that compared to Cplex results, the use of the Branch-and-Cut algorithm implies a reduction of the CPU time as well as the tree size (given by the number of nodes).

Through the experimental results, we also note that our Branch-and-Cut algorithm was performant, being able to guarantee optimality for 69 instances over 170 in general hard instances. Nine instances have been solved to optimality at the root node of the Branch-and-Cut tree (5 for Cplex), and for 68 instances we have a very interesting gap at the root not exceeding 10% (47 instances solved by Cplex have a root gap less than 10%). This proves that we succeed in tightening the DCKP linear relaxation using our valid inequalities.

As it has been mentioned above, we separate 4 families of valid inequalities, i.e., the cliques, the odd cycles, the extended and the lifted covers. Based on experimentations, we can see that the number of generated inequalities of each family depends on the group of instance. For almost all the instances, we notice that the number of generated odd-cycle inequalities is the most important, reaching more than 10,000 for some hard instances. For the other families of inequalities, we generate a reasonable number. Moreover, as said before, the number of generated inequalities of each family of valid inequality directly depends on the instance. For example, when the instances are of small size (i.e., regarding n and m), we generate very small number of cliques and odd cycles. This is obvious because for such instances the graph of conflict is sparse. As much as the instance becomes bigger, we generate more and more cliques and odd cycles since the corresponding conflict graph becomes denser. Obviously, there is a very close relationship between the different families of valid inequalities, namely the cliques and odd cycles, and the properties related to the conflict graph (perfect, tree, claw-free,...). In fact, the conflict graph structure plays a prominent role in determining which families are more likely to appear and be effective in strengthening the linear relaxation of the problem. Recall that, in our case, conflicts between items are randomly generated, which means the structure of the conflict graph is not particular, and that the number of generated cliques and odd cycles depends only on the density of the conflict graph. For the two families of cover inequalities, i.e., the extended and the lifted ones, we remark that the generated number depends not only on the size of the instance, but also on its type and capacity (and hence parameter l). In general, the number of generated cover inequalities is more important for the strongly correlated instances (Tables 3, 4) compared to the uncorrelated ones (Tables 1, 2). It is clearly bigger for instances with $l=5$ than for those with $l=10$, since capacities for the second group is bigger. We also note that for huge instances, (more than 500 items, $l=10$), we are no more able to generate extended and lifted cover inequalities. This is obvious for these families of inequalities. Recall that in order to separate these inequalities, we use a heuristic method solving a knapsack or a knapsack-like problem with a greedy algorithm. The bigger the instance is, the looser the quality of solution of the knapsack subproblem is. Consequently, it would be interesting if we could improve the separation of these families for huge-sized instances.

All the arguments above show that our Branch-and-Cut algorithm is efficient for solving the DCKP. Note, however, that for one instance (see Table 3, instance $n=400$, $\eta =0.07$), Cplex was able to reach optimality but not the Branch-and-Cut algorithm. Our algorithm has oddly a better gap at the root than Cplex’s one (5.32% for the Branch-and-Cut, 8.06% for Cplex), and it was very near to optimality (final gap equal to 0.19%). This is mainly due to the number of generated extended covers and lifted covers inequalities which reach 10,767 and 1839, respectively. At this stage, one can think first in improving the separation procedures that we are using, and second in devising an efficient primal heuristic that can help us pruning some uninteresting branches of the Branch-and-Cut tree.

6 Concluding remarks

In this paper, we studied a variant of the Knapsack Problem, that is when some of the items are in conflict with some others. We presented a 0–1 ILP formulation for the problem and study the associated polytope. New families of valid inequalities are then identified. A facial study of the basic and valid inequalities is held. We then discussed the separation problem of the valid inequalities and used the whole study to develop a Branch-and-Cut algorithm. Experimental results show that the Branch-and-Cut algorithm performs well compared to Cplex, mainly for hard instances. However, as pointed for some cases, it would be interesting to boost our Branch-and-Cut algorithm, first by improving our separation procedures and second by devising efficient primal heuristics. This can indeed help prune uninteresting branches of the Branch-and-Cut tree and accelerate the resolution mainly for hard instances.

It would also be interesting to use the results obtained in this work in order to study some extensions of the DCKP. A possible extension consists in imposing an order for the selection of items. One can also think of other variations extending the problem for more than one dimension, i.e., the Bi-dimensional (or Multi-dimensional) Disjunctively Constrained Knapsack Problem. Another stimulating perspective would be to extend the provided theoretical results to several other problems for which the DCKP appears as a subproblem, such as the Bin Packing Problem with conflicts.