1 Introduction

The main theory of the ensemble methodology is to measure a set of individual pattern classifiers and merge the classifier’s predictions to obtain one result. Therefore, classifier ensembles improve the performance of a single classifier (Tahir et al. 2012; Nanni and Lumini 2007; Harrison et al. 2011). Because of classifier diversity, different classifiers produce various classification results for a certain instance (Christoudias et al. 2008). Usually, multiple classifiers work together to generate prediction results, so as to improve classification accuracy. A classifier ensemble adopts such a strategy to exhibit accuracy and generalization ability. Recently, classifier ensembles have been successfully applied in many fields, e.g., bioinformatics (Okun and Global 2011; Mandal 2014; Bouziane et al. 2015), financial forecasting (Marqués et al. 2012; Teng et al. 2014), big data clustering (Su et al. in press), and even robotic control (Chao et al. 2014; Chen et al. 2014).

Generally speaking, a classifier ensemble with a large number of individual classifiers produces better performance. However, the training time for such a large size ensemble is also enormous. Therefore, classifier ensemble reduction (CER) technology is applied to reduce the redundancy of candidate classifier ensemble subsets, thereby constructing a new subset whose performance is close to or even better than that of the original ensemble (Dash and Liu 1997; Diao et al. 2014; Yao et al. 2014). The benefits of ensemble size reduction include fewer computational and storage overheads and shorter algorithm running time. However, the reduction strategy cannot simply limit the size of a classifier ensemble. Because diversity affects the classifier ensembles’ generalization ability, the reduction process must retain the classifier ensembles’ diversity. If each classifier in an ensemble produces a very similar performance, such a classifier ensemble may not improve its generalization ability (Sun et al. 2014). On the other hand, if an instance is classified into a wrong category by a classifier of an ensemble, other classifiers within the same ensemble may correct the wrong classification by combining the rest of the classifier’s results.

The diversity measurement, therefore, is used to evaluate each single classifier’s diversity within a classifier ensemble. Many diversity measurement methods calculate the correlations amongst classifiers or classification preference of each classifier. Then, the correlations, or preferences, are used to remove those classifiers that have similar performances, and the significant classifiers are retained (Sun et al. 2014). The diversity measurement methods are divided into the following two categories: pairwise diversity measures and non-pairwise diversity measures (Brown et al. 2005). The common pairwise diversity measurement methods include Q statistics, inconsistency, and entropy measurement methods (Brown et al. 2005). In addition, the interrater agreement measures, the Kohavi–Wolpert variance (KW) (Kohavi and Wolpert 1996), and the entropy measure (Cunningham and Carney 2000) are the typical non-pairwise diversity measures.

In addition, searching the best ensemble candidate classifiers is regarded as an NP-Hard problem (Diao et al. 2014). Many heuristic search algorithms, such as evolutionary algorithms (Wróblewski 2001) and particle swarm optimization (Wang et al. 2007), are applied to find the potential solutions. In particular, the harmony search (HS) algorithm is a recently developed meta-heuristic algorithm that simulates the improvisation process of music players (Geem 2010). HS contains many advantages, for example, HS imposes only limited mathematical requirements and is insensitive to initial value settings. Due to the HS algorithm’s simplistic structure and powerful performance, the harmony search algorithm has been very successful in a wide variety of engineering and machine learning tasks (Diao and Shen 2012; Ramos et al. 2011; Mashinchi et al. 2011; Zheng et al. 2014, 2015).

Moreover, an application of HS to feature selection has also been recently developed to minimize the ensemble’s redundancy (Diao et al. 2014). The application exhibited good performance for classification. In particular, the application used three evaluation methods to select potential classifier ensembles. The three evaluators—correlation based, probabilistic consistency based, and fuzzy-rough set theory based feature selections—focused on finding the correlations between each classifier candidate and its prediction result. However, the application did not consider a direct application of diversity measures to the ensemble evaluation to improve the application’s performance.

This paper is an extension of the framework for CER using feature selection techniques, which are implemented in our previous research (Diao et al. 2014; Yao et al. 2014). In this paper, a new classifier evaluation method is proposed to replace the original method in the framework. The new technique applies both the pairwise and non-pairwise diversity measurements to evaluate each ensemble candidate’s performance. Three classical diversity methods and a newly developed method are used to build the pairwise measure. Also, another three methods are used to implement the non-pairwise measure. As a result, by comparing the performances generated by various evaluation methods, one diversity measure with the best performance is chosen to improve the entire CER framework.

The remainder of this paper is organized as follows: Sect. 2 briefly introduces the background and related work of classifier ensembles, diversity of classifier ensembles, and CER framework. Section 3 describes the newly proposed diversity measure method for the ensemble subsets evaluation. Section 4 presents and discusses the experimental results. Section 5 concludes the paper and points out future research.

2 Background

2.1 Accuracy and diversity of classifier ensemble reduction

Inside each classifier ensemble, the differences amongst the individual classifiers are considered the key factors that enable the ensembles to achieve a high prediction accuracy. A combination of multiple classifiers with similar performance is not helpful for improving the entire ensemble’s accuracy. When a part of the classifiers produce incorrect predictions, the rest of the classifiers produce correct predictions. By using a voting mechanism, the incorrect predictions are eliminated. The various predictions of a classifier ensemble are regarded as the ensemble’s diversity. However, there is no unified standard to measure the diversity (Sun et al. 2014). Recently, a number of ensemble measurement methods were proposed to represent the ensemble diversity.

The recent diversity measurement consists of two types: pairwise diversity and non-pairwise diversity measures. The pairwise diversity method calculates the diversity value of each pair of classifiers in a classifier ensemble and then uses the mean value of the diversity values to represent the ensemble’s diversity. The non-pairwise diversity measures directly calculate the diversity values of an ensemble system. Moreover, the common measurement methods are Q statistics, correlation coefficient parameter, disagreement measure, and double-fault measure (Cherkauer 1996; Skalak 1996; Tang et al. 2006). Recently, several other diversity measure methods have been developed, e.g., distance measure (Harrison et al. 2011), percentage correct diversity measure (Banfield et al. 2004), and generalized diversity measure (Partridge and Krzanowski 1997). Not all the diversity measures are used in this paper. Several representative measures are selected to build the proposed evaluation method.

2.2 The framework for classifier ensemble reduction using feature selection techniques

Recently, a new approach to CER has been developed (Diao et al. 2014). The approach works by applying feature selection techniques to minimize redundancy in a data set. The data set is generated via transforming ensemble predictions into training samples and treating classifiers as features. Then, the harmony search is applied to find a reduced subset of such classifier features, while attempting to maximize the feature subset evaluation. Experimental comparative results demonstrate that the approach reduces the size of an ensemble, while maintaining and improving classification accuracy and efficiency.

Figure 1 illustrates the four important steps of the CER approach.

  1. 1.

    Base classifier pool generation: the first step is to generate a diverse base classifier pool. Any of the conventional methods, such as bagging, boosting and random subspaces, can be used to build the base classifiers. In this approach, the bagging and subspaces methods are used to build the base classifier pool. By selecting classifiers from different schools of classification algorithms, the ensemble diversity is naturally added into the base classifier pool through the various foundations of the algorithms themselves.

  2. 2.

    Classifier decision transformation: in this step the classifier decisions are converted to a feature selection supported format. Once the base classifiers are built, the classifier decisions on training instances are also collected. For supervised feature selection methods, a category label is required for each type of instance, and each single classifier’s decision of a training instance is retained with the category label. A new, artificially generated feature format, “Decision Matrix”, is thereby constructed. In the decision matrix, each column represents an artificially generated feature, and each row corresponds to a training instance.

  3. 3.

    Classifier selection: a novel feature selection algorithm, “Feature Selection with Harmony Search” (HSFS) (Diao and Shen 2012), is then performed on the artificial feature data set to evaluate the emerging feature subset using the correlation-based feature selection algorithm (CFS) (Hall 2000) as the default subset evaluator. HSFS optimizes the quality of the discovered subsets, while trying to reduce subset sizes. When harmony search algorithm terminates, the best harmony is translated into a feature subset and returned as the feature selection result. Thus, the feature selection result is the optimized classifier ensemble.

  4. 4.

    Ensemble decision aggregation: when the classifier ensemble is constructed, new instances are classified by the ensemble members, and their results are aggregated to form the final ensemble decision output. Actually, the final aggregated decision is made by the winning classifier that possesses the highest averaged prediction across all classifiers.

The accuracy and diversity of classifier ensembles are recognized as two important evaluating indicators. However, the current CER framework merely considers the classifier diversity in the base classifier pool generation phase. The framework’s main efforts rely on searching effective classifiers while maintaining high accuracy. Diversity evaluation is not involved in the CER framework. Therefore, to improve generalization ability, diversity must be included to evaluate each ensemble member. In summary, this paper attempts to apply various diversity measures to improve the current evaluation method of the CER framework.

Fig. 1
figure 1

The flowchart of the CER framework

Full size image

3 Integrating of classifier diversity evaluations for CER

This paper focuses on not only improving the CER framework’s classification accuracy, but also bringing diversity measures to the third step of the CER procedure shown in Fig. 1. The third step applies harmony search and feature selection algorithms to select the best ensemble members. The harmony search algorithm initializes its harmony memory and the initialization randomly produces n groups of classifier subsets. Then, the search iteration starts; each classifier subset obtains a merit value by the subset CFS evaluation in Fig. 1. The merit value is returned to the harmony search to rank the subsets. If one new subset’s merit value is better than that of the worst subset in the harmony memory, then, the worst subset is replaced by the new merit value. Otherwise, the harmony memory’s content remains unchanged. The iteration continues until a pre-defined repeating iteration is reached. The remaining contents inside the harmony memory are the harmony search’s final results, which are used to form the reduced classifier ensemble.

To involve the diversity measure in the framework, the subset evaluation step must establish the relationships between the ensemble subset’s diversity and the subset’s performance. However, merely considering the diversity evaluation does not reflect each subset’s accuracy, and may even decrease the precision. Thus, both precision and diversity must be evaluated simultaneously while implementing the subset evaluation. In this case, the third step is extended to three modules: (1) precise calculation; (2) diversity measure; and (3) merit calculation.

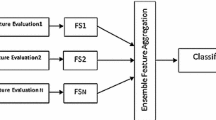
Ensemble candidates are generated by the harmony search algorithm. The precision calculation module generates each candidate’s precision value that is retained for the subsequent merit calculation. The diversity measure applies two types of measure methods to calculate the diversity for each candidate. Both pairwise and non-pairwise measures are used in the module. Pairwise measures contain four methods, one of which is developed in this paper. Non-pairwise measures have three methods. After the diversify calculation, the merit calculation module uses the generated precision and diversity to produce a merit value for each ensemble candidate and sends the value back to the harmony search algorithm. The entire procedure is shown in Fig. 2. The detailed implementation of the three modules is described as follows.

Fig. 2
figure 2

The diversity evaluation

Full size image

3.1 Precise calculation

The classifier subset evaluation algorithm is divided into three steps: the first step is to calculate the average precision, \(P_{\mathrm{precise}}\), of each ensemble candidate. \(P_{\mathrm{precise}}\) is the entire ensemble candidate’s precision rate, rather than a single classifier’s precision rate. In addition, the size of the ensemble candidates is k. Thus, for each ensemble candidate, the number of any two classifiers taken in combination, m, is obtained by:

$$\begin{aligned} m=\frac{k(k-1)}{2}. \end{aligned}$$
(1)

However, for any two classifiers taken in combination, joint accuracy, p, cannot be directly obtained by using the test results of the training data, but rather, is determined by their classification performance. Consider a group of instances with parameters a–d. Then, as shown in Table 1, a denotes the number of instances where both Classifiers A and B are classified correctly; b denotes the number of instances where Classifier A is classified correctly, but Classifier B is classified incorrectly; c denotes the number of instances where Classifier B is classified correctly, but Classifier A is classified incorrectly; d denotes the number of instances where both Classifiers A and B are classified incorrectly. Thus, the joint accuracy p of Classifiers A and B is obtained as follows:

$$\begin{aligned} p=\frac{a}{a+b+c+d}. \end{aligned}$$
(2)

The entire ensemble member’s accurate \(P_{\mathrm{precise}}\) is obtained by Eq. 3. All the single classifier precision values, p, are summated, and then, the summation is divided by the combination number obtained in Eq. 1.

$$\begin{aligned} P_{\mathrm{precise}}=\frac{\sum _{n=1}^{m} p_{n}}{m}=2\frac{\sum _{n=1}^{m} p_{n}}{k(k-1)}, \end{aligned}$$
(3)

where n denotes the nth pair of classifiers; m is determined by Eq. 1.

Table 1 The prediction combinations of each two classifiers
Full size table

3.2 Diversity calculation

The second step is to calculate the diversity, \(Q_{\mathrm{diversity}}\), of each classifier ensemble’s candidate. The diversity calculation contains pairwise and non-pairwise measures. There is a slight difference in the implementation of the two measures. The pairwise measure requires the summation of all the diversity pairs, followed by the calculation of the entire ensemble candidate’s diversity. The non-pairwise measure is obtained directly from the candidate’s diversity.

3.2.1 Pairwise evaluation

Three conventional diversity measure methods, introduced in Sect. 2, are used to measure the diversity of each pair of classifiers. The pairwise diversity also uses the parameters shown in Table 1.

\(q_\mathrm{QS}\) is the Q statistics method, and is defined by:

$$\begin{aligned} q_\mathrm{QS}=\frac{ad-bc}{ad+bc}. \end{aligned}$$
(4)

\(q_\mathrm{DM}\) is the disagreement measure method (Skalak 1996):

$$\begin{aligned} q_\mathrm{DM}= \frac{b+c}{a+b+c+d} \end{aligned}$$
(5)

and \(q_\mathrm{DFM}\) is the double-fault measure method (Giacinto and Roli 2001):

$$\begin{aligned} q_\mathrm{DFM}=\frac{d}{a+b+c+d}. \end{aligned}$$
(6)

In addition, a new diversity measure method is also developed in this paper. The new method is a variant of Eq. 4. Equation 7 presents the calculation method:

$$\begin{aligned} q_\mathrm{VQS}=\frac{bc}{ad+bc}. \end{aligned}$$
(7)

Similar to the ensemble candidate’s precision rate, the entire ensemble candidate’s pairwise diversity, \(Q_{\mathrm{diversity}}\), is obtained as follows: all the pairwise diversity values are summed, and then, the average value of the summated value is calculated; Eq. 8 defines the ensemble’s pairwise diversity:

$$\begin{aligned} Q_{\mathrm{diversity}}^{x}=2\frac{\sum _{n=1}^{m} q_{x}}{k(k-1)}, \end{aligned}$$
(8)

where the x value in \(q_x\) stands for the chosen diversity measure method, which is one of the \(q_\mathrm{QS}\), \(q_\mathrm{DM}\), \(q_\mathrm{DFM}\), and \(q_\mathrm{VQS}\).

3.2.2 Non-pairwise measure

Compared with a pairwise measure, a non-pairwise diversity measure directly obtains the entire ensemble candidate’s diversity value. In this paper, Kohavi–Wolpert variance measure, interrater agreement \(\kappa \) measure, and entropy measure are used.

\(Q_{\mathrm{diversity}}^\mathrm{KW}\) stands for the Kohavi–Wolpert variance (KW) (Kohavi and Wolpert 1996), and is be calculated by:

$$\begin{aligned} Q_{\mathrm{diversity}}^\mathrm{KW}=\frac{1}{NL^{2}}\sum _{j=1}^{N}l(z_{j})(L-l(z_{j})), \end{aligned}$$
(9)

where N denotes the size of the ensemble’s training instances; L denotes the classifier size of an ensemble candidate; \(z_{j}\) denotes the jth instance of the ensemble’s training data set; and \(l(z_{j})\) denotes the account of the classifiers that gives the correct classification result for instance j.

\(Q_{\mathrm{diversity}}^{\kappa }\) is the measurement of interrater agreement \(\kappa \) (Fleiss 1981) (abbreviated in this paper as “interrate \(\kappa \)”).

$$\begin{aligned} Q_{\mathrm{diversity}}^{\kappa }=1-\frac{\frac{1}{L}\sum _{j=1}^{N}l(z_{j})(L-l(z_{j}))}{N(L-1)\bar{p}(1-\bar{p})}, \end{aligned}$$
(10)

where N, L, and \(l(z_{j})\) are the same values in Eq. 9; \(\bar{p}\) is the ensemble’s single member’s average precise rate, which is obtained by:

$$\begin{aligned} \bar{p}=\frac{\sum _{j=1}^{N}\sum _{i=1}^{n}p_{j,i}}{NL}, \end{aligned}$$
(11)

where \(p_{j,i}\) denotes the classification results of the jth instance that are classified by the ith classifier.

The entropy measure method (Cunningham and Carney 2000), abbreviated as E, is calculated by Eq. 12

$$\begin{aligned} Q_{\mathrm{diversity}}^{E}=\frac{1}{N}\sum _{j=1}^{N}\frac{1}{L-\frac{L}{2}}\min \{l(z_{j}),l-l(z_{j})\}, \end{aligned}$$
(12)

where N, L, and \(l(z_{j})\) also have the same values as in Eq. 9.

3.3 Merit calculation

The third step is to combine the results of \(P_{\mathrm{precise}}\) and \(Q_{\mathrm{diversity}}^{x}\) to calculate each ensemble member’s merit value. The merit is returned to the harmony search algorithm. The merit value is, thus, obtained by using the \(P_{\mathrm{precise}}\) and \(Q_{\mathrm{precise}}^{x}\) values:

$$\begin{aligned} merit_{\mathrm{PQE}^{x}} = \frac{k\cdot P_{\mathrm{precise}}}{\sqrt{k+k(k-1)(1-Q_{\mathrm{diversity}}^{x})}}, \end{aligned}$$
(13)

where x stands for the user selected q measure’s index (\(q_\mathrm{QS}\), \(q_\mathrm{DM}\), \(q_\mathrm{DFM}\), \(q_\mathrm{VQS}\), KW, \(\kappa \), and E).

To test various evaluation methods, another merit calculation method is also designed as follows:

$$\begin{aligned} merit_{\mathrm{QPE}} = \frac{k\cdot Q_\mathrm{VQS}}{\sqrt{k+k(k-1)(1-P_{\mathrm{precise}})}}. \end{aligned}$$
(14)

As expected, both Eqs. 13 and 14 imply that if the P and Q values increase, the merit value also increases. In the experiments, these two equations are evaluated separately; therefore, which equation is chosen as the final solution is based the experimental results. Finally, the merit value is returned to the harmony search algorithm as the subset evaluation values.

The entire ensemble subset evaluation procedure is interpreted into a pseudo code shown in Algorithm 1.

figure a

4 Experimental results

To access the capability of the CER framework with the proposed diversity evaluation methods, a number of experiments were conducted. The implementation is mainly based on the CER framework, which is closely connected to the “WEKA” data mining software (Hall et al. 2009). The main ensemble construction method adopted is the bagging approach (Breiman 1996), and the base classification algorithm used is C4.5 (Witten et al. 2011). Also, the CER framework adopts a dynamic parameter adjustment scheme (refer to Diao and Shen 2012 for further information).

A number of real-valued UCI (Asuncion and Newmann 2007) benchmark data sets are used in the experiments. The selected data sets are representative. In particular, several data sets contain a large size of categories. For example, data set “libras” contains 16 categories. Moreover, a data set contains a large number of instances, i.e., data set “ozone” contains 2536 instances. In this case, the data sets demonstrate significant challenges for the construction and reduction of ensembles. The information in the data sets is summarized in Table 2. In addition, stratified tenfold cross-validation (10-FCV) is employed for data validation.

Table 2 Experimental data set
Full size table

The following eight types of diversity evaluation methods tested in the experiments are as follows: (1) the combination of Eqs. 4 and 13 (\(\mathrm{PQE}+\mathrm{VQS}\)); (2) the combination of Eqs. 5 and 13 (\(\mathrm{PQE}+\mathrm{DM}\)); (3) the combination of Eqs. 6 and 13 (\(\mathrm{PQE}+\mathrm{DFM}\)); (4) the combination of Eqs. 7 and 13 (\(\mathrm{PQE}+\mathrm{VQS}\));(5) the combination of Eqs. 9 and 13 (\(\mathrm{PQE}+\mathrm{KW}\)); (6) the combination of Eqs. 10 and 14 (\(\mathrm{PQE}+\kappa \)); (7) the combination of Eqs. 12 and 14 (\(\mathrm{PQE}+\mathrm{Entropy}\)); and (8) the combination of Eqs. 7 and 14 (\(\mathrm{QPE}+\mathrm{VQS}\)). to reduce the impact of random factors caused by the HS algorithm, the experimental outcomes presented are averaged values of ten different 10-FCV runs, i.e., 100 outcomes.

The merit performances of PQE and QPE are tested firstly in the experiments. Table 3 summarizes the two sets of results obtained for PQE (calculated by Eq. 13) and QPE (calculated by Eq. 14), respectively. By using the same diversity measure, PQE exhibits much better accuracy than QPE does. PQE generates better performance in seven data sets among the entire 12 data sets. In addition, the leading range of PQE is very large. Moreover, the sizes of the performances of both methods are very similar. In this case, Eq. 13 is used as the merit evaluation method. Both the pairwise and non-pairwise diversity measures adopt the PQE equation.

Table 4 presents the performance comparison of the classifier ensembles by adopting \(q_\mathrm{QS}\), \(q_\mathrm{DM}\), \(q_\mathrm{DFM}\), and \(Q_\mathrm{VQS}\). The four ensembles are labeled as \(\mathrm{PQE}+\mathrm{QS}\), \(\mathrm{PQE}+\mathrm{DM}\), \(\mathrm{PQE}+\mathrm{DFM}\), and \(\mathrm{PQE}+\mathrm{VQS}\). \(\mathrm{PQE}+\mathrm{QS}\) produces the highest accuracy of eight data sets among the entire 12 data sets. \(\mathrm{PQE}+\mathrm{DM}\) generates four highest accuracies. \(\mathrm{PQE}+\mathrm{VQS}\) has only two. No highest accuracy is generated by \(\mathrm{PQE}+\mathrm{DFM}\). However, \(\mathrm{PQE}+\mathrm{DFM}\) has the smallest ensemble size within ten data sets. Although, \(\mathrm{PQE}+\mathrm{VQS}\) does not generate good performance for accuracy, the size performance is the best in the four ensembles. In addition, the change in the range of \(\mathrm{PQE}+\mathrm{QS}\) is very large. The largest size of \(\mathrm{PQE}+\mathrm{QS}\) is 94.6, the smallest is 7.9. The overall size performance is not stable. \(\mathrm{PQE}+\mathrm{DM}\)’s largest size is 20.7, the smallest is 3.9; the size performance of \(\mathrm{PQE}+\mathrm{DM}\) is relatively better than that of \(\mathrm{PQE}+\mathrm{QS}\). \(\mathrm{PQE}+\mathrm{DFM}\)’s performance is not very stable because its largest size is 87.0, and the smallest is 3.3. By contrast, the change in the size performance of \(\mathrm{PQE}+\mathrm{VQS}\)is not large; the largest size is 25.5 and the smallest is 3.3. By contrast, \(\mathrm{PQE}+\mathrm{QS}\) achieves the best accuracy; \(\mathrm{PQE}+\mathrm{DM}\) and \(\mathrm{PQE}+\mathrm{VQS}\) have advantages on size performance.

Table 3 Classification results of \(\mathrm{PQE}+\mathrm{VQS}\) and \(\mathrm{QPE}+\mathrm{VQS}\)
Full size table
Table 4 Classification results of pairwise diversity measure methods
Full size table

Table 5 presents a performance comparison of the classifier ensembles by adopting the following three non-pairwise measures: the interrater agreement measure \(\kappa \), the KW measure, and the entropy measure. The three ensembles are labeled as \(\mathrm{PQE}+\kappa \), \(\mathrm{PQE}+\mathrm{KW}\), and \(\mathrm{PQE}+\mathrm{Entropy}\), respectively. In the experiments, \(\mathrm{PQE}+\kappa \) produces the highest accuracy of nine data sets among the entire 12 data sets. \(\mathrm{PQE}+\mathrm{KW}\) has two highest data sets, and \(\mathrm{PQE}+\mathrm{Entropy}\) generates only one highest accuracy. Therefore, \(\mathrm{PQE}+\kappa \) is regarded as an evaluation method to improve the CER framework. In addition, \(\mathrm{PQE}+\mathrm{Entropy}\) exhibits a very good performance in ensemble size. The averaged ensemble size is approximately ten.

Table 5 Classification results of the non-pairwise measures
Full size table

To access the precision and size performances of the improved CER framework, the \(\mathrm{PQE}+\mathrm{VQS}\) method, the \(\mathrm{PQE}+\kappa \) method, the \(\mathrm{PQE}+\mathrm{Entropy}\) method, and \(\mathrm{PQE}+\mathrm{QS}\) method are combined to clearly identify which method is the best. To identify whether the performances of the four methods developed in this paper are better than the existing methods, we used the results generated by CFS, random, and base for comparison. In the experiments, the correlation-based feature selection algorithm is used to build the original CER framework. The base classifier pool is built by using C4.5 as the base algorithm. Also, each randomly formed ensemble contains 20 individual classifiers. Table 6 shows the comparison of the six classifier ensembles and a base classifier.

Table 6 Classification performance comparison
Full size table

In Table 6, regarding pairwise diversity methods (\(\mathrm{PQE}+\mathrm{VQS}\) and \(\mathrm{PQE}+\mathrm{QS}\)), with the exception of the comper, libras, sonar, and water data sets, \(\mathrm{PQE}+\mathrm{VQS}\) has the best accuracy performance. Regarding \(\mathrm{PQE}+\kappa \) compared with \(\mathrm{PQE}+\mathrm{QS}\), with the exception of comper and cpart, the overall accuracy performance of \(\mathrm{PQE}+\kappa \) is better than that of \(\mathrm{PQE}+\mathrm{QS}\). By comparison, \(\mathrm{PQE}+\kappa \) produces the highest accuracy in eight data sets within the entire 12 data sets. Regarding all the methods, the \(\mathrm{PQE}+\mathrm{VQS}\), CFS, and random methods each generate, among the 12 data sets, one highest data set for accuracy.

Therefore, the above comparison proves that the diversity evaluation within the CER framework achieves better performance relative to the current classifier ensemble methods. In addition, for the data sets, comper and cpart, there is a significant difference in size performance between the \(\mathrm{PQE}+\kappa \) and CFS methods. Both methods contain a large number of classifiers. The \(\mathrm{PQE}+\mathrm{VQS}\) and \(\mathrm{PQE}+\mathrm{Entropy}\) methods use a fewer classifiers. However, the precision performance of these two methods is better than that of the base classifier. In this case, the \(\mathrm{PQE}+\mathrm{VQS}\) and \(\mathrm{PQE}+\mathrm{Entropy}\) are suitable where relative good accuracy, but fewer classifiers are required.

Figure 3 illustrates the size performances of all the classifier ensembles tested in this paper. The figure contains eight sub-figures, which represent the change in size for the four pairwise ensembles (Fig. 3a–d), the three non-pairwise ensembles (Figs. 3e–g), and the CFS ensemble (Fig. 3h). The numbers (from 1 to 12) along the x axes are the indices of the 12 data sets. Ensemble size (from 0 to 100) is shown along the y axes. As shown in Fig. 3, the performances of \(\mathrm{PQE}+\mathrm{QS}\) and CFS are the most unstable, and the average sizes are also high. The \(\mathrm{PQE}+\mathrm{DFM}\), \(\mathrm{PQE}+\mathrm{VQS}\), \(\mathrm{PQE}+\mathrm{Entropy}\) methods exhibit stable size performance. In terms of accuracy, \(\mathrm{PQE}+\mathrm{VQS}\), \(\mathrm{PQE}+\mathrm{Entropy}\) achieve a balance between size and accuracy.

Fig. 3
figure 3

The size of the four diversity methods

Full size image

4.1 Discussions

Based on the experimental results, in contrast to single classifiers, all the classifier ensembles with both the pairwise and non-pairwise evaluations achieve very high accuracy. In particular, the combination \(\mathrm{PQE}+\kappa \) exhibits the best accuracy; in addition, our previous work showed that the original CER framework with CFS was better than several current popular ensemble methods. In this paper, the CER framework with \(\mathrm{PQE}+\kappa \)’s performance is even better that the original CER’s. This finding may imply that the non-pairwise diversity measure can represent ensemble diversity more correctly.

The size of the seven ensembles are various. \(\mathrm{PQE}+\mathrm{QS}\) and \(\mathrm{PQE}+\kappa \) tend to achieve better accuracy, but their sizes are larger than the other ensembles. \(\mathrm{PQE}+\mathrm{DFM}\) tends to have the smallest size; however, the accuracy is not satisfied. \(\mathrm{PQE}+\mathrm{Entropy}\) and \(\mathrm{PQE}+\mathrm{VQS}\) balance the accuracy and size. Although the running time is not retained. The larger the ensemble size, the longer the running time. Thus, the running time for \(\mathrm{PQE}+\mathrm{Entropy}\) and \(\mathrm{PQE}+\mathrm{VQS}\) is shorter than that for the remaining ensembles.

In the experiments, the same evaluation method shows various performances on different data sets. Different evaluation methods also show varied performances on the same data set. For a certain application, choosing which evaluation method depends on the user’s objective, accuracy or running time. The new diversity method, \(\mathrm{PQE}+\mathrm{VQS}\) developed in this paper has stable size performance and achieves relatively accurate classifications.

5 Conclusion

This paper introduced a novel approach for integrating classifier diversity measures into a framework for CER. The approach was implemented by using four pairwise diversity algorithms and three non-pairwise diversity measure methods to calculate the diversity merits. One of the pairwise diversity measures was developed in this paper. The experimental evaluations demonstrate that the combination of the CER framework and the interrater agreement measurement achieves better classification accuracy. Also, the combination of the CER and the new pairwise diversity measures, developed in this paper, uses fewer ensemble members to maintain relative good accuracy. Smaller ensemble size consumes less computational running time. Therefore, the new pairwise method is suitable when the accuracy requirements are not very strict. However, when the computational running time requirements are more stringent, it is better to use the proposed approach.

Our present work can still be improved upon. In particular, the present work merely uses diversity and precision as the evaluation standards. However, the correlations amongst classifier ensemble and ensemble size were not considered during ensemble selection. In this case, the variances among the classifiers might be useful for future research. Additionally, in the present work, each evaluation method applied only one diversity measure in each evaluation session. Involving more than one diversity measure would be beneficial in the evaluation.