1 Introduction

A large literature on the analysis, classification, and clustering of data is now available (Jain et al. 2004; Law et al. 2005; Banerjee et al. 2004; Xiang et al. 2008). This is fueled by the fact that a large number of real-world problems can be easily approached as categorization tasks. The number of approaches and techniques is overwhelming. In particular, many generative models have been proposed for probabilistic classification (Kahn 2004). The Gaussian mixture model (Li et al. 2006; McLachlan and Peel 2000; Lu and Yao 2005) is perhaps the most well-known and widely used generative approach. Although the Gaussian mixture has proven to be an effective approach for data clustering when the partitions are Gaussian, it is known that this approach can fail in several real-world problems when the data are clearly non-Gaussian as deeply discussed and reported in the literature (Bouguila and Ziou 2006, 2007; Shoham et al. 2003). Indeed, a major difficulty of generative models is that they require the choice of a parent distribution to model the data. Thus, much of the work on finite mixture models has focused on determining appropriate choices for different kinds of data (e.g. discrete, binary, continuous, directional, etc.). For instance, we have shown recently that the Dirichlet (Bouguila and Ziou 2005) and generalized Dirichlet (GD) (Bouguila and Ziou 2006, 2007) distributions could be good alternatives to the Gaussian for data modelling. The main advantage of the GD over the Dirichlet is that it has a more general covariance structure which makes it more flexible and useful for a variety of real life applications from different disciplines. Therefore, in this work, in lieu of considering the classic Gaussian assumption, we base our work on the GD mixture.

The statistical models proposed in (Bouguila and Ziou 2006, 2007) have been based on finite GD mixtures and then needed to address challenging learning problems including model selection (i.e. determination of the optimal number of components), the choice of an initialization approach to avoid convergence to saddle points and over- or under-fitting problems. A recently introduced model provides a new strategy where the number of components is supposed to be infinite which allows to overcome problems related to model selection (Bouguila and Ziou 2010). This approach, based on Dirichlet processes, appears currently to offer the best results in terms of efficiency and model selection accuracy. Moreover, it avoids classic problems related to initialization sensitivity and convergence.

This work is an effort to deal with the classification of data in a flexible fashion and can be viewed as an major extension of the framework previously developed in (Bouguila and Ziou 2010). Indeed, in this paper, we go a step further by focusing on the problem of modelling grouped data where observations are organized into groups that we allow to remain statistically linked by sharing mixture components. Our solution is based on the adoption of a hierarchical nonparametric Bayesian framework namely hierarchical Dirichlet process (Teh et al. 2006; Teh and Jordan 2010), which is motivated by its promising results shown recently when modelling grouped data generated from various fields. Appropriate learning is a key issue when using generative models and is a quite difficult task, especially when dealing with high-dimensional data. Recently, variational Bayes learning has been shown to be an efficient alternative to both frequentist and purely Bayesian techniques (Fan and Bouguila 2013; Fan et al. 2013). We, therefore, develop a principled variational approach to learn the parameters of our hierarchical Dirichlet process of GD distributions model, which can be viewed as the second major contribution of this research work. The third contribution concerns the challenging problems that we have tackled to illustrate the usefulness of our approach namely images categorization and web service intrusion detection.

The rest of the article is organized as follows. In Sect. 2 we present the basic hierarchical Dirichlet process mixture model and its adoption to GD distributions. The model’s learning approach, based on variational inference, as well as the complete fitting algorithm are detailed in Sect. 3. Section  4 presents and discusses the experiments and simulations conducted to assess the viability and efficiency of the proposed model. Section 5 concludes the paper.

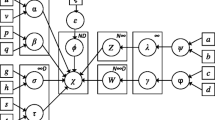
2 Hierarchical Dirichlet process mixture of GD distributions

In this section, we introduce our hierarchical Dirichlet process mixture model of GD distributions, which may also be referred to as the hierarchical infinite GD mixture model.

2.1 Hierarchical Dirichlet process mixture model

The hierarchical Dirichlet process is built on the Dirichlet process (Korwar and Hollander 1973; Ferguson 1983) with a Bayesian hierarchy in which the base distribution of the Dirichlet process is itself distributed according to a Dirichlet process. A two-level hierarchical Dirichlet process model can be defined as the following: given a grouped data set \(\mathcal {X}\) with \(M\) groups, where each group is associated with a Dirichlet process \(G_j\), and this indexed set of Dirichlet processes \(\{G_j\}\) shares a global (or base) distribution \(G_0\) which is itself distributed according to a Dirichlet process with the base distribution \(H\) and concentration parameter \(\gamma \):

$$\begin{aligned} G_0&\sim \mathrm {DP}(\gamma ,H)\nonumber \\ G_j&\sim \mathrm {DP}(\lambda ,G_0) \qquad \text {for}\,\text {each}\, j, j \in \{1, \ldots , M\} \end{aligned}$$
(1)

where \(j\) is an index for each group of the data set. Please notice that the above hierarchical Dirichlet process can be readily extended to contain more than two levels.

In this work, the hierarchical Dirichlet process is represented using the stick-breaking construction (Sethuraman 1994; Ishwaran and James 2001). In the global-level construction, the global measure \(G_0\) is distributed according to the Dirichlet process \(\mathrm {DP}(\gamma ,H)\) as

$$\begin{aligned} G_0&= \sum _{k=1}^\infty \psi _k\delta _{\varOmega _k} \qquad \psi _k = \psi ^{\prime }_k\prod _{s=1}^{k-1}(1-\psi ^{\prime }_s) \nonumber \\&\psi '_k \sim \mathrm {Beta}(1,\gamma ) \qquad \varOmega _k \sim H \end{aligned}$$
(2)

where \(\delta _{\varOmega _k}\) is an atom at \(\varOmega _k\), and \(\{\varOmega _k\}\) is a set of independent random variables drawn from \(H\). The stick-breaking variable \(\psi _k\) satisfies \(\sum _{k=1}^\infty \psi _k=1\), and is obtained by recursively breaking a unit length stick into an infinite number of pieces such that the size of each successive piece is proportional to the rest of the stick. Since \(G_0\) is the base distribution of the Dirichlet processes \(G_j\) and has the stick-breaking representation as shown in Eq. (2), the atoms \(\varOmega _k\) are shared among all \(\{G_j\}\) and only differ in weights according to the property of Dirichlet process (Teh et al. 2006).

Motivated by (Wang et al. 2011), we also apply the conventional stick-breaking representation to construct each group-level Dirichlet process \(G_j\) as

$$\begin{aligned} G_j&= \sum _{t=1}^\infty \pi _{jt}\delta _{\varpi _{jt}} \qquad \pi _{jt} = \pi ^{\prime }_{jt}\prod _{s=1}^{t-1}(1-\pi ^{\prime }_{js}) \nonumber \\&\pi ^{\prime }_{jt} \sim \mathrm {Beta}(1,\lambda ) \qquad \varpi _{jt} \sim G_0 \end{aligned}$$
(3)

where \(\delta _{\varpi _{jt}}\) are group-level atoms at \(\varpi _{jt}\), \(\{\pi _{jt}\}\) is a set of stick-breaking weights which satisfies \(\sum _{t=1}^\infty \pi _{jt}=1\). Since \(\varpi _{jt}\) is distributed according to the base distribution \(G_0\), it takes on the value \(\varOmega _k\) with probability \(\psi _k\). Next, we introduce a binary latent variable \(W_{jtk}\) as an indicator variable, such that \(W_{jtk} \in \{0,1\}\), \(W_{jtk} = 1\) if \(\varpi _{jt}\) maps to the global-level atom \(\varOmega _k\) which is indexed by \(k\); otherwise, \(W_{jtk} = 0\). Thus, we can have \(\varpi _{jt}=\varOmega _k^{W_{jtk}}\). Accordingly, group-level atoms \(\varpi _{jt}\) do not need to be explicitly represented. The indicator variable \(\mathbf {W}= (W_{jt1}, W_{jt2}, \ldots )\) is distributed as

$$\begin{aligned} p(\mathbf {W}|\varvec{\psi })=\prod _{j=1}^M\prod _{t=1}^\infty \prod _{k=1}^\infty \psi _k^{W_{jtk}} \end{aligned}$$
(4)

Since \(\varvec{\psi }\) is a function of \(\varvec{\psi }^{\prime }\) according to the stick-breaking construction of the Dirichlet process as shown in Eq. (2), we can rewrite \(p(\mathbf {W})\) as

$$\begin{aligned} p(\mathbf {W}|\varvec{\psi }^{\prime })=\prod _{j=1}^M\prod _{t=1}^\infty \prod _{k=1}^\infty \left[ \psi _k'\prod _{s=1}^{k-1}(1-\psi _s')\right] ^{W_{jtk}} \end{aligned}$$
(5)

The prior distribution of \(\varvec{\psi }^{\prime }\) is a specific Beta distribution according to Eq. (2)

$$\begin{aligned} p(\varvec{\psi }^{\prime })= \prod _{k=1}^\infty {\mathrm {Beta}}(1,\gamma _k)= \prod _{k=1}^\infty \gamma _k(1-\psi _k')^{\gamma _k-1} \end{aligned}$$
(6)

For the grouped data set \(\mathcal {X}\), let \(i\) index the observations within each group \(j\). We assume that each variable \(\theta _{ji}\) is a factor corresponding to an observation \(X_{ji}\), and the factors \(\varvec{\theta }_j=(\theta _{j1},\theta _{j2},\ldots )\) are distributed according to the Dirichlet process \(G_j\), one for each \(j\). Then, the likelihood function can be defined as

$$\begin{aligned} \begin{aligned}&\theta _{ji}|G_j \sim G_j\\&X_{ji}|\theta _{ji} \sim F(\theta _{ji}) \end{aligned} \end{aligned}$$
(7)

where \(F(\theta _{ji})\) represents the distribution of the observation \(X_{ji}\) given \(\theta _{ji}\). The base distribution \(H\) of \(G_0\) provides the prior distribution for the factors \(\theta _{ji}\). This setting is known as the hierarchical Dirichlet process mixture model, in which each group is associated with a mixture model, and the mixture components are shared among these mixture models due to the sharing of atoms \(\varOmega _k\) among all \(\{G_j\}\).

Since each factor \(\theta _{ji}\) is distributed according to \(G_j\) based on Eq. (7), it takes the value \(\varpi _{jt}\) with probability \(\pi _{jt}\). We then place a binary indicator variable \(Z_{jit} \in \{0,1\}\) for \(\theta _{ji}\). That is, \(Z_{jit} = 1\) if \(\theta _{ji}\) is associated with component \(t\) and maps to the group-level atom \(\varpi _{jt}\); otherwise, \(Z_{jit} = 0\). Thus, we have \(\theta _{ji} = \varpi _{jt}^{Z_{jit}}\). Since \(\varpi _{jt}\) also maps to the global-level atom \(\Omega _k\) as we mentioned previously, we then have \(\theta _{ji} = \varpi _{jt}^{Z_{jit}}=\Omega _k^{W_{jtk}Z_{jit}}\). The indicator variable \(\mathbf {Z}= (Z_{ji1}, Z_{ji2}, \ldots )\) is distributed as

$$\begin{aligned} p(\mathbf {Z}|\varvec{\pi })=\prod _{j=1}^M\prod _{i=1}^N\prod _{t=1}^\infty \pi _{jt}^{Z_{jit}} \end{aligned}$$
(8)

Since \(\varvec{\pi }\) is a function of \(\varvec{\pi }'\) according to the stick-breaking construction of the Dirichlet process as shown in Eq. (3), we then have

$$\begin{aligned} p(\varvec{Z}|\varvec{\pi }^{\prime })=\prod _{j=1}^M\prod _{i=1}^N\prod _{t=1}^\infty \left[ \pi _{jt}^{\prime }\prod _{s=1}^{t-1}(1-\pi _{js}^{\prime })\right] ^{Z_{jit}} \end{aligned}$$
(9)

The prior distribution of \(\varvec{\pi }^{\prime }\) is a specific Beta distribution as described in Eq. (3) as

$$\begin{aligned} p(\varvec{\pi }^{\prime })= \prod _{j=1}^M\prod _{t=1}^\infty {\mathrm {Beta}}(1,\lambda _{jt})= \prod _{j=1}^M\prod _{t=1}^\infty \lambda _{jt}(1-\pi _{jt}^{\prime })^{\lambda _{jt}-1} \end{aligned}$$
(10)

2.2 Hierarchical infinite GD mixture model

In our work, we focus on a specific form of hierarchical Dirichlet process mixture model where each observation within a group is drawn from a mixture of GD distributions. Since Dirichlet process mixture models are often referred to as infinite mixture models, the proposed model can then be considered as a hierarchical infinite GD mixture model. The motivation of choosing GD mixture is due to its good modelling performance as shown, for instance, in Bouguila and Ziou (2006, 2007), Fan and Bouguila (2013), Fan et al. (2013).

If a \(D\)-dimensional random vector \(\mathbf {Y} = (Y_1,\ldots ,Y_D)\) is distributed according to a GD distribution with positive parameters \(\varvec{\alpha } = (\alpha _1,\ldots ,\alpha _D)\) and \(\varvec{\beta }_j = (\beta _1,\ldots ,\beta _D)\), then its probability density function (pdf) is defined by

$$\begin{aligned} \mathrm {GD}(\mathbf {Y}|\varvec{\alpha },\varvec{\beta }) = \prod _{l=1}^D\frac{\varGamma (\alpha _l + \beta _l)}{\varGamma (\alpha _l)\varGamma (\beta _l)} Y_l^{\alpha _l-1}\left( 1-\sum _{f=1}^lY_f\right) ^{\gamma _l} \end{aligned}$$
(11)

where \(\varGamma (\cdot )\) is the gamma function, \(\sum _{l=1}^D Y_l < 1\) and \(Y_l>0\) for \(l = 1,\ldots ,D\), \(\alpha _l>0\), \(\beta _l>0\), \(\gamma _l =\beta _l-\alpha _{l+1}-\beta _{l+1}\) for \(l = 1,\ldots ,D-1\), and \(\gamma _D = \beta _D -1\). It is noteworthy that GD distribution has a more general covariance structure (can be positive or negative) than Dirichlet distribution which makes it more practical and useful.

By applying an interesting mathematical property of the GD distribution which is thoroughly discussed in Boutemedjet et al. (2009), we can use a geometric transformation to transform the original data point \(\mathbf {Y}\) into another \(D\)-dimensional data point \(\mathbf {X}\) with independent features as

$$\begin{aligned} {\mathrm {GD}}(\mathbf {X}|\varvec{\alpha },\varvec{\beta })= \prod _{l=1}^D{\mathrm {Beta}}(X_{l}|\alpha _l,\beta _l) \end{aligned}$$
(12)

where \(\mathbf {X} = (X_{1}, \ldots , X_{D})\), \(X_{1} = Y_{1}\) and \(X_{l} = Y_{l}/(1-\sum _{f=1}^{l-1}Y_{f})\) for \(l>1\), and \({\mathrm {Beta}}(X_{l}|\alpha _l,\beta _l)\) is a Beta distribution defined with parameters \((\alpha _l,\beta _l)\). By doing this, the estimation of a \(D\)-dimensional GD distribution is transformed to \(D\) estimations of one-dimensional Beta distributions which may facilitate the inference process for multidimensional data (Boutemedjet et al. 2009).

Now for the grouped data set \(\mathcal {X}\) with \(M\) groups, we assume that each \(D\)-dimensional data vector \(\mathbf {X}_{ji} = (X_{ji1},\!\ldots \!,X_{jiD})\) is drawn from a hierarchical infinite GD mixture model, then we have the likelihood function of the proposed hierarchical infinite GD mixture model with latent variables as

$$\begin{aligned} p(\mathcal {X})=\prod _{j=1}^M\prod _{i=1}^N\prod _{t=1}^\infty \prod _{k=1}^\infty \left[ \prod _{l=1}^D\mathrm {Beta}(X_{jil}|\alpha _{kl},\beta _{kl})\right] ^{Z_{jit}W_{jtk}} \end{aligned}$$
(13)

Next, we need to place prior distributions over parameters \(\varvec{\alpha }\) and \(\varvec{\beta }\) of the Beta distribution. Although Beta distribution belongs to the exponential family and has a formal conjugate prior, it is analytically intractable. Thus, we adopt Gamma distribution to approximate the conjugate prior by assuming that these Beta parameters are statistically independent as

$$\begin{aligned} p(\varvec{\alpha })&=\mathcal {G}(\varvec{\alpha }|\mathbf {u},\mathbf {v}) =\prod _{k=1}^\infty \prod _{l=1}^D\frac{v_{kl}^{u_{kl}}}{\varGamma (u_{kl})}\alpha _{kl}^{u_{kl}-1}\mathrm{e}^{-v_{kl}\alpha _{kl}}\end{aligned}$$
(14)
$$\begin{aligned} p(\varvec{\beta })&=\mathcal {G}(\varvec{\beta }|\mathbf {g},\mathbf {h})= \prod _{k=1}^\infty \prod _{l=1}^D\frac{h_{kl}^{g_{kl}}}{\varGamma (g_{kl})}\beta ^{g_{kl}-1}\mathrm{e}^{-h_{kl}\beta _{kl}} \end{aligned}$$
(15)

where \(\mathcal {G}(\cdot )\) is the Gamma distribution with positive parameters.

3 Variational model learning

Variational inference (Attias 1999; Bishop 2006) is a deterministic approximation technique that is used to find tractable approximations for posterior distributions of a variety of statistical models. The literature of the past decade is abundant with papers that have considered successfully variational learning. In this section, we propose a truncated variational inference framework to learn the stick-breaking representation of the hierarchical infinite GD mixture model. To simplify notation, we define \(\varTheta = (\mathbf {Z},\mathbf {W},\varvec{\psi }^{\prime },\varvec{\pi }^{\prime },\varvec{\alpha },\varvec{\beta })\) as the set of latent variables and unknown random variables. Similarly, the set of all observed variables is represented by \(\mathcal {X}\). The central idea in variational learning is to find an approximation \(q(\varTheta )\) for the true posterior distribution \(p(\varTheta |\mathcal {X})\) by maximizing the lower bound of the logarithm of the marginal likelihood \(p(\mathcal {X})\). By applying Jensen’s inequality, this lower bound can be found as

$$\begin{aligned} \mathcal {L}(q) = \int q(\varTheta )\ln [ p(\mathcal {X},\varTheta )/q(\varTheta )] \mathrm{d}\varTheta \end{aligned}$$
(16)

In our work, we apply the truncation technique as described in (Blei and Jordan 2005) to truncate the variational approximations of global- and group-level Dirichlet processes at \(K\) and \(T\), such that

$$\begin{aligned} \psi _K^{\prime }&= 1, \quad \sum _{k=1}^K\psi _k = 1, \quad \psi _k = 0 \;\;\text {when}\;\; k>K \end{aligned}$$
(17)
$$\begin{aligned} \pi _{jT}^{\prime }&= 1, \quad \sum _{t=1}^T\pi _{jt} = 1, \quad \pi _{jt} = 0 \;\;\text {when}\;\; t>T \end{aligned}$$
(18)

where the truncation levels \(K\) and \(T\) are variational parameters which can be freely initialized and will be optimized automatically during the learning process. Moreover, we adopt a factorial approximation to factorize \(q(\varTheta )\) into disjoint tractable distributions. Using the truncated stick-breaking representations and the factorization assumption, we then have

$$\begin{aligned} q(\varTheta ) = q(\mathbf {Z})q(\mathbf {W})q(\varvec{\pi }^{\prime })q(\varvec{\psi }^{\prime })q(\varvec{\alpha })q(\varvec{\beta }) \end{aligned}$$
(19)

To maximize the lower bound \(\mathcal {L}(q)\), we need to make a variational optimization of it with respect to each of the factors \(q_i(\varTheta _i)\) in turn. The general expression for the optimal solution to a specific variational factor \(q_s(\varTheta _s)\) is given by

$$\begin{aligned} q_s(\Theta _s) = \frac{\exp \bigl \langle \ln p(\mathcal {X},\Theta )\bigr \rangle _{i\ne s}}{\int \exp \bigl \langle \ln p(\mathcal {X},\Theta )\bigr \rangle _{i\ne s}\mathrm{d}\varTheta } \end{aligned}$$
(20)

where \(\langle \cdot \rangle _{i\ne s}\) is the expectation with respect to all the distributions of \(q_i(\varTheta _i)\) except for \(i = s\).

Therefore, the optimal solutions for the factors of the variational posterior can then be obtained by applying Eq. (20) to each of the factor, such that

$$\begin{aligned}&q(\mathbf {Z})= \prod _{j=1}^M\prod _{i=1}^N\prod _{t=1}^T\rho _{jit}^{Z_{jit}} \end{aligned}$$
(21)
$$\begin{aligned}&q(\mathbf {W})=\prod _{j=1}^M\prod _{t=1}^T\prod _{k=1}^K\vartheta _{jtk}^{W_{jtk}}\end{aligned}$$
(22)
$$\begin{aligned}&q(\varvec{\pi }^{\prime })= \prod _{j=1}^M\prod _{t=1}^T {\mathrm {Beta}}(\pi _{jt}^{\prime }|a_{jt},b_{jt})\end{aligned}$$
(23)
$$\begin{aligned}&q(\varvec{\psi }^{\prime })= \prod _{k=1}^K{\mathrm {Beta}}(\psi _k^{\prime }|c_k,d_k) \end{aligned}$$
(24)
$$\begin{aligned}&q(\varvec{\alpha })= \prod _{k=1}^K \prod _{l=1}^D\mathcal {G}(\alpha _{kl}|\tilde{u}_{kl},\tilde{v}_{kl})\end{aligned}$$
(25)
$$\begin{aligned}&q(\varvec{\beta })= \prod _{k=1}^K \prod _{l=1}^D \mathcal {G}(\beta _{kl}|\tilde{g}_{kl},\tilde{h}_{kl}) \end{aligned}$$
(26)

where the corresponding hyperparameters in the above equations can be calculated as the following:

The hyperparameter \(\rho _{jit}\) of the factor \(q(\mathbf {Z})\) is calculated by

$$\begin{aligned} \rho _{jit} = \frac{\exp (\widetilde{\rho }_{jit})}{\sum _{f=1}^T\exp (\widetilde{\rho }_{jif})} \end{aligned}$$
(27)

where

$$\begin{aligned}&\widetilde{\rho }_{jit} = \sum _{k=1}^K\langle W_{jtk}\rangle \sum _{l=1}^D\left[ (\bar{\alpha }_{kl}-1)\ln X_{jil}+(\bar{\beta }_{kl}-1)\right. \nonumber \\&\quad \,\left. \ln (1-X_{jil})+\widetilde{\mathcal {R}}_{kl}\right] +\langle \ln \pi _{jt}^{\prime }\rangle + \sum _{s=1}^{t-1}\langle \ln (1-\pi _{js}^{\prime })\rangle \end{aligned}$$
(28)
$$\begin{aligned} {\widetilde{\mathcal {R}}}&= \ln \frac{\varGamma (\bar{\alpha }\!+\!\bar{\beta })}{\varGamma (\bar{\alpha })\varGamma (\bar{\beta })} \!+\! \bar{\alpha }[\varPsi (\bar{\alpha }\!+\!\bar{\beta }) - \varPsi (\bar{\alpha })]\big (\big \langle \ln \alpha \big \rangle \!-\!\ln \bar{\alpha }\big )\nonumber \\&\quad \,+\bar{\beta }[\varPsi (\bar{\alpha }+\bar{\beta }) - \varPsi (\bar{\beta })]\big (\big \langle \ln \beta \big \rangle -\ln \bar{\beta }\big ) \nonumber \\&\quad \,+\frac{1}{2}\bar{\alpha }^2[\varPsi ^{\prime }(\bar{\alpha }+\bar{\beta })- \varPsi ^{\prime }(\bar{\alpha })]\bigl \langle (\ln \alpha -\ln \bar{\alpha })^2\bigr \rangle \nonumber \\&\quad \,+\frac{1}{2}\bar{\beta }^2[\varPsi ^{\prime }(\bar{\alpha }+\bar{\beta })- \varPsi ^{\prime }(\bar{\beta })]\bigl \langle (\ln \beta -\ln \bar{\beta })^2\bigr \rangle \nonumber \\&\quad \,+\bar{\alpha }\bar{\beta }\varPsi ^{\prime }(\bar{\alpha }+\bar{\beta })(\bigl \langle \ln \alpha \bigr \rangle -\ln \bar{\alpha }) (\bigl \langle \ln \beta \bigr \rangle -\ln \bar{\beta }) \end{aligned}$$
(29)

where \(\varPsi (\cdot )\) is the digamma function.

The hyperparameter \(\vartheta _{jtk}\) of the factor \(q(\mathbf {W})\) is calculated by

$$\begin{aligned} \vartheta _{jtk} = \frac{\exp (\widetilde{\vartheta }_{jtk})}{\sum _{f=1}^K\exp (\widetilde{\vartheta }_{jtf})} \end{aligned}$$
(30)

where

$$\begin{aligned} \widetilde{\vartheta }_{jtk}&= \sum _{i=1}^N\langle Z_{jit}\rangle \sum _{l=1}^D\left[ (\bar{\alpha }_{kl}-1)\ln X_{jil}+(\bar{\beta }_{kl}-1)\right. \nonumber \\&\left. \ln (1-X_{jil}) +\widetilde{\mathcal {R}}_{kl}\right] +\langle \ln \psi _k^{\prime }\rangle + \sum _{s=1}^{k-1}\langle \ln (1-\psi _s^{\prime })\rangle \nonumber \\ \end{aligned}$$
(31)

The hyperparameters \(a_{jt}\) and \(b_{jt}\) of the factor \(q(\varvec{\pi }')\) are calculated by

$$\begin{aligned} a_{jt}=1+\sum _{i=1}^N\langle Z_{jit}\rangle , \qquad b_{jt} = \lambda _{jt} + \sum _{i=1}^N\sum _{s=t+1}^T\langle Z_{jis}\rangle \end{aligned}$$
(32)

The hyperparameters \(c_k\) and \(d_k\) of the factor \(q(\varvec{\psi }^{\prime })\) are calculated by

$$\begin{aligned} c_k=1+\sum _{j=1}^M\sum _{t=1}^T\langle W_{jtk}\rangle , \quad d_k = \gamma _k +\sum _{j=1}^M\sum _{t=1}^T\sum _{s=k+1}^K\langle W_{jts}\rangle \end{aligned}$$
(33)

The hyperparameters \(\tilde{u}_{kl}\) and \(\tilde{v}_{kl}\) of the factor \(q(\varvec{\alpha })\) are calculated by

$$\begin{aligned} \tilde{u}_{kl}&= u_{kl} + \sum _{j=1}^M\sum _{t=1}^T \langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \bar{\alpha }_{kl}\left[ \varPsi (\bar{\alpha }_{kl}+\bar{\beta }_{kl})\right. \nonumber \\&\quad \,\,\left. - \varPsi (\bar{\alpha }_{kl})+ \bar{\beta }_{kl} \varPsi '(\bar{\alpha }_{kl}+\bar{\beta }_{kl})(\langle \ln \beta _{kl}\rangle -\ln \bar{\beta }_{kl})\right] \end{aligned}$$
(34)

and

$$\begin{aligned} \tilde{v}_{kl} = v_{kl}-\sum _{j=1}^M\sum _{t=1}^T\langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \ln X_{jil} \end{aligned}$$
(35)

The hyperparameters \(\tilde{g}_{kl}\) and \(\tilde{h}_{kl}\) of the factor \(q(\varvec{\beta })\) are calculated by

$$\begin{aligned} {\tilde{g}}_{kl}&= g_{kl} + \sum _{j=1}^M\sum _{t=1}^T \langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \bar{\beta }_{kl}\left[ \varPsi (\bar{\alpha }_{kl}+\bar{\beta }_{kl})\right. \nonumber \\&\quad \left. -\, \varPsi (\bar{\beta }_{kl})+ \bar{\alpha }_{kl} \varPsi ^{\prime }(\bar{\alpha }_{kl}+\bar{\beta }_{kl})(\langle \ln \alpha _{kl}\rangle -\ln \bar{\alpha }_{kl})\right] \nonumber \\ \end{aligned}$$
(36)

and

$$\begin{aligned} {\tilde{h}}_{kl} = h_{kl}-\sum _{j=1}^M\sum _{t=1}^T\langle W_{jtk}\rangle \sum _{i=1}^N\langle Z_{jit}\rangle \ln (1-X_{jil}) \end{aligned}$$
(37)

The expected values in the above formulas are given by

$$\begin{aligned}&\bar{\alpha }_{kl} = \frac{\tilde{u}_{kl}}{\tilde{v}_{kl}}, \quad \bar{\beta }_{kl} = \frac{\tilde{g}_{kl}}{\tilde{h}_{kl}},\nonumber \\&\langle Z_{jit}\rangle =\rho _{jit}, \quad \langle W_{jtk}\rangle =\vartheta _{jtk} \end{aligned}$$
(38)
$$\begin{aligned}&\langle \ln \alpha _{kl}\rangle = \varPsi (\tilde{u}_{kl}) -\ln \tilde{v}_{kl},\nonumber \\&\langle \ln \beta _{kl}\rangle =\varPsi (\tilde{g}_{kl}) - \ln \tilde{h}_{kl} \end{aligned}$$
(39)
$$\begin{aligned}&\langle \ln \pi _{jt}^{\prime }\rangle =\varPsi (a_{jt})-\varPsi (a_{jt}+b_{jt}) \end{aligned}$$
(40)
$$\begin{aligned}&\langle \ln (1-\pi _{jt}^{\prime })\rangle =\varPsi (b_{jt})-\varPsi (a_{jt}+b_{jt}) \end{aligned}$$
(41)
$$\begin{aligned}&\langle \ln \psi _k^{\prime }\rangle =\varPsi (c_k)-\varPsi (c_k+d_k) \end{aligned}$$
(42)
$$\begin{aligned}&\langle \ln (1-\psi _k^{\prime })\rangle = \varPsi (d_k)-\varPsi (c_k+d_k) \end{aligned}$$
(43)

Since the solutions to the variational factors are coupled together through the expected values of other factors, this optimization process can be solved in a way analogous to the EM algorithm and the complete algorithm is summarized in Algorithm 1. The convergence of this variational learning algorithm is guaranteed and can be monitored through inspection of the variational lower bound (Bishop 2006).

figure a

4 Experiments

4.1 Design of experiments

We evaluate the effectiveness of the proposed hierarchical infinite GD mixture model (referred to as HInGD) on two challenging real-life problems. The first one concerns visual scenes classification and more specifically the discrimination between different breeds of cats and dogs from images. This task is extremely challenging since cats and dogs are highly deformable and different breeds may differ only by a few subtle phenotypic details (Parkhi et al. 2012). The second application is web service intrusion detection which has attracted a lot of attention recently. We conducted our experiments using a computer with Intel’s Core i7 processor @2.00 GHz. In our experiments, we initialize the global truncation level \(K\) to 600, and the group truncation level \(T\) to 100. This is because in general, the number of clusters in the global level is much larger than the one in the group level. The initial values of involved hyperparameters are set as the following: \((u_{kl}, v_{kl}, g_{kl}, h_{kl}, \lambda _{jt},\gamma _k) = (0.25,0.01,0.25,0.01,0.1,0.1)\). These specific choices were chosen according to our experimental results and were found convenient in our case. As a formal approach to choose the initial hyperparameters values does not exist, it may be helpful in practise to run the optimization several times using different initializations to find a good maximum since multiple maxima may exist in the variational bound. It is noteworthy that the Bayesian nature of the proposed learning algorithm makes it less sensitive to initialization as compared to frequentist techniques for instance.

4.2 Images categorization

4.2.1 Methodology

Image categorization has been the topic of extensive research in the past which may be motivated by its various applications such as object detection, recognition, and retrieval (Lamdan et al. 1988; Agarwal and Roth 2002; Matas et al. 2002; Lazebnik et al. 2004; Rasiwasia and Vasconcelos 2008). Here, we focus on a specific image categorization problem that has received some attention recently namely the classification of images representing cats and dogs (Parkhi et al. 2012). We perform this classification using the proposed HInGD. Our categorization methodology is summarized as following: first, we extract and normalize PCA-SIFT descriptorsFootnote 1 (36-dimensional) (Ke and Sukthankar 2004) from raw images using the Difference-of-Gaussian (DoG) detector (Mikolajczyk and Schmid 2004). Then, these extracted image features are modelled using the proposed HInGD. Specifically, each image \(\mathcal {I}_j\) is considered as a “group” and is therefore associated with an infinite mixture model \(G_j\). Thus, each extracted PCA-SIFT feature vector \(X_{ji}\) of the image \(\mathcal {I}_j\) is supposed to be drawn from the infinite mixture model \(G_j\), where the mixture components of \(G_j\) can be considered as “visual words”. A global vocabulary is constructed and is shared among all groups (images) through the common global infinite mixture model \(G_0\) of our hierarchical model. This setting matches the desired design of a hierarchical Dirichlet process mixture model. It is noteworthy that an important step in image categorization approaches with bag-of-visual words representation is the construction of visual vocabulary. Nevertheless, most of the previously invented approaches have to apply a separate vector quantization method (such as \(K\)-means) to build the visual vocabulary, where the size of the vocabulary is normally chosen manually. In our approach, the construction of the visual vocabulary is part of our hierarchical Dirichlet process mixture framework, and, therefore, the size of the vocabulary (i.e. the number of mixture components in the global-level mixture model) can be automatically inferred from the data thanks to the property of nonparametric Bayesian model. Then, the “bag-of-words” paradigm is employed and a histogram of “visual words” for each image is computed. Since the goal of our experiment is to determine which image category (breeds of cats and dogs) that a testing image \(\mathcal {I}_j\) belongs to, we also need to introduce an indicator variable \(B_{jm}\) associated with each image (or group) in our hierarchical Dirichlet process mixture framework. \(B_{jm}\) denotes that image \(\mathcal {I}_j\) comes from category \(m\) and is drawn from another infinite mixture model which is truncated at level \(J\). This means that we need to add a new level of hierarchy to our hierarchical infinite mixture model with a sharing vocabulary among all image categories. In this experiment, we truncate \(J\) to 50 and initialize the hyperparameter of the mixing probability of \(B_{jm}\) to 0.05. Finally, we assign testing images to the appropriate categories according to Bayes’ decision rule.

4.2.2 Data set

We conducted our experiments of categorizing cats and dogs using a publicly available database namely the Oxford-IIIT Pet database (Parkhi et al. 2012).Footnote 2 This database contains 7,349 images of cats and dogs in total with 12 different breeds of cats and 25 different breeds of dogs. Each of these breeds contains about 200 images. We randomly divided this database into two halves: one for training (to learn the model and build the visual vocabulary), the other one for testing. Sample images from the database are shown in Fig. 1 (cats) and Fig. 2 (dogs).

Fig. 1
figure 1

Sample cat images from the Oxford-IIIT Pet database. a Abyssinian, b Bengal, c Birman, d Bombay, e British Shorthair, f Egyptian Mau, g Persian, h Ragdoll

Full size image
Fig. 2
figure 2

Sample dog images from the Oxford-IIIT Pet database. a Basset hound, b Boxer, c Chihuahua, d Havanese, e Keeshond, f Pug, g Samyod, h Shiba inu

Full size image

4.2.3 Results

In this experiment, our goal is to demonstrate the advantages of using hierarchical Dirichlet process framework over the conventional Dirichlet process one, as well as GD distribution over the Gaussian. Therefore, we compared the categorization results using the proposed HInGD model with three other mixture models including infinite GD mixture (InGD) model, hierarchical infinite Gaussian mixture (HInGau) model and infinite Gaussian mixture (InGau) model. All of these models were learned using variational inference. For the experiments of using InGD and InGau models, the visual vocabularies were built using the \(K\)-means algorithm and the sizes of the visual vocabularies were manually set to 500. We evaluated the categorization performance by running the approach 30 times.

First, we focus on discriminating different breeds of cats (12 breeds) and dogs (25 breeds), respectively. The average breed discrimination performances of our approach and the three other tested approaches are shown in Table 1. According to these results, the proposed HInGD approach was able to provide the highest categorization accuracies (54.72 % for cats and 42.93 % for dogs) among all tested approaches. The differences in accuracy between the HInGD and the other tested models are statistically significant according to Student’s \(t\) test (i.e. for different runs, we have observed \(p\) values between 0.017 and 0.038 in the case of discriminating cats images, and \(p\) values between 0.022 and 0.041 for discriminating dogs images). Moreover, HInGD and HInGau outperformed InGD and InGau, respectively, which demonstrates the merits of using hierarchical Dirichlet process framework over the conventional Dirichlet process. Better modelling capabilities of using GD mixture models over Gaussian mixtures are also illustrated in Table 1, in terms of higher categorization accuracies obtained by HInGD and InGD than HInGau and InGau.

Table 1 The average categorization performance (%) and the standard deviation obtained over 30 runs using different approaches
Full size table

Next, we evaluated our approach and the other three approaches on discriminating different breeds of cats and dogs using the whole Oxford-IIIT Pet database (i.e. we do not separate cat and dog images). The corresponding results are summarized in Table 2. As we can see in this table, the proposed HInGD approach again provided higher categorization accuracy rate (40.78 %) than the other tested approaches (the differences are statistically significant as shown by a Student’s \(t\) test, \(p\) values between 0.029 and 0.043).

Table 2 The average categorization performance (%) and the standard deviation obtained over 30 runs using different approaches
Full size table

4.3 Web service intrusion detection

4.3.1 Problem statement

Recent advances in web technologies and the constant growth of the Internet have led to many online service applications. Examples include e-commerce, social networks, online banking, business intelligence, web search engines, etc. An important feature of these web services is that they are based on software applications running at the server-side and generating new web content in an online fashion, which makes them flexible to exchange information on the Internet (Pearce et al. 2005; Desmet et al. 2005; Mehdi et al. 2012). The flexibility of web services poses also vulnerabilities which make them the targets for attacks (e.g. code injection attacks, SQL/XML injection, buffer overflow attacks, denial of service, etc.) by cyber-criminals who can collect confidential information from servers or even compromise them (Pinzen et al. 2010; Dagdee and Thakar 2008; Yee et al. 2007; Gruschka and Luttenberger 2006; Jensen et al. 2007). Then, there is an urgent need to protect the servers on which the applications are running (Zolotukhin et al. 2013; Zolotukhin and Hamalainen 2013; Jensen et al. 2009; Corona and Giacinto 2010). Indeed, intrusion detection systems (IDSs) need to be deployed. An overview of current intrusion detection techniques and related issues was proposed in Zhou et al. (2010) and Tsai et al. (2009). Recently, data mining and machine learning approaches have been used in this growing area to improve the performance of existing systems (Patcha and Park 2007; Laskov et al. 2005; Zanero and Savaresi 2004; Fan et al. 2011; Horng et al. 2011; Khan et al. 2007). The key idea for these works is to use machine learning techniques (e.g. decision trees, artificial neural networks, support vector machines, mixture models, etc.) to train a classifier and to recognize attacks based on a list of features, which generally reduces the intrusion detection problem to an adversarial learning task (Lowd and Meek 2005).

Based on the analysis methods, IDSs are usually classified into two main categories: misuse (i.e. signature-based) detection and anomaly detection systems (Northcutt and Novak 2002). In misuse detection systems, the goal is to detect the occurrence of attacks that have been previously identified as intrusions. For this type of IDS, attacks must be known a priori. Misuse detection can be viewed then as a supervised learning problem. Alternatively, anomaly detection systems detect unknown attacks by observing deviations from normal activities of the system. It is based on the assumption that intrusive activities are noticeably different from normal system activities and hence detectable. Data clustering and unsupervised learning approaches have been widely used to develop anomaly detection systems. Several of recent clustering approaches quantify deviation from normal behaviour using thresholds (see, for instance, Pereira and Jamhour 2013; Zolotukhin et al. 2013; Zolotukhin and Hamalainen 2013). Unlike these approaches we consider here our HInGD to model normal traffic data and then to automatically detect potential intrusions (i.e. anomalous traffic).

4.3.2 Results

The proposed framework is tested using logs collected from a real-life web service (from several Apache servers) in a two-week time interval. The collected data set contains normal requests, anomalies as well as intrusions. More specifically, our training data are collected at the beginning and is composed of 10,000 requests. The majority of these requests are legitimate, but some are attacks (e.g. cross-site scripting, SQL injections, buffer overflows, etc.). After using these data to train our mixture model, by considering 1 g, 2 g, and 3 g representations (an n-gram is a sub-sequence of n overlapping items from a given sequence) as done in Zolotukhin and Hamalainen (2013), new requests are considered and classified as normal or abnormal. More specifically, we performed our approach as a classifier to detect abnormal requests by assigning the testing request to the group (normal or abnormal) that most likely generated it. These new requests constitute the testing set and their number is equal to 35,000.

The evaluation of the performance of our approach has been based on the following measures:

  • True-positive rate: the number of correctly detected intrusions over the number of intrusions in the testing set.

  • False-positive rate: the number of normal requests considered as intrusions over the total number of normal requests in the testing set.

  • True-negative rate: the number of correctly classified normal requests over the total number of normal requests in the testing set.

  • False-negative rate: the number of misclassified intrusions over the number of intrusions in the testing set.

  • Accuracy: the number of correctly classified requests over the total number of requests in the testing set.

  • Precision: the number of correctly classified intrusions over the number of intrusions.

To demonstrate the advantages of our approach, we compared it with the SDEM and SDPU approaches in Yamanishi et al. (2004) based on Gaussian mixture models and kernel mixtures. Moreover, we performed comparisons with the well-known nearest-neighbour (KNN) technique and three recent state-of-the art approaches, namely GHSOMs (Zolotukhin et al. 2013), diffusion maps (Kirchner 2010), and the algorithm proposed in Zolotukhin and Hamalainen (2013), respectively. For the KNN approach, we have tested several values of \(K\) and found that the best performance was achieved when \(K = 9\) according to the experimental results. For other tested approaches, we adopted the same initial experimental settings as in their original works. We evaluated the performance of each tested approach in detecting web service intrusion with 1 g representation and the corresponding results are illustrated in Table 3. According to this table, HInGD has provided the best performance among all tested approach in terms of the highest true-positive rate (98.71 %), the lowest false-positive rate (0.95 %), the highest true-negative rate (99.03 %), the lowest false-negative rate (0.99 %), the highest accuracy (98.26 %), and the highest precision (98.79 %). The fact that better performance provided by HInGD than the ones obtained by SDEM and SDPU implies that, the hierarchical Dirichlet process framework with GD mixtures works better than the SDEM algorithm with a finite Gaussian mixture and the SDPU algorithm with a kernel mixture in detecting web service intrusion. The performances achieved by SDEM and SDPU are comparable (the differences are not statistically significant, \(p\) values between 0.39 and 0.51). The difference is statistically significant when the HInGD is compared to SDEM and SDPU (\(p\) values between 0.037 and 0.048 for all evaluation measurers), respectively. Moreover, HInGD performed better than GHSOMs, and the approaches proposed in Kirchner (2010) and Zolotukhin and Hamalainen (2013) demonstrate the merits of using our approach over these state-of-the art approaches in web service intrusion detection. We may also observe that in Table 3, the KNN approach has provided the worst performance among all tested approaches. This can be explained by the fact that KNN approach has a suboptimal generalization power and is not robust to noisy data, also. Furthermore, we have tested the performance of our approach in detecting web service intrusion with 2-, and 3-g representation and the results are shown in Tables 4 and 5. According to these tables, we can see that the difference between the results obtained using the three representations is not important in our case. The results shown demonstrate also that our statistical framework is promising. Future works could be devoted to the analysis of the influence of the features representations on the results.

Table 3 Performance (%) of using different approaches with 1 g representation in detecting web service intrusion
Full size table
Table 4 Performance (%) of using different approaches with 2 g representation in detecting web service intrusion
Full size table
Table 5 Performance (%) of using different approaches with 3 g representation in detecting web service intrusion
Full size table

5 Conclusion

Our main goal in this paper, which we believe we have reached, was to develop a flexible statistical model for data modelling and classification. Our scheme is based on a powerful nonparametric Bayesian approach namely hierarchical Dirichlet process and a flexible probability density function namely the GD distribution, and a principled variational learning approach. The proposed framework has been shown to be statistically plausible, principled and well behaved and then can deal with many real-world problems. Indeed, it has provided state-of-the art results on two challenging applications namely visual objects categorization and web service intrusion detection. It is noteworthy that the proposed model is clearly scalable and appropriate for applications generating large scale data. We are currently investigating several future works related to the proposed model such as integrating feature selection to improve more its generalization capabilities, and extending the learning approach to online settings to take into account dynamic data.