A decision rule-based soft computing model for supporting financial performance improvement of the banking industry

Abstract

This study attempts to diagnose the financial performance improvement of commercial banks by integrating suitable soft computing methods. The diagnosis of financial performance improvement comprises of three parts: prediction, selection and improvement. The performance prediction problem involves many criteria, and the complexity among the interrelated variables impedes researchers to discover patterns by conventional statistical methods. Therefore, this study adopts a dominance-based rough set approach to solve the prediction problem, and the core attributes in the obtained decision rules are further processed by an integrated multiple criteria decision-making method to make selection and to devise improvement plans. By using VIKOR method and the influential weights of DANP, decision maker may plan to reduce gap of each criterion for achieving aspired level. The retrieved attributes (i.e., criteria) are used to collect the knowledge of domain experts for selection and improvement. This study uses the data (from 2008 to 2011) from the central bank of Taiwan for obtaining decision rules and forming an evaluation model; furthermore, the data of five commercial banks in 2011 and 2012 are chosen to evaluate and improve the real cases. In the result, we found the top-ranking bank outperformed the other four banks, and its performance gaps for improvements were also identified, which indicates the effectiveness of the proposed model.

1 Introduction

Banks play a crucial role in facilitating and stabilizing the economy of a nation. Since the financial crisis in 2008, the importance of monitoring and forecasting future financial performance (FP) of banks has been significantly aware by central banks all over the world. As a consequence, there has been an increasing interest in exploring the relationship between historical data (mainly financial ratios and special indicators for the banking industry) and future FP. While bank performance has been traditionally analyzed using financial ratios with statistical methods, the complexity of multiple dimensions and criteria has motivated researchers to adopt advanced quantitative techniques from the other fields (Fethi and Pasiouras 2010). In this study, we propose an integrated model by infusing soft computing and multiple criteria decision-making (MCDM) methods to resolve the problem.

The diagnosis of a bank’s FP can serve multiple purposes in practice: detecting bankruptcy, evaluating credit scores of banks, making investment decisions, and helping the management teams of banks plan for improvements. Owing to the needs from the practical fields, many methods have been tried to solve the problem, and we roughly divide the used methods into two categories: statistics and computational intelligence. Conventional studies mainly rely on statistical methods; however, statistical models are constrained by certain unrealistic assumptions (Liou 2013). Take the most commonly used regression model for example: the assumption of the independence of variables and the assumed linearity relationship, both are required to form regressions. Those unrealistic assumptions cause limitations in exploring the entwined relationships of complex problems in practice (Liou 2013; Tzeng and Huang 2011).

As for the computational intelligence, MCDM is reasonable to solve the addressed problem, due to its main focus in handling multiple variables. Among the MCDM methods, data envelopment analysis (DEA) might be the most commonly used technique, applied to evaluate the performance or efficiency of banks (Fethi and Pasiouras 2010). Some other group decision methods were also adopted, such as multiple-group hierarchical discrimination (Zopounidis and Doumpos 2000), analytic network process (ANP) (Niemira and Saaty 2004), and UTilities Additives DIScriminantes (UTADIS) (Kosmidou and Zopounidis 2008). The group decision methods transform the opinions of domain experts into evaluation models for ranking or selecting alternatives. On the other side, machine learning-based approach, such as artificial neural network (ANN) (Zhao et al. 2009; Ao 2011), supports vector machine (SVM) (Luo et al. 2009; Wu et al. 2007, 2009), genetic programming (Ong et al. 2005; Huang et al. 2006), decision tree (DT) (Ravi and Pramodh 2008), all have their own advantages in handling nonlinear data. In addition, the rough set approach (RSA) is a mathematical theory (Pawlak 1982), using computational algorithm to induct findings from large and imprecise data. The rising computational capability of computer makes those machine learning-based techniques to be more efficient and effective in handling large data set.

Although various computational methods (techniques) have been applied to predict the FP of banks, the aforementioned studies mainly depended on single approach to reach their goals: either constructing models from the opinions of experts (such as ANP) or inducting patterns (such as rules or logics) from large data set (Verikas et al. 2010). An integrated model that can leverage different approach’s advantages is still underexplored. Thus, not to be constrained by a single approach, this study decomposes the FP diagnosis problem into three stages, and devises a reasonable infusion model to solve it. At the first stage, considering the large number of related variables for assessing FP, the extended RSA is proposed to obtain the critical variables with decision rules from historical data. At the second stage, the implicit knowledge of domain experts is retrieved to comprehend the interrelationship among variables and the influential weights of each criterion. At this stage, the DANP (DEMATEL-based ANP) (Hsu et al. 2012) is adopted by requesting experts to compare only two variables (i.e., compare the relative influence of criterion $C_{A}$ to criterion $C_{B})$ in each time, which is easier for experts to give opinions regarding a complex problem. At the final stage, a compromised outranking method VIKOR (Opricovic and Tzeng 2004) is incorporated to identify the performance gap of each bank on each criterion. The VIKOR model may rank the alternatives—while facing certain conflicting and non-commensurable criteria—by minimizing the total performance gap to be zero, i.e., reach the aspiration level in each criterion. To demonstrate the proposed model, a group of real commercial banks is examined as an empirical case. The raw data come from the quarterly released reports (from 2008 to 2012) of the central bank of Taiwan.

The remainder of this paper is organized as follows: Sect. 2 briefly reviews the used methods. Section 3 introduces the required steps in three stages. Section 4 uses the real data (34 commercial banks) from the central bank of Taiwan as an empirical case. Section 5 analyzes the data with discussions. Section 6 provides conclusion and remarks.

2 Preliminary

This study infuses several computational methods to resolve the diagnosis of FP in banks, and this section briefly reviews the origins and concepts of the used methods.

2.1 RSA and Dominance-based rough set approach (DRSA)

The RSA (rough set approach), a mathematical theory (Pawlak 1982), aimed to explore the vagueness and ambiguity of complex data. The classical RSA achieved success in discovering useful knowledge in various applications—such as the prediction of financial distress (Dimitras et al. 1999), credit assessment (Liu and Zhu 2006); however, RSA was constrained in dealing with the non-ordered data of classification problems, and many real-world problems have to handle data with preference-ordered attributes. For example, a company with higher profitability is usually preferred while making investment decision. The need to preserve the ordinal characteristic of attributes gave rise to the development of DRSA. Developed by Greco et al. (2001, 2002), the DRSA has been applied to discover implicit knowledge in various applications, such as finding the customers’ preference in the airline industry, obtaining marketing guidance for customer relationship management, and analyzing credit risk in finance. Compared with the classical RSA, the DRSA method not only classifies decision classes, but also generates decision rules associated with each class. Moreover, the DRSA has the capability to discern objects with reduced attributes. In this study, the reduced dimensions (criteria) could decrease the complexity of FP modeling for the next stage.

2.2 DEMATEL technique

The DEMATEL technique was proposed by the Battelle Memorial Institute of Geneva in 1972 (Gabus and Fontela 1972) for solving complex social problems. The technique helps decision makers explore the interrelated and entwined relations among criteria, which can support to identify the influential directions and weights of the considered variables (criteria) while making evaluation (Liou 2013; Tzeng and Huang 2011; Wu 2008; Tzeng and Huang 2012; Peng and Tzeng 2013; Lin and Tzeng 2009; Shen et al. 2014). The DEMATEL technique provides an analytical approach to retrieve the knowledge of experts regarding a complex problem. Many topics have been explored by the DEMATEL technique, such as evaluating the performance of e-learning (Tzeng et al. 2007), creating the aspired intelligent global manufacturing and logistics systems (Tzeng and Huang 2012), selecting knowledge management strategies (Wu 2008), evaluating medical information (Furumoto and Tabuchi 2002), and developing a value-created system of science park (Lin and Tzeng 2009).

2.3 ANP and DANP (DEMATEL-based ANP)

The ANP (Saaty 2004) was extended from the analytic hierarchy process (AHP) (Saaty 1988) to allow for interdependence among considered criteria. The ANP decomposes problem into clusters (dimensions), and each cluster contains multiple variables/criteria for evaluation. To improve the equal weighting assumption of the typical ANP method (in clusters of un-weighted super-matrix), the DEMATEL technique was introduced to combine with the basic concept of ANP for solving the addressed problem, called DANP (DEMATEL-based ANP). The DANP method is adopted in this study to explore the influential weights of the selected financial variables for forming an evaluation model.

2.4 VIKOR method

In a typical MCDM problem, decision makers often have to consider multiple criteria simultaneously with conflicting (competing) outcomes on different criteria (Tzeng and Huang 2011). Take the evaluation of stocks for example, stock $A$ might outperform stock $B$ on profitability, but the operational efficiency of stock $A$ might be worse than stock $B$. The VIKOR (means multi-criteria optimization and compromise solution in Serbian) was introduced to solve the ranking/selection problem in the presence of several non-commensurable and conflicting criteria, based on the proposed ranking index to measure how close an alternative is to the aspiration level on multiple criteria (Opricovic and Tzeng 2007). In other words, the performance gap of each alternative on each criterion are measured to form a compromised ranking index by VIKOR, and the final scores of each alternative can be synthesized to make ranking and selection. At the final stage of the proposed model, the VIKOR method is incorporated to synthesize with the influential weights from DANP, and the performance gaps of each alternative on each criterion can be obtained accordingly. Finally, this research emphasizes on how to reduce the performance gaps of each alternative on each criterion based on influential network relation map (INRM)—referring directional (cause–effect) influences among dimensions/criteria—to achieve aspiration level of each variable (criterion) for improvements.

3 The integrated soft computing model

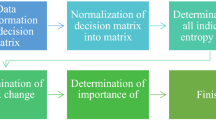
This section introduces the conceptual framework of the integrated model (Fig. 1) and the infused computational methods, including the DRSA method for selecting critical financial attributes, the DANP for finding influential weights of criteria (by the DEMATEL-adjusted weights in ANP) and the VIKOR method for ranking the sample banks.

Fig. 1

The illustration of the infused methods for the proposed model

The integrated model comprises of three stages, and the three stages should be conducted in sequence. The first stage focuses on exploring and retrieving patterns (i.e., decision rules and indispensable attributes) from the historical data, and decision maker should make judgment regarding the acceptance level to proceed for the second stage. If there were no consistent patterns in the historical data, the model would not move to the next stage. The second stage begins with DEMATEL analysis to explore the directional influences of each dimension and criterion, and the result can be integrated with ANP method to obtain the weights of each criterion for FP evaluation. The third stage, the VIKOR method is incorporated to synthesize the final scores of each sample bank for making selection. Furthermore, the measured performance gap of each alternative on each criterion could be obtained to plan for improvements.

3.1 DRSA method for selecting critical variables

At the first stage, DRSA begins with an information table (or called as an information system, abbreviated as IS), and objects are often placed in rows, while attributes are located in columns. If an attribute represents a criterion, it often has a preference-ordered characteristic. The data table is in the form of a 4-tuple information system $IS=( {U,Q,V,f})$, where $U$ is a finite set of universe, $Q=\left\{ {q_1 ,q_2 ,\ldots ,q_{n}} \right\}$ is a finite set of $n$ attributes, $V_q$ is the value domain of attribute $q$, $V=\bigcup \nolimits _{q\in Q} {V_q }$ and $f:U\times Q\rightarrow V$ is a total function where $f( {x,q})\in V_q$ for each $q\in Q$ and $x\in U$. The set $Q$ is often divided into condition set $C$ (multiple attributes or criteria) and decision set $D$ (one single decision attribute).

Define $\ge _q$ as a complete outranking relation on $U$ with respect to a criterion $q\in Q$, in which $x\ge _q y$ denotes “$x$ is at least as good as $y$ with respect to criterion $q$”. If $\ge _q$ represents a complete outranking relation, it means that $x$ and $y$ are always comparable with respect to criterion $q$. Let $Cl=\left\{ {Cl_t ,t=1,\ldots ,m} \right\}$ be a set of decision classes of $U$, in which $t\in T$, and for each $x\in U$ belongs to only one class $Cl_t \in Cl$. Assumes that decision classes are preference ordered, i.e., for all $r,s=1,\ldots ,m$, if $r\succ s$, the decision class $Cl_r$ is preferred to $Cl_s$. Then, given a set of decision class $Cl$, we may define downward and upward unions of classes as Eqs. (1, 2):

$$\begin{aligned} Cl_t^\le&=\bigcup \limits _{s\le t} {Cl_s }\end{aligned}$$

(1)

$$\begin{aligned} Cl_t^\ge&=\bigcup \limits _{s\ge t} {Cl_s} \end{aligned}$$

(2)

With the downward union and upward union of classes, we may define the dominance relation $D_P$ for $P\subseteq C$, where $C$ belongs to the criteria subset (conditional set) of $Q$. If we say object $x\,P$-dominates $y$ with respect to $P$, then it means $x\ge _q y$ for all $q\in P$, denoted by $xD_P y$. The $P$-dominating set and $P$-dominated set may be denoted by Eqs. (3, 4):

$$\begin{aligned} D_P^+ ( x)&=\left\{ {y\in U:yD_P x} \right\} \end{aligned}$$

(3)

$$\begin{aligned} D_P^- ( x)&=\left\{ {y\in U:xD_P y} \right\} \end{aligned}$$

(4)

The $P$-dominating set and $P$-dominated set can be used for representing a collection of upward and download unions of decision classes. Then, the $P$-lower and $P$-upper approximations of an upward union $Cl_t^\ge$ with respect to $P\subseteq C$ may be defined by $\underline{P}( {Cl_t^\ge })$ and ${\overline{P}} ( {Cl_t^\ge })$, respectively, as Eqs. (5, 6) show:

$$\begin{aligned}&\underline{P}( {Cl_t^\ge })=\left\{ {x\in U:D_P^+ \subseteq Cl_t^\ge } \right\} \end{aligned}$$

(5)

$$\begin{aligned}&\overline{P} ( {Cl_t^\ge })=\bigcup \limits _{x\in Cl^\ge } {D_P^+ } ( x)=\left\{ {x\in U:D_P^- ( x)\cap Cl_t^\ge \ne \varnothing } \right\} \end{aligned}$$

(6)

The $P$-lower approximation $\underline{P}\left( {Cl_t^\ge }\right)$ comprises of all objects $x$ from $U$ whereas all objects $y$ have at least the same evaluation with regard to all criteria $P$ belong to class $Cl_t^\ge$ or better, according to Eq. (3). The $P$-upper approximation of an upward union $Cl_t^\ge$ with respect to $P\subseteq C$, that can be interpreted as the set of all the objects belonging to $Cl_t^\ge$. Similarly, the $P$-lower approximation and $P$-upper approximation of $Cl_t^\le$ can be defined as Eqs. (7) and (8) respectively.

$$\begin{aligned}&\underline{P}( {Cl_t^\le })=\left\{ {x\in U:D_P^- \subseteq Cl_t^\le } \right\} \end{aligned}$$

(7)

$$\begin{aligned}&{\overline{P}} ( {Cl_t^\le })=\bigcup \limits _{x\in Cl^\le } {D_P^- } ( x)=\left\{ {x\in U:D_P^+ ( x)\cap Cl_t^\le \ne \varnothing }\right\} \end{aligned}$$

(8)

The $P$-lower ($P$-upper) approximation can be interpreted as the sets that denote certain (plausible) relationship. Thus, the $P$-boundary ($P$-doubtable regions) of $Cl_t^\ge$ and $Cl_t^\le$ is defined as below:

$$\begin{aligned} Bn_P \left( {Cl_t^\le }\right)&=\overline{P} \left( {Cl_t^\le }\right) -\underline{P}\left( {Cl_t^\le }\right) \end{aligned}$$

(9)

$$\begin{aligned} Bn_P \left( {Cl_t^\ge }\right)&=\overline{P} \left( {Cl_t^\ge }\right) -\underline{P}\left( {Cl_t^\ge }\right) \end{aligned}$$

(10)

The classification of $Cl$ can be further defined by the ratio $\gamma _{P} ( {Cl})$ for the criteria $P\subseteq C$ as Eq. (11).

$$\begin{aligned} {\gamma _{_{P}}} ( {Cl})=\frac{\left| {U-\left( {\bigcup \nolimits _{t\in \left\{ {2,\ldots ,m} \right\} } {Bn_P ( {Cl_t^\le })} }\right) } \right| }{\left| U \right| } \end{aligned}$$

(11)

In Eq. (11), $\left| \bullet \right|$ is the cardinality of a set. The ${\gamma _{_\mathrm{P}}} ( {Cl})$ represents the ratio of all correctly classified objects for criteria $P\subseteq C$. With the dominance-based rough approximation of upward and downward unions of decision classes, a generalized description of decision rules can be obtained in terms of “if antecedent, then consequence”. For a decision rule $r\equiv$ “if $f_{i_1 } ( x)\ge r_{i_1 }$&...& $f_{ip} ( x)\ge r_{ip}$, then $x\in Cl_t^\ge$”, and an object $y\in U$ supports $r$ if $f_{i_1 } ( y)\ge r_{i_1 }$&...& $f_{ip} ( y)\ge r_{ip}$. The total number of $y$ in the $IS$ is denoted as the SUPPORTs of the decision rule $r$, which indicates the relative strength that a rule can provide. Furthermore, for each minimal subset $P\subseteq C$ that can satisfy $\gamma _{{_P}} ( {Cl})=\gamma _{{_C}} ( {Cl})$ is termed as a REDUCT of $Cl$, and the intersection of all REDUCTs represents the indispensable attributes for maintaining the quality of approximation. In this study, the obtained attributes with relatively high supports are used to devise an integrated MCDM model for the next stage. The details of DRSA may be found in previous works (Greco et al. 2001, 2002; Błaszczynski et al. 2013).

3.2 DANP method

At the second stage, it begins with collecting opinions of experts for the selected criteria from DRSA. Experts are asked to judge the direct effect that they feel factor/criterion $i$ will have on factor/criterion $j$, indicated as $a_{ij}$. The scale ranges from 4 (very high influence) to 0 (no influence). The initial average matrix takes the arithmetic mean of each expert’s feedbacks for forming the initial average matrix A as Eq. (12):

$$\begin{aligned} A=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {a_{11}} &{} \ldots &{} {a_{1j}}&{} \ldots &{} {a_{1n} } \\ \vdots &{}&{} \vdots &{}&{} \vdots \\ {a_{i1}} &{} \ldots &{} {a_{ij}}&{} \ldots &{} {a_{in} } \\ \vdots &{}&{} \vdots &{}&{} \vdots \\ {a_{n1}} &{} \ldots &{} {a_{nj} }&{} \ldots &{} {a_{nn} } \\ \end{array} }} \right] \end{aligned}$$

(12)

Then, the initial average matrix should be normalized for obtaining the direct-influence matrix D $.$ The matrix $\varvec{D}=[d_{ij} ]_{n\times n}$ can be obtained by Eqs. (13) and (14):

$$\begin{aligned}&\varvec{D}=k\varvec{A}\end{aligned}$$

(13)

$$\begin{aligned}&k=\min \left\{ {\frac{1}{\max _i \sum \nolimits _{j=1}^n {a_{ij} } },\frac{1}{\max _j \sum \nolimits _{j=1}^n {a_{ij} } }} \right\} ,\nonumber \\&\quad \quad \quad i,j\in \left\{ {1,2,\ldots ,n} \right\} \end{aligned}$$

(14)

In the next, the total-influence matrix T for forming influential network relationship map (INRM) can be obtained by Eqs. (15) and (16), and I denotes the identity matrix in those two equations.

$$\begin{aligned}&\varvec{T}=\varvec{D}+\varvec{D}^2+\cdots +\varvec{D}^w=\varvec{D}(\varvec{I}-\varvec{D}^w)(\varvec{I}-\varvec{D})^{-1}\end{aligned}$$

(15)

$$\begin{aligned}&\varvec{T}=\varvec{D}(\varvec{I}-\varvec{D})^{-1}=[\varvec{t}_{ij} ]_{n\times n} ,\nonumber \\&\quad \quad \quad \text{ when }\,w\rightarrow \infty ,\,\varvec{D}^w\cong [0]_{n\times n} \end{aligned}$$

(16)

Using Eqs. (17) and (18), the sum of rows and the sum of columns of the total-influence matrix $\varvec{T}=[t_{ij} ]_{n\times n}$ are expressed as vector $\varvec{r}=( {r_1 ,\ldots ,r_i ,\ldots ,r_n })^\prime$ and vector $\varvec{c}=( {c_1 ,\ldots ,c_j ,\ldots ,c_n })^\prime$. The superscript $\prime$ denotes transpose operation of matrix. Therefore, the operations of $\varvec{r}+\varvec{c}$ and $\varvec{r}-\varvec{c}$ can form two column vectors as Eqs. (17) and (18) for $i,j\in \left\{ {1,2,\ldots ,n} \right\}$ and $i=j$:

$$\begin{aligned} \varvec{r}&=\left[ {\sum \limits _{j=1}^n {t_{ij} } } \right] _{n\times 1} =( {r_1 ,\ldots ,r_i ,\ldots ,r_n })^{\prime }\end{aligned}$$

(17)

$$\begin{aligned} \varvec{c}&=\left[ {\sum \limits _{i=1}^n {t_{ij} } } \right] ^{'}_{1\times n} =( {c_1 ,\ldots ,c_j ,\ldots ,c_n })^{\prime } \end{aligned}$$

(18)

The next step integrates the DEMATEL and the ANP to develop the un-weighted super-matrix. Based on the total-influence matrix T obtained from the DEMATEL technique, the matrix T may be normalized to be $\varvec{T}_C^N$ as Eq. (19).

(19)

After the normalization of the total-influence matrix T, the un-weighted super-matrix can be obtained by transposing $\varvec{T}_C^N$, denoted by setting $\varvec{W}=({\varvec{T}_C^N })^{'}$. In addition, to adjust the weights among dimensions, the dimensional matrix $\varvec{T}_D$ is normalized to become $\varvec{T}_D^N$ as in the Eqs. (20, 21).

$$\begin{aligned}&\varvec{T}_D =\left[ {{\begin{array}{lll} {t_D^{11} } &{} \ldots &{} {t_D^{1n} } \\ \vdots &{} \ddots &{} \vdots \\ {t_D^{n1} } &{} \ldots &{} {t_D^{nn} } \\ \end{array} }} \right] \end{aligned}$$

(20)

$$\begin{aligned}&\varvec{T}_D^N =\left[ {{\begin{array}{lll} {t_D^{11} /d_1 } &{} \ldots &{} {t_D^{1n} /d_1 } \\ \vdots &{} \ddots &{} \vdots \\ {t_D^{n1} /d_n } &{} \ldots &{} {t_D^{nn} /d_n } \\ \end{array} }} \right] =\left[ {{\begin{array}{lll} {t_D^{N11} } &{} \ldots &{} {t_D^{N1n} } \\ \vdots &{} \ddots &{} \vdots \\ {t_D^{Nn1} } &{} \ldots &{} {t_D^{Nnn} } \\ \end{array} }} \right] \end{aligned}$$

(21)

The adjusted super-matrix can be obtained by multiplying $\varvec{T}_D^N$ by un-weighted super-matrix $\varvec{W}$, and the limiting super-matrix can be derived from multiplying by itself multiple times until the weights become stable and converged as weighted super-matrix $\varvec{W}^N=\varvec{T}_D^N \varvec{W}$. The influential weights of each criterion can then be obtained by $\mathop {\lim }\nolimits _{z\rightarrow \infty } ({\varvec{W}^N})^z$. In general, the process of raising power $z$ can be stopped as the limiting super-matrix becomes stable.

3.3 VIKOR method

After forming the integrated evaluation model as Subsection 3.2 and 3.3, the performance score of each alternative on each criterion can be collected from domain experts referring to the actual FP of each alternative on conditional attributes. The VIKOR method is applied to synthesize—with the influential weights from DANP—the final ranking index for each alternative.

The VIKOR (Tzeng et al. 2002a, b; Opricovic and Tzeng 2002, 2003, 2007; Tzeng et al. 2005) begins with an $L_{p}$-metric, used as an aggregation function to form compromise ranking, and the ideas were based on the works of Yu (1973) and Zeleny and Cochrane (1982). Assume that there are $m$ alternatives, expressed as $A_{1}$, $A_{2}$,..., $A_{m}$. The performance on the $j$th criterion is denoted as $f_{kj}$ for alternative $k$, and $w_j$(i.e., from DANP) is the influential weight of the $j$th criterion, where $j=1,2,{\ldots },n$, and $n$ is the number of the criteria. The form of $L_{p}$-metric is as Eq. (22):

$$\begin{aligned} L_k^P&= \left\{ {\sum \limits _{j=1}^n {\left[ {w_j \left( {\left| {f_j^*-f_{kj} } \right| }\right) /\left( {f_j^*-f_j^- }\right) } \right] ^P} } \right\} ^{1/P},\nonumber \\&1\le p\le \infty ;k=1,\ldots ,m \end{aligned}$$

(22)

In the next, the indexes $S_k$ [in Eq. (23)] and $R_k$ [in Eq. (24)] can be calculated while $P=1$ and $P=\infty$, respectively.

$$\begin{aligned} S_k&=L_k^{P=1} =\sum \limits _{j=1}^n {\left[ {w_j \left( {\left| {f_j^*-f_{kj} } \right| }\right) /\left( {\left| {f_j^*-f_j^- } \right| }\right) } \right] }\end{aligned}$$

(23)

$$\begin{aligned} R_k&=L_k^{P=\infty } =\max _j \left\{ w_j \left( {\left| {f_j^*-f_{kj} } \right| }\right) /\right. \nonumber \\&\quad \left. \left( {\left| {f_j^*-f_j^- } \right| }\right) \vert j=1,2,\ldots ,n \right\} \end{aligned}$$

(24)

By modified VIKOR (Liu et al. 2012; Lu et al. 2013, 2014), in Eqs. (23, 24), symbol $f_j^*$ denotes the best value (also termed as the aspired level) on the $j$th criterion, and $f_j^-$ the worst value on the $j$th criterion. The obtained $S_k$ and $R_k$ can form the compromise ranking index $Q_k$ based on the weighted group utility (i.e., weight=$v)$ and individual regret (i.e., $\hbox {weight}=1-v$) in Eq. (25).

$$\begin{aligned} Q_k =v\times \frac{( {S_k -S^*})}{( {S^--S^*})}+( {1-v})\times \frac{( {R_k -R^*})}{( {R^--R^*})} \end{aligned}$$

(25)

In traditional approach, the symbols $S^*=\min _k \{S_k \vert k=1,2,\ldots ,m\}$ and $S^-=\max _k \{S_k \vert k=1,2,\ldots ,m\}$; also, the symbols $Q^*=\min _k \{Q_k \vert k=1,2,\ldots ,m\}$ and $Q^-=\max _k \{Q_k \vert k=1,2,\ldots ,m\}$ in Eq. (25). However, if we set $f_j^*$ as the aspired level and $f_j^-$ as the worst value, then we can get $S^*=Q^*=0$ and $S^-=Q^-=1$. Therefore, Eq. (25) can be re-written as Eq. (26).

$$\begin{aligned} Q_k =v\times S_k +( {1-v})\times R_k \end{aligned}$$

(26)

3.4 The overall algorithm (required steps) for the proposed three-stage model

To summarize the proposed model, the involved steps for the three stages are listed in sequence as below:

• Step 1 Discretize the raw financial figures for the conditional attributes and decision attribute for DRSA at the first stage. The used three-level discretization method will be further explained in Subsection 4.2.

• Step 2 Apply DRSA algorithm to induct decision rules from the discretized information system. In the empirical case, the data will be divided into the training set and the testing set. Once the classification result can meet the expected classification accuracy, the obtained strong decision rules with core attributes (by setting a support-cut threshold) will be further analyzed for the second stage.

• Step 3 Calculate the initial average matrix A as Eq. (12) by collecting opinions from domain experts. Among the core attributes obtained from Step 2, experts are asked to compare the relative influence that they feel criterion $i$ has on criterion $j$. Then, the direct-influence matrix D can be calculated from A by Eqs. (13, 14).

• Step 4 Obtain the influential weight of each criterion in the core attributes by Eqs. (15–21) until the limiting super-matrix becomes stable.

• Step 5 Collect opinions from experts regarding the performance score of each bank on each criterion in the core attributes by questionnaires. The actual financial figures of example banks and the industrial average on each criterion are provided in the questionnaire, and domain experts are requested to rate the performance score that they feel for the target banks on each criterion.

• Step 6 Synthesize the final score for each bank by the VIKOR method. Using Eqs. (22)–(25), decision maker may choose the weight $v$ to form the compromise ranking index $Q_i$ for each bank.

• Step 7 Plan for improvements based on the obtained performance gap information and cause–effect relationship from INRM.

4 Empirical case: commercial banks in Taiwan

This study divided the problem into three stages; the first stage used DRSA to find out critical variables and strong decision rules for predicting future FP, and the second stage collected opinions from domain experts to form the influential weights of each criterion for evaluation. Furthermore, at the third stage, to examine the evaluation model, the historical data (the raw financial data in 2011) of five commercial banks were used to obtain the performance scores on each criterion from experts to synthesize with the influential weights of DANP. The actual FP changes of the five sample banks in 2012 were compared with the final result from the proposed model, and the performance gaps were also identified for a sample bank.

4.1 Data

The raw data come from the quarterly released reports of the central bank in Taiwan, under the title of “Condition and Performance of the Domestic Banks” [23]. There were 34 commercial banks included for the analysis, and we mainly used the year-end reports from 2008 until 2011 to construct the DRSA model. There were two reasons regarding the selection of this time period: (1) the financial crisis was revealed since 2008, and the management teams of banks were highly influenced to conduct their operations afterwards; (2) the government (i.e., the central bank) was also involved to make additional supports and requirements for the banking industry after 2008. The financial results and operational performance might be different compared with previous patterns; therefore, we selected the period from 2008 to 2012 for the empirical case.

The data from 2008 to 2011 were used as the training set, and the data in 2012 as the testing set. The report comprises of six dimensions: (1) Capital Sufficiency; (2) Asset Quality; (3) Earnings and Profitability; (4) Liquidity; (5) Sensitivity of Interest Rate; and (6) Growth Rates of Main Business. The six dimensions include 25 variables (financial ratios or special indicators for the banking industry). The short description and definition for each variable (criterion) are shown in Table 1. Furthermore, this study used the growth rate of ROA (return on assets) in the subsequent year to define Good or Bad decision class, and the parameters used in the proposed and the compared approaches are in the Appendix.

Table 1 Description of variables used in the central bank’s report

4.2 Selection of the variables by DRSA model

The 25 financial ratios of a bank in each year were ranked and transformed into “1”, “2” and “3” to represent “low”, “middle” and “high”, respectively, and the 25 ratios represent the conditional attributes in the DRSA. For example, the top 1/3 stocks (34/3 = 11 stocks) on the ratio $E_{1}$ were categorized as “3” in the model. As for the decision class, we categorized the banks with more than 10 % growth in ROA as “Good” decision class and the banks with more than 10 % decline as “Bad”. The banks that performed in the middle (i.e., $-10\,\% \le \Delta ROA\le 10\,\%$) were not used to induct decision rules. As a whole, there were 84 records (the training set) used in the DRSA modeling.

The training set was examined by a threefold cross-validation for five times, and its average and standard deviation (SD) were compared with the results of discriminant analysis (DISCRIM) and decision tree (DT) in Table 2. DRSA generated 92.38 % classification accuracy in average, which was better than the results of DISCRIM and DT. Therefore, the training set was regarded acceptable for obtaining decision rules using DRSA.

The jMAF software (Błaszczynski et al. 2013) developed by the Laboratory of Intelligent Support Systems was used for DRSA, and the software DTREG was used for the calculations of DISCRIM and DT; 33 decision rules were retrieved from the training set, and those decision rules successfully re-classified the 84 objects with 97.62 % (82/84 $=$ 97.62 %) accuracy. To validate the DRSA model, the untouched testing set (21 banks) was examined by the 33 decision rules, and the accuracy of approximation reached 95.24 % (20/21 $=$ 95.24 %), which indicated its effectiveness in modeling.

Table 2 Classification accuracy of the training set

To select the crucial variables for the next stage, this study only included the variables (attributes) that appeared in the decision rules with more than five supports, termed as “support-cut”. After setting the support-cut to five, nine decision rules (Table 3) were obtained from the 33 rules with 12 attributes. We organized the 12 attributes (key financial ratios and indicators) with their original dimensions in Table 4. The 12 attributes were applied to construct a DANP model in the second stage.

Table 3 Decision rules (SUPPORTs $>$ 5)

4.3 Construction of the DANP evaluation model

The 12 variables obtained from the first stage were designed to collect the implicit knowledge from experts regarding the FP prediction problem. This study collected the questionnaires from domain experts as inputs to get the DANP influential weights for the 12 variables. All of the domain experts (eight experts in total) have more than 10-year working experience in banking or financial industry; their job titles include senior consultant, vicepresident, chief financial officer (CFO), senior analyst, director, associate professor (retired government official) and manager.

Table 4 Selected 12 criteria in four dimensions

Table 5 Total-influence matrix T

Table 6 Dimension matrix $\varvec{T}_D$

Table 7 Normalized dimension matrix $\varvec{T}_D^N$

Table 8 The un-weighted super-matrix $\varvec{W}=(\varvec{T}_{C}^{N})'$

Table 9 The adjusted super-matrix $\varvec{W}^N=\varvec{T}_D^N \varvec{W}$

The initial average influence matrix A was normalized by Eqs. (13) and (14) to get the normalized direct-influence matrix D. Using Eqs. (15) and (16), the total-influence matrix T was obtained as Table 5. Applying the DEMATEL technique to adjust the ANP weights, the dimension matrix $T_D$ (Table 6) and the normalized dimension matrix $T_D^N$ (Table 7) were obtained by Eqs. (20) and (21).

The un-weighted super-matrix $\varvec{W}=(\varvec{T}_C^N)'$ is the transpose matrix of the normalized direct-influence matrix. The un-weighted super-matrix $\varvec{W}$ is shown in Table 8. The weighted super-matrix ($\varvec{W}^N=\varvec{T}_D^N \varvec{W})$ thus may be obtained by multiplying $\varvec{T}_D^N$ by $\varvec{W}$ (Table 9). The stable limiting super-matrix was arrived by raising power $z$ of $\lim _{z\rightarrow \infty } (\varvec{W}^N)^z$, and the final influential weights of each criterion are shown in Table 11 with the evaluation of target banks.

4.4 Synthesize performance scores by VIKOR method

After constructing the integrated model in the aforementioned two stages, this study selected five commercial banks: (1) E. Sun Commercial Bank ($A)$; (2) Standard Chartered Bank (Taiwan) ($B)$; (3) Mega International Commercial Bank ($C)$; (4) Taipei Fubon Commercial Bank ($D)$; (5) Taishin International Bank ($E)$, and requested experts to give rating scores for the five banks on the 12 criteria. To be consistent with the reasoning processes of DRSA model, experts were provided with the raw financial ratios and the contemporary industry averages on the 12 variables of the five banks, and they were requested to give ratings as “Bad”, “Middle” and “Good” for the five banks on each criterion.

Table 10 The average performance scores$^{\mathrm{a}}$ of the five sample banks

Table 11 VIKOR–DANP evaluation result of the five sample banks

In Table 9, the performance scores of each bank on each criterion were collected from the same group of domain experts (for forming DANP model). Since the highest score on each criterion is “3”, this study set the aspired level on each criterion as “3”, and the performance gaps of each bank on each criterion were calculated and shown in Table 11. Take the performance score of Bank $A$ on criterion $C_{1}$ for example, the raw score was 2.125 (Table 10, bold value), and the transformed performance gap was calculated by $(3-2.125)/(3-0)=0.292$ (Table 11, bold value). The influential weights obtained from DANP showed that $L_{1}$, $E_{3}$ and $L_{2}$ were the top three influential criteria in predicting future FP, and we may conclude that liquidity ratios have dominant effect in the evaluation model. Among the 12 variables, both $L_{1}$ and $L_{2}$ appeared in the decision rules associated with at least Good decision class with high SUPPORTs.

5 Result and discussion

By synthesizing the influential weights (in DANP) by VIKOR, the compromise ranking index $Q_{\mathrm{k}}$ indicates that Bank $A$ is the top choice by different weights in $v$ (i.e., $v=1$, $v=0.7$, and $v=0.5$). Although the ranking (i.e., Bank $A\succ$ Bank $B\succ$ Bank $C)$ of the top three banks is consistent among the three $Q_{\mathrm{k}}$ values [$v$ equals 1, 0.7, and 0.5 in Eq. (26)], the 4${\mathrm{th}}$ and 5${\mathrm{th}}$ ranked banks are different, while $Q_{\mathrm{k}}$ equals to 0.5. While $Q_{\mathrm{k}}$ equals to 1 or 0.7 (puts more emphasis on group utility), the ranking index $Q_{\mathrm{k}}$ suggests that Bank $E\succ$ Bank $D$; on the contrary, while $Q_{\mathrm{k}} =0.5$, the result is Bank $D\succ$ Bank $E$. The actual $\Delta$ ROA of Bank $D$ and Bank $E$ in 2012 are 10 and $-$10 %, which is consistent with the ranking result while $Q_{\mathrm{k}}=0.5$; therefore, to weight the group utility and the individual regret equally could be a good choice in this empirical case.

Table 12 The five example banks’ FSAW measurements and performance scores

To make comparison using the other aggregation operator, the fuzzy simple additive weighting (FSAW) method was further applied in the study. The rated performance score on each criterion for each bank followed the same approach as mentioned in Subsection 4.4; in addition, the FSAW further considers every expert’s differences in subjective judgments regarding “Bad”, “Middle” and “Good”, each expert was also requested to fill out their subjective fuzzy membership parameters regarding “Bad”, “Middle” and “Good”. The commonly adopted triangular membership function (with FSAW) was then used to transform the experts’ judgments into performance scores.

The brief explanation of FSAW is as follows. Assume that there are $s$ experts for making the fuzzy performance measurement ($s$ = 8 in this study), and $E_{kj}^h$ denotes the $h$th expert’s fuzzy measurement for the $k$th bank on criterion $j$. This study selects the average operation to obtain the representative result for the $k$th bank on the criterion $j$, which may be expressed by Eq. (27).

$$\begin{aligned} E_{kj}=( {E_{kj}^1 \oplus E_{kj}^2 \oplus \cdots \oplus E_{kj}^s })/s=( {L_{kj}^s ,M_{kj}^s ,H_{kj}^s }) \end{aligned}$$

(27)

Assume that $w_j$ denotes the influential weights for criterion $j$ (refer to Subsection 3.2), then the fuzzy synthetic performance measurement for the $k$th bank can be expressed as Eq. (28), where $n$ is the number of total criteria for evaluation ($n$ = 12 in this study). Finally, the fuzzy synthetic performance measurement $E_k$ can be defuzzified into the performance score $P_k$ for the $k$th bank as Eq. (29).

$$\begin{aligned} E_k&= \left( {\frac{\sum \nolimits _{j=1}^n {w_j } \times L_{kj}^s }{n},\frac{\sum \nolimits _{j=1}^n {w_j } \times M_{kj}^s }{n},\frac{\sum \nolimits _{j=1}^n {w_j } \times H_{kj}^s }{n}}\right) \nonumber \\&= \left( {L_{k}^w ,M_{k}^w ,H_{k}^w }\right) \end{aligned}$$

(28)

$$\begin{aligned} P_k&= L_{k}^w +\frac{\left( {H_{k}^w -L_{k}^w }\right) +\left( {M_{k}^w -L_{k}^w }\right) }{3} \end{aligned}$$

(29)

The five example banks’ FSAW performance scores $P_{k}$ are shown in Table 12. We may find that, in the bottom of Table 12, the final ranking sequence is $A\succ B\succ C\succ D\succ E$. This ranking sequence is the same as the result from VIKOR by setting $v$ = 0.5 (refer to Table 11). Although the final ranking sequence of the five banks using VIKOR with different setting in $v$ (i.e., $v$ = 1, 0.7, and 0.5) and FSAW are not totally the same, the ranking for the top three banks is consistent (i.e., Bank $A\succ$ Bank $B\succ$ Bank $C)$, which implies the stability of the proposed approach.

The use of FSAW with certain multiple criteria decision-making methods for ranking has been applied in many problems, such as measuring the competitiveness of manufacturing companies (Kao and Liu 1999) and the facility location selection problem (Chou et al. 2008); however, the FSAW may only be used in ranking or selection, which is not capable to support decision makers to plan for improvements. This is the main reason why we adopt the modified VIKOR at the final stage to aggregate the performance gaps for each bank.

Combining the findings from DEMATEL and VIKOR analyses, the proposed hybrid MCDM model not only can make ranking and selection, but also supports banks to plan for improvements. Take the top ranked Bank $A$ for example; if Bank $A$ attempts to improve its FP in the subsequent period, it should take the dimension Earnings and Profitability ($E)$ as the top priority, because the aggregated performance gap (gap on dimension $E=(0.069\times 0.625)+(0.105\times 0.042)+(0.084\times 0.667)=0.104$, refer to Table 11) on dimension $E$ is the highest among the four dimensions (according to the aforementioned calculation method, the performance gaps of Bank $A$ on dimensions $C$, $L$, and $G$ are 0.066, 0.056, and 0.024, respectively. Moreover, according to Table 13 [transformed from Table 6, and refer to Eqs. (17–18)], the relative influences and cause–effect analysis of dimensions could be obtained.

Table 13 Influential weights of dimensions

In Fig. 2, the performance gaps to the aspired levels (on each dimension) of Bank $A$are illustrated with the directional influences (from the DEMATEL analysis) among the four dimensions.

Fig. 2

Performance gaps to aspired levels with directional influences (dimensions)

Based on DEMATEL, the calculation of $r_i^D -c_i^D$ could divide dimensions into the cause group ($r_i^D -c_i^D >0)$ and the effect group ($r_i^D -c_i^D <0)$. The dimension Capital Structure ($C)$ might cause changes in dimension Earnings and Profitability ($E)$, the dimension $C$ also has the highest influential weight (i.e., $r_i^D +c_i^D =1.927$) among the three dimensions (i.e., $C=1.927$, $L=1.642$, and $G=1.854$). Therefore, a reasonable improvement plan should focus on improving the dimension $C$ to yield the highest marginal effect. This kind of analysis could not be obtained by a single MCDM method, which is also the major advantage of the proposed model in practice.

Aside from the ranking and improvement planning, the proposed model not only found out the decision rules to identify future improvements, but also generated decision rules to detect deteriorating FP in the subsequent period (Table 2). This finding can be applied to detect symptoms of potential crises, which acts as a warning mechanism. As the commercial banks are crucial to the stability of economy, the obtained decision rules may provide useful rules for identifying early symptoms of potential crises.

6 Conclusion and remarks

To conclude, this study proposed an integrated soft computing model to resolve the FP prediction problem; also, the incorporated hybrid model (DANP with VIKOR) may rank and identify the performance gaps of banks. The complexity of the multiple dimensions and criteria of financial reports impedes decision makers to conclude useful patterns from large and imprecise data set; therefore, this study chose DRSA to induct the patterns and critical variables for predicting FP. This study successfully selected 12 critical ratios from the original 25 financial attributes with the capability to discriminate positive (negative) FP changes. In addition, several easy-to-understand decision rules (Table 2) that may predict future performance improvement/deterioration with strong SUPPORTs were found.

With fewer variables (from 25 to 12 criteria in this study), domain experts were able to give opinions for forming the DANP model. Since the experts were requested to compare the relative influence of one criterion against the other, it is more likely to retrieve reliable knowledge from experts by pairwise comparisons. The constructed DANP model could analyze the interrelationships among the criteria, and the influential weights of each criterion were also found. Besides, the obtained DEMATEL analysis at this stage divided dimensions (criteria) into a cause group and an effect group, which could be integrated with VIKOR method to guide FP improvements. To summarize the new concepts and purposes for the adopted methods and soft computing techniques in the proposed model, the comparison Table 14 is as below:

To examine the constructed model, the raw financial data of the five sample banks and the industrial averages were provided to the experts to rate each criterion of the five banks. At this stage, the compromised ranking method VIKOR was used to aggregate the performance gaps of each alternative for ranking. The selected top choice Bank $A$ outperformed the other four banks in 2012, which indicated the effectiveness of the proposed model. Furthermore, the selected Bank $A$ was illustrated to identify its top priority dimension for improvement, and the way to explore the source dimension for improvements—by combining VIKOR and DEMATEL analysis—was also discussed. Thus, the present study contributes to the application of soft computing and MCDM methods in the banking industry.

Table 14 New concepts and purposes for the proposed model

Despite the contributions of this study, there are still several limitations. First, only the ordinal three-level discretization was adopted for the DRSA model, and the obtained decision rules or accuracy of approximation might be different using the other discretization methods. Future studies may incorporate some other machine learning techniques to find the optimal discretization intervals. Second, the DRSA model only used one period-lagged data to predict FP (i.e., associate the data of a bank’s conditional attributes in $t-1$ period with its decision class in period $t)$. Some latent tendency in relatively long-lagged periods (e.g., more than 2 years) might not be captured in the model. Finally, though the present study may identify the performance gaps of banks with suggested improvement priority, it is still at the experimental stage. The involvements of banks to evaluate the feasibility and the plausible effects of the guiding rules may form a loop to plan for continuous improvements; future studies are suggested to work in this direction.

Appendix

See Table 15.

Table 15 Main parameters used in the proposed and compared approaches