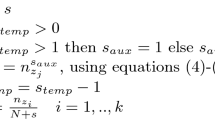Extending information processing in a Fuzzy Random Forest ensemble

Abstract

Imperfect information inevitably appears in real situations for a variety of reasons. Although efforts have been made to incorporate imperfect data into classification techniques, there are still many limitations as to the type of data, uncertainty, and imprecision that can be handled. In this paper, we will present a Fuzzy Random Forest ensemble for classification and show its ability to handle imperfect data into the learning and the classification phases. Then, we will describe the types of imperfect data it supports. We will devise an augmented ensemble that can operate with others type of imperfect data: crisp, missing, probabilistic uncertainty, and imprecise (fuzzy and crisp) values. Additionally, we will perform experiments with imperfect datasets created for this purpose and datasets used in other papers to show the advantage of being able to express the true nature of imperfect information.

1 Introduction

Classification has always been a challenging problem (Ahn et al. 2007; Fernández et al. 2009). Many techniques and algorithms have been developed to address this issue. In the past few years, we have also observed an increase in the development of multiple classifier systems, which usually have delivered better results than individual classifiers (Opitz and Maclin 1999). However, these techniques and algorithms must work with information that is not as always precise and accurate.

Imperfect information inevitably appears in realistic domains and situations. Instrument errors or corruption from noise during experiments may give rise to information with incomplete data when measuring a specific attribute. In other cases, the extraction of exact information may be excessively costly or unfeasible. Moreover, it might be useful to complement the available data with additional information from an expert, which is usually elicited by imperfect data (interval data, fuzzy concepts, etc). In most real-world problems, data have a certain degree of imprecision. Sometimes, this imprecision is small enough for it to be safely ignored. On other occasions, the imprecision of the data can be modeled by a probability distribution. However, there is a third kind of problems, where the imprecision is significant, and a probability distribution is not the most natural way to model it. This is the case of certain practical problems where the data are inherently fuzzy (Casillas and Sánchez 2006; Otero et al. 2006; Sánchez et al. 2008, 2009).

For these cases, it is necessary to incorporate the handling of information with attributes which may present missing and imprecise values in the classifier’s learning and classification phases.

In this paper, we focus on the use of a Fuzzy Random Forest (FRF) ensemble for classification and illustrate its power for handling imperfect data, extending the treatment of imperfect information to multiple classifier systems. FRF uses a fuzzy decision tree as base classifier. Therefore, FRF leverages the robustness of fuzzy decision trees and tree ensembles, the power of randomness to increase the diversity of the trees in the forest, and the flexibility of fuzzy logic to manage imperfect data.

In Sect. 2, we describe the types of imperfect data. In Sect. 3 we review the major elements that constitute the FRF ensemble. In Sect. 4, we describe the types of imperfect data supported by the FRF ensemble and we devise an augmented ensemble that can operate with other types of imperfect data (crisp, missing, probabilistic uncertainty and imprecise (fuzzy and crisp) values.). In Sect. 5, we perform experiments with imperfect datasets created for this purpose and datasets used in other papers to show the advantage of being able to express the true nature of imperfect information. Finally, we present our conclusions in Sect. 6.

2 Imperfect data

There is a wide range of classification techniques based on different theoretical proposals (Duda et al. 2001; Mackay 2003; Quinlan 1993; Witten and Frank 2000). Unfortunately, most of the conventional techniques did not consider the sources of uncertainty. As a result, incomplete and imprecise data have usually been discarded or ignored in the classifier’s learning and in its subsequent classification process. However, these data are inevitable when dealing with real-world applications.

Let us first define our concept of imperfect information. Then we can label classification techniques according to the type of imperfect information allowed in the input data.

Imprecision and uncertainty can be considered as two complementary aspects of imperfect information (Bonissone 1997; Coppi et al. 2006; Dubois and Prade 1988). From a practical viewpoint, an item of information can be represented as a four-tuple (attribute, object, value, confidence). The attribute is a function which assigns a value (or a set of values) to the object. The value is a subset of the reference domain associated with the attribute. Confidence indicates the likelihood of the item of information. In this context, imprecision is related to the value of the item of information, while uncertainty is related to the confidence in the item. Thus, an item of information will be precise when its value cannot be subdivided. Otherwise, we will talk about imprecision. Furthermore, when there are no crisp constraints on the set of values that an imprecise item can take, we will talk about fuzzy imprecision. On the other hand, uncertainty is a property of belief. We say that we are certain of an event if we assign it a maximum belief value. We can define uncertainty as the absence of certainty, and this may arise from the randomness of some experimenting (objective uncertainty), or from subjective judgements by human reasoning (subjective uncertainty). In Dubois and Guyonnet (2011) the concepts of imprecision and uncertainty are described in terms of stochastic and epistemic uncertainties. Stochastic uncertainty arises from random variability related to natural processes. Epistemic uncertainty arises from the incomplete/imprecise nature of available information. While stochastic uncertainty is adequately addressed using classical probability theory, several uncertainty theories have been developed in order to explicitly handle incomplete/imprecise information that basically are convex probability sets, random sets, and possibility theory.

Therefore, it would be useful to incorporate the treatment of this type of data in both learning and classification phases of our algorithm. We will deal with heterogeneous attributes expressed by crisp values, missing values, values with objective uncertainty, values with subjective uncertainty, non-fuzzy imprecise values, fuzzy imprecise values, or linguistic labels.

Some techniques can only work with attributes with nominal domains and the domain of the numerical attributes needs to be discretized, as in the case of Bayesian networks and techniques based on imprecise probabilities, but currently studies are being developed that allow these techniques to work with numeric attributes without being discretized (Langseth et al. 2009; Quaeghebeur and Cooman 2005). Other techniques can only work with numerical attributes and only allow a nominal attribute if it is considered a class, as in the case of neuronal networks or classifiers that generate discriminant functions. Techniques that can work with both types of attributes include those based on classification/regression trees, those based on sample patterns via the definition of heterogeneous distance functions and, in general, those methods that generate rules, as they allow rules to be expressed using both types of attributes (with the exception of association rules, which only work with discrete domains).

Great efforts have been made to incorporate uncertainty and imprecision into the learning and classification phases of the well-known classification techniques. Although not exhaustively, some methods allow treatment of examples with some missing attribute, as is the case for techniques based on density estimation from sample patterns (Witten and Frank 2000), regression/classification tree construction techniques (Duda et al. 2001; Quinlan 1993), the classifier based on discriminant functions made up of multivariant normals (McLachlan and Krishnan 1997), clustering based on mixture models (Ruiz et al. 1998), Bayesian networks (Hernández et al. 2004), etc. Techniques based on tree construction and mixture models also allow observations with nominal attributes which present uncertain values from the probabilist viewpoint as well as continuous attributes expressed by classical intervals (non-fuzzy imprecision) (Quinlan 1993; Ruiz et al. 1998). Treatment of attributes expressed by fuzzy values is also incorporated into the tree construction techniques (Janikow 1996, 1998), into neuronal networks (Mitra and Pal 1995) and mixture models (Garrido et al. 2010). The last of these techniques allows us to express uncertain values with imprecise probabilities, thus allowing the treatment of subjective uncertainty.

In general, we can say that there are many restrictions to the type of imperfection allowed in the input examples or in the data. For this reason, we propose to extend the treatment of imperfect information with a classification technique based on multiple classifier systems. This technique is the FRF ensemble. Beside its ability to handle imperfect information, FRF also proved to be effective when dealing with regular data, e.g., without imperfect information (Bonissone et al. 2010).

3 Fuzzy Random Forest: an ensemble based on fuzzy decision trees

FRF was originally presented in Bonissone et al. (2010). In this section we describe the basic elements that compose a FRF ensemble and the types of data that are supported by this ensemble in both learning and classification phases.

3.1 Fuzzy Random Forest learning

FRF learning phase uses Algorithm 1 to generate the FRF ensemble whose trees are fuzzy decision trees.

Each tree in the FRF ensemble is a fuzzy tree. Algorithm 2 shows the fuzzy decision tree learning algorithm.

Algorithm 2 has been designed so that the trees can be constructed without considering all the attributes to split the nodes. We select a random subset of the total set of attributes available at each node and then choose the best one to make the split. Algorithm 2 is an algorithm to construct trees based on ID3, where the numeric attributes have been discretized by a fuzzy partition. The domain of each numeric attribute is represented by trapezoidal fuzzy sets, $A_1,\ldots ,A_f$ so each internal node of the tree, whose division is based on a numerical attribute, generates a child node for each fuzzy set of the partition.

Moreover, Algorithm 2 uses a function, denoted by χ _t,N (e), that indicates the degree with which the example e satisfies the conditions that lead to node N of tree t. Each example e is composed of attributes which can take crisp, missing, or fuzzy values belonging to the fuzzy partition of the corresponding attribute. Each of these examples (according of the attribute value) has the following treatment:

• Each example e used in the training of the tree t has been assigned an initial value 1 (χ _t,root (e) = 1) indicating that this example was initially found only in the root node of tree t.

• According to the membership degree of the example e to different fuzzy sets of partition of a split based on a numerical attribute:

  • If the value of e for that attribute is crisp, the example e may belong to one or two children nodes, i.e., the example will descend to a child node associated with membership degree greater than 0 ($\mu_{fuzzy\_set\_partition}(e)>0$). In this case $\chi_{t,child node}(e)=\chi_{t,node}(e)\times \mu_{fuzzy\_set\_partition}(e).$

  • If the value of e for that attribute is a fuzzy value, it must match one of the sets of the fuzzy partition of the attribute. In this case, e will descend to the child node associated with that set. In this case, χ _{t,child node} (e) = χ _t,node (e).

  • When the example e has a missing value in an attribute i which is used as a test in a node node. In this case, the example descends to each child node $node_h,h=1,\ldots,H_i$ with a modified value proportionately to the weight of each child node. The modified value for each node _h is calculate as

    $$ \chi_{node_h}(e)=\chi_{node}(e) \cdot \frac{T\chi_{node_{h}}}{T\chi_{node}} $$

    where Tχ _node is the sum of the weights of the examples with known value in the attribute i at node node and Tχ _{node_h} is the sum of the weights of the examples with known value in the attribute i that descend to the child node node _h .

3.2 Fuzzy Random Forest classification

In this section we describe how the classification is carried out using the FRF ensemble. First, we introduce the notation used. Then, we present two alternative strategies to obtain the decision of the FRF ensemble for a target example. In the Appendix, we present concrete instances of these strategies (different combination methods) used in this paper.

3.2.1 Notations

The following is the notation used in this paper:

• T is the number of trees in the FRF ensemble. We will use the index t to refer to a particular tree.

• N _t is the number of leaf nodes reached by an example, in the tree t. We will use the index n to refer to a particular leaf reached in a tree.

• I is the number of classes. We will use the index i to refer to a particular class.

• e is an example which will be used either as an example of training or as a test.

• χ _t,n (e) is the degree of satisfaction with which example e reaches the leaf n from t tree, as we indicated in Sect. 3.1.

• Support for the class i is obtained in each leaf as $\frac{E_i}{E_n}$ where E _i is the sum of the degrees of satisfaction of the examples with class i in leaf n and E _n is the sum of the degrees of satisfaction of all examples in that leaf.

• L_FRF is a matrix with size ($T\times MAX_{N_t}$) with $MAX_{N_t}=max\{N_1,N_2,\ldots ,N_T\},$ where each element of the matrix is a vector of size I containing the support for every class provided by every activated leaf n on each tree t. Therefore, the matrix L_FRF contains all the information generated by the FRF ensemble when it is used to classify an example e and from which it makes its decision or class with certain methods of combination. L_FRF _t,n,i refers to an element of the matrix that indicates the support given to the class i by the leaf n of tree t.

• T_FRF is a matrix with size (T × I) that contains the confidence assigned by each tree, t, to each class i. The matrix elements are obtained from the support for each class in the leaves reached when applying some combination method. An element of matrix is denoted by T_FRF _t,i .

• D_FRF is a vector with size I that indicates the confidence assigned by the FRF ensemble to each class i. The matrix elements are obtained from the support for each class in the leaves reached when applying some combination method. Denote an element of this vector as D_FRF _i .

3.2.2 Strategies for fuzzy classifier module in the FRF ensemble

The fuzzy classifier module operates on fuzzy trees of the FRF ensemble using one of these two possible strategies:

Strategy 1 Combining the information from the different leaves reached in each tree to obtain the decision of each individual tree and then applying the same or another combination method to generate the global decision of the FRF ensemble. In order to combine the information of the leaves reached in each tree, the Faggre1₁ function is used and the Faggre1₂ function is used to combine the outputs obtained with Faggre1₁. Figure 1 shows this strategy.

Fig. 1

Strategies for fuzzy classifier module

Strategy 2 Combining the information from all reached leaves from all trees to generate the global decision of the FRF ensemble. We use function Faggre2 to combine the information generated by all the leaves. Figure 1 shows this strategy.

In Bonissone et al. (2010) a set of combination methods are defined. In the Appendix of this paper we will describe the different combination methods (for Strategy 1 and Strategy 2) which will be used in the experimental results of this paper. In these methods, the final decisions are both weighted and non weighted.

Strategy 1 is implemented in Algorithm 3.

Faggre1₁ is used in Algorithm 3 to obtain the matrix T_FRF. In this case, Faggre1₁ aggregates the information provided by the leaves reached in a tree. Later, the values obtained in each tree t, will be aggregated by means of the function Faggre1₂ to obtain the vector D_FRF. This algorithm takes a target example e and the FRF ensemble, and generates the class value c as decision of the FRF ensemble.

To implement Strategy 2, Algorithm 3 is simplified so that it no longer adds the information for each tree, but it uses the information of all leaves reached by example e in the different trees of the FRF ensemble. Algorithm 4 implements Strategy 2 and uses the example e to classify and the FRF ensemble as target values, and provides the value c as class proposed as decision of the FRF ensemble. Faggre2 aggregates the information provided by all leaves reached in the different trees of the FRF ensemble to obtain the vector D_FRF.

As we can see, the output of FRF ensemble (regardless of the strategy) is obtained from vector D_FRF, which contains the membership degree of the target example to each class. Finally, the FRF ensemble assigns the class c with maximum value to example e.

4 Extending FRF ensemble

FRF ensemble is a versatile technique, which is able to adapt itself to new elements. Having introduced the FRF ensemble, we now describe an extension of this technique to allow the incorporation of new imprecise data. This extension involves changes in the learning and classification phases of the technique. In this section, we will describe the new types of imprecise data that we will incorporate and the new elements and changes needed to carry out the FRF ensemble’s extension.

4.1 New types of imprecise data

In Sect. 3.1 we described the types of data supported by the FRF ensemble, in both the learning and classification phases, as originally proposed in Bonissone et al. (2010). Now, we want to extend the information processing in the FRF ensemble to incorporate data containing attributes measured by interval values and attributes measured by fuzzy values which may be different from the fuzzy values which constitute the fuzzy partition of the attribute and therefore the degree of similarity of these fuzzy values to each element of the fuzzy partition of the attribute can be less than 1. Furthermore, we want to allow the class attribute to be set-valued. Figure 2 illustrates the proposed extension.

Fig. 2

Extending information processing in FRF

In FRF ensemble when a numeric attribute is discretized using a fuzzy partition, the only fuzzy values allowed in the input data for this attribute are elements of that partition. For example, if an attribute X is discretized according to the partition shown in Fig. 3a, the only fuzzy values allowed in the input data are A ₁, A ₂ or A ₃.

Fig. 3

Management of fuzzy values in FRF ensemble (a) and in Extended FRF ensemble (b)

In Extended FRF ensemble, fuzzy values different from A ₁, A ₂ and A ₃ are allowed as input data (Fig. 3b). The degree of similarity of the fuzzy value with each of the values A ₁, A ₂ and A ₃ will be used to modify the value χ _t,node of the example in both the learning and classification stages of the Extended FRF ensemble.

To incorporate these new types of data, we need to modify the following elements of FRF ensemble:

• Define an extended function to measure the membership degree of these new types of data in the fuzzy partitions of the numerical attributes used by the ensemble.

• The definition of this function requires a modification of the information gain function in both learning and classification phases of FRF ensemble.

• To incorporate set-valued classes, we need to modify and define the learning and classification phases.

Let us further analyze these new elements and their required modifications.

4.2 Fuzzy and interval values

To incorporate attribute values measured by a fuzzy value (fuzzy set) different from the sets of the partition of the attribute, or attributes measured by interval values, we must extend the function that measures the membership degree of these types of values to the different fuzzy sets forming the partition of the numeric attributes. This new function (denoted by $\mu _{simil}(\cdot)$) captures the change in the value χ _{t, node} (e) of the example e when it descends in the fuzzy tree. e has attributes whose values are expressed by intervals or fuzzy values that do not match any of the fuzzy values of the partition used by the fuzzy tree and therefore by the ensemble. This function will be used in both learning and classification phases of extended FRF ensemble.

In these cases, we use the function $\mu_{simil}(\cdot)$ that, given the attribute “Attr” to be used to split a node, measures the similarity between the values of the fuzzy partition of the attribute and fuzzy values or intervals of the example in that attribute. When the example e must descend to different child nodes, the function $\chi(\cdot)$ is calculated as χ _t,childnode (e) = χ _t,node  ×  μ _simil (e).

Using the $\mu_{simil}(\cdot)$ function, we allow a new treatment of missing values in FRF ensemble. In Sect. 3, we noted that a missing value descends through the tree distributing its weight evenly between the child nodes of a node. By incorporating intervals values in FRF ensemble, we can express a missing value as an interval that includes the entire domain of an attribute. Thus, using the above $\mu_{simil}(\cdot)$ function, the example descends to all child nodes distributing its weight proportionally among them, according to the size of each fuzzy set of the partition. In a given problem, function $\mu_{simil}(\cdot)$ will be defined by a particular similarity measure.

4.3 Set-valued classes

As described in Sect. 3, the examples in the dataset are weighted examples (initially with weight 1). When we incorporate in FRF ensemble examples whose class can be expressed by a set of values, it is necessary to modify the way we treat this weight in the learning phase of FRF ensemble. Thus, step 3.2 of Algorithm 2 should calculate the information gain considering the example as belonging to each potential class. For this, the example in step 1 of the algorithm must be replicated for each class of its class attribute, using an associated weight indicating uncertainty about the class of example. In the classification phase, the example with set-valued class is not replicated and therefore its initial weight is 1. Example descends through various branches of the tree and different leaf nodes are activated. Each of these activated leaf nodes assigns a weight to each possible classes. According to the combination method used, we obtain from the FRF ensemble a weight for each class. The resulting weight vector of classes is denoted by D _FRF .

At this point, when we perform a test of the extended FRF ensemble results to classify a dataset we can follow the decision process:

As result of this test, we obtain the interval [min_error, max_error] where min_error is calculated considering only errors indicated in the variable errors from the previous process and max_error is calculated considering as errors errors + success_or_error.

4.4 Changes of learning and classification algorithms

Algorithms 2, 3, and 4 should now be modified to allow the FRF ensemble to learn, infer, and classify from an example expressed with the types of values presented in Sect. 4.1. This subsection shows the modification of these algorithms.

Algorithm 2 is modified in steps 1 and 3.2 as we show in Algorithm 5.

Algorithm 3 “FRF Classification (Strategy 1)” is modified according to Algorithm 6.

Finally, Algorithm 4 “FRF Classification (Strategy 2)” is modified in steps 1. and 3. as is shown in Algorithm 7.

5 Experiments and results

In this section we describe several computational results that show the behavior of FRF ensemble with different types of imperfect data. We also show that the substitution of imperfect data by crisp values produces different results (different precision of the ensemble) to those obtained using the original imperfect data. Based on these results, we stress the need to keep the original data, which express the true nature of the measurement process or source of information.

The experiments are grouped as follows:

(a) The experiments of Sect. 5.2 are designed to measure the behavior of the FRF ensemble with missing and fuzzy data. Furthermore, these data will be replaced by other values:

• Missing values that can affect both numeric and nominal attributes,

  • missing values will be replaced by the mean value of the attribute in the case of numerical attributes or by the predominant value in the case of nominal attributes.

• Fuzzy values,

  • fuzzy values are replaced by intervals gathering support,

  • fuzzy values are replaced by the mean of α − cut = 1,

  • fuzzy values are replaced by the mean of α − cut = 0,

  • fuzzy values are replaced by the center of gravity of fuzzy set.

(b) The experiments of Sect. 5.3 are designed to measure the behavior of FRF ensemble using datasets and results proposed in (Palacios et al. 2009, 2010).

5.1 Datasets and parameters for FRF ensemble

To obtain these results we have used several datasets from the UCI repository (Asuncion and Newman 2007) and real-world datasets about medical diagnosis and high-performance athletics (Palacios et al. 2009, 2010), whose characteristics are shown in Table 1. The table shows the number of examples (|E|), the number of attributes (|M|), and the number of classes (I) for each dataset. “Abbr” indicates the abbreviation of the dataset used in the experiments.

Table 1 Datasets

All FRF ensembles use a forest size of 100 trees. The number of attributes chosen at random at a given node is $\log _2 (|\cdot|+1),$ where $|\cdot|$ is the number of available attributes at that node, and each tree of the FRF ensemble is constructed to the maximum size (node pure or set of available attributes is empty) and without pruning. All partitions used in experiments of the Sect. 5.2 are fuzzy. These partitions are obtained by the NIP1.5 tool available in “http://heurimind.inf.um.es/”. As described in Palacios et al. (2009 and Palacios et al. (2010), for experiments in Sect. 5.3, the fuzzy partitions are uniform.

Function μ _simil (e) is defined for $f=1,\ldots , F_i,$ as

$$ \mu_{simil}(e)= \displaystyle \frac{\int (\min \{\mu_{e}(x),\mu_{f}(x)\}){\rm d}x}{\sum_{f=1}^{F_i} \int (\min \{\mu_{e}(x),\mu_{f}(x)\}){\rm d}x} $$

where

• μ _e (x) represents the membership function of the fuzzy or interval value of the example e in the attribute i.

• μ _f (x) represents the membership function of the fuzzy set of the partition of the attribute i.

• F _i is the cardinality of the partition of the attribute i.

In those datasets with imprecise outputs we have considered a uniform distribution on the possible values for the class in each example. That is, each example with set-valued class is replicated as many times as possible classes it may belong, and each replica is assigned an initial weight of $\frac{1}{n\_values\_classes\_of\_examples}.$

In each experiment, we will use different datasets with different types of imperfect information. When, for absence of datasets with some kind of imperfection, we have to create them, we use the tool NIP1.5. All datasets and fuzzy partition created will be available in “http://heurimind.inf.um.es/” with the results obtained in this paper.

5.2 Experimentation with missing and fuzzy data

First, we will experiment with crisp datasets that have been augmented by a percentage of missing or fuzzy values. This percentage does not affect the class attribute. Experimentation with these datasets has been included to test the effect on the accuracy of the classifier when we include in the datasets imperfect data expressed as imperfect and when the imperfect data included are replaced by other data.

The aim of these experiments is to see if we can safely replace imperfect data by imputed or calculated data to allow the application of more traditional techniques (that cannot handle imperfect data).

Each dataset has been modified by introducing a 5% of missing or 5% of fuzzy values.

Datasets with missing values (MIS) have been transformed into others where missing values were replaced by the mean or predominant value (PMV) of corresponding attribute.

Datasets with fuzzy values (FUZ) have been transformed into various datasets, substituting the fuzzy values by (a) an interval value (INT) for the α − cut = 0, (b) the value of the center of gravity (CG), (c) the mean value for the α − cut = 0 (Mad), and (d) the mean value for the α − cut = 1 (Mbc).

The results obtained from this experiment are shown in Table 2. The table indicates the percentage of average classification accuracy of the FRF ensemble (mean and standard deviation) for a 5 × 10-fold cross-validation test, across all datasets.

Table 2 FRF ensemble results for 5% of missing and 5% of fuzzy values

From Table 2 we can observe that the results seem to change considerably when we transform the original dataset with imperfection into one with imputed (calculated) data. To reach a more formal conclusion, we performed a statistical study of significant differences following the recommendations by García et al. (2009).

For datasets with missing values, there are significant differences between having 5% missing values (MIS) and replacing them by imputed mean or predominant values (PMV) (in all cases except for the dataset PIM). In these cases, the best results are obtained with datasets with 5% of missing values.

For datasets with 5% fuzzy values, the analysis is the following:

• Dataset APE: FUZ, Mbc and CG have significant differences with respect to INT, all of them being better than INT.

• Dataset BRE: no significant differences found.

• Datasets HEA: FUZ have significant differences with respect to INT, Mbc, Mad, and CG, with FUZ being the best.

• Dataset PIM: FUZ, Mbc, Mad, and CG have significant differences with respect to INT, all of them being better than INT.

• Dataset IRP: no significant differences found.

• Dataset SMO: FUZ have significant differences with respect to INT and Mbc, with FUZ being the best.

With these experiments we tried to see if it was possible to replace imperfect data by imputed or calculated data to apply traditional techniques (that cannot handle imperfect data). From our analysis, we conclude that when we perform these replacements, the quality of the results tend to suffer.

5.3 Experimentation with low-quality data

These experiments were conducted to test the accuracy of FRF ensemble applied to real-world datasets with imperfect values and compare the results with the ones obtained by the GFS classifier proposed in (Palacios et al. 2009).

In these experiments we used the available datasets in “http://sci2s.ugr.es/keel/” and the available results in (Palacios et al. 2009, 2010). These are datasets from two different real-world problems. The first one is related to the composition of teams in high-performance athletics and the second one is a medical diagnosis problem.

5.3.1 High performance athletics

The score of an athletics team is the sum of the individual scores of the athletes in the different events. It is the coach’s responsibility to balance the capabilities of the different athletes in order to maximize the score of a team according to the regulations. The variables that define each problem are as follows:

• There are four indicators for the long jump that are used to predict whether an athlete will pass a given threshold: the ratio between the weight and the height, the maximum speed in the 40 m race, and the tests of central (abdominal) muscles and lower extremities.

• There are also four indicators for the 100 m race: the ratio between weight and height, the reaction time, the starting or 20 m speed, and the maximum or 40 m speed.

A more detailed description of this problem may be found in (Palacios et al. 2009). The datasets used in this experiment are the following:

• Dataset “Long-4”: Dataset used to predict whether an athlete will improve certain threshold in the long jump, given the indicators mentioned earlier. The set has 25 examples (25 athletes), 4 attributes, 2 classes, and no missing values. All attributes, including the output attribute, are interval-valued.

• Dataset “100ml-4-I”: Used for predicting whether a mark in the 100 meters sprint race is being achieved. Actual measurements are taken by three observers and are combined into the smallest interval that contains them. The set has 25 examples, 4 attributes, 2 classes, and no missing values. All attributes, including the output attribute, are interval-valued.

• Dataset “100ml-4-P”: Same dataset as “100ml-4-I”, but the measurements have been replaced by the subjective grade the trainer has assigned to each indicator (i.e. “reaction time is low” instead of “reaction time is 0.1 sec”).

As in (Palacios et al. 2009), we have used a tenfold cross-validation design for all datasets. Table 3 shows the results obtained in (Palacios et al. 2009) and the ones obtained by the FRF ensemble with the eight combination methods proposed in Appendix. Except for the crisp algorithm proposed in (Palacios et al. 2009), in this table, the interval [mean_min_error, mean_max_error] obtained for each dataset according to the decision process described in Sect. 4.3, is shown. Data from the last row are those obtained in Palacios et al. (2011) repeating the experiments 100 times with bootstrapped resamples of the training set and where each partition of test contains 1,000 tests. This way of obtaining an estimate of the error is more expensive but gets a best estimate and is named exhaustive evaluation.

Table 3 Comparative results of FRF with the ones obtained in (Palacios et al. 2009) for datasets 100ml-4-I, 100ml-4-P and Long-4 with five labels/attribute

In Figs. 4 and 5 are shown the boxplots with the best results of FRF ensemble. Observe that the boxplots of the imprecise experiments are not standard. We have used the extended boxplot proposed in (Palacios et al. 2009). They propose to use a box showing the 75% percentile of the maximum and the 25% percentile of the minimum error (thus the box displays at least the 50% of data). In addition, they represent the interval-valued median of the maximum and minimum result. For this reason, they draw two marks inside the box.

Fig. 4

Boxplots 100ml-4-I and 100ml-4-P with five labels/attribute. cT and cTst are the results for train and test, respectively, of the crisp algorithm proposed in Palacios et al. (2009). LowT and LowTst are the results for train and test of the extended algorithm proposed in Palacios et al. (2009). T-FRF an Tst-FRF are the results for train and test of FRF_MWLT1 to 100ml-4-I and FRF_MIWF1 to 100ml-4-P

Fig. 5

Boxplots Long-4 with five labels/attribute. cT and cTst are the results for train and test, respectively, of the crisp algorithm proposed in Palacios et al. (2009). LowT and LowTst are the results for train and test of extended algorithm proposed in Palacios et al. (2009). T-FRF and Tst-FRF are the results for train and test of FRF_SM2

The results obtained by the extended GFS proposed in (Palacios et al. 2009) and FRF ensemble are very promising because we are representing the information in a more natural and appropriate way, and in this problem, we are allowing the collection of knowledge of the coach by ranges of values and linguistic terms. The results of FRF ensemble are very competitive.

5.3.2 Diagnosis of dyslexic

Dyslexia is a learning disability in people with normal intellectual coefficient and without further physical or psychological problems explaining such disability. Dyslexia may become apparent in early childhood, with difficulty putting together sentences and a family history. Recognition of the problem is very important in order to give the infant an appropriate teaching. A more detailed description of this problem can found in (Palacios et al. 2009, 2010).

In these experiments, we have used three different datasets. Their names are “Dyslexic-12’, “Dyslexic-12-01”, and “Dyslexic-12-12”. Each dataset has 65 examples, 4 classes, and 12 attributes. The output variable for each of these datasets is a subset of the labels that follow:

• No dyslexic.

• Control and revision.

• Dyslexic.

• Inattention, hyperactivity, or other problems.

Both input and the output exhibit imprecision and missing values. These three datasets differ only in their outputs:

• “Dyslexic-12” comprises the four mentioned classes.

• “Dyslexic-12-01” does not make use of the class “control and revision”, whose members are included in class “no dyslexic”.

• “Dyslexic-12-12” does not make use of the class “control and revision”, whose members are included in class “dyslexic”.

All experiments are repeated 100 times for bootstrap resamples with replacement of the training set. The test set comprises the “out of the bag” elements. As mentioned above, the boxplots of the imprecise experiments are not standard. We have used the extended boxplot proposed in Palacios et al. (2009).

The results are shown in Table 4. We compare the results obtained by FRF ensemble with the best ones obtained in (Palacios et al. 2010). Again, in this table, the interval [mean_min_error, mean_max_error] obtained for each dataset according to the decision process described in Sect. 4.3 is shown. In this table, the test values to GGFS are also obtained by an exhaustive evaluation (Palacios et al. 2010), taking a sample of values in the support of imprecise input. The statistical significance of the differences is displayed in Figs. 6 and 7. FRF ensemble is a significant improvement over the crisp GFS.

Table 4 Comparative results of FRF ensemble and the ones obtained in (Palacios et al. 2010) for datasets Dyslexic-12, Dyslexic-12-01, and Dyslexic-12-12

Fig. 6

Boxplots Dyslexic-12 and Dyslexic-12-01 with four labels/attributes. cT and cTst are the results for train and test, respectively, of crisp algorithm CF_0 proposed in Palacios et al. (2010). LowT and LowTst are the results of the extended algorithm CF_0 proposed in Palacios et al. (2010). T-FRF and Tst-FRF are the results for train and test of FRF _SM2

Fig. 7

Boxplots Dyslexic-12-12 with four labels/attribute. cT and cTst are the results for train and test, respectively, of crisp algorithm CF_0 proposed in Palacios et al. (2010). LowT and LowTst are the results for train and test of the extended algorithm CF_0 proposed in Palacios et al. (2010). T-FRF and Tst-FRF are the results for train and test of FRF _SM2

6 Summary

We have presented FRF ensemble, which is an ensemble based on fuzzy decision trees. The FRF ensemble can manage imperfect data directly and has a good classification performance with relatively small ensemble sizes. The FRF ensemble has been extended to include the treatment of new types of imperfect data in both input and output attributes. This technique is very versatile due to the ease with which we can extend it to new situations.

We have presented experimental results obtained by applying the FRF ensemble to various datasets. On the imperfect datasets (with missing and fuzzy values) the results obtained by the FRF ensemble are very interesting. Our conclusion, as many papers in the literature are indicating, is that it is necessary to design and/or adapt classification techniques so they can manipulate real data that can be imperfect in some cases. The transformation of these imperfect values to (imputed) crisp values may cause undesirable effects with respect to accuracy of the technique.

Finally, FRF ensemble has been applied to real-problems datasets, such as the composition of teams in high-performance athletics and a medical diagnosis problem. The results obtained by FRF ensemble are promising, leading to the conclusion, as in (Palacios et al. 2009, 2010), that by using ranges of values and linguistic terms instead of crisp, imputed numbers, we better capture the nature of the underlying information.

Appendix: Combination methods

In this appendix, we use the notation above defined in Sect. 3.2. For each strategy for fuzzy classifier module in the FRF ensemble that is described in Sect. 3.2 we can define several functions Faggre1₁, Faggre1₂ and Faggre2. The overall set of functions is described in Bonissone et al. (2010). In this appendix, the utilized methods in this paper are described in detail:

1.1 Non-trainable methods

In these combination methods, a transformation is applied to the matrix L_FRF in Step 2 in Algorithms 3 and 4 so that each leaf reached assigns a simple vote to the majority class.

$$ \begin{aligned} {\rm For}\,t &= 1,\ldots,T \\ &{\rm For}\, n = 1,\ldots, N\\ & \quad {\rm For}\,i = 1,\ldots, I\\ &\qquad L\_FRF {-}mod_{t,n,i} = \left\{ \begin{array}{ll} 1 & {\rm if}\ i=\arg\displaystyle\max_{j, j=1,\ldots,I} \{L\_FRF_{t,n,j}\}\\ 0 &{\rm otherwise} \\ \end{array}\right. \end{aligned} $$

Within this group we define the following methods. We get two versions depending on the strategy used:

• Simple Majority vote:

• Strategy 1→ method SM1

  The function Faggre1₁ in Algorithm 3 is defined as

  $$ Faggre1_1(t,i,L\_FRF)=\left\{ \begin{array}{ll} 1 & {\rm if}\ i=\arg\displaystyle\max_{j, j=1,\ldots,I} \left\{ \sum_{n=1}^{N_t} L\_FRF-mod_{t,n,j} \right\}\\ 0 & {\rm otherwise} \\ \end{array}\right. $$

  In this method, each tree t assigns a simple vote to the most voted class among the N _t reached leaves by example e in the tree.

  The function Faggre1₂ in Algorithm 3 is defined as

  $$ Faggre1_2(i,T\_FRF)=\sum_{t=1}^{T} T\_FRF_{t,i} $$

• Strategy 2 → method SM2

  For Strategy 2, it is necessary to define the function Faggre2 combining information from all leaves reached in the ensemble by example e. Thus, the function Faggre2 in Algorithm 4 is defined as

  $$ Faggre2(i,L\_FRF)= \sum_{t=1}^{T} \sum_{n=1}^{N_t} L\_FRF_mod{t,n,i} $$

1.2 Trainable explicitly dependent methods

• Majority vote Weighted by Leaf:

  In this combination method, a transformation is applied to the matrix L_FRF in Step 2 of Algorithms 3 and 4 so that each leaf reached assigns a weighted vote to the majority class. The vote is weighted by the degree of satisfaction with which example e reaches the leaf.

  $$ \begin{aligned} {\rm For}\,t &= 1,\ldots,T \\ &{\rm For}\, n = 1,\ldots, N\\ & \quad {\rm For}\,i = 1,\ldots, I\\ &\qquad L\_FRF {-}mod_{t,n,i} = \left\{ \begin{array}{ll} \chi_{t,n(e)} & {\rm if}\ i=\arg\displaystyle\max_{j, j=1,\ldots,I} \{L\_FRF_{t,n,j}\}\\ 0 & {\rm otherwise} \\ \end{array}\right. \end{aligned} $$

  Again, we have two versions according to the strategy used.

• Strategy 1 → method MWL1

  The functions Faggre1₁ and Faggre1₂ are defined as

  $$ Faggre1_1(t,i,L\_FRF)=\left\{ \begin{array}{ll} 1 & {\rm if}\ i=\arg\displaystyle\max_{j, j=1,\ldots,I} \left\{ \sum_{n=1}^{N_t} L\_FRF-mod_{t,n,j} \right\}\\ 0 & {\rm otherwise} \\ \end{array}\right. $$
  $$ Faggre1_2(i,T\_FRF)=\sum_{t=1}^{T} T\_FRF_{t,i} $$

• Strategy 2 → method MWL2

  The function Faggre2 is defined as

  $$ Faggre2(i,L\_FRF)= \sum_{t=1}^{T} \sum_{n=1}^{N_t} L\_FRF_{t,n,i} $$

  • Majority vote Weighted by Leaf and by Tree:

  Again, in this combination method, a transformation is applied to the matrix L_FRF in Step 2 of Algorithms 3 and 4 so that each leaf reached assigns a weighted vote to the majority class. The vote is weighted by the degree of satisfaction with which example e reaches the leaf.

  $$ \begin{aligned} {\rm For}\,t &= 1,\ldots,T \\ &{\rm For}\, n = 1,\ldots, N\\ & \quad {\rm For}\,i = 1,\ldots, I\\ &\qquad L\_FRF {-}mod_{t,n,i} = \left\{ \begin{array}{ll} \chi_{t,n}(e) & {\rm if}\ i=\arg\displaystyle\max_{j, j=1,\ldots,I} \{L\_FRF_{t,n,j}\}\\ 0 & {\rm otherwise} \\ \end{array}\right. \end{aligned} $$

  In addition, in this method a weight for each tree obtained is introduced by testing each individual tree with the OOB dataset. Let $\overline{p}=(p_1,p_2,\ldots,p_T)$ be the vector with the weights assigned to each tree. Each p _t is obtained as $\frac{N\_success\_OOB_t}{size\_OOB_t}$ where N_success_OOB _t is the number of examples classified correctly from the OOB dataset used for testing the tth tree and size_OOB _t is the total number of examples in this dataset.

  Strategy 1 → method MWLT1

  The function Faggre1₁ is defined as:

  $$ Faggre1_1(t,i,L\_FRF)=\left\{ \begin{array}{ll} 1 & {\hbox{if}}\ i=\arg\displaystyle\max_{j, j=1,\ldots,I} \left\{ \sum_{n=1}^{N_t} L\_FRF-mod_{t,n,j} \right\}\\ 0 & {\hbox{otherwise}} \\ \end{array}\right. $$

  Vector $\overline{p}$ is used in the definition of function Faggre1₂:

  $$ Faggr1_2(i,T\_FRF)=\sum_{t=1}^{T} p_t \cdot T\_FRF_{t,i} $$

  Strategy 2 → method MWLT2

  The vector of weights $\overline{p}$ is applied to Strategy 2.

  $$ Faggre2(i,L\_FRF)=\sum_{t=1}^{T} p_t \sum_{n=1}^{N_t} L\_FRF_{t,n,i} $$

  • Minimum Weighted by Leaf and by membership Function:

    In this combination method, a transformation is applied to the matrix L_FRF in Step 2 of Algorithms 3.

    $$ \begin{aligned} {\rm For}\,t &= 1,\ldots,T \\ &{\rm For}\, n = 1,\ldots, N\\ & \quad {\rm For}\,i = 1,\ldots, I\\ &\qquad L\_FRF {-}mod_{t,n,i} = \chi_{t,n}(e) \times \frac{E_i}{E_n} \end{aligned} $$

    Strategy 1 → method MIWLF1

    The function Faggre1₁ is defined as:

    $$ Faggre1_1(t,i,L\_FRF)=\left\{ \begin{array}{ll} 1 & {\hbox{if}} \ i=\displaystyle\arg\max_{j, j=1,\ldots,I}\left\{ min(L\_FRF-mod_{t,1,j},L\_FRF-mod_{t,2,j},\right.\\ & \phantom{si\ i=\displaystyle\arg\max_{j, j=1,\ldots,I}}\left.\ldots ,L\_FRF-mod_{t,N_t,j})\right\} \\ 0 & {\hbox{otherwise}} \\ \end{array}\right. $$

    The function Faggre1₂ incorporates the weighting, defined by a fuzzy membership function, for each tree:

    $$ Faggre1_2(i,T\_FRF)=\sum_{t=1}^{T} \mu_{pond}\left(\frac{errors_{(OOB_t)}}{size_{(OOB_t)}}\right) \cdot T\_FRF_{t,i} $$

    The membership function is defined by μ _pond (x):

    $$ \mu_{pond}(x)=\left\{\begin{array}{ll} 1 & 0 \leq x \leq (pmin+marg)\\ \frac{(pmax+marg)-x}{(pmax-pmin)} & (pmin+marg)\leq x \leq (pmax+marg)\\ 0 & (pmax+marg) \leq x \\ \end{array}\right. $$

    where

    • pmax is the maximum rate of errors in the trees of the FRF ensemble ($pmax=\max_{t=1,\ldots,T}\left\{\frac{errors_{(OOB_t)}}{size_{(OOB_t)}}\right\}$). The rate of errors in a tree t is obtained as $\frac{errors_{(OOB_t)}}{size_{(OOB_t)}}$ where errors _{(OOB_t)} is the number of classification errors of the tree t (using the OOB _t dataset as test set), and size _{(OOB_t)} is the cardinal of the OOB _t dataset. As we indicated above, the OOB _t examples are not used to build the tree t and they constitute an independent sample to test tree t. So we can measure the goodness of a tree t as the number of errors when classifying the set of examples OOB _t ;

    • pmin is the minimum rate of errors in the trees of the FRF ensemble; and

    • $marg=\frac{pmax-pmin}{4}$

1.3 Trainable implicitly dependent methods

Within this group we define the following methods:

• Minimum Weighted by membership Function: In this combination method, no transformation is applied to matrix L_FRF in Step 2 of Algorithm 3.

  Strategy 1 → method MIWF1

  The function Faggre1₁ is defined as

  $$ Faggre1_1(t,i,L\_FRF)=\left\{ \begin{array}{ll} 1 & {\rm if}\ i=\displaystyle\arg\max_{j, j=1,\ldots,I}\left\{ min(L\_FRF_{t,1,j},L\_FRF_{t,2,j}, \right. \\ & \phantom{si\ i=\displaystyle\arg\max_{j, j=1,\ldots,I}}\left.\ldots ,L\_FRF_{t,N_t,j})\right\} \\ 0 & {\rm otherwise} \\ \end{array}\right. $$

  The function Faggre1₂ incorporates the weighting defined by the previous fuzzy membership function for each tree:

  $$ Faggre1_2(i,T\_FRF)=\sum_{t=1}^{T} \mu_{pond}\left(\frac{errors_{(OOB_t)}}{size_{(OOB_t)}}\right) \cdot T\_FRF_{t,i} $$