Enhanced opposition-based differential evolution for solving high-dimensional continuous optimization problems

Abstract

This paper presents a novel algorithm based on generalized opposition-based learning (GOBL) to improve the performance of differential evolution (DE) to solve high-dimensional optimization problems efficiently. The proposed approach, namely GODE, employs similar schemes of opposition-based DE (ODE) for opposition-based population initialization and generation jumping with GOBL. Experiments are conducted to verify the performance of GODE on 19 high-dimensional problems with D = 50, 100, 200, 500, 1,000. The results confirm that GODE outperforms classical DE, real-coded CHC (crossgenerational elitist selection, heterogeneous recombination, and cataclysmic mutation) and G-CMA-ES (restart covariant matrix evolutionary strategy) on the majority of test problems.

1 Introduction

Many real-world problems may be formulated as optimization problems with variables in continuous domains (continuous optimization problems). In the past decades, different kinds of nature-inspired optimization algorithms have been designed and applied to solve optimization problems, e.g., simulated annealing (SA; Kirkpatrick et al. 1983), evolutionary algorithms (EAs; Bäck 1996), differential evolution (DE; Storn and Price 1997), particle swarm optimization (PSO; Kennedy and Eberhart 1995), ant colony optimization (ACO; Dorigo et al. 1996), estimation of distribution algorithms (EDA; Larranaga and Lozano 2001), etc.

Although these algorithms have shown good optimization performance in solving lower dimensional problems (D < 100), many of them suffer from the curse of dimensionality, which implies that their performance deteriorates quickly as the dimension of the problem increases. The main reason is that in general the complexity of the problem increases exponentially with its dimension. The majority of evolutionary algorithms lose the power of searching the optima solution when the dimension increases. So, more efficient search strategies are required to explore all the promising regions in a given time budget (Tang et al. 2007).

Opposition-based learning (OBL), introduced by Tizhoosh (2005), is a machine intelligence strategy, which considers current estimate and its opposite estimate at the same time to achieve a better approximation for a current candidate solution. It has been proved (Rahnamayan et al. 2008a) that an opposite candidate solution has a higher chance to be closer to the global optimum solution than a random candidate solution. The idea of OBL has been used to enhance population-based algorithms (Rahnamayan et al. 2006a, b, 2008b; Wang et al. 2007). Opposition-based DE (ODE) is one of these successful applications, which shows excellent search abilities in solving both low-dimensional and high-dimensional problems (Rahnamayan et al. 2008b; Rahnamayan and Wang 2008). In this paper, we present an enhanced ODE algorithm to solve high-dimensional continuous optimization problems more efficiently. The proposed approach is called GODE, which employs a generalized opposition-based learning (GOBL) concept (Wang et al. 2009a, b).

The rest of the paper is organized as follows. In Sect. 2, the classical DE algorithm is briefly introduced. Section 3 presents some reviews of related work on large-scale global optimization. The GOBL and its analysis are given in Sect. 4. Section 5 gives an implementation of the proposed algorithm, GODE. In Sect. 6, the test suite, parameter settings, results and discussions are presented. Finally, the work is concluded in Sect. 7.

2 Differential evolution

Differential evolution (DE), proposed by Storn and Price (1997), is an effective, robust and simple global optimization algorithm. According to frequently reported experimental studies, DE has shown better performance than many other evolutionary algorithm (EAs) in terms of convergence speed and robustness over several benchmark functions and real-world problems (Vesterstrom and Thomsen 2004).

There are several variants of DE (Storn and Price 1997). According to the suggestions of Herrera et al. (2010a), the rand/1/exp strategy shows a better performance to solve high-dimensional problems. Our proposed algorithm is also based on this DE scheme. Let us assume that $X_{i}(t)(i=1,2,\ldots,N_p)$ is the ith individual in population P(t), where $N_p$ is the population size, t is the generation index, and P(t) is the population in the tth generation. The main idea of DE is to generate trial vectors. Mutation and crossover are used to produce new trial vectors, and selection determines which of the vectors will be successfully selected into the next generation.

• Mutation: For each vector $X_{i}(t)$ in Generation t, a mutant vector V is generated by

  $$ V_i(t) = X_{i_1}(t)+F \left(X_{i_2}(t)-X_{i_3}(t)\right), $$

  (1)
  $$ \qquad i \neq i_1 \neq i_2 \neq i_3, $$

  where $i=1,2,\ldots,N_p$ and $i_1, i_2$, and i₃ are mutually different random integer indices within $[1,N_p]$. The population size $N_p$ should be satisfied $N_p \geq 4$ because i, i₁, $i_2$, and $i_3$ are different. $F \in [0,2]$ is a real number that controls the amplification of the difference vector $(X_{i_2}(t)-X_{i_3}(t))$.

• Crossover: Like genetic algorithms, DE also employs a crossover operator to build trial vectors $(U_i(t) = \{U_{i,1}(t),U_{i,2}(t),\ldots, U_{i,D}(t)\})$ by recombining two different vectors. In this paper, we use the rand/1/exp strategy to generate the trial vectors.

• Selection: A greedy selection mechanism is used as follows:

  $$ X_{i}(t) = \left\{\begin{array}{ll} U_{i}(t), & \hbox{if}\;f(U_i(t))\leq\, f(X_i(t)) \\ X_{i}(t), & \hbox{otherwise}\\ \end{array}\right. $$

  (2)

Without loss of generality, this paper only considers minimization problem. If, and only if, the trial vector $U_i(t)$ is better than $X_i(t)$, then $X_i(t)$ is set to $U_i(t)$; otherwise, the $X_i(t)$ remains unchanged.

3 Related works

In the past several years, the research on solving high-dimensional optimization problems has attracted much attention. Some excellent works have been proposed. In this section, a brief overview of these approaches is presented.

Yang et al. (2008) proposed a multilevel cooperative co-evolution algorithm based on self-adaptive neighborhood search DE (SaNSDE) to solve large-scale problems. Hsieh et al. (2008) presented an efficient population utilization strategy for PSO (EPUS-PSO) to manage the population size. Brest et al. (2008) introduced a population size reduction mechanism into self-adaptive DE, where the population size decreases during the evolutionary process. Tseng and Chen (2008) presented multiple trajectory search (MTS) by using multiple agents to search the solution space concurrently. Zhao et al. (2008) used dynamic multi-swarm PSO with local search (DMS-PSO) for large-scale problems. Rahnamayan and Wang (2008) presented an experimental study of opposition-based DE (ODE; Rahnamayan et al. 2008b) on large-scale problems. The reported results show that ODE significantly improves the performance of standard DE. Wang and Li (2008) proposed a univariate EDA (LSEDA-gl) by sampling under mixed Gaussian and lévy probability distribution. Rahnamayan and Wang (2009) introduced an effective population initialization mechanism when dealing with large-scale search spaces.

Molina et al. (2009) presented a memetic algorithm by employing MTS and local search chains to deal with large-scale problems. García-Martínez and Lozano (2009) proposed a continuous variable neighborhood search algorithm based on evolutionary metaheuristic components. Muelas et al. (2009) used a local search mechanism to improve the solutions obtained by DE. Duarte and Marti (2009) presented an adaptive memory procedure based on scatter search and Tabu search to guide search in solving large-scale problems. Wang et al. (2009b) used an enhanced ODE based on generalized opposition-based learning (GODE) to solve scalable benchmark functions. Gardeus et al. (2009) proposed an enhanced unidimensional search (EUS) by employing an intensification mechanism.

4 Generalized opposition-based learning

4.1 Opposition-based learning

Opposition-based Learning (OBL; Tizhoosh 2005) is a new concept in computational intelligence, and has been proven to be an effective concept to enhance various optimization approaches (Rahnamayan et al. 2006a, b, 2008b; Wang et al. 2007). When evaluating a solution x to a given problem, simultaneously computing its opposite solution will provide another chance for finding a candidate solution closer to the global optimum (Rahnamayan et al. 2006a).

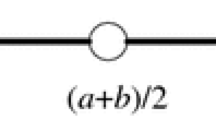
Opposite number (Rahnamayan et al. 2006a): Let $x\in [a,b]$ be a real number. The opposite of x is defined by:

$$ x^*=a+b-x. $$

(3)

Similarly, the definition is generalized to higher dimensions as follows.

Opposite point (Rahnamayan et al. 2006a): Let $X=(x_1,x_2,\ldots,x_D)$ be a point in a D-dimensional space, where $x_1,x_2,\ldots,x_D\in R$ and $x_j\in [a_j, b_j],\ j\in{1,2,\ldots,D}$. The opposite point $X^* = (x_1^*,x_2^*,\ldots,x_D^*)$ is defined by:

$$ x_j^*=a_j+b_j-x_j. $$

(4)

By applying the definition of opposite point, the opposition-based optimization can be defined as follows.

Opposition-based optimization (Rahnamayan et al. 2006a): Let $X=(x_1,x_2,\ldots,x_D)$ be a point in a D-dimensional space (i.e., a candidate solution). Assume f(X) is a fitness function, which is used to evaluate the candidate’s fitness. According to the definition of the opposite point, $X^* = (x_1^*,x_2^*,\ldots,x_D^*)$ is the opposite of $X=(x_1,x_2,\ldots,x_D)$. If $f(X^*)$ is better than f(X), then update X with $X^*$; otherwise keep the current point X. Hence, the current point and its opposite point are evaluated simultaneously to continue with the fitter one.

4.2 The concept of GOBL

Based on the concept of OBL, we proposed a generalized OBL as follows (Wang et al. 2009a). Let x be a solution in the current search space S, $x\in [a,b]$. The new solution $x^*$ in the opposite space $S^*$ is defined by (Wang et al. 2009a):

$$ x^* = \Updelta - x, $$

(5)

where Δ is a computable value and $x^*\in [\Updelta -b,\Updelta - a]$. It is obvious that the differences between the current search space S and the opposite search space $S^*$ are the center positions of search space. Because the size of search range (indicates the size of interval boundaries) of S and $S^*$ are b − a, and the center of current search space moves from ${\frac{a+b}{2}}$ to ${\frac{2\Updelta-a-b}{2}}$ after using GOBL.

Similarly, the definition of GOBL is generalized to a D-dimensional search space as follows.

$$ x_j^* = \Updelta - x_j, $$

(6)

where $j=1,2,\ldots,D$.

By applying the GOBL, we not only evaluate the current candidate x, but also calculate its transformed candidate $x^*$. This will provide more chance of finding candidate solutions closer to the global optimum.

However, the GOBL could not be suitable for all kinds of optimization problems. For instance, the transformed candidate may jump away from the global optimum when solving multimodal problems. To avoid this case, a new elite selection mechanism based on population is used after the transformation, in which $N_p$ (population size) fittest candidates will survive in the next generation. The elite selection mechanism is described in Fig. 1. Assume that the current population P(t) has three candidates ($N_p=3$), $x_1, x_2$ and $x_3$, where t is the index of generations. According to the concept of GOBL, we get three transformed candidates $x^*_1$, $x^*_2$ and $x^*_3$ in population GOP(t). Then, we select three fittest candidates from P(t) and GOP(t) as a new population $P^{\prime}(t)$. It can be seen from Fig. 1, $x_1, x^*_2$ and $x^*_3$ are three new members in $P^{\prime}(t)$. In this case, the transformation conducted on $x_1$ did not provide another chance of finding a better candidate solution. With the help of the elite selection mechanism, $x^*_1$ is eliminated in the next generation.

Fig. 1

The elite selection mechanism based on population

4.3 Four different schemes of GOBL

Let $\Updelta = k(a+b)$, where k is a real number. The new GOBL model is defined by:

$$ x^* = k(a+b) - x. $$

(7)

Let us consider four typical GOBL schemes with different values of k as follows.

• 1. $k=0$ (symmetrical solutions in GOBL, GOBL-SS). The GOBL-SS model is defined by

  $$ x^* = - x, $$

  (8)

  where $x \in [a,b]$ and $x^* \in [-b, -a]$. The current solution x and opposite solution $x^*$ are on the symmetry of origin (0).

• 2. $k={\frac{1}{2}}$ (symmetrical interval in GOBL, GOBL-SI). The GOBL-SI model is defined by

  $$ x^* = {\frac{a+b}{2}}- x, $$

  (9)

  where $x \in [a,b]$ and $x^* \in \left[-{\frac{b-a}{2}}, {\frac{b-a} {2}}\right]$. The interval of the opposite space is on the symmetry of origin.

• 3. $k=1$ (opposition-based learning, OBL).

  When $k=1$, the GOBL model is equal to equation (3), where $x \in [a,b]$ and $x^* \in [a, b]$.

• 4. $k=rand(0,1)$ (Random GOBL, GOBL-R)

The GOBL-SI model is defined by

$$ x^* = k(a + b) - x, $$

(10)

where k is a random number within $[0, 1], x \in [a, b]$ and $x^* \in [k(a+b)-b, k(a+b)-a]$. The center of the opposite space is at a random position between $-{\frac{a+b}{2}}$ and ${\frac{a+b} {2}}$.

For a given problem, it is possible that the opposite candidate may jump out of the box-constraint $[X_{\rm min}, X_{\rm max}]$. When this happens, the GOBL will be invalid, because the opposite candidate is infeasible. To avoid this case, the opposite candidate is assigned to a random value as follows.

$$ x^* = rand(a,b),\quad\hbox{If}\;x^*\notin[X_{\rm min},X_{\rm max}] $$

(11)

where rand(a, b) is a random number within [a, b], and [a, b] is the interval boundaries of current search space.

To illustrate the mechanism of GOBL clearly, Figs. 2 and 3 present the visualization of the four different GOBL models. By the suggestion of our previous study (Wang et al. 2009a), the GOBL-R surpasses the other three GOBL models. So the proposed approach GODE is also based on the GOBL with random k in this paper.

Fig. 2

(1) The GOBL-SS model, (2) the GOBL-SI model

Fig. 3

(3) The OBL model, (4) the GOBL-R model

4.4 GOBL-based optimization

By staying within variables’ interval static boundaries, we would jump outside of the already shrunken search space and the knowledge of the current converged search space would be lost. Hence, we calculate opposite particles by using dynamically updated interval boundaries $[a_j(t),b_j(t)]$ as follows (Rahnamayan et al. 2008b).

$$ X_{i,j}^*=k[a_j(t)+b_j(t)]-X_{i,j} $$

(12)

$$ a_j(t)=\min(X_{i,j}(t)),\;b_j(t)=\max(X_{i,j}(t)) $$

(13)

$$ X_{i,j}^*=rand(a_j(t),b_j(t)),\;\hbox{If} \ X_{i,j}^* \notin [X_{min}, X_{max}] $$

(14)

$$ i=1,2,\ldots,N_p,\;j=1,2,\ldots,D, k=rand(0,1), $$

where $X_{i,j}$ is the jth vector of the ith candidate in the population, $X_{i,j}^*$ is the opposite candidate of $X_{i,j}$, $a_j(t)$ and $b_j(t)$ are the minimum and maximum values of the jth dimension in the current search space, respectively, $rand(a_j(t),b_j(t))$ is a random number within $[a_j(t), b_j(t)]$, $[X_{min}, X_{max}]$ is the box-constraint, $N_p$ is the population size, rand(0,1) is a random number within [0,1], k is generated anew in each generation (i.e., the same value of k is used for the whole population), and $t = 1,2,\ldots,$ indicates the generations.

5 Generalized opposition-based differential evolution

In our previous work (Wang et al. 2009a), GOBL was applied to PSO and the experimental results showed that the GOBL with random k works better than the other three GOBL models in many benchmark problems. So, the proposed approach GODE is also based on the random GOBL model in this paper.

Like ODE (Rahnamayan et al. 2008b), the GODE uses similar procedures for opposition-based population initialization and dynamic opposition with GOBL. The parent DE is chosen as a parent algorithm and the proposed GOBL model is embedded in DE to improve its performance. However, the embedded strategy of GODE is different from ODE [See Table 3 in Rahnamayan et al. (2008b)]. In the ODE, the opposition is regarded as a jump or mutation strategy. GODE considers the opposition as another search mechanism besides DE, so GODE alternately executes GOBL and DE. In the ODE, the opposition occurs with a probability, and the parent DE executes every generation. But in the GODE, if the probability of opposition p _o is satisfied, then execute the GOBL; otherwise execute the classical DE.

The framework of GODE is shown in Algorithm 1, where P is the current population, GOP is the opposite population after using GOBL, $P_i$ is the ith individual in P, $GOP_i$ is the ith individual in GOP, k is a random number within [0, 1], $p_o$ is the probability of GOBL, $N_p$ is the population size, D is the dimension size, $a_j(t), b_j(t)$ is the interval boundaries of current population, $rand(a_j(t), b_j(t))$ is a random number within $[a_j(t), b_j(t)], CR \in (0,1)$ is the predefined crossover probability, $rand_j()$ is a random number within [0,1], FEs is the number of fitness evaluations, and $MAX\_{{FEs}}$ is the maximum number of evaluations.

6 Experimental studies

6.1 Experimental setup

There are 19 high-dimensional continuous optimization functions used for the following experiments. Functions F1–F6 were chosen from the first six functions provided by CEC 2008 Special Session and Competition on Large Scale Global Optimization (Tang et al. 2007). Functions F7–F11 were proposed for ISDA 2009 Workshop on Evolutionary Algorithms and other Metaheuristics for Continuous Optimization Problems—A Scalability Test (Herrera and Lozano 2009). The rest of the eight functions, F12–F19, are hybrid composition functions built by combining two functions belonging to the set functions F1–F11. The specific descriptions of F1–F19 can be found in Herrera et al. (2010b). In this paper, we focus on investigating the optimization performance of GODE on problems with and D = 50, 100, 200,  500, 1,000.

Experiments were conducted to compare four algorithms including DE (Storn and Price 1997), real-coded CHC (Eshelman and Schaffer 1993), G-CMA-ES (Auger and Hansen 2005) and the proposed GODE algorithm on the test suite. The parameter settings of DE, CHC and G-CMA-ES are described in (Herrera et al. 2010a). For GODE, the parameters N _p , F, CR, and $p_o$ are fixed to 60, 0.5, 0.9 and 0.05, respectively. By the suggestions of Herrera et al. (2010a), the rand/1/exp scheme is employed in GODE.

In the experiments, and each algorithm is run 25 times for each test function. The maximum number of fitness evaluations $\hbox{MAX}\_{{\rm FEs}}$ is 5,000*D. Each run stops when the maximum number of evaluations is achieved. Throughout the experiments, the Best, Median, Worst and Mean error values over 25 runs are recorded (for a solution x, the error measure is defined as $F(x)-F(op)$, where op is the global optimum of the function). All the results below 1E–14 have been approximated to 0.0.

6.2 Results

Table 1 shows the results of GODE on functions F1–F19 with dimension D = 50, 100, 200,  500, 1,000. As seen, GODE obtains promising performance on the majority of test functions on each dimension. But GODE fails to solve F3 and its hybrid composition functions F13 and F17. It also has some difficulties when solving F4 for D = 500, 1,000, while it achieves good results for smaller dimensionality. For functions F8, GODE could hardly find reasonable solutions on each dimension. When the dimension increases to 1,000, GODE fails to solve F7 and F15. In our test, the fitness values of these two functions are larger than the maximum value $(10^{308})$ that double precision float number can represent. This problem can be solved by using higher precision data types, such as “long double” in C/C++. Although we used “long double” to represent the fitness value, GODE was implemented in Microsoft Visual C++ 6.0, which uses the same size of bytes (8 bytes) to represent “double” and “long double”. So, we did not list the results of these two functions for $D=1000$.

Table 1 Experimental results of GODE for D = 50, 100, 200,  500, 1,000

6.3 Comparison of GODE with DE, CHC and G-CMA-ES

This section investigates the performance comparison of GODE with DE, CHC and G-CMA-ES for D = 50, 100, 200,  500, 1,000 (the results of G-CMA-ES for D = 1,000 are not included due to the large computation time for runs for some functions). Tables 2, 3, 4, 5 and 6 present the average error values of the above four algorithms on D = 50, 100, 200,  500, 1,000, respectively. The best results among the four (three for D = 1,000) algorithms are shown in bold.

Table 2 Mean error values achieved by DE, CHC, G-CMA-ES and GODE on D = 50

Table 3 Mean error values achieved by DE, CHC, G-CMA-ES and GODE on D = 100

Table 4 Mean error values achieved by DE, CHC, G-CMA-ES and GODE on D = 200

Table 5 Mean error values achieved by DE, CHC, G-CMA-ES and GODE on D = 500

Table 6 Mean error values achieved by DE, CHC, G-CMA-ES and GODE on D = 1000

From the results, it can be seen that both DE and GODE achieve promising results in all test cases except for F8, while CHC and G-CMA-ES fall into local optima on the majority of test functions. Compared to DE, GODE achieves better results on nine functions (F4, F6, F8, F9, F11, F12, F14, F16 and F18) in terms of their average error values, while DE performs better on one function F13. For functions F2, F3 and F17, DE outperforms GODE on some dimensions. Both GODE and DE achieve the same results on six functions: F1, F5, F7, F10, F15 (except for $D=1,000$) and F19 (except for $D=1,000$). These comparison results clearly demonstrate that the achieved improvements of GODE are due to usage of the proposed GOBL strategy.

G-CMA-ES outperforms GODE on three functions, F2, F3 and F8. Especially for F8, only G-CMA-ES achieves excellent results, while the other three algorithms could hardly search reasonable results. Both GODE and C-CMA-ES obtain the same results for F1 and F5 on $D=200$. For the rest of the 14 functions, GODE obtains better performance than G-CMA-ES.

Real-coded CHC is the worst algorithms among the four algorithms. It only obtains promising results on F1, which is a simple and unimodal function. For the rest of the functions, the performance of CHC is seriously affected with increasing dimensions. It suggests that CHC is not a good choice for solving large-scale problems.

6.4 Statistical comparisons of different algorithms

Non-parametric tests can be used for comparing algorithms, the results of which represent average values for each problem, in spite of the inexistence of relationships among them. It is encouraged to use non-parametric tests to analyze the results obtained by evolutionary algorithms for continuous optimization problems in multiple problem analysis (García et al. 2009a, b; Luengo et al. 2009).

To compare the performance of multiple algorithms on the test suite, average ranking of Friedman test is conducted according to the suggestions of García et al. (2010). Tables 7, 8, 9, 10 and 11 show the average ranking of GODE, DE, CHC and G-CMA-ES on D = 50, 100, 200,  500 and 1,000, respectively. For each dimension, the performance of the four algorithms (three for D = 1,000) can be sorted by average ranking into the following order: GODE, DE, G-CMA-ES and CHC. It means that GODE and CHC are the best and worst ones among the four algorithms, respectively.

Table 7 Average rankings of the algorithms when D = 50

Table 8 Average rankings of the algorithms when D = 100

Table 9 Average rankings of the algorithms when D = 200

Table 10 Average rankings of the algorithms when D = 500

Table 11 Average rankings of the algorithms when D = 1000

To investigate the significant differences between the behavior of two algorithms, we conduct other tests: Nemenyi’s, Holm’s, Shaffer’s and Bergmann-Hommel’s. For each test, we calculate the adjusted p values on pairwise comparisons of all algorithms.

Tables 12,13,14,15 and 16 show the results of adjusted p values on and D = 50, 100, 200,  500 and 1,000, respectively. The computation of the results is used by the software MULTIPLETEST package (provided on the Web site: http://sci2s.ugr.es/sicidm). Under the null hypothesis, the two algorithms are equivalent. If the null hypothesis is rejected, then the performances of these two algorithms are significantly different. In this paper, we only discuss whether the hypotheses is rejected at the 0.05 level of significance. For D = 50, Nemenyi’s procedure rejects hypotheses 1–3, while Holm’s, Shaffer’s and Bergmann-Hommel’s procedures reject hypotheses 1–4. For D = 100, Nemenyi’s, Holm’s and Shaffer’s procedures reject hypotheses 1–3, while Bergmann-Hommel’s procedure rejects hypotheses 1–4. For D = 200, Nemenyi’s, Holm’s and Shaffer’s procedures reject hypotheses 1–3, while Bergmann-Hommel’s procedures rejects hypotheses 1–4. For D = 500 and 1,000, all the four tests reject hypotheses 1–4 and 1–3, respectively.

Table 12 Adjusted p values for D = 50

Table 13 Adjusted p values for D = 100

Table 14 Adjusted p values for D = 200

Table 15 Adjusted p values for D = 500

Table 16 Adjusted p values for D = 1000

Besides the above four tests, we also conduct Wilcoxon’s test to detect significant differences between the behavior of two algorithms. Table 17 shows the p values of applying Wilcoxon’s test between GODE and other three algorithms for D = 50, 100, 200,  500 and 1,000. The p values below 0.05 are shown in bold. From the results, it can be seen that GODE is significantly better than CHC and G-CMA-ES on each dimension. Though GODE is not statistically better than DE on each dimension, GODE outperforms DE according to the results of average ranking.

Table 17 Wilcoxon test considering functions F1–F19 on each dimension

6.5 Computational running time

In this section, we investigate the computation running time and the computational time complexity of the proposed algorithm. For each test function, the average running time on the 25 runs are recorded. The computational conditions are listed as follows.

• System: Windows 7 professional edition

• CPU: Intel(R) Core(TM)2 Duo CPU E8500 (3.16GHz)

• RAM: 4G

• Language: C++

• Compiler: Microsoft Visual C++ 6.0

• MAX_FEs: 5000*D (D=50, 100, 200, 500 and 1,000)

The average computation running time of GODE on the test suite is given in Table 18. As seen, the computation time increases dramatically with increasing of dimensions. To investigate how the computational running time grows in relation to the number of dimensions, we analyze the computational time complexity of GODE as follows.

Table 18 The average computation running time (in seconds) achieved by GODE

Assume that O(F(D)) is the computational time complexity of a fitness evaluation function F(D) on dimension D. For GODE, the computational time complexity is $O(D^2)+O(D) \cdot O(F(D))$. So, the computational time complexity of GODE depends on O(F(D)). For the 19 test functions used in the experiments, O(F(D)) is O(D) except for F8; on this function, $O(F(D))=O(D^2)$. So the computational time complexity of GODE is $O(D^3)$ for F8 and $O(D^2)$ for the rest of functions.

To verify the above analysis, we use two regression models, cubic ($T=a_0+a_1{\times}D+a_2 {\times}D^2+a_3 {\times}D^3$, where $a_0,a_1,a_2,a_3 > 0$) and quadratic ($T=b_0 + b_1\times D + b_2\times D^2$, where $b_0, b_1, b_2 > 0$), to approximate the results of computational running time for F8 and the rest of functions, respectively. To measure how well the regression line approximates the real data points, we calculate the values of “R square”, which evaluates the goodness of fit of the line. It represents the percentage variation of the data explained by the fitted line. A value of 1.000 indicates that the regression line perfectly (100%) fits the real data. Table 19 shows the values of “R square”. As seen, the regression model perfectly fits the real data for each test function. It confirms that the computational time complexity of GODE is $O(D^3)$ for F8 and $O(D^2)$ for the rest of the functions. The results suggest that GODE is applicable for large-scale problems.

Table 19 Computational time complexity analysis using regression model

7 Conclusion

In this paper, a novel DE algorithm based on generalized opposition-based learning (GODE) is proposed. The GOBL is an enhanced opposition-based learning, which transforms candidates in current search space to a new search space. By simultaneously evaluating solutions in the current search space and transformed space, we can provide more chance of finding better solutions. A scalability test over 19 high-dimensional continuous optimization problems with and D = 50, 100, 200,  500 and 1,000, provided by the current special issue, are conducted.

GODE as well as DE obtains promising performance on the test suite (except for F8), while CHC and G-CMA-ES could hardly obtain reasonable results on many functions. Compared to DE, GODE performs better on the majority of test functions. It demonstrates that the proposed GOBL is helpful to solve these kinds of challenging problems.

Statistical comparisons of GODE with DE, CHC and G-CMA-ES show that GODE and CHC are the best and worst ones among the four algorithms. GODE is significantly better than CHC and G-CMA-ES on each dimension. Though GODE is not significantly better than DE, GODE performs better than DE according to the results of average ranking.

However, GODE is not suitable for all kinds of problems, such as F3 and its hybrid composition functions F13 and F17. GODE also has some difficulties when solving F8, while G-CMA-ES could find the global optimum on this function.

The proposed GOBL can be embedded and investigated on other population-based algorithms. More applications on GOBL will be studied. Moreover, possible directions for our future work also include the investigation of diversity analysis, the weaknesses and limitations of GOBL, the convergence analysis, etc.