Automatic circle detection on digital images with an adaptive bacterial foraging algorithm

Abstract

This article presents an algorithm for the automatic detection of circular shapes from complicated and noisy images without using the conventional Hough transform methods. The proposed algorithm is based on a recently developed swarm intelligence technique, known as the bacterial foraging optimization (BFO). A new objective function has been derived to measure the resemblance of a candidate circle with an actual circle on the edge map of a given image based on the difference of their center locations and radii lengths. Guided by the values of this objective function (smaller means better), a set of encoded candidate circles are evolved using the BFO algorithm so that they can fit to the actual circles on the edge map of the image. The proposed method is able to detect single or multiple circles from a digital image through one shot of optimization. Simulation results over several synthetic as well as natural images with varying range of complexity validate the efficacy of the proposed technique in terms of its final accuracy, speed, and robustness.

1 Introduction

Past few decades have seen a massive growth in the field of biologically inspired metaheuristics for search and optimization. Computational cost having been reduced almost dramatically; researchers from all corners are showing more interest in following the underlying principles of nature to solve nearly intractable optimization problems. Following this tradition, practitioners in the field of computer vision are also applying such metaheuristics to difficult problems arising in the field. For example, Wachowiak et al. (2004) applied the particle swarm optimization (PSO) algorithm (Kennedy et al. 2001; Abraham et al. 2006; Liu et al. 2007a, b), which draws inspiration from the intelligent group behavior of social creatures, to the problem of biomedical image registration. Le Hégarat-Mascle et al. (2007) proposed a non-stationary Markov model-based image regularization algorithm, which uses another swarm intelligence algorithm known as ant colony optimization (ACO) (Dorigo and Gambardella 1997). De-Sian and Chien-Chang (2008) applied ACO for improving the edge detection from digital images. Very recently, Santamaría et al. (2009) used memetic algorithms (MAs) (Ong and Keane 2004) that are based on synergy of evolutionary or any population-based approach with separate individual learning or local improvement procedures, in 3D Reconstruction of Forensic Objects.

Automatic identification and extraction of geometric shapes from images are very useful in a number of tasks because such shapes are often present in human-made environments. They are also widely used as a part of man-designed symbols. In particular, circle and ellipse detection problems have been widely studied in the shape recognition community by using the deterministic techniques like Hough transform (HT) (Illingworth and Kittler 1988; Leavers 1993; Duda and Hart 1972), which often necessitates high computation and storage requirements particularly for high-dimensional applications. In order to overcome these limitations, researchers have proposed new approaches to HT, e.g., the probabilistic HT (Shaked et al. 1996), the randomized HT (Xu et al. 1990), and the fuzzy HT (Han et al. 1993). Lam and Yuen (1996) came up with a hybrid approach based on hypothesis filtering and HT to detect circles. New integral transforms have also been proposed in this context, e.g., see Becker et al. (2002). As an alternative to the HT-based techniques, the shape recognition problem in computer vision has been handled with stochastic search methods that include random sample consensus (Fischer and Bolles 1981), simulated annealing (SA) (Bongiovanni and Crescenzi 1995), and genetic algorithm (GA) (Goldberg 1989). Stochastic algorithms like GA exhibit adaptive and robust search behavior can produce near optimal solutions very fast due to possessing a large amount of implicit parallelism. However, they cannot promise to achieve the solution every time. Recently there has been a growing interest of researchers in using GA for important shape detection tasks, e.g., Roth and Levine (1994) proposed use of GA for primitive extraction of images. Lutton et al. carried out a further improvement of the aforementioned method recently in 2000 (Lutton and Martinez 1994). Yao et al. (2004) came up with a multi-population GA to detect ellipses. Ayala-Ramirez et al. (2006) presented a GA-based circle detector. Their approach is capable of detecting multiple circles on real images but fails frequently to detect small and imperfect circles.

Passino (2002) proposed a powerful algorithm for real parameter optimization, now known as the bacterial foraging optimization algorithm (BFOA) (Liu and Passino 2002). BFOA tries to mimic the individual and grouped foraging behavior of Escherichia coli, a bacteria living in our intestines. Until date the algorithm has found successful applications in several real world problems like optimal controller design (Liu and Passino 2002), harmonic estimation (Mishra 2005), transmission loss reduction (Tripathy et al. 2006), and power delay filter design (Mishra and Bhende 2007; Das et al. 2009a, b; Kim et al. 2007; Biswas et al. 2007). This work presents an attempt to detect circles (recognizing them by their shapes) from digital images using an adaptive variant of the classical BFOA. The work is not an extension of the HT techniques described earlier and presents an altogether new approach to this classical problem of computer vision. We use the Canny edge detector (Canny 1986) to generate the edge-map from a gray-scale image. The adaptive BFOA is then applied to search the entire edge-map for circular shape. Each bacterium here models a trial circle and an objective function has been derived over the domain of such trial circles in order to measure to what degree a trial circle matches to an actual circle on the edge map of the image. The better a test circle approximates the actual edge-circle, the lesser becomes the value of this function. Minimization of the objective function with BFOA ultimately leads to the fast and robust extraction of circular shapes from the given image. Comparison with one state-of-the-art GA-based method and a randomized Hough transform (RHT) (Xu et al. 1990) algorithm on multiple images indicate the superiority of the proposed method.

The rest of the paper is organized as follows. In Sect. 2, we provide a brief review of classical BFOA. In Sect. 3, we derive the adaptation scheme of the chemotactic step in BFOA leading to its faster convergence with a mathematical justification. Section 4 describes bacteria representation and also lays out the mathematical basis of the objective function. Results of computer simulation over several images have been presented in Sect. 5, and finally the paper is concluded in Sect. 6 with a discussion of future research directions.

2 The classical BFOA: an overview

Now suppose that we want to find the minimum of $J(\theta )$ where $\theta \in \Re^{p}$ (i.e., $\theta$ is a p-dimensional vector of real numbers), and we do not have measurements or an analytical description of the gradient $\nabla J(\theta ).$ BFOA mimics the four principal mechanisms observed in a real bacterial system: chemotaxis, swarming, reproduction, and elimination-dispersal to solve this non-gradient optimization problem. Below we introduce the formal notations used in BFOA literature and then provide the complete pseudo-code of the BFO algorithm. A more detailed description of the steps of BFOA is out of the scope of this paper and can be found in Passino (2002), Liu and Passino (2002) and Dasgupta et al. (2008).

Let us define a chemotactic step to be a tumble followed by a tumble or a tumble followed by a run. Let j be the index for the chemotactic step. Let k be the index for the reproduction step. Let l be the index of the elimination-dispersal event. Also let

p :

Dimension of the search space,

S :

Total number of bacteria in the population,

N _c :

The number of chemotactic steps,

N _s :

The swimming length

N _re :

The number of reproduction steps,

N _ed :

The number of elimination-dispersal events,

P _ed :

Elimination-dispersal probability,

C (i):

The size of the step taken in the random direction specified by the tumble.

Let $P(j,k,l) = \{ \theta^{i} (j,k,l)|i = 1,2, \ldots ,S\}$ represent the position of each member in the population of the S bacteria at the jth chemotactic step, kth reproduction step, and lth elimination-dispersal event. Here, let $J(i,j,k,l)$ denote the cost at the location of the ith bacterium $\theta^{i} (j,k,l) \in \Re^{p}$ (sometimes, we drop the indices and refer to the ith bacterium position as $\theta^{i}$). Note that we will interchangeably refer to J as being a “cost” (using terminology from optimization theory) and as being a nutrient surface (in reference to the biological connections). For actual bacterial populations, S can be very large (e.g., S = 109), but p = 3. In our computer simulations, we will use much smaller population sizes and will keep the population size fixed. BFOA, however, allows p > 3 so that we can apply the method to higher dimensional optimization problems. Below, we briefly describe the four prime steps in BFOA. We also provide a pseudo-code of the complete algorithm.

• 1. Chemotaxis This process simulates the movement of an E. coli cell through swimming and tumbling via flagella. Suppose $\theta^{i} (j,k,l)$ represents ith bacterium at jth chemotactic, kth reproductive and lth elimination-dispersal step. $C(i)$ is a scalar and indicates the size of the step taken in the random direction specified by the tumble (run length unit). Then in computational chemotaxis, the movement of the bacterium may be represented by

$$ \theta^{i} (j + 1,k,l) = \theta^{i} (j,k,l) + C(i){\frac{\Updelta (i)}{{\sqrt {\Updelta^{T} (i)\Updelta (i)} }}}, $$

(1)

where $\Updelta$ indicates a unit length vector in the random direction.

• 2. Swarming An interesting group behavior has been observed for several motile species of bacteria including E. coli and S. typhimurium, where stable spatio-temporal patterns (swarms) are formed in semisolid nutrient medium. A group of E. coli cells arrange themselves in a traveling ring by moving up the nutrient gradient when placed amidst a semisolid matrix with a single nutrient chemo-effecter. The cells when stimulated by a high level of succinate, release an attractant aspartate, which helps them to aggregate into groups and thus move as concentric patterns of swarms with high bacterial density. The cell-to-cell signaling in E. coli swarm may be represented by the following function.

$$ \begin{aligned} & J_{\text{cc}} (\theta ,P(j,k,l)) = \sum\limits_{i = 1}^{S} {J_{\text{cc}} (\theta ,\theta^{i} (j,k,l))} \\ & \quad = \sum\limits_{i = 1}^{S} {\left[ { - d_{\text{attractant}} \exp \left( { - w_{\text{attractant}} \sum\limits_{m = 1}^{p} {(\theta_{m} - \theta_{m}^{i} )^{2} } } \right)} \right] + } \sum\limits_{i = 1}^{S} {\left[ {h_{\text{repellant}} \exp \left( { - w_{\text{repellant}} \sum\limits_{m = 1}^{p} {(\theta_{m} - \theta_{m}^{i} )^{2} } } \right)} \right]} , \\ \end{aligned} $$

(2)

where $J_{\text{cc}} (\theta ,P(j,k,l))$ is the objective function value to be added to the actual objective function (to be minimized) to present a time varying objective function. The coefficients $d_{\text{aatractant}} ,w_{\text{attractant}} ,h_{\text{repellant}} ,$ and $w_{\text{repellant}}$ control the strength of the cell-to-cell signaling. More specifically $d_{\text{aatractant}}$ is the depth of the attractant released by the cell, $w_{\text{attractant}}$ is a measure of the width of the attractant signal (a quantification of the diffusion rate of the chemical), $h_{\text{repellant}} = d_{\text{attractant}}$ is the height of the repellant effect (a bacterium cell also repels a nearby cell in the sense that it consumes nearby nutrients and it is not physically possible to have two cells at the same location), and $w_{\text{repellant}}$ is a measure of the width of the repellant. For a detailed discussion on the function $J_{\text{cc}}$ please see, Passino (2002) and Liu and Passino (2002).

• 3. Reproduction The least healthy bacteria eventually die while each of the healthier bacteria (those yielding lower value of the objective function) asexually split into two bacteria, which are then placed in the same location. This keeps the swarm size constant.

• 4. Elimination and dispersal To simulate this phenomenon in BFOA some bacteria are liquidated at random with a very small probability while the new replacements are randomly initialized over the search space.

3 A simple adaptation scheme for chemotactic step of the BFOA

3.1 Mathematical foundation

Let us consider a single bacterium cell that undergoes chemotactic steps according to (1) over a one-dimensional objective function. The bacterium lives in continuous time and at the tth instant its position is given by $\theta (t).$ Below we list a few assumptions that are considered for the sake of gaining mathematical insight.

• 1. The objective function $J(\theta )$ is continuous and differentiable at all points in the search space.

• 2. The chemotactic step size C is not very large.

• 3. The analysis applies to the regions of the fitness landscape where gradients of the function are small, i.e., near to the optima.

Let, at time $t$ position of an individual bacterium be $\theta$ and value of objective function (to be minimized) be $J(\theta ).$ Also assume that, after a very small time interval $\Updelta t,$ its position changes by an amount $\Updelta \theta .$ Then the new value of the objective function becomes $J(\theta + \Updelta \theta ).$ According to the chemotactic step used in BFOA, the bacterium changes its position only if the modified objective function value is less than the previous one, i.e., $J(\theta ) > J(\theta + \Updelta \theta )$, i.e., $J(\theta ) - J(\theta + \Updelta \theta )$ is positive, i.e., ${\frac{J(\theta ) - J(\theta + \Updelta \theta )}{\Updelta t}}$ is positive. (As time is unidirectional, $\Updelta t$ is a positive infinitesimally small quantity. So, sign of any number is retained after it is divided by $\Updelta t.$)

The decision-making (i.e., whether to take a step or not) activity of the bacterium can be modeled by a unit step function $u(x)$ as,

$$ \begin{aligned} u\left( {{\frac{J(\theta ) - J(\theta + \Updelta \theta )}{\Updelta t}}} \right) & = 1,\quad {\text{if}}\;{\frac{J(\theta ) - J(\theta + \Updelta \theta )}{\Updelta t}} > 0, \\ & = 0,\quad {\text{otherwise}} .\\ \end{aligned} $$

Thus,

$$ {\frac{\Updelta \theta }{\Updelta t}} = u\left( {{\frac{J(\theta ) - J(\theta + \Updelta \theta )}{\Updelta t}}} \right)C\Updelta , $$

(3)

where C indicates the chemotactic step height and $\Updelta$ indicates the direction of tumble (here it can assume only two values 1 or −1 with uniform probabilities). Note that modeling the decision-making activity of a bacterium with unit step function reinforce the local search behavior since a step is taken only if it keeps on minimizing (i.e., improving the fitness of a bacterium) following the directives of original BFOA. In that case, the advancement is done with an intensity C in $\Updelta$ direction. Here, we have assumed in unit time bacterium takes a chemotactic step. ${\frac{\Updelta \theta }{\Updelta t}}$ is the velocity.

$$ \Rightarrow \quad {\frac{\Updelta \theta }{\Updelta t}} = u\left[ { - {\frac{J(\theta + \Updelta \theta ) - J(\theta )}{\Updelta t}}} \right]C\Updelta . $$

Now velocity of the bacterium is given by,

$$ V_{\text{b}} = \mathop {Lt}\limits_{\Updelta t \to 0} {\frac{\Updelta \theta }{\Updelta t}} = u\left[ { - \left( {\mathop {Lt}\limits_{\Updelta \theta \to 0} {\frac{J(\theta + \Updelta \theta ) - J(\theta )}{\Updelta \theta }}} \right)\mathop {Lt}\limits_{\Updelta t \to 0} {\frac{\Updelta \theta }{\Updelta t}}} \right]C\Updelta , $$

(4)

$$ \Rightarrow \quad V_{\text{b}} = \theta^{'} = u\left[ { - {\frac{{{\text{d}}J(\theta )}}{{{\text{d}}\theta }}}\,{\frac{{{\text{d}}\theta }}{{{\text{d}}t}}}} \right]C\Updelta , $$

$$ \Rightarrow \quad V_{\text{b}} = u( - GV_{\text{b}} )C\Updelta , $$

(5)

where G = J′(θ) = gradient of the objective function at θ. Since the unit step function $u(x)$ has a jump discontinuity at $x = 0,$ to simplify the analysis further, we replace $u(x)$ with the continuous logistic function $\phi (x)$ (Anwal 1998), where

$$ \phi (x) = {\frac{1}{{1 + e^{ - kx} }}}. $$

(6)

We note that, $u(x) = \mathop {Lt}\nolimits_{k \to \infty } \phi (x) = \mathop {Lt}\nolimits_{k \to \infty } {\frac{1}{{1 + e^{ - kx} }}}$

Figure 1 illustrates how the logistic function may be used to approximate the unit step function used for decision-making in chemotaxis. For analysis purpose, k cannot be infinity. We restrict ourselves to moderately large values of k (say k = 10) for which $\phi (x)$ fairly approximates $u(x).$ The following subsection describes the error limit introduced by this assumption. Thus, for moderately high values of k $\phi (x)$ fairly approximates $u(x).$ Hence from (5),

$$ V_{\text{b}} = {\frac{C\Updelta }{{1 + e^{{kGV_{\text{b}} }} }}}. $$

(7)

According to assumptions (1) and (3), if C and G are very small and k ~ 10, then we may have $|kGV_{\text{b}} | \ll 1.$ In that case, we neglect higher order terms in the expansion of $e^{{kgv_{\text{b}} }}$ and have $e^{{kgv_{\text{b}} }} \approx 1 + kGV_{\text{b}} .$ Substituting it in (7), we obtain,

$$ \begin{aligned} \,&V_{\text{b}}= {\frac{C\Updelta }{{2 + kGV_{\text{b}} }}}, \\ \,&\Rightarrow \quad V_{\text{b}} = {\frac{C\Updelta }{2}}\,{\frac{1}{{1 + {\frac{{kGV_{\text{b}} }}{2}}}}}, \\ \,&\Rightarrow \quad V_{\text{b}} = {\frac{C\Updelta }{2}}\left( {1 - {\frac{{kGV_{\text{b}} }}{2}}} \right)\quad \begin{array}{*{20}c} {\left[ {\because \left| {{\frac{{kGV_{\text{b}} }}{2}}} \right| \ll 1\;{\text{Neglecting higher}}} \right.} \hfill \\ {\left. {{\text{order}}\;{\text{terms}}\;{\text{and }}\left( {1 + {\frac{{kGV_{\text{b}} }}{2}}} \right)^{ - 1} \approx \left( {1 - {\frac{{kGV_{\text{b}} }}{2}}} \right)} \right]}. \hfill \\ \end{array} \\ \end{aligned} $$

After some manipulation we have,

$$ V_{\text{b}} = {\frac{2C\Updelta }{4 + kGC\Updelta }} $$

(8)

$$ \begin{gathered} \Rightarrow \quad V_{\text{b}} = {\frac{C\Updelta }{2}}\,{\frac{1}{{1 + {\frac{kCG\Updelta }{4}}}}}, \hfill \\ \Rightarrow \quad V_{\text{b}} = {\frac{C\Updelta }{2}}\left( {1 - {\frac{kGC\Updelta }{4}}} \right)\begin{array}{*{20}c} {\left[ {\because \left| {{\frac{kGC\Updelta }{4}}} \right| \ll 1,\;{\text{as}}\;\left| \Updelta \right| = 1\;{\text{and}}} \right.} \hfill \\ {\left. {\text{neglecting the higher order terms}} \right],} \hfill \\ \end{array} \hfill \\ \end{gathered} $$

$$ \Rightarrow \quad V_{\text{b}} = - {\frac{{kC^{2} }}{8}}G + {\frac{C\Updelta }{2}}, $$

(9)

$$ \Rightarrow \quad {\frac{{{\text{d}}\theta }}{{{\text{d}}t}}} = - \alpha G + \beta , $$

(10)

where $\alpha$ is ${\frac{{ - kC^{2} }}{8}}$ and $\beta$ is ${\frac{C\Updelta }{2}}.$

Fig. 1

The unit step and the logistic functions

The classical gradient descent algorithm (CGDA) (Fletcher 1987) is given by the following dynamics in single dimension:

$$ {\frac{{{\text{d}}\theta }}{{{\text{d}}t}}} = - \alpha G, $$

(11)

where $\alpha$ is the learning rate.

Similarity between Eqs. 9, 10, and 11 suggests that chemotaxis is a modified CGDA where $\alpha ,$ which is a function of chemotactic step size, can be identified as the learning rate of chemotaxis.

3.2 Oscillation problem: need for adaptive chemotaxis

If magnitude of the gradient decreases consistently, near the optima or very close to the optima $\alpha$ of Eq. 15 becomes comparable to $\beta .$ Then gradually $\beta$ becomes dominant. When $\left| G \right| \to 0,\left| {{\frac{{{{\rm d}}\theta }}{{{{\rm d}}t}}}} \right| \approx \left| \beta \right| = \left| {{\frac{C\Updelta }{2}}} \right| = {\frac{C}{2}}\quad [\because \left| \Updelta \right| = 1].$Let us assume the bacterium has reached close to the optimum. But as we have derived $\left| {{\frac{{{{\rm d}}\theta }}{{{{\rm d}}t}}}} \right| = {\frac{C}{2}},$ the bacterium does not stop taking chemotactic steps. It oscillates about the optima. This crisis can be remedied if step size C is made adaptive according to the following relation,

$$ C = {\frac{\psi |J(\theta )|}{|J(\theta )| + \lambda }} = {\frac{\psi }{{1 + {\raise0.7ex\hbox{$\lambda $} \!\mathord{\left/ {\vphantom {\lambda {\left| {J(\theta )} \right|}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left| {J(\theta )} \right|}$}}}}}. $$

(12)

Here, λ and $\psi$ (>1) are positive constants. Thus from (12), we see, if $J(\theta ) \to 0,$ then $C \to 0.$ Therefore, there would be no oscillation if the bacterium reaches optima. The functional form of (12) causes C to vanish near the optima. Besides, it plays another important role described below. From (12), we have, when $J(\theta )$ is large ${\frac{\lambda }{|J(\theta )|}} \to 0$ and consequently $C \to \psi ( > 1).$ This has an important physical significance. If magnitude of cost function is large for an individual bacterium, it is in vicinity of the noxious substance. It will then try to move to a place with better nutrient concentration by taking large steps. On the other hand, the bacterium when in nutrient rich zone, i.e., with small magnitude of the objective function value, tries to retain its position. Naturally, its step size becomes small. Dasgupta et al. (2008) have illustrated the effectiveness of the above-mentioned adaptation scheme over several numerical benchmarks.

4 The ABFOA-based circle detection algorithm

4.1 The scheme for population initialization

An individual member of the population of sample circles is actually a trial solution. Each sample circle is represented as a bacterial position $\vec{\theta } = [x_{0} ,y_{0} ,r_{0} ]^{\text{T}} ,$ where first two components of the vector are $x$ and $y$ co-ordinates of the center of that circle and third term stands for the radius.

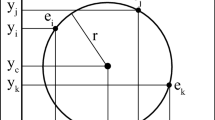
Let $(x_{k} ,y_{k} ,r_{k} )$ be the kth test circle in the population, where $k = 1, \ldots ,S,\;S$ is the population size, i.e., it denotes total number of test circles. In initialization phase, random values within suitable range are assigned to each of the three entries of the vectors. Two statistical properties of sample points on a candidate circle are used in this regard, where one property is used to find a suitable value for co-ordinates of probable center of the test circle and, another is used to model its probable radius. These two properties are described below. Let us consider $2N$ number of equally spaced sample points on a circle of radius $r_{0}$ and center at $(x_{0} ,y_{0} ).$ Figure 2 shows a similar case where $N = 4.$ Now, ith sample point may be designated by $(x(i),y(i)).$

Fig. 2

An edge-circle with sample points depicted in blue

Here, $x(i) = x_{0} + r_{0} \cos {\frac{\pi }{N}}i$ and $y(i) = y_{0} + r_{0} \sin {\frac{2\pi }{N}}i,\quad i = 1, \ldots ,2N.$

Let $(\overline{X} ,\overline{Y} )$ be defined as,

$$ \overline{X} = {\frac{1}{2N}}\sum\limits_{i = 1}^{2N} {x(i)} ,\quad \overline{Y} = {\frac{1}{2N}}\sum\limits_{i = 1}^{2N} {y(i)} . $$

(13)

Now, $\overline{X} = {\frac{1}{2N}}\sum\nolimits_{i = 1}^{2N} {x(i)} = {\frac{1}{2N}}\sum\nolimits_{i = 1}^{2N} {\left( {x_{0} + r_{0} \cos {\frac{\pi }{N}}i} \right)} = x_{0} + r_{0} {\frac{1}{2N}}\sum\nolimits_{i = 1}^{2N} {\cos {\frac{\pi }{N}}} i$

$$ \therefore \, \overline{X} = x_{0} + r_{0} {\frac{\sin \pi }{{\sin {\frac{\pi }{2N}}}}}\cos {\frac{\pi (2n + 1)}{4n}} \Rightarrow \overline{X} = x_{0} \quad \left[ {\because \sin \pi = 0} \right]. $$

Similarly, we can show that $\overline{Y} = y_{0} .$

$$ \therefore \, \overline{X} = x_{0} ,\quad \overline{Y} = y_{0} . $$

(14)

Let us also define

$$ \sigma = \sqrt {{\frac{1}{2N}}\left( {\sum\limits_{i = 1}^{2N} {(x(i) - \overline{X} )^{2} + (y(i) - \overline{Y)}^{2} } } \right)} , $$

(15)

$$ \begin{aligned} \Rightarrow \quad \sigma^{2} & = {\frac{1}{2N}}\left( {\sum\limits_{i = 1}^{2N} {(x(i) - x_{0} )^{2} + (y(i) - y_{0} )^{2} } } \right),\quad [\because \overline{X} = x_{0} ,\overline{Y} = y_{0} ], \\ \Rightarrow \quad \sigma^{2} & = {\frac{1}{2N}}\left( {\sum\limits_{i = 1}^{2N} {\left( {r_{0} \cos {\frac{\pi }{N}}i} \right)^{2} + \left( {r_{0} \sin {\frac{\pi }{N}}i} \right)^{2} } } \right) \\ \Rightarrow \sigma^{2} &= r_{0}^{2} {\frac{1}{2N}}\left( {\sum\limits_{i = 1}^{2N} {\left( {\cos {\frac{\pi }{N}}i} \right)^{2} + \left( {\sin {\frac{\pi }{N}}i} \right)^{2} } } \right), \\ \Rightarrow \quad \sigma^{2} & = r_{0}^{2} , \\ \end{aligned} $$

$$ \Rightarrow \quad \sigma^{2} = r_{0}^{2} . $$

(16)

To initialize kth test-circle we form a set of $2m_{k}$ edge-points drawn at random from the edge-map, where $2m_{k} = {\text{rand}}(L,U)$ such that $L,U$ specify upper and lower limit of $2m_{k} .$ Let $(x(i),y(i))$ be the ith edge-point, $i = 1, \ldots ,2m_{k}$ and $(x_{k} ,y_{k} ,r_{k} )$ denotes the kth test circle to be initialized. Now, we assign values to three entries of the vector taking guidelines of Eqs. 13 and 15.We assign

$$ \begin{aligned} &x_{k}= {\frac{1}{{2m_{k} }}}\sum\limits_{i = 1}^{{2m_{k} }} {x(i)} ,\quad y_{k} = {\frac{1}{{2m_{k} }}}\sum\limits_{i = 1}^{{2m_{k} }} {y(i)} \\ &{\text{and}}\quad r_{k} = \sqrt {{\frac{1}{{2m_{k} }}}\left( {\sum\limits_{i = 1}^{{2m_{k} }} {(x(i) - x_{k} )^{2} + (y(i) - y_{k} )^{2} } } \right)} . \\ \end{aligned} $$

This initialization scheme is adopted with the expectation that the selected edge points may lie on the actual circle or very close to it, so that we may reach a good approximation of the center and radius.

4.2 The objective function

We are assuming that in the edge-map edge pixels are simply represented by ‘1’ and back-ground pixels by ‘0’. Figure 3 illustrates a similar situation. Let us consider a test circle be denoted by $(x_{0} ,y_{0} ,r_{0} ).$ And let $A$ be the edge matrix. We denote the objective function be $J.$ Let for the above-mentioned test circle, its value be $J_{0} .\;\therefore J_{0} = J(A,x_{0,} y_{0} ,r_{0} ).$ _.

Fig. 3

a An $5 \times 5$ image matrix and b its corresponding edge-matrix

We define another function $P(x,y),$ which returns pixel value of a point $(x,y).$

$$ \begin{aligned} P(x,y) & = 1,\quad {\text{if }}(x,y)\,{\text{is an edge - point}} \\ & = 0,\quad {\text{otherwise}}. \\ \end{aligned} $$

So the edge-matrix $A = \left( {a_{ij} } \right) = \left( {P(i,j)} \right).$ As an example, for image in Fig. 3a, $P(2,3) = P(3,2) = P(3,4) = P(4,3) = 1$ (for the edge pixels marked in red) and for other non-edge pixels (white colored in Fig. 3a), e.g., $P(1,1) = P(2,2) = P(3,3) = P(3,1) = P(5,5) = 0.$

For sampling, we consider the family of circles with center at $(x_{0} ,y_{0} )$ with a radius varying in a range from $r_{0} - \delta$ to $r_{0} + \delta .$ This forms the test-band, $\delta$ being a constant. After some trial and error, we found that taking $\delta = {\frac{{r_{0} }}{6}}$ is comfortable enough for this specific application. After this, $N_{\text{S}}$ sample points are taken for each circle in test-band. Sample points are positioned on the circle maintaining equal distance between each other. Let ith sample point on a circle of test-band, having radius $r_{0} + j\;( - \delta \le j \le \delta )$ be denoted by $(x_{i}^{j} ,y_{i}^{j} ).$

$$ \therefore\,x_{i}^{j} = (r_{0} + j)\cos {\frac{2\pi }{{N_{\text{S}} }}}i,\quad y_{i}^{j} = (r_{0} + j)\sin {\frac{2\pi }{{N_{\text{S}} }}}i, $$

(17)

$$ i = 1,2, \ldots N_{S} \quad {\text{and}}\quad j = - \delta , - \delta + 1, \ldots , - 1,0,1, \ldots ,\delta - 1,\delta . $$

In this work, to deal with real world images containing incomplete and noisy circles, we define a distance function $\mu$ to measure the degree of belongingness of a sample point to the circumference of the central circle of the test band (i.e., circle with radius $r_{0}$). Value of this distance function is $\mu_{i}^{j}$ for sample point $(x_{i}^{j} ,y_{i}^{j} )$ and it is defined as:

$$ \mu_{i}^{j} = P\left( {x_{i}^{j} ,y_{i}^{j} } \right)\exp \left( { - {\frac{1}{{2\sigma^{2} }}}(r + j - r_{0} )^{2} } \right). $$

(18)

If $(x_{i}^{j} ,y_{i}^{j} )$ is not an edge-point, we can infer $\mu_{i}^{j} = 0$, i.e., a zero belongingness to the circumference of the central circle $[\because P(x_{i}^{j} ,y_{i}^{j} ) = 0].$ Let us consider now the case that $(x_{i}^{j} ,y_{i}^{j} )$ is an edge-point. Then $\mu_{i}^{j} = \exp \left( { - {\frac{1}{{2\sigma^{2} }}}(r + j - r_{0} )^{2} } \right)$ and note that $\mu_{i}^{j} = 1$ if $j = 0$ and $r = r_{0}$, i.e., the distance function is unity or maximum when sampled edge-point lies on central circle. It decreases when $\left| j \right|$ increases and, it follows the distribution shown in Fig. 4. If $\sigma$ decreases the function becomes more sharp cut-off or narrow-band. Now, normalized objective function corresponding to $(x_{0} ,y_{0} ,r_{0} )$ for the edge matrix $A$ is defined as following,

$$ J(A,x_{0,} y_{0} ,r_{0} ) = 1 - {\frac{1}{{(2\delta + 1)N_{S} }}}\sum\limits_{i = 1}^{{N_{\text{S}} }} {\sum\limits_{j = - \delta }^{\delta } {\mu_{i}^{j} } } $$

$$ \Rightarrow \quad J(A,x_{0,} y_{0} ,r_{0} ) = 1 - {\frac{1}{{(2\delta + 1)N_{\text{S}} }}}\sum\limits_{i = 1}^{{N_{\text{S}} }} {\sum\limits_{j = - \delta }^{\delta } {P(x_{i}^{j} ,y_{i}^{j} )\exp \left( { - {\frac{1}{{2\sigma^{2} }}}(r + j - r_{0} )^{2} } \right)} } . $$

(19)

Note that this function is a heuristic that weighs each edge-point according to the distance of the candidate circle. Here, we would also like to point out that most of the existing GA-based circle detection methods (e.g., Ayala-Ramirez et al. 2006) encode one circle in one chromosome with the coordinates of three points on that circle. They usually evaluate fitness of the encoded circle by taking several sample points on the test circle and checking their status (whether edge pixel, etc.). Now two circles can have maximum two points of intersection. Due to digital approximation of the circle, the number may be greater than two by small amount but still not large enough to draw a comprehensive inference to guide the search process. To circumvent this limitation in this work, we take a band of circles symmetrically distributed around actual test circle. Sample points are taken on the periphery of each circle and then we test whether they are edge-point or not. Therefore, the probability of detecting the circle increases even when the edge pixels are not completely connected. To differentiate between points on actual test circle and that of lying on circle on test band, a distance function is assigned to each sample point. The function is basically a Gaussian deviate and it reaches the maxima when point is on the central circle of the band and decreases on both sides.

Fig. 4

Test-band for a test circle. Red circle shows the central circle. Two blue circles show the boundaries of test-band

4.3 Multiple circle detection

The proposed algorithm with slight modification can detect multiple circular objects on real image. At first, an upper limit of the number of circular shapes is specified. The method is run on the original edge-map until convergence is achieved for first circle detection. This shape is then masked on the edge-map and the ABFOA circle-detector is then again run on the edge-map. The procedure is repeated until the maximum number of circles is attained. In this approach, there is a possibility of false detection as the actual number of circles present may be lesser than the maximum number specified. To overcome this, once the process is terminated, all the detected circles are validated by analyzing their connectivity of circumference segments using the method of Kelly and Levine (1997).

5 Computer simulation results

5.1 Test images

The test bed includes 15 synthetic (handcrafted) gray-scale images and 15 natural test images each of size 256 × 256 pixels. The natural images include a circular-shaped object among various other configurations. All the images were preprocessed using a standard edge-detector (Canny or Sobel edge-detector in image-processing toolbox, MATLAB 7.0). We have reported detailed results for six images in order to save space.

5.2 Parametric setup

Table 1 presents the parameters of ABFOA algorithm used here. Once set (after a considerable number of trials and error) values of the parameters were kept unaltered for all the test images without allowing any type of hand tuning.

Table 1 Parameter setup for ABFOA

Detailed meaning of all these parameters has been provided in Sect. 2. In order to make an objective evaluation of the proposed method, circular shapes in three of the natural images were detected manually and the circles detected by our algorithm were then compared with the hand-label ones (considered as the ground truth images) using a new heuristic score.

For the GA algorithm described in Ayala-Ramirez et al. (2006), we take the population size = 70, crossover probability = 0.55, mutation probability = 0.10, number of elite individuals = 2. We also took as selection method, the roulette wheel selection and as a crossover method, the 1-point crossover. The parametric setup appears as the best set, configured by Ayala-Ramirez et al. (2006) after lot of hand tuning experiments. The same fitness function as the one described by Ayala-Ramirez et al. (2006) has been used for the GA implementation.

5.3 Error score and success rate

To test accuracy of the algorithm obtained result is compared with ground truth. First, the circle in the edge-map is detected manually and it is referred as the ground-truth image. Next three peripheral points are taken on the manually detected circle. We know that through three non-collinear points only one circle can pass. So from previous three points, we get integer-approximated (as we are dealing with digital circle) center and radius of the ground-truth circle (GTC). Let center of the GTC be $(x_{\text{GTC}} ,y_{\text{GTC}} )$ and its radius be $r_{\text{GTC}} .$ Let the chosen points on the GTC be $(x_{1} ,y_{1} ),(x_{2} ,y_{2} ),$ and $(x_{3} ,y_{3} ).$Then

$$ \begin{aligned} &x_{\text{GTC}} = {\frac{{\left| {\begin{array}{*{20}c} {x_{2}^{2} + y_{2}^{2} - (x_{1}^{2} + y_{1}^{2} )} & {2(y_{2} - y_{1} )} \\ {x_{3}^{2} + y_{3}^{2} - (x_{1}^{2} + y_{1}^{2} )} & {2(y_{3} - y_{1} )} \\ \end{array} } \right|}}{{4(x_{2} - x_{1} )(y_{3} - y_{1} ) - (x_{3} - x_{1} )(y_{2} - y_{1} )}}} \\ &{\text{and}}\quad y_{\text{GTC}} = {\frac{{\left| {\begin{array}{*{20}c} {2(x_{2} - x_{1} )} & {x_{2}^{2} + y_{2}^{2} - (x_{1}^{2} + y_{1}^{2} )} \\ {2(x_{3} - x_{1} )} & {x_{3}^{2} + y_{3}^{2} - (x_{1}^{2} + y_{1}^{2} )} \\ \end{array} } \right|}}{{4(x_{2} - x_{1} )(y_{3} - y_{1} ) - (x_{3} - x_{1} )(y_{2} - y_{1} )}}}. \\ \end{aligned} $$

If center and radius of the detected circle found by algorithm is denoted by $(x_{\text{D}} ,y_{\text{D}} )$ and $r_{\text{D}} ,$ then we can define an error score in the following way,

$$ {\text{ES}} = \eta (\left| {x_{\text{GTC}} - x_{\text{D}} } \right| + \left| {(y_{\text{GTC}} - y_{\text{D}} } \right|) + \mu \left| {r_{\text{GTC}} - r_{\text{D}} } \right| $$

(20)

First term represents shift of center of the detected circle from that of GTC and second term signifies difference of their radii. η and μ are two weights associated with each term in (20). They may be chosen according to the accuracy required. We have taken $\eta = 0.05$ and $\mu = 0.1.$ This particular choice of parameters ensures that radii difference gets priority to the difference of the centers of the manually detected circle and the machine-detected circle. Here we assume that if ES is found to be less than 1, then the algorithm gets a success, otherwise, we say that it has failed to detect the edge-circle. Note that for $\eta = 0.05$ and $\mu = 0.1,$ ES < 1 means the maximum difference of radius tolerated is 10 while the maximum mismatch in the location of the center can be 20 (in number of pixels). From this consideration, success rate (SR) is defined as percentage of reaching success in certain number of trials.

5.4 Simulation strategy

The algorithm has been developed from scratch on a Pentium IV 2.4 GHz PC using C language under windows XP environment. Fifty independent runs of the proposed algorithm were carried out with different seeds of random number generator over each test image.

5.5 Presentation of results

In Table 2, we report the final heuristic score (between ground truth and the actual image with circle detection), as well as the time taken for each image. In Table 2, we have provided three synthetic images and their counterparts processed with the proposed algorithm. Table 3 presents the same experimental results on natural images. In order to test the robustness of our algorithm, we have added salt and pepper noise to the synthetic images before the algorithm was applied. It also illustrates the performance of the algorithm in presence of such noisy and corrupted pixels. In all cases, we have reported the results for median-run solution (when the runs were ranked according to their final fitness values). In order to test the effectiveness of the adaptive chemotaxis scheme, we compared the performance of ABFOA with that of the classical BFOA over the same test-bed. In all the test cases, ABFOA yielded more accurate final results consuming lesser amount of computational time. Figure 5 indicates the superior performance of ABFOA in terms of convergence speed over natural image 1 and synthetic image III (the noisy version). We omit rest of the graphical results of the comparison as they show a similar trend.

Table 2 Synthetic images and detected circles

Table 3 Natural images and detected circles

Fig. 5

Convergence characteristics: a for natural image I, b for synthetic image III (noisy version)

Table 4 provides a visual illustration of the performances of classical BFOA, ABFOA and the GA algorithm described in (Ayala-Ramirez et al. 2006) on two hard problem instances (one natural and one synthetic image). The results are for the median of 50 independent runs of each algorithm. It is interesting to observe that the deviation between the detected circle and actual circle is least for ABFOA. Table 5 shows the average time taken, success rate (in %), and average error score (calculated following Eq. 20) for the three competitor algorithms over six test images considered in Tables 2 and 3. The best entries are marked in bold in this Table. A close inspection of Table 5 reveals that the ABFOA based method was able to achieve highest success rate and minimum error taking least computational time in majority of the cases.

Table 4 Performances of ABFOA, Classical BFOA, and GA based method (Ayala-Ramirez et al. 2006) on a natural image (row 1) and a synthetic image (row 2) corrupted with salt and pepper noise

Table 5 Average time taken and success rate of ABFOA, classical BFOA and the GA based method (Lam and Yuen 1996) over the six test images

A non-parametric statistical significance test called Wilcoxon’s rank sum test for independent samples (Wilcoxon 1945; García et al. 2008) has been conducted at the 5% significance level on the error score (ES) data of Table 5. Table 6 shows reports the P-values produced by Wilcoxon’s rank sum test for comparison of the error scores of two groups (one group corresponding to ABFOA and the other corresponding to a competitor algorithm) at a time. As a null hypothesis, it is assumed that there is no significant difference between the mean values of two groups. Whereas, the alternative hypothesis is that there is significant difference in the mean values of the two groups. All the P values reported in the Table are less than 0.05 (5% significance level). This is strong evidence against the null hypothesis, indicating that the better mean values of the performance metrics produced by ABFO is statistically significant and has not occurred by chance.

Table 6 P values produced by Wilcoxon’s rank sum test taking comparing ABFOA with other algorithms on the Error Score (ES) data of Table 5

Table 7 demonstrates relative performance of ABFOA in comparison to the RHT algorithm described in Ong and Keane (2004). Images taken for the test are complicated and also comprises of different geometrical figures. RHT finds out the circle located in the figures satisfactorily but ABFOA is found to determine the position of circles with higher accuracy. Table 8 reports the corresponding average time taken, success rate (in %), and average error score (calculated following Eq. 20) for ABFOA and RHT algorithms over three test images considered in Table 7.

Table 7 Relative performance of ABFOA and HT

Table 8 Average time taken and success rate of ABFOA and HT over the 3 test images

6 Discussion and conclusion

This paper has presented a novel application of the BFOA to the task of automatic circle detection from gray images. To the best of our knowledge, BFOA has not been applied to any such computer-vision related task till date. An adaptive version of the basic BFOA has been used in order to improve its convergence behavior. In addition, a new fitness function was derived specifically for the circle detection task. As can be perceived from the result provided in Tables 3 and 5, ABFOA detects most of the circles in an image with little visual distortion even in the presence of noisy background pixels. Unlike most of the conventional papers on circle detection and instead of relying on visual perception only we have formulated a score function [presented in (20)], which can objectively evaluate the mismatch between a manually detected circle and a machine-detected circle. From Table 4, we observe that for natural images with more complexity the heuristic score is relatively high and the average time elapsed is higher as well. Through the use of non-parametric Wilcoxon’s rank sum test, we demonstrated that the ABFOA-based method could outperform both GA (as described in Ayala-Ramirez et al. 2006) and classical BFOA in a statistically significant fashion. Since both classical BFOA and ABFOA use the same initial population, bacteria representation scheme and fitness function, it is evident that the superior performance of ABFOA is attributed to its adaptation scheme of the chemotactic step-size C.

Although Table 7 indicated that ABFOA can yield better results on complicated and noisy images as compared to the RHT, note that the objective of our paper is not to devise a circle-detection algorithm that could beat all the HT based methods discovered earlier, but to show that a new swarm intelligence algorithm called BFOA with the suggested modifications can serve as an attractive alternative of the GA that has been used earlier to extract circular shapes from objects successfully. This way, the work undertaken here, encourages further research on the application of BFOA to the tasks related to shape extraction in computer vision. Future research will focus on hybridizing ABFOA with different HT based techniques for automatic shape extraction. In addition, application of the ABFOA based techniques for automatic shape recognition by mobile robots may also be studied. In future, we shall also attempt to compare the performance of our ABFOA based algorithm with other evolutionary computation techniques on the circle detection problem quantitatively.