1 Introduction

Streamflow process is the key component of the hydrological cycle, which is complex, and hard to predict accurately (Cheng et al. 2016; Neto et al. 2018). It has been largely affected by several parameters, namely precipitation, temperature, evapotranspiration, and characteristics of land use and drainage basin (Adnan et al. 2019). The reliable and precise prediction of streamflow process has great importance in designing, planning, optimizing, utilizing, and management of water resources (Adnan et al. 2018; Roy and Singh 2019). Streamflow prediction models are generally classified in two broad categories (Solomatine and Ostfeld 2008); (i) physically-based model, and (ii) data-driven model. The physically-based models require a wide range of data such as human interventions, land use, physiographic characteristics of the drainage basin, rainfall amount, intensity, and its distribution (Ochoa-Tocachi et al. 2016; Teutschbein et al. 2018), while data-driven models construct the mathematical relationship (linear or non-linear) between the streamflow and its constraints (Yaseen et al. 2015; Zhang et al. 2018). Elshorbagy et al. (2010a, b) examined the predictive capability of several data-driven approaches (i.e., neural networks, genetic programming, evolutionary polynomial regression, support vector machines, M5 model trees, K-nearest neighbors and multiple linear regression) in modeling the various hydrological components like evapotranspiration, soil moisture, and rainfall-runoff. They found the successful application of data-driven models in hydrological applications. The conventional models which are linear, are unable to capture the non-linearity and non-stationarity of hydrological applications. The moving average (MA) model, auto regressive (AR) model, auto regressive moving average (ARMA) model, and auto regressive integrated moving average (ARIMA) model are linear models that have received wide application in hydrological time-series forecasting (Wu et al. 2009; Wu and Chau 2010; Valipour et al. 2013; Valipour 2015). Consequently, the researchers have focused on constructing artificial intelligence (AI) based models that are accomplished to disabling the drawbacks of conventional models (Yaseen et al. 2016; Adnan et al. 2019).

Over the last two decades, on the global scale, the AI techniques integrated with numerous meta-heuristics algorithms received the extensive application in streamflow modelling and forecasting (Granata et al. 2016; Ghorbani et al. 2018; Hadi and Tombul 2018; Yaseen et al. 2018, 2019b; Rauf et al. 2018; Al-Sudani et al. 2019; He et al. 2019; Rasouli et al. 2020; Van et al. 2020; Safari et al. 2020). Huang et al. (2019) applied random forest (RF), support vector machine (SVM), artificial neural network (ANN), Bayesian model averaging (BMA), and Copula-BMA techniques to forecast monthly runoff at Huangzhuang station located in Hanjiang river basin, China. They found the better performance of RF, ANN, and Copula-BMA models. Rahmani-Rezaeieh et al. (2019) forecasted daily streamflow in Shahrchay river catchment, Iran using ensemble gene expression programming (EGEP), and they found the superior performance of proposed EGEP model for daily streamflow prediction in study basin. Rezaie-Balf et al. (2019) simulated daily streamflow at Bilghan, Siira, and Gachsar stations, Iran by using hybrid ensemble empirical mode decomposition-variational mode decomposition (EEMD-VMD) integrated with GEP and random forest regression (RER). The results indicated the better performance of the EEMD-VMD-GEP model than the EEMD-VMD-RER for streamflow simulation at such stations. Hussain and Khan (2020) applied multilayer perceptron (MLP), support vector regression (SVR) and RF models to forecast the monthly flow in the Hunza River, Pakistan, and they found that the RF model outperformed to the others in the study basin. Pandhiani et al. (2020) predicted monthly streamflow in Berman and Tualang rivers, Malaysia by employing least squares-SVM (LS-SVM), M5P tree, and RF data-driven models. Results of appraisal reveal that the RF models performed better than the LS-SVM and M5P tree models in predicting streamflow at both rivers.

Currently, the nature-inspired meta-heuristics algorithms like Particle Swarm Optimization (PSO), Grey Wolf Optimizer (GWO), Fruit Fly Algorithm (FFA), Gravitational Search Algorithm (GSA), Genetic Algorithm (GA), Differential Evolution (DE), Shuffled Frog Leaping Algorithm (SFLA) in conjunction with numerous machine learning techniques have been successfully applied for streamflow/rainfall-runoff/river flow modeling (Wang et al. 2013; Danandeh Mehr 2018; Ghorbani et al. 2018; Adnan et al. 2019; Meshram et al. 2019; Samadianfard et al. 2019; Yaseen et al. 2019a; Tikhamarine et al. 2019b; Afan et al. 2020; Tikhamarine et al. 2020b; Mohammadi et al. 2020). The key parameters of any meta-heuristic algorithm are; exploitation, exploration, or intensification and diversification. Diversification means creating diverse solutions to explore the global search space, while intensification means focusing on local area research by exploiting the information that is currently a good solution in this region (Mirjalili et al. 2014, 2016; Mirjalili 2015a; Mirjalili and Lewis 2016). Mirjalili and Lewis (2016) introduced the concept of WOA for solving many optimization and modeling problems and demonstrated superiority in finding the best global solutions.

The objective of the present research is to predict the daily time-series of streamflow at Naula watershed situated in the upper Ramganga river catchment. To this end, the novelty of the current research is presented in different aspects. First, the support vector regression (SVR) optimized with six meta-heuristic algorithms (i.e. ALO, MVO, SHO, HHO, PSO, and BO) were applied. Afterward, from a practical point of view, the non-linear components and the number of input variables are of great importance, for robust forecasting. So, the Gamma Test (GT) has been used to identify the optimal combinations of input variables. Accordingly, the hybrid SVR models namely SVR-ALO, SVR-MVO, SVR-SHO, SVR-HHO, SVR-PSO, and SVR-BO were proposed and their prediction accuracy was assessed over observed streamflow through statistical indicators and graphical inspection. It is worth mentioning that the performance of the proposed hybrid SVR models were examined for the first time in this study for daily streamflow prediction at the Naula Basin.

2 Study location and data acquisition

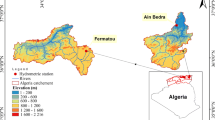
The Naula watershed positioned in upper Ramganga River catchment between longitude: 79o 06′ 15′′ E to 79o 31′ 15′′ E, and latitude: 29o 42′ 00′′ N to 30o 06′ 20′′ N with the varying elevation of 709 m to 3079 m above MSL in Ranikhet forest sub-division of Uttarakhand State, India (Fig. 1). The basin has a hilly terrain, steep slope with the rectangular shape of the area is 1023 km2. The rainfall occurs maximum during monsoon season started from June to September months, and mean annual rainfall is 1014 mm in the basin. The daily rainfall and streamflow data of monsoon season (1st June 2000 to 30th September 2004) were obtained from Soil Conservation Divisional Forest Office (SCDFO), Ranikhet, Uttarakhand State, India. The total available data of rainfall and streamflow was portioned into two sets (i) calibration dataset comprises 427 samples (70%: 1st June 2000 to 31st July 2003), and (ii) validation comprises 183 samples (30%: 1st August 2003 to 30th September 2004). The statistical properties of rainfall and streamflow for calibration and validation periods are presented in Table 1, which exposed that the rainfall/streamflow distributed Xmin = 0.000 mm/7.360 m3/s, Xmax = 98.200 mm/1484.640 m3/s, Xavg = 3.917/229.250, Xstd = 9.979/190.939, Xskw = 4.614/2.002, and Xkur = 28.999/7.397 during calibration, Xmin = 0.000 mm/1.730 m3/s, Xmax = 117.200 mm/2160.400 m3/s, Xavg = 4.625/253.432, Xstd = 11.985/253.351, Xskw = 5.528/3.631, and Xkur = 43.695/19.895 during validation. Figure 2 demonstrates the time-series plot of available rainfall and streamflow data in the study basin.

Fig. 1
figure 1

Study location map of Naula watershed (Uttarakhand)

Full size image
Table 1 Daily statistical parameters of hydro-meteorological data at Naula watershed
Full size table
Fig. 2
figure 2

Time series plot of daily rainfall and streamflow at study basin

Full size image

3 Methodology

3.1 Gamma test (GT)

GT is an impartial and multi-objective technique in identifying the significance of every input variable. The concept of this method was first announced by Stefánsson et al. (1997). Then it was employed by other scholars (Tsui et al. 2002; Remesan et al. 2008; Moghaddamnia et al. 2009; Noori et al. 2011; Kakaei Lafdani et al. 2013; Malik et al. 2017b, 2018, 2020a, c). GT compute the minimum standard error for each combination of input–output variables through the continuous nonlinear procedure. Suppose we have a set of data observations in the form;

$$\left\{ {\left( {x_{i} , y_{i} } \right),\quad 1 \le i \le M} \right\}$$
(1)

In which input vectors \(x_{i} \in R^{m}\) are m dimensional vector (with a pattern quantity of M) confined to some closed bounded set \(C \in R^{m}\) and, without loss of generality, the corresponding outputs \(y_{i} \in R\) are scalars. The vectors x holds predicatively beneficial factors influencing the output y. The only assumption is that the underlying relationship of the system under investigation is of the following form:

$$y = f\left( {x_{1} \ldots x_{m} } \right) + r$$
(2)

where f = smooth function, and r = random variable that represent the noise. With loss of generality it can be assumed that the r distribution is zero, and that variance of the noise \(Var\left( r \right)\) is bounded. The domain of a possible model is now restricted to the class of smooth functions which bounded first partial derivatives. The Gamma statistic (Γ) is an estimate of the model output variance that cannot be accounted for by smooth data model.

The GT is based on \(N\left[ {i,k} \right]\), which are the kth \(\left( {1 \le k \le p} \right)\) nearest neighbours \(x_{{N\left[ {i,k} \right]}}\) \(\left( {1 \le k \le p} \right)\) for each vector \(x_{i}\) \(\left( {1 \le i \le M} \right)\). Specifically, the GT is derived from the Delta function of the input vectors:

$$\delta_{M} \left( k \right) = \frac{1}{M} \mathop \sum \limits_{i = 1}^{M} \left| {x_{{N\left[ {i,k} \right]}} - x_{i} } \right|^{2}$$
(3)

In which \(\left| \ldots \right|\) represent the Euclidean distance, and the corresponding Gamma function of the output values:

$$\gamma_{M} \left( k \right) = \frac{1}{2M}\mathop \sum \limits_{i = 1}^{M} \left| {y_{{N\left[ {i,k} \right]}} - y_{i} } \right|^{2}$$
(4)

where \(y_{{N\left[ {i,k} \right]}}\) = corresponding y value of kth nearest neighbor of xi in Eq. (3). To compute Γ a least-square regression line is constructed for the p points (\(\delta_{M} \left( k \right), \gamma_{M} \left( k \right)\)):

$$y = \beta C + \varGamma$$
(5)

where y = the output vector, β and Γ = the gradient and intercept of regression line (C = 0). The output from the regression line provides beneficial information for model construction. A small value of Γ indicates the more suitable input parameter. The gradient indicates the complexity of the model, high gradient means complicated fitting. The standard error (SE) indicates the reliability of the Г; small SE means more reliable Г. Vratio indicates the predictability of the given output based on employed inputs, and expressed as:

$$V_{ratio} = \frac{\Gamma}{{\sigma^{2} (y)}}$$
(6)

where \(\sigma^{2} \left( y \right)\) is output variance, Г is the gamma function. Lower value of Vratio shows a high degree of predictability for the target y. Gamma, SE, and Vratio having smaller values indicate the mathematical model (e.g. SVR-ALO, SVR-MVO, SVR-SHO, SVR-HHO, SVR-PSO, and SVR-BO) of decent quality. In the presented study, the best input combinations were decided by utilizing the least value of Γ, SE, and Vratio (Moghaddamnia et al. 2009; Piri et al. 2009; Malik et al. 2017a, 2019b).

3.2 Support vector regression (SVR)

A support vector machine (SVM) is an observer-based learning method introduced by Vapnik (1995). This model has been applied successfully in many fields, including water resources and streamflow prediction. The first use of the SVM model in water topics and rainfall-runoff modeling was presented by Dibike et al. (2001). The support vector machine is an efficient learning system based on bounded optimization theory that uses the principle of structural minimization principle. In general, support vector machines are divided into two categories: the first one is the support vector classifier (SVC) which deals with classification issues and the second one is the support vector regression (SVR) which performs the regression and forecasting issues. The SVR regression function is expressed as:

$$f (x) = w \times \phi \left( {\text{x}} \right) + b$$
(7)

where w: weight vector in the feature space, ϕ: transfer function, and b is the bias. To find a suitable SVR function f (x), the problem of regression can be declared as:

$${\text{Minimize}}\;\frac{1}{2}\left\| w \right\|^{2} + C\mathop \sum \limits_{i = 1}^{N} \left( {\xi_{i} + \xi_{i}^{*} } \right)$$
(8)
$${\text{Subject to the condition}}:\left\{ {\begin{array}{*{20}l} {y_{i} - f\left( x \right) \le \varepsilon + \xi_{i} } \hfill \\ {f\left( x \right) - y_{i} \le \varepsilon + \xi_{i}^{*} } \hfill \\ {\xi_{i} ,\xi_{i}^{*} \ge 0,\; i = 1, 2, 3, \ldots ,N} \hfill \\ \end{array} } \right.$$
(9)

where C, \(\xi_{i}\) and \(\xi_{i}^{*}\) are penalty parameter and two slack variables, respectively. By utilizing the Lagrangian functions, the solution of the non-linear regression function can be given based on the optimization as follows:

$$f\left( x \right) = \mathop \sum \limits_{i = 1}^{N} \left( {\alpha_{i} - \alpha_{i}^{*} } \right) K\left( {x,x_{i} } \right) + b$$
(10)

where \(K\left( {x,x_{i} } \right)\), \(\alpha_{i}\), \(\alpha_{i}^{*}\) are kernel function and dual variables, respectively. C, \(\alpha_{i}\) and \(\alpha_{i}^{*}\) > 0. There are several kernel functions like linear, sigmoid, polynomial, and radial basis function (RBF) while choosing the appropriate kernel function is important. The RBF kernel can be considered as the most popular kernel used in the literature. Therefore, the RBF kernel was adopted for this research. The RBF kernel is defined as:

$$K\left( {x,x_{i} } \right) = { \exp }\left( { - \gamma \left\| x_{i} - x^{2} \right\| } \right)$$
(11)

where γ is the kernel parameter, which means that C, γ, and ε are the three parameters that are responsible for the SVR performance.

A detailed description of the SVR and SVM models can be found in (Gunn 1998). In this study, LIBSVM version 3.23 developed by Chang and Lin (2011) was used with MATLAB software to implement SVR development models.

3.3 Meta-heuristic algorithms

3.3.1 Harris hawks optimization (HHO)

The HHO algorithm is a novel developed algorithm based on swarm’s intelligence. The HHO algorithm was developed and expanded by Heidari et al. (2019). Usually, the hawks work lonely except the Harris hawks that work together for hunting and chasing. The HHO algorithm mimics the cooperative behavior and hunting mechanism of Harris’ hawks in nature. The proposed HHO algorithm was successfully used for optimization and engineering applications (Moayedi et al. 2019a, 2020). The hunting mechanism of proposed HHO includes four movements; tracing, encircling, approaching, and attacking. This mechanism is based on three principle stages from exploration, a transition from exploration to exploitation and exploitation. Figure 3 shows how HHO works based on three basic phases.

Fig. 3
figure 3

Stages of HHO algorithm (Heidari et al. 2019)

Full size image

The first phase is the capability of exploration, which is listed as:

$$X\left( {t + 1} \right) = {\text{ }}\left\{ {\begin{array}{ll} {X_{{rand}} \left( t \right) - r_{1} \left| {X_{{rand}} \left( t \right) - 2r_{2} X\left( t \right)} \right|} \hfill & {if\;q \ge 0.5} \hfill \\ {X_{{rabbit}} \left( t \right) - X_{a} \left( t \right) - r_{3} \left( {LB + r_{4} \left( {UB - LB} \right)} \right)} \hfill & {if\;q < {\text{0}}.{\text{5}}} \hfill \\ \end{array} } \right.$$
(12)
$$X_{a} \left( t \right) = \frac{1}{N}\mathop \sum \limits_{1}^{N} X_{i} \left( t \right)$$
(13)

where \(X_{a} \left( t \right)\) is the average location of the Harris hawk, N is the number of all Harris hawks (search agent number), \(X\left( {t + 1} \right)\) is the location of the hawk in the following iteration t + 1, \(X_{i} \left( t \right)\) is the position of the current Harris Hawk at iteration t, \(X_{rand} \left( t \right)\) is a randomly selected hawk between, \(X_{rabbit} \left( t \right)\) is the location of the rabbit (prey); LB and UB are the lower and upper bands, respectively, and \(q\), \(r_{1}\), \(r_{2}\), \(r_{3}\) and r4 are random values varying between 0 and 1.

The second stage is the transition from exploration to exploitation, in this stage, the energy of hawks is reduced during the hunt. The hunt escaping energy (E) can be formulated as:

$$E = 2E_{0} \left( {1 - \frac{t}{T}} \right)$$
(14)

where E0 is the initial energy during each progression (E0 ∈ −1, 1) and T is the maximum size about the iterations. In the HHO algorithm, the rabbit’s state may be determined based on the contrast direction of E. In this equation, E stands for the rabbit energy, and E0 ∈ (−1, 1) indicates the inlet energy for every step. HHO may compute the rabbit state dependent on the variation trend of E.

The third stage is the exploitation phase, which predominantly plans to improve local solutions from recently available solutions. This stage is the hawk’s sudden attack on the prey identified in the past stage based on the prey escape and hawk hunting. Based on both values of E and r, in the phase of exploitation is considered to select the besiege type to catch the rabbit the hard one is taken when \(\left| E \right| < 0.5\) and the soft one is taken when \(\left| E \right| \ge 0.5\), the HHO algorithm has proposed four strategies to mimic the attacking stage; soft besiege, soft besiege with progressive rapid dives, hard besiege, and hard besiege with progressive rapid dives (Moayedi et al. 2019b; Heidari et al. 2019).

3.3.2 Bayesian optimization (BO)

Bayesian optimization (BO) is a type of optimization algorithms which are called Sequential Model-Based Optimization (SMBO) algorithms. This algorithm based on the Bayesian theorem and implements observations of previous data of the loss function in order to determine the calculated next position as the best performance (Bergstra et al. 2011).

The basic idea of the BO algorithm is to assume a prior distribution model and using the information obtained later to continually refine the expected model to make the model with respect to the actual distribution. The BO algorithm can improve the outcome, find the optimum parameters and achieve optimal accuracy using the information of previous evaluation (iteration) and solve the optimization problem using two main components; Gaussian regression process (probabilistic surrogate model) and acquisition function (expected improvement) by taking the advantage of the full information provided by the optimization history to make the optimization search efficient and effective (Shahriari et al. 2016).

Gauss process regression predicts the probability distribution of an objective function that can be used to create an acquisition function while the BO uses the acquisition function to balance between exploration and exploitation phases during each iteration. The acquisition function with strong exploration capability favors sampling from regions of high uncertainty in the design space, while an acquisition function with a strong exploitation capability favors samplings that are likely to provide an improvement over the currently best observation (Brochu et al. 2010).

In this study, the objective function to be optimized is daily streamflow prediction which is assessed through the optimization of the SVR hyperparameters based on reducing the root mean square error between the observed and predicted daily streamflow using MATLAB software. The BO algorithm coupled with SVR is widespread used in the literature (Law and Shawe-Taylor 2017; Alade et al. 2019; Kouziokas 2020a, b). For more details about the BO algorithm, readers can refer to (Brochu et al. 2010; Shahriari et al. 2016).

3.3.3 Spotted hyena optimizer (SHO)

SHO is a new bio-inspired based metaheuristic technique for optimization problems. It was developed by Dhiman and Kumar (2017) based on four steps of prey hunting on which spotted hyenas depend on nature. These four behaviors can be summarized as; encircling, hunting, attacking prey (exploitation), and search for prey(exploration), unlike the gray wolf optimizer which contains only three steps. The SHO has provided robust performance for solving the optimization and engineering problems (Dhiman and Kumar 2018; Dhiman et al. 2018; Kumar and Kaur 2019). The encircling behaviors can be represented mathematically as follows:

$$D_{h} = \left| {B \cdot X_{P} \left( t \right) - X\left( t \right)} \right|$$
(15)
$$X\left( {t + 1} \right) = X_{P} \left( t \right) - E \cdot D_{h}$$
(16)

where \(D_{h} is\) the distance between the spotted hyena and the prey, t is the current iteration, \(X_{P} \left( t \right)\) is the location of prey, \(X \left( t \right)\) is the location of a spotted hyena, E and B are coefficients calculated using the following equations;

$$B = 2 \cdot r_{1}$$
(17)
$$E = 2h.r_{2} - h$$
(18)
$$h = 5 - \left( {Iteration*\left( {5/Maximum\_Iteration} \right)} \right)$$
(19)

where h is linearly reduced from 5 to 0 during the iterations to ensure a balance between exploration and exploitation,\(r_{1}\) and r2 are random values between [0,1]. Hunting process can be illustrated mathematically as follows:

$$D_{h} = \left| {B \cdot X - X_{k} } \right|$$
(20)
$$X_{k} = X_{h} - E \cdot D_{h}$$
(21)
$$C_{h} = X_{k} + X_{k + 1 } + \cdots + X_{k + N }$$
(22)
$$N = count_{nos} \left( {X_{h} ,X_{h + 1} , X_{h + 2} , \ldots ,\left( {X_{h} + M } \right)} \right)$$
(23)

where M is a random value between [0.5 − 1]. For the purpose of developing a mathematical model for attacking prey, the mathematical formula for attacking prey is formulated as follows:

$$X\left( {t + 1} \right) = C_{h} /N$$
(24)

where \(X\left( {t + 1} \right)\) is the best solution obtained so far. More details about using the SHO algorithm, readers are referred to (Dhiman and Kumar 2017, 2018).

3.3.4 Multi-verse optimizer (MVO)

The MVO algorithm is introduced by Mirjalili et al. (2016). The multi-verse optimizer algorithm is inspired by the theory of multi-verse in astrophysics based on three cosmological concepts; black hole, white hole, and wormhole. A white hole has never seen in our universe, but physicists think that the big bang may be accepted as a white hole and can be the basic component for the birth of a universe. These three ideas perform exploration, exploitation, and local search according to the mathematical formulation that there are two basic coefficients: traveling distance rate (TDR) and wormhole existence probability (WEP). The former coefficient is for identifying the wormhole’s existence probability in universes. It is required to increase linearity over the iterations to emphasize exploitation as the progress of the optimization procedure. TDR is also a factor to show the distance rate that an object may be teleported by a wormhole around the best universe obtained so far (Mirjalili et al. 2016).

The MVO algorithm has been applied and evaluated in engineering and optimization tasks and many areas and has achieved high performance (Hu et al. 2016; Trivedi et al. 2016; Peng et al. 2017; Fathy and Rezk 2018).

In the MVO algorithm, the TDR and WEP must be calculated to update the solutions. These parameters dictate the number of times and the amount of solutions change during the optimization process the TDR and WEP are defined as follows:

$$TDR = 1 - \left( {\frac{{t^{{\left( {\frac{1}{P}} \right)}} }}{{T^{{\left( {\frac{1}{P}} \right)}} }}} \right)$$
(25)
$$WEP = W_{\hbox{min} } + t*\left( {\frac{{W_{min} - W_{max} }}{T}} \right)$$
(26)

where Wmin indicate the minimum (commonly equal to 0.2), Wmax is the maximum (commonly equal 1), t is the current iteration, P is the exploitation accuracy and T is the maximum_iteration. After specifying the WEP and TDR parameters, the solution position can be created based on the following formula:

$$X_{i}^{j} = \left\{ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {X_{j} + TDR + \left( {\left( {Ub_{j} - lb_{j} } \right)*r_{4} + lb_{j} } \right)} \hfill & {if\; r_{2} < WEP\; and \;r_{3} < 0.5} \hfill \\ {X_{j} - TDR + \left( {\left( {Ub_{j} - lb_{j} } \right)*r_{4} + lb_{j} } \right)} \hfill & {if\; r_{2} < WEP\; and\; r_{3} \ge 0.5} \hfill \\ \end{array} } \right.} \hfill \\ {X_{{{\text{roulette }}\;{\text{wheel}}\; {\text{selection}}}}^{j} \quad\quad\quad\quad\quad\quad\quad if\; r_{2} \ge WEP} \hfill \\ \end{array} } \right.$$
(27)

where r1, r2, r3 and r4 are random values between [0, 1], \(X_{j}\) is the jth parameter of the best universe obtained so far, Ubj and lbj are the upper and lower bounds of the jth element, respectively; \(X_{\text{roulette wheel selection}}^{j}\) is the jth element of a solution chosen by the roulette wheel selection mechanism and \(X_{i}^{j}\) is the jth parameter in the ith universe. More information about this meta-heuristic algorithm can be found in Aljarah et al. (2020) and Mirjalili et al. (2016).

3.3.5 Particle swarm optimization (PSO)

PSO was developed for the first time by Kennedy and Eberhart (1995). The PSO concept mimics the movement of birds in the search for food in nature. PSO has been effectively utilized for solving engineering, classification and optimization problems and fast finding the optimal solutions using two main parameters: position (x) and velocity (V) (Chau 2006; García Nieto et al. 2014; Sudheer et al. 2014; Zhang et al. 2014; Kuntoji et al. 2018; Tikhamarine et al. 2020a). The main parameters of position and velocity can be explained mathematically as follows:

$$V_{i} \left( {t + 1} \right) = wV_{i} \left( t \right) + r_{1} c_{1} (X_{{pbest_{i} }} - X_{i} \left( t \right) + r_{2} c_{2} \left( {X_{{gbest_{i} }} - X_{i} \left( t \right)} \right)$$
(28)

where pbest is the best position of the ith particle and gbest is the best global value obtained from various particles in each iteration. The new position of the next iteration can be updated using the following formula:

$$X_{i} \left( {t + 1} \right) = X_{i} \left( t \right) + V_{i} \left( {t + 1} \right)$$
(29)

where w is the coefficient of inertia, r1 and r2 are random coefficients, c1 and c2 are the acceleration coefficients and \(V_{i} \left( {t + 1} \right)\) is the next velocity. More details about PSO can be found in Kennedy and Eberhart (1995) and Mirjalili et al. (2020).

3.3.6 Ant lion optimizer (ALO)

ALO is a novel optimization algorithm developed by Mirjalili (2015b). The ALO algorithm mimics the hunting mechanism of ant-lions in nature (insect). The mechanism of the ant lion algorithm is based on five steps for prey hunting. These steps can be listed as; random walk of ants, build traps, entrapment of ants in traps, hunt prey, and rebuild traps. ALO has been successfully applied and evaluated in engineering and optimization problems and has provided robust performance compared to other optimization algorithms (Mouassa et al. 2017; Tharwat and Hassanien 2018; Kose 2018; Dinkar and Deep 2019).

The different steps of the ALO mechanism can be mathematically described by the following equations: i.e. random walk, as follows:

$$X\left( t \right) = [0, cumsum\left( {2r\left( {t_{1} } \right) - 1} \right),cumsum(2r\left( {t_{2} } \right) - 1, \ldots ,cumsum\left( {2r\left( T \right) - 1} \right]$$
(30)

where \(X\left( t \right)\) is the random walks of ants, t is the step of random walk, T is the maximum_Iterationn and r(ti) is a stochastic function defined as follows:

$$r\left( t \right) = \left\{ {\begin{array}{*{20}c} {1\; if \;rand > 0.5 } \\ {0\; if\; rand \le 0.5} \\ \end{array} } \right.$$
(31)

where rand is a random number in the range of [0,1]. Hunting process of the ALO algorithm can be illustrated mathematically as follows:

$$X_{i} \left( t \right) = \frac{{\left( {X_{i} \left( t \right) - \alpha_{i} } \right)*(d_{i} \left( t \right) - c_{i} \left( t \right))}}{{\left( {b_{i} - \alpha_{i} } \right)}} + c_{i} \left( t \right)$$
(32)

where αi, bi are the minimum and maximum of random walk corresponding to the ith variable. respectively. ci(t), di(t) are the minimum and maximum of ith variables at ith iteration and can be defined as;

$$c_{i} \left( t \right) = Antlion_{j} \left( t \right) + c\left( t \right)$$
(33)
$$d_{i} \left( t \right) = Antlion_{j} \left( t \right) + d\left( t \right)$$
(34)
$$c\left( t \right) = c\left( t \right)/I$$
(35)
$$d\left( t \right) = d\left( t \right)/I$$
(36)

where \(Antlion_{j}\) is the position of selected jth antlion at ith iteration. \(c_{i} \left( t \right)\), \(d_{i} \left( t \right)\) are the minimum and maximum of ith variables at ith iteration, Antlionj is the position of selected jth antlion at ith iteration and I is the ratio and it is defined as follows;

$$I = 10^{w} \frac{t}{T}$$
(37)

where w is a constant that changes based on the current iteration (Table 5). After trapping in antlion’s traps, the Ant hunting by Antlion and rebuilding the pit to catch new prey can be described with the following formula.

$$Antlion_{j} \left( t \right) = \left\{ {\begin{array}{*{20}l} {Ant_{i} \left( t \right) \;if\quad f\left( {Ant_{i} \left( t \right)} \right) > f\left( { Antlion_{j} \left( t \right)} \right)} \hfill \\ {\left( { Antlion_{j} \left( t \right) \; if\quad f(Ant_{i} \left( t \right)} \right) \le f\left( { Antlion_{j} \left( t \right)} \right)} \hfill \\ \end{array} } \right.$$
(38)

where Anti(t) is the position of selected ith ant at ith iteration.

The antlions update their position according to the ants’ location to increase their chance of catching new prey. In each iteration, the best antlion obtained (the best solution) saved as an elite. Since the elite are the hardest antlion that can direct the remaining antlions movements along with the iterations. The elitist mechanism can be described as;

$$X\left( {t + 1} \right) = \left( {R_{A} + R_{E} } \right)/2$$
(39)

where \(X\left( {t + 1} \right)\) is the best solution obtained so far, RA is a random walk around the chosen ant-lion with the roulette wheel while and RE is a random walk around the best antlion at ith iteration.

Further theories, literature review, and applications of the ALO algorithm can be found in Heidari et al. (2020).

3.4 Hybrid SVR models

In order to successfully implement the SVR model and achieve good performance, SVR parameters must be carefully defined. The accuracy of SVR model performance, in general, depends on the selection of appropriate parameters that can be considered an optimization problem and need to find the global optimal solution to achieve the best performance that can be obtained so far. The meta-heuristic algorithms were used to identify the three responsible parameters of the SVR model (C, γ, and ε). The best choices of SVR parameters are not known to the problem. Thus, some form of model identification (parameter search) should be performed. The goal is to find these parameters well to predict unknown data with sufficient accuracy with the minimal error between predicted and target variables, where the proposed algorithms have been evaluated based on the lowest RMSE value in training stage.

In the present study, we follow the search space for the SVR hyperparameters used in literature (Sudheer et al. 2014). The parameters C, γ, and ε are searched in the exponential space C ∈ (10−5, 105), γ ∈ (0, 101) and γ ∈ (0, 101). The association of the SVR model with the meta-heuristic algorithms selected (HHO, MVO, SHO, PSO, ALO, and BO) can build the following hybrid models; (SVR-HHO, SVR-MVO, SVR-SHO, SVR-PSO, SVR-ALO, and SVR-BO) respectively. The flowcharts of the proposed SVR hybrid models are summarized in Fig. 4.

Fig. 4
figure 4

Flowchart of the proposed hybrid SVR models

Full size image

3.5 Statistical performance indicators

The prediction accuracy of SVR-ALO, SVR-MVO, SVR-SHO, SVR-HHO, SVR-PSO and SVR-BO models were examined by using various statistical performance indicators and through graphical appraisal (i.e. time-series plot, scatter plot, and Taylor diagram). The statistical performance indicators are root mean square error (RMSE), scatter index (SI), coefficient of correlation (COC), and Willmott index (WI) (Willmott 1981; Malik and Kumar 2015, 2020; Tao et al. 2018; Malik et al. 2019a, c, 2020b; Tikhamarine et al. 2019a).

$$RMSE = \sqrt {\frac{1}{N} \mathop \sum \limits_{i = 1}^{N} (Q_{obs, i } - Q_{pre,i} )^{2} }$$
(40)
$${\text{SI}} = \frac{{\sqrt {\frac{1}{N} \mathop \sum \nolimits_{i = 1}^{N} (Q_{obs, i } - Q_{pre,i} )^{2} } }}{{\overline{{Q_{obs } }} }}$$
(41)
$$COC = \frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{N}} \left( {Q_{obs,i } - \overline{{Q_{obs } }} } \right) \left( {Q_{for,i} - \overline{{Q_{pre} }} } \right) }}{{\sqrt {\mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{N}} (Q_{obs,i } - \overline{{Q_{obs } }} )^{2} \mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{N}} (Q_{pre,i} - \overline{{Q_{pre} }} )^{2} } }}$$
(42)
$${\text{WI}} = 1 - \left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{N} (Q_{pre,i} - Q_{obs, i} )^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} (\left| {Q_{pre,i} - \overline{{Q_{obs } }} } \right| + \left| {Q_{obs,i } - \overline{{Q_{obs } }} } \right|)^{2} }}} \right]$$
(43)

where \(Q_{obs }\) and Qpre = observed and predicted streamflow values, N = number of observations, \(\overline{{Q_{obs } }}\) and \(\overline{{Q_{pre } }}\) = mean of observed and predicted streamflow values, \(\left| {Q_{pre,i} - \overline{{Q_{obs } }} } \right|\) = absolute difference between predicted and observed mean, and \(\left| {Q_{obs,i } - \overline{{Q_{obs } }} } \right|\) = absolute difference between observed and their mean. By utilizing the Eqs. (40-43), the model has a minimum value of error matric (RMSE and SI) and a higher value of COC and WI were nominated better for daily streamflow prediction at the study basin.

4 Results and discussion

4.1 Optimal input selection using GT

The selection of optimal input variables in modelling complex hydrological processes is very tedious and time-consuming. In recent times, to overcome this problem Gamma test (GT) has been utilized widely in various fields (Piri et al. 2009; Kakaei Lafdani et al. 2013; Rashidi et al. 2016; Malik et al. 2019b). In this study, the impression of the individual parameter was evaluated on output (Qt) by constructing the eight different combinations (Table 2) through different input parameters (Rt, Rt−1, Rt−2, Rt−3, Qt−1, Qt−2, Qt−3) at Naula watershed (Qt is the streamflow at time t, and Rt is the rainfall at time t). It was observed from Table 2 that the first combination includes all seven input parameters (called an initial set); the second combination comprised of six input parameters (All - Rt) means omitted Rt from the initial set; the third combination contains six input parameters (All - Rt−1), means omitted Rt-1 and include Rt to the initial set, and so on for rest of the combinations as specified in Table 2. Based on GT results summarized in Table 2 the parameters Rt, Rt−1, Qt−1, and Qt−2 have a significant influence on output (Qt). The selected parameters are designated as important constraints based on the maximum value of gamma (Г), standard error (SE) and Vratio statistics, and further used for model construction and streamflow forecasting in the study basin.

Table 2 Optimal input variable nomination at Naula watershed using GT
Full size table

Based on four nominated variables (Rt, Rt-1, Qt-1, and Qt-2), five diverse combinations were constructed (Table 3), and the best one was selected based on the minimum score of Г, SE, and Vratio (Noori et al. 2011; Malik et al. 2019b). The results of GT on five different combinations are summarized in Table 4, which exposed that the combination Rt, Rt−1, Qt−1, Qt−2 had the lowest value of gamma statistics (Г = 17514.139, SE = 2088.613, Vratio = 0.390, and Mask = 1111), and utilized for daily streamflow forecasting at Naula watershed.

Table 3 Various hybrid SVR models optimized with six meta-heuristic algorithms at Naula watershed
Full size table
Table 4 GT statistics of different input models at Naula watershed
Full size table

4.2 Streamflow prediction through hybrid SVR models

The controlling parameters of the HHO, MVO, SHO, PSO, ALO, and BO algorithms used in this study are listed in Table 5. The performance of optimized SVR-ALO, SVR-MVO, SVR-SHO, SVR-HHO, SVR-PSO, and SVR-BO models for selected combination (Rt, Rt−1, Qt−1, and Qt−2) during calibration and validation periods are summarized in Table 6. It was observed from Table 6 that the SVR optimized with several meta-heuristic algorithms produced RMSE (92.038 to 123.04 m3/s), SI (0.401 to 0.537), COC (0.780 to 0.881), and WI (0.840 to 0.928) in the calibration period and the RMSE (181.31 to 213.169 m3/s), SI (0.715 to 0.841), COC (0.577 to 0.717), and WI (0.690 to 0.777) in the validation period. From Table 6, it is clearly exposed that the SVR-HHO-5 model produced the highest level of accuracy in terms of RMSE (92.038/181.31 m3/s), SI (0.401/0.715), COC (0.881/0.717), and WI (0.928/0.777) during calibration/validation periods, and closely followed by the SVR-ALO-5 model. Also, the SVR-HHO-5 model follows the criteria of minimum values of error metrics (RMSE and SI) and higher values of COC, and WI for periods of calibration and validation. Furthermore, the results reveal the poor performance of the SVR-BO model in predicting the daily streamflow at the study basin. With respect to the performance of hybrid SVR models, during periods of calibration and validation the hierarchy follows the order of SVR-HHO > SVR-ALO > SVR-PSO > SVR-BO > SVR-SHO > SVR-MVO, and SVR-HHO > SVR-ALO > SVR-MVO > SVR-SHO > SVR-PSO > SVR-BO, respectively. The prediction accuracy of the SVR-ALO, SVR-MVO, SVR-SHO, SVR-PSO, and SVR-BO models concerning the RMSE during calibration/validation periods was reduced by 4/3%, 25/13%, 24/14%, 22/14% and 23/15% applying the SVR-HHO. To support the findings of this study, it was compared with other studies conducted on streamflow simulation on different time-scales by utilizing hybrid machine learning models (Adnan et al. 2019; Huang et al. 2019; Nourani et al. 2019; Roy and Singh 2019; Xie et al. 2019; Zakhrouf et al. 2019; Tikhamarine et al. 2019b, 2020b), also they report the successful application of hybrid machine learning models for daily or monthly streamflow/runoff simulation based on error matrix and graphical inspection in various catchments with different environmental conditions over the globe. Table 7 compares the accuracies of the models with respect to 10 initializations. The average RMSE and COC values of the 10 runs reveals that the SVR-HHO-5 has better accuracy (RMSE: 91.936 and 181.951 m3/s and COC: 0.881 and 0.717) in the calibration and validation phases compared to other models.

Table 5 Initial parameter settings for the algorithms
Full size table
Table 6 Performance indicators values of hybrid SVR and BNN models at Naula watershed
Full size table
Table 7 Performance comparison of hybrid SVR models with respect to 10 initializations
Full size table

Figure 5a–f shows the comparison of predicted and observed streamflow values of SVR-ALO, SVR-MVO, SVR-SHO, SVR-HHO, SVR-PSO, and SVR-BO models through time-series plot (left-side) and scatter plot (right-side) during the calibration period, whereas Fig. 6a–f demonstrate a comparison of predicted and observed streamflow values of SVR-ALO, SVR-MVO, SVR-SHO, SVR-HHO, SVR-PSO, and SVR-BO models through time-series plot (left-side) and scatter plot (right-side) during validation period, respectively. As observed from Figs. 5a–f and 6a–f all the optimized SVR models overpredict the low streamflow values for calibration (up to 160 m3/s) and validation (up to 140 m3/s) periods. Furthermore, the hybrid SVR models underestimate peak daily streamflow, especially in the validation period. The main reason for this might be the fact that the calibration data range does not cover that of the validation as explained in Sect. 2. The other possible reason is a small sample of extreme values in the calibration period and hybrid models cannot adequately learn the process. The regression line and 1:1 (45° line) are closer to each other, for the SVR-HHO-5 model with a coefficient of determination (R2) = 0.7764 (Fig. 5d) and 0.5135 (Fig. 6d) for both periods, respectively. The graphical comparison of assessment reveals that the SVR embedded with the HHO algorithm (SVR-HHO) provides better estimates than the SVR-ALO, SVR-MVO, SVR-SHO, SVR-PSO, and SVR-BO models for both periods.

Fig. 5
figure 5

Time-series (left) and scatter plots (right) of observed and predicted daily streamflow values by a SVR-ALO-5, b SVR-MVO-5, c SVR-SHO-5, d SVR-HHO-5, e SVR-PSO-5, and f SVR-BO-5 models for calibration period at Naula watershed

Full size image
Fig. 6
figure 6

Time-series (left) and scatter plots (right) of observed and forecasted daily streamflow by a SVR-ALO-5, b SVR-MVO-5, c SVR-SHO-5, d SVR-HHO-5, e SVR-PSO-5, and f SVR-BO-5 models for validation period at Naula watershed

Full size image

To assess the performance of newly proposed SVR and BNN models spatially the Taylor diagram (Taylor 2001) was utilized, which summarized the multiple aspects such as standard deviation, root mean squared error, and coefficient of correlation in a single frame through the polar plot. Figure 7a, b illustrates the spatial pattern of predicted streamflow values by SVR-ALO, SVR-MVO, SVR-SHO, SVR-HHO, SVR-PSO, and SVR-BO models concerning observed ones during calibration and validation periods. It was noticed from Fig. 7a, b the SVR-HHO-5 model estimates are close to the observed values (reference field) with a higher coefficient of correlation and least standard deviation, and root mean squared error during calibration and validation periods, respectively.

Fig. 7
figure 7

Taylor diagram of observed and predicted daily streamflow values by SVR-ALO-5, SVR-MVO-5, SVR-SHO-5, SVR-HHO-5, SVR-PSO-5, and SVR-BO-5 models during a calibration, and b validation periods at Naula watershed

Full size image

The results of this research expose a promising application of Harris Hawks Optimization (HHO) algorithm integrated with support vector regression (SVR) for daily streamflow prediction. Thus, this study concludes that the newly developed hybrid SVR-HHO model can be a trustworthy and dynamic optimization approach for streamflow modeling.

5 Conclusion

In this research, daily streamflow was predicted by using six meta-heuristic algorithms viz. Ant Lion Optimization (ALO), Multi-verse Optimizer (MVO), Spotted Hyena Optimizer (SHO), Harris Hawks Optimization (HHO), Particle Swarm Optimization (PSO), and Bayesian Optimization (BO) combined with Support Vector Regression (SVR) at Naula watershed. The significant variables and optimal inputs were decided through the application of the Gamma test (GT). The outcomes produced by hybrid SVR models were compared to the observed values based on performance indicators (root mean square error, scatter index, coefficient of correlation, and Willmott index), and by graphical examination (time-series plot, scatter plot and Taylor diagram). A comparison of results assessment revealed that the hybrid SVR-HHO model outperformed the other models in predicting daily streamflow with the inputs of current rainfall, 1 and 2-day antecedent rainfall, and streamflow (Rt, Rt−1, Qt−1, and Qt−2) at Naula basin. Also, this research explored the latent capability of GT in defining the extensive input parameters and best combination with less time-consuming for daily streamflow prediction at the study basin.

In future studies, it is recommended that the potential ability of these six meta-heuristic algorithms (i.e. ALO, MVO, SHO, HHO, PSO, and BO) and two more viz. Whale Optimization Algorithm (WOA) and Grey Wolf Optimizer (GWO) embedded with simple and advance machine learning techniques may also be calibrated and validated for various catchments on global scale.