1 Introduction

Reliability of a structure is the probability that it performs its intended function over a given period of time. Structural reliability is concerned with the probability of occurrence of limit state violation for engineered structures. Limit state includes safety of the structure against collapse, limitations on damage, or other safety criteria. The probability of limit state violation is identical to the probability of failure.

Because fatigue is the most common degradation mechanism in material strength and stiffness due to cyclic stress–strain operation, expressing the limit state in terms of fatigue strength and damage caused by cyclic loading defines the fatigue reliability problem. Fatigue failures are attributed to dynamic response (either a deflection, a strain, or a stress), which is a random process X(t), of a stable structure. These do not include failures under fixed or random static loads, failures due to static or dynamic instability, or failures caused by corrosion and abrasion (Lin 1967). Fatigue failure occurs when the damage to the structure accumulates to a critical level (allowable fatigue strength); this is due to X(t) fluctuations at small and moderate excursions which are not large enough to cause first-excursion failures.

For deepwater structures, fatigue reliability analysis is a challenging task due to the complex nature of dynamic structure response and the large uncertainty caused by the dynamic external load (wind, wave, and current).

A riser is a critical element of a production system, which links the floating unit (e.g. an FPSO vessel or a semi-submersible) to the seabed manifold. There are three main categories of risers:

  1. (i)

    drilling risers,

  2. (ii)

    workover/completion risers, and

  3. (iii)

    export/production/injection risers.

Drilling risers are rigid with vertical configuration. They contain a rigid internal drill pipe. Workover/completion risers are also rigid and commonly have vertical configurations. The external casing contains an internal pipe for transportation of system components and tools required for the various operations. Production/export/injection risers transport fluid (oil and gas) from the seabed to the surface and vice versa. The most severe consequences of failure are typically associated with these risers. A wide variety of different configurations exist under this riser category. Vertical top-tensioned rigid risers are historically most commonly employed for production. Tension force is applied to prevent buckling of a long, slender riser and to reduce deflections. These risers may also be non-rigid without any requirement of top tensioning. The details of configurations, operations, and functional requirements of the above-stated riser categories are given by Leira (1998).

The current paper presents the fatigue reliability analysis of a rigid riser with vertical configuration (the most common type of production riser) under Morison-type wave loading. Riser dynamic response is a random process and is commonly analyzed either in the frequency domain (Tucker and Murtha 1973; Kirk et al. 1979) or the time domain (Harper 1979). The analysis of dynamic response in the frequency domain is valid for linear systems with Gaussian excitation, where the response is also Gaussian. Non-linearity in a riser system arises due to Morison-type hydrodynamic forces. Commonly used spectral analysis techniques are unable to predict deviations from a Gaussian form due to non-linearity.

Numerical time-domain simulation methods are able to account for system non-linearity. However, the solution routine is time consuming (Brouwers 1982). The method is not suitable for fatigue reliability analysis, which depends on a large number of sea states over a long duration of time. It also does not help in identifying general trends in riser response. Furthermore, in quantifying response-modeling uncertainty in reliability-based fatigue analysis, the method of stress analysis becomes less attractive. Approximate formulae for response of slender risers in deepwater have been given by Verbeek and Brouwers (1986).

The current study has been carried out with the following objectives:

  • to conduct fatigue analysis under non-linear response using analytical expressions for rigid slender risers in deepwater considering the long-term non-stationary behavior of sea states,

  • to prescribe a methodology based on reliability that bridges the gap between simple design fatigue models based on a factor of safety approach, and time consuming and computationally extensive numerical models, and

  • to discuss the validity of a lognormal format in calculating time to fatigue failure.

2 Riser fatigue reliability modeling methodology

The riser fatigue modeling framework is illustrated in Fig. 1; detailed discussion of each step is presented in subsequent sections.

Fig. 1
figure 1

Riser fatigue reliability modeling methodology

Full size image

2.1 Fatigue problem definition

Morison-type wave loading is considered for the response analysis, whereas the riser strength is related to a damage model. Uncertainty associated with each component, i.e. load and strength, is also incorporated in the present analysis.

2.1.1 Fatigue reliability, loading and response

A structural element is considered failed if its resistance, R, is less than the resultant stress, S, acting on it. The probability of failure, P f , can be presented mathematically as:

$$ P_{f} = p{\left({R \leqslant S} \right)} $$
(1a)

or in general

$$ P_{f} = p{\left[ {G{\left({R,S} \right)} \leqslant 0} \right]} $$
(1b)

where G(R,S) is termed the limit state function. The probability of failure is identical to the probability of limit state violation. Thus reliability, Re, (i.e. the probability of success) can be expressed as:

$$ \hbox{Re} = 1 - P_{f} $$
(2)

Fatigue reliability involves the measure of fatigue damage and resistance over fatigue lifetime. The classical approach to describe the fatigue life is based on the S–N curve approach (ASCE 1982).

The S-N curve is based on experimental data obtained from deterministic loading conditions and is represented mathematically as:

$$ {\rm NS}^{b}_{a} = c $$
(3)

where S a is stress amplitude, N is number of cycles to failure, and b and c are positive empirical material constants.

Equation (3) holds for all values of S a >  0 for models in which an endurance limit does not exist.

The problem in calculating fatigue life using the S–N curve is to establish a rational means of combining test data based on cyclic stresses of fixed amplitude and frequency to predict the real structural failure under the range of amplitudes and frequencies of concern. Miner (1945) gave the solution of this problem in the form of a linear cumulative damage rule. This theory is well known as Miner’s rule. It is based on the S–N curve, which gives the number of cycles to failure, N ξ, at a constant stress amplitude ξ for the entire N ξ cycles. The basic assumption in Miner’s rule is that if this stress level is applied for only n ξ < N ξ cycles, then the fraction of total fatigue life consumed is n ξ/N ξ = Δξ, at stress amplitude ξ. The quantity Δξ is known as the damage fraction. Failure is assumed to occur when the sum of all the applicable damage fractions reaches unity. The total damage Δ is expressed mathematically as (Lin 1967):

$$ \Delta = {\sum {\frac{{n_{\xi}}}{{N_{\xi}}}}} $$
(4)

However, Miner’s original paper reported the failure in the range of 0.61 ≤ Δ ≤ 1.45. The large uncertainty in Δ arises from the empirical nature of Eq. (4) and it becomes a random variable denoted as \({\hat{\Delta}.}\) The lognormal distribution with unit median and a coefficient of variation of about 0.3 for \({\hat{\Delta}}\) is used to account for modeling error associated with Miner’s rule, after Wirsching (1984). Replacing the parameter Δ with the variable \({\hat{\Delta},}\) the nature of the cumulative damage rule becomes probabilistic.

Another damage model assumes an evolutionary probabilistic structure from the start (Bogdanoff 1978). In this model, use is made of various Markovian processes. Unlike Miner’s rule, in this model the order and severity of the loading must be known. Furthermore, damage states are not uniquely related to measurable physical quantities. Due to these reasons, the method is not attractive to the offshore industry and Miner’s rule is preferred because of its ease in dealing with probabilistic structures.

The fatigue process may be physically separated into two regimes: (1) crack initiation, and (2) crack propagation or sub-critical crack growth. The importance of these regimes depends upon the nature of the structure and service loads applied to it. For example, under high cyclic fatigue with low stress fluctuations, the crack initiation period consumes a substantial percentage of the usable fatigue life. When stress fluctuations are high, or cracks and notches are present, fatigue cracks initiate quite early and a significant portion of the service life may be spent in propagating the crack to critical size. In low cycle fatigue (total life less than 100,000 cycles), the two regimes are of equal importance. For those structures where defects are practically unavoidable due to fabrication, crack propagation may virtually begin with the first load application.

For reliability analysis purposes, the riser is considered free of initial cracks and other defects and is expected to have high cycles during its service life. So the S–N diagram and Miner’s rule are used to relate stress to total fatigue life.

Total damage \({\hat{\Delta}}\) at failure may be expressed as (combining Eqs. (3) and (4)):

$$ \hat{\Delta} = \frac{1}{c}{\sum {n_{\xi} \xi^{b}}} $$
(5)

The variable \({\hat{\Delta}}\) defines the resistance of the structure element for fatigue reliability. Considering the expected damage E[D] in the structure associated with the stresses, the limit state function in fatigue reliability can be prescribed as:

$$ G{\left(X \right)} = \Delta - E{\left[ {D{\left(t \right)}} \right]}$$
(6)

The mathematical expression for probability of fatigue failure from Eqs. (1) and (6) can be given as:

$$ P_{f} = p{\left[ {\Delta - E{\left[ {D(t)} \right]\leq0}} \right]} $$
(7)

Subtracting this probability of failure from unity gives the fatigue reliability of the element. The discussion on expected damage is presented in the following section.

2.1.2 Expected fatigue damage

As a riser experiences random stresses X(t), the damage accumulated in the structure should also be considered as a random variable in time (stochastic process), denoted here by D(t). The objective is to find the mathematical expression for the expectation of this damage, E[D(t)]. Equation (5) is considered as the basis for deriving the expression for E[D(t)]. The expression for the expected damage under stationary condition using the spectral approach is extensively documented in the literature as:

$$ E{\left[ {D_{T}} \right]} = T\frac{1}{c}E{\left[ {M_{T}} \right]}{\left({2{\sqrt 2}} \right)}^{b} {\left({\sigma_{X}} \right)}^{b} \Gamma {\left({\frac{b}{2} + 1} \right)} $$
(8)

Wave loadings may be considered stationary for a 3-h period, during which they cause stationary stresses in the riser. Therefore, the assumption of stationarity is not applicable for calculating the long-term expected total damage of the riser structure in Eq. (8).

However, the long-term non-stationary response process can be measured as a sum of a large number of short-term stationary processes (Chakrabarti 1990).

Accounting for the non-stationary process, Eq. (8) can be presented as:

$$ E{\left[ {D_{T}} \right]} = {\left({2{\sqrt 2}} \right)}^{b} Tc^{{- 1}} \Gamma {\left({\frac{b}{2} + 1} \right)}{\sum\limits_{i = 1}^k {{\left[ {p_{i}\cdot E{\left[ {M_{T}} \right]}_{i}\cdot{\left({\sigma^{b}_{X}} \right)}_{i}} \right]}}} $$
(9)

or

$$ E{\left[ {D_{T}} \right]} = \frac{{T\Omega}}{c} $$
(10)

where p i is the probability of occurrence of an environmental loading in terms of wave statistics during the structure life (site specific), and

$$ \Omega = {\left({2{\sqrt 2}} \right)}^{b} \Gamma {\left({\frac{b}{2} + 1} \right)}{\sum\limits_{i = 1}^k {{\left[ {p_{i}\cdot E{\left[ {M_{T}} \right]}_{i}\cdot {\left({\sigma^{b}_{X}} \right)}_{i}} \right]}}} $$
(11)

2.1.3 Incorporating uncertainty

For a narrow band process, the variance of the total damage is small near the time of failure (Lin 1967). So the uncertainty in the expected damage at failure seems negligible.

However, in the analysis there are other sources of uncertainty. These sources are inherent to scatter in laboratory test data, the effects of fabrication and workmanship, stress analysis and fatigue strength of the structure during service life.

In the past, significant efforts were made to quantify uncertainty in the factors of fatigue damage expression; details can be found in ASCE (1982), Wirsching(1984), and Wirsching and Chen (1988).

In light of these studies, the true nature of E[D T ] may be predicted as:

$$ \hat{E}{\left[ {D_{T}} \right]} = \frac{{T\hat{B}^{b} \Omega}}{{\hat{c}}} $$
(12)

where \({\hat{B}}\) is a ratio of actual stress to estimated stress. It is a random variable that quantifies modeling errors in fatigue stress estimation. Wirsching (1984) considers uncertainty in \({\hat{B}}\) stemming from five sources: (1) fabrication and assembly operations, (2) seastate description, (3) wave load predictions, (4) nominal member loads, and (5) estimation of hot spot stress concentration factors. Contrary to the previously used parameter c, here \({\hat{c}}\) is considered as a random variable. It accounts for the uncertainty associated with the scatter in S–N data, considering the slope of the curve, b, to be constant. These uncertainties are modeled in terms of the mean, the variance and the probability distribution functions. The related probabilistic characteristics of random variables used in this work are reported in Table 1 (after Wirsching 1984).

Table 1 Statistical properties of random variables
Full size table

In the fatigue expression, the expected damage also becomes a random variable, \({\hat{E}{\left[ {D_{T}} \right]},}\) due to the random nature of variables \({\hat{B}}\) and \({\hat{c}.}\) Furthermore, the uncertainty in each random variable will influence the uncertainty in \({\hat{E}{\left[ {D_{T}} \right]}}\) to a different extent.

2.2 Riser dynamic response modeling

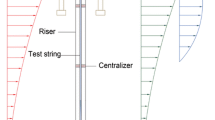
For a slender riser in deep water (risers about 0.5 m or less in diameter in water depths of approximately 150 m or more), Brouwers (1982) proposed three different regions: a wave active zone at the top, a boundary layer at the bottom, and a riser main section in between (Fig. 2). The wave active zone lies near mean sea level and in this zone the riser is exposed to direct wave loading due to wave-induced motions. According to wave theory, wave-induced motions decay exponentially in magnitude from mean sea level over a length λ w (magnitude of 10–40 m in practice). This length may be calculated by the following expression:

$$ \lambda_{w} = \frac{g}{{\omega^{2}_{z}}} $$
(13)

where g is gravitational acceleration and ω z is the characteristic (mean zero-up crossing) frequency of the sea surface elevation.

Fig. 2
figure 2

Regions of riser response

Full size image

The height of the riser above mean sea level is, in general, of the same order of magnitude as that of λ w . The wave active zone is the region which is extended from the riser top to a distance of the order λ w below mean sea level. Below this region, wave induced water particle displacements and associated forces can be disregarded.

Boundary layers appear at discontinuities in the riser due to top and bottom connections. The boundary layer length, λ b , can be given as:

$$ \lambda_{b} = {\sqrt {\frac{{EI}}{{T_{r}}}}} $$
(14)

where

E:

is Young’s modulus of elasticity,

I:

is moment of inertia about neutral axis,

EI:

is bending stiffness of riser,

T r :

is effective riser tension.

The characteristic length over which the response in the riser main section varies is presented here as λ m . This length may be defined as the minimum of the dynamic lengths λ i , and λ d , and riser length L:

$$ \lambda_{m} = \min {\left[ {\lambda_{i,} \lambda_{d,} L} \right]} $$
(15)

where

$$ \lambda_{i} = \pi T^{{1/2}}_{r} {\left({m + m_{A}} \right)}^{{- 1/2}} \omega^{{- 1}}_{z} $$
(16)
$$ \lambda_{d} = \lambda_{i} \delta^{{- 1/2}} $$
(17)
$$ \delta = \frac{{0.5\rho dC_{D} \sigma_{v}}}{{m + m_{A}}} $$
(18)

where

λ i :

= half the wavelength of a lightly damped (δ < < 1) tensioned string,

λ d :

= half the wavelength of a highly damped (δ = O(1)) tensioned string,

δ:

= damping parameter,

σ v :

= standard deviation of FPSO vessel displacement,

ρ:

= density of seawater,

C D :

= drag coefficient ≈ 1,

m:

= riser mass per unit length,

m A :

= added mass of sea water.

As long as λ i or λ d is approximately equal to or shorter than the riser length L, the response in the main section will be dynamic. Otherwise, the response is quasi-static; tension forces dominate inertia and damping forces. The lengths of the boundary layer and wave-active zone are much shorter than the half wavelength of the riser so the response will be quasi-static in these regions (inertia and damping forces may be disregarded and the response is governed by a balance between tension and bending forces).

The response of the riser in the wave-active zone is linearly related to force and is quasi-static in nature. Probability distributions of response, normalized with respect to standard deviation, are the same as those of the force (Brouwers 1982). The non-linearity in the system arises because of the water-particle velocity term in the drag force of Morison-type wave loading. Brouwers and Verbeek (1983) have derived the probability distribution of peak forces based on Borgman’s narrow-band model. The probability distribution of force reduces to a narrow band Gaussian process with Rayleigh distribution only in the inertia-dominated regime, as does the response. In the inertia regime, the loading remains linear. However, in the drag-dominated regime where non-linearity arises in the system, the response deviates non-conservatively from Rayleigh distribution and the use of Eq. (8) will give a small magnitude of expected total damage. To overcome this problem, Brouwers and Verbeek (1983) have related the expected fatigue damage based on non-linear distribution and the expected fatigue damage from Rayleigh distribution by the following relation:

$$ f(b,K) = \frac{{E{\left[ D \right]}_{{\rm non - lin}}}}{{E{\left[ D \right]}_{{\rm lin}}}} = (3K^{2} + 1)^{{- {\left({b/2} \right)}}} \frac{1}{{\Gamma {\left({\frac{b}{2}} \right)}}}{\left[ {\gamma {\left({\frac{b}{2,}\frac{1}{{8K^{2}}}} \right)} + 2^{{1 + {\left({b/2} \right)}}} K^{b} \exp {\left({\frac{1}{{8K^{2}}}} \right)}\Gamma {\left({b,\frac{1}{{4K^{2}}}} \right)}} \right]} $$
(19)

where Γ(a) is the Gamma function and γ(a,z) and Γ(a,z) are incomplete Gamma functions as defined by Abramowitz and Stegun (1970).

Factor f(b,K) is the ratio of non-linear to linear expected fatigue damages and is a function of the slope of the S–N curve (b) and drag inertia parameter (K).

The problem due to deviation of the peak response magnitude from the Rayleigh distribution in calculating E[D T ] can be addressed by introducing the factor f(b,K) in Eq. (8) and may be presented as:

$$ E{\left[ {D_{T}} \right]} = {\left({2{\sqrt 2}} \right)}^{b} Tc^{{- 1}} \Gamma {\left({\frac{b}{2} + 1} \right)}{\sum\limits_{i = 1}^k {{\left[ {p_{i} f_{i} (b,K)E{\left[ {M_{T}} \right]}_{i}.{\left({\sigma^{b}_{X}} \right)}_{i}} \right]}}} $$
(20)

The variation of f(b,K) with K and for three different slopes is shown in Fig. 3. It is evident that f(b,K) is approximately equal to unity in the limit of K → 0 (inertia force dominant regime) and reaches a maximum value when K → ∞ (drag force dominant regime). The variation of this factor is significant in the region 0.3 < K < 10 for the three different slopes.

Fig. 3
figure 3

Variation of factor f(b,K) with parameter K for three different slopes of the S–N curve (after Brouwers and Verbeek 1983)

Full size image

The comparison of narrow-band, non-linear distributions in the drag and inertia dominated limits with those obtained from a wide band model (spectral width = 0.7) was made by Brouwers and Verbeek (1983). The narrow-band model yielded results in the proximity of the results obtained from the wide-band model. This justifies the use of a narrow-band assumption in the current study. For a narrow-band random process, the total number of peaks is almost the same as the number of zero crossings at positive slopes.

The number of response peaks can be considered equal to the number of wave peaks in the wave active zone. For deep waters, the probability density function of sea elevation is Gaussian with zero mean. The number of wave peaks per unit time may be approximated from the expected rate of zero crossings from below for a stationary Gaussian process with a zero mean, by the following expression:

$$ E{\left[ {M_{T}} \right]} = E{\left[ {N_{+} {\left(0 \right)}} \right]} = \frac{1}{{2\pi}}\frac{{{\mathop \sigma \limits^ \bullet}_{\eta}}}{{\sigma_{\eta}}} $$
(21)

or in terms of spectral moments:

$$ E{\left[ {M_{T}} \right]} = \frac{1}{{2\pi}}{\sqrt {\frac{{m_{2} (\omega)}}{{m_{0} (\omega)}}}} $$
(22)

The kth spectral moment can be defined as:

$$ m_{k} = {\int\limits_0^\infty {\omega^{k} S_{\eta} (\omega)}}{\rm d}\omega $$
(23)

where ω is an angular frequency and S η is a single sided wave spectrum.

The right-hand side of Eq. (22) is equal to the number of expected equivalent cycles per unit time between two consecutive zero crossings with positive slope. Spectral moments can be based on either angular frequency, ω, or cyclic frequency, f, and the relationship between them is given as:

$$ m_{k} {\left(\omega \right)} = {\left({2\pi} \right)}^{k} m_{k} {\left(f \right)} $$
(24)

The analytical expression for the standard deviation of bending moment (σ M ) for this zone can be expressed as (Verbeek and Brouwers 1986):

$$ \sigma_{M} = 0.21\rho C_{M} d^{2} \omega^{2}_{z} \lambda^{2}_{b} H_{s} \alpha (x){\sqrt {{\left({1 + 3K^{2} (x)} \right)}}} $$
(25)

where

H s :

is significant wave height

\({\omega_{z} = {\sqrt {\frac{{m_{2} (\omega)}}{{m_{0} (\omega)}}}}}\) :

is mean wave zero-crossing frequency

C M :

is hydrodynamic inertia coefficient ≈ 2

d:

is hydrodynamic diameter of a riser

The drag-inertia parameter K(x) can be defined as:

$$ K{\left(x \right)} = 0.125\frac{{\beta {\left(x \right)}}}{{\alpha {\left(x \right)}}}\frac{{C_{D} d}}{{C_{M} d^{2}}}H_{s} $$
(26)

The x-dependent constants α(x) and β(x) are defined (for the orientation of x, see Fig. 2):

  • for x ≤ 0 (below mean sea level)

    $$ \begin{aligned} \alpha {\left(x \right)} &= \frac{1}{2}{\left({1 + \lambda_{b} /\lambda_{w}} \right)}^{{- 1}} {\left\{{\exp {\left({x/\lambda_{w}} \right)} - \exp {\left({{\left({x - 2L_{1}} \right)}/\lambda_{b}} \right)}} \right\}}\\ &\quad + \frac{1}{2}{\left({1 - \lambda_{b} /\lambda_{w}} \right)}^{{- 1}} {\left\{{\exp {\left({x/\lambda_{w}} \right)} - \exp {\left({x/\lambda_{b}} \right)}} \right\}} \end{aligned} $$
    (27)
    $$ \begin{aligned} \beta {\left(x \right)} &= \frac{1}{2}{\left({1 + 2\lambda_{b} /\lambda_{w}} \right)}^{{- 1}} {\left\{{\exp {\left({2x/\lambda_{w}} \right)} - \exp {\left({{\left({x - 2L_{1}} \right)}/\lambda_{b}} \right)}} \right\}}\\ &\quad + \frac{1}{2}{\left({1 - 2\lambda_{b} /\lambda_{w}} \right)}^{{- 1}} {\left\{{\exp {\left({2x/\lambda_{w}} \right)} - \exp {\left({x/\lambda_{b}} \right)}} \right\}}; \quad \hbox{where} \quad \lambda_{b,} \lambda_{w} \ne 0 \end{aligned} $$
    (28)

  • for x >  0 (above mean sea level)

    $$ \alpha {\left(x \right)} = \frac{1}{2}{\left({1 + \lambda_{b} /\lambda_{w}} \right)}^{{- 1}} {\left\{{\exp {\left({- x/\lambda_{b}} \right)} - \exp {\left({{\left({x - 2L_{1}} \right)}/\lambda_{b}} \right)}} \right\}} $$
    (29)
    $$ \beta {\left(x \right)} = \frac{1}{2}{\left({1 + 2\lambda_{b} /\lambda_{w}} \right)}^{{- 1}} {\left({1 + \lambda_{b} /\lambda_{w}} \right)}\alpha {\left(x \right)} $$
    (30)

In the above expressions L 1 is the extension of the riser above mean sea level. The parameters α(x) and β(x) are at most equal to unity and both reach a maximum value at some distance below mean sea level.

The parameter of σ X in Eq. (20) may be given as:

$$ \sigma_{X} = \frac{{\sigma_{M} d/2}}{I} $$
(31)

In the solution for bending moment Verbeek and Brouwers (1986) assumed that the standard deviation of sea surface elevation (≈H s /4) would be much smaller than the boundary layer length. The effects of free-surface fluctuations would then be small. Furthermore, they neglected the dynamic effects from the response of the main riser section.

To the first order, the horizontal deflection of the riser in the wave active zone may be assumed equal to the horizontal deflection of the FPSO vessel imposed at the top. The effect of direct wave loading on horizontal deflection is negligible, which is of O(|w|λ2 w /λ2 m ) and λ2 w /λ2 m < < 1. Here |w| is the characteristic magnitude of wave-induced horizontal water particle displacement; e.g. standard deviation of sea surface elevation.

The analytical formulation by Verbeek and Brouwers (1986) for the dynamic response in the riser main section can be represented as the vector sum of a ‘quasi-static’ component and a ‘resonant’ component. The quasi-static component describes the static deflection of the riser owing to FPSO displacement at the top and the resonant component represents the dynamic response in one of the natural modes of the riser.

The natural frequency can be calculated as:

$$ \omega_{n} = \frac{{n\pi}}{{2L}}\frac{{T^{{1/2}}_{t} + T^{{1/2}}_{b}}}{{(m + m_{A})^{{1/2}}}} $$
(32)

For a lightly damped riser of length L ∼ λ i the response will be predominantly in the first natural mode, in the second mode when L ∼ 2λ i and in the nth mode when L ∼ nλ i . Maximum response occurs when one of the natural frequencies coincides with the frequency of excitation, i.e. when L = λ i , 2λ i ,...,nλ i .

The response in the lightly damped riser main section and the boundary layer at the bottom may be considered conservatively Rayleigh distributed. So for these two regions in the limit of K → 0, the ratio factor f(b,K) in Eq. (20) approaches unity. The period of response can be given by the natural period of the riser, and the expression for E[M T ] takes the form:

$$ E{\left[ {M_{T}} \right]} = \frac{1}{{2\pi}}\omega_{n} $$
(33)

For analytical expressions of σ M in the main section, we refer to Verbeek and Brouwers (1986).

In the main section, currents cause additional damping and reduce the amplitude of the resonant response. However, a current may excite a dynamic response through vortex shedding, i.e. vortex-induced vibrations (VIVs). The discussion on expected damage due to VIVs is beyond the scope of this work.

The current study is limited to the reliability analysis of slender deep-water risers under wave loading. A reliability analysis of a multi-bore riser in the wave-active region is undertaken as a representative example. The two main reasons for selecting this region are (i) the response in the wave-active zone is the most sensitive to wave height parameter, and (ii) the response deviates from a Rayleigh distribution.

2.3 Reliability analysis

The stress response will be incorporated in the reliability analysis. The following solution approaches are employed in carrying out reliability analyses:

  1. 1.

    simulation methods, and

  2. 2.

    closed form format.

The method of closed form solution can be obtained by quantifying uncertainties of stress and resistance/strength variables in terms of a lognormal distribution. The result of simulation methods will provide a base to validate the result of the simple closed form format. The probability of failure can be calculated on a yearly basis of riser service life. Finally, setting the target reliability, which depends on type of structure and ease of repair, service design life can be estimated.

2.3.1 Closed form solution

Quantifying the uncertainties of variables \({\hat{\Delta}}\) and \({\hat{E}{\left[ {D_{T}} \right]},}\) an expression for reliability can be derived using the lognormal distribution. The parameters of the lognormal distribution for \({\hat{E}{\left[ {D_{T}} \right]}}\) would be:

$$ \mu_{{\ln \hat{E}{\left[ {D_{T}} \right]}}} = \ln \Omega + \ln T + (b\mu_{{\ln \hat{B}}} - \mu_{{\ln \hat{c}}}) $$
(34)

alternatively:

$$ \mu_{{\ln \hat{E}{\left[ {D_{T}} \right]}}} = \ln \tilde{E}{\left[ {D_{T}} \right]} $$
(35)

where \({\tilde{E}{\left[ {D_{T}} \right]}}\) is the median value of the random variable \({\hat{E}{\left[ {D_{T}} \right]}.}\)

Using the reproductive property of the lognormal distribution it can be shown that:

$$ \tilde{E}{\left[ {D_{T}} \right]} = \frac{{T \tilde{B}^{m} \Omega}}{{\tilde{c}}} $$
(36)

where tildes (∼) represent median values of random variables. T is time period in seconds.

The variance in terms of the coefficient of variation (CV) may be given as:

$$ \sigma^{2}_{{\ln \hat{E}{\left[ {D_{T}} \right]}}} = \ln {\left[ {{\left({1 + CV^{2}_{{\hat{c}}}} \right)}{\left({1 + CV^{2}_{{\hat{B}}}} \right)}^{{b^{2}}}} \right]} $$
(37)

Similarly, the parameters of the distribution for the strength variable \({\hat{\Delta}}\) are:

$$ \mu_{{\ln \hat{\Delta}}} = \ln \tilde{\Delta} $$
(38)

and

$$ \sigma^{2}_{{\ln \hat{\Delta}}} = \ln {\left[ {{\left({1 + CV^{2}_{{^{{\hat{\Delta}}}}}} \right)}} \right]}. $$
(39)

Furthermore, the performance function \({\hat{G} = \hat{\Delta}/\hat{E}{\left[ {D{\left(t \right)}} \right]}}\) will also have a lognormal distribution with the following parameters:

$$ \mu_{{\ln \hat{G}}} = \mu_{{\ln \hat{\Delta}}} - \mu_{{\ln \hat{E}{\left[ {D_{T}} \right]}}} $$
(40)
$$ \sigma^{2}_{{\ln \hat{G}}} = \sigma^{2}_{{\ln \hat{\Delta}}} + \sigma^{2}_{{\ln \hat{E}{\left[ {D_{T}} \right]}}} $$
(41)

In terms of the coefficient of variation (CV) of random variables Eq. (41) takes the form:

$$ \sigma^{2}_{{\ln \hat{G}}} = \ln {\left[ {{\left({1 + CV^{2} (\hat{\Delta})} \right)}{\left({1 + CV^{2} (\hat{c})} \right)}{\left({1 + CV^{2} (\hat{B})} \right)}^{{b^{2}}}} \right]} $$
(42)

At any value of the lognormal distributed \({\hat{G} < 1,}\) the performance function would be in the failure state. So the failure probability is:

$$ P_{f} = \Phi {\left({\frac{{\ln 1 - \mu_{{\ln \hat{G}}}}}{{\sigma_{{\ln \hat{G}}}}}} \right)} = \Phi {\left({- \frac{{\mu_{{\ln \hat{G}}}}}{{\sigma_{{\ln \hat{G}}}}}} \right)} $$
(43)

or

$$ P_{f} = \Phi {\left({\frac{{\ln \tilde{E}{\left[ {D_{T}} \right]} - \mu_{{\ln \hat{\Delta}}}}}{{\sigma_{{\ln \hat{G}}}}}} \right)} $$
(44)

where Φ (.) is the standard normal distribution function, N(0,1).

Expression (43) can be presented in the reliability index format as:

$$ P_{f} = \Phi {\left({- \beta} \right)} $$
(45)

where the reliability index β can be prescribed as:

$$ \beta = \frac{{\mu_{{\ln \hat{G}}}}}{{\sigma_{{\ln \hat{G}}}}} $$
(46)

Our derived Eq. (44) is different from the expression recommended by various structural codes, which is (Souza and Goncalves 1997):

$$ P_{f} = \Phi {\left({\frac{{\ln D - \mu_{{\ln \hat{\Delta}}}}}{{\sigma_{{\ln \hat{\Delta}}}}}} \right)} $$
(47)

In the above expression, the admissible damage factor D is not considered as a random variable and uncertainty in the analysis is accounted for by the resistance \({(\hat{\Delta})}\) only.

To characterize the probabilistic nature of fatigue analysis and to utilize extensive data on the quantification of uncertainty of the stress part, Eq. (44) should be preferably used instead of Eq. (47).

2.3.2 Simulation methods

The ‘Direct’ Monte Carlo simulation approach is often used to estimate the probabilistic characteristics of the limit state function given by Eq. (6). In this technique, the independent variables are sampled at random. After feeding them in a performance function, sample points of G are obtained. Each point is checked to see whether it is inside or outside the failure domain. This is accomplished in the simulation by using the indicator function I(X):

$$ I{\left(X \right)} = \left\{\begin{aligned} 1, \quad G{\left(X \right)} \leqslant 0 \\ 0, \quad G{\left(X \right)} > 0 \\ \end{aligned} \right. $$
(48)

where G(X) is the performance function. The indicator function is evaluated at each sampled point. The failure probability is estimated as the average number of hits in the failure domain during the N trials, which can be presented as:

$$ P_{f} \approx \frac{1}{N}{\sum\limits_{i = 1}^N {I{\left({X_{i}} \right)}}} $$
(49)

Obviously the number of trials (N) required is directly related to the desired accuracy for P f .

Broding et al. (1964) suggested that a first estimate of the N simulations for a given confidence level C in the failure probability P f can be obtained from:

$$ N > \frac{{- \ln (1 - C)}}{{P_{f}}} $$
(50)

At a 95% confidence level with P f  = 10−3, the required number of simulations is more than 3,000. Error analysis using Shooman’s (1968) recommendation of calculating N shows that for N = 10,000 samples with expected P f =  10−3, the error in P f will be less than 20% at 95% confidence. Others have recommended the number of simulations in the range of 10,000–20,000 (Melchers 1987).

In Equation (6), the mean of the \({\hat{E}{\left[ {D_{T}} \right]}}\) distribution can be calculated from Eq. (34) or alternatively by Eq. (35), and the variance from Eq. (37). The mean and the variance for the variable \({\hat{\Delta}}\) can be estimated from Eqs. (38) and (39), respectively.

The estimated failure probability should approach the true value when N approaches infinity (Ayyub 2003). The variance of the estimated probability failure can be approximately measured using the variance expression for a binomial distribution as:

$$ {\rm Var}(P_{f}) \approx \frac{{{\left({1 - P_{f}} \right)}P_{f}}}{N} $$
(51)

The coefficient of variation (CV) would be:

$$ {\rm CV}(P_{f}) \approx \frac{1}{{P_{f}}}{\sqrt {\frac{{{\left({1 - P_{f}} \right)}P_{f}}}{N}}} $$
(52)

At the desired P f value of 0.01 and N = 1,000, the magnitude of CV from Eq. (52) would be 0.315. To maintain this level of uncertainty at P f  = 0.001 the N should be increased from 1,000 to 10,000. This discussion shows that direct simulation can be computationally prohibitive for small failure probabilities. To control the high uncertainty associated with a direct sampling approach, the following procedure is adopted. Considering the fact that \({\hat{\Delta}}\) is lognormal, the probability of failure can be given as:

$$ P_{f} = \Phi {\left({\frac{{\ln \hat{D} - \mu_{{\ln \hat{\Delta}}}}}{{\sigma_{{\ln \hat{\Delta}}}}}} \right)}. $$
(53)

The simulation algorithm becomes: (1) generate \({\hat{E}{\left[ {D_{T}} \right]},}\) (2) calculate P fi as given by Eq. (53) and return. Therefore the sample mean of the probability of failure is given by:

$$ \bar{P}_{f} = \frac{{{\sum\limits_{i = 1}^N {P_{{fi}}}}}}{N} $$
(54)

The uncertainty in terms of coefficient of variation (CV) associated with this estimation can be expressed as:

$$ CV_{{\bar{P}_{f}}} = \frac{{\sigma_{{\bar{P}_{{fi}}}}}}{{\bar{P}_{f}}} $$
(55)

where

$$ \sigma_{{\bar{P}_{f}}} = \frac{{{\left[ {\frac{1}{{N - 1}}{\sum\limits_{i = 1}^N {(P_{{fi}} - {\bar{P}}_{f})^{2}}}} \right]}^{{\frac{1}{2}}}}}{N} $$
(56)

The mean values of probability of failure \({(\bar{P}_{f})}\) do not change considerably when the simulation exceeds 5,000 cycles. Therefore, 5,000 simulation cycles are suggested to be used.

2.3.3 Closed form solution (based on time to fatigue failure)

The limit state function for crack initiation can also be formulated in terms of time to fatigue failure \({\hat{T}}\) as:

$$ \hat{G}{\left(X \right)} = \hat{T} - T_{s} $$
(57)

where the parameter T s is the intended service life of the structure. The fatigue life \({\hat{T}}\) may be approximated by setting the expected damage equal to its critical failure value \({\hat{\Delta}}\) in Eq. (12) (Lutes et al. 1984; Souza and Goncalves 1997).

$$ \hat{T} = \frac{{\hat{c}\hat{\Delta}}}{{\hat{B}^{b} \Omega}}*\frac{1}{{365\times24\times3600}} $$
(58)

where the conversion factor \({\frac{1}{{365\times24\times3600}}}\) converts the unit of \({\hat{T}}\) from seconds to years. By virtue of the lognormal behavior of variables in Eq. (58), \({\hat{T}}\) will also follow a lognormal distribution with the following parameters:

$$ \mu_{{\ln \hat{T}}} = (\mu_{{\ln \hat{c}}} + \mu_{{\ln \hat{\Delta}}} - b\mu_{{\ln \hat{B}}}) + \ln {\left({\frac{1}{\Omega}} \right)} - 17.267 $$
(59)

where \({-17.267 = \ln {\left({\frac{1}{{365\times24\times3600}}} \right)}}\) alternatively:

$$ \mu_{{\ln \hat{T}}} = \ln \tilde{T} $$
(60)

where \({ \tilde{T} = \frac{{\tilde{c} \tilde{\Delta}}}{{\tilde{B}^{b} \Omega}}*{\left({\frac{1}{{365\times24\times3600}}} \right)}}\)

Variance is given as:

$$ \sigma^{2}_{{\ln \hat{T}}} = \ln {\left[ {{\left({1 + {\rm CV}^{2} (\hat{\Delta})} \right)}{\left({1 + {\rm CV}^{2} (\hat{c})} \right)}{\left({1 + {\rm CV}^{2} (\hat{B})} \right)}^{{b^{2}}}} \right]} $$
(61)

Using the mathematical properties of lognormal distribution for \({\hat{T}}\) the expression of P f will be:

$$ P_{f} = \Phi {\left({\frac{{\ln T_{s} - \ln \tilde{T}}}{{\sigma_{{\ln \hat{T}}}}}} \right)} $$
(62)

Eq. (45) can be used to give the probability of failure in terms of a reliability index β; however, now β will take the form:

$$ \beta = \frac{{\ln {\left({\tilde{T}/T_{s}} \right)}}}{{\sigma_{{\ln \hat{T}}}}} $$
(63)

This lognormal format was first proposed by Wirsching (1984). Quantifying all the uncertainties in the fatigue expression as lognormal will give a closed form solution for P f . However, it can be argued that the lognormal behavior should not be advocated as a fatigue life model because the shape of the hazard function is difficult to rationalize (Bury 1999). The reason is that the lognormal hazard rate function rises from the origin to a peak and then it slowly decreases (i.e. it is an initially increasing failure rate and later a decreasing failure rate). A fatigue phenomenon corresponds to a wear-out region of the bathtub curve and should be characterized by increasing failure rate.

Sweet (1990) provides approximations for the location of the peak of the hazard rate function, T max, of the lognormal distribution. For large values of \({\sigma_{{\ln \hat{T}}}}\) (approximately of the magnitude of 3), the expression for T max is:

$$ T_{{\max}} \approx \exp {\left({\mu_{{\ln \hat{T}}} - \sigma^{2}_{{\ln \hat{T}}}} \right)} $$
(64)

For small values of \({\sigma_{{\ln \hat{T}}}}\) (approximately of the magnitude of 0.3), the expression for T max becomes:

$$ T_{{\max}} \approx \exp {\left({\mu_{{\ln \hat{T}}} + 1 - \sigma^{2}_{{\ln \hat{T}}}} \right)} $$
(65)

The parameter \({\sigma_{{\ln \hat{T}}}}\) from Eq. (61) and Table 1 can be calculated as 1.0295. Using this value and considering the large \({\sigma_{{\ln \hat{T}}}}\) approximation, Eq. (64) prescribes T max in terms of median time to failure \({(\tilde{T})}\) as:

$$ T_{{\max}} \approx 0.347 \tilde{T} $$
(66)

and for the small \({\sigma_{{\ln \hat{T}}}}\) approximation, Eq. (65) takes the form:

$$ T_{{\max}} \approx 0.942 \tilde{T} $$
(67)

The intended lifetime T s is based on the reliability index, β. For a riser, the typical value of β is 2 (Wirsching and Chen 1988). So the service life in terms of \({ \tilde{T}}\) from Eq. (63) can be given as:

$$ T_{s} \approx 0.128 \tilde{T} $$
(68)

T s is less than T max given by Eqs. (66) and (67). This shows that during the intended design life the hazard rate remains an increasing function conforming to the shape of the bathtub curve in the wear out region (under the quantification of uncertainties as presented in Table 1 and the selective reliability index of 2). To the best of our knowledge, the justification of using the lognormal format in fatigue reliability analysis has not been presented elsewhere.

3 Application of fatigue reliability modeling methodology

The methodology is applied to evaluate the fatigue reliability of a multi-bore riser for a floating production system in a northern North Sea environment. The configuration and the dimensions of the production riser system are given by Verbeek and Brouwers (1986). The long-term sea state data in terms of the significant wave height are obtained from Souza and Goncalves (1997) and reported in Table 2. The associated average time period is calculated using the Pierson–Moskowitz spectrum.

Table 2 Sea states used in analysis
Full size table

4 Results and discussion

Fatigue reliability analysis is carried out by employing the various methods already discussed in Sect. 2.3. The simulations are carried out using MATLAB 6.5. The approach is very time efficient, and running time for the above 9 sea-state was less then 5 s on a Pentium Pro III, 550-MHz processor. The results are reported in Table 3. Both closed form solutions give the same reliability index. Results obtained from the simulation method are of comparable magnitude with the results obtained from the closed form solutions. Although the relative error is approximately 55% at a service life of 2 years, the order of magnitude of the probability of failure is same. The minimum target reliability index (β) for the riser is defined as 2 by Wirsching and Chen (1988). This corresponds to a probability of failure of 0.02275. Thus, a service life of 9 years is recommended in the current example. The analysis is based only on Morison-type wave forces, for which the riser response is critical in the wave-active zone. Vortex induced vibrations (VIVs) due to current loading are critical in the riser main section. The fatigue damage associated with VIVs should also be calculated separately and then used in calculating the service life along with the wave force fatigue damage. However, the treatment of VIVs in calculating the service life is beyond the scope of the current work.

Table 3 Fatigue reliability results
Full size table

5 Concluding remarks

Different reliability methodologies are used in fatigue reliability analysis. To characterize the probabilistic nature of fatigue analysis, uncertainty is included in both the stress and resistance components. In the stress component, uncertainty arises due to the uncertainty associated with the scatter in S–N curve data and with a random variable that quantifies modeling error. Uncertainty in the strength part is due to the modeling error associated with Miner’s rule. These uncertainties are well documented in the literature and are considered as lognormally distributed.

Lognormal quantification of uncertainty results in the formulation of closed form solutions. The closed form solution based on a lognormal format is particularly useful in rapid calculations of ‘notional’ P f values.

The behavior of the hazard rate function of lognormal distribution is rationalized for predicting fatigue life. It has been shown that the hazard function remains increasing in the fatigue failure regime. It starts decreasing far away from the failure regime.

A simulation method is also used to study the problem. However, instead of using the direct Monte Carlo simulation, a simple algorithm is used to avoid the large uncertainty associated with both the small P f values and the small number of simulations.

Nonlinear behavior of a riser can be modeled effectively considering a narrow-band process. Approximate formulae, which have already been successfully tested in the time domain analyses, are very attractive in calculating the fatigue life of the riser. They become more effective when the modeling uncertainty is accounted for in the reliability-based design.