1 Introduction

In the colouring problem, we are asked to colour the vertices of a given graph with the smallest possible number of colours so that no two adjacent vertices receive the same colour. If such a colouring with k colours exists, the graph is k-colourable.

The colouring problem is one of the most studied problems on graphs. It is also one of the first problems known to be NP-hard [10]. In other words, it is unlikely that there is a polynomial time algorithm for solving this problem. This is true even in very special cases such as in planar graphs [9], line graphs [15], regular graphs [7] or if the number of colours k is fixed and at least three [9] (known as the k-colouring problem). On the other hand, for k≤2 the problem is polynomially solvable, as is the general problem for many structured classes of graphs such as interval graphs [11], chordal graphs [11], comparability graphs [11], and more generally for perfect graphs [12]. In these cases, the special structure of the classes in question allows for polynomial algorithms.

We study the colouring problem in the class of AT-free graphs, i.e., graphs with no asteroidal triple (a triple of vertices such that between any two vertices of the triple there is a path disjoint from the closed neighbourhood of the third vertex). This class is a generalization of interval and co-comparability graphs as well as some non-perfect graphs such as the complements of triangle-free graphs. Unlike other standard optimization problems such as independent set or clique whose complexity on AT-free graphs is known (the former is solvable in polynomial time, while the latter is NP-hard [3]), the complexity of colouring is not known on AT-free graphs.

As a first step towards resolving this, we propose in this paper a polynomial time algorithm for 3-colouring of AT-free graphs. We prove the following theorem.

Theorem 1.1

There is an O(n 2 m) time algorithm to decide, given an AT-free graph G with n vertices and m edges, whether or not G is 3-colourable and to also construct a 3-colouring of G if it exists.

We show this in three stages:

  1. (1)

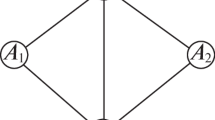
    we reduce the problem to AT-free graphs with no induced diamonds (Fig. 2a),

  2. (2)

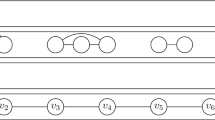
    we show how to decompose every AT-free graph with no induced diamond and no K 4 (Fig. 2b) into triangular strips (Fig. 1)

    Fig. 1
    figure 1

    The triangular strip of order k

    Full size image
    Fig. 2
    figure 2

    (a) Diamond, (b) K 4, (c) 5-cycle, (d) 5-wheel

    Full size image

    using stable cutsets, and

  3. (3)

    we prove that we are allowed to contract minimal stable separators without changing the answer to the problem.

This reduces the problem to graphs whose each block is a triangular strip or has at most two vertices; all such graphs are easily seen to be 3-colourable. If at any stage we encounter a K 4, a complete subgraph on four vertices, we declare the graph not 3-colourable. A sketch of an algorithm resulting from this is presented below as Algorithm 1. (Note that G/ S denotes the graph we obtain from G by contracting (identifying) the vertices of S into a single vertex.)

Algorithm 1
figure 3

Find a 3-colouring of an AT-free graph

Full size image

Note that, in this algorithm, once Line 5 is reached, the graph is guaranteed to be 3-colourable. This follows from the fact that AT-free graphs with no induced diamond and no K 4 are 3-colourable (we prove this as Theorem 1.3). Consequently, to obtain a decision algorithm, one can modify the procedure in Algorithm 1 to announce that “G is 3-colourable” once Line 5 is reached.

In light of this algorithm, we remark that there are also other non-perfect classes of graphs, such as the graphs with no induced path on five [20] or six [19] vertices, for which 3-colouring is known to be polynomially solvable even though colouring is NP-complete [16]. (In fact, in the former case, k-colouring for every fixed k is polynomially solvable [14].) In these cases, we are essentially able to reduce the problem to 2-satisfiability which is solvable in polynomial time [1]. Our approach for AT-free graphs differs from this in that it instead focuses on efficient decompositions of AT-free graphs to graphs for which 3-colouring can be decided in polynomial time. This is akin to and largely inspired by the celebrated decomposition of perfect graphs [4] even though this decomposition does not (as of yet) yield a polynomial time algorithm for colouring of perfect graphs; note that, however, a recent progress towards this goal has been made [23].

In the following sections, we examine the main ingredients to the proof of correctness of our algorithm which are summarized in the following two theorems.

Theorem 1.2

Let G be an AT-free graph with at least three vertices and with no induced diamond and no K 4. Then either

  1. (i)

    G is a triangular strip, or

  2. (ii)

    G contains a stable cutset.

Theorem 1.3

Every AT-free graph G with no induced diamond and no K 4 is 3-colourable. Moreover, if G contains a minimal stable separator S, then there exists a 3-colouring of G in which all vertices of S have the same colour.

Afterwards, in the subsequent two sections, we explain implementation details needed to guarantee the running time O(n 2 m). In particular, we prove some interesting properties of minimal stable separators of AT-free graphs.

In the final section, we discuss some generalizations and other cases of AT-free graphs with polynomial complexity of the colouring problem.

2 Notation

In this paper, a graph is always simple, undirected, and loopless.

For a vertex v of a graph G, we denote by N G (v) the set of vertices adjacent to v in G, and write N G [v]=N G (v)∪{v}. We drop the index G and write N(v) and N[v] whenever it is clear from the context. For X⊆V(G), we write G[X] for the subgraph of G induced by X, and write G−X for the subgraph of G induced by V(G)∖X. A set X⊆V(G) is stable, if G[X] contains no edges. As usual, K n denotes the complete graph (i.e., the graph with all possible edges) on n vertices, and diamond is the (unique) graph on 4 vertices with 5 edges (see Fig. 2).

We say that a path P of a graph G is missed by a vertex x if no vertex of P is adjacent to x. A triple of vertices x,y,z of a graph G is asteroidal if between any two vertices of the triple there exists a path missed by the third vertex.

We write G/ S for the graph we obtain from G by contracting (i.e., identifying) all vertices of S into a single vertex (while suppressing parallel edges and loops). That is,

A set S⊆V(G) disconnects vertices a,b in G if a and b are in different connected components of G−S. We say that S is a cutset of G if it disconnects some vertices a,b. We say that S is a minimal separator of G if there exist vertices a and b such that S disconnects a and b, but no proper subset of S disconnects them. A cutpoint of G is a vertex v such that {v} is a cutset. A block of G is a maximal connected induced subgraph of G having no cutpoints.

Note that a minimal separator is not necessarily an inclusion-wise minimal cutset. For example, consider the 4-cycle a,b,c,d with a pendant edge de. The set {b,d} is a minimal separator, since it disconnects a from c while no proper subset of {b,d} disconnects a from c. However, {b,d} is not an inclusion-wise minimal cutset since {d}⊆{b,d} is also a cutset.

Further note that we sometimes allow G to be disconnected; in that case, any set S⊆V(G) is a cutset of G unless S includes all but at most one connected component K of G and S∩V(K) is not a cutset of K. In particular, the empty set is a cutset of G and it is also a minimal separator of G. On the other hand, a non-empty set S⊆V(G) is a minimal separator of G if and only if it is a minimal separator of some connected component of G. Indeed, if S≠∅ disconnects some vertices a,b and no proper subset of S disconnect a,b, then there is a connected component K of G that contains both a and b. This implies that S∩V(K) is a minimal separator of K. In fact, S⊆V(K) by the minimality of S. The converse is immediate.

For a complete terminology, see [11, 24].

3 Removing Diamonds

In this section, we explain how to reduce the problem to the case of AT-free graphs with no induced diamonds. We show that if we have a diamond in G, i.e., we have adjacent vertices u,v such that their common neighbourhood contains two non-adjacent vertices, then we can contract any maximal set S of pair-wise non-adjacent common neighbours of u,v and the resulting graph remains AT-free. It is also 3-colourable if and only if G is, since in any 3-colouring of G all vertices of S must have the same colour. Thus we show the following.

Theorem 3.1

If u,v are adjacent vertices of an AT-free graph G and S is a maximal stable set in N(u)∩N(v), then G/ S is AT-free. Moreover, G is 3-colourable if and only if G/ S is.

To prove this, we use a more general tool that allows contracting specific sets in G without creating asteroidal triples. We say that a set S⊆V(G) is externally connected in G, if for each x∈V(G) with N[x]∩S=∅, the set S is contained in a (single) connected component of G−N[x].

Lemma 3.2

Let G be an AT-free graph and S⊆V(G) be an externally connected set in G. Then G/ S is AT-free.

Proof

Let s denote the vertex of G/ S to which we contracted the vertices of S, and suppose that G/ S contains an asteroidal triple {x,y,z}. Let P be a path in G/ S from y to z missed by x. If s is not on P, then P is also a path in G, and if x=s, then every vertex of S misses P in G. So, suppose that s belongs to P and is not one of the endpoints of P. Let u,v be the two neighbours of s on P. By the construction of G/ S , there exist vertices a,b∈S, such that ua,vb∈E(G). Since xs∉E(G/ S ), we have N G [x]∩S=∅, and since S is externally connected in G, we conclude that a and b, and hence, u and v are in the same connected component of G−N G [x]. Consequently, there is a path in G from y and z missed by x. Similarly, if s is one of the endpoints of P, say y=s, then we conclude that there exists a path in G missed by x between z and each vertex of S. This proves that if s is not one of x,y,z, then x,y,z is an asteroidal triple of G, and otherwise, if say x=s, then a,y,z is an asteroidal triple of G for every a∈S. But this is a contradiction, since G is AT-free. Thus the claim is proved. □

From this lemma, we immediately obtain a proof of Theorem 3.1 as well as two other corollaries that we shall make use of later.

Lemma 3.3

If G is AT-free and G[S] is connected, then G/ S is AT-free.

Proof

By Lemma 3.2, it suffices to show that S is externally connected. This is obvious, since S induces a connected subgraph in G−N[x] for N[x]∩S=∅. □

Lemma 3.4

If G is AT-free and S is a minimal separator, then G/ S is AT-free.

Proof

Again, it suffices to show that S is externally connected. Consider x∈V(G) with N[x]∩S=∅, and let K denote the connected component of G−S that contains x. Since S is a minimal separator, there is a connected component K′ of G−S different from K such that each vertex of S has a neighbour in K′. Therefore, G[V(K′)∪S] is connected, and so, S belongs to a connected component of G−N[x], since clearly N[x]∩(V(K′)∪S)=∅. This proves that S is externally connected. The claim now follows from Lemma 3.2. □

Proof of Theorem 3.1

For the first part of the claim, it again suffices to prove that S is externally connected. Consider x∈V(G) with N[x]∩S=∅. Therefore x is not adjacent to any vertex of S implying that S∪{x} is a stable set. By the maximality of S, x is non-adjacent to one of u,v. By symmetry, suppose that xu∉E(G). Then S∪{u} is in a connected component of G−N[x] since G[S∪{u}] is connected. So, we conclude that S is indeed externally connected.

For the second part of the claim, let s be the vertex of G/ S to which we contracted S. If we have a 3-colouring of G/ S , then we can extend this colouring of G by colouring all vertices of S with the colour of s. Conversely, if we have a 3-colouring of G, then u,v have different colours in this colouring, and hence, all vertices of S must have the same colour. So, we use this colour for s and colour all other vertices of G/ S as in G. This clearly yields a 3-colouring of G/ S . □

4 Structural Decomposition

In this section, we prove Theorem 1.2 asserting that every AT-free graph with no induced diamond and no K 4 decomposes into triangular strips via stable cutsets.

The triangular strip of order k is the graph formed by taking three disjoint paths \(P^{1}=v^{1}_{1},v^{1}_{2},\ldots,v^{1}_{k}\), \(P^{2}=v^{2}_{1},v^{2}_{2},\ldots,v^{2}_{k}\), \(P^{3}=v^{3}_{1},v^{3}_{2},\ldots,v^{3}_{k}\) and adding a triangle on \(v^{1}_{i},v^{2}_{i},v^{3}_{i}\) for each i=1,…,k. In other words, the triangular strip of order k is the Cartesian product of an induced path on k vertices and a triangle. (See Fig. 1 for an illustration.) We say that the triangles \(v^{1}_{1},v^{2}_{1},v^{3}_{1}\) and \(v^{1}_{k},v^{2}_{k},v^{3}_{k}\) of the triangular strip of order k are the end-triangles.

We say that G is a triangular strip if G is isomorphic to the triangular strip of order k for some k. Clearly, every triangular strip is AT-free and contains no induced diamond or K 4. Note also that triangular strips have no stable cutsets; in other words, the two conditions of Theorem 1.2 are mutually exclusive.

Let G be an AT-free graph with |V(G)|≥3, no induced diamond, and no K 4. First, we observe that it suffices to prove Theorem 1.2 for 2-connected graphs G, since any cutpoint (and also the empty set if G is disconnected) forms a stable cutset of G. Since G contains no diamond and no K 4, no two triangles of G share an edge. We show that, actually, no two triangles share a vertex provided G is 2-connected.

Lemma 4.1

Let G be a 2-connected AT-free graph with no induced diamond and no K 4. Then every vertex of G is in at most one triangle.

Proof

Let x be a vertex that belongs to two different triangles, namely, a triangle x,a,b and a triangle x,u,v. Clearly, {u,v}∩{a,b}=∅, since otherwise x,u,v,a,b induces a diamond or a K 4 in G. For the same reason, there is no edge between the vertices u,v and a,b.

Since G is 2-connected, G−x is connected, and hence, there is a path between the vertices u,v and a,b in G−x. Let P be a shortest such path. Without loss of generality, P is a path from u to a. Let y be the second vertex on P (after u). Clearly, yv∉E(G) and xy∉E(G), since otherwise y,v,u,x induces a diamond or a K 4. Also, y is non-adjacent to at least one of a,b, since otherwise y,a,b,x induces a diamond. In particular, yb∉E(G), since otherwise ya∉E(G) and u,y,b is a shorter path from u,v to a,b contradicting the minimality of P.

We now show that {y,v,b} is an asteroidal triple of G. Indeed, v,x,b is a path from v to b missed by y, and v,u,y is a path from v to y missed by b. Finally, P′=P∖{u}∪{b} is a path from y to b missed by v, since vy∉E(G) and v has no neighbour on P∖{u,y} by the minimality of P. □

By the above lemma, every vertex of G is in at most one triangle. If some vertex v is in no triangle, then N(v) is a stable cutset of G unless V(G)=N[v] in which case v is a cutpoint because G is assumed to have at least three vertices.

This implies that we may assume that every vertex of G is in exactly one triangle. In other words, G contains a triangular strip (of order 1). We show that by taking a maximal such strip, we either get the whole graph G or find a stable cutset in G, thus proving Theorem 1.2. To simplify the proof of this, we need the following lemma.

Lemma 4.2

Let G be an AT-free graph with no induced diamond and no K 4, and let H be a (not necessarily induced) subgraph of G isomorphic to a triangular strip. Then

  1. (i)

    H is induced in G, and

  2. (ii)

    no vertex of H has a neighbour in G−V(H) except for end-triangles of H.

Proof

Let \(v^{i}_{j}\) for i=1,2,3 and j=1,…,k for some k be the vertices of H. Suppose that H is not induced in G, and let \(v^{i}_{j} v^{i'}_{j'}\) be an edge of G not in H such that j<j′ and j′−j is smallest possible. By symmetry, we assume i′=1, and i∈{1,2}. Clearly, j≠j′.

First, we observe that \(v^{i}_{j}\) is non-adjacent to \(v^{2}_{j'}\) and \(v^{3}_{j'}\), otherwise \(v^{i}_{j},v^{1}_{j'},v^{2}_{j'},v^{3}_{j'}\) induces a diamond or K 4 in G. This also implies j′−j≥2. By the choice of j,j′ and the fact that j′−j≥2, we conclude that \(v^{i}_{j}\) is non-adjacent to \(v^{3}_{j+1},v^{3}_{j+2},\ldots,v^{3}_{j'}\), and \(v^{3}_{j+1}\) is non-adjacent to \(v^{1}_{j'}\). By the same token, \(v^{2}_{j'}\) is non-adjacent to \(v^{1}_{j+1}\) and \(v^{3}_{j+1}\). We show that \(\{v^{i}_{j}, v^{3}_{j+1}, v^{2}_{j'}\}\) is an asteroidal triple in G. Indeed, the path \(v^{i}_{j},v^{1}_{j'},v^{2}_{j'}\) is missed by \(v^{3}_{j+1}\), and the path \(v^{3}_{j+1},v^{3}_{j+2},\ldots,v^{3}_{j'},v^{2}_{j'}\) is missed by \(v^{i}_{j}\). Finally, \(v^{2}_{j'}\) is non-adjacent to at least one of \(v^{1}_{j},v^{3}_{j}\) otherwise \(v^{1}_{j},v^{2}_{j},v^{3}_{j},v^{2}_{j'}\) induces a diamond or K 4 in G. If \(v^{3}_{j} v^{2}_{j'}\notin E(G)\), then the path \(v^{i}_{j},v^{3}_{j},v^{3}_{j+1}\) is missed by \(v^{2}_{j'}\). Otherwise, \(v^{1}_{j}v^{2}_{j'}\notin E(G)\) in which case \(v^{i}_{j},v^{1}_{j},v^{1}_{j+1},v^{3}_{j+1}\) is a path (or walk) missed by \(v^{2}_{j'}\). This proves (i).

For (ii), let x∉V(H) be a vertex adjacent to \(v^{i}_{j}\) for some i∈{1,2,3} and some j∈{2,…,k−1}. By symmetry, we may assume i=1. Then, clearly, x is non-adjacent to both \(v^{2}_{j}\) and \(v^{3}_{j}\), since otherwise \(x,v^{1}_{j},v^{2}_{j},v^{3}_{j}\) induces a diamond or K 4 in G. First, suppose that x is also adjacent to \(v^{1}_{j+1}\). Then x is non-adjacent to both \(v^{2}_{j+1}\) and \(v^{3}_{j+1}\), since otherwise \(x,v^{1}_{j+1},v^{2}_{j+1},v^{3}_{j+1}\) induces a diamond or a K 4. But now \(\{x,v^{3}_{j},v^{2}_{j+1}\}\) is an asteroidal triple in G. Indeed, the path \(x,v^{1}_{j},v^{3}_{j}\) is missed by \(v^{2}_{j+1}\), the path \(v^{3}_{j},v^{3}_{j+1},v^{2}_{j+1}\) is missed by x, and the path \(v^{2}_{j+1},v^{1}_{j+1},x\) is missed by \(v^{3}_{j}\). So, we may assume \(xv^{1}_{j+1}\notin E(G)\), and by symmetry, also \(xv^{1}_{j-1}\notin E(G)\).

Suppose that x is non-adjacent to both \(v^{2}_{j+1}\) and \(v^{3}_{j-1}\). Then \(\{x,v^{2}_{j+1},v^{3}_{j-1}\}\) is an asteroidal triple in G. Indeed, the path \(x,v^{1}_{j},v^{2}_{j},v^{2}_{j+1}\) is missed by \(v^{3}_{j-1}\), the path \(v^{2}_{j+1},v^{2}_{j},v^{3}_{j},v^{3}_{j-1}\) is missed by x, and the path \(v^{3}_{j-1},v^{3}_{j},v^{1}_{j},x\) is missed by \(v^{2}_{j+1}\). So x has at least one neighbour among \(v^{2}_{j+1}, v^{3}_{j-1}\). By the same token, x has at least one neighbour among \(v^{3}_{j+1},v^{2}_{j-1}\). Clearly, x cannot be adjacent to both \(v^{2}_{j+1},v^{3}_{j+1}\) or to both \(v^{2}_{j-1},v^{3}_{j-1}\), since we get an induced diamond in G on \(x,v^{1}_{j+1},v^{2}_{j+1},v^{3}_{j+1}\), or on \(x,v^{1}_{j-1},v^{2}_{j-1},v^{3}_{j-1}\). So, by symmetry, we may assume that x is adjacent to \(v^{2}_{j-1}\) and \(v^{2}_{j+1}\) and non-adjacent to \(v^{3}_{j-1}\) and \(v^{3}_{j+1}\). But then \(\{x,v^{3}_{j-1},v^{3}_{j+1}\}\) is an asteroidal triple in G. Indeed, the path \(x,v^{2}_{j+1},v^{3}_{j+1}\) is missed by \(v^{3}_{j-1}\), the path \(v^{3}_{j+1},v^{3}_{j},v^{3}_{j-1}\) is missed by x, and the path \(v^{3}_{j-1},v^{2}_{j-1},x\) is missed by \(v^{3}_{j+1}\).

That concludes the proof of (ii). □

Now, we are finally ready to prove Theorem 1.2.

Proof of Theorem 1.2

As remarked in the discussion above, we may assume that G is 2-connected, and contains a triangle (triangular strip).

Let H be the largest triangular strip induced in G. If V(H)=V(G), then G is a triangular strip, and we are done. Otherwise, there exists a vertex v∈V(G)∖V(H) adjacent to a vertex of H. By Lemma 4.2, v is adjacent to a vertex c of an end-triangle of H; let a,b be the other two vertices of this triangle. Clearly, va,vb∉E(G) since otherwise v,a,b,c induces a diamond or K 4 in G.

First, we note that N(b)∖{a} and N(a)∖{b} are stable sets, since otherwise a or b is in two triangles which is not possible by Lemma 4.1. Therefore, also N(a)∩N(v) and N(b)∩N(v) are stable sets of G, since a,b∉N(v). Moreover, we prove that there are no edges between the two sets. Suppose otherwise, and let u∈N(a)∩N(v) and w∈N(b)∩N(v) be adjacent. We observe that if u∈V(H), then u belongs to a triangle in H and the triangle u,v,w. But these triangles are different since v∉V(H), contradicting Lemma 4.1. Hence, u∉V(H), and by the same token, w∉V(H). Thus G[V(H)∪{u,v,w}] contains a spanning triangular strip which is, by Lemma 4.2, induced in G. This, however, contradicts the maximality of H.

Now, suppose that there are no edges between N(b)∖{a} and N(a)∩N(v). In other words, S=(N(b)∖{a})∪(N(a)∩N(v)) is a stable set. We show that S is a stable cutset of G separating a from v. Suppose otherwise, and let P be a shortest path in G−S from a to v. Let z be the second vertex on P (after a). Since N(a)∩N(v)⊆S, we conclude zv∉E(G). Also, zc∉E(G), since otherwise a,b,c,z induces a diamond or K 4 in G. By the same token, zb∉E(G). This implies that {b,v,z} is an asteroidal triple in G. Indeed, the path v,c,b is missed by z, the path z,a,b is missed by v, and P∖{a} is a path from z to v missed by b, since all neighbours of b except for a are in S.

By the same token, if there are no edges between N(a)∖{b} and N(b)∩N(v), we conclude that G contains a stable cutset. So, we may now assume that there exists x∈N(a)∩N(v) adjacent to some y∈N(b)∖{a}, and x′∈N(b)∩N(v) adjacent to some y′∈N(a)∖{b}. We show that this is impossible. Clearly, y,y′∉N(v), since there are no edges between N(a)∩N(v) and N(b)∩N(v). Also, y is non-adjacent to a,c,x′, since otherwise b is in two triangles which is impossible by Lemma 4.1. By the same token, y′ is non-adjacent to b,c,x while x is non-adjacent to b,c and x′ is non-adjacent to a,c. In particular, this shows that x,x′,y,y′ are distinct vertices different from a,b,c,v. We now show that G contains an asteroidal triple.

Suppose that yy′∉E(G). Then {y,y′,v} is an asteroidal triple of G. Indeed, the path y,x,v is missed by y′, the path y′,x′,v is missed by y, and the path y,b,a,y′ is missed by v. Hence, we may assume yy′∈E(G) in which case {x,c,x′} is an asteroidal triple of G. Indeed, the path x,a,c is missed by x′, the path c,b,x′ is missed by x, and the path x,y,y′,x′ is missed by c.

That concludes the proof. □

5 Proof of Theorem 1.3

The proof is by induction on |V(G)|. Let G be an AT-free graph with no induced diamond and no K 4. If G has at most 2 vertices, the claim is trivially satisfied.

Therefore, we may assume |V(G)|≥3. If G has a stable cutset, then by (possibly) removing some of its vertices, we can find a minimal stable separator in G. So, if G has no minimal stable separator, then it must be, by Theorem 1.2, a triangular strip with vertices \(v^{i}_{j}\) for i=1,2,3 and j=1,…,k for some k. We obtain a 3-colouring of G by assigning each \(v^{i}_{j}\) the colour ((i+j) mod 3)+1.

So, we may assume that G contains a minimal stable separator S. If S is empty, then G is disconnected and we obtain a 3-colouring of G by independently colouring its connected components by induction. If S has one element, then G has a cutpoint and we obtain a 3-colouring of G by 3-colouring its blocks by induction, and permuting the colours in blocks so that they match on cutpoints. In both cases, all vertices in S have the same colour. So, we may assume |S|≥2.

To prove the claim, it now suffices to show that for every connected component K of G−S, there exists a 3-colouring of G[V(K)∪S] in which all vertices of S have the same colour.

Let K be a (fixed) connected component of G−S. Let S′ denote the set of vertices of S with at least one neighbour in K. If S′≠S, then S′ is a minimal stable separator in G′=G−(S∖S′). By induction, there exists a 3-colouring of G′ in which all vertices of S′ have the same colour. By restricting this colouring to V(K)∪S and colouring the vertices of S∖S′ with the common colour of the vertices of S′, we obtain the required 3-colouring. (Note that the vertices of S∖S′ are isolated in G[V(K)∪S].)

Hence, we may assume that every vertex of S has a neighbour in K. Further, since S is a minimal separator, there exists a connected component K′ of G−S different from K such that each vertex of S also has a neighbour in K′. Let G′ denote the graph G[V(K)∪V(K′)∪S]/ V(K′), and let x denote the vertex of G′ to which we contracted V(K′). By Lemma 3.3, G′ is AT-free. Moreover, G′ contains no induced diamond or K 4, since any such subgraph is either in G, or contains x, but x belongs to no triangle of G′. Also, S is a minimal separator in G′. Hence, if G′ has fewer vertices than G, then, by induction, there exists a 3-colouring of G′ in which all vertices of S have the same colour. This colouring when restricted to V(K)∪S yields the required 3-colouring.

It follows that we may assume that G−S has exactly two connected components, one of which is K, the other consists of a single vertex x, and every vertex of S is adjacent to x and has a neighbour in K.

Now, let S ∗ be a smallest subset of S such that \(\bigcup_{u\in S^{*}}N(u)=\bigcup_{u\in S}N(u)\). Suppose that S ∗ contains three distinct vertices u,v,w. By the minimality of S ∗, there exist vertices u′,v′,w′ such that u′∈N(u)∖(N(v)∪N(w)), v′∈N(v)∖(N(u)∪N(w)) and w′∈N(w)∖(N(u)∪N(v)). Clearly, u′,v′,w′∈V(K) since S is a stable set and u,v,w are adjacent to x. Suppose that u′v′∉E(G). Then {u′,v′,x} is an asteroidal triple in G. Indeed, the path u′,u,x is missed by v′, the path v′,v,x is missed by u′, and x misses any path in K between u′ and v′. Hence, we must conclude u′v′∈E(G), and by the same token, u′w′,v′w′∈E(G). However, then {u,v,w} is an asteroidal triple in G. Indeed, the path u,u′,v′,v is missed by w, the path u,u′,w′,w is missed by v, and the path v,v′,w′,w is missed by u. Hence, we conclude |S ∗|≤2.

If S ∗≠S, we consider the graph G′=G−(S∖S ∗). Clearly, S ∗ is a minimal separator in G′, and hence, there exists, by induction, a 3-colouring of G′ in which all vertices of S ∗ have the same colour. We extend this colouring to G by assigning the vertices of S∖S ∗ the common colour of the vertices of S ∗. By the definition of S ∗, this gives the required 3-colouring.

Hence, we may assume that S consists of exactly two vertices u and v. We let A=N(u)∖N(v), B=(N(u)∩N(v))∖{x}, and C=N(v)∖N(u). By the minimality of S ∗, we have A≠∅ and C≠∅. Moreover, each vertex a∈A is adjacent to every vertex c∈C, since otherwise {a,c,x} is an asteroidal triple of G. Indeed, the path a,u,x is missed by c, the path c,v,x is missed by a, and any path between a and c in K is missed by x. Further, A is a stable set in G, since any adjacent a,a′∈A yield an induced diamond u,a,a′,c for any c∈C. By the same token, C is a stable set. Finally, B is a stable set, since any adjacent b,b′∈B yield an induced diamond b,b′,u,v in G.

Suppose that there is b∈B adjacent to some a∈A, and let c∈C. We show that N(b)∖{u}⊆N(c). Suppose otherwise and let w∈N(b)∖{u} be such that wc∉E(G). Clearly, bc∉E(G) since otherwise u,a,b,c induces a diamond in G. Also, wu,wa∉E(G) since otherwise w,a,b,u induces a diamond or K 4 in G. Finally, wx∉E(G), since w is not one of u,v and x is only adjacent to u,v. It follows that {w,x,c} is an asteroidal triple in G. Indeed, the path w,b,a,c is missed by x, the path c,a,u,x is missed by w, and the path x,u,b,w is missed by c. This proves that N(b)∖{u}⊆N(c).

Now, by induction, there exists a 3-colouring of G−b in which u and v have the same colour. We extend this colouring to G by assigning b the colour of c. Clearly, b and u have different colours in this colouring, since otherwise c,u,v have the same colour, impossible since cv is an edge in G−b. Also, b has colour different from its other neighbours, since N(b)∖{u}⊆N(c). So, this gives the required 3-colouring.

It follows that we may assume that there are no edges between A and B. In other words, A∪B is a stable set. It is also a minimal separator of G[V(K)∪{u,v}] that disconnects u from v, since u,a,c,v and u,b,v are paths from u to v for each a∈A, b∈B, and c∈C. So, by induction, there is a 3-colouring of G[V(K)∪{u,v}] in which all vertices of A∪B have the same colour. If B≠∅, then recolouring u with the colour of v yields the required 3-colouring. Thus, we may assume B=∅.

Now, suppose that there is a∈A with N(a)⊆C∪{u}. If |A|≥2, then {u,v} is a minimal separator in G−a, and hence, there exists, by induction, a 3-colouring of G−a in which u,v have the same colour. Recall that N(a′)⊇C∪{u} for all a′∈A. So, by assigning a the colour of any vertex in A∖{a}, we obtain the required 3-colouring. Hence, we may assume A={a}, and we observe that C is a minimal separator of G−u that disconnects a from v. By induction, there is a 3-colouring of G−u in which all vertices of C have the same colour. To obtain the required 3-colouring, we colour u with the colour of v and recolour a with the colour different from the colour of u and the common colour of the vertices of C.

Hence, we may assume that there exists w∈N(a)∖(C∪{u}) for some a∈A, and by symmetry, we also have z∈N(c)∖(A∪{v}) for some c∈C. We show that in this case G contains an asteroidal triple. Clearly, w and z are both different from and non-adjacent to all of u,v,x. If wc∈E(G) or wz∈E(G), then {w,u,v} is an asteroidal triple. Indeed, the path w,a,u is missed by v, the path w,c,v or w,z,c,v is missed by u, and the path u,x,v is missed by w. So, wc,wz∉E(G), and by symmetry, za∉E(G). But now {z,w,x} is an asteroidal triple. Indeed, the path w,a,c,z is missed by x, the path w,a,u,x is missed by z, and the path z,c,v,x is missed by w.

That concludes the proof.

6 Minimal Separators

In this section, we focus on some properties of minimal stable separators of AT-free graphs. These properties will be used in the next section to construct an efficient implementation of Algorithm 1 as promised by Theorem 1.1.

As remarked in Sect. 4, if the neighbourhood of some vertex x is a stable set, then either N(x) is a stable cutset of G, or x is a cutpoint of G, or |V(G)|≤2. It turns out that a partial converse of this is also true as shown in the following lemma.

Lemma 6.1

If S is a minimal stable separator of an AT-free graph G, then there exists a vertex x∈V(G) with N(x)⊇S.

Proof

Let S be a counterexample to the claim and let S ∗ be a smallest subset of S for which there is no vertex x with N(x)⊇S ∗. Clearly, |S ∗|≥2.

First, suppose that |S ∗|=2. Hence, S ∗={x,y} for some vertices x,y. Since S is a minimal separator, there are connected components K,K′ of G−S such that each vertex of S has a neighbour in both K and K′. In particular, we have u∈N(x)∩V(K) and v∈N(x)∩V(K′). Clearly, uy,vy∉E(G) by the minimality of S ∗. This implies that {u,v,y} is an asteroidal triple of G. Indeed, the path u,x,v is missed by y. Also, since S is a minimal separator, we have a path P in G[V(K)∪{y}] from y to u, and a path P′ in G[V(K′)∪{y}] from y to v. Clearly, P is missed by v and P′ is missed by u.

Therefore, we may assume |S ∗|≥3, and we let x,y,z be any three vertices of S ∗. By the minimality of S ∗, there exist vertices a,b,c such that N(a)⊇S ∗∖{x}, N(b)⊇S ∗∖{y}, and N(c)⊇S ∗∖{z}, and also ax,by,cz∉E(G). But this implies that {x,y,z} is an asteroidal triple of G. Indeed, the path x,c,y is missed by z, the path y,a,z is missed by x, and the path z,b,x is missed by y.

That concludes the proof. □

We further need the following two observations.

Lemma 6.2

If S is a stable cutset of a connected graph G, and S′⊇S is a stable set, then S′ is also a stable cutset of G.

Proof

Since S is a cutset of G, let K,K′ be two different connected components of G−S. Recall that G is connected; thus there exist vertices a∈V(K), b∈V(K′) with neighbours in S. This implies that a,b∉S′, since S′ is a stable set containing S. Now, if G−S′ is connected, there exists a path P in G−S′ between a and b, and clearly, P is also a path in G−S, since S⊆S′. But this is impossible, since a,b are in different connected components of G−S. Hence, we must conclude that S′ is a cutset of G. □

Lemma 6.3

A set S⊆V(G) is a minimal separator of a graph G with |S|≥2 if and only if there exists a block B of G such that S is a minimal separator of B.

Proof

Let S be a minimal separator of G with |S|≥2. This implies that there exist connected components K,K′ of G−S such that each vertex in S has both a neighbour in K and in K′. Thus, for each distinct x,y∈S, there exist two internally vertex disjoint paths P,P′ between x and y, namely the shortest path between x and y in G[V(K)∪{x,y}]−xy and in G[V(K′)∪{x,y}]−xy, respectively. In particular, G[P∪P′] is a 2-connected subgraph of G, and hence, it belongs to a block of G. Consequently, this block contains both x and y as well as a vertex of K and a vertex of K′.

Since |S|≥2, this proves that there exists a block B of G with S⊆V(B) and such that V(B)∩V(K)≠∅, and V(B)∩V(K′)≠∅. Consider a∈V(B)∩V(K) and b∈V(B)∩V(K′). Firstly, note that S disconnects a,b in B, since if there is a path in B−S between a and b, then this is also a path in G−S between a,b which is impossible since a∈V(K), b∈V(K′) and K,K′ are connected components of G−S.

Secondly, suppose that a proper subset S′ of S disconnects a,b in B. Consider x∈S∖S′, and recall that x has both a neighbour in K and a neighbour in K′. Thus, there exists a path P between a and x in G[V(K)∪{x}] and a path P′ between x and b in G[V(K′)∪{x}]. We claim that both P and P′ completely lie in B. This follows easily from the observation that if two vertices belong to B, then any path between them also belongs to B. Thus, P∪P′ is a path between a and b in B−S′, contradicting the assumption that S′ disconnects a from b in B. So, S is indeed a minimal separator of B.

Conversely, suppose that S is a minimal separator of a block B of G. That is, there are vertices a,b in B such that S disconnects a,b in B and no proper subset of S disconnects a,b in B. Clearly, S disconnects a,b in G, since every path between a,b in G−S is also a path in B−S. For this recall that if the endpoints of a path belong to B, then the whole path belongs to B. Further, if a proper subset S′ of S disconnects a,b in G, then S′ does not disconnect a,b in B because of the minimality of S. Consequently, there is a path in B−S′ between a and b which is also a path in G−S′, contradicting the assumption that S′ disconnects a,b in G. So, S is indeed a minimal separator of G.

Finally, observe that |S|≥1, since B is connected. Moreover, if S={v} for some vertex v, then v is a cutpoint of B, since {v} separates a from b in B. But this is impossible, since, by definition, no vertex of B is a cutpoint of B. Thus, |S|≥2.

That concludes the proof. □

7 The Algorithm

Finally, we are ready to prove Theorem 1.1. To do this, we show that Algorithm 1 is correct and can be implemented to run in time O(n 2 m) on a given an AT-free graph G with n vertices and m edges. The correctness follows easily from Theorems 1.2, 1.3, 3.1 and Lemma 3.4. We therefore focus on the details of O(n 2 m) implementation.

First, we note that the complexity is easily seen to be polynomial, since all the tests in Algorithm 1 are polynomial, including the test in Line 5 which follows from [2]. Also, the algorithm makes at most n recursive calls, since each call reduces the graph by at least one vertex. Further, contracting a set before a recursive call and extending the colouring to G from the contracted graph is easily implementable in time O(n+m). Thus to get the running time O(n 2 m), it suffices to explain how to implement each test of the algorithm in time O(nm).

The test in Line 3 has a direct implementation of complexity O(nm); we try each edge uv of G and construct N(u)∩N(v) by exploring the neighbourhoods of u and v in time O(n).

For Line 7, if G is a triangular strip, we 3-colour G in time O(m) by iteratively removing triangles on vertices of degree 3. If G is not a triangular strip, but the blocks of G are triangular strips or have at most two vertices, we construct the block-cutpoint decomposition of G in time O(n+m) by the standard algorithm of [21]. Then we 3-colour all blocks in time O(n+m) by applying the previous argument to each block. Finally, using the block-cutpoint tree of G, we obtain in time O(n) a 3-colouring of G by combining the 3-colourings of the blocks by (possibly) permuting the colours so they match on the cutpoints of G. This yields an O(n+m) implementation of Line 7.

For the test in Line 1, we do the following. If we execute Line 1 for the first time, we test if G contains a K 4 in time O(m 2)=O(n 2 m) by trying all possible pairs of disjoint edges of G. If we reach Line 1 by recursion to G/ S , and s is the vertex of G/ S to which we contracted S, then we only test if the neighbourhood of s in G/ S contains a triangle. This requires only O(nm) time by trying each vertex-edge pair of G, and it is enough to verify that G/ S contains no K 4, since before contracting S, the graph G was assumed to contain no K 4 (we reached at least Line 3 before the recursive call).

It remains to show how to implement the test in Line 5 in time O(nm). By Lemma 6.3, it suffices to check every block B of G for a minimal stable separator. By Lemma 6.1, if such a separator S of B exists, it is also a stable cutset of B, and hence, there is a vertex x with N B (x)⊇S. Also, |V(B)|≥3, since S disconnects at least two vertices in B, and |S|≥2 by Lemma 6.3. Thus, B is 2-connected, and also contains no diamond and no K 4, since G does (we reached Line 5) and since B is an induced subgraph of G. Consequently, N B (x) contains, by Lemma 4.1, at most two maximal stable sets one of which contains S. But then this set is also a stable cutset of B by Lemma 6.2.

Thus, we proceed as follows. First, we compute the block-cutpoint decomposition of G in time O(n+m), again by the algorithm of [21]. Then we try each vertex x∈V(G) and each block B of G that contains x and has at least three vertices. For each such choice, we test if N B (x) or N B (x)∖{u} or N B (x)∖{v} is a stable cutset of B where uv (if exists) is the unique edge in G[N B (x)]. This can be accomplished in time O(|V(B)|+|E(B)|) by the standard graph search. Since |V(B)|≥3 and B is a block of G, we have |V(B)|≤|E(B)|, and hence, summing over all choices of B yields the complexity O(m). Thus, over all choices of x, the complexity is O(nm).

If a stable cutset S of some block B is found, we reduce it to a minimal stable separator of B by iteratively removing vertices of S and testing if the resulting set is a still a cutset of B. Again, O(nm) time, since it suffices to test each vertex of S once. By Lemma 6.3, the resulting set S is a minimal separator of G and satisfies |S|≥2.

8 Concluding Remarks

In this paper, we have shown how to find in polynomial time a 3-colouring of a given AT-free graph if one exists. To this end, we used a nice structural decomposition of AT-free graphs without diamonds. Note that similar structural results are also known for other restrictions of AT-free graphs [6, 13].

For the more general case, we have recently learned that Haiko Müller et al. announced that for every fixed k, the k-colouring problem on AT-free graphs is also solvable in polynomial time [18]. Their result is yet to be published. This leaves open only the case of the colouring problem on AT-free graphs where the number of colours is unbounded.

We remark that there are special cases of AT-free graphs in which we can solve colouring in polynomial time, for instance, in interval, co-comparability, and more generally in perfect AT-free graphs [12]. This is also true for some non-perfect AT-free graphs. For instance, if G is the complement of a triangle-free graph, then any colour class in a colouring of G has at most two vertices. Therefore, to find an optimal colouring of G we need to pack as many stable sets of size two into G as possible. This is solvable in polynomial time [8, 17], since it is precisely the problem of maximum matching on the complement of G.

What about AT-free graphs that are not complements of triangle-free graphs? It turns out that every connected AT-free graph decomposes into complements of triangle-free graphs by means of star cutsets, i.e., cutsets having a vertex adjacent to all other vertices of the cutset. This can be seen as follows: if a connected AT-free graph contains a stable set of size three, then the closed neighbourhood of at least one of the three vertices disconnects the other two, that is, the closed neighbourhood of one of the three vertices is a star cutset.

Theorem 8.1

If G is a connected AT-free graph, at least one of the following is true:

  1. (i)

    G is the complement of a triangle-free graph.

  2. (ii)

    G contains a star cutset.

Note the similarity with Theorem 1.2. This tells us that to find a polynomial time algorithm for colouring AT-free graphs, it suffices to find a way to combine colourings of AT-free graphs through star cutsets. Recall that this is possible in perfect graphs [5].

Finally, we remark that there exists a similar decomposition of another subclass of AT-free graphs, namely for AT-free graphs with no induced 4-cycles. The following theorem is from [6]. A thick 5-cycle is any graph we obtain by substituting complete graphs (of arbitrary sizes) for the vertices of a 5-cycle (Fig. 2c), and a thick 5-wheel is obtained by substituting complete graphs for the vertices of a 5-wheel (Fig. 2d).

Theorem 8.2

[6]

If G is a connected AT-free graph with no induced 4-cycle, then at least one of the following is true:

  1. (i)

    G is an interval graph.

  2. (ii)

    G is a thick 5-cycle or a thick 5-wheel.

  3. (iii)

    G contains a clique cutset.

Observe that the complement of every thick 5-cycle (thick 5-wheel) is triangle-free. Also, recall that we can optimally colour interval graphs in polynomial time [11] and it is possible to find all clique cutsets also in polynomial time by the algorithm of Tarjan [22]. Further, to get a colouring of a graph with a clique cutset, it suffices to colour the pieces individually and then permute the colours on the pieces so that they match on the cutset. Thus it follows that the colouring problem is solvable in polynomial time on AT-free graphs with no induced 4-cycles.