Introduction

The morphology of fungal mycelia exhibits a remarkable capacity to adapt to different environmental conditions [1]. Because of their considerable spatial extension, and due to their ability to translocate nutrients inside the hyphal network [2–4], the behavior of fungal mycelia is not determined only by local interactions of hyphae with their microscopic environment. In addition, nutrient and information transport processes, respectively, which easily reach the scale of centimeters or meters have to be considered for a comprehensive description of fungal growth. Due to these large differences in relevant scales, environmental and biological factors that determine mycelial development are often difficult to access experimentally, which hinders the quantification of their impact on fungal development.

Due to these difficulties, the mathematical analysis of mycelial growth gains growing attention, since this enables computation of environmental state variables that are otherwise inaccessible. Available mathematical models reach from rather simple reaction–diffusion models [5–7] to sophisticated approaches that considered a substantial number of biological phenomena typically present in mycelial development [8–13]. The best-developed mathematical models took hyphal growth characteristics [13], different types of nutrient translocation within the mycelia [11], acidification of the growth substrate by the fungal development [12], as well as biomass recycling for cellular growth [10] into account. In an original approach presented by Meskauskas et al. [14, 15], growth of fungal hyphae was simulated up to the formation of fruiting bodies applying a vector-based algorithm.

Simulations showed that complex morphologies could be produced from rather simple model structures [5–7], underlining the emergent behavior of mycelial growth. However, comparison of results from different mathematical models indicated that highly similar morphologies could be generated on the basis of rather distinct model assumptions, which was most likely due to the more or less freely chosen parameter sets (compare e.g. [6, 7, 10]). Furthermore, most of the above discussed models did not provide actual spatial or temporal dimensions (with a notable exception in [12]), which made it impossible to compare simulated with experimental results beyond a mere visual inspection. Hence, these modeling approaches provide a conceptual mathematical framework, rather than allowing to assess the significance of model assumptions in a particular experimental system.

Therefore, we came to the conclusion that, in addition to conceptual models, a quantitative modeling strategy is needed to effectively support experimental investigations [16, 17]. Only on the basis of experimentally verifiable results, discrepancies between simulations and experiments can yield the rejection of a model assumption, or guide experimental efforts toward the estimation of the most crucial biological parameters in a particular model system. In addition to choosing a quantitative modeling approach, we aimed at a strong simplification of the mycelial development under consideration by applying the dimorphic yeasts Candida boidinii and Yarrowia lipolytica as model organisms (for explanation see Introduction and Discussion in Part 1 of this study [18]).

We implemented a mathematical model that aimed at correct balancing of nutrient consumption, as well as biomass growth and decay processes that occurred inside the yeast mycelia. It was shown that the growth of C. boidinii colonies on glucose was adequately described by a diffusion-limited growth (DLG) model. Furthermore, it was demonstrated that the decay of individual cells and the free diffusion of cell decay products in the agar do not support sustained colony extension, but result in the formation of islets of proliferating cells that are distributed across the whole colony. The comparison of experiments and simulations for the growth of Y. lipolytica suggested that characteristic features of hyphal development, i.e. apical growth and intrahyphal translocation of cytoplasm or parts thereof, have to be considered for an adequate biological and mathematical description of mycelial growth of this yeast.

Model definition

To abstract the mycelial growth process comprehensively, a hybrid cellular automaton model describing discrete cells and continuous concentrations of nutrient sources [16, 17, 19] was developed. The model was applied to simulate the spatio-temporal evolution of the cell density profile in a growing yeast colony. In particular, the simulations were meant to reproduce the growth characteristics of yeast mycelia under glucose limitation, which were described in the experimental part of this study [18]. Since the growth of the colonies was symmetrical and rectangular in the chosen experimental setup (see Part 1, Fig. 1; [18]), calculations only accounted for one moiety of the colony, i.e. for the region between inoculation site and the outer edge of the growth field, and were restricted to one dimension. The simulations quantitatively predicted a spatio-temporal distribution of discrete cells (or hyphal segments) that could be easily compared to experimental results.

Fig. 1
figure 1

Schematic illustration of model dynamics. Variables: n C,p number of proliferating cells, n C,s number of stationary cells (n C,s′ intermediate number of stationary cells in time step Δt), c N nutrient concentration (c N′ intermediate nutrient concentration in time step Δt), t time, t p discrete time scale for proliferation. Parameters: Δt p time step for growth dynamics, Δt time step for diffusion of chemicals, T C time constant for cell decay. Indices: i position of the lattice node. Asterisk indicates the start site of the algorithm. Double asterisk indicates implementation of distal budding for σ = 1 (Eq. 4). See text for further details. (Roman index numbers serve to facilitate referencing between text and figure)

Full size image

For the mathematical description of yeast colony development, strong simplifications of the actual microbial growth process were necessary. As described in the experimental part of this study [18], yeast colony development was biphasic. Immediately after the inoculation, cells grew in the round yeast-like morphology. After 2–4 days of cultivation, differentiation into filamentous cells was observed. These elongated cells generated a (pseudo) mycelial structure that was covered by a considerable number of round cells. However, because of their phenotypic characteristics (elongated cell morphology, unipolar budding, polarized growth), the filamentous cells clearly determined the behavior of spreading yeast colonies. Therefore, the presence of different cell types was neglected in the mathematical description of the growth process. The development of yeast colonies was described based on the proliferation of unit cells that had the dimensions of pseudohyphal cells or hyphal segments (see below).

Growth dynamics

Proliferating cells (n C,p) and stationary cells (n C,s) resided on the same one-dimensional lattice L(0,…i,…n), with L(0) being the inoculation site and L(n) representing the edge of the growth field. The state s(i, t) of each lattice node was defined by the number of proliferating and stationary cells, and the concentration of nutrient (c N), respectively.

$$ s (i ,t )= (n_{\text{C,p}} (i ,t ) ,n_{\text{C,s}} (i ,t ) ,c_{\text{N}} (i ,t ) ) , $$
(1)

with

$$ n_{\text{C,p}} (i ,t )\in {\text{\{0,1,2,}} \ldots {\text{\} ,}} $$
(2)

and

$$ c_{\text{N}} (i ,t ) ,n_{\text{C,s}} (i ,t )\in ( 0 ,\infty ). $$
(3)

Initially, inoculated or newborn cells were in the proliferating state having the ability to give birth to a daughter cell. In the automaton model, cell divisions were assumed to occur at discrete intervals (Δt p) (Eq. 19) representing the replication time of a cell. Furthermore, it was assumed that newborn cells were preferentially formed at the pole opposite to the mother cell’s birth end [17], leading to a directed growth away from the inoculation site. Distal budding was implemented by placing the fraction n C,p*

$$ n_{\text {C,p}}{^{*}} (i,t_{p} ) = \sigma \cdot n_{\text {C,p}} (i,t_{\text {p}} ) $$
(4)
$$ \sigma = {\text{rand}}(0.7 \ldots 1) $$
(5)

of newborn cells originating from node (i) to the adjacent position (i + 1). (The lower limit for σ was arbitrarily chosen. Model predictions were insensitive to large variations in interval size).

$$ n_{{{\text{C}},{\text{p}}}} (i + 1,t_{\text{p}} + \, \Updelta t_{\text{p}} ) \, = \, n_{{{\text{C}},{\text{p}}}} (i + 1,t_{\text{p}} ) \, + \, n_{{{\text{C}},{\text{p}}}}{^{*}} (i,t_{\text{p}} ). $$
(6)

The remaining cells were distributed randomly to nodes (i) and (i−1). It was assumed that proliferating cells ceased growth and entered the stationary state when the local nutrient concentration dropped to zero (Eq. 7). The transition of a cell from the proliferating to the stationary state was defined to be irreversible:

$$ s_{\text{C}} (i ,t )= \left\{ {\begin{array}{*{20}c} {\text{proliferating}} & {{\text{if}}\quad c_{\text{N}} (i ,t )> 0} \\ {\text{ stationary}} & {\text{else}} \\ \end{array} } \right.. $$
(7)

To account for the apparent cell decay observed in Y. lipolytica colonies (see Part 1, Fig. 3c; [18]), stationary cells (n C,s) were defined to decay exponentially with time constant T C(i), yielding equation

$$ {\frac{{\partial n_{\text{C,s}} (i ,t )}}{\partial t}} = - {\frac{{n_{\text{C,s}} (i ,t )}}{{T_{\text{C}} (i )}}}. $$
(8)

The chosen relation does not explain the regulation of this apparent decay process, which might, e.g. be controlled by the availability of extracellular nutrient. It, however, accounts for the consequences of the decay process by describing the decrease of local cell (biomass) density, thereby providing the basis for the replenishment of the nutrient pool by the cellular decay products (see Eq. 14). The implementation of a decay constant that depended on the position within the colonies accounted for different decay rates observed at different distances from the inoculation site [18]. In the simulations, not more than two different values for the decay constant were used (see below).

Nutrient balance

In the model, proliferating cells took up nutrient with rate (r N,prol) and transformed it into a new unit cell of dry mass m C. r N,prol was calculated from the cell’s dry mass (m C) that was generated within the replication interval Δt p (Eq. 19). The yield (Y) described the efficiency with which a particular nutrient was transformed into dry biomass,

$$ r_{\text{N,prol}} = {\frac{{m_{\text{C}} }}{{\Updelta t_{\text{p}} \cdot Y}}}. $$
(9)

In addition, proliferating and stationary cells consumed nutrient with rate r N,main

$$ r_{\text{N,main}} = m_{\text{C}} \cdot R $$
(10)

to maintain viability, wherein R represented the mass-specific maintenance requirement [20]. Nutrient was balanced by solving the reaction–diffusion equation

$$ {\frac{{\partial c_{\text{N}} (i ,t )}}{\partial t}} = D \cdot {\frac{{\partial^{ 2} c_{\text{N}} (i ,t )}}{{\partial x^{ 2} }}} - r_{\text{N, con}} (i ,t )+ r_{\text{N,rep}} (i ,t) $$
(11)

wherein

$$ r_{\text{N,con}} (i ,t )= { \min }\left[ {r_{\text{N,con}}^{\prime } (i ,t ) ,c_{\text{N}} (i ,t )\cdot \Updelta t_{\text{p}}^{ - 1} } \right] $$
(12)

was the total nutrient consumption rate (r N,con) at lattice node (i).

$$ r_{\text{N,con}}^{\prime } (i ,t )= \left[ {r_{\text{N,prol}} \cdot n_{\text{C,p}} (i ,t )+ r_{\text{N,main}} \cdot (n_{\text{C,p}} (i ,t )+ n_{\text{C,s}} (i ,t ) )} \right] \cdot V_{i}^{ - 1} , $$
(13)

was the maximum uptake rate as derived from Eqs. 10 and 12, and c N (i, t) Δt −1p represented the uptake rate as limited by the locally available nutrient. V i denoted the volume that was assigned to each lattice node. The secondary nutrient resource released upon cell decay was lumped with glucose into a single nutrient pool denoted by c N. Thus, the rate of nutrient replenishment (r N,rep) due to cell decay at lattice node (i) was described by

$$ r_{\text{N,rep}} (i ,t )= T_{\text{C}}^{ - 1} \cdot n_{\text{C,s}} (i ,t )\cdot m_{\text{C}} \cdot V_{i}^{ - 1} . $$
(14)

To account for the limited nutrient reservoir in the agar substrate, boundary conditions were chosen according to

$$ \left[ {{\frac{{\partial c_{\text{N}} (i ,t )}}{\partial x}}} \right]_{i = 0 ,i = n} = 0. $$
(15)

Summary of model dynamics

In the automaton model, cell divisions were defined to occur at discrete intervals (Δt p) representing the time span between birth and maturity of a cell. Consequently, proliferation was modeled on the discrete time scale (t p). In contrast, state transition of cells, diffusion of chemicals, nutrient uptake, as well as cell decay were assumed to occur on the continuous time scale (t). Model dynamics were summarized in Fig. 1. All computed data presented in the manuscript represent the average of five individual simulations.

Parameterization of the models

Experimental setup and simulation dynamics

The automaton model described growth of unit cells, which corresponded to filamentous cells of length l C. The distance between two lattice nodes was chosen according to the unit cell size. From the length of the growth field moiety (l = 26 mm) and the cell length, the lattice size (n) was determined.

$$ n = \left[ {{\frac{l}{{l_{\text{C}} }}}} \right]. $$
(16)

For correct balancing of nutrient in the growth substrate, the agar height (h = 0.9 mm), calculated from the amount of agar filled into the Petri dish (2 mL), and the tile width (w = 1 cm) were incorporated into the model by giving each lattice node a volume (V i ),

$$ V_{i} = h \cdot w \cdot l_{\text{C}} . $$
(17)

From the diffusion constant in agar (D) and the distance between two lattice nodes (l C), the time step (Δt) for the discretization of the continuous time scale (t) was calculated according to

$$ \Updelta t = {\frac{{ 0. 5\cdot l_{\text{C}}^{2} }}{D}}. $$
(18)

The replication time (Δt p) was estimated from the extension rate (v) of the colony diameter and the unit cell length (l C).

$$ \Updelta t_{\text{p}} = {\frac{{ 2\cdot l_{\text{C}} }}{v}} $$
(19)

Accordingly, the cell array was updated in intervals of Δt p (Fig. 1). Values estimated for Δt p and v during growth of the yeasts on glucose are listed in Table 1. The diffusion constant of glucose in water [21] was corrected for the diffusion in agar as described in [22].

Table 1 Biochemical and kinetic parameters used in the simulations of colony development for Y. lipolytica and C. boidinii
Full size table

Growth and decay of the cells

According to Tijhuis et al. [20], the mass-specific nutrient uptake rate to meet maintenance requirements (R) mainly depends on the cultivation temperature and only to a small extent on the particular nutrient resources. The value of R = 0.01 g g−1 h−1 [20] was used in the simulations. The dry mass of a single cell (m C) was estimated using equations

$$ m_{\text{C}} = \, V_{\text{C}} \, \cdot \, \rho_{\text{C}} \cdot {\text{DW}} $$
(20)

and

$$ V_{\text{C}} = \, \pi / 4\cdot d_{\text{C}}^{2} \cdot l_{\text{C}} , $$
(21)

where V C was the experimentally determined volume of a pseudohyphal cell, d C the cell diameter, ρ C the density of the wet biomass (4), and DW represented the dry weight fraction of the total cell mass. The parameter DW was not determined experimentally, but assigned to fit simulated results to data derived from the growth experiments. The biomass yields of C. boidinii and Y. lipolytica on glucose were estimated in shake flask experiments [23]. Time constants for cell decay (T C) were estimated from glucose-limited cultivations of Y. lipolytica [18].

Results and discussion

The mathematical model for the development of yeast mycelia (Eqs. 1–15, Fig. 1) was scaled to the experimental setup, and to the growth dynamics of each model yeast when cultivated in rectangular growth fields on minimal medium containing a starting concentration of 2 g L−1 glucose (Table 1) (for experimental details see Part 1 of this study [18]). Hence, the model facilitated quantitative computation of mycelial development based on different biological processes that were considered.

Simulation of C. boidinii colony development

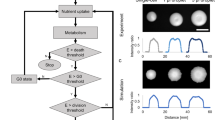
Experimental characterization of the glucose-limited colony development of C. boidinii showed that (pseudo)mycelia ceased to extend when glucose concentration was depleted from the agar substrate (Part 1 of this study [18]). Furthermore, neither cell decay nor biomass recycling was detected. Thus, the model described above was adapted to the growth of C. boidinii by only considering the processes: (I) cell proliferation, (II) diffusion, (III) consumption of nutrient, and (IV) the transition of individual cells from an initially proliferating state to a stationary state in the absence of nutrients (indexes correspond to Fig. 1). Parameters listed in Table 1 were used in the simulations. Both computed and experimentally obtained cell density profiles of C. boidinii populations exhibited a declining shape, formation of new cells was restricted to the outer colony margin, and cell densities in the colony interior remained stable (Fig. 2). This behavior is characteristic for single cell populations, in which proliferation of individuals is exclusively controlled by the availability of extracellular nutrient. Here, nutrient limitation arises from the diffusive transport of glucose. The model (I–IV, see Fig. 1) is thus referred to as the diffusion-limited growth (DLG) model [16]. It correctly predicted the shape (Fig. 3a) and extension (Fig. 3b) of the final cell density profile in C. boidinii colonies. Furthermore, it reproduced the temporal evolution of the total cell number in the colony (Fig. 3c), as well as the total nutrient concentration in the growth field (Fig. 3d) (see [17] for a detailed discussion of sensitivity of predictions to changes in model parameters). In contrast to the experiments, the simulation yielded a pronounced cell density peak close to the inoculation site (Figs. 2, 3a). This behavior was an artifact resulting from the definition of the model: to save computation time, the algorithm simulated the development of only one colony moiety. Thus, in contrast to the inner lattice nodes L(1, 2,…, (n−1)), the position L(0) at x = 0 mm had only one neighbor from where it received newborn cells. The introduction of this asymmetry caused a drop in cell density at the left boundary, but did not affect the overall behavior of the simulations, which was evident from the good agreement between the experimentally determined and the simulated evolution of the total cell number (Fig. 3c). Thus, the described phenomenon was neglected when comparing simulations and experimental data. From the above discussed results, it became evident that the DLG model was not only able to predict final colony morphology and extension, as shown earlier in [17], but also enabled the quantitative computation of the spatio-temporal development with respect to several measurable quantities that were used to experimentally characterize the growth process (Part 1 of this study [18]). Combining experimental findings and simulations, the diffusion-limited growth of autonomous pseudohyphal cells could be identified as the ruling construction principle in glucose-limited C. boidinii colonies.

Fig. 2
figure 2

Comparison of simulated colony development of C. boidinii with experimental results. Evolution of a simulated and b measured cell density profiles at different cultivation times. The model accounted for (I) cell proliferation, (II) diffusion and (III) consumption of nutrient, and (IV) the transition of individual cells from an initially proliferating state to a stationary state in the absence of nutrients (compare indexes to Fig. 1)

Full size image
Fig. 3
figure 3

Comparison of experimentally determined growth characteristics and simulations of the development of C. boidinii colonies. a Cell density profile after 35 days of cultivation. b Colony extension versus time. c Total cell number versus time. d Glucose content of the growth field versus time. The model accounted for (I) cell proliferation, (II) diffusion and (III) consumption of nutrient, and (IV) the transition of individual cells from an initially proliferating state to a stationary state in the absence of nutrients (compare indexes to Fig. 1)

Full size image

Simulation of Y. lipolytica colony development

The results obtained in the experimental part of this study [18] showed that continuous extension of glucose-limited Y. lipolytica populations coincided with an apparent cell decay in the colony interior. It was established that colonies continued to extend in the absence of extracellular glucose utilizing mycelial decay products as a secondary nutrient resource [18]. However, the precise mechanism of the apparent cell decay and biomass recycling are still under question. Although we considered this option very unlikely, the decrease of local biomass concentration may have been caused by the emission of cytoplasm (or parts thereof) into the growth substrate, resulting in the free extracellular diffusion of the decay products. Alternatively, the apparent cell decay may have resulted from the translocation of cytoplasm (or parts thereof) inside the mycelium. Therefore, we developed a mathematical model (Eqs. 1–15, Fig. 1) that was meant to test in silico whether or not the actual decay of cells (or hyphal compartments), and the thereof resulting emission and diffusion of secondary nutrient in the agar substrate, could explain the observed growth characteristics. In this context, it is worth noting that the mathematical description for the growth of filaments that are either built up of true pseudohyphal cells or of hyphal segments is identical. In both cases, the automaton model as defined above, produces either type of such filaments by lining up cells of discrete length. Simulations were adapted to the colony development of Y. lipolytica by extending the basal model (I–IV, see Fig. 1) used to simulate the development of C. boidinii by additionally incorporating (V) cell decay, (VI) nutrient replenishment and (VII) free diffusion of the secondary nutrient, i.e. cell decay products, through the agar substrate. The parameters used in the simulations are listed in Table 1. Two different time constants for cell decay (T C) were applied to account for the significantly different decay rate at the inoculation site when compared to other parts of the mycelium (Table 1). This difference most likely resulted from the presence of round yeast-like cells at the inoculation site, whereas filamentous cells were predominant in the other parts of the colonies (see Part 1 of this study [18]). Accounting for this observation, it was assumed that cells within a radius of 1.5 mm around the inoculation site decayed with time constant T C1 = 615 h, whereas cells outside this radius decayed with T C2 = 342 h, a value representing the average of time constants at distances of 2–6 mm from the colony center (Part 1 of this study [18]).

In Fig. 4, the simulated development of glucose-limited Y. lipolytica colonies was compared to experimental results. Predicted and measured cell density profiles after 1 week of cultivation were in excellent agreement (Fig. 4a). However, neither the colony density profile after 35 days (Fig. 4b) nor the sustained colony extension at longer cultivation times was reproduced by the model (Fig. 4c). The predicted abortion of colony extension was found to be independent of variations in model parameters such as the time constant for cell decay (T C) or the diffusion constant for the nutrient (D) (data not shown). Therefore, the significant discrepancy between simulations and experimental results indicated the presence of additional regulatory mechanisms, or a wrong set of model assumptions, respectively. In any case, colony development of Y. lipolytica on glucose was not adequately explained by the hypothesis that the release and free diffusion of cell decay products in the agar could facilitate sustained colony extension in the absence of glucose.

Fig. 4
figure 4

Comparison of experimentally determined growth characteristics and simulations of the development of Y. lipolytica colonies. Cell density profiles after a 7 days and b 35 days. c Colony extension versus time (black solid line represents regression line for experimental values of colony extension). d Total cell number versus time. The model accounted for (I) cell proliferation, (II) diffusion and (III) consumption of nutrient, (IV) the transition of individual cells from an initially proliferating state to a stationary state in the absence of nutrients, (V) cell decay, (VI) nutrient replenishment, and (VII) free diffusion of cell decay products through the agar substrate (compare indexes to Fig. 1)

Full size image

At first glance, the mathematically predicted abortion of colony extension appeared surprising, since simulations showed that cells continued to decay even after the colony ceased growth (Fig. 4c, d). This behavior must have resulted in a permanent nutrient replenishment of the agar, thus providing the basis for sustained growth (Eqs. 8, 11). However, the reason for this behavior became obvious when the predicted distribution of proliferating cells was analyzed. Long after the colony stopped to extend, proliferating cells were still present everywhere across the colony (Fig. 5a). Secondary nutrient released upon continuous cell decay was utilized by these proliferating cells before it could diffuse outwards to fuel growth in the colony margin. Thereby, cells in the colony boundary became starved and aborted proliferation. The result of this behavior was a final colony extension, which was not larger than the one predicted for the absence of nutrient replenishment (compare to [23]). A general conclusion that can be drawn from these results is that programmed cell death (and the resulting emission of cell decay products), which is often observed in single cellular yeast populations [24], cannot facilitate spatial extension of those colonies, but may rather ensure the maintenance of a proliferating subpopulation of cells inside those colonies.

Fig. 5
figure 5

Comparison of the effect of different growth-controlling mechanisms on simulated cell density profiles and nutrient distributions in Y. lipolytica colonies. a, b Exclusively nutrient-controlled proliferation. c, d Proliferation restricted to the colony margin and controlled by nutrient availability. a, c Distribution of stationary and proliferating cells. b, d Distribution of cells and nutrient. The basal model was the same as for Fig. 4. Values correspond to 35 days of cultivation

Full size image

It was then asked whether the simulations only failed to predict sustained colony extension because the growth-controlling mechanism was not correctly described (Eq. 7, Fig. 1IV), or whether inadequate nutrient or biomass balancing caused the discrepancies between computed and experimental results. Therefore, the simulation routine was changed such that all cells were assigned to the stationary state not only when they were lacking nutrients, but also when they were further than 1 mm behind the colony margin (results of the simulations were not sensitive to changes in the width of this margin; data not shown.) Comparison of computed colony development and experimental results are summarized in Figs. 5 and 6. Since cell growth was restricted to the colony boundary (Fig. 5c), decay products released in the colony interior fed proliferating cells in the outer margin and ensured stable extension of the colony. In contrast to the exclusively nutrient-controlled mechanism, the formation of a nutrient gradient over the colony was predicted (Fig. 5d) indicating the radially outward diffusion of nutrient from the colony center. By restricting growth to the colony boundary, the model quantitatively reproduced the characteristic behavior of glucose-limited Y. lipolytica colonies, which comprised rapid accumulation of cells at the inoculation site (Fig. 6a), the formation of large areas with constant cell density in the course of the cultivation (Fig. 6b), sustained colony extension (Fig. 6c) and biomass accumulation that peaked after 10 days of colony development (Fig. 6d). Please note that the good fit of experimental results to simulated data for a DW of 0.27 also supported the plausibility of biomass estimations by the OD measurements [23].

Fig. 6
figure 6

Comparison of experimentally determined growth characteristics and simulations of the development of Y. lipolytica colonies. The model was the same as in Fig. 4 except that proliferation was restricted to a 1 mm wide zone at the colony boundary. Cell density profiles after a 7 days and b 35 days. c Colony extension versus time. d Total cell number versus time

Full size image

The good agreement between model predictions and experimental results showed that the biochemical aspects of the glucose-limited growth of Y. lipolytica colonies (i.e. nutrient and biomass balance, diffusion and growth dynamics) were adequately described by the model. Assigning all cells outside the colony boundary to the stationary state may be regarded as a (very!) preliminary implementation of hyphal growth characteristics into the simulation routine, since in hyphal mycelia formation of new hyphal segments is largely restricted to the apical tip. Although the presented model does not explain which biological mechanism could facilitate the restriction of cell proliferation to the colony boundary, it does demonstrate the need for this constraint to reproduce the development of Y. lipolytica colonies and quantitatively predicts the consequences of such a mechanism.

Microscopic images of Y. lipoytica colonies showed that the filamentous structures formed by this yeast had a hyphal morphology that enabled intracellular translocation of cytoplasm (Part 1 of this study, [18]). Furthermore, calculations clearly showed that nutrient replenishment originating from an emission of cell decay products into the agar could not reproduce the mycelial growth of this yeast. Taken together, these data suggest that the experimentally determined decrease of biomass density in the colony interior (see Part 1 of this study [18]) was not due to an actual decay of the cells, but rather the consequence of the translocation of cytoplasm toward the apical tips of the hyphae where it served as a secondary nutrient resource. Accordingly, the formation of vacuoles in large portions of the mycelium (Part 1 of this study, Fig. 6; [18]) was the mechanistic consequence of the utilization of mycelial biomass to fuel colony extension. In this context, it is interesting to note that models for the submersed cultivation of fungi, although they do phenomenologically describe the formation of vacuolated hyphae, commonly do not take into account the utilization of cytoplasm for hyphal extension (e.g. [25, 26]).

Summary

In summary, quantitative simulations of the mycelial development of the two model yeasts Y. lipolytica and C. boidinii were compared to experimental results. It could be shown that the growth of C. boidinii colonies on glucose was adequately described by a DLG model. Furthermore, it was demonstrated that the decay of individual cells and the free diffusion of cell decay products in the agar do not support sustained colony extension, but result in the formation of islets of proliferating cells that are distributed across the whole colony. The comparison of experiments and simulations for the growth of Y. lipolytica suggested that characteristic features of hyphal development, i.e. apical growth and intrahyphal translocation of cytoplasm or parts thereof (elsewhere referred to as mobile biomass [10]), have to be considered for an adequate biological and mathematical description of mycelial growth of this yeast. It was demonstrated that the presented modeling approach, as well as the employment of dimorphic yeasts as model organisms, supported research on the development of fungal mycelia, since they allowed for effective hypothesis testing on the basis of quantitative model predictions, as well as a gradual increase in system complexity, respectively. We also feel that our modeling philosophy will complement conceptual mathematical approaches [10, 13] by providing a quantitative framework for the description of mycelial growth processes.