Plankton motility patterns and encounter rates

Abstract

Many planktonic organisms have motility patterns with correlation run lengths (distances traversed before direction changes) of the same order as their reaction distances regarding prey, mates and predators (distances at which these organisms are remotely detected). At these scales, the relative measure of run length to reaction distance determines whether the underlying encounter is ballistic or diffusive. Since ballistic interactions are intrinsically more efficient than diffusive, we predict that organisms will display motility with long correlation run lengths compared to their reaction distances to their prey, but short compared to the reaction distances of their predators. We show motility data for planktonic organisms ranging from bacteria to copepods that support this prediction. We also present simple ballistic and diffusive motility models for estimating encounter rates, which lead to radically different predictions, and we present a simple criterion to determine which model is the more appropriate in a given case.

Introduction

Why do plankters move? One important purpose of motility in planktonic (and other) organisms is to enhance the rate at which food and mates are encountered (e.g. Charnov 1976; Okubo 1986). Encounter rate depends both on the speed at which they move and on their motility pattern (e.g. Gerritsen 1980). For example, a plankter that moves along a very convoluted path may sample the same volume of water repeatedly, which of course reduces the rate at which (new) food is encountered, but this problem is reduced the less convoluted the track of motion is (e.g. Levandowsky et al. 1988; Viswanathan et al. 1999). At the same time, however, motility may also increase the rate at which an organism encounters its predators (e.g. Lima and Dill 1990). There is, thus, an apparent trade-off here between enhancing prey and mate encounter rates while at the same time reducing predator encounter rates. Because of the fundamental significance of these three undertakings (prey and mate encounters, avoiding predators) one can expect strong selection pressure on motility patterns and realized motility patterns optimize the fitness of the individual in terms of this trade-off. Here we describe some fundamental properties of organism motility patterns—ballistic vs. diffusive—and recommend a meaningful way to analyse motility patterns in the encounter context that allows prediction of optimal motility patterns.

Swimming paths: ballistic vs. diffusive

Planktonic organisms exhibit a wide variety of swimming patterns from relatively erratic behaviours such as run—tumble and hop—sink, to more continuous swimming along nearly straight, helical, or sinuous paths. Examples of plankton motility patterns described in the literature include those of bacteria (Berg and Brown 1977; Mitchell et al. 1995; Kiørboe et al. 2002), protists (Buskey and Stoecker 1988; Kamykowski et al. 1992; Buskey et al. 1993; Fenchel and Blackburn 1999; Bartumeus et al. 2003; Kiørboe et al. 2004), copepod nauplii (Buskey et al. 1993; Titelman and Kiørboe 2003), and copepods (Schmitt and Seuront 2001; Doall et al. 2002). Irrespective of the details of these swimming patterns, all such paths have a common characteristic in that at very small scales, the path tends to remain constant in direction whereas at larger scales, a degree of randomness appears. A direct analogy can be drawn here with the seminal work of Taylor (1921); the continuous random motions of particles suspended in a turbulent flow follow paths that are characterized by short-term coherency but long-term stochasticity. For motile organisms this means that if we take l as the straight-line displacement of an animal (Table 1 provides a glossary of symbols in this work), then for small time scales, the path is linear and

$$l \approx \nu t,$$

(1)

where v is the mean speed of swimming. That is, the straight-line displacement increases linearly with time, a characteristic known as ballistic (Fig. 1). On the other hand, at longer time scales as the path becomes more convoluted, the straight-line displacement (net distance travelled) increases at a slower rate as more time is spent backtracking over areas already covered. At these large scales, we can write

$$l \propto t^{1/\delta },$$

(2)

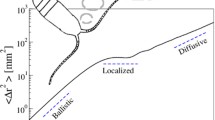
where δ is a coefficient greater than 1. When the kinematics of the path trajectory conform to a random walk (i.e. the probability of changing direction at a given time is independent of what has happened before), then δ=2, and the large-scale dependence of l is diffusive, l∝t ^1/2. These relationships can equally well be expressed in terms of the gross distance travelled, L. For ballistic motion, the net and gross distances travelled are identical, i.e. l=L, whereas for diffusive motion l∝L ^1/2. A log–log plot of l vs. L or t would reveal two distinct regions; one where the slope is 1, and another where the slope becomes 1/2. The temporal scale at which this transition happens is the ‘correlation time scale’ (τ), and the corresponding spatial scale is the ‘correlation length scale’ (λ=ντ). These scales are of more than academic interest since, as we shall see later, they have implications for the rates at which motile organisms encounter their prey as well as their predators.

Table 1 Glossary of symbols and their description

Fig. 1

The transition from ballistic to diffusive motion as a function of the net distance traveled (l) and either gross distance (L) or time (t). In terms of L, the transition occurs at the correlation length scale λ, or equivalently, in terms of time, at the correlation time scale τ. The transition is characterized by a change in slope from 1 (ballistic) to a slope less than 1. For diffusion proper, the slope is 1/2, although super-diffusion characterized by a slope between 1/2 and 1 is also possible

The transition from ballistic to diffusive dispersion was examined more formally by Taylor (1921) for a continuous random walk and leads to time-dependent net displacement of the form

$$l^2 = 2\nu ^2 \tau (t - \tau (1 - {\text{e}}^{ - t/\tau })).$$

(3)

This relationship has the asymptotic properties that

$$l \approx \nu t\quad {\text{for}}\; t \ll \tau, $$

(4)

$$l \approx (2 n D t)^{1/2}\quad {\text{for}}\;t \gg \tau, $$

(5)

where D is the diffusivity in n dimensions, D=ν ²τ/n, and τ is the correlation time scale as above. That is, τ is the time scale of persistence in the direction of the continuous random walk path. Equation 3 is quite general. It is valid for both run-tumble and continuous random walks. For those more familiar with run-tumble motility such as is often exhibited by bacteria and ciliates, the correlation time scale can be calculated as

$$\tau = \sigma / (1- \phi),$$

(6)

where ϕ = the mean cosine of the angle between runs, and σ is the mean time interval between tumbles (Berg 1992). Further, it can be noted that Eq. 3 can be rewritten in terms of the gross travel distance L as

$$l^2 = 2\lambda (L - \lambda (1 - {\text{e}}^{ - L/\lambda })).$$

(7)

Motility examples for different planktonic organisms

Displacement-vs.-time relationships for a wide variety of organisms conform reasonably well to Taylor’s model, Eq. 3. Here we present a number of examples ranging from bacteria to copepods (Fig. 2, Table 2). We used nonlinear regression (sigma plot) to fit this function to the two-dimensional projections of three-dimensional swimming paths from video recordings. Swimming patterns for bacteria and protists were recorded in microscopic preparations or small chambers under either phase contrast or dark-field illumination as described by Kiørboe et al. (2002). Copepod nauplii were filmed while swimming in 1-L aquaria illuminated from the back by collimated infrared light. Finally, adult copepods were filmed while swimming in the middle of a 1-m diameter (75 L) planktonkreisel (Hamner 1990) that was illuminated by white fluorescent light from the side. Swimming paths were digitized using LabTrack software (Bioras, Kvistgård) as described by Kiørboe et al. (2002). Data for bacteria are from Kiørboe et al. (2002), for the flagellates Bodo designis and Spumella sp. from Kiørboe et al. (2004), and for the dinoflagellate Heterocapsa triquetra and the ciliate Balanion comatum from Jakobsen et al. (2005), while the rest of the observations (copepod nauplii of Acartia tonsa and Centropages typicus, and adult copepods Temora longicornis and Calanus hegolandicus) were made for the purpose of this work. About 100 tracks were analysed for each species. Despite pronounced differences between swimming patterns of different species (see examples in Fig. 2), Taylor’s continuous random walk model provided a reasonable fit in all cases (lower panels in Fig. 2), and motility parameters and their standard errors as derived from the mean net displacement fits, could be estimated (Table 2). Note that the speeds listed here are effective ballistic speeds and are not necessarily the same as the animals’ swimming speeds. This is particularly evident for helical swimmers such as Spumella, Balanion and Centropages nauplii. In these cases, the speed is that of the propagation of the helix and can be considerably lower than that of the animal through the water.

Fig. 2

Examples of swimming paths and analyses for a–b bacteria strain 46 (Kiørboe et al. 2002), c–d the flagellate Bodo designis (Kiørboe et al. 2004), e–f the ciliate Balanion comatum (Jakobsen et al. 2005), g–h copepod nauplii of Centropages typicus, and i–j adult copepods Temora longicornis. Only a few representative swimming paths are plotted, although the analysis was conducted on many times this number. A summary of analyses is given in Table 2

Table 2 Motility parameters: v velocity, τ correlation time scale, λ correlation length scale, and D diffusivity, derived from regression analyses of swimming paths of various organisms of size d (equivalent spherical diameter)

Two encounter rate models

When trying to interpret the roles of the relative motion and sensing ability of plankton in determining their encounter rates, one is confronted by a choice of two groups of encounter rate models, both of which are based on sound physical reasoning, but which can give considerably different results both qualitatively and quantitatively. These models can be termed the ballistic and diffusive models, respectively. It is no accident that we use the same terms here as were used in the description of motility patterns.

The ballistic model assumes that organisms swim in straight lines, directed randomly in space. A precise formulation was provided by Gerritsen and Strickler (1977) for randomly swimming predators with a spherical perception volume encountering their randomly swimming prey. Within this framework, turbulent motion (Rothschild and Osborn 1988) and Gaussian velocity distribution (Evans 1989) were later included, producing the model of choice for nearly all predator–prey interactions in the mesozooplankton for the past 15 years (e.g. Saiz and Kiørboe 1995).

Running parallel to this evolution, however, has been the development of models based on the observation that many organisms (e.g. bacteria, ciliates) execute a random walk (Berg 1992), and their interactions thus can be modelled as a diffusive process. These models are often seen in conjunction with micro-organisms interacting with particulate matter (e.g. Jackson 1989; Kiørboe et al. 2002). The model formulation follows directly from Fick’s diffusion law, and the encounter rate can be equated with the flux of organisms entering the predator’s perception volume.

To illustrate these different models, we can consider a simple interaction of particles moving in random directions with speed v encountering a stationary spherical capture zone of radius R. This can be viewed as an idealization of several real-world interactions such as an ambush copepod capturing and feeding on motile protists (e.g. Jonsson and Tiselius 1990; Svensen and Kiørboe 2000; Jakobsen et al. 2005), or bacteria colonizing a cell or a detrital aggregate (e.g. Kiørboe et al. 2004). For the ballistic model, the encounter kernel (essentially the maximum clearance rate) is given by

$$\beta_{\rm ball} = \pi R^{2} \nu.$$

(8)

The models of Gerritsen and Strickler (1977), Rothschild and Osborn (1988) and Evans (1989) all converge at this result when both the predator speed, and turbulent velocity are set to zero. In comparison, if the motion of the particles is taken a priori as a random walk and therefore diffusive, then the normalized, steady-state particle flux (encounter rate) gives β _diff=4π R D, where D=ν ² τ/3 is the diffusivity of the particles, and τ is the mean time interval between tumbles. That is

$$\beta_{\rm diff} = 4/3\pi R \nu^{2} \tau.$$

(9)

The diffusive encounter kernel, Eq. 9, holds only for the steady state (i.e. after much time has elapsed) whereby prey concentration has been reduced within a diffusive boundary layer around the predator. The ballistic model on the other hand, assumes a constant prey concentration around the predator. The models that should more properly be compared are, therefore, the ballistic and the time-dependent diffusive clearance rate that is given by (e.g. Carslaw and Jaeger 1959)

$$\beta _{{\text{diff}}} (t) = \frac{4}{3}\pi R\nu ^2 \tau \left( {1 + \frac{R}{{\sqrt {\pi Dt} }}} \right)$$

(10)

which tends toward Eq. 9 as t→∞. Apart from the leading coefficients, Eqs. 8 and 10 differ in their functional dependence on reaction distance, swimming speed and tumble interval. The question is how to resolve them. Clearly, the two models can only apply when their underlying assumptions are valid. That is, the ballistic model applies when the scale of the interaction, i.e. the perception distance R, is small compared to the run length of the motion λ. Conversely, when the scale of interaction is large, the motion looks diffusive (λ<R), and the diffusive model applies.

Perhaps the most straightforward way to illustrate the difference in encounter rate for these different regimes is through a simple numerical model. We examine a spherical capture zone of R=1 mm radius centred in a 1-l volume cube. We seed the volume with a number of particles that move with uniform speed, v=1 mm s⁻¹, and tumble to a new direction (uniformly random in 3 dimensions) after a mean time interval τ. That is, the probability of tumbling to a new direction in a time step Δt is 1−exp(−Δt/τ). The encounter rate can then be estimated from the number of particles that enter the capture zone each time step. Particles entering the capture zone continue to move but are set to “inactive” and do not count towards any future encounters. Particles passing out of the simulated region are reintroduced through the opposite side, and any of them that were inactive are reactivated.

Results from 2 model runs are presented in Fig. 3, where the swimming speed and perception distance are the same, but the tumble intervals, τ, are 0.1 and 5 s, respectively. The estimated encounter kernel is given by

$$\beta = \frac{{N_{\rm enc} V}}{{N_{\rm act} \Delta t}}.$$

(11)

where N _enc is the number of encounters in the time interval Δt, and N _act is the number of active particles in the simulation volume V.

Fig. 3

Encounter kernel (maximum clearance-rate) estimates from numerical model results for 10⁶ particles simulating their encounter with a 1-mm spherical radius capture zone in a 1-l cubic volume of space. Particles execute a random walk with speed 1 mm s⁻¹, and correlation time scales of a τ=5 s and b τ=0.1 s. The runs are unbiased (uniformly random in 3 dimension) so that ϕ=0 and the correlation time scale matches the tumble interval σ. The ballistic, steady-state and time-dependent diffusive clearance rates are indicted as β_ball, β _diff and β _diff(t), respectively. Equivalently, this can be viewed as the sum of 10⁶ simulations of a single randomly walking particle encountering a stationary spherical capture zone, or indeed, the sum of 10⁶ simulations of a stationary particle encountering a randomly walking spherical capture zone. The simulation time step Δt=0.01 s in both cases

When τ=5 s, λ=ντ=5 mm (Fig. 3a), the measured encounter kernel conforms well to the ballistic estimate and remains constant over time. This may be expected since λ>R. Using the diffusive estimate in this case would overestimate the realized encounter rate by a factor of 2.5. For τ=0.1 s, λ=vτ=0.1 mm (Fig. 3b), the measured clearance rate is initially ballistic, but falls off towards the diffusive limit over time. The fall-off rate appears to be well described by the time-dependent diffusive estimate. In this case, the over all clearance rate is diffusive in nature as may be expected since λ<R. Using the ballistic estimate in this case would overestimate the realized encounter rate by a factor of up to 7.

In summary, then, the ballistic encounter is inherently more efficient than the diffusive encounter, and the motility of any plankter has both a ballistic and a diffusive component. The former applies at small and the latter at larger spatio-temporal scales; specifically when the motility length scale λ=ντ>R, the encounter rate is determined by the ballistic formulation at all times, whereas when the motility length scale λ=ντ<R, the encounter rate is initially determined by the ballistic formulation, but tends towards the diffusive formulation over time scale R ²/D.

Discussion

For most practical applications in the natural sciences, the diffusive approximation for Brownian motion is totally adequate. This is because the spatial scale of the process under consideration (e.g. the size of the source or sink region) is usually many times greater than the typical length of the Brownian runs. One can think of molecular diffusion: the mean free path of a molecule in water at room temperature is about 10⁻¹⁰ m, whereas the process scale (e.g. dissolved organic carbon leaking from a phytoplankton cell) is >1 μm. However, for planktonic interactions, these scales are not well separated, and the transition from ballistic to diffusive processes may be important. The transition zone is sometimes termed meso-diffusive, and the governing dynamics can be approximately described by the telegraph equation (Goldstein 1963; Boudreau 1989; Turchin 1998; Uchaikin and Saenko 2001). The name of this equation derives from its formulation by Lord Kelvin in connection with the first trans-Atlantic telegraph cable in the 1850s. It describes composite dynamics that appear wave-like at short time scales (like ripples spreading from a stone tossed into a pond), and diffusive at longer time scales. Unfortunately, even for simple geometries such as a spherical sink, the telegraph equation does not yield to simple analytic solutions, and it is partly due to this complexity that the ballistic–diffusive transition has not been fully explored.

A common element of nearly all analyses of swimming paths is the relationship between the straight-line displacement of an animal, l, and the length of the path it takes, L. The net-to-gross distance ratio (Buskey 1984), for instance, is given by NGDR = l/L, while the path fractal dimension (Seuront et al. 2004) examines relationship l∞L ^1/δ where δ is the scale-independent fractal dimension. While useful in some applications, both of these metrics have inherent problems. Firstly, NGDR is a time-dependent measure; specifically, for time scales larger than τ, NGDR ∝ t ^1/δ−1. That is, the value of NGDR will depend on the length of time that the swimming motion is observed. On the other hand, fractal analysis is predicated on the assumption that the path is self-similar. That is, the path will have the same structure irrespective of the scale at which it is being analysed. This may be a fine mathematical abstraction, but it is unlikely that any physical process, including plankton motility, is self-similar at all scales (Turchin 1998). There is a length scale, smaller than which the path is characterized by the physical laws of locomotion. The classic analogy of the drunkard’s walk comes to mind—what ever his path may be, the drunkard walks one step at a time. For the swimming paths of plankton, this transition from ballistic (δ=1) to fractal (whether it be diffusive δ=2 or super-diffusive δ<2) occurs at length scales that are directly relevant to their encounter rates with predators, prey and mates.

While the large-scale characteristics of organisms’ motility patterns are likely to be related to their utilization of patchy resources, their small-scale motility characteristics are also likely to be tailored to their encounter rates with other individual organisms (prey, mates or predators). Armed with these observations, it is tempting to make the following predictions:

• 1. Ballistic interactions yield high encounter rates. Therefore we predict that the motility scale of an organism exceeds its prey encounter scale (i.e. perception distance of the organism to its prey).

• 2. Since diffusive interactions yield low encounter rates, we predict that the motility length scale of an organism is less than the scale of its encounter with predators (i.e. the distance at which its predators perceive the organism).

As a corollary, we can note that in classical predator–prey interactions in the plankton, the relative length scale of a predator to its prey is about 10:1 (Hansen et al. 1994 ). Furthermore, we note that the distance at which an organism perceives a prey organism can be quite different from the distance it is perceived by its predator; each scaling approximately with the size of the searching organism. In such cases, both the criteria posed in 1 and 2 may be fulfilled at the same time, as sketched in Fig. 4. This implies that the motility length scale for an organism should be related to the size of the organism itself. This appears to be the case. Plotting the correlation length scale against the equivalent spherical diameter of the animals on a log–log plot gives an almost exact linear slope (Fig. 5a) and suggests that the run length is roughly an order of magnitude larger than the organism, a result that supports but does not immediately confirm the predictions in 1 and 2.

Fig. 4

Predicted optimum relationship between the correlation length scale of an organism’s swimming path (motility length scale), the distance at which it perceives its prey (R _prey) and the distance at which it, in turn, is perceived by its predator (R _predator)

Fig. 5

a Relationship between the size of an organism (d, equivalent spherical diameter) and the correlation length scale of its swimming path (λ). Data are for those organisms analysed in this study, and summarized in Table 2. Regression analysis suggests the relationship λ=7.67×d^1.00 (r²=0.90). b Similar relationship between the size of organisms and their effective diffusivity of motility (D), for which the regression fit gives D=2.8×d^1.71 (r²=0.97) for D given in units cm² s⁻¹ and d in cm

Allometric scaling for the motion of animals has received considerable attention over the years (e.g. Jetz et al. 2004; Woodward et al. 2005; Alexander 2005). Generally such scaling relationships are posed in terms of energy requirements, balancing the area that an animal has to search and exploit in order to meet its metabolic costs. While this is certainly a factor for plankton, here we also suggest that there can be a top-down control on motility such that encounters with predators are reduced.

As an example of how this may work, we can return to the numerical example given in Fig. 3. In this example, we concentrated on illustrating the effect of changing the correlation length scale λ with respect to a fixed reaction distance R, the pertinent parameter being the ratio λ:R. Qualitatively, the same results (i.e. ballistic vs. diffusive interactions) would be seen in changing the reaction distance for a fixed λ. Indeed, the parameter ratios in the examples of Fig. 3 correspond roughly with B. comatum (λ≈100μ) interacting, respectively, with (1) a typical prey such as Rhodomonus salina (R ≈20μ: ballistic) and (2) a typical predator such as the ambush feeding Acartia tonsa adults (R≈1,000 μ; diffusive).

This is not the whole story of course. Motility patterns are not immutable; there may be similarities within a species, but large differences in detail between individuals. For example, in the copepods Centropages typicus and Pseudocalanus elongates, where males search for females (rather than visa versa), the males have much longer correlation length scales than the females, enhancing their chances of encountering a female (Doall et al. 1998; Kiørboe and Bagøien 2005). This happens, of course, at an elevated risk of encountering a predator, a risk that the females restrict by having shorter correlation length scales. Also it appears that motility patterns may change in response to food availability (Tiselius 1992; Bartumeus et al. 2003) and predation risk (Broglio et al. 2001). Food availability may be a strong driving factor in that a decreasing turn rate would increase the organism’s contact rate with food patches. Further it should be noted that the encounter rate is also strongly affected by the predator’s motility. The best an organism can hope for is to keep the contribution from its own motility small. Finally, it should be noted that there are many predator–prey interactions, where predictions 1 and 2 do not apply. Examples include viruses attacking bacteria or phytoplankton and, generally, parasites infesting hosts. Such interactions are probably more important than we normally anticipate.

In addition to motility, the motion of planktonic organisms is also affected by turbulence. Turbulence affects the encounter rate directly by increasing the relative motion between predators and prey (Rothschild and Osborn 1988), but also, in light of the discussion above, indirectly in that it impairs an organism’s ability to maintain a ballistic path. An analogy may be seen here in the “crossing trajectories” effect (e.g. Csanady 1963) wherein the correlation time scale of a sinking particle decreases the faster it moves relative to the turbulent flow. It may be expected that smaller organisms with correspondingly smaller perception distances and slower swimming speeds will be more susceptible to turbulent reorientations in their swimming trajectories. Similar random reorientations are observed at even smaller scales (below the Kolmogorov scale) due to Brownian rotation of swimming microorganisms (e.g. Jackson 1987). The ballistic–diffusive transition for turbulent encounter rates has recently been examined by Mann et al. (2005). There it was found experimentally, that the turbulent flux (i.e. encounter rate) of particles into a perfectly absorbing, drifting sphere showed a slow decrease from an initial ballistic flux to an asymptotic diffusive flux; qualitatively similar to that shown here in Fig. 3b. A curious distinction, however, is that for turbulence, ballistic and diffusive fluxes have the same dimensional dependence, namely βε^1/3 R ^7/3 where ε is the turbulent dissipation rate, and R is the radius of the absorbing sphere (perception distance). This means firstly that the shape of the flux curves measured by Mann et al. (2005) should be of universal form, and secondly that the transition from ballistic to diffusive is scale independent.

In this work we have sought to sift through the various characteristics of motility to identify those that can be related directly to encounter rate processes. The rationale here is that in all likelihood, the evolutionary pressure shaping motile behaviour is an optimization of the rate of beneficial encounters (food, mates) vs. the rate of encounter with predators. The motility parameters that arise out of an application of Taylor’s continuous random walk model to the swimming paths of organisms are directly relevant for encounter rate processes. These parameters govern not only the intensity of the interaction, but also the mechanism by which it is realized. Furthermore, it seems that parameters such as motility length scale and diffusivity (Fig. 5b) are strongly correlated to the size of organisms. It is hoped that this information together with knowledge on mechanisms of remote detection (the nature of the signal; whether hydromechanical or chemical, how it is transmitted and attenuated in the environment, and the organism’s sensitivity) will allow specific hypotheses to be constructed and tested.