Introduction

Allometric scaling laws generalize the size-dependent structural relationships, partitioning and trade-offs between different organs’ or ecosystem elements’ growth. The stand density rule postulated by Reineke (1933) for woody plants, is an early empirically based species invariant scaling law with considerable importance in forest practice and forest science. The −3/2 power law of self-thinning formulated by Yoda et al. (1963) for herbaceous plants is the most prominent example for a scaling law based on Euclidian geometry. West et al. (1997, 1999) and Enquist et al. (1998) posit a scaling law for plants and animals, based on fractal geometry. The allometric coefficients and exponents of such laws give shape to underlying processes and although not elucidated in detail, they make the processes’ results operational for linkages between organismal and ecosystem level, for prognosis and scenario analyses. Simple and general rules still our innate propensity to reduce complexity, however they engender the risk of neglecting individual species peculiarities, which are essential for assessment and understanding the dynamics of organisms, populations or ecosystems.

For the relationship between tree number N and mean diameter \(\bar d\) in fully stocked, even-aged forest stands Reineke (1933) revealed the “stand density rule”

$$N = k\,\bar d^{ - 1.605} $$
(1)

Reineke’s rule can be represented on the ln–ln scale as a straight line

$${\text{ln}}\,N{\text{ = }}k^\prime - 1.605\,{\text{ln}}\,\bar d$$
(2)

with intercept k′=ln k and slope r= −1.605. Reineke obtained this scaling rule by plotting \(\bar d\) and N of untreated forest inventory plots in the USA in an ln–ln grid. He found very similar allometric exponents for various tree species, stand structures, and sites and he attributed a general validity of \(r \cong - {\text{1}}{\text{.605}}\) for forest stands. Therefore, he used the allometric coefficient r=−1.605 for the stand density index \({\text{SDI}}\,{\text{ = }}\,N(25.4/\bar d)^{ - 1.605} \, = \,k(25.4)^{ - 1.605}, \) which describes the density of stands with mean diameter \(\bar d\) and number of stems N by calculating the number of trees per hectare in these stands at 10 inches index diameter (=25.4 cm). Reineke’s rule and SDI has gained considerable importance for the quantification and control of stand density and modelling of stand development in pure stands (Ducey and Larson 1999; Pretzsch 2002; Puettmann et al. 1993; Sterba 1981, 1987) and mixed stands (Puettmann et al. 1992; Sterba and Monserud 1993). For Zeide (2004, p. 7), Reineke’s approach for density assessment by SDI is even “may be the most significant American contribution to forest science”. But, like Gadow (1986) and Pretzsch and Biber (2004) he calls into question the generality of r ≅ −1.605.

With no knowledge of the stand density rule by Reineke (1933), Kira et al. (1953) and Yoda et al. (1963) discovered the −3/2 power law of self-thinning, probably the most prominent example for a controversially discussed scaling law. It describes the relationship between the average shoot weight \(\bar w\) and the plant number N per unit area in even-aged and fully stocked monospecific plant populations as

$$\bar w \propto N^{ - 3/2} $$
(3)

with species invariant scaling exponent −3/2. Yoda et al. (1963) assume that plants are simple Euclidian objects and all plant parts scale isometrically to each other. So Yoda’s allometric coefficient −3/2 is based on the cubic relation between plant diameter \(\bar d\) and biomass \(\bar w\)

$$\bar w\; \propto \;\bar d^{\text{3}} $$
(4)

and the quadratic relation between \(\bar d\) and occupied growing area \(\bar s\)

$$\bar s\; \propto \;\bar d^{\text{2}} .$$
(5)

As average growing area \(\bar s\) is the inverse of number of plants N ( \(\bar s\,{\text{ = }}\,{\text{1/}}N\)), Eq. 5 can be written as \(N\; \propto \;\bar d^{ - {\text{2}}} \,{\text{or }}\,\bar d\; \propto \;N^{ -1/2} \). By insertion in Eq. 4 and rearrangement we get \(\bar w\; \propto (N^{ -1/2} )^{\text{3}} \propto \;N^{ -3/2} \) [cf. Eq. 3]. Equivalently, shoot biomass per unit area W scales over plant number N as \(W \propto N^{ - 1/2}, \) since \(W\,{\text{ = }}\,\bar w\,N,\) \(W \propto NN^{ - 3/2} \propto N^{ - 1/2}. \) Harper (1977, p 183) attested the −3/2 power law, a validity for annual plants and forests as well. White (1981, p 479) even saw the “empirical generality of the rule ... beyond question”. And among others, Long and Smith (1984, p 195) titled it “a true law instead of the mere rule”. The theoretical analyses of the law brought Zeide (1987, p 532) to the result, “Unlike the fixed value of −3/2, the actual slopes convey valuable information about species... that should not be cast away”. Weller (1987, p 37) outgrows the spell of the law and turns it into a research perspective “The differences among slopes may provide a valuable measure of the ecological differences among species and plants, and a powerful stimulus for further research”. He divided the law into two concepts, the “dynamic self-thinning line” and the “species boundary line” (Weller 1987, 1990). A quarter of the century after the first euphoria concerning the law, Begon et al. (1998, p 169) revise their approving attitude towards the law and plead for detection of interspecific peculiarities of allometry. Nevertheless the −3/2 law forms an essential contribution to the recent edition of the textbook Strasburger (cf. Körner 2002, p 967).

By contrast, West et al. (1997, 1999) and Enquist et al. (1998) present a model, which considers that plants are fractal objects and postulates the generality of quarter-power scaling. Their model describes the supply of the entire plant volume by a space-filling fractal network of branching tubes. The assumption is that the energy required for resource distribution in the network is minimized and that the terminal tubes of the network do not vary with body size. In this way, they explain that the metabolic rate of individual plants scale as the 3/4 power of body mass and predict from their model in particular

$$\bar w \propto N^{ - 4/3} $$
(6)

for unmanaged, fully stocked stands. They posit that whole plant resource use q and equivalently metabolic rate, gross photosynthetic rate and growing area scale as \(q \propto w^{3/4}, \) because \(q \propto d^{\text{2}} \) and

$$d \propto w^{3/8} $$
(7)

or

$$w \propto d^{8/3} $$
(8)

with d = tree diameter and w = tree biomass. The maximal number N of trees per unit area in fully stocked, unmanaged stands depends on the resource supply R per unit area and the average resource use \(\bar q\) per individual \(R{\text{ = }}N{\text{ }}\bar q{\text{ }} \propto N{\text{ }}\bar w^{3/4}. \) If R is constant, then \({\text{constant}} \propto N{\text{ }}\bar w^{3/4} \) what yields Eq. 6. Enquist et al. (1998) stress that their model \(\bar w \propto N^{ - 4/3} \) does not predict self-thinning trajectories, but they do not explain why. This restraint makes their model’s predictions somehow immune against falsification. Nevertheless, I compared their postulated exponent of −4/3 with empirical findings on my plots.

Always based on the 3/4 scaling of metabolic rate, West, Brown and Enquist extend their considerations on plants, animals, and even on cells and mitochondria. They apply it on individual, community and ecosystem level and provoke Whitefield’s (2001, p. 343) question whether their approach is a “...theory of everything...”. Kozlowski and Konarzewski (2004) see the models’ positive influence in reviving interest in allometric scaling as a link between process and structure. However, after numerical and empirical scrutiny, they criticize West, Brown and Enquist’s model as neither mathematically correct nor biological relevant or universal. They claim more biological realism and analysis why scaling exponents differ between taxonomic groups.

My contribution to the ongoing debate about “the ultimative scaling law” is not more theory, but more empirical evidence. My database is a unique set of fully stocked, untreated long-term experimental plots in pure common beech, Norway spruce, Scots pine, and common oak stands in central Europe and it covers a 120 years’ observation period. The study is stimulated by the critical attitude towards general and species-invariant scaling rules of Gadow (1986), Niklas et al. (2003), Stoll et al. (2002), Weller (1987, 1990) and Zeide (1987). I focused on species-specific structural and temporal peculiarities under self-thinning.

Hypotheses

H1 addresses Reineke’s stand density rule (cf. Formula 1), which reads in general form

$$N \propto \bar d^r $$
(9)

H1.1 claims for unthinned, fully stocked, even-aged pure stands a constancy of r of Reineke’s rule (exponent r in Formula 9) within stand development. H1.2 assumes that exponent r is equal for all m considered species, i.e. r 1=...=r m . H1.3 claims r 1=r 2=... =r m =−1.605, i.e. the validity of Reineke’s rule.

H2 is focussed on the generalized form of Yoda’s relationship (cf. Formula 3)

$$\bar w \propto N^c $$
(10)

H2.1 postulates constancy of c [exponent c in Formula 10] within stand development. H2.2 postulates that slope c is equal for all m considered species, i.e. c 1=...=c m . H2.3 scrutinizes whether the self-thinning line of the species follows Euclidian geometry, i.e. c 1=...=c m =− 3/2 or fractal scaling, i.e. c 1=...=c m =−4/3.

H3 analyses for each species its self-thinning trajectories’ oscillation around the self-thinning line \(\bar w \propto N^c. \) The value pairs \(\bar w_i \) and N i from the i=1...n consecutive surveys of the plots are used to calculate the period-wise slopes

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} _i = \frac{{\ln (\bar w_{i + 1} ) - \ln (\bar w_i )}}{{\ln (N_{i + 1} ) - \ln (N_i )}} = \frac{{\ln (\bar w_{i + 1} /\bar w_i )}}{{\ln (N_{i + 1} /N_i )}}$$
(11)

for all survey periods. Thus, \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \) quantifies the self-thinning slope in each particular survey period; whereas, \(c = ({\text{d}}\bar w/\bar w)/({\text{d}}N/N) = {\text{d}}\ln (\bar w)/{\text{d}}\ln (N)\) (exponent in Formula 10) describes the self-thinning lines’ slope fitted on the basis of all survey periods.

H3.1 postulates, that the coefficients of variation of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \) are equal for all species, i.e. \({\text{v}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} _1 = \ldots = {\text{v}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} _4 \) H3.2 uses the Pearson correlation \(r_{{\text{v}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} ,\,c} \) between v \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \) and slope c to detect connections between the spatial and temporal dynamic of the self-thinning process.

Data

This and all subsequent sections repeatedly refer to electronic supplementary material available on Springer Verlag’s server. References to this material are numbered as S1, S2 etc. See URL on title page.

H1–H3 are tested for common beech, Norway spruce, Scots pine and common oak on the basis of 28 fully stocked long term experimental plots in even-aged pure stands. The plots are located in southern and central Germany between 07°52′34′′E–12°20′30′′E longitude and 47°50′03′′N–51°36′06′′N latitude (cf. Fig. 1). They represent medium to very good growth conditions in the lowlands and sub-alpine zone between 320 m and 840 m above sea level (cf. S1, S2). The oldest of these experiments have been under observation since the mid-nineteenth century. They form an important database, from which stand management rules, yield tables and training programmes for forestry practice were developed. Due to their unique length, these time-series were the subject of numerous publications on growth and yield of Norway spruce (Assmann 1970; Röhle 1994; Pretzsch and Utschig 2000), common beech (Kennel 1972; Franz et al. 1993; Foerster 1993), Scots pine (Foerster 1990; Küsters 2001; Pretzsch 1985) and common oak (Assmann 1970; Mayer 1958; Utschig and Pretzsch 2001). Thus, Table 1 reports only the most important data from the non-thinned, fully stocked plots used in this study. All plots are untreated A-grade variants from classical thinning experiments in unmanaged pure stands. All included stands are mono-layered, with narrow unimodal diameter distributions with coefficients of variation ranging from 15% to 28%. By definition, A-grade is restricted to the removal of dead trees and aims at the documentation of self-thinning (Verein Deutscher Forstlicher Versuchsanstalten 1902).

Fig. 1
figure 1

Map with distribution of the 28 experimental plots in central and southern Germany. Experiments for the species common beech, Norway spruce, Scots pine and common oak are marked by different symbols. Abbreviations near the symbols refer to location and number of the experiments and indicate the plot number (cf. S1)

Full size image
Table 1 Growth and yield characteristics for the first/last survey of 28 non-thinned, fully stocked experimental plots of common beech, Norway spruce, Scots pine and common oak
Full size table

For above-ground biomass estimation (cf. Eq. 10; Table 2), biomass analyses were carried out on experimental plots with sampling techniques, reported elsewhere (Grote et al. 2003). All together 94 sample trees were included, covering approximately the diameter range of the unthinned plots.

Table 2 Estimates ± standard error for k′ and a of the model \({\text{ln }}w{\text{ }} = k' + a\,{\text{ln }}d\) or adequately \(w = k\,d^a, \) with k’=ln k [w= above ground shoot weight (kg), d= diameter in brest height (cm), k, k′, a= regression coefficients, n= number of harvested sample trees, dmin to dmax minimum to maximum diameter of sample trees (cm)]
Full size table

Methods

Regression algorithm

After ln–ln-transformation, most of the datasets fulfilled the assumptions of linear regression analysis such as normal distributions of residuals, homoscedasticity and independence of residuals. Except RMA regression analysis, for all subsequent calculations, I used SPSS (Version 11.5). Those 10 out of 28 plots with nonlinear self-thinning lines were omitted from the subsequent analysis (cf. Sect. “Results”).

Scaling exponents and scaling coefficients were computed by both, Model I (ordinary least square regression, OLS) and Model II (reduced major axis regression, RMA). Zeide (1987) and Niklas (1994) argue that RMA regression (Model 2) represents the “true relationship” between the variables, as RMA slopes of x on y are exactly the inverse of those of y on x. I applied a program for reduced major axis regression from Bohonak (2002), who suggests that RMA should be used, if error variance of x exceeds one-third of the error variance in y. I also applied ordinary least square regression, to keep comparable with the original work of Yoda et al. (1963) and other studies, based on OLS-slopes. Sackville Hamilton et al. (1995) showed that slope estimates of all different algorithm converge with increasing r 2. As the fitting of Eqs. 9, 10, and 12 yielded mostly r 2>0.9, the differences between OLS and RMA slopes (2.3% in average) had no decisive effect on the final results of this study.

Above-ground shoot biomass’ estimation

Using the 94 sample trees presented in the “Data” section, the model

$${\text{ln }}w{\text{ }} = k' + a\,{\text{ln}}\,d$$
(12)

was fitted by OLS regression. Depending on stem diameter d, the biomass w of each individual tree was estimated, so that mean plant biomass \(\bar w\) and biomass per unit area W can be calculated.

Mathematical representation of the self-thinning line

Weller (1987) and Niklas (1994) argue that most empirical studies about self-thinning rule are methodologically flawed, as they base on ln  \(\bar w\) versus ln N instead of ln W versus ln N. They argue that the relation ln  \(\bar w\) versus ln N is equivalent to plotting total plant biomass/total number of plants ( \(\bar w\)) versus total number of plants/total area (N), so that total number of plants is shared by x and y. As x and y are not independently measured and total number of plants is mostly estimated by sampling, slopes obtained from the first formulation of the rule may be spurious. However, these arguments apply to studies about herbaceous plants rather than to forests. In forests, biased plant numbers play a minor role as biomass is not measured by harvesting all plants, but each individual tree is measured and counted (Prairie and Bird 1989). Thus stem number is the most precisely recorded variable; each tree is permanently marked and any flaws at a survey are corrected at the next survey at the latest. In order to anticipate criticism on account of the used model and to keep comparable with studies applying ln  \(\bar w\) versus ln N (e.g. White 1981; Yoda et al. 1963) and ln W versus ln N (e.g. Weller 1987; Zeide 1987), both relations were analyzed.

Regression with centered data

To obtain individual species’ slopes for the relations \({\text{ln}}\,N\;{\text{versus}}\;{\text{ln}}\,\bar d,\) \({\text{ln}}\,\bar w\;{\text{versus}}\;{\text{ln}}\,N,\) and \({\text{ln}}\,W\;{\text{versus}}\;{\text{ln}}\,N\) all plots per species were integrated in an overall RMA and OLS analysis. Prior to RMA and OLS analysis, the mean values \(\overline {{\text{ln}}\,\bar w} \) and \(\overline {{\text{ln}}\,N} \) were calculated for each stand and used for standardisation \({\text{ln}}\,\bar w_i^\prime {\text{ = ln}}\,\bar w_i - \overline {{\text{ln}}\,\bar w} \) and \({\text{ln}}\,N_i^\prime {\text{ = ln}}\,N_i - \overline {{\text{ln}}\,N}. \) The standardisation has the effect of focussing all straight lines on the mean value ( \(\overline {{\text{ln}}\,\bar w} ,{{\text{ln}}\,N} \)) and eliminating of plot specific intercepts. The regression of \({\text{ln}}\,N\;{\text{versus}}\;{\text{ln}}\,\bar d,\) \({\text{ln}}\,\bar w^\prime \) versus \({\text{ln}}\,N^\prime, \) and ln W versus ln N yielded individual species’ scaling exponents. The slopes resulting from centered data are labeled by apostrophe (e.g. c′).

Results

Relationship w ∝ d a between diameter and biomass

Table 2 displays the species-specific parameters k′ and a of the model ln w = k′ + a ln d [cf. Eq. 12]. Parameter a serves in this study for both, scrutiny whether slope a tends to follow a general scaling law and upscaling from tree diameter d to stand biomass W.

Parameter a is equivalent to scaling exponent a in w ∝ d a (generalized form of Eq. 8) and represents the allometric relationship between diameter and biomass. The observed values for common beech, Norway spruce, Scots pine, and common oak differ considerably from a=3.0, assumed by Yoda et al. (1963), but vary around a=8/3, postulated by West et al. (1997) and Enquist et al. (1998).

Biomass of adult trees or even whole stands can hardly be measured completely. For the subsequent evaluation, individual tree biomass w was estimated in dependence on individual stem diameter d by model ln w = k′ + a ln d [Eq. 12]. Estimates of all individual trees’ biomass w enables calculation of \(\bar w\) and W. Slopes c and d, needed for scrutiny of H2, were derived by regression analysis on the basis of all value pairs (N, \(\bar w\)) and (N, W), respectively.

H1: scrutiny of Reineke’s stand density rule

Reineke’s relationship \(N \propto \bar d^r \) is another representation of \(\bar s \propto \bar d^b, \) as \(\bar s{\text{ = 1/}}N.\) Thus, scrutiny of slope r of \({\text{ln}}\,N{\text{ versus ln}}\,\bar d\) also exposes slope b of \({\text{ln}}\,\bar s{\text{ versus ln}}\,\bar d,\) as both slopes just differ in the sign (r=−b).

H1.1: each of the 28 \({\text{ln}}\,N{\text{ versus ln}}\,\bar d\)-trajectories was analyzed by OLS-regression with regard to quadratic effects by model \(\ln N = o_{\text{1}} + o_{\text{2}} \ln \bar d + o_{\text{3}} \,\ln ^{\text{2}} \bar d\). Negative o3-values indicate a concave curve, as seen from below, while positive o3-values produce a convex curve. Overall, significant quadratic terms (P<0.05) were obtained for 29% of the plots (8 out of 28 plots). Significantly negative quadratic terms were obtained in six cases, significantly positive ones in only two cases. For common beech there were three concave curves (o 3 = −0.02 to −0.001, P<0.05) and one convex curve (o 3 = +0.004, P<0.05). Norway spruce had two concave (o 3=−0.002 to −0.001, P<0.05) and one convex curve (o 3= +0.011, P<0.05). Scots pine had one concave curve (o 3= −0.001, P<0.001). Common oak was consistently linear (o 3 ≅ 0).

H1.2: for the 20 plots with linear \({\text{ln}}\,N{\text{ versus ln}}\,\bar d\)-lines I estimated the plot-wise slopes by OLS and RMA regression (cf. Table 3). RMA slopes r RMA range between −1.222 and −1.873 with −1.628 in average. Arithmetic means for common beech (n=5), Norway spruce (n=6), Scots pine (n=5), and common oak (n=4) are r RMA = −1.765, −1.644, −1.655, −1.399. OLS slopes range from r OLS= −1.204 to −1.865 with −1.594 in average. Means are r OLS= −1.761 for common beech, −1.636 for Norway spruce, −1.551 for Scots pine, and −1.398 for common oak. For the 20 plots with linear relationship \({\text{ln}}\,N{\text{ versus ln}}\,\bar d\) ANOVA was applied, to detect species-specific differences concerning r RMA and r OLS. Levene’s statistic proved for r RMA and r OLS homogeneity of variances for the four species groups (P<0.05). Independent of the regression algorithm, the ANOVA yielded significant differences between the species (P<0.01), with r RMA mean (± standard error) 1.765 (±0.027), 1.644 (±0.009), 1.655 (±0.034) and −1.399 (±0.086) for common beech, Norway spruce, Scots pine, and common oak, respectively. Multiple comparisons of group means by Scheffé’s statistic detected differences between common beech and common oak (P<0.01), Norway spruce and common oak (P<0.05) and Scots pine and common oak (P<0.05). Analysis of r OLS provided similar results.

Table 3 Plotwise scaling exponents r RMA and c RMA for the relations \({\text{ln}}\,N\;{\text{versus}}\;{\text{ln}}\,\bar d\) and \({\text{ln}}\,\bar w\;{\text{versus}}\;{\text{ln}}\,N\), respectively)
Full size table

H1.3: Comparison of r with Reineke’s −1.605. In 60% of the cases (12 of 20 plots) −1.605 lies within the 95% confidence intervall of r RMA (cf. Table 3). Bold letters denote that Norway spruce and Scots pine in majority correspond with Reineke’s slope, whereas the slope of common beech is steeper and the one of common oak is shallower than −1.605. Same evaluation on basis of r OLS yielded 50% of the plots with −1.605 included in the 95% CI. The regression over all centered data \({\text{ln}}\,N^\prime {\text{ versus ln}}\,\bar d^\prime \) yielded slopes r RMA′ between −1.778 and −1.457 (common beech<Norway spruce<Scots pine<common oak) and r OLS′ between −1.773 and −1.423 with the same ranking of the species. Only the 95% confidence intervals of Scots pine’s slopes r RMA′ and r OLS′ include −1.605. Slopes r′ of common beech and Norway spruce are significantly steeper than −1.605; r′ of common oak is shallower than −1.605 (cf. S5).

H2: slopes of the dynamic self-thinning lines \(\bar w \propto N^c \) and \(W \propto N^d \), respectively

Weller (1987, 1990), Zeide (1987) and Niklas (1994) prefered the relation \({\text{ln }}W{\text{ versus ln }}N\) for slope estimation, while Yoda et al. (1963) used \({\text{ln }}\bar w{\text{ versus ln }}N\). To avoid unjustified rejection of my results on account of methodological disagreement, I applied RMA and OLS regression to both relationships. However, as \(d \cong c + {\text{1}}\) the evaluation for c and d yielded always analogous results and I concentrated my report on c.

The \({\text{ln }}\bar w - {\text{ln }}N\)-lines for the four considered tree species (Fig. 2) depict the wide range of stem numbers and biomass, covered by the dataset. Mean shoot biomass per plant \(\bar w\) of common beech, Norway spruce, Scots pine, and common oak, ranges from 9.7 kg to 1,809.9 kg, 13.5 kg to 1,514.4 kg, 12.9 kg to 331.7 kg and 93.4 kg to 982.1 kg, respectively.

Fig. 2
figure 2

Relation between logarithmic mean plant biomass \({\text{ln}}\,\bar w\) and tree number per unit area \({\text{ln}}\,N\) for untreated, fully stocked common beech, Norway spruce, Scots pine, and common oak pure stands. Nonlinear trajectories are depicted as broken lines. Self-thinning lines \({\text{ln}}\,\bar w{\text{ = }}k' - 3/2\,{\text{ln}}\,N\), with Yoda’s slope −3/2 and \(k' = {\text{15, 16, 17}}\) are given as reference

Full size image

H2.1: The OLS-regression of the quadratic model \({\text{ln}}\,\bar w = p_{\text{1}} + p_{\text{2}} \,\ln N + p_{\text{3}} \,{\text{ln}}^{\text{2}} N\) resulted in significantly (P<0.05) negative p 3-coefficients in three out of nine common beech plots (p 3=−0.187 to −0.075), two out of nine Norway spruce plots (p 3=−0.148 and −0.125), two out of six Scots pine plots (p 3=−1.323 and −0.473) and one out of four common oak plots (p 3=−0.135). Thus, in 29% of the cases, the slope is concave from below and becomes shallower within stand development. In one out of nine common beech plots (p 3=+0.456) and one out of nine Norway spruce plots (p 3=+0.119), i.e. in 7% of all cases a significant (P<0.05) convex curve was detected. Comparison between the straight self-thinning lines (Fig. 2, solid lines) and those detected as nonlinear (broken lines) indicates mainly a slight curvature. Altogether in 10 out of 28 cases, the relation \({\text{ln }}\bar w{\text{ versus ln }}N\) deviated significantly (P<0.05) from linearity, i.e. on 36%. The analysis on basis of the relation \({\text{ln }}W{\text{ versus ln }}N\) yielded the same percentages of nonlinear, concave and convex self-thinning lines.

H2.2: For each of the 18 plots with a straight self-thinning line, we estimated slopes c and d, for the relations \({\text{ln }}\bar w{\text{ versus ln }}N\) and \({\text{ln }}W{\text{ versus ln }}N\) by both, RMA and OLS regression. The regression \({\text{ln }}\bar w{\text{ versus ln }}N\) yielded r 2 -values from 0.91 to 0.99, which were highly significant (P<0.001) in all cases. On average (min to max), the RMA-slopes were c RMA =−1.459 (−1.490 to −1.374) for common beech, c RMA =−1.618 (−1.648 to −1.594) for Norway spruce, c RMA =−1.474 (−1.667 to −1.369) for Scots pine, and c RMA =−1.868 (−2.139 to −1.617) for common oak (Table 3). The OLS slopes are in average (min to max) c OLS =−1.457 (−1.489 to −1.366) for common beech, c OLS =−1.610 (−1.630 to −1.586) for Norway spruce, c OLS =−1.449 (−1.600 to −1.358) for Scots pine, and c OLS =−1.830 (−2.087 to −1.575) for common oak.

ANOVA for detection of individual species’ slope c: any interspecific differences of the scaling exponent c were analyzed by ANOVA. Variance analysis included all 18 plots with linear self-thinning lines and was carried out for slopes, estimated by RMA and OLS. Levene’s statistic proved homogeneity of variances for the four species (P<0.05). The hypothesis that the slope c RMA of the relation \({\text{ln }}\bar w{\text{ versus ln }}N\) is equal for all four considered species can be rejected (P<0.01). The mean slopes (± standard error) were c RMA=−1.459 (±0.022), c RMA =−1.618 (±0.009), c RMA =−1.474 (±0.068) and c RMA =−1.868 (±0.151) for common beech, Norway spruce, Scots pine and common oak, respectively. Multiple comparisons of group means by Scheffé’s procedure revealed significant differences between c RMA-values of common beech and common oak (P<0.01) as well as between Scots pine and common oak (P<0.01). Variance analysis on basis of OLS-slopes underlines the differences between the species: Global hypothesis of equality was rejected (P<0.001), group means differed significantly between common beech and common oak (P<0.001), Norway spruce and Scots pine (P<0.05), Scots pine and common oak (P<0.001).

In passing, I emphasize that also the intercept of the self-thinning lines differ considerably between the species (cf. Fig. 2). This fact was recently revealed by Stoll et al. (2002) and will be analyzed in a subsequent report.

H2.3: Table 3 presents slopes, standard errors and 95% confidence intervals for each plot. Those slopes, corresponding with Yoda’s law are printed in bold letters. Yoda’s constant of −3/2 is in 10 out of 18 cases (56%) within the 95% confidence interval of the RMA-slope c RMA. Fractal scaling constant −4/3 is in merely 5 out of 18 cases (28%) within the respective CI. In the majority slopes of common beech (four out of five) and Scots pine (three out of four) approximated −3/2; whereas, Norway spruce (two out of six) and common oak (one out of three) differed significantly. The same evaluation on the basis of OLS-slopes yielded similar results. The relation \({\text{ln}}\,{\ifmmode\expandafter\bar\else\expandafter\=\fi{w}}\ifmmode{'}\else$'$\fi\,{\text{versus}}\,{\text{ln}}\,{N}\ifmmode{'}\else$'$\fi\) was fitted by both, OLS- and RMA-regression analysis. The slopes c OLS′ and c RMA′ (cf. Fig. 4 and S5) all differ significantly from −3/2 as well as from −4/3.

H3: species’ oscillation around the self-thinning line

The representation of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \)-values over mean diameter \(\bar d\) (Fig. 3) shows oscillation around the mean value (broken line). Common beech plots FAB 151/1, HAI 27/1 (a) and common oak plots WAL 88/5 and ROH 90/1 (b) represent a species-specific dynamic of self-thinning. Common beech is characterized by rather low oscillation, compared with common oak. For the 18 plots which have proved to follow linear self-thinning lines, I have applied Eq. 11 in order to analyse interspecific differences in temporal dynamic of self-thinning process.

Fig. 3
figure 3

\(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \)-values over mean diameter \(\bar d\) for common beech plots FAB 15/1 and HAI 27/1 (a) and common oak plots WAL 88/5 and ROH 90/1 (b). The time series were smoothed by cubic spline; broken lines represent mean \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \)-values for common beech and common oak

Full size image

H3.1: Standard deviation and coefficient of variation of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \) reveal differences between the considered species (Table 4). As the variation coefficient \({\text{v}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \) expresses the standardized variation of \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \), it is most suitable for comparing the species groups by ANOVA. Cubic transformation of the \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \)-values assured variance homogeneity between the species groups (P<0.01). ANOVA uncovered significantly different variation coefficients (P<0.001) between the considered species. Multiple comparisons of cell means by Scheffé’s statistic detected significant differences (P<0.05) for common beech versus common oak, Norway spruce versus common oak, and Scots pine versus common oak. Coefficient of variation of Norway spruce, Scots pine, and common oak amount to 123, 156 and 230% compared with common beech (= 100%).

Table 4 Mean, standard deviation and coefficient of variation v \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \) of quotient \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} = \ln \,\left( {{{\bar w_{i + 1} } \mathord{\left/ {\vphantom {{\bar w_{i + 1} } {\bar w_i }}} \right. \kern-\nulldelimiterspace} {\bar w_i }}} \right)/\ln \,\left( {{{N_{i + 1} } \mathord{\left/ {\vphantom {{N_{i + 1} } {N_i }}} \right. \kern-\nulldelimiterspace} {N_i }}} \right)\)
Full size table

H3.2: Pearson’s correlation between slope c RMA and \({\text{v}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \) resulted in \(r_{c_{RMA} {\text{,}}\,{\text{v}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} } \) = −0.614 (P<0.01). With other words, the steeper the slope of \({\text{ln }}\bar w\,{\text{versus}}\,{\text{ln }}N\), the higher the variation around the self-thinning line. In common beech stands, e.g., self-thinning is more rigorous (c RMA′ = −1.409) but more consistent ( \({\text{v}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{c} \) = 30.2%) than in oak stands, where self-thinning is slower (c RMA′=−1.794) but tree losses due to self-thinning come up in batches \(\left( {{\text{v}}\hat c = 69.3\% } \right).\)

Discussion

The partially nonlinear curvature of the relation between ln (stem number) and ln (plant dimension) was mainly caused by storm damage and ice breakage, which opened up crown space and lowered stand density. I applied a rather conservative but objective criterion for telling linear from nonlinear relationships. Nevertheless, mean plant biomass \(\bar w\) and biomass per unit area W have to be interpreted with due care, as biomass of forest stands can hardly be measured completely, but is estimated by scaling functions again (e.g., \(w \propto d^a \)). To avoid artefact due to two-stage biomass sampling, slopes on the basis of the primary variables \(\bar d\) and N were analysed as well. The plus of the used database lies in the length of time series. It displays the “dynamic self-thinning line” for a restricted number of sites. But it is not sufficiently scattered over the whole site spectrum of the considered species to yield a “species boundary line”, which would represent the upper boundary of yield–density relation for a species (Weller 1987, 1990).

Generalization

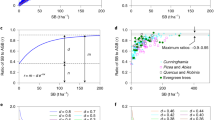
The synopsis of observed and expected scaling exponents in Fig. 4 abates hope for consistent scaling laws for forest trees and stands but helps to bridge the gap between the work of Yoda et al. (1963) and West et al. (1997, 1999). For the allometric exponents of \({\text{ln}}\,w\;{\text{versus}}\;{\text{ln}}\,d\), Euclidian geometry would expect a=3 and fractal geometry a=8/3=2.67. The observed values a=2.50, 2.66, 2.30, and 2.63 for common beech, Norway spruce, Scots pine, and common oak, respectively, vary around a=2.67 (Fig. 4a). They are significantly different from a=3.0 and support the 8/3-scaling law postulated by West et al. (1997) and Enquist et al. (1998) [cf. Eq. 8]. For the relation ln  \(\bar s\) versus ln  \(\bar d\) Euclidian as well as fractal geometry expect b=2.0, rather the observed exponents b=1.77, 1.65, 1.59, 1.42 reveal systematically shallower slopes. They are significantly lower than 2.0 and scatter around 1.605, which is the constant, Reineke revealed more intuitively than biometrically (Fig. 4b). Although a follows more or less fractal scaling and b escapes from theoretical Euclidian and fractal geometry assumptions, the self-thinning lines’ slopes for \({\text{ln }}\bar w{\text{ versus ln }}N\) and \({\text{ln }}W{\text{ versus ln }}N\) roam around c=−1.50 and d=−0.50, respectively (Fig. 4c, d). They are significantly steeper than expected by fractal scaling laws (c=−1.33 and d=−0.33, respectively). Euclidian scaling of one relation and fractal scaling of another are coupled, depending on species.

Fig. 4
figure 4

Observed scaling exponents (mean, 95% confidence intervals) and predicted scaling exponents of Euclidian geometrical scaling (solid vertical line), empirical scaling after Reineke (1933) (dotted vertical line), and fractal scaling (broken vertical line). Depicted are slopes of the relations a \({\text{ln}}\,w\;{\text{versus}}\;{\text{ln}}\,d{\text{ }}\), b \({\text{ln}}\,\bar s\;{\text{versus}}\;{\text{ln}}\,\bar d\), c \({\text{ln}}\,\bar w\;{\text{versus}}\;{\text{ln}}\,N\), and d \({\text{ln}}\,W\;{\text{versus}}\;{\text{ln}}\,N\)

Full size image

The exponent a of \(w \propto d^a \) expresses biomass allocation of a tree with a given diameter, while exponent b of \(\bar s \propto \bar d^b \) expresses the lateral crown expansion. The scaling exponents for common beech account for its high efficiency of space occupation. Compared with Norway spruce and common oak, common beech invests rather less in biomass, but the invested biomass is used more efficiently to occupy additional space. A given diameter growth is coupled with a relatively low biomass growth (Fig. 4a), however, with an increase of growing space \(\bar s\), topped by none of the other considered species (Fig. 4b). The opposite applies to common oak. Despite a comparably high investment in biomass, oak achieves a rather low lateral expansion. Another pattern of shape and biomass allocation shows Norway spruce and Scots pine, where a and b are counteracting. The results confirm Weller (1987, 1990) and Zeide (1987) in their view, that the individual species’ scaling exponents are a key for understanding the species’ ability to cope with crowding and should not be cast away, although generalization across species is tempting.

Scaling exponents for woody plants might be biased because of the progressive accumulation of dead inner xylem, which impairs the relation between average biomass and plant number. In contrast to herbaceous plants, for which the −3/2 law was initially developed, dead tissue in the stem’s core is negligible in the juvenile phase but amounts to 15–20% for common beech, 50% for Norway spruce, 35–40% for Scots pine and 65–70% for common oak in age 100 (Trendelenburg and Mayer-Wegelin, 1955). As the steepness of the slopes, revealed in this study, rank in the same way as the percentage of dead xylem wood (common oak>Norway spruce>Scots pine>common beech), it seems that the percentage of dead wood is behind the species-specific slopes, or at least influences them.

Since slopes c and d of common beech and Scots pine are even flatter than −3/2 and −1/2, respectively, although they should be steeper if we consider the dead core wood accumulation, Yoda’s law appears questionable. Enquist et al. (1998) state without reasons that their −4/3 self-thinning law applies across populations of herbaceous and woody plants of very different size but that it does not explain self-thinning within populations. Fractal scaling slopes −4/3 and −1/3, expected by West et al. (1997, 1999), Enquist et al. (1999, 2001) and Niklas (1994), are flatter than all observed slopes. In view of my results, fractal scaling slopes −4/3 and −1/3 appear in a new light: they might apply to ln  \({ws}\) versus ln N and ln WS versus ln N, where \({{\text{ws}}}\) and WS describes sapwood biomass. In order to judge, if this hypothesis is reasonable, I estimated whole stem biomass using c RMA-slopes and compared them with stem biomass estimated via slope −4/3. The difference [(w−ws)/w 100] of biomass in advanced stand age (300 trees per ha) amount to 20% for common beech, 56% for Norway spruce, 23% for Scots pine and 75% for common oak. These portions of dead xylem correspond to remarkable extend with empirical findings and justify the assumption, that −4/3 is not at all generalizable for ln  \(\bar w\) versus ln N, but applies better to ln  \(\overline {ws}\) versus ln N.

Ecological implication

Allometry under self-thinning reveals the species-specific critical demand on resources of trees of given size. If the number N of trees per area approximates maximum stand density, average growing space \(\bar s\) falls below a critical limit and induces the mortality process especially of trees with growing space s< \(\bar s\). By rearrangement \(\bar w \propto N^c \), \(\bar w \propto \bar s^{ - c} \), \(\bar s \propto \bar w^{ - {{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} c}} \right. \kern-\nulldelimiterspace} c}} \) and differentiation we get \(g = {{({\text{d}}\bar s/\bar s)} \mathord{\left/ {\vphantom {{({\text{d}}\bar s/\bar s)} {({\text{d}}\bar w/\bar w)}}} \right. \kern-\nulldelimiterspace} {({\text{d}}\bar w/\bar w)}}\), where g is reciprocal of Yoda’s exponent taken with the opposite sign (g = −c −1). Rate g reflects the relative gain of growing space \({\text{d}}\bar s{\text{/}}\bar s\) by a given biomass investment \({\text{d}}\bar w{\text{/}}\bar w\). Yoda’s slope c = −3/2 would yield g=0.667. In other words, under self-thinning conditions, regardless of species and site, 1% of biomass investment would always effect 0.667% of space occupation. My evaluation yielded individual species’ c RMA ′-values of −1.409, −1.611, −1.421, and −1.794, so that g = 0.7097, 0.6207, 0.7037, and 0.5574 for common beech, Norway spruce, Scots pine, and common oak, respectively. Thus, common beech and Scots pine prove to be more efficient in space occupation than predicted by Yoda’s constant, Norway spruce and common oak are less efficient. If we define the efficiency of space occupation as the fraction of sequestered space \({\text{d}}\bar s{\text{/}}\bar s\) per fraction of biomass investment \({\text{d}}\bar w{\text{/}}\bar w\) and set common beech as reference, the species’ ranking of efficiency will be: common beech (100%) Scots pine (99%)>Norway spruce (88%)>common oak (79%). If we follow Zeide (1985) who revealed c = \({{{\text{(d}}\bar w{\text{/}}\bar w{\text{)}}} \mathord{\left/ {\vphantom {{{\text{(d}}\bar w{\text{/}}\bar w{\text{)}}} {{\text{(d}}N{\text{/}}N}}} \right. \kern-\nulldelimiterspace} {{\text{(d}}N{\text{/}}N}})\) as a measure for a species’ self-tolerance, we get a ranking of self-tolerance: common beech (100%)<Scots pine (101%)<Norway spruce (114%)<common oak (127%). Thus, a high efficiency of space sequestration is coupled with a low self-tolerance and a rigorous self-thinning process, and vice versa.

Conclusions

In view of the individual species’ slopes, stand density estimation algorithms, founded on generalized allometric relations, appear unsuitable. Questionable is, e.g. Reineke’s stand density index (Reineke 1933), founded on species invariante slope r=−1.605. It is frequently used to quantify stand density (Sterba 1981, 1987; Kramer and Helms 1985). Stand density management diagrams (SDMD), which are applied for many species as a tool for regulating stand density, use the self-thinning line with generalized scaling exponents as upper boundary and are the most prominent silvicultural application of the self-thinning rule (Oliver and Larson 1990). Bégin et al. (2001) list for a considerable number of tree species available SDMDs as guides for stand management. As long as those SDMDs ignore individual species allometry, flawed density control and contraoptimal thinning will result. Equivalent shortcomings apply for prognoses by growth models, which ignore individual species’ scaling exponents. Models, which base thinning and mortality algorithms on generalized scaling exponents (Eid and Tuhus 2001; Xue and Hagihara 2002; Yang and Titus 2002) should be replaced by more flexible approaches (Pittman and Turnblom 2003; Roderick and Barnes 2004; Zeide 2001).

Allometry and peculiarities of space sequestration are a benchmark for a species competitiveness in pure and mixed stands (Bazzaz and Grace 1997). In order to get a better understanding of competitive mechanisms in forest stands, further research should clarify individual species scaling rules rather than to continue search for “the ultimative law”, that appears like hunting for a phantom. In comparison with ecophysiological and biochemical processes, which are not thoroughly understood, size and structure of plants are much easier to measure. Since there is a close feedback between structure and process, organisms’ size and structure can become the key for revelation and prognosis of stand dynamic. Allometric slopes can serve as an interface between process and structure. If the numerous falsification trials concerning the rules from Reineke, Yoda and West, Brown and Enquist lead to a refined understanding of individual species allometry, allpervasive scaling exponents would appear as a stimulating myth.