The coupling interaction of a screw dislocation with a bimaterial interface and a nearby circular inclusion

Abstract

This work deals with the coupling interaction of a screw dislocation with a bimaterial interface and a nearby circular inclusion. Explicit series solutions are obtained by the complex potential and conformal mapping technique. Then the solutions are cast into new expressions with the coupling interaction effects separated. The new expressions converge rapidly and provide good first-order approximation formulae. The interaction energy and image force fields are formulated, evaluated, and shown graphically. It is found that the inclusion severely distorts the neighboring interaction energy contours and image force lines. There must be one unstable equilibrium point in Material 2 where the inclusion is located, whereas there may be zero, one or two equilibrium points (stable or unstable) in Material 1 without any inclusion, which depends on a combination of three material shear moduli and the nondimensional distance between the inclusion and bimaterial interface. It is interesting to notice that the direction of some local image forces in Material 1 may be inversed by a nearby inclusion in Material 2, and the inverse region is close to but not connected to the bimaterial interface.

1 Introduction

The movement of dislocations in the materials can determine the strength of materials and how they will deform under a load, and how they accommodate strain [1]. Bimaterials are extensively used in many engineered-material systems, such as composite structures, electronic packaging and thin-film constructions. The interaction of dislocations with a bimaterial interface is a very important topic, which has attracted considerable attention in the past decades.

Head [2] first derived the image force on a dislocation near a perfect bimaterial interface. He found that the dislocation was either repelled or attracted by the interface, depending on the combination of material constants. Dundurs [3] made a systematic review on the early continuum mechanics studies of elastic interactions between dislocations and inhomogeneities, and he also investigated the interaction of a screw dislocation with the interface. By using the continuous dislocation technique, Huang and Kardomateas [4] presented a method for obtaining the mixed-mode stress intensity factors for interface cracks or cracks parallel to the interface in half-plane configurations. Kuo [5] presented a numerical procedure for the analysis of the elastic field due to an edge dislocation in a multilayered composite. Hejazi et al. [6] derived exact analytical solution in explicit forms for the transient response of Volterra-type dislocation in a half-plane by using the Cagniard-de Hoop method of Laplace inversion. The interactions of dislocations with various imperfect bimaterial interfaces have also been investigated by many researchers (see, for example, [7–9]).

The interaction between dislocations and inclusions of finite size is another important research topic. It is revealed that interaction energy and dislocation force acting on dislocations are influenced by the shape of inclusions, the nature of inclusion/matrix interfaces and the size of inclusions.

The influence of the inclusion shape on the interaction of dislocations with the inclusion has been well studied. Smith [10] analyzed circular and elliptic inclusions. Sendeckyj [11] obtained the elastic fields of a screw dislocation near an arbitrary number of elastic circular cylindrical inclusions, where the inclusions can have arbitrary radii and shear moduli. By using the Eshelby equivalent inclusion method, Li and Shi [12] studied the inclusion of arbitrary shape and obtained a set of simple approximate formulae with satisfactory accuracy. Gutkin et al. [13] derived and analyzed in detail the stress field and strain energy of a screw dislocation in an elastically isotropic solid containing two cylindrical voids by the technique of infinite ensembles of image dislocations. As an extension to the piezoelectric issue, Shen et al. [14] investigated the interaction between a screw dislocation and a piezoelectric fiber composite with a semi-infinite wedge crack. Zeng et al. [15] dealt with the interaction between piezoelectric screw dislocations and two asymmetrical interfacial cracks emanating from an elliptic hole under combined mechanical and electric load at infinity. Zhang et al. [16] presented a numerical solution of interaction between cracks and a circular inclusion in a finite plate, in which distributed dislocations were used to model the cracks and boundaries. The nature of the inclusion/matrix interface plays an important role in the study of the interaction of dislocations with an inclusion. Various interfaces have been considered, which include perfect and imperfect interface [17, 18], uniform coating [19, 20], nonuniform coating [21] and interfacial cracks [22]. When the inhomogeneity is small to nano-size, since the equilibrium lattice spacing in the interface is different from that in the bulk, the interface stress effect must be considered. In recent years, with the extensive preparation and application of nanomaterials, researches on the nano-size began to emerge in large numbers (see, for example, [23–25]).

There often are third-phase inclusions near a bimaterial interface, and a strong coupling interaction of dislocations with the inclusions and the bimaterial interface arises. Such a coupling interaction plays an important role in bimaterial interface properties. However, this coupling interaction cannot be obtained by a linear superposition of existing solutions for an isolated inclusion and an isolated bimaterial interface. A basic understanding of such coupling interaction effects must be gained to achieve the full potential of bimaterials and to design novel bimaterials and bimaterial structures. This work deals with the coupling interaction of a screw dislocation with a bimaterial interface and a nearby circular inclusion, with focus on the derivation of the analytical solution where the coupling interaction effects are separated, and on the revelation of interesting coupling interaction phenomena that cannot be shown by the existing solutions.

2 Model and basic equations

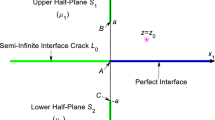
The physical problem under consideration is shown in Fig. 1a, where $S_1, S_2$ and $S_3$ denote the regions occupied by Material 1, Material 2 and the inclusion (with the radius $R_1$), respectively. $\varGamma _1$ and $\varGamma _2$ are the bimaterial interface and the inclusion/Material 2 interface. The origin of a Cartesian coordinate system lies at the center of the inclusion, and the $x$-axis is perpendicular to the bimaterial interface. $h$ represents the distance between the inclusion and bimaterial interface. The materials in three regions are assumed to be transversely isotropic. A screw dislocation with the Burgers vector b is located at an arbitrary point $z_0$ in Material 1 ($S_1$) or Material 2 ($S_2$).

Fig. 1

a A screw dislocation near the bimaterial interface as well as near a circular inclusion. b Mapping regions and characteristic points in the $\zeta$-plane

For the convenience of analysis, the following conformal mapping is introduced:

$$\begin{aligned} z=m(\zeta )=\frac{R_2 \zeta +R_1^2 }{\zeta +R_2 }, \end{aligned}$$

(1)

where $z=x+\hbox {i}y,\, \zeta =\xi +\hbox {i}\eta$ and $R_2 =(R_1 +h)+\sqrt{(R_1 +h)^{2}-R_1^2 }$. The regions $S_1, S_2$ and $S_3$ in the $z$-plane (refer to Fig. 1a) are, respectively, mapped onto the regions ${S}^{\prime }_1$ ($\left| \zeta \right| >R_2$), ${S}_2^{\prime } (R_1 <\left| \zeta \right| <R_2 )$ and ${S}^{\prime }_3$ ($\left| \zeta \right| <R_1 )$ in the $\zeta$-plane (refer to Fig. 1b). The interfaces $\varGamma _1$ and $\varGamma _2$ are mapped onto the concentric circles $\varPi _1$ and $\varPi _2$, respectively. The coordinate origin $O$, the infinity and the points $z_0$ are mapped onto the points ${O}^{\prime }(\zeta =-{R_1^2 }/{R_2 }$), $K (\zeta =-R_2 )$ and $\zeta _0$, respectively.

Referring to [26] and our recent work [27], the displacement $w$, the shear stress components $\tau _{zx}$ and $\tau _{zy}$ and the resultant force $T$ along any arc AB (not pass through interfaces of dissimilar phases) can be expressed in terms of a complex potential function $\varphi (\zeta )$ in the $\zeta$-plane

$$\begin{aligned}&\displaystyle w=\frac{1}{2\mu }\left[ {\varphi (\zeta )+\overline{\varphi (\zeta )} } \right] , \end{aligned}$$

(2)

$$\begin{aligned}&\displaystyle \tau _{xz} -\hbox {i}\tau _{yz} =\frac{{\varphi }^{\prime }(\zeta )}{{m}^{\prime }(\zeta )}, \end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle T=\int \limits _A^B {\tau _{zn} \hbox {d}s} =\int \limits _A^B {\left( {\tau _{xz} \hbox {d}y-\tau _{yz} \hbox {d}x} \right) } =\frac{\hbox {i}}{2}\left[ {\overline{\varphi (\zeta )} -\varphi (\zeta )} \right] _ {{A^{\prime }}}^{B^{\prime }}. \end{aligned}$$

(4)

where $\mu$ is the shear modulus of the material, the overbar represents the complex conjugate, the superscript prime denotes the differentiation with respect to the argument, $\tau _{zn}$ denotes the normal component of the shear stress on any arc $AB$ in the $z$-plane, and $\left[ {\bullet } \right] _{{A}^{\prime }}^{{B^{\prime }}}$ signifies the change in the bracketed function in going from the point ${A}^{\prime }$ to the point ${B}^{\prime }$ along the arc ${A}^{\prime }{B}^{\prime }$, where ${A}^{\prime }{B}^{\prime }$ is the mapping arc in the $\zeta$-plane corresponding to $AB$ in the $z$-plane.

The assumption of perfect bonding between dissimilar materials implies the continuity conditions of displacements and stresses on two interfaces. By introducing three complex potentials, $\varphi _1 (\zeta ),\varphi _2 (\zeta )$ and $\varphi _3 (\zeta )$, in the corresponding regions, Material 1, Material 2 and the inclusion, and using Eqs. (2) and (4), the continuity conditions can be expressed as

(i) displacements continuity conditions

$$\begin{aligned} \left\{ {{\begin{array}{l} {\mu _2 \left[ {\overline{\varphi _1 (t)} +\varphi _1 (t)} \right] _{{S}_1^{\prime } } =\mu _1 \left[ {\overline{\varphi _2 (t)} +\varphi _2 (t)} \right] _{{S}_2^{\prime } } \quad \hbox {on }\,\varPi _1 } \\ {\mu _3 \left[ {\overline{\varphi _2 (t)} +\varphi _2 (t)} \right] _{{S}_2^{\prime } } =\mu _2 \left[ {\overline{\varphi _3 (t)} +\varphi _3 (t)} \right] _{{S}_3^{\prime } }\quad \hbox { on }\,\varPi _2 } \\ \end{array} }} \right. , \end{aligned}$$

(5)

(ii) stresses continuity conditions

$$\begin{aligned} \left\{ {{\begin{array}{l} {\left[ {\overline{\varphi _1 (t)} -\varphi _1 (t)} \right] _{{S}^{\prime }_1 } =\left[ {\overline{\varphi _2 (t)} -\varphi _2 (t)} \right] _{{S}^{\prime }_2 } \quad \hbox {on }\varPi _1 } \\ {\left[ {\overline{\varphi _2 (t)} -\varphi _2 (t)} \right] _{{S}^{\prime }_2 } =\left[ {\overline{\varphi _3 (t)} -\varphi _3 (t)} \right] _{{S}^{\prime }_3 }\quad \hbox { on }\varPi _2 } \\ \end{array} }} \right. , \end{aligned}$$

(6)

where the subscripts, ${S}^{\prime }_1, {S}^{\prime }_2$ and ${S}^{\prime }_3$, refer to the function values as approached from the three corresponding regions, respectively.

3 Complex potential solutions

In this section, the complex potential solutions and their new expressions with various interaction effects separated will be given for the two cases that the screw dislocation is located in Material 2 and Material 1, respectively.

3.1 A dislocation inside Material 2

Referring to Ref. [27], when the screw dislocation is located in Material 2, the complex potential in ${S}_2^{\prime }$ can be written as

$$\begin{aligned} \varphi _2 (\zeta )=\varphi _{\mathrm{2S}} (\zeta )+\varphi _{20} (\zeta )=\frac{\mu _2 b}{2\pi \hbox {i}}\ln \frac{\zeta -\zeta _0 }{\zeta +R_2 }+\varphi _{20} (\zeta ), \end{aligned}$$

(7)

where the first term $\varphi _{\mathrm{2S}} (\zeta )$ is the singular part. In the annular region ${S}_2^{\prime }$ ($R_1 <\left| \zeta \right| <R_2 )$, the holomorphic part $\varphi _{20} (\zeta )$ can be expanded into a Laurent series

$$\begin{aligned} \varphi _{20} (\zeta )=G_P (\zeta )+G_N (\zeta )=\sum _{n=1}^\infty {C_n \zeta ^{n}} +\sum _{n=1}^\infty {D_n \zeta ^{-n}}, \end{aligned}$$

(8)

where the constant term representing the rigid displacement is neglected. Using the continuity conditions of displacements and stresses (5)–(6) and following the works in Refs. [26] and [27], the complex potentials can be obtained

$$\begin{aligned} \varphi _1 (\zeta )= & {} \frac{1+k_1 }{2}\frac{\mu _2 b}{2\pi \hbox {i}}\ln \frac{\zeta -\zeta _0 }{\zeta +R_2 }+\frac{k_3 -1}{2}\frac{\mu _2 b}{2\pi \hbox {i}}\ln \frac{\zeta -{R_1^2 }/{\overline{\zeta _0 } }}{\zeta +{R_1^2 }/{R_2 }}+\frac{1-k_3 }{2}\overline{G_P } ({R_1^2 }/\zeta ) \nonumber \\&+\,\frac{k_1 -1}{2}\overline{G_P } \left( {R_2^2 }/\zeta \right) +\frac{k_1 -k_3 }{2}G_N (\zeta ) \end{aligned}$$

(9)

$$\begin{aligned} \varphi _3 (\zeta )= & {} \frac{1+k_3 }{2}\frac{\mu _2 b}{2\pi \hbox {i}}\ln \frac{\zeta -\zeta _0 }{\zeta +R_2 }+\frac{k_1 -1}{2}\frac{\mu _2 b}{2\pi \hbox {i}}\ln \frac{\zeta -{R_2^2 }/{\overline{\zeta _0 } }}{\zeta +R_2 }+\frac{k_3 -1}{2}\overline{G_N } \left( {R_1^2 }/\zeta \right) \nonumber \\&+\,\frac{1-k_1 }{2}\overline{G_N } \left( {R_2^2 }/\zeta \right) +\frac{k_3 -k_1 }{2}G_P (\zeta ) \end{aligned}$$

(10)

where $\overline{G_P } (\zeta )=\sum \limits _{n=1}^\infty {\overline{C_n } \zeta ^{n}}, \overline{G_N } (\zeta )=\sum \limits _{n=1}^\infty {\overline{D_n } \zeta ^{n}}, k_1 ={\mu _1 }/{\mu _2 }$ and $k_3 ={\mu _3 }/{\mu _2 }$. The complex coefficients $C_n$ and $D_n$ in the solutions (8)–(10) are

$$\begin{aligned} \left\{ {{\begin{array}{l} {C_n =\frac{(k_1 -1)\mu _2 b}{2L\pi \hbox {i}}\left( {(k_3 +1)\frac{(-1)^{n}R_2^{-n} -R_2^{-2n} \overline{\zeta _0 } ^{n}}{n}+(k_3 -1)\frac{(-1)^{n}\beta ^{2n}R_2^{-n} -\beta ^{2n}\zeta _0^{-n} }{n}} \right) } \\ {D_n =\frac{(k_3 -1)\mu _2 b}{2L\pi \hbox {i}}\left( {(k_1 -1)\frac{(-1)^{n}\beta ^{2n}R_2^n -\beta ^{2n}\zeta _0^n }{n}+(k_1 +1)\frac{(-1)^{n}\beta ^{2n}R_2^n -R_1^{2n} \overline{\zeta _0 } ^{-n}}{n}} \right) } \\ \end{array} }} \right. \end{aligned}$$

(11)

where $L=(k_1 +1)(k_3 +1)-(k_1 -1)(k_3 -1)\beta ^{2n}$ and $\beta ={R_1 }/{R_2 }$.

When $\mu _3 =\mu _2$ (i.e., $k_3 =1)$, the solution (8) degenerates into the previous solution of a screw dislocation near a bimaterial interface without any third-phase inclusion [3]

$$\begin{aligned} \varphi _{2} (\zeta )=\varphi _{\mathrm{2S}} (\zeta )+\varphi _{\mathrm{Int0}} (\zeta )=\frac{\mu _2 b}{2\pi \hbox {i}}\ln \frac{\zeta -\zeta _0 }{\zeta +R_2 }+\frac{k_1 -1}{k_1 +1}\frac{\mu _2 b}{2\pi \hbox {i}}\ln \frac{\zeta -{R_2^2 }/{\overline{\zeta _0 } }}{\zeta +R_2 }, \end{aligned}$$

(12)

where $\varphi _{\mathrm{2S}} (\zeta )$ refers to the singular part in Eq. (7) and $\varphi _{\mathrm{Int0}} (\zeta )$ is a holomorphic function, which represents the interaction of the screw dislocation with the bimaterial interface. If $\mu _1 =\mu _2$ (i.e., $k_1 =1$), the solution (8) degenerates into the previous solution of a screw dislocation near a circular inclusion in an infinite medium [10]

$$\begin{aligned} \varphi _\mathrm{2} (\zeta )=\varphi _{\mathrm{2S}} (\zeta )+\varphi _{\mathrm{Inc0}} (\zeta )=\frac{\mu _2 b}{2\pi \hbox {i}}\ln \frac{\zeta -\zeta _0 }{\zeta +R_2 }+\frac{k_3 -1}{k_3 +1}\frac{\mu _2 b}{2\pi \hbox {i}}\ln \frac{\zeta -{R_1^2 }/{\overline{\zeta _0 } }}{\zeta +{R_1^2 }/{R_2 }}, \end{aligned}$$

(13)

where $\varphi _{\mathrm{Inc0}} (\zeta )$ is also a holomorphic function, which represents the interaction of the screw dislocation with a circular inclusion.

In terms of basic solutions (12) and (13), the complex potential $\varphi _2 (\zeta )$ can be cast into a new expression $\varphi _{\mathrm{2New}} (\zeta )$ with various interaction effects separated:

$$\begin{aligned} \varphi _{\mathrm{2New}} (\zeta )=\varphi _{\mathrm{2S}} (\zeta )+\varphi _{\mathrm{Int0}} (\zeta )+\varphi _{\mathrm{Inc0}} (\zeta )+\varphi _{\mathrm{Cpl}} (\zeta ), \end{aligned}$$

(14)

where $\varphi _{\mathrm{Cpl}} (\zeta )$ is the only series term representing the coupling interaction of the dislocation with the bimaterial interface and inclusion. Compared with Eq. (7), $\varphi _{\mathrm{Cpl}} (\zeta )$ is given as

$$\begin{aligned} \varphi _{\mathrm{Cpl}} (\zeta )= & {} (k_1 -1)(k_3 -1)\frac{\mu _2 b}{2\pi \hbox {i}}\sum _{n=1}^\infty {\frac{(-1)^{n}\beta ^{2n}R_2^{-n} -\beta ^{2n}\zeta _0^{-n} }{nL}\cdot \zeta ^{n}} \nonumber \\&+\,\frac{(k_1 -1)^{2}(k_3 -1)}{k_1 +1}\frac{\mu _2 b}{2\pi \hbox {i}}\sum _{n=1}^\infty {\frac{(-1)^{n}\beta ^{2n}R_2^{-n} -\beta ^{2n}R_2^{-2n} \overline{\zeta _0 } ^{n}}{nL}\cdot \zeta ^{n}} \nonumber \\&+\,\frac{(k_3 -1)(k_1 -1)}{(k_3 +1)}\frac{\mu _2 b}{2\pi \hbox {i}}\sum _{n=1}^\infty \left\{ \frac{(k_3 +1)\left[ (-1)^{n}\beta ^{2n}R_2^n -\beta ^{2n}\zeta _0^n \right] }{nL}\right. \nonumber \\&\left. +\,\frac{(k_3 -1)[(-1)^{n}\beta ^{4n}R_2^n -R_1^{2n} \beta ^{2n}\overline{\zeta _0 } ^{-n}]}{nL}\right\} \cdot \zeta ^{-n}, \end{aligned}$$

(15)

Since the coupling interaction $\varphi _{\mathrm{Cpl}} (\zeta )$ is a higher-order interaction effect than $\varphi _{\mathrm{Int0}} (\zeta )$ and $\varphi _{\mathrm{Inc0}} (\zeta )$, the convergence of $\varphi _{\mathrm{2New}} (\zeta )$ is much better than that of $\varphi _2 (\zeta )$, especially in the case when the dislocation is near the inclusion or bimaterial interface. The first-order approximation of Eq. (14) [taking the first term of Eq. (15)] is of high accuracy, which can be shown by using the similar way in our recent work [27].

3.2 A dislocation inside Material 1

Similarly, when the screw dislocation is located in Material 1, the complex potentials in three regions can be derived as

$$\begin{aligned}&\displaystyle \varphi _1 (\zeta ) = \frac{\mu _1 b}{2\pi \hbox {i}}\ln \frac{\zeta -\zeta _0 }{\zeta +R_2 }+\frac{1-k_3 }{2}\overline{{G}_P^{\prime } } \left( {R_1^2 }/\zeta \right) +\frac{k_1 -1}{2}\overline{{G}_P^{\prime } } \left( {R_2^2 }/\zeta \right) +\frac{k_1 -k_3 }{2}{G}_N^{\prime } (\zeta ), \end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle \varphi _2 (\zeta ) = {G}_P^{\prime } (\zeta )+{G}_N^{\prime } (\zeta )=\sum _{n=1}^\infty {{C}_n^{\prime } \zeta ^{n}} +\sum _{n=1}^\infty {{D}_n^{\prime } \zeta ^{-n}}, \end{aligned}$$

(17)

$$\begin{aligned}&\displaystyle \varphi _3 (\zeta ) = \frac{\mu _1 b}{2\pi \hbox {i}}\ln \frac{\zeta -\zeta _0 }{\zeta +R_2 }+\frac{k_3 -1}{2}\overline{{G}_N^{\prime } } \left( {R_1^2 }/\zeta \right) +\frac{1-k_1 }{2}\overline{{G}_N^{\prime } } \left( {R_2^2 }/\zeta \right) +\frac{k_3 -k_1 }{2}{G}_P^{\prime } (\zeta ). \end{aligned}$$

(18)

The complex coefficients ${C}_n^{\prime }$ and ${D}_n^{\prime }$ are

$$\begin{aligned} \left\{ {{\begin{array}{l} {{C}_n^{\prime } =\frac{(k_3 +1)\mu _1 b\left( {(-1)^{n}R_2^{-n} -\zeta _0^{-n} } \right) }{nL\pi \hbox {i}}} \\ {{D}_n^{\prime } =\frac{(k_3 -1)\mu _1 b\left( {(-1)^{n}R_1^{2n} R_2^{-n} -R_1^{2n} \overline{\zeta _0 } ^{-n}} \right) }{nL\pi \hbox {i}}} \\ \end{array} }} \right. , \end{aligned}$$

(19)

where $L=(k_1 +1)(k_3 +1)-(k_1 -1)(k_3 -1)\beta ^{2n}$. The complex potential with various interaction effects separated in Material 1 is obtained similarly

$$\begin{aligned} \varphi _{\mathrm{1New}} (\zeta )= & {} \frac{\mu _1 b}{2\pi \hbox {i}}\ln \frac{\zeta -\zeta _0 }{\zeta +R_2 }+\frac{k_3 -1}{k_3 +1}\frac{\mu _1 b}{2\pi \hbox {i}}\ln \frac{\zeta -{R_1^2 }/{\overline{\zeta _0 } }}{\zeta +{R_1^2 }/{R_2 }}+\frac{1-k_1 }{k_1 +1}\frac{\mu _1 b}{2\pi \hbox {i}}\ln \frac{\zeta -{R_2^2 }/{\overline{\zeta _0 } }}{\zeta +R_2 } \nonumber \\&+\,\frac{(1-k_1 )(k_3 -1)}{(k_1 +1)(k_3 +1)}\frac{\mu _1 b_1 }{2\pi \hbox {i}}\sum _{n=1}^\infty {\frac{M}{L}\cdot \frac{(-1)^{n}\beta ^{2n}R_2^n -R_1^{2n} \overline{\zeta _0 } ^{-n}}{n}\cdot \zeta ^{-n}}, \end{aligned}$$

(20)

where $M=(k_1 -1)(k_3 +1)-(k_1 +1)(k_3 -1)\beta ^{2n}$. The new expression $\varphi _{\mathrm{1New}}$ also more rapidly converges than the original solution $\varphi _1$ in Eq. (16). The first-order approximation of the new expression (20) is of high accuracy.

4 Interaction energy and image force

4.1 Nondimensional expressions of the interaction energy and image force

The interaction energy and image force acting on dislocations are of practical importance in understanding the behavior of inhomogeneous materials. Referring to our recent work [27], the nondimensional interaction energy and image force can be, respectively, written as

$$\begin{aligned}&\displaystyle \tilde{W}_i =\frac{{2\pi }}{\mu _2 b}\,\hbox {Im}\,\left[ {\varphi _{i0} (\zeta _0 )} \right] \quad \zeta _0 \in {S}_i^{\prime }, \end{aligned}$$

(21)

$$\begin{aligned}&\displaystyle \tilde{F}_i =\frac{2\pi R_1 }{\mu _2 b^{2}}\left( {F_{ix} -\hbox {i}F_{iy} } \right) =\frac{2\pi R_1 \hbox {i}}{\mu _2 b}\left[ {\frac{{\varphi }_{i0}^{\prime } (\zeta )}{{m}^{\prime }(\zeta )}} \right] _{\zeta =\zeta _0 } \quad \zeta _0 \in {S}_i^{\prime }, \end{aligned}$$

(22)

where $i=1,2, F_x$ and $F_y$ are the image force components in the $x$-axis and $y$-axis directions, respectively.

In the following subsection, the numerical examples are presented to demonstrate the intricate and interesting coupling interaction induced by the inclusion and bimaterial interface.

4.2 Interaction energy contours and image force lines

In terms of Eqs. (21) and (22), the interaction energy and image force of a screw dislocation can be evaluated for different combinations of parameters (two modulus ratios $k_1 ={\mu _1 }/{\mu _2 }$ and $k_3 ={\mu _3 }/{\mu _2 }$ and a nondimensional distance $h/{R_1 })$. Noting the symmetry of the solutions, we need only to consider two cases of modulus ratios: (1) $k_1 ={\mu _1 }/{\mu _2 }<1$ and $k_3 ={\mu _3 }/{\mu _2 }<1$, (2) $k_1 ={\mu _1 }/{\mu _2 }<1$ and $k_3 ={\mu _3 }/{\mu _2 }>1$.

First consider case (1) and take an extreme modulus ratio $k_3 =0$ (the inclusion is a hole) for the convenience of discussion. For different values of $k_1$ and $h/{R_1 }$, nondimensional interaction energy contours [$\tilde{W}$, refer to Eq. (21)] and image force lines [$\tilde{F}$, refer to Eq. (22)] are depicted in Fig. 2, where the interaction energy contours are denoted by dashed lines with the values of $\tilde{W}$ being marked and the image force lines are denoted by solid lines with the directions of $\tilde{F}$ being marked. Figure 2 shows that the two families of curves are severely distorted. A dislocation near the hole in Material 2 is always attracted by the hole due to $k_3 =0$, at the same time a dislocation near the bimaterial interface in Material 2 is also always attracted by the bimaterial interface due to $k_1 <1$. Therefore, there must be one unstable dislocation equilibrium point ($E_1$, as shown in Figs. 2a–c) between the hole and bimaterial interface in Material 2.

Fig. 2

Interaction energy contours and image force lines for $k_3 ={\mu _3 }/{\mu _2 }=0$, where the dashed lines denote contours of the nondimensional interaction energy $\tilde{W}$ (values of $\tilde{W}$ are marked) and the solid lines show the direction of the nondimensional image force. a $k_1 =0.7$ and $h/{R_1 }=1$; b $k_1 =0.8$ and $h/{R_1 }=0.5$; c $k_1 =0.71335$ and $h/{R_1 }=0.5$

The equilibrium points in Material 1 are more intricate and interesting, which depend on the material elastic dissimilarity as well as the nondimensional distance between the hole and bimaterial interface. When $h/{R_1 }$ is large enough and/or $k_1$ is small enough, the repulsion from the bimaterial interface cannot be exceeded by the attraction from the hole, and the direction of the image force remains unchanged. There is no equilibrium point in Material 1, as shown in Fig. 2a, where $k_1 =0.7$ and $h/{R_1 }=1$. However, when $h/{R_1 }$ is small enough and/or $k_1$ is large enough (but it is still $<$1), two equilibrium points appear. Such a case is shown in Fig. 2b, where $k_1 =0.8$ and $h/{R_1 }=0.5$. Refer to the insets in Fig. 2b, it is seen that $E_2$ is a stable equilibrium point, whereas $E_3$ is an unstable equilibrium point. It is specially interesting that the image force inverse its direction between $E_2$ and $E_3$. Figure 2c shows a transition from Fig. 2a, b, where $k_1 =0.71335$ and $h/{R_1 }=0.5$. The point $E_2$, which coincides with $E_3$, also is a stationary point of the image force on the $x$-axis, and a detailed discussion refers to Sect. 4.3.

Now, consider the case (2) $k_1 <1$ and $k_3 >1$. For an extreme example $k_1 =0$ (i.e., the bimaterial interface reduces to the free surface), nondimensional interaction energy contours and image force lines in Material 1 degenerate to the results in the previous work [27]. For $k_1 \ne 0$, the dislocation in Material 1 is always repelled by the bimaterial interface and the inclusion, and there is no any equilibrium point; the dislocation in Material 2 is attracted by the bimaterial interface, whereas repelled by the inclusion, and there is only one unstable equilibrium point on the left of the hole. It is similar with the extreme example $k_1 =0$ and is not be shown to save space.

It is easy to find that the interaction energy and image force fields in case (3), $k_1 >1$ and $k_3 >1$, and case (4), $k_1 >1$ and $k_3 <1$, are similar to those in case (1), $k_1 <1$ and $k_3 <1$, and case (2), $k_1 <1$ and $k_3 >1$, respectively, except that the interaction energy and image force change their signs. As a result, all the equilibrium points become unstable.

4.3 A discussion on the image force and dislocation equilibrium points

Now further examine the variations of the image force and locations of dislocation equilibrium points. Figure 2 shows that there is always one and only one unstable dislocation equilibrium point in Material 2 with an inclusion. There is no any equilibrium point in Material 1 without inclusion in cases (2) and (4), whereas there may be zero, one or two equilibrium points in Material 1 in case (1) and (3). So the following discussion focuses on cases (1) and (3).

From Fig. 2, it is seen that the equilibrium points always lie on the $x$-axis because of the symmetry, and the image force on the $x$-axis varies most dramatically. Whether equilibrium points will appear depends on two material parameters: $k_1 ={\mu _1 }/{\mu _2}, k_3 ={\mu _3 }/{\mu _2 }$ and a geometrical parameter $h/{R_1 }$.

First consider case (1) and observe the influence of material parameters. Taking $k_3 =0$ and $h/{R_1 }=0.5$, variations of the nondimensional image force $\tilde{F}$ with $\delta /{R_1 }$ for various values of $k_1$ are shown in Fig. 3, where $\tilde{F}={2\pi R_1 F_{1x} }/{\mu _2 b^{2}}$, and $\delta$ is the distance from a point on the $x$-axis to the bimaterial interface. From Fig. 3, it is observed that for a small value of $k_1$ ($k_1 <0.71335$ as $k_3 =0$ and $h/{R_1 }=0.5)$, no equilibrium point in Material 1 appears and the direction of the image force always leaves from the bimaterial interface. When $k_1 >0.71335$, two equilibrium points, $E_2$ and $E_3$, appear and the direction of the image force becomes contrary within the region between $E_2$ and $E_3$. With the increase of $k_1$, $E_2$ moves toward the bimaterial interface (from $E_2 (1)$ to $E_2 (2)$), whereas $E_3$ moves in a contrary direction (from $E_3 (1)$ to $E_3 (2))$. As a result, the image force reversion region expands. When $k_1 =0.71335$, two equilibrium points ($E_2 (0)$ and $E_3 (0))$ coincide.

Fig. 3

Variations of the nondimensional image force $\tilde{F}$ in Material 1 versus $\delta /{R_1 }$ for various values of $k_1$, where $k_3 ={\mu _3 }/{\mu _2 }=0$ and $h/{R_1 }=0.5$

It is interesting to note that the reversion region of the image force induced by the inclusion (hole in the extreme case) does not connect with the bimaterial interface, but has a certain distance from the bimaterial interface. Such an interesting phenomenon was also observed by other researchers. For example, Gutkin and Romanov [29] found that the edge dislocation in a thin two-phase plate might have from one to five equilibrium (stable and unstable) positions because of the reversible image forces, which depend on the Burgers vector orientation and the ratio between the elastic moduli of layers. In addition, in nanoindentation tests of crystals [30, 31], dislocation nucleation first occurs at a position of certain depth from the surface, which does not connect with the surface.

Now, discuss case (3) and examine the influence of the geometrical parameter $h/{R_1 }$. Taking $k_1 =1.3$ and $k_3 =10^{5}$, variations of the nondimensional image force $\tilde{F}$ in Material 1 with $\delta /{R_1 }$ for different values of $h/{R_1 }$ are shown in Fig. 4. From Fig. 4, it is observed that when the inclusion is far from the bimaterial interface, the influence of the inclusion in Material 2 on the image force in Material 1 becomes negligible, and when $h/{R_1 }>0.65561$, no equilibrium point in Material 1 appears. If $h/{R_1 }<0.65561$, two equilibrium points, ${E}_2^{\prime }$ and ${E}_3^{\prime }$, appear and the direction of image forces in the region between ${E}_2^{\prime }$ and ${E}_3^{\prime }$ becomes contrary. With the decrease of $h/{R_1 }, {E}_2^{\prime }$ and ${E}_3^{\prime }$ have the similar trendy of motion with $E_2$ and $E_3$ as shown in Fig. 3.

Fig. 4

Variations of the nondimensional image force $\tilde{F}$ in Material 1 versus $\delta /{R_1 }$ for various values of $h/{R_1 }$, where $k_1 ={\mu _1 }/{\mu _2 }=1.3$ and $k_3 ={\mu _3 }/{\mu _2 }=10^{5}$

As shown in Figs. 3 and 4, both the interaction energy and image force become unbounded as the dislocation approaching the bimaterial interface. This physically unsatisfactory result arises because of the idealization of a singular dislocation. However, the solutions are of practical importance. As pointed out by Dundurs [3], when the distance between the dislocation and bimaterial interface $\delta >3b$ ($b$ is the module of the Burgers vector b) and the mismatch in the moduli is small, such solutions give accurate results.

5 Conclusion

The coupling interaction of a screw dislocation with a circular inclusion and the bimaterial interface is dealt with. Explicit series solutions are obtained by using the complex potential and conformal mapping technique. Then the solutions are cast into new expressions where the coupling interaction effects are separated. The new expressions converge more rapidly, and their simple first-order approximation formulae are of high accuracy.

The interaction energy and image force acting on the dislocation are formulated and shown graphically. It is seen that the coupling interaction effects induced by the inclusion and bimaterial interface severely distort the interaction energy contours and image force lines when the inclusion and the bimaterial interface close to each other and material properties severely mismatch. It is found that there must be an unstable dislocation equilibrium point in Material 2 with a circular inclusion, whereas there may be zero, one or two equilibrium points in Material 1 without any inclusion, which depends on a combination of material properties and the nondimensional distance between the inclusion and bimaterial interface. It is interesting that an inclusion near the bimaterial interface may inverse the direction of image forces in a certain region of another material without any inclusion, and the image force inverse region does not connect with the bimaterial interface.