Modeling of chromosome aberration response functions induced by particle beams with different LET

Abstract

This study is based on our already published experimental data (Kowalska et al. in Radiat Environ Biophys 58:99–108, 2019) and is devoted to modeling of chromosome aberrations in human lymphocytes induced by 22.1 MeV/u ¹¹B ions, 199 MeV/u ¹²C ions, 150 MeV and spread-out Bragg peak (SOBP) proton beams as well as by ⁶⁰Co γ rays. The curvature of the dose–effect curves determined by the linear-quadratic model was considered in the frame of a simple analytical approach taking into account increase in the irradiation dose due to overlapping interaction regions of ion tracks. The model enabled to estimate effective interaction radius which could be compared with the physical expectations. The results were also compared to the Amorphous Track Structure Model of Katz which allows to get some additional information about the ion track structure. The analysis showed that the curvature of the experimental dose–effect curves mainly results from highly efficient repair processes of the DNA damage.

Introduction

The present paper is the second part of our study devoted to the analysis of chromosome aberrations of human lymphocytes induced by particle irradiation with different LET values, recently published in Radiation and Environmental Biophysics (Kowalska et al. 2019). This kind of investigations has a large impact on the cancer hadron radiotherapy and necessary understanding of the biological response to the ionizing radiation. The first part was focused on examination of experimental data, including both statistical distributions of the aberration frequency and resulting dose–effect curves, to demonstrate differences in experimentally determined parameters for different particle irradiations. The experimental data obtained should serve as the basis for a model description of the observed dependencies, which is an issue of the present work.

Among other things, we could show (Kowalska et al. 2019) that the Neyman type A statistical distribution reflecting the ion track structure of the particle radiation field determined by fast δ-electrons can very well describe the observed deviations from the Poisson distribution of aberration frequencies, especially in the case of high-LET ¹¹B ions for which the probability of aberration creation per one hit was close to unity. For other particle beams applied (150 MeV and SOBP protons, ¹²C ions), this parameter was much lower than one and surprisingly increased linearly with the radiation dose. This effect might result from the overlapping of ion tracks, which can locally increase the dose at higher particle fluencies and the corresponding biological response. The question arised why the same effect was not observed by us for boron ions for which the physical ion track radius, and thus, the overlapping probability was comparable to other ion beams. A recent theoretical survival study (Surdutovich and Solov’yov 2018) also demonstrated that the yield of lethal lesions as a function of deposited dose deviates from the exponential dependence at high doses due to the effect of ion track overlapping.

Chromosome aberration yield Y found at the given dose D can be parameterized using the radiotherapy applied linear-quadratic model (LQM):

$$ Y = \alpha \cdot D + \beta \cdot D^{2} $$

(1)

Here, the linear parameter α can be directly related to the probability of the double-strand DNA damage of irradiated cells and for moderate ionization densities should be linearly dependent on the LET value (Ando and Goodhead 2016). The quadratic parameter β can result both from physical and biological effects. Whereas the physical contribution due to the overlapping of ion tracks can be estimated for instance within the Monte Carlo calculations (Friedland et al. 2017), the biological component involving mainly repair mechanisms of the double-strand breaks is not known precisely enough to determine its contribution. Therefore, there are still no ab initio calculations that could fully explain the nonlinear term of the dose–effect curves (Friedland and Kundrat 2013). However, an approximate modeling of repair mechanisms enables to get successful results (Ballarini et al. 2014; Tello et al. 2018). On the other hand, there are powerful phenomenological models that can correctly describe the cell response to the highly non-uniform dose deposited in an ion track.

There are two main approaches that have been extensively developed in the past to explain cell inactivation by ion irradiation in the survival and chromosome aberration experiments: the Katz Model (also known as Amorphous Track Structure Model) (Katz et al. 1971; Katz 1988) and, more recently, the local effect model (LEM). Both models are based on the microscopic description of the amorphous track structure of the radial dose distribution and use the dose response function observed for gamma irradiation for construction of the dose response induced by particle beams. Therefore, these approaches can, in principle, include the contribution arising from repair mechanisms to the extent to which it is included in the gamma response. The LEM model (Scholz and Kraft 1996) utilizes the linear-quadratic parameterization without discussing the origin of the parameters. The only assumption made is that the same local dose density results in the same biological response, equally for the gamma and particle radiation. Contrary to this, the Katz model distinguishes between two different regions of an ion track: the gamma-kill region and the ion-kill region. Whereas the first region can be described by the gamma response function, the second one assumes inactivation of cells by the similar radiation dose density for all particle species. The Katz model leads to a different parameterization of the dose–effect curves. It can, however, take into account the overlapping effect between the ion tracks which can contribute to the gamma-kill region (Cucinotta et al. 1999).

The weak point of both models is their inability to separate the physical effect of overlapping ion tracks from the biological one. In order to estimate their relative relevance, we have developed a simple analytical approach, the effective track radius model (Kowalska et al. 2017) that enables to determine the ion interaction radius from the experimentally determined quadratic parameter of the dose–effect curve. A comparison to the physically expected values will allow us to estimate efficiency of the repair mechanisms for different ion beams. It is especially important in view of our experimental finding that the quadratic term of the dose effect curves does not significantly depend on the LET value of the particle irradiation. Here, we propose a modification of formulas for the effective track radius to fully include the two-dimensional stochastic nature of impinging ions onto biological targets.

The modeling of the dose effect curves presented in the first part of the study and considering possible overlapping effects of ion tracks will be the main goal of this paper.

Materials and methods

Experimental datasets used for the analysis

In this paper, we use the experimental data of chromosome aberrations (CA) presented in the first part of our work (Kowalska et al. 2019) where they have been analyzed with respect to the dose effect curves and statistical distributions of aberration frequencies. All experimental details of irradiation experiments are given in the first part of our work, only a general overview will be given here.

Blood samples—or isolated lymphocytes—obtained from informed, healthy, non-smoking volunteers were exposed to 199 MeV/u ¹²C ions (LET 16 keV/µm), monoenergetic ¹¹B ions (22.1 MeV/ u, LET 76 keV/µm), ⁶⁰Co γ rays and two different proton beams—unmodified 150 MeV proton beam (LET 0.57 keV/µm) and slowed-down protons at the central region of the 10 mm wide plateau of spread-out Bragg peak SOBP (average LET 1.4 keV/µm).

In the case of ¹¹B irradiation, isolated lymphocytes were highly concentrated in nutrient medium and shaped for irradiation as a 1.5 mm thick layer in specially designed plexiglas chambers. Immediately after irradiation, isolated lymphocytes were seeded at a density of 0.5 × 10⁶/ml in RPMI medium supplemented by 20% fetal calf serum, 2 mM L glutamine, 100 U/ml penicillin, 100 μg/ml streptomycin and 1.5% phytohaemagglutinin (PHA).

After exposure to protons, ¹²C ions and ⁶⁰Co γ rays, the blood samples were diluted in 4.5 ml of the same medium. All samples were incubated at 37 °C and 5% CO₂. Cells were fixed at 48 h after PHA stimulation proceeded by 3-h colcemid treatment (200 ng/ml) for metaphase accumulation and stained in 3% Giemsa. Typically, 100–300 metaphases were analyzed for every data point. Chromosomal aberrations were classified according to (Savage 1975). All aberrations of the chromosome and chromatid types visible without karyotyping were recorded. The chromosome-type aberrations comprise paired fragments, dicentrics, centric and acentric rings (the latter also includes double minutes) and translocations visible without karyotyping. The minor fraction of chromatid-type aberrations includes the chromatid-type breaks and chromatid-type exchanges. Gaps were not scored as aberrations.

Dose response curves and ion track overlapping

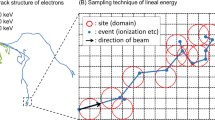
The total number of chromosome aberrations observed for different doses and irradiations can be described by a simple linear-quadratic dose response curve of the form $Y = \alpha \cdot D + \beta \cdot D^{2}$. The major yield of damage Y produced along the particle track corresponds to the linear part of the curve. The quadratic term is usually treated as a result of misrepair of breaks caused by electrons produced in more than one track (Loucas et al. 2013). It has been suggested (Loucas et al. 2013) that the overlapping regions of neighboring ion tracks may lead to higher local doses and therefore increase the biological effectiveness of radiation. In our previous work (Kowalska et al. 2017), we developed an analytical formula to relate the β parameter to the ion track radius and the LET value of the applied radiation. Within the proposed model, the experimentally determined dose–response curves can be described by an effective interaction radius R_eff which can be compared with the physical expectations resulting from the dose distribution of secondary electrons created in the ion track. As the latter is relatively well known, we can compare both values to estimate the efficiency of corresponding biological processes arising mainly from cellular repair mechanisms which can also influence the curvature of the dose–effect curves (Scholz 2006). The schematic view illustrating the idea of overlapping ion tracks is presented in Fig. 1.

Fig. 1

Schematic view of two overlapping ion tracks: a presented on microscopic dose distribution for 1 Gy of B¹¹ irradiation (E 22.1 MeV/u, LET 76 keV/µm) evaluated for us by Friedrich (GSI, Darmstadt, Germany) according to (Friedrich et al. 2012); b as assumed for calculations of the overlapping area assessed as a rectangle of $t$ and $t - r$ side; c and as a section of two overlapping circular shape tracks; t represents effective diameter of track electrons where the areal dose density can be treated as constant, r represents distance between centers of overlapping tracks and ω² stays for an area of a lymphocyte nucleus (within our model, the nucleus area is simplified to a square of ω = 5 μm side length)

To model this effect, we assume that the ion tracks are stochastically distributed over the target area, and thus, the probability of a distance r between centers of two ion tracks can be described by the following probability density function which can be derived from the two-dimensional Poisson distribution:

$$ P\left( r \right) = \frac{1}{{\pi L^{2} }}{\text{e}}^{{ - \frac{{r^{2} }}{{L^{2} }}}} $$

(2)

where L is a correlation parameter related to the mean value of the ion track distance:

$$ \left\langle r \right\rangle = \frac{1}{{\pi L^{2} }}\mathop \int \limits_{0}^{\infty } r{\text{e}}^{{ - \frac{{r^{2} }}{{L^{2} }}}} 2\pi rdr = \frac{\sqrt \pi }{2}L $$

(3)

Its value depends on the dose and thus on the number of tracks N created in the sample of the area ω² (i.e., area of G₀ lymphocyte cell nucleus equal to 25 μm², see Fig. 1a). Both quantities can be connected to each other by the relation describing the average area per track: $\left\langle r \right\rangle^{2} = \frac{{\omega^{2} }}{N}$. Therefore, L can be now determined as: $L^{2} = \frac{{4\omega^{2} }}{N}$.

Supposing that the quadratic term of the dose–effect curve results from overlapping interaction regions of the neighboring tracks where the irradiation dose is doubled, it is important to estimate an average overlapping area. In order to get final analytical expressions, a quadratic shape of ion tracks and a rectangular shape of the overlapping area of length t (see Fig. 1b) as well as a simplified probability density function $\frac{1}{{2\pi L^{2} }}{\text{e}}^{{ - \frac{r}{L}}}$ could be applied (see Kowalska et al. 2017):

$$ S_{\text{overlapping}} = \mathop \int \limits_{0}^{t} \frac{1}{{2\pi L^{2} }}{\text{e}}^{{ - \frac{r}{L}}} \cdot s_{\text{ov}} \cdot 2\pi rdr \approx \frac{1}{{2\pi L^{2} }}\mathop \int \limits_{0}^{t} {\text{e}}^{{ - \frac{r}{L}}} \left( {t - r} \right)t 2\pi rdr \approx \frac{{t^{4} }}{{6L^{2} }} $$

(4)

where $s_{\text{ov}}$ denotes the area of the overlapping tracks. In the case of circular tracks of a radius R, the corresponding expression reads as follows:

$$ s_{\text{ov}} = 2R^{2} { \arccos }\frac{r}{2R} - r\sqrt {R^{2} - \frac{{r^{2} }}{4}} $$

(5)

Now, a more exact expression for the average overlapping area including the two-dimensional probability density function (Eq. 2) and circular tracks (Eq. 5) can be given in terms of Eq. (4) corrected only by a geometrical factor F:

$$ S_{\text{overlapping}} = \mathop \int \limits_{0}^{t} \frac{1}{{\pi L^{2} }}{\text{e}}^{{ - \frac{{r^{2} }}{{L^{2} }}}} \cdot s_{\text{ov}} \cdot 2\pi rdr \approx F\frac{{t^{4} }}{{6L^{2} }} $$

(6)

The geometrical factor F can be calculated numerically (see Fig. 2); it takes on an approximately constant value of 1.17 for L/R > 10. Assuming that R is of order 0.1 μm and the cell nucleus area matches 25 μm², this inequity is satisfied for the number of hits per cell N < 25, confirming applicability of approximations performed. The result above is formally the same we have previously obtained in (Kowalska et al. 2017); however, the factor F is now twice as large because of differences in the normalizations of the probability density functions used.

Fig. 2

Geometrical factor F in dependence on the correlation parameter L (related to the ion track distance), normalized to the track radius R

Within our model, the aberration yield Y is assumed to be simply proportional to the number of non-overlapping ion tracks N and the interaction area of the individual track t²

$$ Y = A \cdot t^{2} \cdot N = \alpha \cdot D $$

(7)

Here, A represents the areal aberration density which is proportional to the dose density ρ as it is assumed in the LEM model. Thus, $A = \alpha \cdot \rho$ where $\alpha$ stays for the linear parameter in the dose–effect curve (Eq. 1). On the other hand, At² also represents the number of aberrations produced by a single track. Additionally, the dose d deposited by a single track can be expressed by the relation $d = \rho \cdot t^{2}$ where the areal dose density $\rho$ is assumed to be constant. Therefore, the total dose deposited in a cell by N tracks reads as follows:

$$ D = N \cdot \rho t^{2} $$

(8)

In the case of overlapping tracks, we can calculate the area of non-overlapping tracks S₁ as the difference between the area of all tracks $\left( {S = Nt^{2} } \right)$ and the area of overlapping tracks $\left( {S_{2} = NS_{\text{overlapping}} } \right)$.

$$ S_{1} = S - S_{2} = Nt^{2} - NS_{\text{overlapping}} $$

(9)

The overall yield of aberrations Y is then a sum of misrejoined breaks from ionization events of a single track Y₁ (corresponding to S₁) and misrejoined breaks Y₂ from the overlapping regions of neighboring tracks (corresponding to S₂). Here, we neglect a small effect of break misrejoining simultaneously in both regions since it is limited to small distances of about 0.7–0.8 µm (Tello et al. 2018):

$$ Y = Y_{1} + Y_{2} = \left( {N\alpha \rho t^{2} - N\alpha \rho S_{\text{overlapping}} } \right) + 2N\alpha \rho S_{\text{overlapping}} $$

(10)

where the factor 2 for Y₂ arises from the double dose cumulated in the overlapping regions. Taking into account the expression for the parameter L and N = D/d, the final equation for the aberration yield Y can be expressed as follows:

$$ Y = \alpha D + \alpha \cdot F \cdot \frac{{\pi Nt^{2} }}{{24\omega^{2} }}D = \alpha D + \frac{{ \pi \alpha t^{2} }}{{24d\omega^{2} }} \cdot F \cdot D^{2} $$

(11)

The coefficient at the quadratic term in the expression above corresponds to the β parameter of the dose–effect curve. Furthermore, the dose d deposited by a single track can be calculated from the LET definition describing the ionization density localized along the whole length x of the irradiated cell nucleus of the material density ρ_m (the cell volume is equal to x³):

$$ d = \frac{{{\text{LET}} x}}{{\rho_{m} x^{3} }} = \frac{\text{LET}}{{\rho_{m} x^{2} }} $$

(12)

Since the effective track radius R_eff is equal to t/2, and the lymphocyte nucleus area ω² ≈  x², we get:

$$ \frac{\beta }{\alpha } = \frac{\pi }{24}\frac{{F\rho_{m} x^{2} }}{{{\text{LET}} \omega^{2} }} \cdot 4R_{\text{eff}}^{2} = \frac{\pi }{6}\frac{{F\rho_{m} }}{\text{LET }}R_{\text{eff}}^{2} $$

(13)

And finally, the effective track radius which can explain experimentally observed curvature of the dose effect curves $\frac{\beta }{\alpha }$ can be obtained from the relation:

$$ R_{\text{eff}} = \sqrt {\frac{{6 \cdot {\text{LET}}}}{{\pi \cdot F \cdot \rho_{m} }}} \cdot \sqrt {\frac{\beta }{\alpha }} $$

(14)

Assuming ρ_m ≈ 1 g/cm³, the following numerical formula to assess R_eff can be used:

$$ R_{\text{eff}} \left[ {\text{nm}} \right] = 510 \cdot \sqrt {{\text{LET}} \left[ {\text{keV}}/{\upmu{\text{m}}} \right]} \cdot \sqrt {\frac{{ \beta \left[ 1 / {\text{Gy}^{2} } \right]}}{{\alpha \left[ 1 / {\text{Gy}} \right]}}} . $$

(15)

The experimental effective track radius R_eff may be compared to a physical one R_eff′, obtained by integration of the radial dose distribution D(r) ~ 1/r² (described by Scholz and Kraft 1996) over the whole physical track range defined by R_max corresponding to the range of fast δ electrons. The dose in the core of the ion track is assumed to be constant up to the radius R_min. Finally, the physical effective radius corresponding to a constant dose distribution can be expressed by the formula:

$$ R_{\text{eff}}^{{\prime }} = R_{\rm{min} } \sqrt {1 + 2\ln \frac{{R_{\rm{max} } }}{{R_{\rm{min} } }}} $$

(16)

where $R_{\rm{max} } = 0.768E - 1.925\sqrt E + 1.257\;{{\upmu}{\text{m}}}$ (Chatterjee and Schaefer 1976) and $R_{\rm{min} } = \frac{v}{c} \cdot 0.0116\;\left[ {{\upmu}{\text{m}}} \right]$ (Chatterjee and Schaefer 1976). Here, v is particle’s velocity, c is the speed of light, and E stands for particle’s kinetic energy per nucleon.

The Katz model

Within the Katz model (Katz et al. 1971, Katz 1978), the structure of the ion tracks plays a very important role. The central part of the ion track connected to a very high free-electron density is responsible for the DNA damages which lead to a lethal cell injury. In the outer part of the ion track (penumbra) of a low electron density, the DNA damages should have a sublethal character, and therefore many cell sub-targets have to be hit before the cell can be killed. The Katz model is usually used to describe the survival experiments of irradiated cell lines whereby cell inactivation arises from two mechanisms: the ion-kill and gamma-kill modes which are associated with the high and low electron density regions of the ion tracks, respectively. Cell surviving fraction SF is the product of surviving fractions connected to both these modes:

$$ {\text{SF}}\left( D \right) = {\text{e}}^{{ - N_{\text{lethal}} }} = \prod_{i} \left( D \right) \cdot \prod_{\gamma } \left( D \right) $$

(17)

where for the ion-kill, the single-target single-hit probability is used:

$$ \prod_{i} \left( D \right) = {\text{e}}^{ - \sigma F} $$

(18)

Here, F denotes the beam fluence and σ determines the part of the total dose deposited in the ion-kill region. Accordingly, the total dose consists of two components, the ion-kill D_i and the gamma-kill D_γ:

$$ D = D_{i} + D_{\gamma } = \frac{\sigma }{{\sigma_{0} }} D + \left( {1 - \frac{\sigma }{{\sigma_{0} }} } \right)D $$

(19)

whereby the ratio $\frac{\sigma }{{\sigma_{0} }}$ defines decomposition of the total dose and the parameter $\sigma_{0}$ corresponds to the cross-sectional area of the cell nucleus. The gamma-kill mode is assumed to be described by m-target single-hit approximation:

$$ \prod_{\gamma } \left( D \right) = 1 - (1 - {\text{e}}^{{ - D_{\gamma } /D_{0} }} )^{m} $$

(20)

Parameters D₀ and m are specific for a given cell line and can be determined by fitting the survival curves obtained experimentally for gamma irradiation. The parameter σ is characteristic for the charged ions used and therefore have to be separately determined for a given radiation quality. On the other hand, the ratio $\frac{\sigma }{{\sigma_{0} }}$ can be estimated if the ion track structure is known (Katz et al. 1971):

$$ \frac{\sigma }{{\sigma_{0} }} = \left[ {1 - {\text{e}}^{{\left( { - Z^{*2} /{{\kappa \beta^{2} }} } \right)}} } \right]^{m} $$

(21)

where Z* is the effective ion charge traversing the target with the relative velocity β = v/c. The parameter κ should be then independent of the applied ions and additionally related to the interaction radius of the ion track a₀:

$$ \kappa = 5 \cdot 10^{2} \cdot D_{0} \cdot a_{0}^{2} \left[ {\text{Gy}}^{ - 1} \cdot {{\upmu} {\text{m}}^{ - 2} } \right] $$

(22)

In the experiments in which the number of chromosome aberrations is measured, the dose response curves can be easily obtained by logarithm of Eq. (17) if we assume that the number of lethal injured cells is proportional to the number of chromosome aberrations:

$$ Y\left( D \right) = - \ln \left( {\text{SF}} \right) = \alpha \frac{\sigma }{{\sigma_{0} }}D - ln\left[ {1 - \left( {1 - {\text{e}}^{{ - \left( {1 - \frac{\sigma }{{\sigma_{0} }}} \right)\frac{D}{{D_{0} }}}} } \right)^{m} } \right] $$

(23)

where α in the first term is the linear parameter of the dose–effect curve obtained for high-LET ions for which the dose–effect is linear. In that case, only ion-kill mode takes place since $\sigma = \sigma_{0}$ and $\sigma F = D$ (see Eq. 18). Thus, the Katz model has only four independent parameters. The $\sigma_{0}$ parameter can be unambiguously determined by fitting the linear dose–effect curve obtained for Boron ions. The D₀ and m parameters can be determined by fitting the dose–effect curve measured for gamma irradiation. Finally, the irradiation experiments of different ions can be described by a corresponding σ parameter which should, however, be determined by the same κ parameter. Furthermore, the $\sigma_{0}$ parameter should be very close to the cross section of the lymphocyte cell of 25 μm².

Results

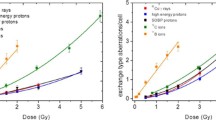
In Fig. 3, dose–response curves of chromosome aberrations fitted by means of the linear-quadratic model (LQ) and the Katz model are presented. Table containing detailed CA data has been already presented in the first part of the study (Kowalska et al. 2019).

Fig. 3

Comparison of the LQ model and the Katz model

Based on the CA dose–effect curves fitted by the LQ model, we could perform an analysis of the effective track radius of different ions. Table 1 contains experimentally determined parameters of the LQ model and β/α ratios for all considered radiation types: ⁶⁰Co γ rays, 150 MeV and SOBP protons, 199 MeV/u ¹²C ions and 22 MeV/u ¹¹B ions. The linear parameter of the dose–response curve (α) increases with increasing LET, while the quadratic parameter (β)—excluding ¹¹B ions—does not change significantly.

Table 1 Parameters of CA dose response fits

Values of the physical maximum track radius and the physical track core radius according to R_max and R_min formulas leading to the physical effective track radius R_eff′ (see Eq. 16) are presented in Table 2 and compared with the experimentally determined effective track radius R_eff (Eq. 15). Additionally, we present the radius of track core assumed for the local effect model (LEM) and described by Elsässer et al. (2008), denoted here as R_LEM. The best agreement between the physical radius and the LEM radius is achieved when the track core is calculated according to the formula $R_{\text{LEM}} = 40\frac{v}{c}$ (nm), where v comprises ion’s velocity and c—the speed of light.

Table 2 Comparison of parameters relevant for calculation of the effective biological interaction radius R_eff and the a₀ parameter of the Katz model

We have adapted the Katz model to study the chromosome aberration dose effect curves and compared its results with the linear-quadratic model (LQ) (see Fig. 3). The parameters of the Katz model and corresponding uncertainties have been obtained by the nonlinear Levenberg–Marquardt fitting procedure and are collected in Table 3. The values of the κ parameter have been calculated according to Eq. (21) separately for each ion beam, taking into account that the effective charge Z* is just equal to the atomic number for all energies and ions applied. In contradiction to the assumptions of the Katz model, the parameters κ and a₀ (Eq. 22) are not constant and increase with the growing LET value of the ion beam. Furthermore, the shape of the dose effect curves calculated within the Katz model significantly deviates from the experimentally observed, especially for higher doses.

Table 3 Parameters of the Katz model: σ corresponds to the cross section of a single subtarget, σ₀ represents the cell nucleus area, m stays for the number of 1-hit targets which are located in a cell nucleus, and D₀ corresponds to the specific dose (see Eqs. 17–23)

Discussion and conclusions

Chromosome aberrations of human lymphocytes induced by particle beams with different LET values, 150 MeV and spread-out Bragg peak (SOBP) proton beams, 199 MeV/u carbon beam and the boron ions of much lower energy 22 MeV/u as well as ⁶⁰Co γ rays, were considered in terms of linear-quadratic dose effect curves which are widely utilized in the clinical radiotherapy. The experimental data used were previously published in the first part of our study (Kowalska et al. 2019) where they were subjected to a detailed statistical analysis of the frequency of chromosome aberrations. The main result of the study was that the probability for the chromosome aberrations per a single ion hit derived from the Neyman type A statistics increases with the radiation dose. This increase is smaller for ion beams of higher LET values and vanishes for boron ions. A similar effect has been observed for dose effect curves, the curvature of which, measured as the ratio of the quadratic and linear parameter (β/α), decreases with increasing LET value and finally disappears for boron ions. Additionally, we have found that the quadratic parameter remains almost constant for all applied radiation qualities, which agrees with our previous results (Kowalska et al. 2017) and results of other authors for protons (George et al. 2015) and carbon ions (Lee et al. 2011).

The main aim of the present study was to model the experimental dose–effect curves and explain the origin of their quadratic term which can generally result from physical effects due to doubling of the local dose by overlapping ion tracks or biological effects of cellular repair mechanisms. To this end we applied our analytical model of the effective track radius (Kowalska et al. 2017) which was here modified to include two-dimensional Poisson statistics of ions impinging the biological targets. Based on the probability function for overlapping of ion track interaction regions, we could estimate the effective radius of these regions which could explain the curvature of the experimental dose–effect curves (β/α ratio). The physically expected values are turned out to be by a factor between 15 (high energy protons) and 40 (SOBP protons) smaller than the experimental ones. Therefore, the unambiguous conclusion can only be that biological repair mechanisms determine the curvature of the dose–effect curves, whereas the ion track overlapping effect can contribute only very slightly. Moreover, our effective radius model cannot explain the observed constant β values. Similarly, the effect of increasing probability for the formation of chromosome aberrations with increasing radiation dose (within the Neyman A statistics) which could be, in principle, related to larger local doses in the overlapping ion track regions must probably be explained with the cellular repair mechanisms, as well.

To describe the dose effect curves, we have also applied the Katz model. Within this model, two different modes: ion-kill and gamma-kill mode, are distinguished and correspond to the ion track regions of high and low ionization density, respectively. The contribution to the dose–effect curves resulting from the gamma-kill mode can be directly determined from the cell response function to the gamma irradiation. Since gamma rays ionize the biological material by means of high energy Compton and photoelectrons, the dose distribution over the irradiated cells is considered homogenous, and therefore, the curvature of the corresponding dose–effect curve should be determined only by the biological repair mechanisms. Consequently, the biological effects in the low ionization track regions are automatically included. The problem, however, arises in the high ionization regions where no repair mechanisms are assumed. This is in contradiction to the well-known phenomenon—even for very high LET irradiation, repair effects are observed. In the case of boron ions for which only ion-kill mode is assumed, we have previously determined that about 60% of the double-strand DNA breaks can be repaired (Kowalska et al. 2018). Despite these reservations, the Katz model was very successfully used in different fields of radiobiology (Katz 1988). In the present study, we achieved an overall agreement with the experimental data using only four fitting parameters. However, the observed linear-quadratic shape of the dose effect curves could not be correctly reconstructed. The discrepancy has already occurred when describing the gamma induced response function. The theoretical curve is too flat to fit experimental points at higher doses. Since the gamma response curve corresponds to the gamma-kill mode of charged particle irradiations, its curve shape is automatically included in all other response functions.

Furthermore, the Katz model enables to determine the ion track interaction radius of the ion-kill region (the a₀ parameter, see Tables 2 and 3) which should be independent of the radiation quality for a given cell line. We observe, however, that the a₀ value increases with the growing LET of applied irradiations—similar to experimentally determined effective interaction radius in our model which is about twice as large as a₀. This finding can be treated as an independent confirmation of our model of overlapping ion tracks. Thus, it is not surprising that the Katz model also cannot explain the constant β values and the increasing DNA damage probability for larger doses. All effects seem to be due to biological repair effects and are much stronger compared to the physical effect of overlapping ion tracks. Consequently, the impact of physical components on cellular effects of ionizing radiation should be studied directly after damage induction, before repair mechanisms are activated.