Silicon and oxygen self diffusion in enstatite polycrystals: the Milke et al. (2001) rim growth experiments revisited

Abstract

Milke et al. (Contrib Mineral Petrol 142:15–26, 2001) studied the diffusion of Si, Mg and O in synthetic polycrystalline enstatite reaction rims. The reaction rims were grown at 1,000°C and 1 GPa at the contacts between forsterite grains with normal isotopic compositions and a quartz matrix extremely enriched in ¹⁸O and ²⁹Si. The enstatite reaction rim grew from the original quartz-forsterite interface in both directions producing an inner portion, which replaced forsterite and an outer portion, which replaced quartz. Here we present new support for this statement, as the two portions of the rim are clearly distinguished based on crystal orientation mapping using electron backscatter diffraction (EBSD). Milke et al. (Contrib Mineral Petrol 142:15–26, 2001) used the formalism of LeClaire (J Appl Phys 14:351–356, 1963) to derive the coefficient of silicon grain boundary diffusion from stable isotope profiles across the reaction rims. LeClaire’s formalism is designed for grain boundary tracer diffusion into an infinite half space with fixed geometry. A fixed geometry is an undesired limitation in the context of rim growth. We suggest an alternative model, which accounts for simultaneous layer growth and superimposed silicon and oxygen self diffusion. The effective silicon bulk diffusivity obtained from our model is approximately equal within both portions of the enstatite reaction rim: D ^eff_Si,En =1.0–4.3×10⁻¹⁶ m² s⁻¹. The effective oxygen diffusion is relatively slow in the inner portion of the reaction rim, D ^eff_O,En =0.8–1.4×10⁻¹⁶ m² s⁻¹, and comparatively fast, D ^eff_O,En =5.9–11.6×10⁻¹⁶ m² s⁻¹, in its outer portion. Microstructural evidence suggests that transient porosity and small amounts of fluid were concentrated at the quartz-enstatite interface during rim growth. This leads us to suspect that the presence of an aqueous fluid accelerated oxygen diffusion in the outer portion of the reaction rim. In contrast, silica diffusion does not appear to have been affected by the spatial variation in the availability of an aqueous fluid.

Introduction

The quantification of component mobility in polycrystals at high pressures and temperatures is crucial for the understanding of a variety of physical and chemical processes in the earth’s crust. The mobility of chemical components may control the kinetics of mineral reactions (Fisher 1978), grain coarsening (Joesten 1991) and crystal creep (Poirier 1985).

Rim growth experiments, in which the growth rate of reaction rims between mutually incompatible phases is determined, have been performed to derive component mobility in polycrystals (Brady 1983; Fisler and Mackwell 1994; Fisler et al. 1997; Liu et al. 1997; Yund 1997). Growth of a reaction rim generally requires material re-distribution between the reactant phases, which, in the absence of a migrating fluid or melt, occurs by diffusion. It is generally found that the thickness of an experimentally grown reaction rim increases linearly with the square root of run duration. This dependency indicates that the rate of rim growth is controlled by the diffusion of the respective chemical components between the reactant phases. It also provides the basis for the derivation of component diffusivities from rim growth rates. The extraction of diffusion coefficients from rim growth experiments is complicated by the fact that the net fluxes of the individual components cannot be determined from rim thickness alone.

The net component fluxes can only be determined if the position of the original interface between the two reactant phases is known. The position of the original interface may be determined through the use of inert markers (Brindley and Hayami 1965; Fisler and Mackwell 1994; Fisler et al. 1997; Yund 1997). Inert markers may, however, be displaced by advancing reaction fronts thus their interpretation may be ambiguous (Yund 1997).

An alternative approach, which is based on the use of isotopically labelled reactants, was employed by Milke et al. (2001). The authors synthesized enstatite reaction rims at quartz-forsterite contacts (see Fig. 1a, b of Milke et al. 2001). As reactants they used quartz, which was extremely enriched in ¹⁸O and ²⁹Si, and forsterite with normal isotopic composition. Growth of an enstatite reaction rim at a quartz-forsterite interface requires transport of Si-bearing species from the quartz towards forsterite and of Mg-bearing species in the opposite direction. If the silicon and oxygen isotopic labels were transported passively with the diffusing species, flat isotopic profiles with step discontinuities at the position of the original quartz-forsterite interface as well as at the enstatite-forsterite and the enstatite-quartz interfaces would be expected (see Fig. 4 of Milke et al. 2001). In this case the position of the original quartz-forsterite interface and, hence, the net material fluxes could be determined unambiguously from a jump discontinuity of the isotopic composition within the enstatite rim. In actual fact, the chemical fluxes are masked by silicon and oxygen self diffusion and initially sharp discontinuities at interfaces are smoothed. The observed stable isotope profiles do not contain any step discontinuities but have a significant slope all across the reaction rim (see Fig. 2 of Milke et al. 2001). On the one hand, this feature hampers the determination of the position of the original quartz-forsterite interface from stable isotope signatures. On the other hand, it offers the possibility to estimate coefficients of oxygen and silicon self diffusion within the polycrystalline enstatite reaction rim during growth.

In their analysis, Milke et al. (2001) used the formalism of LeClaire (1963) to derive the coefficient of silicon self diffusion from the observed ²⁹Si/(²⁸Si+²⁹Si) isotope profile across the enstatite rim. Le Clair’s formalism describes grain boundary diffusion of a tracer into a semi infinite half space with fixed geometry. A model with a fixed geometry is, however, of limited applicability in the context of rim growth. In this contribution we suggest an alternative diffusion model, which accounts for simultaneous rim growth and superimposed silicon and oxygen self diffusion. We treat the reactant forsterite and quartz and the two portions of the enstatite reaction rim as four media with distinct transport properties and continuously evolving geometry. The effective coefficients of silicon and oxygen self diffusion obtained from our model are discussed with respect to the relative contributions of volume and grain-boundary diffusion and with respect to the diffusion mechanisms.

Synthetic isotopically labelled enstatite reaction rims

The experimental procedure used to produce the enstatite reaction rims was described in detail by Milke et al. (2001) and only a brief summary is given here. Five milligrams of chemically pure synthetic forsterite or San Carlos olivine (fo₉₂fa₈) with a particle size of 100–200 μm (mostly single crystals) and normal isotopic composition were dispersed in 20 mg of quartz with a grain size of 25 μm, which was extremely enriched in ²⁹Si and ¹⁸O. The starting material was placed into a Pt capsule without addition of water and without drying before sealing, i.e. a small amount of water was introduced through adsorbed moisture. Run conditions were 1,000°C and 1 GPa. Within 24 h polycrystalline enstatite rims of about 15 μm width formed around forsterite grains (see Fig. 1a, b of Milke et al. (2001)).

Silicon and oxygen isotope compositions across the reaction rims were determined by SIMS step scanning with a spatial resolution of less than 2 μm. The analytical methods and results were described in detail by Milke et al. (2001). The stable isotope data are illustrated in Fig. 4. The ²⁹Si/(²⁸Si+²⁹Si) profile is symmetric across the reaction rim. The ¹⁸O/(¹⁶O+¹⁸O) profile is skewed with a relatively shallow gradient in the outer portion of the rim, and a comparatively steep gradient in the inner portion. Reactant forsterite retained both its original silicon and oxygen isotope compositions. Reactant quartz also retained its original silicon isotope composition. Milke et al. (2001) reported about 8% shift in the overall oxygen isotope composition of quartz from an original ¹⁸O/(¹⁶O+¹⁸O) of 0.6 down to about 0.52 after the experiment. Given a forsterite to quartz ratio of 1/4 by weight (molar ratio of 1/11) an 8% shift in the oxygen isotope composition of quartz would require a concomitant 44% shift towards more ¹⁸O enriched composition in forsterite. Alternatively, enstatite rim compositions would have to be enriched in ¹⁸O with respect to quartz. In actual fact, neither forsterite nor enstatite is sufficiently enriched in ¹⁸O to account for the inferred shift in the oxygen isotope composition of quartz. The quartz starting material was analyzed for its oxygen isotope composition using a conventional fluorination extraction technique. In contrast, the run products were analyzed using SIMS. This leads us to suspect that the apparent shift in the ¹⁸O/¹⁶O+¹⁸O ratios of quartz is an analytical artifact. In the sample presented here, an increase of the ¹⁸O/(¹⁶O+¹⁸O) in quartz towards the reaction rim is observed. This pattern was not found in any other sampling profiles (see Milke et al. 2001, Fig. 2) and is probably an analytical artifact, too. For the diffusion modeling we assume a flat oxygen isotope profile for quartz.

Microstructural evidence

SEM images show an enstatite reaction rim around a single crystal of forsterite in a polycrystalline quartz matrix (Fig. 1). The back scatter electron (BSE) image is based on atomic number contrast, which is very weak between the three phases, superimposed by some surface topography mostly along quartz grain boundaries. The forward scatter electron (FSE) image is based on crystal orientation contrast and distinguishes individual grains in enstatite and quartz. Both images were taken simultaneously under the same SEM settings, which were optimized for best FSE contrast but compromised BSE performance, with the sample surface steeply tilted (70°) under a long working distance (WD=35 mm). The sample surface was ultra-polished using colloidal silica suspension in order to remove any preparation induced surface damage, although a few holes due to pullout of quartz grains could not be avoided. Crystal orientations of the imaged sample area were mapped using electron backscatter diffraction (EBSD, Adams et al. 1993) on a square raster of 177 μm×113 μm at a step size of 0.5 μm. Figure 2 presents selected aspects of the data set, where each of the 80,000 raster points has been assigned a crystal phase and orientation plus parameters for EBSD pattern contrast (image quality, IQ) and indexing reliability confidence index (CI).

Fig. 1

SEM images of an enstatite reaction rim around forsterite in a polycrystalline quartz matrix. Grey shadings reflect atomic number contrast in the BSE image and orientation contrast in the FSE image, respectively. Note that the grain size of newly formed enstatite is generally smaller in the inner portion of the reaction rim than in the outer portion; locally a palisade microstructure is developed in enstatite at the forsterite-enstatite interface; up to 20 μm long enstatite grains crystallized at the enstatite-quartz interface; although somewhat rugged, the enstatite-forsterite reaction front is always sharp, the enstatite-quartz reaction front is characterized by abundant cavities; these cavities may indicate reaction induced porosity at this interface; undulose grey shading in olivine indicates a certain degree of crystal plastic deformation; quartz exhibits a well equilibrated polygonal microstructure

The images and maps verify that the reaction fronts are rather straight (at the size scale of forsterite and quartz grains, i.e. tens of microns), both at the forsterite-enstatite and the enstatite-quartz interface. There are hardly any relicts of forsterite or quartz in the enstatite rim. Phase boundaries are serrated at the size scale of enstatite grains (a few microns, Fig. 2a). Pockets with abundant cavities are observed near the enstatite-quartz interface, in particular at the corners. These cavities may indicate fluid-filled reaction-induced transient porosity near this interface.

Fig. 2a–i

Crystal orientation maps of an enstatite reaction rim around forsterite in a polycrystalline quartz matrix, obtained from EBSD scan with 0.5 μm step size (map size 113×177 μm). On maps, background grey levels reflect the EBSD pattern quality parameter (IQ) outlining grain boundaries. a Indexed mineral phase. b Crystal orientation map of forsterite and quartz, color key corresponds to inverse pole figure representation of RD-direction, labelled RD. Black lines—high angle grain boundaries (>15°), white lines—low angle subgrain boundaries (3°... 15°), green lines—Dauphiné twin boundaries in quartz. c Pole figures of forsterite, blue clusters reflect host grain orientation with some scatter. d Crystal orientation map of enstatite, color key corresponds to inverse pole figure representation of vertical-direction CRD. e Crystal orientation map of outer part of enstatite rim, selected manually. Color separation criteria: green—horizontal interface, yellow—subset of green with [001] horizontal (towards TD, coincides with grain long axes), blue—vertical interface, red—subset of blue with [001] vertical (towards RD, coincides with grain long axes). f Pole figures of inner part of enstatite (marked white in (e), compare symmetry centers with forsterite host orientation. g Pole figures of outer part of enstatite, colors as highlighted in (e)). h Contoured pole figures of inner part of enstatite (same data as in (f) with 10° smoothing width), equal area upper hemisphere projection, contour levels in logarithmic scale: 0.71, 1, 1.41, 2, 2.83, 4 multiples of uniform distribution. i Contoured pole figures of outer part of enstatite (same data as in (g), same parameters as in (h))

Quartz grains are in a size range of about 10–60 μm and have idiomorphic shapes with straight or gently curved boundaries and equilibrated triple junctions with dihedral angles around 120°. Indications of wet quartz-quartz grain boundaries and triple junctions are visible in the bottom part of the images. There is hardly any orientation contrast or subgrain structure within individual quartz grains except for a few Dauphiné twins. Quartz crystal orientations scatter randomly without any preference. All these features of an equilibrated polygonal microstructure suggest that quartz statically recrystallized and grew easily during the experiment.

The forsterite grain shows a few preferentially aligned microcracks parallel to [010] and [001]. Some lattice bending but no subgrains are visible in orientation contrast (FSE image). Very few small forsterite crystals are separated from the host grain both in space and orientation (Fig. 2b, c). The bending relates to crystal rotations around the [010] axis by an angle of about 10° in total. If it was not already present in the starting material, this indicates rather high differential stress on the forsterite grain capable to initialize ductile deformation by dislocation glide, perhaps on the (001)[100] slip system, without any noticeable subgrain formation or recrystallization of forsterite.

Two distinct microstructures are observed within the enstatite rim (Fig. 2d), one with smaller grains in the range of a few μm inside towards the enstatite-forsterite reaction front and the other one with larger grains up to 20 μm outside next to quartz. A palisade texture is locally developed in inner parts of the enstatite reaction rim, with the long axes of the enstatite grains oriented perpendicular to the forsterite replacement front. Enstatite crystal preferred orientations (Fig. 2f, h) were inherited from the forsterite crystal orientation, which is best visible by the pseudo-hexagonal pattern of en[100] maxima around the position of fo[100] near the pole figure centre. It also follows from the approximate orthorhombic symmetry of all three enstatite pole figures with respect to the reference frame of the forsterite crystal axes (dark blue in Fig. 2c). This indicates that enstatite growth at the forsterite-enstatite interface was directed inwards normal to the interface and was mostly limited by the availability of space (compare Milke et al. 2003). The gradual increase in enstatite grain size and the decreasing amount of subgrain boundaries with increasing distance from the forsterite-enstatite interface lead us to suspect that rim growth was accompanied by concomitant grain coarsening. In the outer portion of the reaction rim enstatite is much coarser grained and some grains form idiomorphic crystal faces. Their crystal orientations are mostly related to the orientation of the interface, with preference of [100] perpendicular to and [001] within the contact surface (Fig. 2e, g, i). The grain long axes if visible are preferentially aligned with [001] and parallel to the enstatite-quartz interface. This indicates fastest growth of enstatite parallel to the enstatite-quartz interface in the outer part of the rim. Keeping in mind that the separation into two parts of the enstatite rim relied on some subjective judgement based on grain size, shape and orientation, the outer part (marked in Fig. 2e) covers about 30% of the total enstatite area (nearly equivalent to volume).

Our new microstructural observations clearly show two distinct parts of the enstatite reaction rim, which verifies that it grew from the initial quartz-forsterite interface into both directions under different constraints. This conclusion was already suggested for a different experiment by Milke et al. 2001, who observed a faint difference in the BSE image brightness between inner and outer portions of an enstatite reaction rim around San Carlos olivine. If the boundary between inner and outer part marks the position of the initial quartz-forsterite interface then the estimated area fractions of 70:30 per cent for inner to outer parts indicate that growth rates closely resemble constant volume replacement of forsterite at the enstatite-forsterite interface (see below). The observed deformation induced defect structures in forsterite suggest that the reaction may have induced considerable non-deviatoric stress on forsterite. The 6% volume reduction associated with the bulk reaction was mainly accommodated by compaction of the quartz matrix into void spaces generated at the enstatite-quartz interface.

Mass transfer scenarios

The net material fluxes associated with rim growth may be described in the MgO–SiO₂ chemical system.¹. Rim growth by the solid/solid reaction:

$$ {\text{forsterite}}\;({\text{Mg}}_2 {\text{SiO}}_4 ) + {\text{quartz}}\;({\text{SiO}}_2 ) = 2\;{\text{enstatite}}\;({\text{MgSiO}}_3 ) $$

may occur by either one or any combination of the following three processes: (1) diffusion of MgO from the forsterite-enstatite interface to the enstatite-quartz interface, (2) diffusion of SiO₂ from the enstatite-quartz interface to the forsterite-enstatite interface, (3) interdiffusion of ionic species such as 2 Mg²⁺/Si⁴⁺ (see Fig. 2). The relative fluxes of Si- and Mg-bearing species between the two reaction fronts determines the rates at which the enstatite reaction rim grows from the original interface into either direction. If the position of the original quartz-forsterite interface could be localized within the enstatite reaction rim, the relative fluxes of the chemical components could be constrained. Due to the lack of inert markers and of unambiguous microstructural or textural evidence, the position of the original quartz-forsterite interface is treated here as an unknown variable. This is why relative chemical fluxes cannot be constrained and an entire range of feasible mass balance scenarios will be considered in our further treatment.

The bulk reaction may be split into two half reactions: at the enstatite/forsterite interface the half reaction is:

$$ 1\;{\text{fo}} + \nu \;{\text{SiO}}_{2} = (1 + \nu )\;{\text{en}} + (1 - \nu )\;{\text{MgO}} $$

The corresponding half reaction at the enstatite/quartz interface is:

$$ (1 - \nu )\;{\text{MgO}} + 1\;{\text{qtz}} = (1 - \nu )\;{\text{en}} + \nu \;{\text{SiO}}_2 $$

SiO₂ and MgO represent mobile components, which are transferred by diffusion between the two reaction fronts. ν is a stoichiometric coefficient, which describes the net material fluxes across the reaction rim. All feasible mass balance scenarios are in the range 0≤ν≤ 1; ν=1 represents diffusion of SiO₂ exclusively, and ν=0 represents the case of exclusive MgO transfer (reactions 5 and 6 in Milke et al. 2001). All other scenarios require transport of both SiO₂ and MgO.

If only SiO₂ were transferred, enstatite would only grow inwards from the original quartz-forsterite interface replacing forsterite; if only MgO were mobile, then the enstatite reaction rim would grow into both directions at the same rate producing equal volumes of an internal and an external reaction rim. All other mass balance scenarios (with 0<ν<1) produce reaction rims with internal portions that comprise between 50 and 100% of the total rim volume. A special case arises when ν=0.39. This represents constant volume replacement of forsterite by enstatite at the forsterite-enstatite interface (reactions 7 and 8 in Milke et al. 2001). In this case 69.7% of the enstatite reaction rim grow inwards from the original quartz-forsterite interface. The scenario with ν=1/3 is conservative with respect to oxygen and is equivalent in terms of mass balance to the interdiffusion of 2Mg²⁺ with Si⁴⁺. Based on volume and stable isotope arguments Milke et al. (2001) argued for pure MgO transfer during rim growth and restricted their analysis to this mass balance scenario.

Irrespective of the mass balance scenario, the bulk reaction has a negative volume change of 6% at 1,000°C and 1 GPa. The negative reaction volume must be accommodated through the enstatite reaction rims by compaction of the quartz matrix. Because enstatite forms continuous rims around forsterite grains, all mass balance scenarios except for the one that represents constant volume replacement of forsterite (ν=0.39) require deformation of the enstatite reaction rim during growth. This inevitable leads to reaction induced stress, which may significantly contribute to the free energy of the phases and, hence, have an influence on the chemical potentials of the diffusing components (Mosenfelder et al. 2000). As a consequence, the net material fluxes associated with rim growth will not only depend on the intrinsic component mobility but they will also be influenced by the rheology of the phases involved. A mass balance scenario, which minimizes reaction induced stress, i.e. a scenario close to constant volume replacement of forsterite, may be energetically favourable.

Based on inert marker experiments Fisler et al. (1997) argue for a rather external position of the original quartz-forsterite interface within the enstatite reaction rim. We consider the range of mass balance scenarios between the “only MgO mobile” (ν=0, 50% of the enstatite reaction rim growing inwards from the original interface) and the “forsterite constant volume replacement” scenarios (ν=0.39, 70% of the rim growing inwards from the original interface) as the most probable ones.

Diffusion model

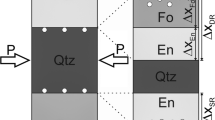
Here we give a brief outline of the mathematical approach used to derive silicon and oxygen self diffusion coefficients from the stable isotope profiles across the enstatite reaction rims. A detailed derivation of the formalism is presented in the Appendix. In our model we treat quartz, forsterite and the two compartments of the enstatite reaction rim as four media with distinct transport properties. The system configuration at t=0 and its evolution with time are illustrated schematically in Fig. 2. Initially, the only two media present are quartz and forsterite, which will henceforth be referred to as medium 1 and 4, respectively. Initially the normalized isotope compositions ² are uniform in forsterite and quartz with values of 0 and 1, respectively. At t=0 a step discontinuity exists at the original forsterite-quartz interface. At t>0 the enstatite reaction rim grows from the original quartz-forsterite interface into both directions. The inner and outer portion of the enstatite reaction rim (en^int and en^ext) represent the media 2 and 3. The quartz- en^ext, the en^ext-en^int. and the en^int-forsterite interfaces are referred to as interfaces 1 through 3. The media are coupled through the conditions of isotopic equilibrium and mass conservation at the interfaces.

In general, the mineral reactions at the interfaces between adjacent media do not conserve volume, and the different media as well as the separation surfaces move with respect to one another during rim growth. This is why separate coordinate systems, x _i , are introduced for each of the media i, where i=1,...,4. As rim thickness increases linearly with the square root of time, the position of interface j between media i and t+1 at time t with respect to coordinate system x _i is X ⁱ _j (t)=(β ⁱ _j *t)^1/2. The β ⁱ _j parameters are obtained from measured rim width, run duration and reaction stoichiometry (see Appendix). The initial and boundary conditions in terms of normalised isotopic compositions are:

$$ R_1 (x_1 > 0,0) = 1,\quad R_4 (x_4 > 0,0) = 0\quad {\text{initial}}\;{\text{conditions}} $$

(1)

$$ R_1 (\infty ,t > 0) = 1,\quad R_4 (\infty ,t > 0) = 0\quad {\text{boundary}}\;{\text{conditions}} $$

(2)

The condition of stable isotope equilibrium between media i and t+1 at interface j is:

$$ R_i (X_j^i ,t) = R_{i + 1} (X_j^{i + 1} ,t)^* \;\alpha _{i - (i + 1)} $$

(3)

where α _i-(i+1) is the equilibrium fractionation factor between the phases comprising the two media i and t+1.

There are three processes of mass transfer, which need to be accounted for at the quartz-enstatite and the enstatite-forsterite reaction fronts. These are the material flux due to direct transfer of the isotopic element from the reactant into the product solid, the flux associated with net chemical transfer between the two reaction fronts, and, finally, the self diffusion of isotopomers down gradients in stable isotope composition in the two media adjacent to the common interface. Accordingly, mass conservation of the isotopic element at the quartz-enstatite reaction front is described by three terms in the equation:

$$ \begin{aligned} & \left[ {D_{{\text{qtz}}} \left( {\frac{{\partial R_{{\text{qtz}}} }} {{\partial x_1 }}} \right)_{X_1^1 } - D_{{\text{en}}} \left( {\frac{{\partial R_{{\text{en}}^{{\text{ext}}} } }} {{\partial x_2 }}} \right)_{X_1^2 } } \right] + \left[ {\nu _{{\text{qtz}}}^1 R_{{\text{qtz}}} (X_1^1 ) + \nu _{{\text{en}}^{{\text{ext}}} }^1 R_{{\text{en}}^{{\text{ext}}} } (X_1^2 )} \right] \\ & \quad + \left[ {\nu _{{\text{SiO}}_2 }^1 \alpha _{{\text{SiO}}_2{\text{-qtz}}} R_{{\text{qtz}}} (X_1^1 ) - \nu _{{\text{MgO}}}^3 \alpha _{{\text{MgO-fo}}} R_{{\text{fo}}} (X_3^4 )} \right] = 0 \\ \end{aligned} $$

(4a)

where $\left( {\frac{{\partial R_{{\text{qtz}}} }} {{\partial x_1 }}} \right)_{X_1^1 } \;{\text{and}}\;\left( {\frac{{\partial R_{{\text{en}}^{{\text{ext}}} } }} {{\partial x_2 }}} \right)_{X_1^2 }$ are the gradients in the stable isotope compositions of quartz and enstatite at the quartz-enstatite reaction front; D _qtz and $D_{{\text{en}}^{{\text{ext}}} }$ are the diffusivities of the isotopic element in the respective media. The parameters $\nu _{{\text{qtz}}}^1 ,\nu _{{\text{en}}^{{\text{ext}}} }^1 \;{\text{and}}\;R_{{\text{qtz}}} {\text{(}}X_{\text{1}}^{\text{1}} {\text{),}}\;R_{{\text{en}}^{{\text{ext}}} } {\text{(}}X_{\text{1}}^{\text{2}} {\text{)}}$ are the molar amounts of the isotopic element contained in quartz and enstatite, which are consumed and produced at the quartz-enstatite reaction front and the respective isotopic compositions. $\nu _{{\text{SiO}}_{\text{2}} }^1$ is the molar amount of the isotopic element contained in SiO₂, which is liberated at the quartz-enstatite reaction front, and $\alpha _{{\text{SiO}}_2{\text{-qtz}}}$ is the SiO ₂-quartz equilibrium fractionation factor for the respective isotopic element. ν ³_MgO is the molar amount of the isotopic element contained in MgO liberated at the enstatite-forsterite reaction front, and α_MgO-fo is the MgO-forsterite stable isotope equilibrium fractionation factor, R _fo(X ⁴₃ ) is the isotopic composition of forsterite at the forsterite-enstatite interface. Similarly, mass conservation at the enstatite-forsterite reaction front requires that:

$$ \begin{aligned} & \left[ {D_{{\text{en}}^{\operatorname{int} } } \left( {\frac{{\partial R_{{\text{en}}^{\operatorname{int} } } }} {{\partial x_3 }}} \right)_{X_3^3 } - D_{{\text{fo}}} \left( {\frac{{\partial R_{{\text{fo}}} }} {{\partial x_4 }}} \right)_{X_3^4 } } \right] + \left[ {\nu _{{\text{en}}^{\operatorname{int} } }^3 {\text{ }}R_{{\text{en}}^{\operatorname{int} } } (X_3^3 ){\text{ }} + \nu _{{\text{fo}}}^3 {\text{ }}R_{{\text{fo}}} (X_3^4 )} \right] \\ & \quad + \left[ { - \nu _{{\text{SiO}}_2 }^1 \alpha _{{\text{SiO}}_2 - {\text{qtz}}} R_{{\text{qtz}}} (X_1^1 ) + \nu _{{\text{MgO}}}^3 \alpha _{{\text{MgO-fo}}} R_{{\text{fo}}} (X_3^4 )} \right]{\text{ }} = 0 \\ \end{aligned} $$

(4b)

There is no net transfer reaction at the interface between the internal and external portion of the enstatite reaction rim, and mass conservation at this interface (interface 2) is described by: ³

$$ \left[ {D_{{\text{en}}^{{\text{ext}}} } \left( {\frac{{\partial R_{{\text{en}}^{{\text{est}}} } }} {{\partial x_2 }}} \right)_{X_2^2 } - D_{{\text{en}}^{\operatorname{int} } } \left( {\frac{{\partial R_{{\text{en}}^{\operatorname{int} } } }} {{\partial x_3 }}} \right)_{X_2^3 } } \right] = 0 $$

(4c)

With the above choice of coordinate systems and model parameterisation, the isotopic composition in each medium is described as a function of space and time coordinates by the general solution for one-dimensional linear diffusion with an extended source:

$$ R(x,t) = a \cdot {\text{erf}}\left( {\frac{x} {{2\sqrt {Dt} }}} \right) + b $$

(5)

Equation 5 may be substituted into Eqs. 3 and 4. Three equations of type (3) and (4) may be written for the three interfaces. Together with the boundary conditions (Eq. 2) this constitutes a system of eight equations in 12 unknowns, where the unknowns are the a _i and b _i parameters with i=1,...,4, and the diffusivities of the isotopic element in the four media. This system of equations may be reduced to a set of four equations, where only the diffusivities of the isotopic element in the four different media remain as unknowns (see Appendix). Each of these equations describes the isotopic composition as a function of space and time coordinates for one of the four media. The diffusivities in the individual media are then estimated from fitting these functions to the observational data with $D_{{\text{qtz}}} ,\;D_{{\text{en}}^{{\text{ext}}} } ,\;D_{{\text{en}}^{{\text{int}}} } ,\;{\text{and}}\;D_{{\text{fo}}}$ as the fitting parameters.

Model characteristics

In Fig. 3 calculated stable isotope profiles are shown for three different mass balance scenarios. The relations between the rates of self diffusion of the isotopic element and chemical mass transfer associated with layer growth may be expressed by a dimensionless ratio $n_i = \left( {\frac{{\sqrt {D_i } }} {{\sqrt {\beta _j^i } }}} \right),$ which may be referred to as a “layer Peclet number”. If n _i is high, then self diffusion dominates over net material transfer and gradients in stable isotope compositions will quickly be degraded. If n _i is low, then the stable isotope composition will be largely controlled by passive transfer of isotopomers during net chemical transfer und sharp isotope fronts, which develop at interfaces between two layers will persist for larger growth increments. If self diffusion is considered to be exceedingly slow as compared to layer growth, then n _i → 0 and flat isotopic profiles with step discontinuities at layer interfaces are predicted (see Fig. 4 of Milke et al. 2001). In Fig. 3 the layer Peclet numbers are set equal in all four media to illustrate the influence of the choice of mass balance scenario. In terms of mass balance ν is varied from 0.0 (i.e. only MgO mobile) to 0.9 to cover the widest possible range of feasible mass balance scenarios. A value of ν=1.0 would imply, that the enstatite rim only grew inwards from the original quartz-forsterite interface. This is a different problem (three media instead of four) and was disregarded in this calculation.

Fig. 3

Schematic illustration of the multilayer moving boundary diffusion model for self diffusion superimposed on enstatite reaction rim growth, at time t=0 the normalized stable isotope compositions of forsterite (medium 4) and quartz (medium 1) are 0 and 1, respectively with a step discontinuity at the original quartz-forsterite interface (interface 2); at t>0 an enstatite rim grows from the original quartz-forsterite interface into both directions generating an enstatite reaction rim with an internal portion (medium 3), which replaces forsterite and an external portion (medium 2), which replaces quartz; replacement is not conservative with respect to volume so that the enstatite-forsterite and the enstatite-quartz interfaces are at different positions with respect to the coordinate systems x ₁ ... x ₄, which are attached to each of the four media; enstatite growth implies net transfer of Si-bearing species, which is denoted as an SiO₂ component here, from the quartz-enstatite interface (interface 1) to the enstatite-forsterite interface (interface 3) and transfer of Mg-bearing species, here denoted as an MgO component, into the opposite direction

Irrespective of the nature of the diffusing species electroneutrality requires that two moles of oxygen are associated with each mole of silicon and, similarly, one mole of oxygen is associated with each mole of magnesium transferred from one reaction front to the other. As a consequence the oxygen and silicon equivalent reaction stoichiometries are different at the reaction fronts. Both, oxygen and silicon isotope profiles were calculated to illustrate the effect of the differences between the oxygen and silicon atom equivalent reaction stoichiometries.

An increase of ν from 0 to 0.9 shifts the original quartz-forsterite interface from a central position within the enstatite reaction rim to an external position. At ν=0.9 only about 4% of the enstatite rim lie outside the original forsterite quartz interface. As the outer portion of the enstatite rim is condensed, the slopes of the calculated oxygen and silicon isotope profiles are increased. Similarly, as the inner portion of the enstatite reaction rim is distended, the slopes of the calculated oxygen and silicon isotope profiles decrease.

For a given value of n _i , the geometries of the oxygen and silicon isotope profiles are somewhat different. These differences are more pronounced for small values of n _i than for large values. They result from the differences in oxygen and silicon atom equivalent reaction stoichiometries at the reaction fronts. In the only MgO mobile scenario (ν=0.0) one third of the oxygen of the enstatite produced at the enstatite-quartz interface stems from MgO, which is derived from the dissolution of forsterite at the enstatite-forsterite interface. This introduces isotopically light oxygen at the enstatite-quartz reaction front and lowers the oxygen isotope curve with respect to a scenario, where no “external” oxygen is introduced. Given that ν=0.0, such a scenario is true for silicon at the enstatite-quartz interface, because no silica is introduced from an external source in this scenario. This is why, for a given value of n _i , the calculated silicon isotope profile lies above the oxygen isotope profile at this interface. For all scenarios, which imply the transfer of Si bearing species, systematic differences exist between the silicon and oxygen isotope profiles in the inner portion of the enstatite rim and in forsterite. These differences can be explained by the introduction of isotopically heavy silicon and oxygen at the forsterite-enstatite interface via SiO₂, which is derived from the dissolution of quartz at the enstatite-quartz interface. A maximum of 50% of the silicon and 33% of the oxygen of the enstatite produced at the forsterite-enstatite interface may stem from externally derived SiO₂. As a consequence the shift towards more enriched isotope compositions is somewhat more pronounced in the silicon than in the oxygen isotope system.

The calculated stable isotope profiles may have kinks at the interfaces, even if the diffusivities are equal in both the adjacent media. This is due to differences in the rates, at which the media grow and are consumed. In the only MgO mobile scenario (ν=0.0) only 5.4 volumetric units of quartz are consumed, whereas 7.5 volumetric units of enstatite are produced per unit time. The isotope signal transferred from quartz to enstatite at the enstatite-quartz reaction front is distended within the outer portion of the enstatite rim. As a consequence the slopes of the isotope profiles in the immediate vicinity of the enstatite-quartz interface are somewhat lower in enstatite than in quartz. This produces a downward convex kink in the isotope profiles at the interface. For the only MgO mobile scenario, this effect is further intensified through the introduction of isotopically light oxygen via the incorporation of MgO derived from the forsterite-enstatite interface. An upward convex kink is produced at the enstatite-quartz interface for the mass balance scenarios with ν=0.4 and 0.9, because then the enstatite produced occupies a smaller volume than the quartz consumed. The stable isotope profiles are smooth across reaction fronts if the layer Peclet numbers in the two adjacent media are equal and the replacement reaction conserves volume such as the constant volume replacement of forsterite by enstatite in the scenario with ν=0.4.

Diffusion coefficients

The coefficients of oxygen and silicon self diffusion in the four media are derived from fitting the error function solutions (Eq. 5) to the observed stable isotope data. Such fits are illustrated for the two extreme mass transfer scenarios (ν=0, ν=0.39) in Fig. 4. Both the oxygen and silicon isotope profiles are flat in forsterite and quartz except for a minute compositional change close to the interfaces with the enstatite reaction rim (Fig. 5). The stable isotope profiles within quartz and forsterite have little information content, i.e. the diffusion coefficients for the forsterite and quartz compartments are poorly constrained from the available stable isotope data and will not be discussed further.

Fig. 4

Model isotope profiles across a 15 μm wide enstatite rim for different mass balance scenarios; oxygen isotope profiles are shown as solid lines, silicon isotope profiles are shown as dashed lines; isotope profiles are shown for different layer Peclet numbers, n _i (see text for explanation); the numbers in the horizontal bars in the top section of each diagram indicate the volumetric proportions of reactant and product phases involved

Fig. 5

Oxygen and silicon isotope profiles across a 15 μm wide enstatite reaction rim between forsterite with normal isotopic compositions and quartz extremely enriched in ¹⁸O and ²⁹Si taken from Milke et al. 2001; isotope compositions are given as normalized isotopic ratios, fits to the data were obtained from a multilayer moving boundary diffusion model; automated non linear optimization tools failed to converge with our model equations, this is why fitting was done by a trial and error method; the “only MgO mobile” (ν=0.0) and the “forsterite constant volume replacement” (ν=0.39) scenarios, which span the entire range of feasible mass balance scenarios, were considered; note: diffusivities are given in units of 10⁻¹⁶ m² s⁻¹; diffusivities in forsterite and quartz are badly constrained by the available data and should not be taken quantitatively, they are only shown for the sake of completeness

The oxygen and silicon bulk diffusivities in the enstatite reaction rim obtained from our model are given in Table 1. The results for the two different mass balance scenarios do not differ by more than a factor of 3 from one another. The diffusion coefficients derived are thus rather insensitive to the choice of mass balance scenario. They are largely independent of the net material fluxes associated with rim growth. The silicon diffusivities obtained are equal within the uncertainty of the analysis in the inner and outer portion of the reaction rim. Irrespective of the mass transfer scenario used, the oxygen diffusivity appears to have been faster by a factor of seven to eight in the outer part of the enstatite reaction rim than in the inner portion of the rim.

Table 1 Effective coefficients of oxygen and silicon self diffusion derived from fitting equations (5) subject to conditions (2), (3) and (4) to the stable isotope profiles across the reaction rim; to illustrate the sensitivity of the analysis to net material fluxes “the only MgO mobile” and the “constant volume replacement of forsterite” scenarios are considered

Discussion

Grain boundary diffusion versus volume diffusion

The stable isotope data from the reaction rims are macroscopic in the sense that their spatial resolution does not allow to identify compositional differences that may exist between grain interiors and grain boundaries. If such heterogeneities existed, they were integrated during stable isotope analysis by SIMS step scanning. Consequently, in our treatment the enstatite reaction rim is regarded as a composite of two continuous media. The diffusion coefficients derived from the available “macroscopic” data must be regarded as effective diffusion coefficients in the sense of Brady (1983). Macroscopic data allow for quantification of the bulk effect of diffusion, but they do not give immediate insight into the diffusion pathways, i.e. they do not allow to directly quantify the relative contributions of volume and grain-boundary diffusion to bulk diffusion. This can only be done through indirect reasoning.

The general observation of a linear relation between rim thickness and the square root of run duration is a good indication of diffusion control on rim growth. ⁴ Diffusion in polycrystals involves both penetration along grain boundaries and lateral spreading into the adjacent grains (Joesten 1991). Based on the assumption that lateral spreading into the grain interiors occurs by volume diffusion, three kinetic regimes are distinguished with respect to the scale of volume penetration relative to grain diameter (Harrison 1961, Joesten 1991): The situation where volume diffusion and grain boundary diffusion are approximately equally fast, so that concentration contours penetrate into a polycrystal as nearly planar fronts, is referred to as Type A kinetics. If, on the other extreme, grain boundary diffusion is much faster than volume diffusion and penetration of the diffusing component into the polycrystal is largely restricted to the grain boundaries, this is referred to as type C kinetics. For both type A and type C kinetics, the bulk effect on a macroscopic scale is displacement of concentration contours at a rate proportional to the square root of time. It has been shown by Fisher (1951) that in an intermediate kinetic regime (type B kinetics) the bulk effect of combined grain boundary and volume diffusion is displacement of concentration contours at a rate that is proportional to the fourth root of time. Type C kinetics is extremely inefficient, because the grain boundary network usually only occupies a very small fraction of the total volume of a polycrystal, and it is very unlikely that reaction rim growth occurred in the regime of type C kinetics. Type B kinetics would be significantly more efficient, but it is incompatible with the observed linear relation between rim thickness and square root of time. The observed growth rate rather suggests that volume diffusion significantly contributed to bulk diffusion and rim growth occurred in the regime of type A kinetics in the sense of Harrison (1961). There are no data on silicon and oxygen volume diffusion in enstatite available. Volume diffusion data from dry experiments on diopside by Bejina and Jaoul (1996) yield D ^v_Si,Di = 5×10⁻²³ m² s⁻¹ at 1,000°C. Taking this as a proxy for silicon volume diffusion in enstatite, a discrepancy of about seven orders of magnitude results between supposedly slow silicon volume diffusion and our estimate for silicon diffusion in enstatite polycrystals. This also renders type A kinetics of Harrison (1961) unlikely and leads us to suspect that fast diffusion along grain boundaries did indeed contribute substantially to bulk diffusion. Volume diffusion at rates on the order of 10⁻²³ m² s⁻¹ is, however, too slow to allow for significant stable isotope exchange between grain interiors and grain surfaces, even if the grain size is only a few μm. Isotopic exchange between the fast diffusion pathways and the grain interiors appears to have occurred by a process which is faster than mere volume diffusion. The dynamic nature of the microstructure in the enstatite reaction rim, i.e. continuous re-crystallization and associated grain boundary migration may have contributed to such an exchange. As the exact nature of the diffusion pathways cannot be determined from the available macroscopic stable isotope data, we suggest that the diffusion coefficients obtained from the stable isotope profiles should be regarded and reported as effective diffusion coefficients.

If the grain size of the polycrystalline aggregate is known, the coefficients of grain boundary diffusion may be estimated from the approximate relation: D ^gb⋅δ≈D^eff⋅d (Brady 1983), where d is grain size and δ is the grain boundary width. For the enstatite reaction rims with d=2 μm our analysis yields values for D ^gb_Si,En *δ in the range of 2–8.6×10⁻²² m³ s⁻¹, depending on the mass balance scenario (see Table 1). This is about two orders of magnitude faster than derived from LeClaire’s formalism by Milke et al. (2001). Their estimation relies on Si volume diffusion data from Bejina and Jaoul (1996) on diopside (D ^v_Si,Di =5×10⁻²³ m² s⁻¹) as proxy for enstatite. Based on the general observation that volume diffusion coefficients increase by about three orders of magnitude if conditions are changed from dry to wet (Freer 1993), the latter authors speculated that, for their wet experiments, a value of D ^gb_Si,En *δ on the order of 10⁻²² m³ s⁻¹ would be a more realistic estimate. Given the considerable uncertainty in the estimation of Si volume diffusion coefficients for enstatite, the agreement between the speculations made by Milke et al. (2001) and our results is surprisingly good. In contrast to their approach, which is based on LeClaire’s formalism, our treatment does not depend on volume diffusion data, which have to be taken from independent sources and are rather badly constrained for enstatite.

Diffusion mechanisms

It is interesting to note that silicon self diffusion was approximately equally fast in the inner and outer portions of the reaction rim. In contrast, oxygen self diffusion was significantly faster in the outer portion of the reaction rim, which replaced quartz, than in the inner portion, which replaced forsterite. This observation is somewhat counter-intuitive as the enstatite grains are considerably larger in the outer part, consequently forming fewer boundaries. Diffusivities should rather be reduced in the more coarse grained portion of the enstatite rim instead of being enhanced, if transport along grain boundaries indeed contributed significantly to bulk diffusion. At present, neither the nature of the diffusing species nor the diffusion mechanisms, which may account for silicon and oxygen self diffusion in the enstatite reaction rim, are known. The fact that the transport properties of the reaction rim are different in the inner and outer part only for oxygen and not for silicon suggests that diffusion of the silicon and oxygen bearing species involved fundamentally different processes. Petrographic evidence suggests that the negative reaction volume was largely accommodated at the enstatite-quartz reaction front and may have caused dilation in the direction perpendicular to this interface. This may have induced migration of volatiles towards the enstatite-quartz interface. The presence of water along grain contacts and in void spaces or at least an increased water fugacity at the outer reaction front may have accelerated oxygen diffusion in polycrystalline enstatite substantially. Even if the solubility of quartz in an aqueous fluid is rather high under the experimental conditions (Newton and Manning 2000), the concentration of oxygen in an aqueous fluid is probably much higher then the concentration of silicon. This renders the fluid a much more efficient transport medium for oxygen than for silicon. The comparatively high oxygen diffusivity in the outer portion of the enstatite reaction rim and the lack of this effect in the silicon system may hence be due to the presence of volatile species at the outer reaction front. In addition, differences in the anion-defect structures and anion-defect densities of enstatite in the two compartments of the reaction rim may also have an influence on oxygen diffusivities. Differences in the defect chemistry of enstatite may well result from the fact that the inner portion of the rim grew on the expense of forsterite, whereas the outer portion replaced quartz.

Conclusions

Growth of polycrystalline enstatite reaction rims at the interfaces between forsterite and isotopically labelled quartz involved net transfer of magnesium bearing species from the enstatite-forsterite interface to the enstatite-quartz interface and a net flux of silicon bearing species in the opposite direction. Silicon and oxygen self diffusion superimposed on the net chemical transport produced diffusion profiles, which allow derivation of the effective coefficients of silicon and oxygen self diffusion within the reaction rim. Within the range of feasible mass balance scenarios, the effective diffusion coefficients derived from a multi-layer moving boundary diffusion model are rather insensitive to the net material fluxes associated with rim growth. Differences in the coefficients for oxygen diffusion between the inner portion of the enstatite reaction rim, which replaced forsterite, and the outer portion of the reaction rim, which replaced quartz, are probably due to the presence of volatile species at the outer reaction front of the reaction rim. Any fluid present was concentrated at the enstatite-quartz interface due to reaction induced dilative stress across the reaction front and thus provided fast passageways for oxygen diffusion. As the pathways of diffusion cannot be determined unambiguously from the available macroscopic stable isotope data, we suggest that diffusion coefficients obtained from rim growth experiments should be regarded and reported as effective diffusion coefficients.

Appendix

An enstatite reaction rim, which forms between mutually incompatible quartz and forsterite, grows into either direction at rates, which depend on the relative fluxes of SiO₂ and MgO between the two reaction fronts. The relative silicon and magnesium fluxes determine the stoichiometries of the half reactions at the reaction fronts:

$$ 1\;{\text{fo}} + \nu \;{\text{SiO}}_{2} {\text{ = }}(1 + \nu )\;{\text{en}}^{{{\text{int}}}} {\text{ + }}(1 - \nu )\;{\text{MgO}}\quad {\text{at}}\;{\text{the}}\;{\text{forsterite - enstatite}}\;{\text{interface}} $$

(6a)

$$ (1 - \nu )\;{\text{MgO}} + 1\;{\text{qtz}} = (1 - \nu )\;{\text{en}}^{{{\text{ext}}}} {\text{ + }}\nu \;{\text{SiO}}_{2} \quad {\text{at}}\;{\text{the}}\;{\text{enstatite - quartz}}\;{\text{interface}} $$

(6b)

For all feasible mass balance scenarios ν is between 0 and 1.

The setting of enstatite rim growth between mutually incompatible forsterite and quartz is illustrated schematically in Fig. 2. As the individual media move with respect to one another during rim growth, separate coordinate systems, x ₁, x ₂, x ₃, x ₄ are introduced for each of the four media. The origin of all coordinate systems is at the original interface between forsterite and quartz at t=0. The coordinate systems move with respect to one another during rim growth at t>0. The x ₁ and x ₂ coordinate systems point into one direction and the x ₃ and x ₄ coordinate systems point into the other direction. The media of interest always lie in the positive domain of each coordinate system. The position of the interface j between media i and t+1 at time t with respect to the coordinate system x _i is referred to as X ⁱ _j (t). To account for the fact that interface positions shift as a linear function of the square root of time we set: X ⁱ _j (t)=(β ⁱ _j *t)^1/2. In our notation the interface displacement rates are all positive. The β ⁱ _j parameters are obtained from measured rim width, d _rim (t), run duration, t, and reaction progress ℑ according to the relations:

$$ d_{{\text{rim}}} = \sqrt {\beta _1^2 t} + \sqrt {\beta _3^3 t} , $$

(7a)

$$ \frac{{\sqrt {\beta _1^2 t} }} {{\sqrt {\beta _3^3 t} }} = \frac{{(1 - \nu )}} {{(1 + \nu )}}, $$

(7b)

$$ \frac{{\sqrt {\beta _3^3 t} }} {{\sqrt {\beta _3^4 t} }} = \frac{{(1 + \nu )\bar \nu _{{\text{en}}} }} {{\bar \nu _{{\text{fo}}} }}, $$

(7c)

$$ \frac{{\sqrt {\beta _1^1 t} }} {{\sqrt {\beta _1^2 t} }} = \frac{{\bar \nu _{{\text{qtz}}} }} {{(1 - \nu )\bar \nu _{{\text{en}}} }}, $$

(7d)

where $\bar \nu _{{\text{qtz}}} = 22.69\,{\text{cm}}^3 \,{\text{mol}}^{ - 1} ,\;\bar \nu _{{\text{fo}}} = 43.66\,{\text{cm}}^3 \,{\text{mol}}^{ - 1} ,\;{\text{and}}\;\bar \nu _{{\text{en}}} = 31.31\,{\text{cm}}^3 \,{\text{mol}}^{ - 1} ,$ are the molar volumes of quartz, forsterite and enstatite at 1,000°C and 1 GPa. ⁵ Reaction progress is calculated from the observed rim thickness according to:

$$ {\Im }(t) = \frac{{d_{{{\text{rim}}}} (t)}} {{2v_{{{\text{en}}}} }} $$

(8)

The position of the enstatite-quartz interface with respect to the coordinate system x ₁, X ¹₁ , is then given by:

$$ X^{1}_{1} (t) = {\Im }(t)v_{{{\text{qtz}}}} = {\sqrt {\beta ^{1}_{1} t} } $$

(9a)

Similarly the positions of the other interfaces are given by:

$$ X^{2}_{1} (t) = {\Im }(t){\left( {1 - \nu } \right)} \cdot v_{{{\text{en}}^{{{\text{ext}}}} }} = {\sqrt {\beta ^{2}_{1} t} } $$

(9b)

$$ X^{3}_{3} (t) = {\Im }(t){\left( {1 + \nu } \right)} \cdot v_{{{\text{en}}^{{{\text{int}}}} }} = {\sqrt {\beta ^{3}_{3} t} } $$

(9c)

$$ X^{4}_{3} (t) = {\Im }(t)v_{{{\text{fo}}}} = {\sqrt {\beta ^{4}_{3} t} } $$

(9d)

With this choice of coordinate systems the general solution for linear diffusion of a tracer in a one dimensional system as given in Eq. 5 adequately describes self diffusion in a moving boundary setting. One equation of this type may be written for each of the four media. Each such equation contains two parameters, a and b, which are not known a priori. The a and b parameters are obtained from solving a set of equations, which is obtained from the conditions of isotopic equilibrium (Eq. 3) and mass conservation (Eq. 4a, Eq. 4b, Eq. 4c) at the contact between two adjacent media and from the boundary conditions (Eq. 2). As the equilibrium stable isotope fractionations between two adjacent media and between the solid phases and the mobile species are very small as compared to the observed variation in stable isotope compositions, all equilibrium fractionation factors are set to unity so that they do not appear any longer in the following equations.

From substitution of the error function solution Eq. 5 into Eq. 3 the following relation is obtained, which expresses isotopic equilibrium at the qtz-en^ext interface (interface 1):

$$ \left[ {a_1 {\text{erf}}\left( {\frac{{\sqrt {\beta _1^1 t} }} {{2\sqrt {D_{{\text{qtz}}} t} }}} \right) + b_1 } \right] - \left[ {a_2 {\text{erf}}\left( {\frac{{\sqrt {\beta _1^2 t} }} {{2\sqrt {D_{{\text{en}}^{{\text{ext}}} } t} }}} \right) + b_2 } \right] = 0 $$

(10)

and mass conservation across the qtz-en^ext interface (interface 1) is expressed as:

$$ \begin{aligned} & \left[ {a_1 {\text{erf}}\left( {\frac{{\sqrt {\beta _1^1 t} }} {{2\sqrt {D_{{\text{qtz}}} t} }}} \right) + b_1 } \right] \cdot \left( {\nu _{{\text{qtz}}}^1 + \nu _{{\text{SiO}}_{\text{2}} }^1 } \right) - \left[ {a_2 {\text{erf}}\left( {\frac{{\sqrt {\beta _1^2 t} }} {{2\sqrt {D_{{\text{en}}^{{\text{ext}}} } t} }}} \right) + b_2 } \right] \cdot \left( {\nu _{{\text{en}}}^1 } \right) \\ & \quad + \left[ {a_4 {\text{erf}}\left( {\frac{{\sqrt {\beta _3^4 t} }} {{2\sqrt {D_{{\text{fo}}} t} }}} \right) + b_4 } \right] \cdot \left( {\nu _{{\text{MgO}}}^3 } \right) + D_{{\text{qtz}}} \left( {\frac{{a_1 }} {{\sqrt \pi }}\frac{1} {{\sqrt {D_{{\text{qtz}}} t} }}\exp \left[ {\frac{{\beta _1^1 t}} {{4D_{{\text{qtz}}} t}}} \right]} \right) \\ & \quad - D_{{\text{en}}^{{\text{ext}}} } \left( {\frac{{a_2 }} {{\sqrt \pi }}\frac{1} {{\sqrt {D_{{\text{en}}^{{\text{ext}}} } t} }}\exp \left[ {\frac{{\beta _1^2 t}} {{4D_{{\text{en}}^{{\text{ext}}} } t}}} \right]} \right) = 0 \\ \end{aligned} $$

(11)

Using the following assignments:

$$ \begin{aligned} n_i & = \frac{{\sqrt {D_i } }} {{\sqrt {\beta _j^i } }} \\ w(i) & = {\text{erf}}\left[ {\frac{1} {{2n_i }}} \right] \\ f\left( i \right) & = n_i \cdot \exp \left[ { - \frac{1} {{4n_i ^2 }}} \right] \\ g\left( i \right) & = \frac{{\sqrt {\beta _j^i } }} {{\sqrt \pi }}\frac{1} {{\sqrt t }} \\ \end{aligned} $$

Equations (10) and (11) reduce to:

$$ \left[ {a_1 w_1 + b_1 } \right] - \left[ {a_2 w_2 + b_2 } \right] = 0 $$

(12)

$$ \left[ {a_1 w_1 + b_1 } \right]\left( {\nu _{{\text{qtz}}}^1 + \nu _{{\text{SiO}}_2 }^1 } \right) - \left[ {a_2 w_2 + b_2 } \right]\left( {\nu _{{\text{en}}}^1 } \right) + \left[ {a_4 w_4 + b_4 } \right]\left( {\nu _{{\text{MgO}}}^3 } \right) + a_1 g_1 f_1 - a_2 g_2 f_2 = 0 $$

(13)

Similarly stable isotope equilibrium and mass conservation at the enstatite-forsterite interface is expressed as:

$$ \left[ {a_3 w_3 + b_3 } \right] - \left[ {a_4 w_4 + b_4 } \right] = 0 $$

(14)

and

$$ \left[ {a_1 w_1 + b_1 } \right]\left( {\nu _{{\text{SiO}}_2 }^1 } \right) + \left[ {a_3 w_3 + b_3 } \right]\left( {\nu _{{\text{en}}}^3 } \right) + \left[ {a_4 w_4 + b_4 } \right]\left( {\nu _{{\text{fo}}}^3 + \nu _{{\text{MgO}}}^3 } \right) + a_3 g_3 f_3 - a_4 g_4 f_4 = 0 $$

(15)

The corresponding relations for the en^int-en^ext interface reduce to:

$$ b_2 - b_3 = 0 $$

(16)

and

$$ \left[ {a_2 w_2 e_2 } \right] + \left[ {a_3 w_3 e_3 } \right] = 0, $$

(17)

where

$$ e_i = \frac{{\sqrt {\beta _j^i } }} {{\sqrt t }} $$

Finally two more relations may be derived from the boundary conditions at x ₁=x ₄=∞:

$$ a_1 + b_1 - 1 = 0 $$

(18)

and

$$ a_4 + b_4 = 0 $$

(19)

Equations 12, 13, 14, 15, 16, 17, 18, and 19 are solved for a ₁, a ₂, a ₃, a ₄, and b ₁, b ₂, b ₃, b ₄, so that the error function solution (Eq. 5) may be written for each of the four media, with the diffusion coefficients of the isotopic element in the four media as the only unknowns. These equations may then be used to obtain the unknown diffusivities from fitting the model curves to the observational data. The a and b parameters are represented by rather complex expressions, which are not shown here due to space constraints. These expressions may be generated from Eqs. 12, 13, 14, 15, 16, 17, 18, and 19, a mathematica notebook, which contains the necessary algebra, is available from the first author upon request.