Activity coefficient and polymerization of aqueous silica at 800 °C, 12 kbar, from solubility measurements on SiO₂-buffering mineral assemblages

Abstract

The activity coefficient of aqueous silica was determined at 800 °C and 12 kbar by measuring the concentration of total dissolved aqueous silica (SiO_2(t)) in H₂O in equilibrium with four buffering mineral assemblages: quartz (Q), kyanite–corundum (KC), enstatite–forsterite (EF), and forsterite–rutile–geikielite (FRG). SiO_2(t) concentrations were determined by reversed equilibration of synthetic minerals with H₂O using a weight gain/weight loss technique, yielding molalities of SiO_2(t) (m _s) of Q, 1.413(1); KC, 0.984(43); EF, 0.276(9); FRG, 0.079(1) (1σ errors). The solubility data can be fitted well according to the homogeneous equilibrium 2 SiO₂ monomers (m) = 1 Si₂O₄ dimer (d) assuming ideal mixing, such that the equilibrium constant (K _md ) is K _md =X _d /X _m ², where X represents the mole fraction of SiO_2(t) occurring as the subscripted species. This formulation is valid irrespective of the hydration states of the silica species because of the small silica concentration at these conditions (≤2.5 mol%). For a standard state of unit activity of the hypothetical pure monomer solution at the P and T of interest, the monomer–dimer model leads to γ _s =X _m /X _s and

$$ {K_{{md}} = {{{\left( {1 - \gamma _{s} } \right)}} \over {2\gamma ^{2}_{s} X_{s} }}} $$

where γ _s and X _s are the activity coefficient and mole fraction of total silica. Our data yield ${K_{{md}} = 155^{{ + 25}}_{{ - 39}} }$ at 800 °C and 12 kbar, in excellent agreement with results from in situ Raman spectroscopy of a quartz-saturated solution at the same P–T. In the system SiO₂–H₂O, a solution in equilibrium with quartz at 800 °C, 12 kbar, contains 2.5 mol% silica, of which 70% occurs in dimers, and γ _s is small (0.30). Even at the low concentration of the FRG buffer (0.1 mol%), the activity coefficient is only 0.75 and the dissolved silica is substantially polymerized (25%).

Introduction

Large-scale transport of silicate mineral components by aqueous fluids is an important factor in the evolution of the Earth's upper mantle and crust in such settings as subduction zones (Manning 1998), batholiths (Ferry 1994), and zones of continental reactivation (Stolz and Davies 1989). The concentration of total dissolved silica (SiO_2(t)) is high in water-rich solutions over a wide range of P and T. Quantitative estimation of silica transport depends on accurate knowledge of the thermodynamic properties of solute silica. Until recently, it was thought that ideal solution of silica monomers accounts adequately for the thermodynamic behavior of SiO_2(t), even in fairly concentrated solutions at high temperatures and pressures (Walther and Helgeson 1977; Berman 1988; Holland and Powell 1998), and calculations of metasomatism in deep-seated environments have employed this concept (e.g., Manning 1995; Newton and Manning 2000a). Recent experimental studies have shown, however, that this assumption is seriously in error at high P and T, even for fairly low SiO_2(t) concentrations (Zhang and Frantz 2000; Zotov and Keppler 2000, 2002; Newton and Manning 2002). Zhang and Frantz (2000) challenged the conventional assumption of ideal solution of monomeric silica at high P and T based on their experimental study of the solubility of silica in H₂O in the model upper mantle system MgO–SiO₂–H₂O. Silica activity in their experiments was buffered according to the reaction 2enstatite = forsterite + SiO_2(t) (reaction EF, Table 1). They synthesized the assemblages enstatite + fluid, enstatite + forsterite + fluid, and forsterite + fluid from oxide mixtures + water of various bulk compositions in the ternary system at 10–20 kbar and 900–1,200 °C in a piston-cylinder apparatus. At constant T and P, the observed phase boundaries of the three assemblages, when projected to the subsystem SiO₂–H₂O, determine the total silica in solution because there is negligible solution of MgO at these conditions (Zhang and Frantz 2000). The principal conclusion of their study was that the observed SiO₂ solubility of the assemblage enstatite-forsterite is two to three times smaller than the solubility to be calculated from the tabulated thermodynamic data for enstatite, forsterite, and quartz, and assuming ideal solution of aqueous silica monomers. The activity coefficient of silica would have to be as low as 0.5 for the measurements of Zhang and Frantz (2000) to be consistent with the thermodynamic data sets (e.g., Berman 1988; Holland and Powell 1998). Zhang and Frantz (2000) suggested that the formation of solute silica polymers could account for the discrepancy.

Table 1. Symbols and abbreviations

Almost simultaneously with the work of Zhang and Frantz (2000), Zotov and Keppler (2000) identified coexisting silica monomers and dimers by in-situ Raman spectroscopy of quartz-saturated solutions in an externally heated diamond cell device. Their experiments were conducted at 500–900 °C and 5–14 kbar along isochoric P–T paths. In the higher P–T region of their investigation, they noted monomer peaks, as well as three peaks that could be attributed to silica dimers. The quantitative assessments of Zotov and Keppler (2002) indicated that the dimers could account for as much as 70% of the solute silica at their highest P–T (900 °C, 14 kbar).

Newton and Manning (2002) measured the solubility of silica in H₂O in equilibrium with forsterite and enstatite at 600–900 °C, 4–14 kbar, by a precise weight change method. Their study used synthetic single crystals of enstatite and forsterite, as well as fine-grained synthetic mechanical mixtures of the two minerals and natural low-Fe enstatite and forsterite. Solubility measurements were reversed at each experimental P and T by approaching equilibrium from silica concentrations initially higher and lower than final EF solubility. As in the study of Zhang and Frantz (2000), the solubilities were much smaller than predicted assuming ideal solution of neutral monomeric silica.

Experimental verification of the partial polymerization of aqueous silica at high P and T indicates that thermodynamic models of silica in solution require revision. This can be done by comparing measured SiO_2(t) concentrations in equilibrium with different buffering mineral assemblages at the same P and T. Because Mg–Si complexes and charged Si complexes can be ignored (Zhang and Frantz 2000; Newton and Manning 2002), results on enstatite + forsterite (Newton and Manning 2002) and quartz (Zotov and Keppler 2000) at the same P and T allow calibration of an activity model. Equilibrium between quartz and aqueous silica monomers (m) can be represented by

$$ {{\mathop {{\rm{SiO}}_{2} }\limits_{{\rm{quartz}}} } = {\rm{SiO}}_{{2(m)}} } $$

(1)

and equilibrium between quartz and aqueous silica dimers (d) by

$$ {{\mathop {{\rm{2SiO}}_{2} }\limits_{{\rm{quartz}}} } = {\rm{Si}}_{{\rm{2}}} {\rm{O}}_{{4(d)}} } $$

(2)

and so on for progressively more polymerized aqueous silica species. Aqueous silica polymers are likely to be H₂O-solvated species, but the extent of solvation varies with P, T, and solution composition (Walther and Helgeson 1977; Walther and Orville 1983). The problem of uncertainty in solvation configuration is avoided by defining as zero the changes in Gibbs free energy of the reactions

$$ {{\rm{SiO}}_{{2(m)}} + x{\rm{H}}_{{\rm{2}}} {\rm{O}} = {\rm{H}}_{{2x}} {\rm{SiO}}_{{2 + x}} } $$

(3)

and

$$ {{\rm{Si}}_{{\rm{2}}} {\rm{O}}_{{4(d)}} + y{\rm{H}}_{{\rm{2}}} {\rm{O}} = {\rm{H}}_{{2y}} {\rm{Si}}_{{\rm{2}}} {\rm{O}}_{{4 + y}} } $$

(4)

Thus, Eqs. (1) and (2) implicitly represent equilibria involving aqueous solvated silica species [Eqs. (3) and (4)] without explicit provision for H₂O solvation (Walther and Helgeson 1977). This approach is useful provided that the activity of H₂O is near unity. Even at the highest SiO₂ concentrations encountered by Zotov and Keppler (2002), the mole fraction of H₂O is immaterially different from unity (minimum of 0.96), and it can be assumed that ${a_{{{\rm{H}}_{{\rm{2}}} {\rm{O}}}} \approx X_{{{\rm{H}}_{{\rm{2}}} {\rm{O}}}} \approx 1}$.

Homogeneous equilibrium among silica monomers and dimers can be represented by

$$ {{\rm{2SiO}}_{{{\rm{2(}}m{\rm{)}}}} = {\rm{Si}}_{{\rm{2}}} {\rm{O}}_{{{\rm{4(}}d{\rm{)}}}} } $$

(5)

Adopting a standard state for SiO_2(t) of unit activity of the hypothetical solution of unit mole fraction of monomers and a reference state of infinite dilution, and assuming ideal solution of monomers and dimers with H₂O (Newton and Manning 2002), the equilibrium constant for Eq. (5) can be written

$$ {K_{{md}} = {{X_{d} } \over {X^{2}_{m} }}} $$

(6)

where the subscript md denotes equilibrium involving monomers and dimers in solution [Eq. (5)] and X is the fraction of SiO_2(t) occurring as the subscripted species on a molar basis. In this model, non-ideality of solute silica would result entirely from decrease of the number of monomers in solution due to Eq. (5) progressing to the right. The activity coefficient of SiO_2(t), γ_s, is given by:

$$ {\gamma _{s} = {{X_{m} } \over {X_{s} }}} $$

(7)

where X _s is the SiO_2(t) mole fraction (${X_{s} = n_{{{\rm{SiO}}_{{2(t)}} }} /[n_{{{\rm{SiO}}_{{2(t)}} }} + n_{{{\rm{H}}_{{\rm{2}}} {\rm{O}}}} ]}$), and

$$ {X_{s} = X_{m} + 2X_{d} } $$

(8)

Combination of Eqs. (6), (7), and (8) yields

$$ {K_{{md}} = {{{\left( {1 - \gamma _{s} } \right)}} \over {2\gamma ^{2}_{s} X_{s} }}} $$

(9)

Where experimental P–T ranges coincide, K _md values deduced by Newton and Manning (2002) are in reasonable agreement with those found by Zotov and Keppler (2002), in spite of the very different kinds of observations and the great difference in silica concentration between quartz saturation in the Zotov and Keppler (2002) study and enstatite–forsterite saturation in the Newton and Manning (2002) study (about five times as concentrated in the former study).

Although there is apparent agreement between the two experimental studies, they do not uniquely determine the activity coefficient because other models could explain the solubility data. For instance, higher polymers (trimers, etc.) may also be present (Zotov and Keppler 2000), with their abundance determined by additional equilibrium constants analogous to K _md of Eq. (6). If the equilibrium constant is independent of polymer size (e.g., Masson 1965), a relation analogous to Eq. (9) for an ideal mixture of all polymers of any geometry (ap) can be derived:

$$ {K_{{ap}} = {{1 - \gamma ^{{1/2}}_{s} } \over {\gamma _{s} X_{s} }}} $$

(10)

(Newton and Manning 2002). Comparison of Eqs. (9) and (10) illustrates that the equilibrium constants and activity coefficients to be deduced from the solubility data differ substantially depending on the energetics and extent of polymerization.

The non-uniqueness of the derived K value means that solubility measurements are necessary on additional SiO₂-buffering assemblages, in order to define the activity–concentration relations over a broad range of concentrations. Most importantly, measurements are needed for some refractory assemblage(s) that buffer SiO₂ concentration in the very dilute range, where, according to Eqs. (9) and (10), the activity coefficient changes rapidly with concentration. It is necessary that the thermodynamic properties of the buffering minerals be well determined, ideally as part of a large internally consistent data set (e.g., Berman 1988; Holland and Powell 1998). This requirement proves to be a stringent one: only a few refractory silica-bearing assemblages can be found for which the known thermodynamic properties are sufficiently reliable for the purpose of defining γ_s–X_s relations.

The present study gives results of measurements of aqueous silica concentrations at 800 °C and 12 kbar on four SiO₂-buffering assemblages that cover a wide span of concentrations. The investigated dissolution reactions and abbreviations are given in Table 1. The broad range in composition permits derivation of an isothermal–isobaric activity–concentration model for aqueous silica in the system SiO₂–H₂O.

Experimental methods

All experiments were conducted in a 0.75-inch (1.91-cm.)-diameter piston-cylinder apparatus with NaCl pressure media and graphite heater sleeves. The same highly polished tungsten-carbide pressure-vessel core and batch of calibrated, matched W3%Re–W25%Re thermocouples were used in all experiments. Accuracy of temperature (±3 °C) and pressure (±300 bar) measurements are discussed in Newton and Manning (2000b). Mass determinations were made with a Mettler M3 microbalance (1σ=2 μg in each weighing step).

Three different kinds of starting material were used. Most experiments used fine-grained mixtures of kyanite–corundum, enstatite–forsterite, and rutile–geikielite. These assemblages were crystallized hydrothermally from reagent-grade oxide mixtures at 900 °C and 10 kbar for 24 h. No extraneous phases were detected optically or by X-ray diffraction. Kyanite was synthesized in the same manner as in Harlov and Newton (1992; properties given therein). Synthesis of the enstatite–forsterite mix is described in Newton and Manning (2002). Crystal sizes were 5–100 μm. Both minerals of a starting mix were present in about equal weight amounts. Trigonal unit-cell constants of a _o =5.052 (2) and c _o =13.896 (4) for geikielite were determined by X-ray diffraction scans (CuK_α, 0.5 °2θ/min) using the rutile peaks as an internal standard. The values coincide, within uncertainties, with synthetic geikielite (ASTM 6-0494). A second kind of starting material in the rutile–forsterite–geikielite system consisted of a hard, sintered compact of well-mixed rutile (70%) and forsterite (30%), which was prepared by pelletizing the mineral mix under pressure and then annealing it at 1,100 °C for 2 h. Chips of the compact weighing about 4 mg were smoothed with a diamond file, polished by rubbing with 600-mesh alundum paper and then cleaned by washing in acetone and water and drying at 350 °C. In one experiment, a natural kyanite crystal (Bahia, Brazil, 0.17 wt% TiO₂, trace of FeO) was used.

Mineral mixes or sintered chips were contained in 2–3-mm-long segments of Pt tubing, welded at one end and lightly crimped at the other. The capsules were usually perforated with between 6 and 20 100–200-μm holes to allow access of the fluid without loss of particulate matter (in two experiments on the geikielite–rutile mix, there was visible evidence after the run of escaped crystals, with attendant anomalous weight changes; these runs were discounted). The perforated inner capsules were placed into 2.5-mm OD Pt tubes with a weighed amount of H₂O and, in most cases, a fragment of a natural quartz crystal to produce a predetermined initial SiO₂ fluid content, and sealed by arc-welding.

Experiments were terminated by turning off the apparatus power. Temperatures fell below 200 °C in about 12 s. Retrieved outer capsules were cleaned of salt by soaking in H₂O. Weights of retrieved capsules demonstrated that no leakage occurred during runs. H₂O contents were redetermined by puncturing and drying at 115 °C for 15 min, followed by 320 °C for 15 min. The weight changes corresponded to the original H₂O contents within 0.3% with no systematic discrepancies relative to the initial H₂O values. This showed that welding-related weight losses, typically about 1 mg, included negligible H₂O.

If the initial SiO₂ concentration was less than the equilibrium amount, the inner capsules lost weight; if there was initial SiO₂ oversaturation, the capsules gained weight through growth of crystals in the inner capsule. Thus, the silica concentrations for all assemblages approached equilibrium from both the undersaturated and oversaturated directions (i.e., were reversed). Experiments have shown that quartz dissolution at these conditions is very fast compared with reaction of the fluid with the experimental charges (Newton and Manning 2002).

Uncertainty in each weighing step was propagated to final solubility determinations. Resulting precision estimates are reported parenthetically as 1σ in the final digit(s) unless otherwise noted. Reported errors do not include the uncertainty in accuracy of P–T of experiments.

Unless otherwise noted, the thermodynamic data of Holland and Powell (1998) were used in all calculations.

Results

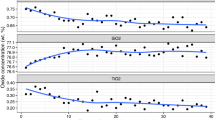
Experimental details are given in Table 2 and shown in Fig. 1, which demonstrates the time independence and reversibility of the SiO₂ molality for each of the assemblages (Q, KC, EF, and FRG, Table 1). The solubility of MgO is below detection (<4 μg, 2σ) at these conditions (Newton and Manning 2002). Additional experiments show that the solubilities of Al₂O₃ and MgO + TiO₂ make only slight contributions to the weight changes (Table 3). SiO_2(t) molalities in KC and FRG experiments were adjusted accordingly (Table 2).

Table 2. Experimental results, 800 °C, 12 kbar

Fig. 1.

Silica concentration vs. experiment duration. 2σ errors in solubility measurements are smaller than the symbol size. Note break in scale. Upward- and downward-pointing triangles denote experiments in which equilibrium was approached from initial under- and oversaturation, respectively. Lines and associated numerical values are the mean solubility (Q, FRG) or the midpoint in the range of permissible solubility (KC, EF). See Table 1 for abbreviations

Table 3. Results of control experiments

Weight losses of the inner capsules in runs GE-6 and GE-8 (Table 2) are inferred to result from the spontaneous nucleation and growth of geikielite, with loss of SiO₂ into the fluid, according to reaction FRG. This interpretation was verified by scanning electron microscopy of the charge of experiment #GE-8. Figure 2A shows that euhedral, equant, and tabular geikielite crystals, up to 80 μm across, are perched on the surface of the sintered rutile–forsterite pellet. Similarly, forsterite was identified in the charges of runs on geikielite–rutile mixes (+ quartz), as shown in Fig. 2B. The forsterite is interpreted to have nucleated and grown according to reaction FRG (Table 1) in reverse.

Fig. 2A–D.

Backscattered-electron micrographs of experimental run products, 800 °C, 12 kbar. A Euhedral geikielite neoblasts on a fine-grained, sintered rutile + forsterite compact, grown by reaction with initially pure H₂O (experiment GE-8, 98 h). B Euhedral, twinned forsterite crystals (fo) in a rutile–geikielite aggregate, grown by reaction with silica oversaturated solution. Geikielite crystals are equant and solution-rounded; rutile is prismatic and euhedral (experiment GE-7, 114 h). C Euhedral corundum platelets occupying solution cavities in kyanite crystal, grown by reaction with initially pure H₂O (experiment KY-2, 94 h). D Doubly terminated quartz crystal, grown in initially pure H₂O from a ground ellipsoid. Faceting developed despite net threefold dissolution of the crystal (experiment QZB-81, 23 h)

The data for reaction FRG are especially important because they define the most dilute SiO₂ concentration point of the present experiments and, hence, represent the closest approach to ideal solutions. The measurements ranging from 89 to 114 h seem to be independent of duration, H₂O volume, or direction of approach to equilibrium (Fig. 1, Table 2). Therefore, we treated them on a statistical basis; the average of the six solubility determinations corresponding to reaction FRG gives a total silica molality (m _s ) of 0.079 when adjusted for a MgO + TiO₂ solubility of 0.022 wt% (Table 3). 1σ in the parent population of FRG experiments is 0.005 molal, yielding a standard error in the mean of 0.002 mol. The latter value was used in all calculations.

Results for reaction EF were given by Newton and Manning (2002). Two determinations at 800 °C, 12 kbar, approached equilibrium from initially under- and oversaturated conditions (Table 2). Because the initially undersaturated experiment has lower final SiO₂ solubility than the initially oversaturated experiment, the measurements bracket the true m _s to between 0.267(2) and 0.285(2). With only two constraints, it must be assumed that there is uniform probability of the true value anywhere within the bracket limits.

The KC experiments also approached equilibrium from initial super- and undersaturation. Figure 2C shows hexagonal corundum crystals formed by dissolution of the natural kyanite in initially pure H₂O, according to reaction KC. Kyanite growth occurred in experiment KY-4, which had excess SiO₂ (Table 2). As with EF results, the three KC experiments bracket m _s to between 0.941(2) and 1.027(2), with equal probability of the actual value anywhere between these constraints.

The two quartz solubility measurements yielded nearly identical molalities (Table 2). The residual quartz was highly faceted (Fig. 2D), even though there were crystal weight losses of three- and eightfold in the two experiments. When considered with the very rapid rate of dissolution at these conditions (Newton and Manning 2002), the recrystallization strongly suggests the attainment of solution equilibrium. This permits averaging the two values to give m _s =1.413(1), which is in good agreement with the prediction of Manning (1994) of 1.50(2).

Discussion

Combination of silica solubility measured at quartz saturation with that at any other reaction B of the form

$$ reactants = products + {\rm{SiO}}_{2(t)} $$

(11)

at the same P and T, fixes the activity of the thermodynamic component SiO₂. Provided that no other components contribute significantly to the weight changes in our experiments, measured SiO_2(t) concentration at any two mineral buffers constrain the ratio of activity coefficients, ${\Gamma }$. Accordingly, the quartz buffer (Q) can be combined with any buffer B to give

$$ \ln \Gamma _{B - Q} \equiv \ln {{\gamma _s^B } \over {\gamma _s^Q }} = {{\Delta G_{B - Q}^ \circ } \over {RT}} + \ln {{X_s^Q } \over {X_s^B }} $$

(12)

where ${\Delta G^{ \circ }_{{B - Q}} }$ is the difference between the standard apparent standard molar Gibbs free energies of buffers B and Q, which is readily derived from standard thermodynamic data sets for minerals.

Reliable values of ${\Delta G^{ \circ }_{{B - Q}} }$ at 800 °C and 12 kbar of KC-Q and EF-Q are provided by the Berman (1988, 1992 update) and Holland and Powell (1998) data sets, which are derived from many experimental phase-equilibrium data involving the minerals enstatite, forsterite, kyanite, corundum, and quartz. Thermodynamic data for rutile are similarly well constrained, but the tabulated Gibbs free energy of formation of geikielite is poorly constrained by the reconnaissance experiments of Haselton et al. (1978) on the equilibrium

$$ {\matrix{ {{{\rm{TiO}}_{{\rm{2}}} }} & { + } & {{{\rm{MgCO}}_{{\rm{3}}} }} & {{\rm{ = }}} & {{{\rm{MgTiO}}_{{\rm{3}}} }} & { + } & {{{\rm{CO}}_{{\rm{2}}} }} \cr {{{\rm{rutile}}}} & {{}} & {{{\rm{magnesite}}}} & {{}} & {{\;{\rm{geikielite}}}} & {{}} & {{}} \cr } } $$

(13)

Derived thermodynamic properties of geikielite differ considerably between the two data sets. However, the recent experimental data of Ferry et al. (2002) on this equilibrium make possible a much improved estimate of ${\Delta G^{ \circ }_{{FRG - Q}} }$. We used the midpoint of bracketed values of ${\Delta _{f} H^{ \circ }_{{geikielite}} }$ based on Ferry et al. (2002) to compute ${\Delta G^{ \circ }_{{FRG - Q}} }$.

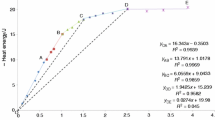
Our solubility constraints, values of ${\Delta G^{ \circ }_{{B - Q}} }$, and ${\log \Gamma _{{B - Q}} }$ calculated using Eq. (12) are listed in Table 4. The ${\log \Gamma _{{B - Q}} }$ constraints (Fig. 3) can be fitted very well with the monomer-dimer model [Eq. (9)]. A ${\log K_{{md}} }$ value of 2.19 satisfies all of the bracketing data using the Holland and Powell (1998) data set (Fig. 3); a similar value of 2.14 is obtained using Berman (1988, updated 1992). The results of Ferry et al. (2002) permit a range of $\Delta _f H_{geikielite}^ \circ ,$ which, in turn, allows a range in the equilibrium constant. The maximum allowable range is that defined by the EF brackets, which translates to ${\Delta _{f} H^{ \circ }_{{geikielite}} }$=–1,568.17 to −1,567.74 kJ/mol, consistent with Holland and Powell (1998), and yields ${\log K_{{md}} }$=2.06 to 2.25 (Fig. 3). The same calculations using Berman (1988, updated 1992) yield ${\Delta _{f} H^{ \circ }_{{geikielite}} }$=–1,570.31 to −1,569.89 kJ/mol and ${{\rm{l}}ogK_{{md}} }$=1.94 to 2.12.

Table 4. Data used in activity determinations, 800°C, 12 kbar. Mole fractions are mean values for Q and FRG but brackets only for KC and EF (see text). HP98 designates thermodynamic data from Holland and Powell (1998), except ${\Delta _{f} H^{ \circ }_{{geikielite}} }$=1,568.00(74) kJ/mol at 25 °C, 1 bar, midpoint calculated from Ferry et al. (2002); B92 designates thermodynamic data from Berman (1988; updated 1992), except ${\Delta _{f} H^{ \circ }_{{geikielite}} }$=1,570.34(67) kJ/mol, from Ferry et al. (2002). See Table 1 for buffer abbreviations

Fig. 3.

${{\rm{Log}}\Gamma _{{B - Q}} }$ vs. mole fraction of total silica in solution at 800 °C, 12 kbar. Values are from Table 4 using thermodynamic data from Holland and Powell (1998). Experimental results on KC and EF experiments plotted with upward and downward pointing triangles. Actual solubility is any value between these limits. Results of FRG and Q experiments shown with filled circles, corresponding to the mean of all experimental results. Variation in ${{\rm{l}}og\Gamma _{{B - Q}} }$ with X _s also shown for monomer-dimer model log K =2.19. Range in permissible values of log K is 2.06–2.25 (see text), yielding ${{\rm{l}}og\Gamma _{{B - Q}} - X_{s} }$ variation shown in light solid lines. The all-polymer model (dashed line) fails to fit all the experiments simultaneously. Abbreviations as in Fig. 1

As noted above, our model does not account explicitly for H₂O solvation. It can be demonstrated that this does not introduce significant error by recasting the monomer and dimer species as H₄SiO₄ and H₆Si₂O₇. Homogeneous equilibrium between these species involves liberation of 1 mol of H₂O for every mol of dimers produced because 2H₄SiO₄ = H₆Si₂O₇ + H₂O. The log K for this equilibrium explicitly involves ${a_{{{\rm{H}}_{{\rm{2}}} {\rm{O}}}} }$. Assuming ideal mixing of silica and H₂O, it is only ~0.01 less than ${\log K_{{md}} }$. Differences in the H₂O solvation configuration between monomers and dimers would have to be very large to change ${\log K_{{md}} }$ significantly.

Using the all-polymer model [Eq. (10)], no single log K _ap value that is consistent with all solubility constraints could be found. This is a result of the less pronounced dependence of K _ap on ${\Gamma }$ at low X _s . A value of ${\log K_{{ap}} }$=1.39 is shown for illustration in Fig. 3.

Our ${\log K_{{md}} }$ value at 800 °C and 12 kbar is the same, within the uncertainties, as that found at the same P–T conditions by Zotov and Keppler (2002) by in situ Raman spectroscopy of quartz-saturated solutions (${\log K_{{md}} }$=2.07±0.07). The close agreement between the present determination of K _md and that of Zotov and Keppler (2002), arrived at by very different techniques, must be in part fortuitous, because the latter reconstruction involved extrapolating the Fournier and Potter (1982) empirical quartz solubility equation, which gives m _s =1.511 at 800 °C and 12 kbar. Nevertheless, the agreement would appear to be a solid justification of the use of the monomer-dimer model, embodied in Eq. (9), in the general P–T range 5–15 kbar and 600–900 °C.

Using ${\log K_{{md}} }$=2.19, Eq. (9) can be rearranged to give the activity coefficient-mole fraction relation of aqueous silica at 800 °C and 12 kbar (Fig. 4). Strong concentration-dependent non-ideality, most pronounced for small concentrations, is evident. For concentrations as dilute as 0.1 mol%, the activity coefficient is markedly different from unity. It is to be emphasized that the construction of Fig. 4 does not depend strongly on the validity of the monomer–dimer model. Equations (6), (7), (8), and (9) serve as a convenient and rational basis for integrating the data, but the activity–concentration relations of Fig. 4 are based mainly on the measured quantities expressed in the brackets of Fig. 3, namely the solubilities and Gibbs free energies for the simple minerals involved, which are among the best determined and most reliable in the thermodynamic data sets.

Fig. 4.

Variation in activity coefficient of total silica with mole fraction of total silica, 800 °C, 12 kbar, based on the monomer-dimer model [Eq. (9)] and ${{\rm{l}}ogK_{{md}} }$=2.19 (bold line). Light, solid lines show the range in possible values consistent with ${\Delta _{f} H^{ \circ }_{{geikielite}} }$ from Ferry et al. (2002) and the EF buffer (see text)

The activity coefficient relations shown in Fig. 4 represent the fraction of total silica present at any concentration that is in the form of monomers, as per Eq. (7). Although the derived fraction of monomers is mainly model-independent, there may well be among the polymerized population a smaller quantity of trimers and even more highly polymerized species (Newton and Manning 2002). The existence of a second critical end point in the system SiO₂–H₂O (Kennedy et al. 1962) implies that higher polymeric species will be present in increasingly greater quantities at higher silica concentrations and at temperatures and pressures beyond those of this study.

The present analysis gives an activity coefficient at quartz saturation at 800 °C and 12 kbar of 0.301. This yields an apparent standard molar Gibbs free energy of reaction of buffer Q (${\Delta G^{ \circ }_{Q} }$) of 43.69 kJ/mol at this P and T. Using the maximum range in ${\Delta _{f} H^{ \circ }_{{geikielite}} }$ defined by the EF brackets limits ${\gamma ^{Q}_{S} }$ between 0.283 and 0.339 and ${\Delta G^{ \circ }_{Q} }$ between 42.64 and 44.24 kJ/mol at 800 °C, 12 kbar.

Geological applications

The present work shows that solubility and metasomatic phase relations involving SiO₂–H₂O fluids under deep crust/upper mantle P–T conditions can be calculated from tabulated thermodynamic data with the aid of activity–concentration relations based on a relatively small number of measured solubility data. The most rigorous calculations are possible for refractory systems where SiO₂ is the most soluble component, as in the ultramafic upper mantle. The solubility of enstatite–forsterite as predicted by the monomer–dimer model is adequate to calibrate activity–concentration relations over an extended P–T region appropriate to deep-Earth conditions. Solubility measurements in addition to those presented by Newton and Manning (2002) are desirable for this purpose, as are, importantly, additional measurements of quartz solubility. Accurate control of quartz solubility may be most important in the >900 °C temperature range, where the deviations of existing experimental data from the Manning (1994) solubility equation are greatest.

Other factors that may enhance the solubility of silica of natural assemblages are alkalis and acid/base relations. It is possible that silica may be present as feldspar-like solute species. The system albite (NaAlSi₃O₈)–H₂O becomes supercritical in an elevated P–T range (Shen and Keppler 1997), and extremely silicate-rich solutions are in equilibrium with albite, which are virtually H₂O-rich melts with SiO₂ near 50 wt%. Alkaline solutions emitted by deep-seated magmas may leach SiO₂ to a greater degree than possible by pure water, as in the fenite aureoles of carbonatite complexes. The most direct application of the present data may be in some subduction zones, where great silica transport is recorded in the form of quartz vein complexes, and where other geochemical criteria suggest that the fluid transporting medium was dominantly H₂O (e.g., Bebout and Barton 1989). The non-ideality of aqueous silica at elevated P–T leads to larger changes in solute transporting power with silica concentration. Compared to an assumed ideal solution of monomers, a polymerized solution requires lower integrated fluid fluxes to transport silica.