Importance of viscoelasticity in the thixotropic behavior of human blood

Abstract

Recent work modeling the rheological behavior of thixo-elasto-viscoplastic (TEVP) materials such as human blood indicates that it has all of the hallmark features of a complex material, including shear-thinning, viscoelasticity, a yield stress, and thixotropy. After decades of modeling steady-state human blood rheological data, and the development of simple steady-state models, like the Casson and Herschel–Bulkley, the advancement and evolution of TEVP modeling to transient flow conditions now has reinvigorated interest. Using recently collected human blood rheological data, over a wide range of flow conditions from steady state to various oscillatory shear flows, we show and compare modeling efforts with the original and a viscoelasticity-enhanced version of the enhanced Apostolidis–Armstrong–Beris (EAAB) model. The viscoelasticity enhancement is then justified by its ability to improve predictions of small and large amplitude oscillatory shear as well as uni-directional oscillatory shear flow. The new viscoelastic parameter is then incorporated into a methodology to estimate the viscoelastic time scale of human blood. Lastly, we compare our new TEVP modeling approach with another recently developed TEVP model, mHAWB, for context.

Introduction

Thixotropic, complex materials continue to be an important topic within rheology. Thixotropy is defined in Colloidal Suspension Rheology as the “continuous decrease in viscosity with time when flow is applied to a sample that has been previously at rest, and subsequent recovery of viscosity when the flow is discontinued” (Goodeve 1939; Mujumdar et al. 2002; Mewis and Wagner 2009; Mewis and Wagner 2012; Larson 2015; Wei et al. 2016). In this context, the viscosity changes are based upon a material’s microstructural breakdown and reformation over different time scales and rates of shear. Typically, thixotropic media are suspended in viscoelastic materials with their own unique viscoelastic time scale of evolution. Lightly structured materials like human blood have overlapping viscoelastic and thixotropic time scales. The viscoelastic modeling upgrade demonstrated in this manuscript will allow for insight into these relative time scales. Certain thixotropic fluids simultaneously possessing both features meet the criteria to be classified as thixo-elasto-viscoplastic materials (TEVP). Thixotropic—containing a microstructure that will break apart and reform based on conditions; elastic—“stretchiness,” or the ability to store energy before the microstructure shatters or breaks apart; viscous—resistance to flow; and plastic—irreversible structure stretching/breaking then shattering (Dullaert and Mewis 2006; Mewis and Wagner 2012; Horner et al. 2018a, 2018b). Examples of TEVP materials include human blood, paint, carbon and silica suspensions, ketchup, yogurt, and toothpaste (Bureau et al. 1979, 1980; Mujumdar et al. 2002; Dullaert and Mewis 2006; Beris et al. 2008; Mewis and Wagner 2012; de Souza Mendes and Thompson 2012, 2013; Dimitriou et al. 2012; Ewoldt et al. 2008; Ewoldt and Bharadwaj 2013; Gurnon and Wagner 2012; Blackwell and Ewoldt 2014; Moreno et al. 2015; Apostolidis et al. 2015; Apostolidis and Beris 2016a, 2016b; Wei et al. 2016; Pratumwal et al. 2017; Ewoldt and McKinley 2017; Clarion et al. 2018; Armstrong et al. 2016a; Armstrong et al. 2017; Armstrong et al. 2018; Horner et al. 2018b; Horner et al. 2019). When a thixotropic material is at rest, typically the microstructure is completely relaxed which contributes to the apparent yield stress. These hallmark features are further described by Mewis and Wagner’s, Larson’s, and the IUPAC definition above (Mewis and Wagner 2009; Mewis and Wagner 2012; Larson 2015).

Blood is a well-known example of a TEVP material with evolving mechanical properties based on microstructure which can be correlated with human health (Bureau et al. 1979, 1980; Apostolidis and Beris 2014; Moreno et al. 2015; Apostolidis and Beris 2016a, 2016b; Armstrong and Tussing 2020). Blood is composed of plasma containing cells, platelets, and other substances essential for human life, and we state here has its own viscoelasticity, and viscoelastic time scale. At lower shear rates, red blood cells will combine to form rouleaux structures in a linear stack, causing an increase in viscosity, thus forming a “microstructure” (Horner et al. 2018a; Horner et al. 2019). The microstructure contributes to the elastic stresses through rouleaux formation and breakdown, as well as viscoelastic stresses since the microstructure surface area will cause resistance to flow. Additionally, as the rouleaux are stretching they are undergoing “plastic, irreversible deformation” before finally breaking apart. At higher shear rates, the red blood cell rouleaux structures will break apart with or without plastic deformation first (Baskurt and Meiselman 2003; Baskurt et al. 2009; Baskurt et al. 2012; Apostolidis et al. 2015; Apostolidis and Beris 2016b; Horner et al. 2018a, 2019), causing a more liquid-like flow. This complex back and forth (evolution) of conformational change of the red blood cells makes it more difficult to accurately model the flow of red blood cells throughout their change in structure. However, recent models by Apostolidis et al. (2015), Armstrong et al. (2018), Horner et al. (2018a, 2019) and Armstrong and Tussing (2020) continue the development of more accurate models to expand the range of its application to modeling and prediction rheological flows. Another notable effect of the viscoelastic time scales is the difference between the viscoelastic time scale of plasma and the viscoelastic time scale of the rouleaux microstructure buildup and breakdown. These two time scales create a complex non-Newtonian flow that exhibits properties of a weak, gel-like, solid at low shear rates and a liquid at higher shear rates.

The ability to model the complex TEVP rheological properties of red blood cells and other materials in the blood has the potential to impact how patient blood samples are analyzed for particular vascular or coronary conditions involving high cholesterol, fibrinogen, or hematocrit (Bureau et al. 1980; Moreno et al. 2015; Apostolidis and Beris 2016b; Horner et al. 2019). There are positive correlations between viscosity of blood plasma and higher instances of vascular disorders (Moreno et al. 2015; Celik et al. 2016). Vascular diseases depend on the health of blood clotting, size of blood vasculature, and viscosity of blood in the patient (Merrill et al. 1966; Merrill 1969; Bureau et al. 1980; Moreno et al. 2015; Apostolidis and Beris 2016a; Clarion et al. 2018). The viscosity of blood cells and the plasma that they are transported in affect the rate that oxygen and other vital nutrients can be transported throughout the body. If the rate is too low, the heart will pump at a more intense rate and create high blood pressure to keep nutrient flow and hormones at a normal level. Identifying high blood viscosity early on through routine blood testing physiological parameters such as fibrinogen, high- and low-density lipoprotein cholesterol, triglycerides, hematocrit, and total cholesterol can help quickly diagnose people at risk of vascular disease. Moreno et al. (2015) as well as Apostolidis and Beris (2016a, 2016b) have correlated hematocrit, fibrinogen, and cholesterol to the viscosity of blood. Other diseases that show a noticeable change in blood rheology are sickle cell anemia, diabetes, and hypertension (Bureau et al. 1979, 1980; Horner et al. 2018a, 2019).

The ability to apply newer model features is aided using Akaike’s information criterion (AIC) to perform cost benefit analysis with respect to number of new parameters added. His formalism is used to penalize increased numbers of parameters and consider the accuracy of the model (Akaike 1974). The AIC assigns a relative value based upon the costs of a more complex model to its accuracy and facilitates a discipline to prevent parameters that are added without a direct correlation with model and microstructure physics (Akaike 1974; Armstrong et al. 2018; Horner et al. 2019).

Our base model evolves from the original Dullaert–Mewis model, a structural kinetic model that focuses on an elastic modulus and shear rate as well as elastic strain (Dullaert and Mewis 2006; Mewis and Wagner 2012). The Dullaert–Mewis structural kinetic model divides total stress into structure-dependent contributions based on elasticity and viscosity. The model also considers time constants, Brownian motion, shear effects on breakdown and buildup, and deformation and relaxation of flocs (Mujumdar et al. 2002; Dullaert and Mewis 2006). The modified Delaware thixotropic model (MDTM) also incorporates the best features from the above cited model (Armstrong et al. 2016a, 2016b). In addition, Dimitriou et al. (2012) introduced a novel methodology that broke total strain and shear rate into elastic and plastic components (Dimitriou et al. 2012). The MDTM is a modified version of the Herschel–Bulkley/Bingham model with a new term “to account for shear aggregation processes, following the approach of Dullaert and Mewis” (Armstrong et al. 2016a). MDTM also utilized portions from Dimitriou et al. (2012), “who developed a framework to separate the strain and shear rate into elastic and plastic components to better capture the EVP behavior of soft materials,” (Armstrong et al. 2016a). Furthermore, MDTM was a structure-based model for thixotropic suspensions and contained a total of 13 parameters. In comparison to models with fewer parameters, MDTM approximated “qualitatively similar” to that of the lower parameters and was deemed “sufficient” (Armstrong et al. 2016a). Apostolidis and coworkers then made the following associations: elastic strain and shear rate would be correlated with stretching microstructure (reversible) and elastic stress contributions, while the plastic strain and shear rate would be associated with permanent changes to the microstructure and plastic contributions imparted on total stress from the microstructure (Apostolidis et al. 2015; Armstrong et al. 2016a, 2017, 2018; Horner et al. 2018a, 2019).

Each of these models contributed to the development of the original Apostolidis–Armstrong–Beris (AAB) model (Apostolidis et al. 2015). Armstrong et al. (2018) then added various structural viscosity contributions analogous to features in the MDTM, thus creating the enhanced Apostolidis–Armstrong–Beris (EAAB) model (Armstrong et al. 2016a; Armstrong et al. 2017; Armstrong et al. 2018). Here, we will add an additional viscoelastic time scale to the effects of the evolving microstructure, which we now understand has a viscoelastic time lag associated with it from Horner and coworkers (Horner et al. 2018b, 2019). We define viscoelastic as follows: property of a material that exhibits both elastic and viscous characteristics simultaneously when undergoing deformation. Viscoelastic materials have elements of both properties. Whereby in our case, the elastic property comes from two places the plasma backbone and the rouleaux that are dynamically building and breaking down during blood flow. In our model, this breakdown and buildup is a function of shear rate. The plasticity comes from the irreversible stretching of the rouleaux before breaking apart. The rouleaux also undergo reversible stretching during some small-deformation, rheological conditions. Typically, the viscoelasticity can be seen experimentally when there is a time lag between a change in the shear rate and when measured stress equilibrates at some finite amount of time after the change. The viscoelastic enhancement of the VE-EAAB model is a time constant of evolution for the effect of the contribution of the continuously evolving structure on total stress (Mewis and Wagner 2012; Horner et al. 2018b; Horner et al. 2019).

Based on analysis of the transient blood data presented here and analysis by Horner et al. (2018a, 2019), it has been determined that to accurately model and predict rheological properties of human blood there must be included an evolutionary time constant for the thixotropic (microstructural) changes as well as a viscoelastic time constant. In addition to introducing the new viscoelastic, structural contribution (to total stress) time constant, we will validate the additional parameter to the EAAB model (Apostolidis et al. 2015; Armstrong et al. 2018) with the model’s ability to predict small amplitude oscillatory shear flow (SAOS), both frequency and amplitude sweeps, as well as cessation of flow, triangle ramp, large amplitude oscillatory shear flow (LAOS), and uni-directional oscillatory shear flow (UD-LAOS) experiments (Armstrong et al. 2016a; Horner et al. 2018a; Horner et al. 2019). The novelty of this work is the fact that both EAAB and VE-EAAB are based on a Kelvin–Voight linear superposition of the various components of the total stress, while the work of Horner et al. uses the Maxwellian, White–Metzner approach (with the Cross model for viscosity) as the basis. It is shown that by adding a viscoelastic time constant to the structural contribution to total stress to the EAAB, we can approach and in some cases equal the accuracy of fits and predictions of Horner et al. (2018a, 2019).

The remainder of the paper is as follows: the “Model descriptions” section, the “Materials and methods” section to detail the experimental protocol, model fitting procedure, and oscillatory shear flow paradigm; results to show both model’s (EAAB and VE-EAAB with comparison to enhanced thixotropic mHAWB) ability to fit steady state and step-up/step-down in shear rate experiments followed by predictions of SAOS, cessation of flow, triangle ramp, LAOS, and UD-LAOS; lastly, the “Results and discussion” section to argue for the inclusion of the additional viscoelastic time constant.

Model descriptions

In this section, we re-introduce the EAAB model in full detail and build onto that with a viscoelastic enhancement. This will allow the new model to have not only a thixotropic time scale of evolution but also a viscoelastic time scale of evolution to accurately account for the lag time of the structural stress contribution to total stress. This is critical for more accurate prediction of the TEVP flow of blood (Apostolidis et al. 2015; Clarion et al. 2018; Armstrong et al. 2018; Horner et al. 2018a, 2019). Recall that the frameworks incorporated for the TEVP rheological modeling of human blood involve two generic approaches as follows:

$$ {\sigma}_{tot}={\sigma}_e\left(\lambda, \dot{\gamma}\right)+{\sigma}_v\left(\lambda, \dot{\gamma}\right) $$

(1)

with the total stress consisting of an elastic component, that is a function of the current level of the microstructure, λ from [0 1], and the shear rate $\dot{\gamma}$ (1/s). The microstructure is a dimensionless number representing a value between 0 and 1, where 0 is fully broken down structure, while a 1 communicates a fully structured complex material with all intermolecular connections intact (Goodeve 1939; Mujumdar et al. 2002; Dullaert and Mewis 2006; Mewis and Wagner 2012; de Souza Mendes and Thompson 2013; Dimitriou et al. 2012; Blackwell and Ewoldt 2014; Armstrong et al. 2016a, 2016b; Armstrong et al. 2017; Clarion et al. 2018; Armstrong et al. 2018; Horner et al. 2018a, 2018b, 2019). Our proposed modification consists of adding an additional viscoelastic component as follows

$$ {\sigma}_{tot}={\sigma}_e\left(\lambda, \dot{\gamma}\right)+{\sigma}_{ve, st}\left(\lambda, \dot{\gamma}\right)+{\sigma}_v\left(\lambda, \dot{\gamma}\right) $$

(2)

where the proposed viscoelastic term, ${\sigma}_{\mathrm{ve},\mathrm{st}}\left(\lambda, \dot{\gamma}\right)$, is the contribution to the total stress that directly manifests from the resistance to flow of the structure, as it evolves, with a modeled viscoelastic time scale of evolution. Equation (3) is the starting point for the enhanced thixotropic mHAWB, our comparison model, which is described later (Armstrong and Tussing 2020). The other modeling approach typically used is a “Maxwellian” paradigm consisting of a form of the following

$$ \boldsymbol{\sigma} +\frac{\eta }{G}\dot{\boldsymbol{\sigma}}=\eta \dot{\gamma} $$

(3)

where σ is the deviatoric stress tensor, $\dot{\boldsymbol{\gamma}}$ is the rate of strain tensor, η is the viscosity and G is the elastic modulus (Mewis And Wagner 2012; Armstrong et al. 2016a; Armstrong et al. 2018). The relaxation time of the system can be approximated as η/G and represents the viscoelastic time scale of evolution of the material (Bird et al. 1987; Bautista et al. 1999; Mewis and Wagner 2012; de Souza Mendes and Thompson 2013; Horner et al. 2018a; Horner et al. 2019). Equation (3) gives a starting point for several models including the White–Metzner, the Oldroyd-8 framework and recently published mHAWB (Bird et al. 1987; Horner et al. 2018a; Horner et al. 2019). In addition, the Bautista Monero Puig (BMP) uses fluidity φ(1/η) with an evolution term for the fluidity, and similar Maxwell construct (Bautista et al. 1999; Armstrong et al. 2018).

We first introduce the original components of the EAAB starting with two correlations by Apostolidis and Beris (2014, 2016a, 2016b) relating the yield stress of blood, σ_y0 to the hematocrit (HCT) and fibrinogen (c_f) as follows:

$$ {\displaystyle \begin{array}{c}{\sigma}_{y0}=\left({\left(\mathrm{HCT}-\left(0.3126\times {c}_{\mathrm{f}}^2-0.468\times {c}_{\mathrm{f}}+0.1764\right)\right)}^2\right)\\ {}\times \left(0.5084{\left({c}_{\mathrm{f}}+0.4517\right)}^2\right)\end{array}} $$

(4)

and the infinite shear viscosity as follows:

$$ {\eta}_{\infty }={n}_p\left(1+2.0703\times \mathrm{HCT}+3.722\times {\mathrm{HCT}}^2\right)\times \mathit{\exp}\left(-7.0276\left(1-\frac{T_0}{T}\right)\right) $$

(5)

whereT₀ = 273.15 + 23 K is the reference temperature the viscosity is measured at, n_p = 1.67 × 10⁻³ Pa s is the reference plasma viscosity, and T is the temperature of the blood (in K) (Apostolidis et al. 2015). From this, we construct the overall constitutive equation

$$ \sigma =G{\gamma}_e+{\sigma}_{\mathrm{ve},\mathrm{st}}+{\eta}_{\infty }{\dot{\gamma}}_p $$

(6)

where G is the elastic modulus, η_∞ is the infinite shear viscosity, γ_e is the elastic strain, ${\dot{\gamma}}_p$ is the plastic shear rate, and σ_{ve, st} is the contribution to stress from the microstructure. At steady state, the plastic shear rate is equal to the imposed shear rate, and the following relation holds true

$$ {\sigma}_{ss}={\lambda}_{ss}{G}_0{\gamma}_{e, ss}+{\lambda}_{ss}{\eta}_{st}\dot{\gamma}+{\eta}_{\infty}\dot{\gamma} $$

(7)

where G₀ is the value of elastic modulus when the material is at rest, and η_st is the structural contribution to viscosity. The ss designation refers to steady state. At steady state, we have the following:

$$ {\lambda}_{\mathrm{ss}}=\frac{\left({tr}_2{\left|\dot{\gamma}\right|}^d+1\right)}{\left({tr}_1{\left|\dot{\gamma}\right|}^a+{tr}_2{\left|\dot{\gamma}\right|}^d+1\right)} $$

(8)

where tr₁ is the thixotropic time constant of the ratio of structure breakage from shear rate and building from Brownian motion, and tr₂ is the ratio of thixotropic time constant of structure aggregation from shear rate to Brownian motion; both a and d are fitting parameters that have been shown in previous literature to facilitate modeling of complex materials undergoing microstructural evolution (Dullaert and Mewis 2006; Blackwell and Ewoldt 2014; Armstrong et al. 2016a, 2016b; Armstrong et al. 2017). Additionally, at steady state, the elastic strain is computed as follows:

$$ {\gamma}_{e, ss}=\left(\frac{\gamma_0}{\lambda^m}\right) $$

(9)

where γ₀ is the critical strain, λ is the structure parameter, and m is a power law dependence which we have found to be 1/3 (Mujumdar et al. 2002; Dullaert and Mewis 2006; Armstrong et al. 2016a, 2016b; Armstrong et al. 2018; Horner et al. 2018b).

Recall that the original Apostolidis et al. (2015) model consisted of the following superposition of elastic and plastic contributions to the total strain and total shear rate as shown below

$$ \gamma ={\gamma}_e+{\gamma}_p\leftrightarrow \dot{\gamma}={\dot{\gamma}}_e+{\dot{\gamma}}_p $$

(10)

where the e and p subscripts represent the elastic and plastic components respectively (Mujumdar et al. 2002; Apostolidis et al. 2015; Armstrong et al. 2018; Horner et al. 2018a, 2019). From here, we describe the computation of ${\dot{\gamma}}_p$

$$ {\dot{\gamma}}_p=\left\{\begin{array}{c}\frac{\dot{\gamma}}{\left(2-\frac{\left|{\gamma}_e\right|}{\gamma_{\mathrm{max}}}\right)}\dot{\gamma}\ge 0\\ {}\frac{\dot{\gamma}}{\left(2+\frac{\left|{\gamma}_e\right|}{\gamma_{\mathrm{max}}}\right)}\dot{\gamma}<0\end{array}\right. $$

(11)

and

$$ {\gamma}_{\mathrm{max}}=\mathit{\min}\left(\frac{\gamma_0}{\lambda^m},{\gamma}_{\infty}\right) $$

(12)

where γ_∞ is the maximum allowable strain (set to 1 for human blood), and γ₀ is the value of the critical strain. Equations (10)–(12) articulate the entire view of how the TEVP model is able to mathematically accomplish the deconstruction of the elastic and plastic components of the strain and shear rate. In addition to this, the model consists of four differential equations in time, shown below for the evolution of elastic strain, γ_e, structure parameter, λ, elastic modulus, G, and the viscoelastic contribution to total stress from structure, σ_{ve, st}.

$$ {\dot{\gamma}}_e={\dot{\gamma}}_p-\frac{\gamma_e}{\gamma_{\mathrm{max}}}\left|{\dot{\gamma}}_p\right| $$

(13)

$$ \dot{\lambda}=\left(\frac{\sigma_{y0}}{\eta_{\infty }}\right){k}_{\lambda}\left(-{tr}_1{\left|{\dot{\gamma}}_{\mathrm{p}}\right|}^a\lambda + tr{{}_2\left|{\dot{\gamma}}_{\mathrm{p}}\right|}^d\left(1-\lambda \right)+\left(1-\lambda \right)\right) $$

(14)

$$ \dot{G}=\left(\frac{\sigma_{y0}}{\eta_{\infty }}\right){k}_G\lambda \left(\lambda {G}_0-G\right) $$

(15)

$$ {\dot{\sigma}}_{ve, st}=\left(\frac{1}{\tau_{ve}}\right)\left({\lambda \eta}_{st}{\dot{\gamma}}_p-{\sigma}_{ve, st}\right) $$

(16)

where in Equations (15)–(16), σ_y0/μ_∞ is the inverse of the characteristic time of relaxation of the sample, k_λ is a dimensionless rate constant of evolution of the microstructure, k_G is the dimensionless rate constant of evolution for the elastic modulus, and τ_ve is a characteristic time of viscoelastic contribution to total stress from microstructure evolution. Table 1 offers a brief synopsis of the two models including parameters, total number of parameters, algebraic equations, ordinary differential equations (in time), and correlations. We acknowledge here that Eqs. (14) and (15) contain a form slightly different from original in Apostolidis et al. (2015), Armstrong et al. (2018), and Horner et al. (2018a, 2019) for the simple fact that here we must imbue the thixotropic term with the greatest capability to fit and then predict the full complement of rheological tests, from steady state to all oscillatory shear experiments. There are three components to overall stress in both EAAB and VE-EAAB. Elastic stress (a function of λ), viscoelastic stress (a function of λ in VE-EAAB)/structural viscous stress in EAAB, and viscous contribution from plasma/free-floating RBCs (not a function of λ mathematically in Eq. (6)).

Table 1 Model equation and parameter roll up (shaded green is “classic” EAAB without viscoelastic enhancement, shaded blue is the VE-EAAB, shaded tan is equations both models have in common) (ODE = ordinary differential equation and refers to number of ordinary differential equations in respective model, algebraic refers to number of algebraic equations in each model, and correlations refers to number of correlations in each model)

As a basis for comparison and to demonstrate that adding a time scale of evolution to the viscoelastic contribution from rouleaux formation to total stress will improve model fits and predictions during transient flow conditions, we will use the recently published enhanced thixotropic mHAWB, (ethixo mHAWB). This construct is based on a White–Metzner framework, using the Cross model for the viscosity as a function of shear rate to capture the contribution to total stress from the free-floating red blood cells and plasma of blood. There is then a linear superposition of this backbone stress and the viscoelastic and elastic contributions to total stress from the formation of rouleaux. Equation (3) is combined with $\eta \left(\dot{\gamma}\right)={\eta}_{\infty }+\frac{\left({\eta}_{\infty }-{\eta}_0\right)}{\left(1+{\tau}_{\mathrm{c}}\dot{\gamma}\right)}$, given by the Cross model where η_∞, η₀, andτ_c are the infinite shear viscosity, the zero shear viscosity, and the Cross constant respectively. This yields the stress in the yx, and the xx direction as follows:

$$ {\sigma}_{\mathrm{yx},\mathrm{c}}+\left(\frac{\eta_{\mathrm{c}}\left({\sigma}_{\mathrm{xx},\mathrm{c}}\right)}{G_{\mathrm{c}}}\right)\frac{{d\sigma}_{\mathrm{yx},\mathrm{c}}}{d t}={\eta}_{\mathrm{c}}\left({\sigma}_{\mathrm{xx},\mathrm{c}}\right)\dot{\gamma} $$

(17)

$$ {\sigma}_{\mathrm{xx},\mathrm{c}}+\left(\frac{\eta_{\mathrm{c}}\left({\sigma}_{\mathrm{xx},\mathrm{c}}\right)}{G_{\mathrm{c}}}\right)\left(\frac{{d\sigma}_{\mathrm{xx},\mathrm{c}}}{d t}-2\dot{\gamma}{\sigma}_{\mathrm{yx},\mathrm{c}}\right)=0 $$

(18)

with

$$ {\eta}_{\mathrm{c}}\left({\sigma}_{\mathrm{xx},\mathrm{c}}\right)=\frac{-b+\sqrt{b^2-4c}}{2} $$

(19)

where

$$ b={\tau}_{\mathrm{c}}\sqrt{\frac{G_{\mathrm{c}}{\sigma}_{\mathrm{xx},\mathrm{c}}}{2}}-{\eta}_0 $$

(20)

and

$$ c=-{\eta}_{\infty }{\tau}_{\mathrm{c}}\sqrt{\frac{G_{\mathrm{c}}{\sigma}_{\mathrm{xx},\mathrm{c}}}{2}} $$

(21)

G_c is the elastic modulus of the plasma with loose red blood cells. Equations (17)–(21) represent the viscoelastic backbone and ethixo mHAWB uses Eq. (8)with $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\tau}_{\lambda }$}\right.$as the pre-factor. Equations (10)–(11) are incorporated for the elastic and plastic components of strain and shear rate, along with

$$ {\dot{\gamma}}_e=\left\{\begin{array}{c}{\dot{\gamma}}_p-\frac{\gamma_e}{\gamma_{\mathrm{max}}}\left|{\dot{\gamma}}_p\right|,\frac{\gamma_e}{\gamma_{\mathrm{max}}}\ge 0\\ {}{\dot{\gamma}}_p-\frac{\gamma_e}{\gamma_{\mathrm{max}}}\left|{\dot{\gamma}}_p\right|+\frac{\gamma_e}{\gamma_{\mathrm{max}}}\frac{{d\gamma}_{\mathrm{max}}}{d t},\frac{\gamma_e}{\gamma_{\mathrm{max}}}<0\end{array}\right. $$

(22)

where

γ_max = γ₀λ, and the elastic contribution from rouleaux to total stress is ${\sigma}_{\mathrm{r},\mathrm{e}}=\frac{\sigma_{\mathrm{y}0}}{\gamma_0}\lambda$. Lastly, the viscoelastic contribution to total stress from the rouleaux is

$$ \frac{d{\sigma}_{\mathrm{r},\mathrm{ve}}}{d t}=\left\{\begin{array}{c}{G}_{\mathrm{r}}{\lambda}^m\left({\dot{\gamma}}_{\mathrm{p}}-\frac{\sigma_{\mathrm{r},\mathrm{ve}}}{\eta_{\mathrm{st}}{\lambda}^m}\right),\frac{d\lambda}{d t}\ge 0\\ {}{G}_{\mathrm{r}}{\lambda}^m\left({\dot{\gamma}}_{\mathrm{p}}-\frac{\sigma_{\mathrm{r},\mathrm{ve}}}{\eta_{\mathrm{st}}{\lambda}^m}\right)+m\frac{\sigma_{\mathrm{r},\mathrm{ve}}}{\lambda}\frac{d\lambda}{d t},\frac{d\lambda}{d t}<0\end{array}\right. $$

(23)

where G_r is the elastic modulus of the rouleaux, and m is a fitting parameter, determined in the literature to be 1.5 (Horner et al. 2018b, 2019; Armstrong and Tussing 2020). The steady-state value of the structure parameter is shown in Eq. (8), and the steady-state value of the total stress is

$$ {\sigma}_{ss}={\sigma}_{ve, ss}+{\eta}_{st}{\lambda}_r^m\dot{\gamma}+{\sigma}_{y0}{\lambda}_{ss} $$

(24)

More detailed model description and derivations can be found here (Horner et al. 2018b; Horner et al. 2019; Armstrong and Tussing 2020).

Materials and methods

This work utilizes human blood samples that were collected by a licensed nurse practitioner at the Nurse Managed Primary Care Center located at the University of Delaware STAR campus in compliance with the University of Delaware’s Institutional Review Board (Study Number 767478-2) (Horner et al. 2018a; Horner et al. 2018b; Horner et al. 2019). We follow an identical blood collection protocol as Horner et al. (2018a, b and 2019). “The protocol is consistent with guidelines established by the International Society for Clinical Hemorheology” (Baskurt et al. 2009; Horner et al. 2018a; Horner et al. 2018b; Horner et al. 2019). Additional samples from the same donors were collected from each donor and subsequently sent to Quest Diagnostics for complete blood count, lipid panel, and fibrinogen activity testing (Baskurt and Meiselman 2003; Baskurt et al. 2009; Baskurt et al. 2012; Horner et al. 2019). All rheological tests were conducted using the ARESG2 strain-controlled rheometer from TA Instruments equipped with a double-wall Couette geometry (Horner et al. 2018a; Horner et al. 2018b; Horner et al. 2019). The experimental protocol and technical details of the ARESG2 rheometer remain unchanged from the work of Horner et al. (2018a, 2018b, 2019), Esteridge et al. (2000), and Williams et al. (1985). To prevent damage to the red blood cells, shear rates within the rheometer never exceeded 1000 s⁻¹. A preshear of 300 s⁻¹ for 30 s was implemented between subsequent tests to remove any memory effects from the previous test. The physiological test results for donors 1 and 2 are included in the main text (Horner et al. 2018a, 2019).

The first rheological test was the steady state test conducted at 16 different shear rates logarithmic spacing (Horner et al. 2018a, 2018b, 2019). Following this a small amplitude, large amplitude oscillatory shear tests and a series of step-up and step-down as well as triangle ramp experiments were done. The performance of our proposed model enhancement is assessed based on the accuracy, as shown by the cost function F_cost. To minimize F_cost, a global stochastic optimization algorithm was used (Armstrong et al. 2016a; Armstrong et al. 2016b; Armstrong et al. 2018; Horner et al. 2018a, 2019).

Once the model parameters have been fit to the steady state and a series of four step-up and four step-down in shear rate rheological experiments, the parameters are fixed. Following this, the entire set of model parameters is utilized to predict a series of transient rheological experiments, including SAOS both frequency and amplitude sweep, cessation of flow, a series of triangle ramp experiments, large amplitude oscillatory shear (LAOS), and uni-directional oscillatory shear (UD-LAOS). The cost functions will be accumulated for each series of experiments and compared for the VE-EAAB model and the EAAB for two donors, with the ethixo mHAWB used as a basis of comparison. The results will be shown graphically and numerically. Recall for oscillatory shear flow starting with an applied strain of γ = γ₀ sin (ωt), with the first time derivative the shear rate $\dot{\gamma}={\omega \gamma}_0\mathit{\cos}\left(\omega t\right)$, where γ₀ is the strain amplitude and ω is the oscillation frequency in rad/s (Singh et al. 2018; Giacomin and Dealy 1993). For SAOS by definition, this is the linear regime whereby the stress signal consists of a liquid-like response described by G″ (Pa) and a solid-like response described by G′ (Pa) (Hyun et al. 2002; Cho et al. 2005; Ewoldt et al. 2008; Ewoldt et al. 2010; Hyun et al. 2011; Dimitriou et al. 2012; Ewoldt 2013; Ewoldt and Bharadwaj 2013; Bharadwaj and Ewoldt 2014; Bharadwaj and Ewoldt 2015; Blackwell and Ewoldt 2014; Ewoldt and McKinley 2017; Song and Hyun 2018). Equation (25) shows the stress reconstruction in the linear regime

$$ \sigma (t)={\gamma}_0\left(G^{\prime}\mathit{\sin}\left(\omega t\right)+G^{{\prime\prime}}\mathit{\cos}\left(\omega t\right)\right) $$

(25)

where G′ is the storage modulus and G″ is the loss modulus. We compare our models’ respective ability to predict G′ and G″ as well as the intensity of the 3rd harmonic divided by the intensity of the 1st harmonic given as

$$ {I}_{3/1}=\frac{\sqrt{{G_3^{\prime}}^2+{G_3^{{\prime\prime}}}^2}}{\sqrt{{G_1^{\prime}}^2+{G_1^{{\prime\prime}}}^2}} $$

(26)

with the ${G}_i^{\prime, "}$, where i represents the harmonic number, from the Fourier decomposition of the stress signal over a cycle at steady alternance given by

$$ \sigma (t)={\gamma}_0\sum \limits_{i=1, odd}^N\left[{G}_i^{\prime}\mathit{\sin}\left( i\omega t\right)+{G}_i^{{\prime\prime}}\mathit{\cos}\left( i\omega t\right)\right] $$

(27)

where i is the harmonic number, G′ is the storage modulus (when i = 1), and G″ is the loss modulus (when i = 1). Equation (26) is calculated with the real and imaginary parts of the third harmonic, divided by real and imaginary parts of the first harmonic. This quantity is known as the relative intensity of the third harmonic. When higher harmonics are required to reconstruct the stress, one has entered the LAOS regime. Rogers and coworkers have recently developed an analogous framework to analyze a wider range of transient flow, called sequence of physical processes (SPP) which are able to calculate elastic and viscous transient moduli at every data point (Rogers 2012; Rogers and Lettinga 2012; Lee and Rogers 2017; Lee et al. 2019; Rogers 2017; Park and Rogers 2018; Carey-De La Torre and Ewoldt 2018; Donley et al. 2019a, 2019b).

The LAOS predictions shown in the results section below compare LAOS over three cycles, starting at time t = 0 s, with cost function accumulated over the three cycles as the difference between the model prediction and the data (the predictions shown in results show only last cycle, while at alternance). The triangle ramp experiments consist of a ramp up in shear rate starting at time t = 0, to a maximum shear rate, followed by a ramp down back to 0 as shown in Eq. (28) (seen in Fig. S1 Supplemental Material).

$$ {\displaystyle \begin{array}{c}\dot{\gamma}=\alpha tt\le {t}_{1/2}\\ {}\dot{\gamma}=\alpha \left({t}_{\mathrm{max}}-t\right)t>{t}_{1/2}\end{array}} $$

(28)

where t_max is the maximum time of the triangle ramp, and α is the slope of the increase in shear rate.

In the results section, we compare predictions to these rheological experiments with EAAB, VE-EAAB, and ethixo mHAWB constant by holding the best fit parameter values constant. We compare an amplitude sweep at frequency of 12.56 (rad/s), and a frequency sweep at γ₀ = 10(−) along with three separate triangle ramp experiments. To calculate the F_cost for the SAOS experiment, we incorporate each model to calculate the moduli over the last period at alternance, the time stable oscillatory response. The quantities $G^{\prime },G",{G}_3^{\prime },\boldsymbol{and}{G}_3^{"}$ are evaluated through harmonic regression. This is executed with MATLAB by solving the linear equation Ax = b where A is the array containing the transient harmonic data (only 1st and 3rd harmonics included), b is a vector containing the transient measures, and x is the vector containing the moduli for each harmonic (Horner et al. 2018a, 2019; Armstrong and Tussing 2020).

The most challenging rheological experiments to predict are the LAOS and UD-LAOS. The UD-LAOS is a linear superposition of a constant shear rate and oscillatory shear flow. This experiment will speed up, then slow down, while the LAOS will also change directions during a period of oscillation. The UD-LAOS predictions and data are shown in results section below (Fig. 11) and are plotted in the traditional sense whereby the effect of the constant shear flow is factored out and only the oscillation is shown for consistency of presentation with the LAOS predictions and data (Fig. 10) (Horner et al. 2018a, 2019). The UD-LAOS strain and shear rate expressions are shown below

$$ \gamma (t)={\gamma}_0\mathit{\sin}\left(\omega t\right)+{\gamma}_0\omega t $$

(29)

$$ {\gamma}_0(t)={\gamma}_0\omega cos\left(\omega t\right)+{\gamma}_0\omega $$

(30)

where all these parameters (γ₀, ω) are same as described above.

The original EAAB by Armstrong et al. (2018) and the new VE-EAAB (described fully in Table 1) are both first fit to the steady state data of the human blood using a stochastic, global optimization algorithm with MATLAB. More details on this parameter fitting algorithm can be found here (Armstrong et al. 2016a, 2016b). The steady-state residual sum of squares is shown below; note that the difference between model prediction of the stress and the actual stress is normalized by the actual stress because we are fitting stress data over several orders of magnitude. The cost function which is minimized for the steady-state parameter fit is defined as follows

$$ {F}_{\boldsymbol{cost},\mathrm{ss}}=\sqrt{\sum \limits_{i=1}^{N=16}{\left(\frac{\left({y}_i-{f}_i\right)}{y_i}\right)}^2}/N $$

(31)

where y_i is the steady-state measurement of stress, f_i is the model prediction, and N are the number of points. Plots of shear rate vs. time for donor 2 are shown in Figs. S2 and S3, of the Supplemental Material. With the steady-state parameters then fixed, the two transient parameters for the original EAAB and the three transient parameters for the VE-EAAB are then fit to a series of four step-up in shear rate and four step-down in shear rate experiments simultaneously. The differences between model prediction and actual measured stress are not normalized during the transient parameter fitting procedure. The residuals are accumulated and minimized with the optimization algorithm over log spaced points throughout the step-up and step-down rheological experiments. The cost function that is used for the transient parameter fit is thus defined

$$ {F}_{\boldsymbol{cost},\boldsymbol{steps}}=\sum \limits_{j=1}^8\left(\sqrt{\sum \limits_{i=1}^{65}{\left({y}_i-{f}_i\right)}^2}/N\right)/8 $$

(32)

Lastly, a comparison will be made to determine if the addition of new parameters contributed to a better representation of the actual stress signatures by incorporating straight cost function comparison of the steady-state and transient data, as well as use of the Akaike information criteria shown below which assesses a penalty for additional model parameters

$$ AIC=2k+2\mathit{\ln}(RSS) $$

(33)

where

$$ \mathrm{RSS}=\sum \limits_{i=1}^{n=16}{\left(\frac{\left({y}_i-{f}_i\right)}{y_i}\right)}^2 $$

(34)

where k is number of model parameters and RSS is the residual sum of squares. Equation (34) shows the RSS for the case of the steady-state residual sum of squares. The AIC will be used to compare the EAAB to the new VE-EAAB and will factor in a penalty for additional parameters used.

The results section will then show the fits and predictions as well as numerically compare the cost functions and AIC. The results will show a comparison of the models in predicting a series of transient, linear, and nonlinear, and several types of oscillatory shear flows graphically and numerically with F_cost using one set of human blood rheology data. The second set of human blood data fits and sets predictions are shown in the Supplemental Material. The transient experiment cost function is computed as follows

$$ {F}_{\boldsymbol{cost},\boldsymbol{trans}}=\sqrt{\sum \limits_{i=1}^N{\left({y}_i-{f}_i\right)}^2}/N $$

(35)

The cost function of the LAOS is a summation of the sum of the difference between model prediction and data over three periods of LAOS. Equation (35) is not normalized; therefore, the LAOS experiments at lower strain amplitude and frequency tend to contribute less to the overall average LAOS and UD-LAOS F_cost values. The model predictions are qualitatively not as good at the smaller strain amplitudes, and the F_cost values for each strain amplitude and frequency combinations are smaller in magnitude.

Results and discussion

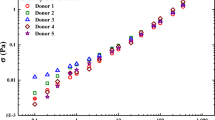
We start with Table 2, a listing of relevant physiological parameters from the analysis of the blood of donors 1 and 2, followed by Figs. 1a–e, 2a–e, and 3a–e, the steady-state flow curve and step-up/step-down fits with human blood using the EAAB, VE-EAAB, and ethixo mHAWB models. The literature has previously demonstrated that the mechanical properties of blood are correlated with hematocrit, fibrinogen, and cholesterol (Moreno et al. 2015; Apostolidis and Beris 2014, 2016a, 2016b). Recall from the methods section that the steady-state parameters were first fit to steady state, and then fixed during the transient parameter or second phase of the model parameter fitting procedure. The model parameter values for donor 1 are shown in Table 3 and the F_cost comparison is shown in Table 4. For donor 2, the fitting and prediction results are shown in the Supplemental Material, Tables S1a and S1b. During the steady-state fit, both versions of the model are identical, as the new viscoelastic time constant of evolution only applies to transient data.

Table 2 Donor physiological test results

Fig. 1

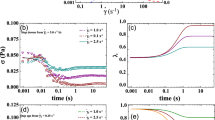
EAAB model fit for a steady-state human blood data; b set of 3 step-up in shear rate from $\dot{\gamma}$ = 5.0 s⁻¹ to 0.1, 1.0, and 2.5 s⁻¹; c corresponding structure parameter curves; d step-down in shear rate to $\dot{\gamma}$ =0.25 s⁻¹ from 1, 2.5, and 5 s⁻¹; and e corresponding structure parameter curves. Bold red box indicates areas of interest due to poor fit (σ_e is elastic contribution to total stress designated by green dashed line; σ_ve is the viscoelastic contribution to total stress designated by blue dashed line) (donor 1) (dataset 1 2020)

Fig. 2

VE-EAAB model fit for a steady-state human blood data; b set of 3 step-up in shear rate from $\dot{\gamma}$ = 5.0 s⁻¹ to 0.1, 1.0, and 2.5 s⁻¹; c corresponding structure parameter curves; d step down in shear rate to $\dot{\gamma}$ = 0.25 s⁻¹ from 1, 2.5, and 5 s⁻¹; and e corresponding structure parameter curves (σ_e is elastic contribution to total stress designated by green dashed line; σ_ve is the viscoelastic contribution to total stress designated by blue dashed line) (donor 1) (dataset 1 2020)

Fig. 3

ethixo mHAWB model fit for a steady-state human blood data; b set of 3 step-up in shear rate from $\dot{\gamma}$ = 5.0 s⁻¹ to 0.1, 1.0, and 2.5 s⁻¹; c corresponding structure parameter curves; d step down in shear rate to $\dot{\gamma}$ = 0.25 s⁻¹ from 1, 2.5, and 5 s⁻¹; and e corresponding structure parameter curves (σ_e is elastic contribution to total stress designated by green dashed line; σ_ve is the viscoelastic contribution to total stress designated by blue dashed line) (donor 1) (dataset 1 2020)

Table 3 Parameter values for steady-state and step-up/step-down fits (donor 1) (green, blue, and pink highlights refer to parameters fit to transient data)

Table 4 F_cost, RSS, and AIC comparison for EAAB, VE-EAAB, and ethixo mHAWB (donor 1) (parameter values fit to steady-state data are highlighted yellow, while green, blue, and pink highlights refer to parameters fit to transient data)

Comparing Figs. 1a–e, 2a–e, and 3a–e shows that fitting the original EAAB model with only a thixotropic time constant of evolution misses key features of the human blood as it steps down and the structure rebuilds, and as it steps up and the structure is broken down after an overshoot as the microstructure is presumably loaded, then breaks. The addition of the time constant for viscoelastic evolution of structure imparts on the model the ability to accurately fit these key features during rouleaux breakdown and rebuilding as seen in Fig. 2b, d. Figure 3 shows the comparison to the ethixo mHAWB. Because the ethixo mHAWB contains two viscoelastic time constants of evolution, one for the viscoelastic contribution from the plasma and loose red blood cell backbone of blood, and the other for the contribution to total stress from the buildup and breakdown of rouleaux, it slightly out-performs both the EAAB and VE-EAAB. The ethixo mHAWB also has a structural time constant of rouleaux buildup and breakdown. This gives the ethixo mHAWB a slight advantage; however, it is clear from Figs. 1 and 2 that the addition of the viscoelastic time constant to the EAAB makes a significant improvement to accuracy qualitatively and quantitatively. The thixotropic and viscoelastic unique times of evolution are on the order of seconds and to deconvolute them would not be trivial. Through analysis of Figs. 1a–e, 2a–e, and 3a–e, the time scales are on the order of 0.1–1 s for viscoelastic changes and 0.5–4 s for the structure rebuilding and destruction. The immediate undershoots for the step-down in shear rate and overshoots for the step-up in shear rate experiments are viscoelastic effects on the order of 0.1–0.5 s (shown most clearly in Figs. 1b, d, 2b, d, and 3b, d), while the thixotropic rebuilding and breaking down of structure are on order of > 0.5–5 s (as shown most clearly in Figs. 1c, e, 2c, e, and 3c, e). Both time scales most likely correlate strongly with the unique physiological characteristics of the donor blood used for the rheological experiments. Table 3 shows the best fit parameters values. The steady-state fit is identical for both models, as the time evolution parameters cannot be fit without transient data. In comparing the λ value evolution in Figs. 1c, e, 2c, e, and 3c, e, consistency is shown for the rebuilding and breaking of the rouleaux during the step-up and step-down in shear rate experiments. In other words, as expected, the structure parameter (and rouleaux) are rebuilding during each of the four step-down in shear rate experiments and breaking down in the step-up in shear rate experiments. This is because at the lower shear rates, the red blood cells can now interact (albeit weakly) and rebuild the rouleaux and undergo the opposite trend when the shear rate is increased. The yield stress and infinite shear viscosity are computed directly with correlations from Apostolidis and Beris (2014, 2016a, 2016b) using physiological parameters from the laboratory, hematocrit, and fibrinogen. We note the immediate decrease to F_cost with initial parameter fitting to the step-up/step-down experiments shown qualitatively in Figs. 1, 2, and 3 and quantitatively in Table 4. The benefit of the modification is clear: by adding a viscoelastic enhancement to the EAAB, the new model is now able to compete with mHAWB in terms of accuracy.

Having now fit all parameters, we enter the prediction phase of the model comparison. Shown in Figs. 4a–c, 5a–c, and 6a–c are the qualitative fits of (a) the frequency sweep, (b) the amplitude sweep (both with the fit to I₃/I₁), and (c) series of three triangle ramps, respectively. Table 5 shows the quantitative comparison using F_cost of all three. Acknowledged here is the failure of the original EAAB to successfully predict all the SAOS experiments, taking it out of the running to be the most accurate version of the model. The EAAB model captures the SAOS qualitatively as well as has the lowest quantitative F_cost and in addition is able to quantitatively dominate the triangle ramp predictions as shown in Table 5 (Tomaiuolo et al. 2016; Armstrong et al. 2018; Horner et al. 2018a, 2019). The VE-EAAB shows a significant improvement over the EAAB and represents a step forward toward better model predictions by incorporation of a viscoelastic time constant of evolution for the stress contribution from rouleaux, approaching the predictive ability and accuracy of the ethixo mHAWB. The benefit of the modification is clear: by adding a VE enhancement to the EAAB, the new model is now able to compete with mHAWB with respect to accuracy.

Fig. 4

SAOS flow data and a EAAB frequency sweep predictions; b EAAB amplitude sweep (discrete point triangles for G′ and squares for G″; dashed green line for G″ model predictions and dashed blue line for G′ model predictions); and c EAAB triangle ramp predictions frequency sweep at three different α (triangle, circle, and square discreet point are data; lines are model predictions (donor 1) (dataset 1 2020)

Fig. 5

SAOS flow data and a VE-EAAB frequency sweep predictions; b VE-EAAB amplitude sweep (discrete point triangles for G′ and squares for G″; dashed green line for G″ model predictions and dashed blue line for G′ model predictions); and c VE-EAAB triangle ramp predictions frequency sweep at three different α (triangle, circle, and square discreet point are data; lines are model predictions (donor 1) (dataset 1 2020)

Fig. 6

SAOS flow data and a ethixo mHAWB frequency sweep predictions; b ethixo mHAWB amplitude sweep (discrete point triangles for G′ and squares for G″; dashed green line for G″ model predictions and dashed blue line for G′ model predictions); and c ethixo mHAWB triangle ramp prediction frequency sweep at three different α (triangle, circle, and square discreet point are data; lines are model predictions (donor 1) (dataset 1 2020)

Table 5 SAOS and triangle ramp F_cost comparison

The following predictions involve the cessation of flow experiment. This experiment incorporates blood at steady state, then stepping down to a shear rate very close to zero, while the rheometer continues to measure the stress. Figures 7, 8, and 9 seem to demonstrate that the viscoelastic time of evolution is approximately 0.1–0.5 s, while the thixotropic time scale is approximately 0.5–4 s. This is corroborated with Figs. 1c, e, 2c, e, and 3c, e. The parameter values from Table 2 with respect to the EAAB and VE-EAAB models have values of this approximate order of magnitude. EAAB has a thixotropic time scale of evolution of 8 s, while the VE-EAAB model has a thixotropic time scale of evolution of 0.77 s and viscoelastic time scale of evolution of 0.08 s (shown in Table 1). The ethixo mHAWB model has two viscoelastic time scales one for the solvent backbone of approximately 0.1 s, and one for the viscoelastic time scale of the stress contribution from the rouleaux of approximately 0.2 s (shown in Table 1, while the viscoelastic time scale of evolution for the contribution to total stress from the rouleaux is calculated as $\raisebox{1ex}{${\eta}_{st}$}\!\left/ \!\raisebox{-1ex}{${G}_{\mathrm{r}}$}\right.$. The ethixo mHAWB has a thixotropic time scale of evolution of 1.3 s. From this experiment, the relaxation time of blood can be estimated (if the model chosen to use for this calculation is accurate). By comparing Figs. 7a, 8a, and 9a, it becomes clear that the viscoelastic enhancements facilitate a more accurate prediction of cessation of flow, and arguably will provide for a better estimate of the relaxation time when comparing Fig. 7a, b. By our estimate, according to the more accurate Figs. 8 and 9a, b, the relaxation time (or time for blood to recover the structure of its “at rest” state) is approximately 1–4 s, while the original model without enhancements predicts a time of less than 1 s. In addition, Figs. 2c, e and 3c, e show much better quality of fit and therefore have more accurately reflected the characteristic time of structure evolution. This is an important development, as we now have a better understanding of the thixotropic time constant of the evolution of the microstructure of human blood (Ewoldt et al. 2015).

Fig. 7

a Cessation of flow predictions from 0.5, 5, and 10 s⁻¹ to 0 (symbols are data; lines are EAAB predictions); b λ predictions. Red box indicates area of relative weakness of prediction (donor 1)

Fig. 8

a Cessation of flow predictions from 0.5, 5, and 10 s⁻¹ to 0 (symbols are data; lines are VE-EAAB predictions); b λ predictions (donor 1) (dataset 1 2020)

Fig. 9

a Cessation of flow predictions from 0.5, 5, and 10 s⁻¹ to 0 (symbols are data; lines are ethixo mHAWB predictions); b λ predictions (donor 1) (dataset 1 2020)

From here, we demonstrate in Figs. 10 and 11 the comparison of predictive capability of the two versions of the model with LAOS and UD-LAOS flow, by showing both the elastic and viscous projections (along with ethixo mHAWB as a basis for comparison). Previous work has shown similar rheological experiments, and model fits (Sousa et al. 2013; Apostolidis et al. 2015; Horner et al. 2018a, 2019); however, here we show an expanded set of predictions over three oscillation frequencies: ω = 0.5,1, 5(rad/s) and six strain amplitudes: γ₀ = 0.5,1.0,5.0,10,50, and100(−) for donor 1 (donor 2 shown in the Supplemental Material). This is to demonstrate the range of the VE-EAAB model to make accurate predictions. We envision our progression of fits and predictions from easiest to most challenging: SS being at the easiest-to-fit end of the rheological fitting/predicting spectrum; the step-up/step-down rheological experiments, starting from steady state at initial shear rate (aka a point on the steady-state flow curve) to a final shear rate (aka a different point on the steady-state flow curve). Recall that analysis of these curves shown in Figs. 1b, d, 2b, d, and 3b, d elucidates the approximate viscoelastic time frame of evolution. From here the next rung, or level of difficulty with respect to the fitting/prediction pyramid, are the SAOS predictions, then the triangle ramps. This is because by definition SAOS experiments are linear tests, in which the microstructure is “gently probed,” not destroyed (Rogers 2012; Ewoldt and Bharadwaj 2013; Ewoldt and McKinley 2017; Rogers 2017; Armstrong et al. 2018; Donley et al. 2019a, 2019b). Noting here that the triangle ramp experiments start from rest and thus at an assumed fully structured state.

Fig. 10

LAOS viscous projections of a EAAB (black lines), b VE-EAAB (gray lines), and c ethixo mHAWB (maroon lines) and LAOS elastic projections of d EAAB predictions (solid black lines), e VE-EAAB predictions (solid gray lines), and f ethixo mHAWB (maroon lines). LAOS data is red circles (donor 1) (dataset 1 2020)

Fig. 11

UD-LAOS viscous projections of a EAAB (black lines), b VE-EAAB (gray lines), and c ethixo mHAWB (maroon lines) and UD-LAOS elastic projections of d EAAB predictions (solid black lines), e VE-EAAB predictions (solid gray lines), and f ethixo mHAWB (maroon lines). LAOS data is red circles (donor 1) (dataset 1 2020)

The LAOS flow via its twice a cycle change of directions imparts an additional structure breaking capability than the UD-LAOS that does not change direction. Although, for blood rouleaux that are held very weakly together with intermolecular forces, this effect is not as pronounced (Armstrong et al. 2016a, 2016b; Armstrong et al. 2017). Analysis of only the data from both sets of elastic and viscous projections from both the UD-LAOS and LAOS indicates that at the higher strain amplitudes the signal tends to show more liquid-like, or viscous features, and at the lower strain amplitudes, the stress signal does begin to show solid-like, elastic features. We note here also that in the intermediate strain amplitudes shown in Figs. 10 and 11, we see there are clear features of both liquid-like and solid-like features as the microstructure is evolving here before breaking down again when the shear rate is increasing. VE-EAAB is also able to show qualitatively various places where there are “cross-overs” in the viscous projections. At the lower strain amplitudes, the data show some level of noise from the instrument. Recall that each of the LAOS predictions accumulates the difference between the data and prediction over three periods and is not normalized, meaning that the units of F_cost are (Pa). Each distinct F_cost is shown for each combination of frequency and strain amplitude in Tables 6 and 7 for LAOS and UD-LAOS, respectively. The VE-EAAB demonstrates qualitatively and quantitatively that it can more robustly predict the LAOS and UD-LAOS rheological experiments, as compared to the original EAAB, with the addition of just one viscoelastic parameter. This allows the Kelvin–Voigt like construct of the EAAB to move closer to, and becoming on-par with the predictive capability of the more “Maxwellian” ethixo mHAWB. Done with the addition of just one new parameter, as is seen in Tables 6 and 7, which is the most important take away here. There is a larger improvement in predictive capability for the LAOS predictions using the VE-EAAB than seen in UD-LAOS predictions because during LAOS, the oscillation not only slows down and speeds up over a cycle but also changes direction. This is in general more difficult for TEVP models like the old EAAB to capture due to lack of robust viscoelastic model enhancements.

Table 6 LAOS F_cost comparison

Table 7 UD-LAOS F_cost comp

As seen in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11 and in Table 8, the viscoelastic and thixotropic enhancements applied to the VE-EAAB model allow the model the necessary and independent time constants for both the viscoelastic and thixotropic evolution to outperform the EAAB model. The addition of a single parameter for the evolution of viscoelastic component to stress from the microstructure had made an improvement on all the transient fits and predictions. The model is now more able to make versatile predictions over small, large, and uni-directional oscillatory shear flow consistently. In addition to the structural contribution to total stress, viscoelastic time constant of evolution, the thixotropic term now considers the effects of shear aggregation. The AIC analysis shown in Table 4 and Table S1b as well as the F_cost comparison shown in Tables 4, S1b, and 8 communicates that the addition of one parameter to the EAAB is compensated by the additional accuracy in terms of a smaller AIC and cost function.

Table 8 F_cost comparison roll up for steady-state and step-up/step-down fit; SAOS, I₃/I₁, triangle ramp, cessation of flow, LAOS, and UD-LAOS predictions (Donor 1)

In summary, the VE-EAAB model out-performs the EAAB model prediction of all the transient rheological experiments. There is significant improvement with respect to the step-up/step-down in shear rate predictions, cessation of flow predictions, and LAOS predictions. With respect to the LAOS experiments, this is a function of the application of two simultaneous characteristic times to adequately model the highly nonlinear flow and capture the contributions of the evolving rouleaux. The model fits, predictions, and comparisons of donor 2 are similar to those of donor 1 and are shown in the Supplemental Material.

Conclusions

We see that a more robust model that considers the physics of blood microstructure evolution, with addition of viscoelastic enhancement, can now make more accurate predictions over a wide range of shear conditions, as demonstrated by comparing the EAAB to the VE-EAAB. A single, additional viscoelastic parameter was able to significantly improve the accuracy of the EAAB. There is a cost in number of parameters; however, considering the accuracy over such a wide range of rheological experiments, the parameter addition is justified. The additional viscoelastic parameter is tied directly to the physics of human blood rouleaux breakdown and buildup and is a useful addition to the original model. The AIC analysis and comparison between the EAAB and VE-EAAB justifies the additional parameter. The additional parameter of the VE-EAAB gives the model accuracy approaching that of (if not equal to in the prediction of most experiments) the ethixo mHAWB. This work has also shown a series of successful fits and then predictions for a wide range of rheological experiments from steady-state flow curve to SAOS, LAOS, and UD-LAOS, which in the past has been difficult for a single model. Using the viscoelastic enhancements to the EAAB model, we propose a viscoelastic, thixotropic, and relaxation time for human blood based, in part on the new model’s ability to predict the step-up/step-down in shear rate and cessation of flow experiments.

We close with discussion of future work which endeavors to quantitatively show the range of parameter values for healthy human blood, with average values and standard deviations, as well as foreshadows a methodology to meaningfully, statistically correlate physiological values from the lab to rheological model parameter values that tie directly to the physics of human blood flow as we accumulate more complete sets of rheological data for human blood. We can also directly compare rheological data sets by analyzing differences in mechanical properties such as elasticity and viscosity using well published, advanced software like MITLAOS, and SPP to make direct comparisons between different donors with different physiology (Ewoldt et al. 2008; Donley et al. 2019a, 2019b; Sankar and Hemalatha 2007).