An investigation of squeeze flow as a viable technique for determining the yield stress

Abstract

A systematic study of squeeze flow (SF) was performed on different concentrations of Carbopol with varying yield stresses. A sample of constant volume was placed between two parallel plates and a series of constant force steps applied, following the plate separation as a function of time. Precise rheological measurements of the model yield stress fluids were performed in addition to the well-controlled SF tests. These rheological measurements were used in conjunction with the SF equations to determine the time-dependent plate separation, allowing a direct comparison of theory and experiment throughout the entire test. The limiting height achieved during constant force SF reveals information about the yield stress of the fluid as predicted by the theory. It appears that by carefully controlling the experimental conditions of the squeeze test one can obtain yield stress values that agree with the rheological measurements within 10%. Additionally, the validity of the lubricational theory was tested; not only for the determination of the yield stress but throughout the flow as well.

Introduction

Squeeze flow (SF) is the process in which a fluid is squeezed between two approaching parallel plates resulting in a radial flow, outward from the center. SF is utilized by many people to probe the rheology of certain soft materials and may offer a more cost-effective alternative to conventional rheometry. This method is advantageous with respect to traditional rheometry in that a sample can be placed within the measuring geometry with minimal disruption to its underlying structure, preserving the rheological properties of the original sample. Additionally, SF yields a 3D flow in which fracture, shear-banding, and wall slip do not develop as easily as in simple shear flow.

Industrial applications of SFs include the compression molding of ceramic and metals as well as the production of various types of foods (Campanella and Peleg 1987a, b, 2002), personal care products, chemicals, and pharmaceuticals. Materials with a yield stress are typically used so that the material can be molded with minimal addition of liquid and once formed will retain its characteristic shape. Additionally, the strength of some adhesives relies on a stretching flow (the reverse of a SF) of fluids exhibiting a yield stress. A detailed review of SF was recently given by Engmann et al. (2005).

It has been shown (Coussot 2005) that the steady-state flow curve in simple shear of many fluids of different structures exhibiting a yield stress can be conveniently fit by a Herschel Bulkley (HB) relation:

$$\tau <\tau _0 \Rightarrow \dot {\gamma }=0;\;\tau >\tau _0 \Rightarrow \tau =\tau _0 +k\dot {\gamma }^n$$

(1)

Where τ and $\dot {\gamma }$ are the shear stress and shear rate magnitudes, τ ₀ the yield stress, k the consistency, and n the power law exponent. To describe 3D flows it is necessary to have a 3D form for the constitutive equation, which is generally done with the help of a Von Mises yielding criterion and an extrapolation from Eq. 1 (see Coussot 2005).

SF theory for yield stress fluids under no-slip conditions was initially studied by Scott (1931). He was able to equate the pressure gradient with the plate velocity. Though unable to find a closed form solution to the problem, he was the first to predict the limiting height, h _∞, of such a fluid. Peek (1932) was in disagreement with Scott because of its prediction of an unsheared zone near the centerline leading to a kinematic inconsistency resulting in the SF paradox (Lipscomb and Denn 1984). This problem was later revisited by Covey and Stanmore (1981) in which, on the basis of the lubrication assumption (i.e. predominance of radial velocity and vertical velocity gradient), closed form solutions were found for the pressure gradient in the large and small asymptotic limits however the intermediate regions remained to be solved numerically. Adams et al. (1994) assumed a form of the pressure gradient and was able to obtain a closed form solution over the entire range of velocities with limited error in the intermediate regions.

The fully elongational (perfect-slip) case has been well developed (Yang 1998) and used in the development of a partial slip model proposed by Sherwood and Durban (1998). In SF works performed with plasticine (Estellé et al. 2006), it was shown that a circular central zone develops with no slip occurring and is surrounded by slipping layers. This observation was later incorporated into a new slip model for Bingham fluids by Estellé and Lanos (2007).

Previous studies examining the reliability of SF for determining a paste’s yield stress considered an assortment of various common household soft materials (Meeten 2000, 2002). A series of constant force steps were employed following the evolution of the interplate separation towards a limiting height thus determining the yield stress. In these studies, smooth glass plates were used as the contacting surface, a detail that could easily lead to imprecise measurement. Later studies by the same author acknowledged the importance of a rough surface for limiting slip effects (Meeten 2004a, b, 2008). The results of the SF experiments were compared with rheological measurements performed with both a four-bladed vane and serrated parallel plates. A global agreement was found which, in some instances, resulted in substantial discrepancy, such that there still remains a significant uncertainty. Moreover, it is difficult to ascertain what the origins of this discrepancy effectively are. To address this question we think it is useful to focus on a specific material and control, at best, the different aspects of the test.

We wish to address the unanswered questions of this problem, most notably how well does SF predict the yield stress of a material under no-slip conditions. In particular, we wish to take a closer look at the determination of yield stress from precise rheological measurements; both the collection as well as the interpretation. We use these rheological measurements in conjunction with the solution of the SF theory to provide the predicted dynamic height evolution. In doing so, we will answer the question as to the validity of the 3D flow equation as well as verify the lubricational regime; not just for the determination of the yield stress but during the flow as well. Additionally, we choose just one, model, yield stress fluid in a variety of different concentrations to avoid any differences in the microstructural properties one encounters when using a variety of materials. Carbopol is a priori an ideal candidate as a yield stress fluid because of its ability to replicate great ranges of shear thinning and yield stress behavior through adjustments of the pH as discussed by Curran et al. (2002). Additionally, it is generally regarded as being relatively free of thixotropic effects (Piau 2007; Coussot et al. 2006; Tabuteau et al. 2007) making it a model yield stress fluid.

In this study precise rheological tests were first performed, characterizing the flow properties of Carbopol. A sandblasted cone and plate geometry was used when performing two different tests on the material: the stress ramp test and the constant stress tests, supplying two different perspectives. Secondly, well-controlled SF tests were performed, with great attention being made towards the surfaces of the plates. Both smooth plates and rough plates were considered. The precise rheological test data were then combined with the SF theory allowing a direct comparison of the predictions of the theory with the well-controlled SF tests.

Experimental methods

Materials

Carbopol U10 was used in the experiments as the model yield stress fluid in four different concentrations (weight percent): 0.4%, 1.0%, 1.5%, and 2.0%. Upon closer examination, it has been observed that Carbopol is essentially a glass comprised of individual, elastic sponges (Piau 2007) whose structure gives rise to its model yield stress behavior.

The preparation of Carbopol gel begins with a Heidolf plastic agitator being added to a glass container filled with the appropriate amount of water and set at a rate of 1,000 rpm. The appropriate amount of raw Carbopol powder was then slowly added to the stirring water and allowed to incorporate for 15 min. After that an appropriate amount of sodium hydroxide was quickly added to the solution, elevating the pH of the acidic solution, and the agitator displaced throughout the entire container to ensure homogenous incorporation. Once incorporated the Carbopol solution was mixed for approximately 1 week in a metallic industrial mixer allowing full homogenization and finally stored in an airtight plastic container. It has been shown that the yield stress is a large function of the pH of the solution and the objective was to ensure that the pH was in the appropriate range to ensure a stable yield stress value. It was ensured that no air bubbles were present in any of the samples prior to their use. Additionally, a 30-ml clear syringe was used when collecting and applying the specified sample and any bubbles became highly visible. If bubbles were present, the sample was disposed of and a new sample withdrawn.

In this study, the 1.0%, 1.5%, and the 2.0% Carbopol were all found to have yield stresses in a very similar range. It is believed that this is an effect of the pH of the fluid not being at the expected value. Indeed it became apparent that the accidental introduction of metal oxides could have a large impact on the resulting yield stress. Since the Carbopol samples were stirred for 1 week in a metallic industrial mixer, it is believed that this effectively veered the pH levels from the expected values. Great care was made towards minimizing the introduction of any further oxides or any non-neutral pH from the plastic storage container to the experiment; all instruments thoroughly cleaned with soap and water and fully dried before implementation. Additionally, each sample was treated in the exact same manner such that if a discrepancy was introduced to a sample it was introduced in the exact same manner to all of the samples.

Stress-controlled rheometry

Stress-controlled rheological tests were performed with a Bohlin Instruments—C-VOR stress-controlled rheometer equipped with a sandblasted cone and plate geometry (4° and 40 mm diameter). Samples were placed within the geometry using a spoon. The cone was slowly lowered onto the sample, with great care not to entrain any air bubbles. Excess sample was removed from the perimeter. The sample was then covered with a specially fitted aluminum cover which sealed around the geometry leaving only a minute hole at the top which allowed the cone to fit in, greatly minimizing any evaporation that occurs. A slight, annular void of material sometimes occurred at the air/sample interface during the tests, slightly evolving in time. Essentially, this hole at the periphery meant that a slightly smaller radius of material was being sheared. This gap was measured at periodic intervals throughout the experiments and the appropriate corrections to the stress were made.

Two types of stress-controlled rheological tests were performed to determine the flow properties of each of the concentrations of Carbopol. First, stress ramp tests, wherein the stress was increased linearly in time for 5 min and then decreased linearly in time for 5 min. The strain rate was followed as a function of the stress. Secondly, constant stress tests were performed, wherein the sample was pre-sheared at a high stress for 1 min and the stress immediately reduced to the stress in question where it was maintained and the strain rate followed as a function of time for a 10-min period. This procedure might be a more accurate depiction of the SF process in which the stress is high throughout the sample and decreases as the sample approaches the limiting height.

Squeeze flow tests

SF experiments were conducted using a dual-column testing system (Instron model 3365) with a position resolution of 0.118 μm and position reproducibility of 15 μm. The column was equipped with a 10 N static load cell (Instron model 2530-428) which was able to measure the force to within ±10^− 5 N. To control the force throughout each experiment the force is relayed to a well-tuned feedback loop which appropriately adjusted the velocity, ensuring the target force is achieved. Typically, the feedback mechanism was able to maintain the force to within ±1% of the desired force. The static load cell connected the motion control of the column to a 57-mm diameter smooth aluminum plate. The lower plate was a solid ultra-smooth PVC cylinder. Though the plates are of different materials, and thus could give rise to differing slip velocities on the upper and lower surfaces, we are interested in qualitatively showing that slip occurs. In the rest of the paper, our main interest lies in the no-slip case in which sandpaper has been added to the surfaces.

Two types of tests were performed. In the first test the smooth upper and lower plate were used as the contacting surface. In the second test, P180 grit waterproof sandpaper (average particle diameter 82 μm) was attached to the top and bottom plate using a double-sided adhesive tape. This roughness was deemed sufficient for preventing wall slip as its dimensions were greater than the dimensions of the swollen microgel particles which comprised the Carbopol solution (reported to be in the range of 2 to 20 μm (Piau 2007)).

The plates were first brought into contact and the top plate adjusted to ensure the plates were parallel to the utmost degree. Initially, the top and bottom plates were brought into contact with a force of 5 N and the gauge length set to zero. The compliance of the whole SF set-up (apparatus + plates + sandpaper) was then collected for later correction. Two separate sets of compliance measurements were collected: one for the smooth plates and one for the rough plates. The data was collected as follows: the plates are brought into contact at a very slow, constant velocity. Once contact is established the SF apparatus begins to yield a small, yet finite amount. As the constant velocity continues, the apparatus continues to yield and the corresponding force collected. At the end of the collection, the relation between the force applied and the yielding distance of the SF apparatus is known. This information was later used when the SF experiments are performed. It is assumed that when force is applied during the SF experiments the same yielding of the SF apparatus occurs as in the compliance measurements. This effect is then subtracted from the data to obtain the most accurate height measurement possible. This effect is typically on the order of several tenths of microns and an error of 10 μm on the limiting height typically leads to an error of approximately 1% to 3% on the yield stress. Accounting for this effect removes a significant source of error from our comparison of experiment and theory.

In the following SF tests a constant volume of sample was used; with the radius of the sample increasing as the interplate separation decreases. This is in contrast to the approach that is typically employed involving a constant area of contact between the plates and the sample; the volume of sample decreasing as the interplate separation decreases. Though this constant area setup has advantages such as a well-characterized area of contact and no moving interfaces within the geometry (which could potentially make it more useful in studying slippage), it adds additional complications to studies; namely the buildup of material just outside of the plate perimeter creating an additional, transient pressure term which is difficult to characterize. Since the aim of our study was to examine the no-slip case, we found it more beneficial to use the constant volume approach and to limit slip by treating the surfaces of the plates with sandpaper.

When performing the SF tests a 2 ml sample of Carbopol was placed on the lower plate using a 30-ml plastic syringe. The bottom plate was adjusted such that the sample’s center of mass was directly beneath the center of the top plate, ensuring an even spread. Next, the top circular plate was slowly lowered onto the sample to an initial starting separation of 3 mm, care being taken not to entrain any air bubbles, pressing the sample into a disk-like shape (h ₀/R is initially 0.206, where h ₀ is the initial interplate separation and R is the radius of the sample). Once the initial height was reached the test began immediately.

Constant force was then applied to the sample via the top circular plate and the resulting plate separation measured as a function of time. The critical interplate separation, h _c, was recorded after 8 min—a time that was determined from the theory to be at a height less than 1% above the limiting height, $h_\infty \;\left( {\mbox{i.e.}\;{\left( {h_{\rm c} -h_\infty } \right)} \mathord{\left/ {\vphantom {{\left( {h_{\rm c} -h_\infty } \right)} {\left( {h_0 -h_\infty } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {h_0 -h_\infty } \right)}<0.01} \right)$ for our materials in the specific range of yield stress they cover—and the force was then increased, driving the fluid towards a new limiting height. The transitional increase in the force occurred at a target rate of 1 N/min. This setting was chosen as it allowed the feedback controller to follow the target rate quite nicely and prevented an overshoot of the target force. In all, three force steps were applied to each sample resulting in three respective critical heights. Forces were chosen such that the material’s radius never exceeded the radius of the top plate (the smaller of the two). It should be noted that although constant force is being applied to the plates, the stress that is applied to the fluid is not constant and in fact decreases throughout the duration of the test. This makes for a more complex 3D flow pattern compared to the non-transient, 2D flows of conventional rheometers and justifies a more careful comparison of data with theory.

The second set of experiments was performed with sandpaper applied to the upper and lower plates, minimizing the effects of slip. The “volume loss” in the voids of the sandpaper was tested by measuring the diameter of the sample at the end of the experiment with the predicted diameter; knowing the height, the volume, and assuming a cylindrical shape. This volume loss was significant if the sandpaper was not pretreated. To prevent the attenuation of fluid into the voids of the sandpaper, a generous amount of extra sample was applied to the surface of the sandpaper before each test and the excess removed by scraping the surface with a palette knife. Between tests, both plates were removed and thoroughly scrubbed with soap and water and allowed to dry before repeating the above steps before the next test commences.

Results

Stress-controlled rheometry

The stress ramp tests were used to generate a flow curve for each of the samples of Carbopol. Only the data collected on the decreasing portion of the ramp were considered, ensuring that the measurements correspond to the liquid regime and not the viscoelastic solid regime, as it is this liquid regime that is applicable to the squeeze flow theory. A typical result is shown in Fig. 1. A least squares fitting routine was used to fit the stress ramp test with a HB curve and the results shown as a dotted line in Fig. 1.

Fig. 1

The flow curve for 1.5% Carbopol, which is typical of all concentrations of Carbopol. The dotted line shows the Herschel-Bulkley fit to the stress ramp tests (τ ₀ = 101.2 Pa, k = 47.1 Pa sⁿ, n = 0.416). The inset shows the shear rate as a function of the time during the constant stress tests for different stress levels. The results of the constant stress experiments are given after 2, 4, 6, 8, and 10 min, represented by circles of increasing darkness. A Herschel-Bulkley fit (solid line) was made to the results after 10 min of flow by adjusting the k and τ ₀ parameters, keeping n invariant (τ ₀ = 105.8 Pa, k = 48.3 Pa sⁿ, n = 0.416)

For a further view of the behavior, experiments were carried out with the help of an alternative technique; the samples were subjected to constant stress values for long periods of time (Fig. 1 inset). Stable values of the apparent shear rate were observed for a stress larger than a critical value—in this case ∼140 Pa—and a slow decrease in time of the shear rates for stresses below this critical value. The values of these constant stress tests after several times are shown in the main area of Fig. 1. An HB fit was then made, using the same least-squares fitting routine, to the data after 10 min of flow this time by adjusting only the k and τ _o parameters, keeping n constant. This fit to the 10 min of flow shows a slight increase in the yield stress for all concentrations of Carbopol and is the data that will be used for the remainder of the paper.

Squeeze flow tests

Figure 2 shows the results for a squeeze flow with the 1.5% Carbopol under the imposed conditions of the experiment. The interplate separation throughout the duration of the experiment shows three distinct drops whose shape is typical of all four concentrations of Carbopol. These results give information as to the reproducibility of measurement showing, in all, six experiments: three performed using the smooth plates and three performed with the rough plates. The maximum deviation of the smooth results is 68.6 μm and the maximum deviation of the rough results is 30.9 μm with the results being less than 5% deviation from this average for the smooth plates and less than 2% deviation from the average for the rough plates. This uncertainty might find its origin in the various, slightly uncontrolled, aspects of the test (exact shape, positioning, and volume of the sample). This suggests that herein lies the global uncertainty of our squeeze flow data, which is typically of the order of 3%. For the analysis below, the results of each respective setup (i.e smooth and rough) will be replaced by an average.

Fig. 2

Typical interplate separation showing the reproducibility of measurement for 1.5% Carbopol when imposed to the three subsequent force levels: 1 N, 2 N, and 3 N. There are three experiments shown for each of the smooth and rough plates

Theory and simulation

Squeeze flow theory

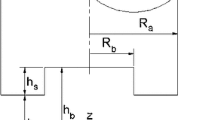
Consider a thin circular disk of fluid of thickness 2b and radius R between two parallel plates. The distance from the central axis is r while the height from the plane parallel to the plates and situated in the middle of the sample is z. The plates are squeezed together at a velocity $V={2db} \mathord{\left/ {\vphantom {{2db} {dt}}} \right. \kern-\nulldelimiterspace} {dt}$ inducing a flow. When b < < R the so-called lubrication assumption (radial velocity much larger than the vertical velocity terms and vertical shear dominant) is valid and upon application, the r-component of the momentum equation becomes:

$$0=-\frac{\partial P}{\partial r}+\frac{\partial \tau _{rz} }{\partial z}.$$

(2)

In which P is the pressure and τ _rz is the radial shear stress. Using the constitutive equation in simple shear (Eq. 1) we have τ _rz  = ετ, in which $\varepsilon ={\left| {\dot {\gamma }} \right|} \mathord{\left/ {\vphantom {{\left| {\dot {\gamma }} \right|} {\dot {\gamma }}}} \right. \kern-\nulldelimiterspace} {\dot {\gamma }}$ where $\dot {\gamma }={\partial v_r } \mathord{\left/ {\vphantom {{\partial v_r } {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}$. When τ _rz  = ετ ₀ one obtains the boundary between the yielded and unyielded domains occurring at $\hat {z}=\pm X^{-1}$, in which $\hat {z}=z \mathord{\left/ {\vphantom {z b}} \right. \kern-\nulldelimiterspace} b$ and $X={b\left( {{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial r}}} \right. \kern-\nulldelimiterspace} {\partial r}} \right)} \mathord{\left/ {\vphantom {{b\left( {{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial r}}} \right. \kern-\nulldelimiterspace} {\partial r}} \right)} {\tau _0 }}} \right. \kern-\nulldelimiterspace} {\tau _0 }$. Assuming no slip at the wall the dimensionless form of the velocity profile can be obtained:

$$\begin{array}{l} \hat {v}_r \left( {\hat {z}} \right)\!=\!\frac{1}{\left( {m+1}\right)}\frac{1}{X}\Big[ \left( {-X\left| {\hat {z}} \right|-1} \right)^{m+1}-\!\left( {\!-\!X\!-\!1} \right)^{m+1} \Big] \\\\\mbox{ for\ } \! \left|{X^{-1}} \right|\!\le\! \left| {\hat {z}} \right|\!\le\! 1, \\\\ \hat {v}_r \left( {\hat {z}} \right)\!=\!-\frac{1}{\left( {m+1}\right)}\frac{1}{X}\left( {-X-1} \right)^{m+1}\ \\\\\mbox{ for }\ 0\le\! \left| {\hat {z}} \right|\le \left| {X^{-1}} \right|, \end{array}$$

(3)

Where $m=1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-\nulldelimiterspace} n$ and $\hat {v}_r ={v_r k^m} \mathord{\left/ {\vphantom {{v_r k^m} {\left( {b\tau _0^m } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {b\tau _0^m } \right)}$. The pressure gradient can then be obtained from the conservation of mass utilizing the mean velocity:

$$\left( {m\!+\!1} \right)\hat {r}SX^2\!-\!\frac{m\!+\!1}{m\!+\!2}\left( {-X\!-\!1} \right)^{m+2}-\left( {-X\!-\!1} \right)^{m+1}\!=\!0,$$

(4)

Where $\hat {r}=r \mathord{\left/ {\vphantom {r R}} \right. \kern-\nulldelimiterspace} R$ and $S={-RVk^m} \mathord{\left/ {\vphantom {{-RVk^m} {\left( {4b^2\tau _0 ^m} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {4b^2\tau _0 ^m} \right)}$. Flow stoppage occurs when ∣ X ^− 1 ∣ approaches 1 and for constant volume Ω the limiting height is obtained:

$$ h_\infty =2b_\infty =\left( {\frac{2\Omega ^{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-\nulldelimiterspace} 2}\tau _0 }{3\sqrt \pi F}} \right)^{2 \mathord{\left/ {\vphantom {2 5}} \right. \kern-\nulldelimiterspace} 5}. $$

(5)

This is the approach of Covey and Stanmore (1981) who went on to provide closed form solutions for the pressure in the asymptotic limits of large and small S. Adams et al. (1994) assumed a form of the pressure gradient:

$$X\approx -1-\left( {m+2} \right)^{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m}\left( {\hat {r}S} \right)^{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m} $$

(6)

and was able to obtain a closed form solution over the entire range of S with limited error in the intermediate regions.

Simulation

Two governing equations for SF were solved numerically: the exact solution provided by Covey and Stanmore and the approximation provided by Adams. Both were solved using the HB parameters determined from the fit of the constant stress experiments.

For the exact solution, the relationship between the dimensionless pressure gradient X and the term S (containing velocity and height information) was determined by solving Eq. 4 using a Newton–Raphson iterative method. For good convergence, Adams’ approximation supplied the initial guess. The pressure, and thus the force, was then determined by integrating X from the periphery of the sample to its center. From this the relationship between the force upon the plates, the plate velocity and the height is easily determined.

To simulate the conditions of the experimental test, a force profile was assumed which included three force steps, each 8 min in duration, to a cylindrical volume of 2 ml at an initial height of 3 mm. To be as precise as possible, a steep ramp of 1 N/min (the target of the feedback control loop) was used to accurately depict the finite transition from one constant force to the next. Knowing the assumed force profile and the initial height allows the velocity to be determined. This initial value problem was then integrated forward in time using an explicit Runge-Kutta method. A perfectly cylindrical sample is assumed throughout the simulation such that as the height decreases, the radius increases accordingly. The simulation was then repeated, this time using the approximate relationship between the force, velocity, and height given by Adams.

Surface tension effects

Let us compute the work resulting from the variations of the interfaces during a squeeze flow by an elementary vertical length dh. The surface energy change is the sum of the changes in the interfacial energy between the solid and the ambient gas (dW _SG ), the material and the ambient gas (dW _LG ), and the solid and the material (dW _SL ). These energies are proportional, respectively, to the changes in the surfaces of the solid–gas (dS _SG ), the material–gas (dS _LG ), and the solid–material (dS _SL ) interfaces, via a coefficient equal to the interfacial tension, respectively γ _SG , γ _LG , and γ _SL , which are related by the Young equation γ _SG  = γ _LG cosθ + γ _SL , where θ is the wetting angle between the three phases. We have dS _SG  = − dS _SL  = − 4πRdR and, from the mass conservation (πR ² h = Cst.), we deduce ${dh} \mathord{\left/ {\vphantom {{dh} h}} \right. \kern-\nulldelimiterspace} h={-2dR} \mathord{\left/ {\vphantom {{-2dR} R}} \right. \kern-\nulldelimiterspace} R$. At last, assuming that the shape of the liquid–gas interface can be described by a single radius of curvature (r ₀) of the interface in the direction perpendicular to the tangent in the horizontal plane, we have $S_{LG} = 2\pi^{2}r_{0}R$ and $dS_{LG} =2\pi ^2\left( {r_0 dR+Rdr_0 } \right)$.

From natural considerations (water molecules surround any other elements of the gel) γ _LG can be considered as typically equal to the surface tension of water with air, i.e. 0.072 Pa m. For a thin layer of a simple liquid the shape of the interface would be governed by the wetting conditions and we would have $r_0 =h \mathord{\left/ {\vphantom {h {2\cos \theta }}} \right. \kern-\nulldelimiterspace} {2\cos \theta }$. For a yield stress fluid the problem is more complex. A finite element treatment of surface tension affects for SF was performed which included the free surface flow of material outside of the plates (Karapetsas and Tsamopoulos 2006). This study showed little impact of the Capillary number on the shape of the interface and attributed this effect to the dominance of yield stress effects. This suggests that in our case, when material does not flow out of the plates, the free surface is also not significantly impacted by the Capillary number, and is more probably governed by the flow of the yield stress fluid and the corresponding viscous dissipations. In this context, we can wonder whether one must use for the wetting angle θ the usual value for a water–solid–gas interface or another value affected by the effective curvature somewhat governed by the solid behavior of the gel. We cannot precisely solve this problem. However, we can reasonably assume that r ₀ is of the order of magnitude of h/2, which is sufficient for our purpose since the corresponding terms in the energy will be negligible. Indeed we find for the work required:

$$dW_s\! =\!-\pi \gamma _{LG} \left( {4R\cos \theta +\pi h} \right)dR\!\approx\! -4\pi \gamma _{LG} R\cos \theta dR $$

(7)

so that we have to provide some energy to the system if θ > π/2 and the system gains some energy if θ < π/2.

The minimum viscous work, i.e. for a vanishing velocity, needed for this elementary squeeze is $dW_v =-F_c dh=-2\pi \tau _c R^3dh \mathord{\left/ {\vphantom {{dW_v =-F_c dh=-2\pi \tau _c R^3dh} {3h}}} \right. \kern-\nulldelimiterspace} {3h}={2\pi \tau _c R^2dR} \mathord{\left/ {\vphantom {{2\pi \tau _c R^2dR} 3}} \right. \kern-\nulldelimiterspace} 3$. Finally the ratio of the surface to the viscous work writes:

$$\left| {\frac{dW_s }{dW_v }} \right|=\frac{6\gamma _{LG} \cos \theta }{\tau _c R} $$

(8)

In our experiments this ratio ranges from 0.13 cos θ to 0.43 cos θ; meaning that surface tension effects have a potential significance. In our case the solid surface was covered with a thin layer of gel so that θ ≈ 0 could be expected for usual wetting conditions. However, a direct inspection of the air–gel interface during squeezing suggests an angle of contact around π/2, most likely due to the abovementioned coupling between the flow history and surface effects for a yield stress fluid. This implies that surface tension effects were not significant in our case but, because of the uncertainty of the exact value of θ, are likely the main source of uncertainty for the data.

Discussion

Figure 3 shows typical interplate separation values for both the smooth and the rough plates. As expected, the samples generally tend to achieve a limiting height towards the end of each of the 8-min durations with each one being lower than the previous. However, the smooth plates show a lower final height at the end of each of the 8-min periods when compared with the results of the rough plates and show a continued, progressive decrease leading to a lower final height at the end of the 8 min in the interplate separation hinting that there is a significant residual flow; a strong indication of wall slip. Recently, Meeten (2008) analyzed the effect of plate roughness on the squeeze flow of a gas–liquid foam finding significant slip for plates of insufficient roughness; in his case, an order of magnitude difference of the plates’ critical separation between the polished and the roughest plates. We observe the same general effect for our material, though to a lesser degree.

Fig. 3

Typical interplate separation for 1.5% Carbopol when imposed to the three subsequent force levels: 1 N, 2 N, and 3 N. The solid line and the dotted line correspond to the solution of the 3D squeeze flow theory under the exact same force profile and Herschel-Bulkley parameters determined from rheometry for Covey and Stanmore and that of Adams, respectively (τ ₀ = 105.8 Pa, k = 48.3 Pa sⁿ, n = 0.416)

Figure 3 also shows the numerical solution of both Covey and Stanmore as well as the numerical solution employing the approximation of Adams. The Adams solution tends to be lower than the exact solution, an effect that is caused by a very slight underestimation of the pressure gradient for certain ranges of the dimensionless variable S.

A more precise comparison of the experimental SF results with the numerical results is shown in Fig. 4 for the second and third drops, respectively. Not only do the experiments performed with the rough plates show an increase in the plate separation after each of the 8-min periods but they also show a slowed height evolution when compared with the smooth plates near the end of each period. The predicted dynamic evolution does a good job representing the experimental results throughout each force step, and even the progressive decrease near the end of the 8-min period. In each case the experimental results fall consistently below the theory (∼60 μm) and could be the result of a slight overestimation of the yield stress or an inaccurate gauge length setting due to the sandpaper’s irregular surface (82 μm average particle diameter). Figure 5 shows what happens to the theoretical curve if we assume a slightly smaller yield stress (and corresponding slight smaller k coefficient). The results fall nicely along the experimental curve of the rough surface but not with smooth surface. This excellent agreement with the predictions of Covey and Stanmore means that the theory perfectly captures the apparent flow characteristics and that the remaining discrepancy of the exact vertical position of the height versus time curve is due to the uncertainty of the experimental conditions for SF (see Section “Squeeze flow tests”) and the uncertainty of the yield stress determination from rheometry (see Section “Stress-controlled rheometry”).

Fig. 4

The reaction of the sample to the second (top) and third (bottom) force step that is imposed and the exact numerical solution for the experiments described in Fig. 3. The figure time has been shifted for its origin to coincide with the onset of the force step and both axes displayed in logarithmic form

Fig. 5

Average interplate separation for 1.5% Carbopol when imposed to second force step (2 N). The axes have been rescaled in logarithmic form. The lines correspond to the solution of the 3D squeeze flow theory of Covey and Stanmore with adjusted τ ₀ and k parameters to best fit the data of the rough plates (solid line) (τ ₀ = 90.0 Pa, k = 30.0 Pa sⁿ, n = 0.416) and the data of the smooth plates (dashed line) (τ ₀ = 75.0 Pa, k = 25.0 Pa sⁿ, n = 0.416)

From the critical height after each of the 8-min periods, it is possible to calculate the yield stress of each sample according to Eq. 5. Figure 6 shows a comparison of the critical height obtained from the SF experiments and that determined from the theory using the rheological results. The results are in relatively good agreement; the rough plates giving the closest results. As expected, the results for the smooth plates lie beneath the predicted value, a consequence of slip occurring at the wall.

Fig. 6

Comparison of the critical height, h _c, obtained from the SF experiment and that of the theory using the rheological results. Filled symbols correspond to experiments performed with smooth plates and the empty ones to those performed with the rough plates

Figure 7 shows a comparison of the yield stress determined from the critical height of the SF experiments and that obtained from the rheological tests. Again, the results are in relatively good agreement with the rough plates giving the most accurate results with over 91% of the measurements being within 10% error or less. The group has a standard deviation from the rheological measurements of 6.46 Pa and a maximum error of 18.2%. Once again, the SF results with the smooth plates tend to be beneath those of the rheological measurements a direct result of the continued, progressive decrease occurring after the 8 min.

Fig. 7

Comparison of the yield stress determined from the critical height of the SF experiments and that obtained from rheometry. For comparison, the solid line has a slope of 1

Conclusion

A model yield stress fluid was studied using two main methods and the results of both methods compared with each other. First, precise rheological measurements were made for a model yield stress fluid, from two alternative views/techniques: stress ramp tests and the constant stress tests. The second method involved well-controlled SF tests which were performed using both smooth plates and rough plates. The solution of SF theory was used in conjunction with the precise rheological measurements and allowed the direct comparison of the predicted dynamic height evolution with the results of the well-controlled SF tests. The results support the role of the 3D flow models; not only in their determination of a limiting height but throughout the flow as well. Two models were explored, the exact model presented by Covey and Stanmore and a model incorporating an approximation of the pressure gradient proposed by Adams. In our case, there was a slight discrepancy between the exact model and the one incorporating the approximation highlighting the importance of being precise. Based upon the critical height for each force achieved during the SF, a yield stress could be calculated. The well-controlled SF tests do a good job agreeing with yield stress determined from the precise rheological measurements with over 91% of the measurements being within 10% or less. It is crucial that the tests be performed with rough plates as the smooth plates were found to consistently underestimate the yield stress as compared with the precise rheological measurements. It was found that surface tension effects could induce a substantial deviation in the results but that usually this uncertainty is significantly less. In order to decrease this uncertainty the tests should be performed so as to obtain larger radii for the expanding sample. Further discrepancies between the theory and the data could be due to such complicated phenomena as thixotropy and migration which are their own topics undergoing a substantial amount of research.