Electrophoretic mobility of latex spheres in the presence of divalent ions: experiments and modeling

Abstract

Electrophoretic mobilities (EPM) of negatively charged latex spheres were measured as a function of salt type and salt concentration. The measured values of EPM were analyzed using a standard electrokinetic model that includes double layer relaxation and the Poisson–Boltzmann model of diffuse double layer. Calculated values of EPM were in good agreement with experimental data taken in simple 1:1 (KCl) and 1:2 (Na₂SO₄) electrolyte solutions without using any fit parameters. For 2:1 electrolytes (CaCl₂ and MgCl₂), however, the magnitude of EPM calculated by the model was higher than the measured values of EPM at higher electrolyte concentrations. The difference between measured and calculated EPM was reduced by assuming the distance of slipping plane x _s = 0.25 nm or by assuming the decrease of the magnitude of surface charge density from −0.07 to −0.025 C/m². These are probably due to the accumulation of divalent counterions in the vicinity of a particle’s surface.

Introduction

Various important properties of colloidal dispersion, such as stability, rheology, and adsorption etc., can be related to the charging behavior of colloidal particles [1–3]. Electrophoresis is a widely used technique to investigate charging properties of colloidal particles. With this technique, we measure the moving velocity of charged particles induced by an applied electric field and obtain electrophoretic mobility (EPM), which is defined by the ratio of the migration velocity to the applied field.

The EPM reflects the sign and the magnitude of surface potential of colloidal particles. Nevertheless, it is not straightforward to interpret quantitatively surface potentials from EPM; theories are needed to convert EPM to electrokinetic or zeta potential ζ. In the earliest studies, von Smoluchowski [4], Henry [5], and Huckel [6] derived approximate expressions for the relationship between ζ and EPM. Their theories are, however, limited to low surface potentials and neglects the relaxation (polarization) effect of electric double layer (EDL). More elaborated theories were developed by Booth [7], Overbeek [8], Wiersmema et al. [9], and O’Brien and White (OW) [10] to take into account the effect of relaxation of EDL surrounding a charged particle. While the OW theory requires numerical computation to be solved, some analytical approximate expressions are also available [11–14]. The theories predict the maximum of the magnitude of EPM in the relationship EPM versus ζ because the EDL polarization reduces the migration velocity of a highly charged particle.

Many experimental studies of EPM have been carried out using latex particles, which are considered as model colloidal particles, because the particles are spherical and monodisperse. Electrokinetic behavior of latex spheres, however, has often been referred to as atypical or anomalous, that is, the magnitude of EPM has shown a maximum when plotted against electrolyte concentration [15–20]. To explain this atypical mobility, several mechanisms such as specific co-ion adsorption, hairy layer, and ion correlations, which are not included in the standard Poisson–Boltzmann (PB) and electrokinetic OW theories, have been proposed [15–17, 21–23].

Antonietti and Vorwerg [19] measured the EPM of latex sphere, bearing a constant surface charge density, in KCl and MgSO₄ solutions, and observed the maximum in the relationship between absolute values of EPM and electrolyte concentrations. In addition, they found that the maximum can be described by a simple theoretical calculation with the approximated version of OW theory, to calculate EPM from the surface potential, and the Gouy–Chapman (GC) theory derived from the PB equation, to convert charge density into surface potential. A similar conclusion has been made by Borkovec et al. [18] who analyzed their mobility data of amidine latex in KCl solution by using the GC and the OW theories. While they used the standard (PB and OW) theory and did not take into account discrete natures of ions, theoretical calculations reasonably agreed well with experimental EPM values for larger particles. The PB and OW approach was also successful in predicting EPM behaviors of other particles in 1:1 electrolyte solutions [24, 25]. It is clear that the maximum is not atypical but results from a consequence of classical EDL and standard electrokinetic theories.

Recently, attention has been paid to the effect of multivalent counterions on EPM of colloidal particles. Quesada-Perez et al. [21] analyzed EPM data of latex particles carrying a constant charge in Mg(NO₃)₂, Ca(NO₃)₂, and La(NO₃)₃ solutions. They have suggested that ion correlations must be included in theoretical calculations to obtain the quantitative agreement between theory and experiment in the presence of multivalent counterions. By contrast, Chow and Takamura have shown that the OW and PB approach reasonably describes the EPM of particles in emulsions, not in suspensions, even in the presence of divalent counterions such as Ca²⁺ and Mg²⁺ [26]. However, they did not obtain good agreement between theory and experiment for the EPM of latex particles in the presence of divalent ions and mainly focused on the shortcoming of the PB and OW theories at a lower salt concentration [27]. Antonietti and Vorwerg [19] measured mobility only in symmetrical electrolyte solutions and did not find the quantitative agreement between theory and experiment, while they showed that the maximum of the magnitude of EPM results from the standard theories. At present, a detailed discussion on the applicability of the standard PB and OW theories on the prediction of EPM of latex particles, especially in a solution of asymmetric electrolytes, is still lacking.

In the present study, the EPM of sulfate latex spheres was measured in KCl, Na₂SO₄, CaCl₂, and MgCl₂ solutions. Measured data were compared with the theoretical evaluations using the standard electrokinetic and PB theories to elucidate the validity of the theories.

Experimental

Commercially available surfactant-free polystyrene sulfate latex spheres (1–2,800; Interfacial Dynamics Corporation) were used as colloidal particles. The sulfate groups on the particle surface are considered to be strong acid and thus to carry a constant negative charge irrespective of pH and ionic strength. The manufacturer reports that the diameter 2a, the density, and the surface charge density σ of the spheres were 2.8 ± 0.14 μm, 1.055 g/cm³, and −0.07 C/m², respectively. Four salt (KCl, Na₂SO₄, CaCl₂, and MgCl₂) solutions and suspensions were prepared from pure water (Elix, Millipore). The electric conductivities of the freshly purified water were around 0.5 μS/cm.

EPM was measured by means of an improved laser Doppler velocimetry, the mixed mode measurement–phase analysis light scattering technique (Zetasizer NANO-ZS, Malvern). Details of the technique are described elsewhere [28]. Measurements of EPM were carried out as a function of salt concentration, 0.1–100 mM, and at a temperature of 298 K. The particle concentrations were 17–34 mg/L. The EPM values were insensitive to changes of particle concentration. Samples were prepared from latex suspensions by adding appropriate volumes of water and stock salt solutions to adjust the particle and salt concentrations. The values of the suspension pH were checked by a combination electrode (6.0234.110, Metrohm) and were 5.70 ± 0.21. The pH value was considered to be due to the dissolved carbonate from air.

Modeling

Measured electrophoretic mobilities were compared with calculated ones by using the theoretical models based on the standard electrokinetic and Poisson–Boltzmann theories. Methods of modeling are written below.

As stated above, this study used latex particles carrying a constant surface charge density σ. The surface charge density can be related to the surface potential ψ ₀ through the PB equation as [1, 29]

$$\sigma = \frac{{\varepsilon _{\text{r}} \varepsilon _0 \kappa k_{\text{B}} T}}{e}f\left( {y_0 } \right)$$

(1)

with

$$\kappa = \left( {\frac{1}{{\varepsilon _{\text{r}} \varepsilon _0 k_{\text{B}} T}}\sum\limits_{i = 1}^N {z_i^2 e^2 n_i } } \right)^{\frac{1}{2}} ,$$

(2)

$$f\left( y \right) = \left[ {1 - \exp \left( { - y} \right)} \right]\left[ {\frac{{2\sum\limits_{i = 1}^N {n_i \left[ {\exp \left( { - z_i y} \right) - 1} \right]} }}{{\left[ {1 - \exp \left( { - y} \right)} \right]^2 \sum\limits_{i = 1}^N {z_{_i }^2 n_{_i } } }}} \right]^{\frac{1}{2}} ,$$

(3)

$$y_0 = \frac{{e\Psi _0 }}{{k_{\text{B}} T}},$$

(4)

where 1/κ is the Debye length in a solution containing N ionic species with the valence of ith ion specie z _i and the number concentration of ith ion n _i. The Debye length 1/κ is regarded as a measure of the thickness of diffuse double layer. Other parameters, k _B, T, ɛ _r, ɛ ₀, and e, are the Boltzmann constant, absolute temperature, the relative permittivity of liquid, the permittivity of a vacuum, and the elementary charge, respectively. When the surface potential is low, the surface charge–potential relationship, Eq. 1, can be simplified as

$$\sigma = \varepsilon _{\text{r}} \varepsilon _0 \kappa \Psi _0 $$

(5)

which is given by the solution of the linearized PB equation.

Assuming that the evaluated surface potential ψ ₀ equals an electrokinetic or so-called zeta potential ζ, we can use the potential as an input parameter to calculate electrophoretic mobility μ. With the Smoluchowski equation, one can calculate electrophoretic mobility μ in a solution with a viscosity η using

$$\mu = \frac{{\varepsilon _{\text{r}} \varepsilon _0 }}{\eta }\zeta .$$

(6)

When the potential is low, an approximated relation

$$\mu = \frac{\sigma }{{\eta \kappa }}$$

(7)

is applicable by combining Eqs. 5 and 6 [30]. Both Eqs. 6 and 7 neglect the relaxation effect retarding particle velocity. To take into account the influence of the relaxation effect, the O’Brien and White theory [13] can be used to calculate mobility of a sphere with a radius a through a computer program.

Approximate analytical expressions to calculate mobility of spheres from zeta potential have been proposed [11–14]. Among them, Ohshima’s expressions [11, 12] were adopted in this study because they are more accurate and available in the presence of asymmetrical electrolytes. Ohshima’s equations are valid when κa ≥ 30. This condition was fulfilled in the present study. Before describing Ohshima’s expressions, several parameters need to be defined as follows: the drag coefficient of the ith ion specie λ _i

$$\lambda _i = \frac{{N_{\text{A}} e^2 \left| {z_i } \right|}}{{\Lambda _{_i }^0 }},$$

(8)

where N _A is Avogadro’s number and $\Lambda _i^0$ is the limiting conductance of ith ion specie, the dimensionless zeta potential

$$\tilde \zeta = \frac{{e\zeta }}{{k_{\text{B}} T}},$$

(9)

the scaled drag coefficient of ith ion specie

$$m_i = \frac{{2\varepsilon _{\text{r}} \varepsilon _0 k_{\text{B}} T}}{{3\eta z_i^2 e^2 }}\lambda _i .$$

(10)

Electrophoretic mobility μ in z:z symmetrical electrolyte solution such as KCl is given by

$$\mu = \operatorname{sgn} \left( \zeta \right)\frac{{\varepsilon _{\text{r}} \varepsilon _0 }}{\eta }\left\{ {\left| \zeta \right| - \frac{{2F}}{{1 + F}}\left( {\frac{{k_{\text{B}} T}}{{ze}}} \right)\ln \left[ {\frac{{1 + \exp \left( {{{z\left| {\tilde \zeta } \right|} \mathord{\left/ {\vphantom {{z\left| {\tilde \zeta } \right|} 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}{2}} \right]} \right\}$$

(11)

with

$$F = \frac{2}{{\kappa a}}\left( {1 + 3m} \right)\left\{ {\exp \left( {{{z\left| {\tilde \zeta } \right|} \mathord{\left/ {\vphantom {{z\left| {\tilde \zeta } \right|} 2}} \right. \kern-\nulldelimiterspace} 2}} \right) - 1} \right\},$$

(12)

$$m = \frac{{2\varepsilon _{\text{r}} \varepsilon _0 k_{\text{B}} T}}{{3\eta z^2 e^2 }}\lambda ,$$

(13)

where m is the scaled drag coefficient of counterions and the function sgn (x) is 1 when x > 0 or −1 when x < 0.

Mobility for negatively charged particles in a 2:1 electrolyte solution like CaCl₂ and MgCl₂ is written by

$$\mu = \frac{{\varepsilon _{\text{r}} \varepsilon _0 }}{\eta }\left\{ {\zeta + \frac{{2F}}{{1 + F}}\left( {\frac{{k_{\text{B}} T}}{e}} \right)\ln \left[ {\frac{1}{2}\exp \left( {\frac{{ - \tilde \zeta }}{2}} \right) + \frac{1}{2}\sqrt {\frac{1}{3}\exp \left( { - \tilde \zeta } \right) + \frac{2}{3}} } \right]} \right\}$$

(14)

with

$$F = \frac{{\sqrt 3 }}{{\kappa a}}\left( {1 + 3m_ + } \right)\left\{ {\exp \left( { - \tilde \zeta } \right) - 1} \right\}$$

(15)

$$m_ + = \frac{{\varepsilon _{\text{r}} \varepsilon _0 k_{\text{B}} T}}{{6\eta e^2 }}\lambda _ + $$

(16)

where m ₊ is the scaled drag coefficient of counterion.

For negatively charged particles in a 1:2 electrolyte solution such as Na₂SO₄,

$$\mu = \frac{{\varepsilon _{\text{r}} \varepsilon _0 }}{\eta }\left\{ {\zeta + \frac{{2F}}{{1 + F}}\left( {\frac{{k_{\text{B}} T}}{e}} \right)\ln \left[ {\frac{1}{2} + \frac{1}{2}\sqrt {\frac{2}{3}\exp \left( { - \tilde \zeta } \right) + \frac{1}{3}} } \right]} \right\}$$

(17)

with

$$F = \frac{{\sqrt 6 }}{{\kappa a}}\left( {1 + 3m_ + } \right)\left\{ {\exp \left( {{{ - \tilde \zeta } \mathord{\left/ {\vphantom {{ - \tilde \zeta } 2}} \right. \kern-\nulldelimiterspace} 2}} \right) - 1} \right\}$$

(18)

$$m_ + = \frac{{2\varepsilon _{\text{r}} \varepsilon _0 k_{\text{B}} T}}{{3\eta e^2 }}\lambda _ + $$

(19)

where m ₊ is the scaled drag coefficient of counterion.

The Ohshima equations [12] described above were used to evaluate electrophoretic mobilities of the latex spheres in KCl, Na₂SO₄, CaCl₂, and MgCl₂ solutions. In the calculation, the values of the limiting conductance $\Lambda _i^0$ (10⁻⁴ S m² mol⁻¹) were 73.48, 59.47, 53.06, 76.31, and 80.0 for K⁺, (1/2)Ca²⁺, (1/2)Mg²⁺, Cl⁻, and (1/2)SO4²⁻, respectively [31, 32].

Results and discussion

The relationship between electrophoretic mobility and KCl concentration is shown in Fig. 1. In the figure, symbols stand for the experimental data, indicating that the magnitude of EPM shows a maximum around 1–10 mM and decreases at lower and higher KCl concentrations. The solid, dotted, and dashed lines were calculated by Ohshima’s theory, Eqs. 1 and 11; the Smoluchowski equation, Eqs. 1 and 6; and the linearized Poisson–Boltzmann theory, Eq. 7, respectively. Calculations were made using a constant surface charge density σ of −0.07 C/m² and the assumption that the surface potential ψ ₀ equals the zeta potential ζ. Figure 1 demonstrates that the Smoluchowski and linearized PB theories predict the continuous decrease of the magnitude of EPM with increasing salt concentration and overestimate the absolute EPM values at lower salt concentrations. In contrast, Ohshima’s theory, including the relaxation effect of electric double layer, describes the minimum in the relationship between EPM and salt concentration. In addition, Ohshima’s theory quantitatively agrees well with experimental data without using any fit parameters. The reduction of absolute EPM values at lower <1 mM and higher >10 mM salt concentrations is ascribed to the relaxation effect; the relaxation must be considered to describe EPM behavior. In later figures, theoretical curves calculated with the Ohshima and PB theories are plotted.

Fig. 1

Electrophoretic mobility against KCl concentration. The circles stand for experimental data. The solid, dotted, and broken lines were evaluated by Eqs. 1 and 11, Eqs. 1 and 6, and Eq. 7, respectively

Figure 2 demonstrates EPM behavior obtained in Na₂SO₄ solution. The symbol and line in Fig. 2 denote experimental data and theoretical calculation, respectively. While the dispersion contains divalent co-ions, the behavior is similar to those found in KCl solution; EPM passes through a clear minimum and the calculated values agree with experimental data. The similarity suggests that the present physical picture of electric double layer, based on the PB equation and the relaxation of diffuse layer, is acceptable to describe EPM behavior as long as the valence of counterions is unity.

Fig. 2

Electrophoretic mobility against Na₂SO₄ concentration. The circles stand for experimental data. The solid line was evaluated by Eqs. 1 and 17

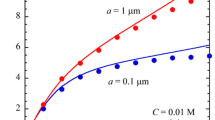
Symbols in Fig. 3 are measured values of EPM in the presence of divalent counterions MgCl₂ and CaCl₂. It is clear from the figures that the values of EPM taken in MgCl₂ and CaCl₂ are almost the same. This insignificant effect of types of divalent counterions is similar to the data cited by Quesada-Perez et al. [21], although Bastos and de las Nieves [20] reported that mobility of latex spheres in the presence of Mg²⁺ is lower than that in the presence of Ca²⁺. The weak dependence of EPM on kinds of divalent counterions implies that no specific interaction is expected between the counterions and the surface. The figure also indicates that the presence of divalent counterions reduces the magnitude of EPM and makes the EPM minimum less pronounced when compared to those obtained in the solution of monovalent counterions. The reason of the reduction is considered to be due to more effective screening of diffuse double layer by divalent counterions. Measured data are compared with theory below.

Fig. 3

Electrophoretic mobility against salt concentration. The circles and triangles stand for experimental data taken in MgCl₂ and CaCl₂, respectively. The solid, dotted, and broken lines were evaluated by Ohshima’s theory assuming the distance to shear plane x _s = 0, 0.25, and 0.5 nm, respectively, with the surface charge density σ = −0.07 C/m²

The solid line in Fig. 3 was estimated for the EPM in MgCl₂ solution by using Eqs. 1 and 14 with the same assumptions as used for the monovalent counterion cases: a constant surface charge density σ of −0.07 C/m² and ψ ₀ = ζ. The calculated mobility values for MgCl₂ are nearly identical to those for CaCl₂ and thus are not shown. As seen in Fig. 3, the evaluated values agree well with experimental data at low salt concentrations 0.1−0.5 mM. At higher concentrations, however, the magnitude of calculated EPM is higher than the measured ones. The disagreement suggests the need of additional effects to explain EPM behavior in the presence of divalent counterions. In order to decrease the discrepancy, modifications by introducing a shear plane and by reducing the magnitude of surface charge are examined.

Previous researchers have reduced the discrepancy between theory and experiment in EPM versus concentration curves by assuming a distance x _s from the plane of the origin of surface potential ψ ₀ to the plane of shear where zeta potential ζ is defined [18, 19, 24–27]. The value of x _s is regarded as the thickness of an immobile fluid layer near the surface, although how to determine the exact x _s value is still an open question. Assuming the existence of the shear plane, Borkovec et al. [18] found that calculated EPM values were in good agreement with the measured ones in KCl solution. Reasonable values of x _s are considered to be within the order of magnitude of subnanometer, which is close to the radius of hydrated ions [33]. In a solution of 2:1 electrolyte, zeta potential ζ can be evaluated from surface potential ψ ₀ by the following equation [1, 29]:

$$\zeta = \frac{{k_{\text{B}} T}}{e}\ln \left[ {\frac{3}{2}\left\{ {\frac{{1 + \left( {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}} \right)\gamma \exp \left( { - \kappa x_{\text{s}} } \right)}}{{1 - \left( {{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}} \right)\gamma \exp \left( { - \kappa x_{\text{s}} } \right)}}} \right\}^2 - \frac{1}{2}} \right]$$

(20)

with

$$\gamma = \frac{3}{2}\frac{{\left[ {{{2\exp \left( {y_0 } \right)} \mathord{\left/ {\vphantom {{2\exp \left( {y_0 } \right)} 3}} \right. \kern-\nulldelimiterspace} 3} + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}} \right]^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} - 1}}{{\left[ {{{2\exp \left( {y_0 } \right)} \mathord{\left/ {\vphantom {{2\exp \left( {y_0 } \right)} 3}} \right. \kern-\nulldelimiterspace} 3} + {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}} \right]^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} + 1}}.$$

(21)

Combining Eqs. 1, 14, and 20 with x _s = 0.25 and 0.5 nm generated dotted and broken lines in Fig. 3, respectively. Figure 3 shows that the good agreement between theory and experiment is found for x _s = 0.25 nm. The value of x _s is comparable to radii of hydrated ions and is thus considered to be reasonable. The results validated the usefulness of the standard PB and OW (Ohshima) theories for the evaluation of latex EPM in the presence of divalent counterions. The existence of immobile fluid layer is probably due to the increase of counterions concentration near a particle’s surface resulting from stronger attractive force between divalent counterions and the surface. It is plausible that a raised concentration reduces the mobility of solution. Quesada-Perez et al. [21] suggested that the PB and OW calculation is unable to fit mobility data even if the plane of shear is assumed. Their suggestion contradicts the finding of the present study. Ion correlation is not necessarily for the particles used in this work and might become significant for the particles with very high surface charge density at high salt concentration. The theoretical model including the effects of ion correlations also requires adjusting the size of hydrated ion to describe EPM [22]. The calculation of this work is rather simple and it can be said that it is practically more useful.

The influence of reducing the magnitude of surface charge with x _s = 0 nm is shown in Fig. 4. The symbols and lines stand for experiments and calculations, respectively. The solid, dotted, and broken lines were evaluated by assuming σ = −0.07, −0.025, and −0.015 C/m², respectively. The figure indicates that decreasing the surface charge density has an effect similar to that obtained by increasing x _s as previously reported [18]. The good agreement between theory and experiment is obtained when σ = −0.025 C/m². The apparent reduction of surface charge means the partial neutralization of the surface charge by adsorption of counterions. This also results from the stronger attractive force between divalent counterions and the surface.

Fig. 4

Electrophoretic mobility against salt concentration. The circles and triangles stand for experimental data taken in MgCl₂ and CaCl₂, respectively. The solid, dotted, and broken lines were evaluated by Ohshima’s theory assuming the surface charge density σ = −0.07, −0.025, and −0.015 C/m², respectively, with the distance to shear plane x _s = 0 nm

The mobility can be described by assuming reasonable values of the distance to shear plane and/or apparent surface charge even in the presence of divalent ions. These assumptions are considered to be related to the strong attraction between divalent counterions and the surface. The attraction is probably not specific but due to physical interactions because the values of EPM in MgCl₂ and CaCl₂ are comparable. We need physical models to explain the existence of shear plane or reduced surface charge.

Conclusion

Electrophoretic mobility of negatively charged latex spheres bearing strong acid (sulfate) groups was measured as a function of the solution concentration and type of electrolytes. The measured values of EPM were analyzed on the basis of the standard electrokinetic model, including double layer relaxation, and the Poisson–Boltzmann model of diffuse double layer. Calculated values of EPM were in good agreement with experimental data taken in simple 1:1 (KCl) and 1:2 (Na₂SO₄) electrolyte solutions without using any fit parameters. For 2:1 (CaCl₂ and MgCl₂) electrolytes, on the other hand, the magnitude of EPM calculated by the model overestimated the measured values of EPM in higher electrolyte concentrations. The difference between measured and calculated EPM was reduced by assuming the distance of shear plane x _s = 0.25 nm or by assuming the decrease of the magnitude of surface charge density from −0.07 to −0.025 C/m².