Charging El Niño with off-equatorial westerly wind events

Abstract

The buildup of the warm water in the equatorial Pacific prior to an El Niño event is considered a necessary precondition for event development, while the event initiation is thought to be triggered by bursts of westerly wind. However, in contrast to the view that warm water slowly builds up years before an El Niño event, the volume of warm water in the equatorial Pacific doubled in the first few months of 2014 reaching values that were consistent with the warm water buildup prior to the extreme 1997/1998 El Niño. It is notable that this dramatic warm water buildup coincided with a series of westerly wind bursts in the western tropical Pacific. This study uses linear wave theory to determine the effect of equatorial and off-equatorial westerly wind events on the Warm Water Volume (WWV) of the Pacific. It is found that westerly wind events have a significant impact on equatorial WWV with all events initially acting to increase WWV, which highlights why WWEs are so effective at exciting ENSO. In fact, our results suggest that the single westerly wind burst, which peaked in the first few days of March in 2014, was largely responsible for the coincident dramatic observed increase in WWV. How long the equatorial region remains charged, however, depends on the latitude of the westerly wind event. For instance, a single equatorially symmetric westerly wind event ultimately acts to discharge WWV via the reflection of upwelling Rossby waves, which makes it difficult to more gradually build WWV given multiple WWEs. In contrast, when the wind events occur off the equator, the subsequent discharge is significantly damped and in some cases the equatorial region can hold the heat charge for the duration of the simulations (~6 months). As such, off-equatorial WWEs can not only charge equatorial region WWV in the short term, but are also a mechanism to more gradually build equatorial region WWV in the longer term. Given that these off-equatorial WWEs have a relatively small projection onto the equatorial Kelvin wave, we argue these events can be considered as a mechanism to modulate the background state in which ENSO operates.

1 Introduction

The tropical Pacific Ocean is home to Earth’ s largest source of interannual climate variability: the El Niño-Southern Oscillation (ENSO). ENSO refers to an interannually recurring warming (El Niño) and cooling (La Niña) of the eastern and central tropical Pacific Ocean Sea Surface Temperature (SST), and a related large-scale seesaw in atmospheric sea level pressure between the Australia–Indonesian region and the south-central tropical Pacific, known as the Southern Oscillation. This overlying atmospheric feature is largely seen as a positive feedback, known as the Bjerknes feedback (Bjerknes 1969), which creates ENSO events as it acts to amplify disturbances in eastern equatorial Pacific SST. ENSO exerts profound worldwide effects (e.g., McPhaden et al. 2006) and while our understanding of ENSO has significantly increased over the last three decades (McPhaden et al. 2006; Chang et al. 2006), its irregular behaviour and predictability continues to challenge scientists.

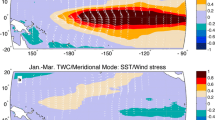
Our improved understanding of ENSO is highlighted by the success of theories such as the Recharge/Discharge Oscillator (RDO) of Jin (1997). Jin’s (1997) theory summarizes the established relationship between ENSO and the warm water volume (WWV) of the tropical Pacific (e.g., Wyrtki 1985; Cane and Zebiak 1985; Zebiak 1989). For instance, mass exchanges between the equatorial and off-equatorial regions indicate that warm water, which slowly builds in the equatorial Pacific prior to El Niño (Wyrtki 1985), is transported out of the equatorial region during El Niño (Fig. 1). In the RDO, this wind-stress curl-driven meridional transport results from a quasi-equilibrium equatorial Sverdrup balance. It is this discharge of WWV and heat during an El Niño that sets up the conditions that tend to terminate the event (e.g., Meinen and McPhaden 2000). Recent research has extended Jin’s (1997) theory, doubling the variance of modeled WWV changes during events, by adding the WWV changes due to the meridional movement of ENSO’s zonal winds (McGregor et al. 2012, 2013, 2014).

Fig. 1

a Equatorial Pacific WWV (5S–5S and 120E–80 W) and Niño 3.4 region (N34) SSTA. The grey lines in the b represent composites of WWV during the 10 El Niño events that have occurred since 1980, while the solid black line represent the composite mean. The additional blue and magenta lines respectively highlight the 1997/98 El Niño event composite and the WWV of 2014

While the RDO was originally proposed to explain ENSO as a slow and symmetric cycle, observations suggest that strong El Niño events are event-like disturbances that operate around a stable basic state, and that the onset of an event requires an initiating trigger which is separate from the dynamics of the cycle itself (e.g., Kessler 2002; Fedorov et al. 2014). These initiating impulses are thought to be largely due to high frequency wind variability, in particular Westerly Wind Events (WWEs) over the western/central tropical Pacific (e.g., Geise and Harrison 1990, 1991; Harrison and Vecchi 1997), which are also modulated by ENSO induced changes in underlying SST (e.g., Kessler 2001; Kessler et al. 1995, Kessler and Kleeman 2000; Eisenman et al. 2005). For example, the 1997/98 El Niño, which has been referred to as the “El Niño of the (last) century” due to the extremely large magnitude of its preceding anomalies of WWV and the resulting SSTA, was shown to be excited by three sequential WWEs (McPhaden 1999; McPhaden and Yu 1999; Vialard et al. 2001).

Even if El Niño is event-like rather than cyclic, growth and termination is largely consistent with the RDO (e.g., Meinen and McPhaden 2000; Hasegawa and Hanawa 2003; Bosc and Delcroix 2008). As such, the buildup of the WWV in the equatorial Pacific prior to the El Niño event is still considered a necessary precondition for the development of an El Niño (Wyrtki 1985; Meinen and McPhaden 2000; An and Kang 2001). In fact McPhaden (2012) find that WWV anomalies in the 1980s and 1990s provided a reliable indicator for peak SST anomalies some 9 months later. It is also interesting to note, however, that anomalies of WWV since ~ 2000 CE only provide a indication of peak east Pacific SST anomalies some 3 months later (McPhaden 2012).

The high Pacific WWV of early 2014 (Fig. 1) and the two relatively strong WWEs that occurred in the western Pacific in February and March led climate scientists to wonder if the resulting El Niño would rival the catastrophic 1997–1998 El Niño event (e.g., Tollefson 2014). However the predictions for a strong 2014 El Niño event did not materialize. In retrospect one can argue that this situation is not completely without precedent as not all strong WWE sequences resulted in the development of extreme El Niño events (e.g., Lengaigne et al. 2004; Fedorov et al. 2014; Lian et al. 2014). The recent study of Menkes et al. (2014) suggests that the absence of WWEs between April and June limited the growth of anomalies through 2014. While not specifically investigating the evolution of 2014, the studies of Fedorov et al. (2014) and Lian et al. (2014) suggest that event type and magnitude are strongly dependent on the phase of the WWV at the time of the WWE.

Here we focus on the fact that equatorial Pacific WWV doubled in the first few months of 2014, concurrent with the observed strong WWVs; this differs from the view of a slow buildup (Fig. 2). This co-occurrence suggests that the WWEs, which are thought to trigger El Niño events, could also be responsible for the buildup of equatorial Pacific WWV prior to the event largely through the generation of downwelling Kelvin waves. It is also interesting that higher than normal WWV has persisted in the equatorial Pacific for the last 14-months (from February 2014 to March 2015). Thus, the purpose of this paper is to understand these peculiar observational features and reconcile them with existing ENSO theories. We will systematically examine the response of the equatorial Pacific’s WWV to single and multiple idealized WWEs situated in different regions of the western Pacific in an effort to better understand the cause of the rapid WWV increase observed in early 2014 along with the persistence of WWV changes (Figs. 1b, 2c). These WWV changes and their underlying dynamical cause will be elucidated largely using linear equatorially trapped wave theory. The remainder of the paper is organized as follows. Section 2 discusses details of observed WWEs. Section 3 reviews the linear low frequency ocean response to a wind stress perturbation, while the WWV response to equatorially symmetric and asymmetric WWEs is presented is Sect. 4. Links with the observations are detailed in Sect. 5, while a discussion and conclusion is provided in Sect. 6.

Fig. 2

Longitude time plots of TAO-TRITON array observed a zonal wind anomalies, and b 20 °C isotherm depth anomalies, plotted alongside of c the equatorial Pacific WWV for the 2013–2014 period. The dashed magenta line is to mark the beginning of 2014 (data sourced from TAO Project Office of NOAA/PMEL)

2 WWE in the observations

In order to systematically identify and analyze observed WWEs, we largely follow the criteria of Harrison and Vecchi (1997) and divide the western central Pacific up into 8 regions. The Northwest (NW) [5°N–15°N, 120°E–150°E], North (N) [5°N–15°N, 150°E–180°E], Northeast (NE) [5°N–15°N, 180°E–210°E], West (W) [5°S–5°N, 130°E–155°E], Central (C) [5°S–5°N, 155°E–180°E], East (E) [5°S–5°N, 180°E–210°E], South (S) [15°S–5°S, 150°E–180°E], and Southeast (SE) [15°S–5°S, 180°E–210°E] regions. However, rather than using a minimum 10 m zonal wind speed anomaly, we follow Chiodi and Harrison (2015) and instead use an area averaged minimum zonal surface wind stress anomaly. To this end, we utilize daily average ERA-interim surface winds for the period 1979–2014. These winds are converted to wind stresses using the quadratic stress law: (τ_x, τ_y) = ρ_a C_d (U₁₀, V₁₀) W, where ρ_a is the density of air (kg/m³), C_d is a dimensionless drag coefficient, U₁₀ and V₁₀ are the zonal and meridional 10 m surface winds, while W is the wind speed given by W = (U ²₁₀  + V ²₁₀ )^0.5. The long-term mean and annual cycle was removed to form daily anomalies of surface wind stress.

The minimum zonal wind stress speed was set to 0.04 Nm⁻². This is equivalent to the area average of an idealized WWE, following the analytical model of Harrison and Vecchi (1997) (detailed here in Sect. 4 by Eqs. 17–18), with a zonal wind speed of 7 m s⁻¹ and all other parameter values set to approximately the average value of all eight regions identified by Harrison and Vecchi (1997). The wind speed of 7 m s⁻¹, which is stricter than the low cutoff (2 m s⁻¹) used by utilized by Harrison and Vecchi (1997), is utilized to focus on the larger WWEs. This value of 7 m s⁻¹, however, is consistent with the work of Eisenman et al. (2005).

Thus, here WWEs are defined as any period of 3 or more days for which the zonal wind stress anomaly, averaged over one of the eight regions and smoothed by a three-point triangle filter in time, exceeds 0.04 Nm⁻². To label and organize the events, an event’s center day was defined to be the day for which the zonal wind anomaly, averaged over the region, was greatest. With these classification criteria, we identified our full list of WWEs, by region (type) and center date. The event peak was identified as day of the maximum zonal stresses, while the duration was calculated as the number of days the zonal wind speed remained above the 0.04 Nm⁻² threshold. As in Harrison and Vecchi, we also added an additional subclassification of WWEs from our full list into overlapping and nonoverlapping events. Overlapping events are defined as those events that were identified in two adjacent regions and whose center dates were within 3 days of each other.

In this 36-year period of ERA-interim we identify 1318 western to central Pacific WWEs in the 36 years, and 948 (>71 %) of these occur in the off-equatorial region (the NW, N, NE, S and SE regions) (see Table 1). This result suggests that roughly 26 off-equatorial (10 equatorial) large WWE occur each year, which is one per fortnight. However, there are clearly WWEs with amplitudes significantly larger than our cut off (Fig. 3). For instance, there are 216 WWEs (6 per year) that have maximum area average wind stress magnitudes that are double that used the average parameter idealized experiments of Sect. 4.1, and 31 WWEs (just less than 1 per year) that have maximum area average wind stress magnitudes that are three times larger than that used the average parameter idealized experiments of Sect. 4.1. For further illustration we show some examples of large observed equatorial and off-equatorial WWEs in Fig. 4.

Table 1 The number of WWEs identified during 1979–2014, in each of the classifying regions, for the complete list and for the nonoverlapping list (see Sect. 2)

Fig. 3

Histograms of ERA-interim WWE peak magnitudes for the a equatorial (including the W, C, and E regions), and b off-equatorial (including the NW, N, NE, S, and SE regions) regions calculated over the period 1979–2014

Fig. 4

Five of the largest observed off-equatorial WWE in a, c, e, g, and i (left column) and five of the largest observed off-equatorial WWE in b d, f, h, and j, where the vectors are the five day average (centered around the event peak) surface wind stresses (N m⁻²) and the background shading is its curl (N m⁻³), while event peak date is indicated the title of each panel

3 Linear ocean response

To study the effect of meridionally displaced WWEs on WWV, we use a simplified linear two-layer ocean model. The active model upper layer is separated from the underlying motionless lower layer by an interface that represents the tropical thermocline. The dynamics and thickness of the upper layer are modeled by the linear shallow water equations with the equatorial β plane approximation (f = βy). The non-dimensionalized equations are:

$$u_{t} - yv + \eta_{x} = X$$

(1)

$$\zeta^{2} v_{t} + yu + \eta_{y} = Y$$

(2)

$$\eta_{t} + \eta_{x} + \eta_{y} = 0$$

(3)

where the subscripts indicate partial derivatives. Here, u and v are the upper layers zonal and meridional currents, respectively, η is the model thermocline depth, x and y are zonal and meridional distances and t is time. The equations were nondimensionalised by using u* = uc; v* = v(λ/L)c; x* = xL; y* = yλ; t* = t(L/c); η* = Hη; and (X*,Y*) = (X,Y)(c ² /L), where the wind stress forcing (X*,Y*) = (τ ^x , τ ^y )(ρH) ⁻¹ is applied as a body force which acts over the entire layer; L is the basin zonal width (L ~ 15.5e⁶); c = (g’H) ^1/2; λ = (c/β) ^1/2; and ζ = λ/L. The density, ρ = 1000 kg/m³, while the reduced gravity parameter, g’ = 0.0263 m s⁻², and the mean depth of the upper layer, H = 300 m, giving a gravity wave speed of 2.8 m s⁻¹, consistent with observational estimates (Chelton et al. 1998).

In the limit as ζ approaches 0, which approximately occurs here since the zonal length scale is much larger than the meridional length scale, only the long low frequency waves remain. This low frequency response (with v _t  = 0 and Y = 0 in Eq. 2, also known as the longwave approximation) of the unforced shallow water equations is described by linear theory as the sum of long equatorial Kelvin waves and long equatorial Rossby waves (e.g., Matsuno 1966). Thus, we expect, and numerous studies and texts have shown (ref; Clarke 2007), that Eqs. (4–6) represents the solution to the forced shallow water Eqs. (1–3).

$$\eta \left( {x,t} \right) = q_{0} \left( {x,t} \right)\psi_{0} + \mathop \sum \limits_{n = 1}^{\infty } q_{n} \left( {x,t} \right)\left[ {\frac{{\psi_{n + 1} }}{{\sqrt {n + 1} }} + \frac{{\psi_{n - 1} }}{\sqrt n }} \right]$$

(4)

$$u\left( {x,t} \right) = q_{0} \left( {x,t} \right)\psi_{0} + \mathop \sum \limits_{n = 1}^{\infty } q_{n} \left( {x,t} \right)\left[ {\frac{{\psi_{n + 1} }}{{\sqrt {n + 1} }} - \frac{{\psi_{n - 1} }}{\sqrt n }} \right]$$

(5)

$$v\left( {x,t} \right) = \mathop \sum \limits_{n = 0}^{\infty } v_{n} \left( {x,t} \right)\psi_{n}$$

(6)

where the Hermite functions ψ_n, provide the meridional structure of the response and are given by,

$$\psi_{n} = \frac{{e^{{\frac{{ - y^{2} }}{2}}} H_{n} \left( y \right)}}{{(2^{n} n!\pi^{1/2} )^{1/2} }}$$

(7)

with H _n (y) being the Hermite Polynomials of order n. Here, q ₀ represents the amplitude of the forced Kelvin wave, while q _n (n = 1, 2, …) represents the amplitude of the forced n^th meridional Rossby mode. As in the unforced solutions, Kelvin waves propagate eastward with a speed of c, while the nth order Rossby waves propagate westward with a speed of −c/(2n + 1).

Thus, the only remaining component to understand the forced response is to calculate the amplitude (q) of the resulting Kelvin and Rossby waves. To this end, we follow Clarke (2007) and add (1) and (3) and subtract (3) from (1), giving:

$$\left( {\eta + u} \right)_{t} + \left( {\eta + u} \right)_{x} - yv + v_{y} = X$$

(8)

$$\left( {u - \eta } \right)_{t} + \left( {\eta - u} \right)_{x} - yv - v_{y} = X$$

(9)

Substituting (4–6) into (8), multiplying by ψ₀ and integrating from y = −∞ to ∞ gives the equation for the amplitude of the forced Kelvin wave:

$$q_{0t} + q_{0x} = \frac{1}{2}\mathop \int \limits_{ - \infty }^{\infty } X\psi_{0} dy$$

(10)

Moving onto the forced amplitude of Rossby waves, we substitute (4–6) into (8), multiply by ψ _l+1 (l = 1, 2, …) and integrate from y = −∞ to ∞ giving:

$$\frac{{2\left( {q_{nt} + q_{nx} } \right)}}{{\left( {n + 1} \right)^{{\frac{1}{2}}} }} - \sqrt 2 \sqrt {n + 1} v_{n} = \mathop \int \limits_{ - \infty }^{\infty } X\psi_{n + 1} dy\quad \left( {n = 1,2, \ldots } \right)$$

(11)

Further, substituting (4–6) into (9), multiplying by ψ _l-1 (l = 1, 2, …) and integrating from y = −∞ to ∞ gives:

$$\frac{{2\left( {q_{nx} - q_{nt} } \right)}}{{\left( n \right)^{{\frac{1}{2}}} }} - \sqrt 2 \sqrt n v_{n} = \mathop \int \limits_{ - \infty }^{\infty } X\psi_{n - 1} dy\quad \left( {n = 1,2, \ldots } \right)$$

(12)

Subtracting (11) from (12) to eliminate v _n then leads to the equation for the amplitude of the forced nth order Rossby wave:

$$\left( {2n + 1} \right)q_{nt} - q_{nx} = \frac{1}{2}\mathop \int \limits_{ - \infty }^{\infty } \sqrt {n + 1} \left( n \right)X\psi_{n + 1} - \sqrt n \left( {n + 1} \right)X\psi_{n - 1} dy\quad \left( {n = 1,2, \ldots } \right)$$

(13)

Thus, by specifying the temporal and spatial structure of any given wind anomaly we can use the method of characteristics to solve for the amplitude of the forced oceanic Rossby and Kelvin wave response (q) (e.g., Clarke 2007). Note, throughout this paper we will refer to these amplitudes as projection coefficients as they are calculated by projecting the surface wind stress forcing onto the various Hermite functions (ψ_n).

Here the modeled Pacific Ocean is essentially infinite in latitude and has a zonal domain between 140°E and 280°E. Utilizing the longwave approximation (Cane and Sarachik 1977), the western boundary condition becomes:

$$\mathop \int \limits_{ - \infty }^{\infty } u dy = 0\quad ({\text{at}}\,{\text{x}} = 140^\circ {\text{E}})$$

(14)

As the only eastward propagating waves available in this model are Kelvin waves, the western boundary condition means that the Rossby wave mass transport at the western boundary must be balanced by the Kelvin wave mass transport (e.g., Kessler 1991). At the eastern boundary, as Rossby waves are the only westward propagating wave, they must satisfy the boundary condition of u = 0 at x = 280°E when a Kelvin impinges on the boundary. The amplitude of the Rossby waves reflected from the eastern boundary follows Battisti (1988), and is calculated as:

$$q_{1} = q_{0} \left( {\frac{1}{2}} \right)^{1/2}$$

(15)

for the n = 1 Rossby wave and:

$$q_{n + 1} = q_{n - 1} \left( {\frac{n}{n + 1}} \right)^{1/2}$$

(16)

for the higher order symmetric Rossby waves (n = 2,4,6,…).

As we are interested in the WWV of the Pacific along with the response of individual waves, it interesting to calculate the WWV (defined as the volume of water above the model thermocline between 5°S and 5°N) along a small strip with a zonal extent of dx ~ 27 km (0.25° horizontal grid spacing) of Rossby and Kelvin waves with the amplitude set to unity (q = 1) (Fig. 5a). This is calculated from Eq. (4) for each of the waves separately by fixing x and t (so a single longitude and time), setting q = 1, using the scaling η = Hη, then integrating in the y direction over the equatorial region (i.e., between 5°S and 5°N) and multiplying by dx. It is clear that if each modes had similar wave lengths (zonal extents), only the equatorial Kelvin wave and the n = 1 Rossby wave have a significant impact on the equatorial WWV. This means that although here we solve for the projection coefficients (or amplitudes) of the first 19 Rossby modes, a large component of the presentation of this studies results will focus on the Kelvin and n = 1 Rossby wave response.

Fig. 5

a The meridional structure of the equatorial Kelvin wave (black line) and the first eight Rossby wave modes. b Presents the dimensionalised equatorial WWV along a single line of longitude (calculated on 0.25° longitudinal grid) for the equatorial Kelvin wave and the first eight Rossby waves

4 Idealized WWB response

Here, we use linear shallow water wave theory described above to examine the extent to which different types of WWEs and in particular their latitudinal position can modulate the equatorial Pacific WWV. To characterize the WWEs in a simple manner, we utilize the analytical model of Harrison and Vecchi (1997), shown here:

$$U\left( {t,x,y} \right) = U_{o} \exp \left[ { - \left( {\frac{{x - X_{o} + c_{x} t}}{{L_{x} }}} \right)^{2} } \right]\exp \left[ { - \left( {\frac{{y - Y_{o} + c_{y} t}}{{L_{y} }}} \right)^{2} } \right]\exp \left[ { - \left( {\frac{t}{{T_{e} }}} \right)^{2} } \right]$$

(17)

This produces WWEs which are Gaussian in time (t), latitude (y) and longitude (x). This parameterization can capture the evolution of composited WWEs in the western/central Pacific (Harrison and Vecchi 1997). U is the modeled zonal wind anomaly field, U _o is the maximum point anomaly, (X ₀, Y ₀) is the geographic center, (c _x , c _y ) is the translational velocity (which is set to zero here), (L _x , L _y ) are the spatial e -folding scales, T _e is the temporal e folding scale. The modeled surface wind anomalies are converted to stresses using the linear stress law:

$$\tau_{x} = \rho_{a} C_{D} \gamma U$$

(18)

where, ρ_a is the density of air, C_D is the dimensionless drag coefficient, and, as in Zavala-Garay et al. (2003), γ, represents the mean wind speed (6 m s⁻¹ in this study).

4.1 Average parameter experiment

In this initial set of experiments using (17–18) as forcing, we set e-folding time scale (T = 3 days), maximum point anomaly (U_o = 21 m/s), latitudinal (L_y = 0.7 × 10⁶ m) and longitudinal (L_x = 1.85 × 10⁶ m) e –folding scales to approximately the average value of all eight regions identified by Harrison and Vecchi (1997). Setting U_o to 21 m/s gives an area average wind stress of 0.12 Nm⁻² around the peak of the WWE, which is near the upper bounds of the observational range. The translational velocities are set to zero, so the applied WWB does not propagate. We also fix X₀ to 190°E, and vary Y₀ from 0° to 14° latitude, with a spacing of 2° latitude, giving eight simulations within the experiment set. This choice of coefficients ensures that the applied WWBs have a consistent structure, magnitude and temporal evolution, with the only difference being the latitude that the WWBs are applied (i.e., the geographic center).

Analyzing the resulting WWV changes from these eight initial WWE forced simulations (Fig. 6a) reveals two large differences amongst the members: (1) the closer to the equator the WWE, is the larger the initial WWV increase/recharge; and (2) the experiments with the larger initial WWV increase leave the equatorial region in a discharged state after about 100 days, while those with more modest changes in WWV, driven by off-equatorial WWEs are largely maintained right through the 180 day simulation. Further analysis reveals that the changes in WWV are made up of three main components:

Fig. 6

(top) The time evolution of equatorial region WWV (m³) from the eight average parameter experiments, where the line color represents the latitude of the maximum WWE forcing. (middle) The WWV contributions of the forced equatorial Kelvin wave and its reflected Rossby waves. (bottom) The WWV contributions of the forced Rossby waves and their reflected equatorial Kelvin wave

• 1. The first component is the initial build up of WWV, which has magnitudes consistent with Ekman convergence, and it is clear that the WWEs that are centered on (symmetric about) the equator are the most effective at generating these initial WWV changes (Fig. 6a, b). As only the equatorial Kelvin wave and the n = 1 Rossby wave have significant equatorial WWV signals (Fig. 5), these WWV increases are largely seen as increases in the projected sum of the Kelvin and the n = 1 Rossby wave (Fig. 6). The differences in the magnitude of the WWV increase between these simulations come about as the more equatorially symmetric WWEs generate an equatorward Ekman transport in both hemispheres, while those with off-equatorial WWEs only generate an equatorward Ekman transport in one hemisphere.

• 2. The second component of this WWV change is the persistence of this initial WWV anomaly (~50 days, or ~40 days after the forcing peak), which is largely governed by the time that it takes the forced equatorial Kelvin wave to reach the Pacific’s eastern boundary. This wave acts to transfer mass from the WWE forcing region to the east at ~2.8 m s⁻¹, and upon reaching the eastern boundary the impinging equatorial Kelvin wave generates coastal Kelvin waves that propagate polewards along this boundary generating Rossby waves which shed off the eastern boundary (Moore and Philander 1977). The volume of the reflected n = 1 Rossby wave is largely maintained within the equatorial region, while the volume carried by coastal Kelvin waves and higher mode (n > 1) Rossby waves is effectively drained from the equatorial region (Fig. 6b). Given that the reflected n = 1 Rossby wave amplitude is set at 1/√2 of the incoming Kelvin wave (Eq. 15) the equatorial region retains (loses) approximately 25 % (75 %) of its Kelvin wave volume at the eastern boundary.

• 3. The third component of the WWV change is due to Rossby waves (Fig. 6c). In all of these experiments the wind-generated Rossby waves, which also have a WWV signal (Fig. 5), slowly propagate westward, and upon impinging on the western boundary these Rossby waves efficiently generate an equatorial Kelvin wave to satisfy the boundary condition. Despite the smaller amplitude of the resulting Kelvin wave (e.g., Kessler 1991), the WWV signal of these impinging Rossby waves is enhanced by the western boundary reflection as the resulting Kelvin wave propagates three times faster away from the boundary than the impinging Rossby waves (Sect. 3).

  The difference between the experiments, however, is the magnitude and sign of the n = 1 Rossby wave projection (Fig. 7b). For WWE close to the equator (latitudes ≤ 6°) the WWV increase of the forced downwelling Kelvin wave basically comes from the upwelling equatorial Rossby waves straddling the equator. As the n = 1 Rossby waves have a strong WWV projection (Fig. 5b), the upwelling Rossby wave signal offsets the Kelvin wave WWV increase. When roughly 3/4 of the Kelvin wave mass is transferred to the off-equatorial region after impinging on the eastern boundary, the n = 1 Rossby wave volume decrease becomes the dominant structure in the equatorial region WWV changes. As discussed above, this equatorial region WWV decrease is enhanced further when the Rossby wave impinges on the western boundary. This final state is consistent with the Sverdrup balance at 5° latitude, which suggests the response to an equatorially symmetric wind burst is to transport mass polewards, effectively discharging WWV.

  Fig. 7

  

  The basin wide sum of projection coefficients (or wave amplitudes, q) for the a equatorial Kelvin wave, and b n = 1 Rossby wave, after 20 days of the average parameter WWE plotted as a function of forcing meridional length in Rossby radii of deformation (x-axis) and forcing latitude (y-axis)

  For the WWE at 8° latitude, the WWV decrease of the small negative n = 1 Rossby wave projection and its reflected Kelvin wave is roughly equivalent to the WWV increase of the n = 1 Rossby waves reflected from the eastern boundary. Thus, the equatorial region has only a very small WWV change after the initial boundary reflections.

  For WWE at or polewards of 10° latitude, on the other hand, the Kelvin wave and n = 1 Rossby waves (for L_y = 2 Rossby radius of deformation) are both downwelling waves (Fig. 7). Therefore, even after the Kelvin waves eastern boundary volume loss, the equatorial regions remaining WWV increase is made up of the forced n = 1 Rossby wave, the resulting Kelvin wave reflected from the western boundary, and the eastern boundary reflected n = 1 Rossby wave, all of which are downwelling waves. The differences in the persistence of the original WWV between the equatorial to off-equatorial WWE is largely due to its projection onto the n = 1 Rossby waves. This off-equatorial WWE does generate an upwelling Rossby wave, but it is centered polewards of the maximum wind speed (~10° latitude), which due to the slow propagation speeds and poor boundary reflection of these higher order Rossby waves (Kessler 1991) does not have a significant impact on the equatorial region WWV in our simulations. Thus, the adjusted state is consistent with the Sverdrup transport at 5° latitude, which suggests that WWE transports mass equatorward acting to recharge equatorial region WWV. This suggests that off-equatorial WWEs, those centered at or poleward of 8° latitude, provide an additional mechanism to recharge and maintain residual WWV for the entire duration of the simulations (180 days).

4.2 Mutliple average parameter experiment

Here we carry out an additional three sets of experiments using (17–18) for forcing, each of which utilize the parameters selected in Sect. 4.1. What is different between these three experiment sets and the previous set (described in Sect. 4.1), is the number and timing of WWE applied, with the first experiment set being forced with two WWE events (one WWE every 60 days), the second experiment set being forced with three distinct WWE events (one WWE every 40 days), while the second experiment is forced with six back to back WWE events (one WWE every 20 days). Moreover, each of these experiments is run with eight different WWE forcing latitudes (from 0°–14°). We know from the earlier work of Meinen and McPhaden (2000) and McPhaden (2012), that the WWV buildup prior to an El Niño event is related to the peak magnitude of eastern Pacific SSTA during the event. Thus, here these experiments are designed to better understand whether multiple WWEs can be used to build equatorial region WWV.

Focusing on the WWV response of equatorially or near equatorially symmetric WWE (lat < 5°) from each experiment set (Fig. 8), we find that after the wave pulses of the initial WWE reach the eastern and western boundaries, the recharging effect of subsequent WWEs is not large enough to offset the long-term WWV boundary discharging. Thus, the peak WWV is reached sometime prior to the first generated equatorial Kelvin wave reaching the eastern boundary (<50 days). On the other hand, as a proportion of the WWV increase of off-equatorial WWEs (lat > 6°) is maintained for the duration of these simulations (180 days), the induced equatorial convergence of multiple WWEs acts to build (recharges) WWV in a step like manner (Fig. 8).

Fig. 8

The time evolution of equatorial region WWV (m³) from the three multiple WWE experiments of Sect. 4.2, where WWEs are applied once every a 60-days, b 40-days, and c 20-days in the first 100 days. The eight lines in each panel represent the latitude of the maximum WWE forcing

We note that the experiments are relatively simple and we have not considered the changing magnitude of the WWEs or WWEs with the central latitude evolving over time. However, these results suggest that it would be very difficult to build WWV larger than that produced by an initial WWE with equatorially or near equatorially symmetric WWEs alone, while multiple off-equatorial wind bursts act to gradually build the Pacific WWV (Fig. 8). It is also noted that being a linear ocean model, the oceanic and WWV response of easterly wind surges (Chiodi and Harrison 2015) should be the of the response to WWEs. Thus, multiple easterly wind surges have the potential to significantly build equatorial region WWV, after 100–160 days.

4.3 Sensitivity to parameter choice

We also examined the sensitivity of the WWV changes to the changes in the analytical WWB model parameters, U_o, T_e, L_x, and L_y, as what we have been using up until this stage is considered as the average WWE. We examine U_o for the range between 7 to 28 m s⁻¹ (giving area average wind stress anomalies within the observed range of 0.04 to 0.16 Nm⁻², Fig. 3), T_e for the range between 1.5 and 6 days, L_x between 1.15 × 10⁶ m (3.3) and 2.55 × 10⁶ m (7.3) and L_y between 0.1 × 10⁶ m (0.29) and 1.3 × 10⁶ m (3.7), where the bracketed numbers are non-dimensionalized quantities.

Due to the linearity of the model we find the dynamical interpretation of the results presented above to be relatively robust. Changes in U_o, T_e, and L_x simply lead to changes in the amplitude of the WWV changes that can be largely represented by multiplying the original WWV changes reported above (Fig. 6a) by a constant (not shown). For instance, the response of the WWV doubles as we go from U_o = 7 m/s to U_o = 14 m/s. The only subtlety that needs mentioning is for the L_x case. The differing length scales of the WWE in this scenario leads to slightly different arrival times of the generated Rossby and Kelvin waves at the western and eastern boundaries respectively, which culminates in slight variations of the phase of WWV around these boundary arrival times.

As expected from the role of Sverdrup balance in controlling WWV, changes in L_y, on the other hand, lead to some interesting dynamical changes (Fig. 9). Considering that the equatorial region WWV only has significant contributions from the Kelvin and n = 1 Rossby waves (Fig. 5b), the initial WWV can be thought of as the sum of the basin wide forced Kelvin and n = 1 Rossby wave projection coefficients (Fig. 7). Note, the basin wide projection coefficients of each of the waves is calculated by summing the wave amplitudes (q _o , q ₁ ) from Eq. (4) over the entire basin width (x), at t ~ 30. The actual WWV contribution of each of the waves can be calculated by simply multiplying the summed amplitudes by the respective dimensionalised WWV of the mode (Fig. 5b).

Fig. 9

Modeled equatorial region WWV (m³) of the average parameter WWE experiment after a 30-days, b 60-days, c 90-days, and d 120-days, plotted as a function of forcing meridional length in Rossby radii of deformation (x-axis) and forcing latitude (y-axis)

Now, lets consider the initial WWV of the equatorially centered WWE case of the L_y sensitivity experiments. Increasing L_y leads to an increasing Kelvin wave amplitude, it is noted that the Kelvin wave amplitude appears to be reaching its maximum value at max L_y (Fig. 7a). The maximum projection onto the n = 1 Rossby wave, on the other hand, occurs between L_y = 1,2 Rossby radii of deformation and decreases for values greater than (less than) the latter (former) (Fig. 7b). For length scales longer than two, the equatorial WWEs increasingly project onto the higher order even Hermite functions, and thus Rossby waves (not shown), of which the n = 2 Hermite projection acts to decrease the n = 1 Rossby wave projection (see Eq. 13). For length scales less than one, the n = 0 Hermite function (Fig. 7a) and thus n = 1 Rossby wave projection simply decreases (Fig. 7b), and as the Rossby wave has a larger WWV signal (Fig. 5b) there is a reduction in WWV. This combines to mean that the initial increase in equatorial Pacific WWV to an equatorially symmetric WWE increases as L_y increases (Fig. 9a). The discharge of WWV of the equatorially centered WWE case, after the WWE induced Kelvin and Rossby waves impinge respectively on the eastern and western boundaries, and the uneven projection of the WWE onto the Kelvin wave and n = 1 Rossby wave signal ensure that the discharge is less for larger L_y for values of L_y > 1. The discharge of WWV also decreases as L_y decreases for values of L_y < 1 as the n = 1 Rossby wave projection also gets smaller (Figs. 7b, 9).

Secondly, lets consider WWE occurring at 6° latitude as this latitude has the largest WWV anomalies for L_y < 2 after 30-days (Fig. 9a). Increasing L_y leads to an increasing Kelvin wave amplitude, and it does not appear to be reaching a horizontal asymptote at the maximum L_y (Fig. 7a). In terms of the n = 1 Rossby wave projection, for L_y ~ <1.5 there is a positive projection of the WWE, while for L_y greater than this there is a negative projection (Fig. 7b). This change in the n = 1 Rossby wave projection leads to a dramatic change in the persistence of WWV anomalies. The positive n = 1 Rossby wave projection is similar to the situation described in Sect. 4.1 for WWE located at 10° latitude, and as seen in Fig. 6 there and Fig. 9 here, the initial increase in WWV is largely maintained right through the 180 day simulation. For values of L_y > 2, the persistence of the WWV anomaly is basically a competition between the magnitudes of the western boundary reflected upwelling Kelvin wave and eastern boundary reflected n = 1 downwelling Rossby wave, where for L_y ~ 2 they are roughly even, while for L_y > 2 the reflected upwelling Kelvin wave dominates (Fig. 9).

In fact, if we only wanted to find the optimal latitude a WWE with a given L_y needed to be located to have a positive WWV anomaly that is maintained throughout the entire 180 day simulation, it is clear that the latitude increases as L_y increases (Fig. 9b, c, d). The persistence of WWV can be thought of in terms of the weighted (i.e., where the projection coefficients are weighted according to the reflective properties of the meridional boundaries) Kelvin wave and n = 1 Rossby wave projection coefficients. As discussed above, a Kelvin wave impinging on the eastern boundary loses roughly ¾ of its equatorial region WWV, while an n = 1 Rossby wave imping on the western boundary increases the equatorial region WWV by 70 %. Thus, in the absence of damping, the forced equatorial WWV response after the initial eastern and western boundary reflection (~ 90–120 days) is given by sum of the forced n = 1 Rossby wave and Kelvin wave projection coefficients, where the former (later) is weighted by 1.7 (0.25) to reflect the effects of western (eastern) boundary reflection. The changing n = 1 Rossby wave projection is best described in terms of Sverdrup transports. As L_y increases, the latitude of the WWE must also increase in order to maintain the strongest wind stress curl (Sverdrup transport) at the meridional boundary of the equatorial region. In terms of the wave projections, when a WWE projects positively onto the Kelvin wave (the n = 0 Hermite function, Eq. 7), it also projects negatively onto the n = 1 Rossby wave (the n-1 Hermite function in Eq. 13). Thus, in order for a WWE to project positively onto the n = 1 Rossby wave the WWE must have a stronger projection onto the n = 2 Hermite Function (the n + 1 term in Eq. 13) than onto the n = 0 Hermite function (the n − 1 term in Eq. 13).

5 The effect of observed WWEs on WWV

We have shown so far that WWE events can generate large changes in WWV, and those WWE that have their maximum wind speeds centered around the equator have the largest initial impact on WWV through a projection on the equatorial Kelvin wave (ψ₀), but ultimately end up discharging WWV through the n = 1 Rossby mode (ψ₁). On the other hand, those WWE with their maximum wind speeds centered polewards of 6° latitude have less of an initial impact on WWV, but the initial charging of WWV can persist for the entire duration of the integrations. While the magnitude of the idealized experiments presented in Sect. 4.1 are roughly one-third of the observed WWV increase of 0.89 × 10¹⁴ between January and April of 2014, considering the maximum values of the parameters U_o, L_x and T_e (Sect. 4.3) allows the WWV of the idealized simulations to equal the WWV changes observed in 2014. However, due to the idealized nature of our experiments to date, the question as to whether the spatial structure and amplitude of the observed WWEs have a significant impact on the observed longterm WWV, even in the absence of positive air–sea coupling, still remains.

Thus, here we intend to analyze the SWM response of each of the 216 WWEs that have maximum area average wind stress magnitudes > 0.08 Nm⁻² (Sect. 2). To this end, we project the Pacific basin zonal wind stresses of each of these observed WWEs onto the Kelvin (Eq. 10) and Rossby (Eq. 13) waves for the duration of the event. We then analyse the resulting Kelvin wave and n = 1 Rossby wave projection in order to understand the initial WWV (at ~20 days) and the adjusted WWV (e.g., after ~90–120 days). Here, we neglect damping and estimate the adjusted WWV (e.g., after 90–120 days) as the weighted sum of these two equatorial modes where the Kelvin wave projection is reduced (~25 % weighting) and the n = 1 Rossby wave projection is amplified (~170 % weighting). This weighting of the projection coefficients reflects the effect of eastern and western boundary reflections on the equatorial region WWV, where 75 % of the mass is lost via the eastern boundary reflection of a Kelvin wave while the n = 1 Rossby wave WWV is amplified by 70 % via the western boundary reflection.

Figure 10a displays the adjusted WWV (weighted sum of projection coefficients), plotted against the initial WWV (sum of the projection coefficients) for each of the observed WWEs. We also generate a similar plot for the idealized experiments carried out in Sect. 4.1 for comparison (Fig. 10b). What is clear from this plot of the observed WWE experiments, is that the observed events produce initial WWV changes that can be larger than the observed WWV increase of 2014 (Fig. 2). Further to this, both the equatorial and off-equatorial WWEs have the potential to dramatically increase observed equatorial region WWV in the space of a couple of weeks (i.e., the duration of the WWE).

Fig. 10

The initial equatorial region WWV (after 30-days) plotted against the adjusted WWV (after 90–120 days, estimated from the weighted Kelvin and n = 1 Rossby wave projection coefficients) for the a observed WWE experiments, and b idealized WWE experiments. The equatorial (off-equatorial) region WWE are distinguished in each panel by blue dots (black plus signs), while the least squares line of best fit is shown in cyan (gray). The non-overlapping 2014 WWE events are highlighted by magenta squares. The black (blue) text is each panel represents the relationship between off-equatorial (equatorial) WWE induced initial and adjusted WWV, where r is the correlation, and b is the linear regression slope

We also find that equatorial WWE have the potential to produce an adjusted (after 90–120 days) discharged state that is twice as large as the original WWV recharge, but the linear relationship between the two states suggests that on average the adjusted state is roughly the mirror of the initial response (Fig. 10a, b). Consistent with the findings of our idealized experiments, off-equatorial WWEs have a much weaker projection onto the n = 1 Rossby wave, than equatorial WWEs (Fig. 9). Thus, on average the adjusted discharged state (after 90–120 days) is much smaller than that of an equatorial WWE with an equivalent initial WWV change. This is summarized by the linear regression between the two states, as seen in Fig. 10. There is also the potential for a positive projection of the off-equatorial WWEs onto the n = 1 Rossby wave with 12 % (19) of the 157 off-equatorial WWEs projecting positively onto both the Kelvin and n = 1 Rossby waves. Meaning that, outside of any additional forcing, a portion of the induced equatorial region positive WWV change will persist for more than 180 days.

In regards to the WWEs of 2014, we find that there were 5 events from the full list that have peak area averaged magnitudes that are greater than 0.08 Nm⁻² and all of these events occurred prior to the end of March 2014 (Fig. 11). However, three of these events are considered to be overlapping. These are the events that peak on the 1st, 4th and 6th of March, in the W, NW and N regions respectively. Highlighting the adjusted (weighted sum of projection coefficients) and initial (sum of the projection coefficients) WWV of these three non-overlapping wind bursts (the overlapping events are considered as one long event) we can see that the early March WWE had the most dramatic effect on equatorial region WWV (Fig. 10a). In fact, the initial response of the WWV is an increase of 0.52 × 10¹⁴ m³, which is quite similar to the observed WWV increase of 0.89 × 10¹⁴ between January and April of 2014 (Fig. 1b). In terms of the adjusted response to this particular 2014 WWE, the projection coefficients suggest that there would be minimal discharging due to the relatively small n = 1 Rossby wave projection of this WWE. Thus, the WWV would return to a similar place to where it started from after roughly 100 days, which is also remarkably similar to what was observed.

Fig. 11

The five large (area average magnitude > 0.8 N m⁻²) WWEs of 2014. Wind stresses (N m⁻², vectors) and wind stress curl (N m⁻³, shading) for the five day average around the event peak are displayed, while event peak date and region are indicated the title of each panel

6 Discussion and conclusions

In this study we used linear equatorial wave theory to examine the response of the equatorial Pacific’s WWV to single and multiple idealized WWEs in the western Pacific where the latitude of the maximum wind speed is also varied. We also investigated the WWV response to 216 of the equatorial Pacific basins largest WWEs. This was carried out using linear equatorially trapped wave theory in an effort to better understand the causes of the dramatic WWV increase observed in early 2014, and its relationship to the series of accompanying WWEs. These simple models are known to represent the large scale ocean dynamics of El Niño events relatively well, however, it is currently unclear how much impact unresolved features like the high-shear equatorial currents and detailed bathymetric features at the boundaries can impact the results presented here.

We find that both equatorial and off-equatorial WWEs can significantly increase the equatorial Pacific WWV, with our results suggesting that a single large WWE can increase the equatorial Pacific WWV by more than 1.0 × 10¹⁴, which is larger than the average WWV preceding El Niño events. In fact, our results suggest that the single observed WWE that occurred at the beginning of March 2014 was solely responsible for doubling the equatorial Pacific WWV observed around this time, in contrast to the slow-recharging concepts paraphrased in various ENSO theories. We also show that the initial WWV increase, which is consistent with the Ekman convergence into the equatorial region, can be thought of as the sum of the Kelvin and n = 1 Rossby wave projection as these are the only two modes that have a significant equatorial region WWV signal. The adjusted state (after both the eastern and western boundary reflection which is roughly 100-days after initialization), on the other hand, can be estimated by the weighted sum of these two equatorial modes where the Kelvin wave projection is reduced (~25 % weighting) and the n = 1 Rossby wave projection is amplified (~170 % weighting). This weighting of the projection coefficients neglects the effects of damping and is obtained by calculating the effect of eastern and western boundary reflections on the equatorial region WWV, where the Kelvin wave WWV signal is decreased by 75 % via its eastern boundary reflection while the n = 1 Rossby wave WWV signal is increased by 70 % via its western boundary reflection.

We find that equatorial WWE (i.e., those that have their maximum wind speeds within 5° latitude of the equator) are most efficient in generating initial changes in equatorial region WWV. This is largely because they have the biggest projection onto the equatorial Kelvin wave, and are thus most effective at triggering changes in eastern equatorial Pacific SST and the onset of an El Niño event, if their effect on eastern equatorial Pacific SST can be further amplified by the seasonal air-sea instability, which occurs in boreal summer. This is consistent with the study of Geise and Harrison (1991) and highlights why WWEs are so effective at exciting ENSO. However, these same WWEs project negatively onto the n = 1 Rossby wave, which in the absence of a seasonal air-sea instability of the Bjerkness feedback, ultimately leaves the equatorial region in a discharged state after roughly 100-days. This discharge is largely consistent with that expected from the RDO. Extending the earlier work of Lengaigne et al. (2004) whose results suggest that not all large WWEs lead to El Niño events, our results suggest that poorly timed WWE’s (i.e., one that occurs when the eastern Pacific is weakly coupled with the overlying atmosphere) may even be detrimental to the development of an El Niño due to the resulting discharged state of the Pacific Ocean. Further to this, the fact the each equatorial WWE ultimately leaves the equatorial region WWV in a discharged state also makes it difficult to more gradually build WWV given multiple WWEs, which is an interesting aside given that peak El Niño anomalies have been linked with the magnitude of WWV preceding the event.

We also analyse the response to off-equatorial WWEs, these are the WWEs that have their maximum wind speeds between 5° and 15° latitude. These off-equatorial WWEs have been shown in the past literature to not be that important for eastern Pacific SST due to the reduced magnitude of their Kelvin wave contribution (Geise and Harrison 1991), which our results support. However, our results show that these off-equatorial WWEs are an effective mechanism to “charge” the equatorial region. For instance, the average initial (~after 30 days) WWV change of the 140 off-equatorial WWEs (those with area average wind stress magnitudes greater than 0.08 Nm⁻²) observed since 1979 is roughly 33 % of the dramatic WWV increase observed in early 2014 (0.89 × 10¹⁴). Based on the results discussed above we prefer to use the terminology “charge”, rather than “recharging”, as these off-equatorial WWE do not have to be related to a cool central/eastern Pacific SSTs like the equatorially symmetric easterly wind stress anomalies that act to recharge equatorial WWV during an La Niña event.

Perhaps the most interesting aspect of the off-equatorial WWEs is their projection onto the n = 1 Rossby wave, which ranges from a relatively small negative projection through to a relatively small positive projection. It is this smaller projection, relative to the Kelvin wave projection, that allows the off-equatorial WWEs to produce significant WWV. The sign of the projection, however, is important due to its western boundary amplification and hence its dominant weighting in the WWV after 100-days. As such, a small negative projection ensures that the equator is not substantially discharged after adjustment, which implies that if an event is not triggered by the Kelvin wave component of the WWE then the system still remains in a neutral state which has the potential to still support El Niño event initiation. A positive n = 1 Rossby wave projection, on the other hand, results in the equatorial Pacific remaining charged for some time after the WWE, which is a state, that according to our experiments, can accumulate WWV with further off-equatorial WWEs in a step like manner. As such, off-equatorial WWEs must be considered a viable mechanism to not only charge equatorial region WWV in the short term, but also as a mechanism to more gradually build equatorial region WWV in the longer term.

In the context of Jin’s (1997) RDO theory, the transport associated with an off-equatorial WWE with a small negative n = 1 Rossby wave projection can be considered an unbalanced, as the net WWV after the initial wave adjustment is close to zero. On the other hand, off-equatorial WWEs with a positive n = 1 Rossby wave projection can essentially be considered a balanced transport as the adjusted impact is consistent with Sverdrup theory. Given the relatively minimal impact of these off-equatorial WWEs on equatorial region winds, it is fair to say that both of these events would not be incorporated in current ENSO theories. Further to this, given that these off-equatorial WWEs also have the potential to modulate equatorial WWV with a relatively small projection onto the equatorial Kelvin wave, and thus a relatively small likelihood of triggering an El Niño event, these events can be considered as a mechanism to modulate the background state in which ENSO operates and they may also be related to the peak amplitude of El Niño events.