1 Introduction

Decision makers in a wide variety of sectors are increasingly asking for quantitative projections of changes in climate on regional scales. Such projections are available from the outputs of (downscaled) Global Climate Models (GCMs), or directly from Regional Climate Models (RCMs). The outputs from the climate models can be further processed by impact models, e.g. hydrological models. The climate change projections are subject to large uncertainties, for example, even the sign of the change in mean precipitation varies across models in many areas (Meehl et al. 2007). An important issue for decision makers and scientists is how to rank and quantify these uncertainties. The relative contribution of emission induced climate change to the simulated changes is important for decision makers developing adaptation strategies.

The uncertainties of climate projections originate from three sources, namely model uncertainty, scenario uncertainty and uncertainty due to internal climate variability (Hawkins and Sutton 2009). Model uncertainties arise from the way specific processes and feedbacks are modelled. Scenario uncertainty originates from incomplete knowledge of external factors influencing the climate system, for example future emission of greenhouse gases or population growth. Internal climate variability is the natural variability of the climate system and uncertainty arises from non-linear dynamical processes and unknown initial conditions. The relative importance of these three sources of uncertainty varies with prediction lead time and with the scale of spatial and temporal averaging (Hawkins and Sutton 2009; Räisänen 2001). For multi-decadal time scales and global spatial scales, the dominant uncertainties for temperature are model uncertainty and scenario uncertainty. The importance of internal climate variability increases at shorter time scales (Cox and Stephenson 2007) and smaller spatial scales (Hawkins and Sutton 2009).

A number of studies have demonstrated that internal climate variability is a much more important factor for projected changes in precipitation than for temperature (Murphy et al. 2004; Räisänen 2001). Giorgi and Bi (2009) studied the time at which the magnitude of the multi-model ensemble mean precipitation change exceeds the total interexperiment standard deviation of the changes in the mean precipitation. They found that for most regions this occurs somewhere in the 21st century and for some regions even in the early 21st century. These authors further stressed that the contribution of inter-model spread to the total interexperiment standard deviation is substantially larger than that of internal multi-decadal climate variability. Hawkins and Sutton (2011) continued on this study and found that internal climate variability is the most important source of uncertainty for many regions for lead times up to 30 years. Model uncertainty is generally dominant thereafter and scenario uncertainty is very small. These results apply to large regions (≈2,500 × 2,500 km2). Rowell (2012) studied the sources of uncertainty in the changes in mean precipitation at the end of the 21st century in four GCM ensembles. He found that model uncertainty is the dominant source of uncertainty for the projected changes in tropical and polar regions, and that internal climate variability becomes more important at mid-latitudes.

The papers cited above deal with the contribution of internal climate variability to the total uncertainty of the change in mean precipitation. For many regions, also the changes in extreme precipitation are important as they can have large impacts on flood risk. The uncertainty of the changes in extreme precipitation, has only been studied to a limited extent. Räisänen and Joelsson (2001) compared the changes in the annual mean and maximum precipitation in two 10-year control and 10-year future regional climate model simulations driven by different GCMs. They concluded that the differences between the changes in these two model experiments could be largely explained by internal climate variability as a result of the short lengths of the climate model simulations. Brekke and Barsugli (2013) studied the sources of uncertainty in the changes in the 2-year and 100-year return levels of the local 1-day annual maximum precipitation in the United States (US). Both model uncertainty and internal climate variability were found to be important sources of the uncertainty in the projected changes in these return levels for the end of the 21st century over much of the US.

This paper focuses on the contribution of internal climate variability to changes in extreme precipitation and discharge in the river Rhine basin. For current and future water management in the densely populated Rhine basin, flood risk is one of the major concerns. Van Pelt et al. (2012) gave various estimates of the future changes in extreme precipitation over the basin using different climate model simulations, but did not quantify the role of internal climate variability. In this paper the same ensemble with different GCMs and another ensemble of multiple realisations from a single GCM (with perturbed initial conditions) are considered to assess the contribution of internal climate variability.

A bootstrap method was applied to estimate the variance of the changes in three precipitation characteristics due to internal climate variability. This variance is compared to the total interexperiment variance of the changes in the ensemble. The non-linear delta method of Van Pelt et al. (2012), in combination with time series resampling, was used to obtain representative series of daily precipitation for future climate conditions at the scale of the Rhine basin consistent with the changes in the various GCM simulations. Return levels of extreme 10-day precipitation, associated with return periods between 10 and 1,000 years were then derived for the end of the 21st century. The spread of these return levels in the two GCM ensembles is compared. A similar comparison is made for extreme river discharges in the Rhine basin. River discharge was obtained by driving a hydrological model with the transformed precipitation and temperature time series.

The paper is structured as follows: The two GCM ensembles and the observed data are described in Sect. 2. Methodological issues, including an analysis of variance to distinguish internal climate variability from the variability due to systematic differences between GCMs, are dealt with in Sect. 3. The results of the analysis of variance are discussed in Sect. 4. The return levels of extreme 10-day precipitation and river discharge are presented in Sect. 5. In Sect. 6 the findings and conclusions are discussed.

2 Climate model ensembles and observations

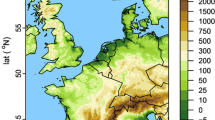
In Table 1 an overview is given of the two GCM ensembles that have been used for this study. Both ensembles refer to transient GCM simulations, using the IPCC SRES A1B scenario for future greenhouse gas emissions. The GCM simulations from the Coupled Model Intercomparison Project Phase 3 (CMIP3) archive were conducted with different GCMs. The ESSENCE ensemble (Sterl et al. 2008) is a 17-member ensemble simulation with the ECHAM5/MPI-OM coupled climate model which has been developed at the Max-Planck-Institute for Meteorology in Hamburg. All members share the A1B greenhouse gas forcing, but their initial state of the atmosphere was perturbed. This results in different realizations due to internal climate variability in the modelling system. The grid size and structure vary between the GCMs, therefore the output was regridded to a common 2° lat by 2.5° lon grid. At this resolution the Rhine basin is covered by eight grid cells (see Fig. 1). For all GCMs a 35-year control period (1961–1995 from the historically forced part of the simulation until 2000) and a 20-year future period (2081–2100 from the SRES A1B forced part of the simulation after 2000) were used, see also Van Pelt et al. (2012). The 20-year future period was chosen because this was the longest common future period for which daily precipitation was available for all GCMs.

Table 1 GCM simulations used in this study
Full size table
Fig. 1
figure 1

The Rhine basin covered by 2°lat by 2.5°lon GCM grid cells. The grey lines represent the 134 HBV sub-basins

Full size image

For the reference years 1961–1995, observations of precipitation and temperature for the Rhine basin were available from the International Commission for the Hydrology of the Rhine basin (CHR). This CHR-OBS dataset (De Wit and Buishand 2007) contains area-averaged daily precipitation and temperature for 134 sub-basins, aligned with the spatial structure of the hydrological Hydrologiska ByrånsVattenbalansavdelning (HBV) model (Bergström and Forsman 1973) of the Rhine basin, see also Fig. 1. For most of the Rhine basin the area-average rainfall of the sub-basins was based on all rainfall data from dense national networks. A newer and longer precipitation data set has become available (Photiadou et al. 2011), but this was not used in the present study because the HBV model was calibrated to the old CHR-OBS dataset. The HBV model is a semi-distributed conceptual model for the entire Rhine basin upstream from Lobith, where the river enters the Netherlands. Daily precipitation and temperature time series are used as input for the HBV model. The model uses temperature to calculate potential evapotranspiration and snow accumulation and -melt.

3 Methodology

3.1 Delta change approach and resampling

An advanced delta change approach was used to transform the daily precipitation and temperature observations in each HBV sub-basin into time series that are representative of future conditions at this scale consistent with the GCM climate change signal. Advanced, means here that the method accounts for the fact that changes in extreme precipitation may be different from changes in the mean. The approach is extensively described in Van Pelt et al. (2012). The transformed precipitation and temperature series were used as input for the HBV model to determine future discharge changes of the Rhine (see Sect. 5). For precipitation the procedure is presented schematically in Fig. 2. First, a non-linear transformation is applied to the aggregated observed 5-day precipitation amounts of the eight GCM grid cells. A 5-day aggregation level was considered in this transformation because flooding in the Rhine basin often occurs after multi-day precipitation (Disse and Engel 2001; Ulbrich and Fink 1995). In a subsequent step the (observed) daily precipitation amounts of the sub-basins are adjusted to the transformed 5-day precipitation amounts at the GCM grid cells.

Fig. 2
figure 2

Schematic overview of the advanced delta change approach. The upper panels represent the observed 5-day precipitation at the GCM grid level and the simulated 5-day precipitation for the control and future climates. The observed precipitation at the sub-basin level was aggregated to the GCM grid cells by taking a weighted average over the sub-basins. The middle panel shows the equations for the transformation of the 5-day precipitation sums at the GCM grid cell scale (with transformation coefficients a, b and \({{\bar{E}_{90}^{\text{F}} } \mathord{\left/ {\vphantom {{\bar{E}_{90}^{\text{F}} } {\bar{E}_{90}^{\text{C}} }}} \right. \kern-0pt} {\bar{E}_{90}^{\text{C}} }}\)). The lower panels demonstrate the transformation of the daily precipitation of the sub-basins using a change factor R, which is the ratio of the transformed (P*) and the observed (P) 5-day precipitation amount at the GCM grid cells (for each sub-basin within a grid cell and for each day within a 5-day period the sub-basin precipitation is multiplied with the same R-value). This figure is based on Fig. 1 in Van Pelt et al. (2012)

Full size image

The transformation of the 5-day precipitation amounts can be mathematically represented as (see also Leander and Buishand 2007):

$$P^{*} = aP^{b } \quad {\text{for}} \; P \le P_{90}^{\text{O}}$$
(1)
$$P^{*} = {{\bar{E}_{90}^{\text{F}} } \mathord{\left/ {\vphantom {{\bar{E}_{90}^{\text{F}} } {\bar{E}_{90}^{\text{C}} }}} \right. \kern-0pt} {\bar{E}_{90}^{\text{C}} }} \cdot \left( {P - P_{90}^{\text{O}} } \right) + a\left( {P_{90}^{\text{O}} } \right)^{b}\quad{\text{for}}\,P > P_{90}^{\text{O}}$$
(2)

where P and P* respectively, represent the observed and transformed (i.e. the future) precipitation over a 5-day interval at a GCM grid cell, \(P_{90}^{\text{O}}\) denotes the 90 % quantile of the observed 5-day precipitation amounts, and a and b are the transformation coefficients (a, b > 0). These coefficients were derived from the changes in the 60 and 90 % quantiles of the (non-overlapping) 5-day precipitation sums in the GCM simulation, between the periods 1961–1995 and 2081–2100. The 60 % quantile was chosen because this quantile is generally closer to the mean than the median due to the positive skewness of the precipitation distribution. The 90 % quantile is in the lower tail of the distribution of the seasonal maximum 5-day precipitation amounts (Van Pelt et al. 2012). For instance, in a 3-month season, this quantile is exceeded with probability 0.85 assuming independence between the 5-day precipitation amounts (Van Pelt et al. 2012). For 5-day precipitation amounts exceeding \(P_{90}^{\text{O}}\) a separate Eq. (2) was used to better reproduce the changes in the upper tail of the precipitation distribution. It scales the excess \(E_{90} = P - P_{90}^{\text{O}}\) with the change in the mean excess \(\left( {{{\bar{E}_{90}^{\text{F}} } \mathord{\left/ {\vphantom {{\bar{E}_{90}^{\text{F}} } {\bar{E}_{90}^{\text{C}} }}} \right. \kern-0pt} {\bar{E}_{90}^{\text{C}} }}} \right)\) in the GCM simulation. This scaling changes the slope of an extreme-value plot of 5-day precipitation maxima but not its curvature, see Van Pelt et al. (2012) for details. The mean excesses for the control and future periods were obtained as:

$$\bar{E}_{90}^{\text{C}} = \mathop \sum \nolimits E_{90}^{\text{C}} /n^{\text{C}} \quad {\text{and}}\quad \bar{E}_{90}^{\text{F}} = \mathop \sum \nolimits E_{90}^{\text{F}} /n^{\text{F}}$$
(3)

where n C and n F are the number of 5-day periods in which the 90 % quantile is exceeded in the control and future period, respectively. As an alternative, the scaling of the excesses E 90 could be based on regional peaks-over-threshold modeling. For peaks-over-threshold modeling of rainfall data, it is often assumed that the excesses follow a Generalized Pareto (GP) distribution (Roth et al. 2012; Weiss and Bernardara 2013). Equation 2 is then obtained if the shape parameter of this distribution remains unchanged in the future climate (Kallache et al. 2011; Van Pelt et al. 2012). Apart from assuming a GP distribution for the excesses, a regional peaks-over-threshold model also makes assumptions about the spatial variation of the distribution parameters. These assumptions need not to be fulfilled for the application of Eq. 2, but they are useful for an accurate description of the changes in the distribution of extreme rainfall. Regional extreme-value modeling is the most straightforward approach if the interest is in the changes in precipitation extremes only.

The 60 and 90 % quantiles and the mean excesses were determined for each calendar month separately. To reduce sampling variability (due to the finite length of the available time series) of the parameters in Eqs. 1 and 2, these quantities were temporally smoothed using a 3-month moving average with a weight of ½ placed on the calendar month of interest and weights of ¼ on the preceding and following calendar months. Sampling variability was reduced further by assuming that b and the scaling factor \({{\bar{E}_{90}^{\text{F}} } \mathord{\left/ {\vphantom {{\bar{E}_{90}^{\text{F}} } {\bar{E}_{90}^{\text{C}} }}} \right. \kern-0pt} {\bar{E}_{90}^{\text{C}} }}\) of the excesses are constant over the eight GCM grid cells covering the Rhine basin. The medians of the temporally smoothed estimates of these parameters over the eight grid cells for each calendar month were used in Eqs. 1 and 2.

After the transformation of the 5-day precipitation at the GCM grid cells, the daily precipitation amounts for the sub-basins are scaled with a change factor R = P*/P (see Fig. 2, lower panels). This change factor is calculated for each subsequent 5-day period and each grid cell.

Temperature time series representative of the future climate were also obtained by using a delta change method. The observed daily temperature was transformed for each sub-basin taking into account the changes in the mean and standard deviation of the daily temperatures from the GCM simulation (Shabalova et al. 2003):

$$T^{*} = \frac{{\sigma^{\text{F}} }}{{\sigma^{\text{C}} }}\left( {T - \bar{T}^{\text{O}} } \right) + \bar{T}^{\text{O}} + \bar{T}^{\text{F}} - \bar{T}^{\text{C}}$$
(4)

where T and T* respectively, represent the observed and transformed daily temperature. \(\bar{T}^{\text{O}}\) is the mean of the observed daily temperature. \(\bar{T}^{\text{F}}\), \(\sigma^{\text{F}}\) are the mean and standard deviation of the daily temperature in the future climate and \(\bar{T}^{\text{C}}\), \(\sigma^{\text{C}}\) are the mean and standard deviation of the daily temperature in the control climate. As for precipitation the mean and standard deviation were determined for each calendar month and each grid cell, but in this case no spatial smoothing was applied. The standard deviation was temporally smoothed using the same 3-month moving average as for the quantiles and mean excesses of the 5-day precipitation sums.

To estimate return levels of 10-day precipitation and discharge associated with long return periods (up to 1,000 years, which means that the level is exceeded each year with a probability of 1/1,000) a 3,000-year synthetic time series of daily precipitation and temperature was available for each HBV sub-basin from the work of Beersma (2002). To create these time series, multi-site daily values of precipitation and temperature were sampled simultaneously with replacement from the 35-year records of historical observations. For each simulation step the 10 nearest neighbours of the last generated day were searched within a moving window of 61 days. The moving window is used to reproduce the effect of seasonal variation. Details of the resampling procedure are given in Buishand and Brandsma (2001) and Wójcik et al. (2000). The 3,000-year synthetic time series were subsequently transformed to future time series using the delta change methods for precipitation and temperature as described above and used as input for the hydrological model.

3.2 Analysis of variance

An analysis of variance (ANOVA) model was formulated to disentangle the contributions from model uncertainty, i.e. systematic differences between GCMs, and internal climate variability. For each GCM experiment the simulated change x i can be represented as (Räisänen 2001):

$$x_{i} = M + \delta_{i} + \eta_{i }$$
(5)

where M is the mean change between the current and future climate in an infinite number of GCM simulations under the same forcing scenario, δ i is a model-related random deviation and η i is a random deviation associated with internal climate variability in experiment i. In this study x i refers to the relative change in the mean, the 90 % quantile (P 90) or the mean excess (\(\bar{E}_{90}\)) of the 90 % quantile. The changes in P 90 and \(\bar{E}_{90}\) determine the change in extremes. It is assumed that the deviations δ i and η i have both zero means and that they are uncorrelated, both within each experiment, i.e. E(δ i η i ) = 0, and between experiments.

For an ensemble of k GCM experiments, the total interexperiment variance V is defined as:

$$V = \frac{1}{k - 1} \mathop \sum \limits_{i = 1}^{k} \left( {x_{i} - \bar{x}} \right)^{2}$$
(6)

where \(\bar{x}\) is the average of the \(x_{i}^{\prime} {\rm s}\). For the ANOVA model in Eq. 5, it can be shown that the mean of V is given by:

$${\text{E}}\left( V \right) = D + \frac{1}{k}\mathop \sum \limits_{i = 1}^{k} N_{i}$$
(7)

where D = var (δ i ) = E (δ 2 i ) and N i  = var (η i ) = E (η 2 i ). This corresponds to Eq. 8 in Räisänen (2001) with his variable e 2 equal to (k − 1)V/k. Thus, the variance due to internal climate variability N i varies from model to model, while the systematic differences between the GCMs are expressed by the variance D.

The variance component due to model uncertainty (D) can be estimated from the total interexperiment variance (V), if we know the variances due to internal climate variability (N i ) for each GCM experiment. To determine N i , each GCM should be run multiple times with different initial conditions. This would result in an ensemble similar to ESSENCE for each GCM. However, such ensembles were not available for the GCMs used in this study. Therefore, we used a bootstrap method to estimate the variances due to internal climate variability N i . This leads to the following estimate of the second term of the right hand side of Eq. 7:

$$\widehat{N} = \frac{1}{k}\mathop \sum \limits_{i = 1}^{k} \widehat{N}_{i}$$
(8)

where \(\widehat{N}_{i}\) is the bootstrap estimate of \(N_{i}\).

The bootstrap samples were generated by taking random samples with replacement from the 35-year time series for the control period and the 20-year time series for the future period. The new 35-year and 20-year bootstrap time series for each GCM simulation were created separately by selecting individual years from either the control or the future period. This process was repeated B = 1,000 times, so we get B estimates for the changes in the mean, P 90 and\(\bar{E}_{90}\). \(\widehat{N}_{i}\) was taken as the sample variance of these estimates. A balanced bootstrap was chosen, which means that taken over all bootstrap samples the individual years are equally represented. The bootstrap assumes independence between years and absence of systematic trends within the control and future GCM periods. Räisänen (2001) demonstrates that for precipitation the estimate of internal climate variability is not much affected by these assumptions. The bootstrap was also applied to the members of the ESSENCE ensemble. For the latter, the estimated variances from the bootstrap should correspond to the total interexperiment variance because the model related deviation δ i equals zero in this ensemble by definition.

4 Results

4.1 Influence of internal climate variability on changes in the mean

In Fig. 3 the changes in the basin-average precipitation and temperature in the CMIP3 ensemble projected for the end of the 21st century are compared with those in the ESSENCE ensemble. The figure shows that for the summer half-year (April–September) the spread of the relative changes in precipitation in the CMIP3 ensemble is much larger than the spread in the ESSENCE ensemble. Assuming a similar internal climate variability within the ESSENCE and the CMIP3 ensembles, the model uncertainty would be considerably larger than the uncertainty due to the internal climate variability. For the winter half-year (October–March), the spread between the changes in the CMIP3 simulations is more similar to that in the ESSENCE ensemble, which suggests that in winter the influence of internal climate variability on the relative change in precipitation is large. For temperature, the spread between the different CMIP3 GCM simulations is much larger than the spread within the ESSENCE ensemble both for the summer and winter halves of the year and the whole year. This confirms the results of other studies that for temperature the contribution of internal climate variability to the total interexperiment variance (V) is smaller than for precipitation (Murphy et al. 2004; Räisänen and Palmer 2001). The remaining part of this study only focuses on changes in winter half-year precipitation, as these changes are most important for flood risk in the river Rhine basin.

Fig. 3
figure 3

Relative change in average precipitation (a) and absolute change in average temperature (b) in the Rhine basin for the summer and winter halves of the year and the whole year. The changes refer to changes between the control (1961–1995) and future (2081–2100) climates

Full size image

A good indicator for the spread of the relative changes between GCMs due to internal climate variability is the coefficient of variation (CV) of the precipitation sums in the winter half-year, i.e. the ratio of their interannual standard deviation (σ) to their mean. Assuming independence between years, the variance of the relative change x can be approximated as (Stuart and Ord 1987):

$$\text{var}\ x \approx \left( {\frac{{\mu^{F} }}{{\mu^{C} }}} \right)^{2} \left[ {\frac{{\left( {CV^{C} } \right)^{2} }}{{n^{C} }} + \frac{{\left( {CV^{F} } \right)^{2} }}{{n^{F} }}} \right]$$
(9)

where μ C and μ F are the means for the control (C) and future (F) periods, CV C and CV F are the CVs for the control (C) and future (F) periods, and n C and n F are the number of years in the control (C) and future (F) periods.

Table 2 shows that the CV for the CMIP3 ensemble is smaller than for the ESSENCE ensemble, both for the control and the future period. According to Eq. 9, the spread of the relative changes in the average winter precipitation should then be smaller for the CMIP3 ensemble than for the ESSENCE ensemble if these changes were purely due to internal climate variability. This is not the case in Fig. 3 owing to systematic differences between the GCMs in the CMIP3 ensemble. These systematic differences are larger than the figure suggests because of the smaller internal variability in the CMIP3 ensemble.

Table 2 Coefficient of variation (CV) and standard deviation (σ) of the winter half-year precipitation sums for the control (C) and future (F) periods
Full size table

Table 2 also shows that the CV and interannual standard deviation of the simulated precipitation for the control period are smaller than those of observed precipitation. This underestimation may partly be due to the fact that our GCM grid cells cover a somewhat larger area than the CHR-OBS dataset. The underestimation of the internal climate variability in the ESSENCE and CMIP3 ensembles implies that the spread of the relative changes in the basin-average winter precipitation in both ensembles (as shown in Fig. 3) is probably too small.

Table 2 further compares the total interexperiment variance (V) with the estimate of variance due to internal climate variability (\(\widehat{N}\)), the latter of which was obtained using a bootstrap method (Sect. 3.2). For the CMIP3 ensemble, \(\widehat{N}\) is about 30 % of the total variance. For the 17 members of the ESSENCE ensemble the total variance and the estimate of the variance due to the internal climate variability are roughly equal, as expected. The small difference between \(\widehat{N}\) and V for the ESSENCE ensemble can be related to sampling uncertainty as expressed by their standard errors. For V the relative standard error is about 30 % and the standard error is larger than the difference between \(\widehat{N}\) and V. The standard error of V is based on 1,000 bootstrap samples of the relative changes of the ESSENCE members. The standard error (se) of \(\widehat{N}\) was obtained from:

$$se^{2} = \frac{1}{k(k - 1)}\mathop \sum \limits_{i = 1}^{k} \left( {\widehat{N}_{i} - \widehat{N}} \right)^{2}$$
(10)

where i refers to the individual ESSENCE members.

4.2 Influence of internal climate variability on changes in extreme multi-day precipitation

Figure 4 shows that the spread of the relative changes in P 90 is larger for the CMIP3 ensemble than for the ESSENCE ensemble, which suggests some influence of systematic differences between the GCMs in the CMIP3 ensemble, i.e. model uncertainty. The CMIP3 and ESSENCE ensembles show similar spread of the relative changes in \(\bar{E}_{90}\), but these changes are larger for the CMIP3 ensemble. Both ensembles show an increase in P 90 and \(\bar{E}_{90}\) for the end of this century. For the ESSENCE ensemble the mean change in \(\bar{E}_{90}\)is comparable with that in P 90 (and that in the average winter precipitation). The relative changes in \(\bar{E}_{90}\) in the CMIP3 ensemble are larger than those in P 90 and in the average winter precipitation.

Fig. 4
figure 4

The relative changes in P 90 and mean excess \(\bar{E}_{90}\) for the winter half-year. The results refer to the changes between the control (1961–1995) and future (2081–2100) climates

Full size image

Table 3 shows that for the change in P 90 the internal climate variability (\(\widehat{N}\)) explains about 55 % of the interexperiment variance V of the CMIP3 ensemble. This is more than what was found for the average winter precipitation (about 30 %) in Sect. 4.1. The spread of the relative changes of \(\bar{E}_{90}\) can be fully explained by the internal climate variability. This does not imply that there is no model uncertainty in the changes of this extreme-value characteristic. Table 3 shows that the variance due to natural variability is much larger for the changes in \(\bar{E}_{90}\) than for the changes in the average winter precipitation and P 90. This may not be the case for the variance due to model uncertainty. The contribution of the model uncertainty to the total uncertainty is then smaller for the changes in \(\bar{E}_{90}\) and this contribution can then be masked due to sampling variability. The fact that the increase of \(\bar{E}_{90}\) in the CMIP3 ensemble tends to be larger than in the ESSENCE ensemble points at systematic differences between the climate model simulations in the two ensembles. The difference in mean change is about three times its standard deviation due to natural variability. For the ESSENCE ensemble the interexperiment variance (V) for \(\bar{E}_{90}\) corresponds roughly with the variance due to internal climate variability (\(\widehat{N}\)), as was the case for the average winter precipitation, but for P 90, \(\widehat{N}\) is twice as large as V. This is mainly due to the large uncertainty of V, as represented by its standard error. An approximate F-test shows that the differences between \(\widehat{N}\) and V are not significant at the 5 % level. Because of the large standard error of V, the discrimination between model uncertainty and internal climate variability is very inaccurate for an ensemble of 15 climate model simulations. For changes in seasonal mean precipitation, Rowell (2012) found substantial sampling variability in the ratio of the model uncertainty to the total uncertainty by computing this ratio for 1,000 random samples of 17 climate models from a 280-member ensemble.

Table 3 Variance components for the relative change in the average precipitation in the winter half-year (see also Table 2), the 90 % quantile of 5-day precipitation sums (P 90) and the mean excess (\(\bar{E}_{90}\)) for the CMIP3 and ESSENCE ensembles. V denotes the total interexperiment variance as defined in Eq. (5). \(\widehat{N}\) denotes the variance from internal climate variability (with the standard errors in parentheses for the ESSENCE ensemble)
Full size table

In both ensembles the smallest values of \(\widehat{N}\) are found for the 90 % quantile (P 90). The variance of the relative change in a statistic is related to the CVs of the statistic in the control and future climate (for the variances of the relative changes in P 90 and \(\bar{E}_{90}\) a similar expression as Eq. 9 applies). These CVs are shown in Table 4. The CV of P 90 is generally smaller than the CV of the average winter precipitation. The relatively low CV of P 90 is due to the relatively large mean value of this statistic. The excesses \((E_{90} = P - P_{90}^{\text{O}}\)) have a relatively small mean value compared to P 90 and Table 4 shows that the mean excesses have a much larger CV than P 90 and the average winter precipitation. This leads to the relatively large values of \(\widehat{N}\) for the mean excesses in Table 3 and the relatively large spread for the change of the mean excess in Fig. 4. Note further that for P 90 the CVs for the CMIP3 ensemble are comparable to those for the ESSENCE ensemble, in contrast to the CVs for the average winter precipitation.

Table 4 Coefficient of variation (CV) of the average precipitation in the winter half-year, the 90 % quantile of 5-day precipitation sums (P 90) and the mean excess \(\varvec{ }\left( {\bar{E}_{90} } \right)\)
Full size table

5 Future changes in precipitation and discharge for long return periods

The advanced delta change method was applied to resampled 3,000-year synthetic time series of daily precipitation (see also Sect. 3.1). This allowed for an analysis of return levels of extreme precipitation with associated return periods up to 1,000 years for both the CMIP3 and ESSENCE ensemble. In addition, the (transformed) resampled precipitation and temperature time series were used as input for the hydrological HBV model. With the HBV model discharge time series (of 3,000 years) were created for the river Rhine. The 1,250-year return level of the Rhine discharge at Lobith is the safety standard for dikes along the non-tidal part of the river in the Netherlands.

Both for the resampled 3,000-year time series for the control climate and the transformed resampled time series for the future climate, the 10-day maximum precipitation amounts in the winter half-year were determined. Return levels of these maxima are shown in Fig. 5a for return periods from 10 to 1,000 years. For return periods less than 1,000 years the return levels were derived empirically from the ordered sample of the 10-day maxima. For the 1,000-year return level, a distribution was fitted to the 15 largest values using an approach due to Weissman (1978). For all GCM simulations in the ESSENCE and CMIP3 ensembles, the transformation leads to an increase in the return levels. This is in line with the increase in the extreme-value characteristics P 90 and \(\bar{E}_{90}\) of the 5-day precipitation sums, shown in Fig. 4.

Fig. 5
figure 5

a Ranges of the return levels of the future 10-day maximum basin-average precipitation in the winter half-year for four return periods. The results are shown for the transformed resampled observations based on the CMIP3 and ESSENCE ensembles. The grey horizontal line denotes the return levels of the 10-day basin-average precipitation from the resampled observations (i.e. the reference or control climate). b Ranges of the return levels of future annual maximum discharge at Lobith, for the same return periods, based on the transformed resampled observations as input to the hydrological HBV model for the river Rhine

Full size image

Although for each return period the increase in the return level is on average somewhat higher for CMIP3 than for ESSENCE, the spread within these ensembles is roughly similar and resembles the spread of the changes in \(\bar{E}_{90}\). This could have been expected because the changes in the return levels of 10-day maximum precipitation are related to the changes in the upper tail of the distribution of the 5-day precipitation amounts, which strongly depend on the changes in \(\bar{E}_{90}\), in particular for long return periods. It may therefore be assumed that the modelled spread of the return levels in the CMIP3 ensemble can largely be explained by internal climate variability. However, the differences in the mean increase of the return levels in the CMIP3 and ESSENCE ensembles are an indication of systematic differences between climate model simulations. Unfortunately, it is not possible to analyse the results of Fig. 5a in a similar way as was done for the mean, P 90 and \(\bar{E}_{90}\). Bootstrapping of the 3,000-year daily time series would give the variance resulting from the finite length of the resampled time series rather than the finite lengths of the GCM simulations.

In Fig. 5b the annual maximum discharge is shown for the same return periods. The spread between the return levels is also similar for the ESSENCE and CMIP3 ensembles. The results for discharge are comparable to those for precipitation in Fig. 5a, which suggests that the change in the 10-day maximum precipitation in the winter half-year is a good indicator for the changes in high discharge levels at Lobith. Consequently, we may assume that also for extreme discharges a large fraction of the total interexperiment variance in the CMIP3 ensemble can be attributed to internal climate variability.

It should be stressed that the spread of the return levels in Fig. 5 relates to differences in climate model simulations. This spread does not represent the total uncertainty. Uncertainties associated with the resampling procedure, time series transformation and hydrological modeling are not taken into account. These uncertainties are large since long return periods are of interest. The total uncertainty will therefore be much larger than the ranges in Fig. 5 suggest.

6 Discussion and conclusions

In this paper we studied the spread of the projected changes of mean and extreme precipitation for the end of the 21st century over the river Rhine basin in the CMIP3 and ESSENCE ensembles. An ANOVA model was formulated to distinguish between the contributions from model uncertainty and internal climate variability. The results were discussed for average winter half-year precipitation and two extreme-value characteristics, P 90 and \(\bar{E}_{90}\). These characteristics were important parameters in an advanced delta change method that was applied to obtain representative time series of future climate conditions at the local scale. Resampled 3,000-year time series were used to estimate return levels of extreme 10-day precipitation in the winter half-year for return periods up to 1,000 years. This long time series was used as input for the hydrological HBV model, to allow for the estimation of the return levels of extreme river discharges.

Most GCM simulations showed an increase in the average winter precipitation over the Rhine basin for the end of the 21st century. It was found that the variability of the simulated precipitation in the winter half-year was smaller than that of the observed winter precipitation in both the ESSENCE and the CMIP3 ensembles. All GCMs in the CMIP3 and ESSENCE ensembles showed an increase in the extreme-value characteristics P 90 and \(\bar{E}_{90}\). This resulted in an increase in the return levels of the 10-day precipitation amounts for return periods from 10 to 1,000 years. The river discharge showed a similar change for this range of periods.

For the Rhine basin it is shown that about 30 % of the variance of the relative changes in the basin-average winter precipitation as projected by the CMIP3 ensemble can be explained by internal climate variability. This result is comparable to what was found in other studies (Hawkins and Sutton 2011; Räisänen 2001). Our results for the changes in winter precipitation maxima over the Rhine basin suggest that the contribution of internal climate variability increases towards more extreme precipitation. The variance of the relative changes in the mean excess \(\bar{E}_{90}\)in the CMIP3 ensemble could be totally explained by internal climate variability. This suggests that the spread in the estimated return levels of extreme 10-day precipitation and river discharges for the end of the 21st century is mainly due to internal climate variability rather than systematic differences between climate models. On the other hand, the significant difference between the mean increase of the return levels in the CMIP3 and ESSENCE ensembles is an indication of differences between climate models. The latter is more in line with the results of Brekke and Barsugli (2013) for the changes in the return levels of 1-day annual maximum precipitation in the US at the end of the 21st century for 9 members of the CMIP3 ensemble where model uncertainty was a significant source of uncertainty. It should be noted, however, that 1-day annual maxima usually pertain to the warm season, whereas our study is restricted to precipitation extremes in the cold season.

The large influence of internal climate variability on the changes in extremes is a source of concern for developers of climate change scenarios for impact modelling. Kay et al. (2009) concluded that understanding natural variability is critical in assessing the importance of climate change impacts on hydrology. Because of natural variability, the spread of the changes in an ensemble of climate model simulations generally overestimates the uncertainty of the true human induced climate change signal. A challenging task is to develop climate change scenarios representing only the climate-model and greenhouse-gas emission uncertainties.

Surprisingly, the variance due to internal climate variability turned out to be smaller for the change in P 90 than for the change in the average winter precipitation. This implies in fact that a change in P 90 over the Rhine basin can be easier detected than a change in the long-term mean. Note that this phenomenon may depend on the scale of the region because the effect of spatial pooling on the variance of the change in P 90 may be different from that on the variance of the change in the average winter precipitation. The effect of spatial pooling also depends on geography and the season of interest. Our result is in accordance with Räisänen and Joelsson (2001) who observed that the internal climate variability of the 1-day annual maximum precipitation is reduced stronger at larger spatial scales than the internal climate variability of the annual mean precipitation, and with Hegerl et al. (2004) who, noted that changes in moderately extreme precipitation should be better detectable than changes in the annual mean precipitation because of a greater consistency between the change patterns in these extremes in climate model simulations.

Ultimately, the discrimination between internal climate variability and model uncertainty in this study is quite inaccurate owing to the limited ensemble size. Especially the standard error of the interexperiment variance V turned out to be large. Larger ensembles are needed to distinguish model uncertainty in the changes of extreme precipitation characteristics well from internal climate variability. Ensembles with multiple runs of each GCM could also be useful. Averaging over these runs reduces the influence of internal climate variability. Kendon et al. (2008) and Kew et al. (2011) advocated the use of multiple runs to improve the detection of changes in moderately extreme precipitation.

The influence of internal climate variability can also be reduced by spatial and temporal smoothing. Kendon et al. (2008) point out that spatial smoothing is, however, much less effective than analysing multiple runs. Moreover, in the present study the exponent b and the relative change in \(\bar{E}_{90}\)were taken constant over the Rhine basin. It has further been shown that the effect of temporal smoothing on the spread of the relative changes during the winter half-year is small (Van Pelt et al. 2012). For the estimation of the changes in \(\bar{E}_{90}\) in particular, it may be worthwhile to consider a longer time slice for the future climate than the 20-year period in the present study.

The estimates of the return levels of 10-day precipitation and discharge were based on 3,000-year synthetic time series of daily precipitation and temperature. Despite the length of these time series the uncertainty of extreme events (either 10-day precipitation or river discharge), with return periods as long as 1,000 years, is high owing to the short record of historical observations used as basis for the resampling. Also, the assumption is made, that there is no change in the shape of the right tail of the distribution, which may lead to substantial systematic errors. Another source of uncertainty is the validity of the hydrological model concepts for conditions leading to higher discharges than those observed. The method followed in this study is, however, currently one of the best options available to estimate (changes in) return levels of river discharges associated with long return periods. Even though the uncertainties are high, the knowledge about changes in extremes is very relevant for adaptation measures of our safety system, which is designed to withstand long return period events.