Dynamics of the coupled human–climate system resulting from closed-loop control of solar geoengineering

Abstract

If solar radiation management (SRM) were ever implemented, feedback of the observed climate state might be used to adjust the radiative forcing of SRM in order to compensate for uncertainty in either the forcing or the climate response. Feedback might also compensate for unexpected changes in the system, e.g. a nonlinear change in climate sensitivity. However, in addition to the intended response to greenhouse-gas induced changes, the use of feedback would also result in a geoengineering response to natural climate variability. We use a box-diffusion dynamic model of the climate system to understand how changing the properties of the feedback control affect the emergent dynamics of this coupled human–climate system, and evaluate these predictions using the HadCM3L general circulation model. In particular, some amplification of natural variability is unavoidable; any time delay (e.g., to average out natural variability, or due to decision-making) exacerbates this amplification, with oscillatory behavior possible if there is a desire for rapid correction (high feedback gain). This is a challenge for policy as a delayed response is needed for decision making. Conversely, the need for feedback to compensate for uncertainty, combined with a desire to avoid excessive amplification of natural variability, results in a limit on how rapidly SRM could respond to changes in the observed state of the climate system.

1 Introduction

Solar radiation management (SRM) has been suggested as a possible tool to offset some or all of the radiative forcing due to anthropogenic greenhouse gases (GHG) and thus reduce the risks of associated climatic changes (Keith 2000). A negative radiative forcing could be introduced, for example, using stratospheric aerosols (Crutzen 2006) or marine cloud brightening (Latham 1990).

A common objection to geoengineering is that we do not understand the climate system well enough to contemplate meddling with it. For example, Prinn asks: “How can you engineer a system whose behaviour you don’t understand?” ¹ We agree that ignorance about the climate system is a good reason for caution about both geoengineering and continued emissions of carbon dioxide. It is not true, however, that we cannot control a system we don’t understand. Feedback enables us to control systems that we only partially understand and imperfectly measure. From heart pacemakers to aircraft, feedback is routinely used in spite of imperfect models. Control theory provides tools to guide the development of such control systems. Here we apply control theory to the challenge of using solar goengineering to limit climate change despite ignorance about the climate system.

If there were no uncertainty in either the radiative forcing or the climate response to this forcing, the desired level of solar reduction could be determined without any observations of the climate state. However, there will always be uncertainty in the radiative forcing due to GHG, the radiative forcing resulting from the application of SRM, and in the different (and possibly nonlinear) climate responses to each of these. As a result, predetermining the required amount of solar reduction based on a model will not, in general, result in the desired outcome. Instead, the SRM forcing could be adjusted to compensate for these uncertainties, e.g., in response to the difference between the observed and some target climate state. This introduces a new, intentional anthropogenic feedback process into the climate system, creating a coupled human–climate system with new dynamics (as in Jarvis et al. 2009). Indeed, even if this feedback wasn’t explicitly planned as part of the implementation strategy, a prolonged deviation from any agreed upon target climate state could lead to a desire to adjust the amount of solar reduction. We avoid here any discussion of what governance process might be required to determine a target climate state, and focus only on the technical question of how to maintain such a desired target in the presence of uncertainty. While feedback of other climate variables might also be used, we focus here on managing the global mean temperature. Both the approach and the issues raised are generally applicable.

This use of feedback for control has been proposed in Jarvis and Leedal (2012) as a modeling aid in geoengineering simulations; Jarvis and Leedal (2012) also introduce the idea that feedback would be useful in SRM implementation to manage the associated deep uncertainties. Here we use simulations to illustrate the role that feedback might play in SRM implementation, and describe the effects of feedback as a function of control parameters. We consider a standard “Proportional-Integral” (PI) control algorithm where the amount of solar reduction depends on both the difference between the actual and desired global mean temperature and the integral of this error over time; the latter term ensures that the desired temperature is maintained in steady state despite uncertainty (shown below in Sect. 3). In addition to exploring how the dynamic behaviour depends on these proportional and integral control actions (determined by their respective gains), we also consider the effect of time delay. For example, a plausible strategy might be to average the climate observations over the previous N years to adjust the strength of solar geoengineering. In addition to filtering (smoothing) the observations, this averaging introduces time delay between the observation and the feedback response; any additional time required for decision making would result in further time delay.

A fundamental result from control theory involves the “waterbed effect”, where improving the ability of the feedback-control to compensate for variation in one frequency range (e.g., to maintain a target temperature despite time-varying GHG forcing) will always result in an increased response to any disturbance or variability at other frequencies. This trade-off is evident here in the amplification of natural variability. In addition to the desired ability to maintain some target despite uncertainty in either the forcing or the response, (1) any intentional feedback will necessarily respond to natural climate variability in addition to the time-varying GHG forcing; not only will this feedback suppress natural variability at low frequencies, but it will amplify the variability at some higher frequencies, and (2) any time delay increases this amplification for given feedback gains (and hence response time), or conversely limits the magnitude of the feedback gains that is allowable while still avoiding excessive amplification or even instability, described in Sect. 4 below. There is thus competition between the objective of steering the climate to the desired target state, and that of avoiding a spurious response to natural climate variability.

The basic concept behind the waterbed limitations is straightforward. The feedback needs to “push” the system in the desired direction, but there is a time lag between applying a radiative forcing and the resulting climate response. As a result, there is always some frequency for which the feedback response to a perturbation will be out-of-phase with the intended response—because a time delay means a frequency-dependent phase shift. This results in the feedback amplifying natural variability at that frequency, with the potential for oscillatory behaviour. The extent of amplification depends on how strongly the feedback responds to any deviation between observed and desired climate states, it also depends on both how strongly and how quickly the climate responds to the imposed radiative forcing. ² The same limitations apply if the phase lag is due to the thermal inertia of the climate system itself, or whatever time delay and lags are introduced through decision-making or from the temporal averaging of observations.

A static analysis would only predict the steady-state behaviour, and would not capture these dynamic (time-dependent) effects. Analysis thus requires a dynamic model that describes the transient climate response to time-varying forcing. Here we use a box-diffusion model (e.g. Lebedoff 1988; Morantine and Watts 1990) to predict the global mean temperature behavior as a function of feedback parameters. Simulations using the HadCM3L fully-coupled AOGCM (Jones 2003) are then used to evaluate whether the results derived using this simple model are sufficient to understand and predict the dynamic behavior resulting from implementing feedback-control of the global mean temperature in a meaningfully complex regime. Note that an accurate model of the climate system is not required for feedback to be effective at regulating the desired variable.

Our HadCM3L simulations involve a simple scenario of initiating SRM in year 2040 with the goal of returning the global mean temperature to 2020 levels. This is sufficient to illustrate both the ability for feedback-control to achieve the desired goal under uncertainty and the inherent trade-off between this objective and the effects on natural variability. However, a more realistic implementation scenario for SRM might begin with a small amplitude testing phase (as in MacMynowski et al. 2011a) followed by a more gradual ramp-up of forcing that allows for the evaluation of unintended consequences. Testing might help improve the best guess of the required SRM radiative forcing, leading to smaller errors that would require feedback compensation.

The dynamic model used for design is discussed in Sect. 2. Section 3 introduces the necessary analysis tools to explore the effects described above as a function of feedback parameters. The predicted behaviour using PI control is illustrated in Sect. 4 using the box-diffusion model. The predictions are evaluated in a more complex regime using HadCM3L simulations in Sect. 5, including an evaluation of regional temperature and precipitation changes, and a brief illustration of managing other variables.

2 Box-diffusion model

Computing the transient response of a linear system to a time-varying input requires a convolution integral in the time domain, but involves only multiplication in the frequency domain; equivalently, the Laplace transform converts a differential equation to an algebraic one; compare Eq. (3) to Eqs. (1–2) below. This property is particularly useful in understanding coupled (linear) systems, so the analysis of feedback here is most straightforward in the frequency-domain. A semi-infinite diffusion model was shown in MacMynowski et al. (2011b) to fit the frequency-dependent response of the global mean temperature in HadCM3L over a wide range of frequencies; this model also fits the transient response of most of the CMIP5 models (Caldeira and Myhrvold 2013).

Here we include a surface layer of fixed heat capacity C to better predict the response at short time-scales. For a radiative forcing F(t), the surface temperature T(t) and deep ocean temperature T _d (z, t) satisfy

$$ C\frac{{\rm d}T}{{\rm d}t}=F-\lambda T+ \beta\left.\frac{\partial T_d}{\partial z}\right|_{{z=0}} $$

(1)

$$ \frac{\partial T_d}{\partial t} = \kappa\frac{\partial^2 T_d}{\partial z^2}, $$

(2)

with boundary condition T _d (0, t) = T(0, t) (taking the top of the deep ocean as z = 0). Here λ describes the natural climate feedback (the change in radiation due to a change in surface temperature), C = cρ H is the surface layer heat capacity per unit area, κ the thermal diffusivity, and β = cρκ for density ρ and specific heat capacity c.

This box-diffusion model can be solved using the Laplace transform (as in Lebedoff 1988, Morantine and Watts 1990, see also Appendix 1) to describe the temperature anomaly T(s) resulting from a radiative forcing perturbation F(s) by the relationship T(s) = G(s)F(s), where s = iω is the Laplace variable, with $i=\sqrt{-1}$, and ω the angular frequency. (We do not distinguish here between variables in the time-domain and in the frequency-domain except by the argument T(t) or T(s) if it is not otherwise clear from context.) This gives

$$ G(s)=\frac{T(s)}{F(s)}=\frac{1}{\lambda+\beta(s/\kappa)^{1/2}+Cs} $$

(3)

G(s) is the ratio of the Laplace transform of the response variable T(s) to the input F(s), and is referred to as the transfer function between them (e.g. Åström and Murray 2008; Li and Jarvis 2009; MacMynowski and Tziperman 2010). Note that G(s) is simply a complex number for any ω, with G(0) describing the steady state temperature response to a step change in radiative forcing, in this case 1/λ. The magnitude |G(s)| gives the response magnitude at each frequency, and the phase of G(s) gives the phase shift between input (radiative forcing) and output (temperature). Equation (3) is compared with the calculated frequency response from HadCM3L in Fig. 1; the latter was computed by introducing 1 % sinusoidal variations in solar forcing into the model (MacMynowski et al. 2011b). The efficacy of radiative forcing due to solar reductions is less than that due to CO₂ (Hansen et al. 2005); in this model, the radiative forcing from 2 × CO₂ (3.7 W m⁻²; IPCC 2007) is offset by a 2.3 % reduction in solar constant (MacMartin et al. 2013). Using this factor to convert the solar reduction into radiative forcing, then the best fit to the calculated frequency response yields λ = 1.2 W m⁻² K⁻¹,  τ = β ²/(λ ² κ) = 13 years, and C = 3.2 × 10⁶  J m⁻² K⁻¹. Note that the heat capacity C is only the value needed to correct the high-frequency behaviour of the diffusion model and is not intended to represent the heat capacity of the ocean mixed layer; most of the mixed layer contribution is already captured in the estimated parameters of the diffusion model (Watterson 2000). As noted, the transient behaviour of most CMIP5 models is consistent with a semi-infinite diffusion model (i.e., C = 0), indicating that the mixed layer in these models does not behave as a single heat capacity with a single distinct time constant (Caldeira and Myhrvold 2013). There are several models that are exceptions to this behaviour (e.g., Held et al. 2010). Increasing the heat capacity C would increase the phase lag at high frequencies in Fig. 1 and would affect the choice of feedback gains in what follows, but not the general conclusions. While this simple model is tuned to match HadCM3L, we note in Sec. 4 the effect that model mismatch would have.

Fig. 1

Frequency response G(s) of global mean temperature in response to 1 % perturbations in solar forcing calculated for HadCM3L (from MacMynowski et al. 2011b), and least-squares fit to a box-diffusion model. The direct calculation involved simulations with sinusoidal variations in solar forcing, and computing the amplitude and phase of the global mean temperature relative to the forcing at each frequency. Parameters of the best fit to this data are given in the text

Natural climate variability d(s) in the global mean temperature can also be included, so that T(s) = G(s)F(s) + d(s). The power spectrum of natural climate variability is approximately 1/f for frequency f (Fraedrich et al. 2004). The frequency-dependent amplitude spectrum of d(s) is thus similar to the frequency-dependence of Eq. (3) as noted in MacMynowski et al. (2011b). For illustrative purposes herein, a sufficiently good model of the natural climate variability is thus to choose d(s) = G(s)w(s), where w(s) is an uncertain radiative forcing that is approximately white noise on the time-scales of interest here (annual to multi-decadal). The power spectral density of w(s) can be chosen so that the resulting spectrum of d(s) approximately matches that of the natural variability (see Fig. 7). Only the spectrum of natural variability matters here, and not whether this is a realistic description of the mechanism of natural variability.

Time-domain calculations with this model are given in Appendix 1.

3 Feedback overview

A block diagram illustrating the coupled human–climate feedback system is shown in Fig. 2. The dynamic system characterized by the transfer function G(s) describes how the global mean temperature (or more generally, the variable(s) being controlled) responds to imposed radiative forcing F, including the radiative forcing associated with anthropogenic climate change F _d , the intentional solar geoengineering component F _s , and the perturbations w responsible for natural variability. The solar geoengineering forcing might in general include a best estimate $\hat{F}$ of the radiative forcing required to maintain T = T _ref in the presence of F _d , as well as the component F _c that corrects for errors in this estimate based on feedback of the observed climate state. The dynamic system K(s) describes how the forcing F _c is adjusted in response to observed changes; this is the added feedback-control correction.

Fig. 2

Block diagram of geoengineering feedback, assuming for simplicity that radiative forcing from SRM (F _s ) and from other sources (F _d ) simply add. The radiative forcing “noise” w can be included to simulate natural climate variability. The climate system is represented by the transfer function G(s), generating temperature anomaly T in response to radiative forcing. The system K(s) computes the feedback in response to the deviation between observed and desired temperature. Also included is a “feedforward” of the best estimate of the SRM radiative forcing $\hat{F}$ required to maintain T = T _ref in the presence of the disturbance F _d

With no feedback (K(s) = 0), the temperature is obtained from the inverse Laplace transform of $T(s)=G(s)(F_d(s)+\hat{F}(s)+w(s))$. If the dynamics G(s) and the radiative forcing F _d (s) are known, then $\hat{F}(s)$ can be chosen so that T only differs from T _ref by natural variability, although implementing this would also require certainty in the efficacy of solar geoengineering. Given uncertainty, then using the best estimate of $\hat{F}$ will yield some error that could be corrected with feedback; we define $F_r=F_d+\hat{F}$ as the residual radiative forcing due to imperfect estimation of the “feedforward” term $\hat{F}$; this is the component that we introduce feedback to compensate for. We focus here on the design and effects of the feedback and do not explicitly consider $\hat{F}$ in our simulations; the simulations are thus representative of the feedback action required to correct F _r rather than F _d . A more accurate estimate $\hat{F}$ would lead to smaller requirements on the feedback to correct the residual errors, and a correspondingly smaller change in the characteristics of natural variability.

With feedback, the response is obtained from Fig. 2 by solving the following two equations, which are algebraic in the frequency domain:

$$ T=G(s)(F_d+\hat{F}+F_c+w) $$

(4)

$$ F_c = -K(s)(T-T_{\rm ref}) $$

(5)

This gives the temperature error T _e relative to the desired temperature (T _e  = T − T _ref), in terms of the residual radiative forcing F _r as

$$ T_e=\frac{G(s)}{1+G(s)K(s)}(F_r+w)=G_{fb}(s)(F_r+w) $$

(6)

Note that this is identical to what one would derive statically (Hansen et al. 1984; Roe and Baker 2007), but here G(s) and K(s) represent the dynamics, so that this can be used to solve for the transient as well as the steady-state behaviour. Furthermore, K(s) is chosen and represents a human feedback system (see below) as opposed to being a property of the climate system.

Now consider the effect of feedback K(s). First, note that if the feedback is chosen proportional to the temperature error, F _c  = k _p T _e or K(s) = k _p , then from (3),

$$ G_{fb}(s)=\frac{1}{(\lambda+k_p)+\beta(s/\kappa)^{1/2}+Cs} $$

(7)

Since 1/λ is the equilibrium climate response without feedback, proportional feedback can be understood as simply reducing the climate sensitivity, i.e., reducing the equilibrium climate temperature response to an increase in GHG radiative forcing F _d . However, there will still be some steady-state temperature error for $\hat{F}\neq F_d$. One way to see this is to note that maintaining non-zero F _c in this case requires non-zero T _e  = F _c /k _p , that is, with only proportional feedback, forcing is only applied if there is an error.

Next, consider also including a term proportional to the integral of the error since the feedback was initiated; the reason for including this will be clear shortly. This integral term results in a feedback response to any persistent error:

$$ F_c(t)=k_p T_e(t)+k_i \int\limits_{t_0}^t T_e(\tau)\hbox{d}\tau $$

(8)

(In our simulations, we implement this feedback with decisions at discrete time intervals,

$$ F_c(n)=k_p T_e(n)+k_i\sum\limits_{j=0}^n T_e(j) $$

(9)

with calculations given in Appendix 2, but we present the analysis here in continuous-time for simplicity.) Taking the Laplace transform of (8) yields

$$ K(s)=k_p+k_i/s $$

(10)

Substitution into (6) then gives

$$ G_{fb}(s)=\frac{s}{k_i+s(\lambda+k_p+\beta(s/\kappa)^{1/2}+Cs)} $$

(11)

Recalling that G _fb (0) is the equilibrium climate response, integral feedback results in zero error in steady state (G _fb (0) = 0) provided that the resulting system is stable. It is still useful to include some amount of proportional control in addition to integral control, as described in the next section. In general, a proportional-integral-derivative (PID) structure could be useful, however the derivative term is unnecessary here as will be discussed below.

The ratio of the response G _fb (s) with feedback to the response T _e  = G(s)(F _r  + w) without feedback is defined as the sensitivity function:

$$ S(s)=\frac{G_{fb}(s)}{G(s)}=\frac{1}{1+G(s)K(s)} $$

(12)

(This terminology, from engineering, is not to be confused with the “climate sensitivity” used to mean the equilibrium response to 2 × CO₂). If the product G(s)K(s) is small at some frequency, then the sensitivity function will be close to unity (feedback has no effect), while if |G(s)K(s)| is large, then the sensitivity will be small (feedback has a significant effect). If at some frequency the magnitude |S(s)| > 1, then the feedback amplifies the climate response that would have been present without feedback at that frequency. A key result from control theory (e.g., Theorem 11.1 in Åström and Murray 2008) is that for any real system (as opposed to idealized cases with the ability to instantaneously respond to observed changes), there will always be some frequency region where |S(i ω)| > 1 (amplification). Furthermore, it can be shown that

$$ \int\limits_0^\infty \log|S(i\omega)|d\omega=0 $$

(13)

This describes a “waterbed effect”: attenuation in some frequency band must result in amplification in some other frequency band (see Fig. 5; the area corresponding to amplification is at least as large as that corresponding to attenuation.)

Compensating for uncertainty or changes in anthropogenic climate change can be equivalently stated as attenuating the effects of radiative forcing. That is, at low frequencies, we need |S| < 1 to have smaller temperature error T _e than there was without the use of feedback; see Eq. (6). A more rapid response to differences between desired and actual temperature corresponds to a larger frequency range over which there is attenuation. However, the feedback acts equally on both the anthropogenic radiative forcing for which it is intended to compensate, and on the source of natural climate variability; also in Eq. (6). Thus Eq. (13) describes a fundamental trade-off between (1) how rapidly the feedback can react to any change in radiative forcing, the climate response to forcing, or goals (described by the frequency range over which there is attenuation, so log|S| < 0), and (2) how much amplification there must be of natural variability in some higher-frequency range (i.e., log|S| > 0). This is true for any feedback law; next, we describe this more concretely for proportional-integral (PI) control.

This constraint holds for feedback of any variable. If solar geoengineering were adjusted to maintain some other variable, then in general G(s) would differ, and thus the appropriate choice of K(s) would differ, but the trade-off would remain; see Sect. 5.

4 Dependence on feedback parameters

The Proportional-Integral (PI) control law is given in Eq. (8). More complicated controllers are possible; e.g., Jarvis and Leedal (2012) also include learning the uncertain system dynamics from the observed response in order to choose a better feedforward $\hat{F}$; this gradually improved estimate reduces the requirements on feedback to correct for errors. However, the most important effects of using feedback can be illustrated using PI control.

In addition to considering how the dynamic behaviour (the response time and the effect on natural variability) depend on the feedback gains k _p and k _i , we also consider the effect of time delay. Time delay might result from the time required to reach a decision on altering the radiative forcing of solar geoengineering, or from averaging the climate response over time with the intent of minimizing the response to natural climate variability. For example, a decision to adjust the SRM forcing level could be made every N years, based on the average global mean temperature over the previous N years. This means that by the time a decision is made, the information used is on average N/2 years old, and on average, the last decision was made N/2 years ago, leading to a delay of N years. The Laplace transform of a pure time delay of N years is e ^−Ns, which has unit magnitude but introduces phase lag of ω N radians at angular frequency ω = 2π f. The N-year averaging does not have the same effect on the behaviour as a pure time delay would; the corresponding Laplace transform is given in Appendix 2. However the effects are similar, so the phase lag of a time delay can be used to understand the effect of the averaging, and also, the averaging is representative of the effects that would arise due to time delays from decision-making or in implementation.

First, note that the magnitude of the sensitivity function |S(s)| in Eq. (12) is the inverse of the distance between the product G(s)K(s) and the point −1. The product G(s)K(s) is plotted in Figs. 3 and 4 for the “high gain” case in Table 1. The shaded region in Fig. 3 corresponds to |S(s)| ≥ 1, that is, to amplification of natural variability.

Fig. 3

Sensitivity analysis: the product G(s)K(s) is plotted in the complex plane for representative choices of feedback gains (“high” gain case in Table 1). The shaded region indicates sensitivity function larger than one (amplification of natural variability), while any part of GK outside the shaded region corresponds to attenuation. Amplification increases closer to the −1 point, which represents the stability boundary. The parametric curves GK are plotted with zero time delay (unachievable in practice, but would allow no amplification at any frequency), with decisions every N = 1 year based on average temperature in the previous year, and with decisions every N = 2 years based on the average temperature over previous 2 years. Frequency is not explicit in this plot; the ‘+’ marks correspond to periods of 4, 8, and 12 years; see also Figs. 4 and 5

Fig. 4

G(s)K(s) plotted as a function of frequency for N = 1 with magnitude in the upper panel and phase in the lower panel, for the “high” gain case in Table 1 (solid), and for the same integral gain but with zero proportional gain (dashed). For frequencies much less than 1/10 (years)⁻¹, the magnitude |GK| ≫ 1 and we expect significant attenuation (see Fig. 5); this frequency is determined primarily by the choice of integral gain (compare with response times in Fig. 8). When the magnitude |GK| ≃ 1 (indicated by filled circle), then the phase of the complex number GK is important in determining the response, with significant amplification if the phase is close to −180° (see Fig. 3). For a given choice of integral gain, then introducing some non-zero proportional gain improves the phase at frequencies where |GK| ≃ 1 (the frequency where |GK| = 1 is indicated with dashed lines in each case)

Table 1 Feedback gains used in generating Figs. 3, 4, 5 and 6, and in simulations with HadCM3L in Sect. 5

From Fig. 3, introducing time delay shifts the curves clockwise (greater phase of the complex number GK). For a constant choice of feedback gains, this increases the range of frequencies over which the feedback amplifies variability, increases the maximum amplification, and for a sufficiently large delay, will result in instability. This amplification is evident in Fig. 5, where the sensitivity function S(i ω) is plotted as a function of frequency, both for the “high gain” cases in Fig. 3 and the “low gain” cases in Table 1. Reducing feedback gains reduces the peak amplification, but results in slower response time to any changes.

Fig. 5

Sensitivity function computed for the gains in Table 1; the “high gain” cases (solid lines) correspond to those in Fig. 3. Note the “waterbed” effect. The peak amplitude of 1.6 for the case with 1-year averaging (solid blue line) is also illustrated in Fig. 3

Figure 6 shows the corresponding response in the time domain. The high gain case with N = 2 results in substantial overshoot in response to any sudden change, followed by a damped oscillation. In steady-state conditions, the peak at a 6–7 years period in Fig. 5 results in significant amplification of natural variability, evident in Fig. 6b. The corresponding power spectra of variability with and without feedback are shown in Fig. 7 from a 1,000 year time simulation; the ratio of these indeed matches the predicted sensitivity function.

Fig. 6

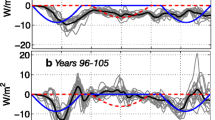
Time-domain response with feedback, illustrating convergence of temperature to some target value (left) and the amplification of natural variability in certain frequency ranges (right). a An idealized scenario where the feedback is turned on in year zero to return the temperature to the target value, with $\hat{F}=0$ for simplicity. Natural variability is removed for clarity of illustration. Higher gain (solid lines) results in faster response, but with the potential for overshoot, particularly for longer time delay of N = 2 (red). For N = 2, forcing is updated every 2 years (indicated by square). b The high-gain case for N = 2, now including natural variability. Background variability at a 6–7  years period is amplified. Gains are given in Table 1

Fig. 7

Power spectrum of temperature variability with (green) and without feedback (blue), calculated using the box-diffusion model with imposed white noise radiative forcing to represent natural variability. The actual variability of the global mean temperature is shown in red for comparison with the no-feedback case here, estimated from detrended annual anomalies using NOAA NCDC data from 1880–2011. The power spectral density of the white noise [w(s) in Eq. (4)] is chosen so that the model variability reasonably approximates the actual spectrum. Only the high-gain case with N = 1 is shown; lower gain results in less amplification. The ratio of the spectrum with and without feedback is the sensitivity function shown in Fig. 5

From Fig. 6a, higher gain results in more rapid correction of errors between the actual and desired climate state; this implies a faster feedback response to any changes in anthropogenic radiative forcing, any nonlinear change in the climate response to this forcing, or any change in desired target (e.g., if the current target is deemed to be insufficient for some reason). However, from Figs. 6b, or 5, higher gain also results in higher amplification of natural variability. These trade-offs are shown as a function of integral (k _i ) and proportional (k _p ) gains in Fig. 8, for two different choices of averaging time N.

Fig. 8

Contours indicate the dependence of response time (top row, years) and peak amplification (bottom row) as a function of proportional (k _p ) and integral (k _i ) gains, with units as in Table 1. The left pair of panels correspond to making decisions every N = 1 years based on the average temperature over the previous year, the right pair correspond to N = 2. The red (N = 2) and blue (N = 1) squares (“high”) and circles (“low”) correspond to the gains in Table 1, used in Figs. 3, 4, 5 and 6, and in HadCM3L simulations. The peak amplification is the maximum value of the sensitivity function (see e.g. Fig. 5). Response time is defined as the number of years required to reach within 1/e of a target temperature (see e.g. Fig. 6a), giving an indication of how rapidly the feedback can compensate for errors or changes in either the forcing, the climate system, or the goal. The response characteristics are not a simple exponential function of time: for high integral gain, the response oscillates before converging, particularly for N = 2. The shaded region indicates where this overshoot exceeds 1/e, so the time before the system stays within 1/e of the final value exceeds the response time given by the contours

The calculations required to compute Fig. 8 are given in Appendix 2. The peak amplification plotted for each choice of k _i and k _p is the maximum over any frequency of the sensitivity function, as in Fig. 5. We define the response time to be the time it takes (see e.g. Fig. 6a) for the system to reach within 1/e of the target temperature. At high values of the integral gain, particularly for N = 2, there is substantial overshoot, and so the time it takes before the system stays within 1/e of the target temperature can be longer than it would be for smaller integral gain; this region is shaded.

Also note that for any given integral gain, the smallest value of the peak amplification occurs for some non-zero proportional gain. This can be understood from Eq. (10) and Fig. 3. At higher frequencies, the phase of k _p  + k _i /s is less negative than the phase of k _i /s alone, shifting the curves in Fig. 3 away from the point −1 and the shaded region of amplification. The added phase is shown more clearly in Fig. 4. This effect is countered by the increased magnitude of k _p  + k _i /s relative to k _i /s alone; trading off these two effects leads to an optimum value of k _p for any choice of k _i which minimizes peak amplification. Figure 4 can be used to design reasonable values of the proportional and integral feedback control gains (see e.g. Åström and Murray 2008). Note that our choices of proportional gain in Table 1 are roughly those that give the minimum peak amplification for a given response time. Finally, note from Fig. 4 that it is not necessary here to include the derivative term of a PID control structure. Near the frequency where the magnitude |G(s)K(s)| = 1, then G(s) is proportional to s ^−1/2 and with only PI gains, the “slope” of K(s) will be between s ⁻¹ and s ⁰. A large derivative gain would give a slope of s ⁺¹, and the product GK would then be increasing with frequency rather than decreasing. A small derivative gain could be useful to compensate for the more negative slope of G(s) at high frequencies (and corresponding more negative phase) if the surface layer heat capacity C were large.

Figure 8 illustrates the trade-offs between response time and peak amplfication. For example, to keep peak amplification <20 %, the minimum possible response time for any choice of gains is 3.4 years with N = 1, increasing to 6.3 years with N = 2; for 10 % amplification, the fastest response time increases to 6.7 or 11 years for N = 1 or N = 2.

Finally, one further essential aspect to feedback can also be seen from Fig. 8: an indication of how accurately the climate dynamics must be known in order for feedback to be effective. Without feedback, if the climate response to either GHG or solar forcing was uncertain by a factor of two, then applying the best estimate of the required radiative forcing would result in either half or double the desired response. (If both the response to GHG and SRM radiative forcing were uncertain by the same amount, the desired result would still be obtained as long as the radiative forcings were known.) With feedback, an uncertainty in the effectiveness of SRM is equivalent to an uncertainty in the feedback gains, that is, whether G(s) differs by a factor of two or K(s) differs by a factor of two, the product GK will still differ by the same factor of two, leading to the same change in sensitivity, same change in peak amplification, and same change in time constant. For example, a factor of two uncertainty in SRM effectiveness might correspond to having intended to use the “low” feedback gains in Fig. 8, but the behaviour instead being that of the “high” feedback gains. This leads to an uncertainty in the response time, but no change in the steady-state response. This robustness to model uncertainty is an important purpose of using feedback. Note that for a sufficiently large feedback gain, a further increase might lead to instability. However, there is no need to choose gains this large, especially as the peak amplification is quite substantial at much lower gain than that which would lead to instability.

Summarizing the effects of feedback control choices:

• Proportional feedback is equivalent to reducing the climate sensitivity; there will still be steady-state error in response to uncertain radiative forcing even with feedback.

• Including an integral term in the feedback means that, at least in steady-state, the error will be zero (as long as the system remains stable).

• In addition to the desired effect, feedback will respond to natural climate variability, attenuating low frequency variability, but also amplifying variability in some frequency ranges.

• Any time delay exacerbates the amplification of climate variability, as evidenced from Fig. 5.

• Higher integral gain results in both a more rapid response to changes, but also a higher amplification of natural variability.

• For any given integral gain, there is an optimal choice of proportional gain that minimizes this amplification.

• Uncertainty in the climate response is equivalent, in terms of behaviour, to uncertainty in the feedback gains. With appropriately chosen gains, the behaviour with feedback is reasonably robust to uncertainty in the magnitude of the climate response to forcing.

5 HadCM3L simulations

In order to verify that the predictions made above using a simple box-diffusion model of the climate are indeed reflective of what might occur in a more complex climate system, we simulate the effect of the gain choices in Table 1, with a delay of N = 1 and N = 2 years, in the HadCM3L fully coupled atmosphere-ocean general circulation model.

This model has resolution of 3.75° in longitude by 2.5° in latitude in both the atmosphere and ocean, with 19 vertical levels in the atmosphere and 20 in the ocean (Jones 2003). This model has been used for simulating SRM (Lunt et al. 2008), for exploring regional effects of SRM (Ricke et al. 2010), and for optimizing the spatial/temporal distribution of solar reduction in SRM (MacMartin et al. 2013). HadCM3 is a participant in the Geoengineering Model Intercomparison Project (GeoMIP; Kravitz et al. 2011); intercomparisons show HadCM3 achieves similar results to other AOGCMs in simulating geoengineering by reducing the solar constant (Kravitz et al. 2013). Feedback is implemented by (1) simulating 1 year of climate response, (2) computing the corresponding feedback response to this ‘observed’ climate state, externally to the GCM, (3) updating the solar constant, and (4) restarting the GCM simulation for the next year. The actual time it would take for the solar forcing to be changed is not considered here; if geoengineering were implemented using stratospheric aerosols, for example, this might take several months at least, while changes to marine cloud brightening could likely be made much more rapidly.

The model is forced with RCP4.5 concentrations (Meinshausen et al. 2011). Feedback is initiated in year 2040, with the goal of returning the global mean temperature to the same value as in 2020; this introduces an initial step in the desired climate state. We are not arguing for this particular implementation scenario, but simply using this scenario to describe how feedback might be used and what its effects could be.

The global mean temperature response with feedback is shown in Fig. 9, using the same gains chosen for the box-diffusion model (Table 1), and $\hat{F}=0$ for simplicity. In all four cases, the feedback indeed results in convergence of the global mean temperature to the desired value, with the higher gains leading to more rapid convergence. However, as expected from Fig. 6b, with N = 2 and higher gains, this coupled human–climate system oscillates about the desired reference temperature, with colder periods resulting in a desire for less solar reduction, but by the time that reduction is in effect, the temperature is too warm, resulting in a desire for more solar reduction, and so forth. The temperature response to this variation is larger over land than over oceans as shown in Fig. 10 (see also Sutton et al. 2007; MacMynowski et al. 2011b); other climate variables also respond to this time-varying solar reduction.

Fig. 9

Simulation results from HadCM3L for two different choices of feedback gains (higher gain for upper plots, lower gain for lower plots), and for N = 1 (left) and N = 2

Fig. 10

Temperature pattern associated with the near-oscillatory variability in Figs. 9b and 11b. A composite map is created by averaging the temperature distribution during years where the oscillation reaches its maximum temperatures, and a similar composite map created for years of minimum temperature; the difference between these is plotted. The dominant temperature response to this frequency of solar forcing is over land

The HadCM3L simulations were continued until 2500 to provide a longer time-record for assessing the change in climate variability. The sensitivity function (ratio of amplitude spectrum with feedback to that without) corresponding to the same four cases are shown in Fig. 11, along with the predictions made using the box-diffusion model in Fig. 5. In all cases, despite the added complexity, the dynamic behaviour of the coupled human–climate feedback system in HadCM3L is well captured by the predictions made using the simple box-diffusion model. The feedback-control allows the target global mean temperature to be reached without requiring any knowledge of the GHG radiative forcing, the relative efficacy of solar reductions, nor details of the climate model beyond the box-diffusion model that was used to choose reasonable values for the feedback gains.

Fig. 11

Sensitivity function computed from HadCM3L simulation results and compared with predictions (red) for the same gain cases as in Fig. 9. The power spectrum of global mean temperature is computed both without SRM and with feedback regulation of SRM; the sensitivity is the ratio of the amplitude spectra

Figure 12 illustrates that using solar reductions to maintain the global mean temperature in the presence of greenhouse gas forcing also reduces regional temperature anomalies, as expected from previous studies (e.g., Govindasamy and Caldeira 2000; Moreno-Cruz et al. 2011). The root-mean-square (rms) difference between the 2080–2100 average temperature and the 2020 target value (averaging years 2010–2030) is 0.4 °C with the solar reduction, compared to 1.6 °C without. The rms difference in precipitation over land relative to the 2020 target also decreases when the solar reduction is adjusted to maintain global mean temperature, although the reductions are more modest (from 0.14 to 0.08 m/year; a 40 % decrease). These temperature and precipitation residuals are not associated with the use of feedback, but result from the fact that spatially-uniform solar reductions do not yield the same pattern of climate change as greenhouse-gases. A non-uniform solar reduction could reduce these residuals (MacMartin et al. 2013).

Fig. 12

Regional temperature (left, °C) and precipitation (right, m/year) averaged over years 2080–2100 relative to the average over 2010–2030, without solar geoengineering (top row) and with geoengineering that uses feedback to maintain the global mean temperature at 2020 levels (bottom row). The temperature change is non-zero everywhere despite the global mean change being small (0.06 °C), however the temperature changes are significantly smaller compared to those without geoengineering. Solar reductions are less effective at compensating the precipitation changes that result from increased greenhouse gas concentrations

Feedback could also be used to manage variables other than the global mean temperature. Figure 13 shows an example using feedback of land-averaged precipitation. This is not intended to be a realistic target, but it illustrates that higher variability does not limit the use of feedback. Both the spectrum of natural variability and the transfer function G(s) have only a weak dependence on frequency for this variable (MacMynowski et al. 2011a, b). The phase lag from G(s) is thus small, and choosing only integral control ensures that the total phase of the product GK remains near −90°, and the curve GK remains far from the point −1 (see Fig. 3). The remaining analysis is similar to feedback-control of temperature: the sensitivity function can be estimated, and has characteristics similar to Fig. 5, including the amplification of natural variability in some frequency range, and the “waterbed” effect where increasing the rejection in some part of the frequency band results in increased amplification at some other frequencies. The solar reduction computed by the feedback algorithm depends on both F _r (the “signal”) and w (the “noise”). Because the signal-to-noise ratio is lower for this variable than for temperature, either there will be larger variability in the desired solar reduction, or lower gains will be required, resulting in slower compensation of changes. As Fig. 13 shows, it is possible to maintain the average value of a “noisy” variable like precipitation without introducing comparable variations in the desired solar reduction. The high inter-annual variability evident in the top panel of Fig. 13 is averaged by the integral action of the feedback-controller.

Fig. 13

Using feedback starting in 2040 to return land-average precipitation to its 2020 value in HadCM3L. The upper plot shows the precipitation with and without solar reduction, the lower plot shows the corresponding solar reduction determined by the feedback algorithm

6 Conclusions

Some form of solar geoengineering may eventually be considered as a possible element of a strategy to minimize climate change risks. The amount of solar reduction in any solar geoengineering scheme would need to be adjusted in response to the observed climate in order to meet any specific objective. Even if feedback was not explicitly planned as part of the implementation strategy, some feedback would be almost inevitable as the implementation of SRM is inherently sequential—there is an implicit repeated decision to be made about the level of replenishment of the SRM forcing, and this decision will unavoidably be influenced by the climate response.

This feedback would compensate for inevitable uncertainty in the climate system dynamics including equilibrium climate sensitivity, the radiative forcing due to greenhouse gases, and the radiative forcing due to the application of SRM. However, in addition to this desired effect, this feedback would also react to natural climate variability, attenuating it at low frequencies, but amplifying it at higher frequencies. This attenuation/amplification is unavoidable, with the peak amplification depending on the choice of gains, and exacerbated by any time delay introduced into the feedback implementation. The frequency of peak amplification depends on the dynamics of the climate response, the time delay, and the choices of feedback gains (e.g., the peak is at a 5–10 year period for the models and range of parameter choices simulated here). The effect that these changes in natural variability might have on humans or ecosystems is unknown, but policy regimes would want to minimize such effects, at the very least to avoid introducing unnecessary solar reductions.

The amplification of natural variability can be minimized by first choosing the best guess for the level of solar reduction required to achieve the desired climate response (thus minimizing the compensation required by feedback), and second, by minimizing any time delay between changes in the climate and the corresponding feedback response. While possibly counter-intuitive, the amplification of natural variability is minimized not by averaging over longer time periods before making a decision, but by adjusting the solar reduction more often: the desired averaging is already incorporated within the integral control of the feedback algorithm, and additional averaging only increases the delay between observing and responding to climate changes. This result highlights the policy challenges of SRM as the narrow technical requirements for effective feedback control may be incompatible with political requirements for a stable decision-making process that is able to gain legitimacy, as such a process may require substantial time delay.

The effect of changing the feedback-control gains by a factor of two is to change both the rate of convergence and the degree of amplification of natural variability. However, for appropriately chosen gains, the system will still converge to the desired target state. A consequence of this is that one could be significantly wrong about the dynamics of the system and still achieve the desired result; that is, the use of SRM need not require a good model of the climate if feedback is used to manage the amount of solar reduction.

We have used feedback of the global mean temperature to illustrate the dynamic effects introduced by using feedback. All of these conclusions would apply regardless of what variable was being controlled, although there may be smaller signal to noise ratio and larger model uncertainty associated with some variables such as precipitation. Controlling the global mean temperature also does not give a spatially-uniform temperature response. Multiple objectives, including regional goals, might be simultaneously maintained by adjusting the spatial and/or temporal distribution of solar reduction as in MacMartin et al. (2013); this would lead to a multivariable control structure.

More complex feedback algorithms may be appropriate. An adaptive algorithm as in Jarvis and Leedal (2012) could better estimate model parameters to adjust $\hat{F}$ and minimize the need for feedback (i.e., by reducing the uncertainty). Model predictive (or receding-horizon) control could adjust forcing levels using a more complicated model including any known nonlinear effects as well as the linear dynamics considered here, including predictions of future emissions, and including constraints on solar reduction or its rate of change. While these algorithms might improve the compensation of anthropogenic climate change, the fundamental constraints described here will still hold. Acting on the observed state with any form of control enables one to partially overcome the effects of uncertainty, but at the cost of amplifying variability.

Appendices

Appendix 1: Time-domain calculations with box-diffusion model

Equations (1–2) can be solved using the Laplace transform. From (2), the temperature in the deep ocean satisfies

$$ T_d(s,z)=M(s)e^{-\sqrt{s/\kappa}z} $$

(14)

for some function M(s), where s is the Laplace variable. Subtituting this into the Laplace transform of (1) and solving for M yields (3).

From Laplace transform tables, the response of a semi-infinite diffusion model (Eq. (3) with C = 0) to a unit step change in radiative forcing at t = 0 is

$$ g_{sd}(t)=\frac{1}{\lambda}\left(1-e^{t/\tau}\hbox{erfc}(\sqrt{t/\tau})\right) $$

(15)

where erfc denotes the complementary error function. With the surface layer included, the step response can be obtained by first factoring G(s) in Eq. (3) as

$$ G(s)=\frac{1/\xi}{\sqrt{s}+b}-\frac{1/\xi}{\sqrt{s}+a} $$

(16)

similar to the derivation in Lebedoff (1988) or Morantine and Watts (1990), where we introduce

$$ \xi=\sqrt{\beta^2/\kappa-4C\lambda}=\lambda\sqrt{\tau-4C/\lambda} $$

(17)

and $a,b=(\beta/\sqrt{\kappa}\pm\xi)/(2C)$ satisfying (aξ)⁻¹ − (bξ)⁻¹ = λ ⁻¹. As in (15), the step response is then

$$ g_{bd}(t)=1/\lambda-1/(b\xi)e^{b^2t}\hbox{erfc} (b\sqrt{t})+1/(a\xi)e^{a^2t}\hbox{erfc}(a\sqrt{t}) $$

(18)

For 4C ≪ λ τ as here, then a ²≃ λ ² τ/C ² and b ²≃ 1/τ, and the first two terms in Eq. (18) are approximately the same as the step response of the semi-infinite diffusion model in Eq. (15), while the final term provides a correction for small t/τ. In calculating this final term, note that for $a\sqrt{t}\gg 1$ then

$$ e^{a^2t}\hbox{erfc}(a\sqrt{t})\simeq \frac{(2/\sqrt{\pi})}{(a\sqrt{t}+\sqrt{a^2t+2})} $$

(19)

The simulations here consider only the average temperature over each year. For semi-infinite diffusion, the average temperature in the nth year after a step change in radiative forcing is

$$ \int\limits_{t=n-1}^{t=n}g_{sd}(t)dt= \frac{1}{\lambda}-\frac{1}{\lambda}\left(2\sqrt{\tau t/\pi}+\tau e^{t/\tau}\hbox{erfc}(\sqrt{t/\tau})\right)_{n-1}^n $$

(20)

$$ =\frac{1}{\lambda}[1-q(\tau^2;n)] $$

(21)

where this defines the function q(a;n). Then for the box-diffusion model,

$$ h(n)=\int\limits_{t=n-1}^{t=n}g_{bd}(t)dt= \frac{1}{\lambda}+\frac{1}{\xi}\left[\frac{q(a;n)}{a}-\frac{q(b;n)}{b}\right] $$

(22)

Simulations here also assume that the radiative forcing is held constant over each year. Given a sequence of forcings f(k) applied during year k, then since the sequence h(n) gives the annual-average temperatures due to a unit step forcing starting at k = 0, the temperature response to the sequence f(k) can be expressed as

$$ T(n)=\sum_{k=1}^{n}h(k)f(n-k)=\sum_{k=0}^{n-1}h(n-k)f(k) $$

(23)

Appendix 2: Frequency-domain calculations

The dynamic response of the climate system with feedback, shown in Figs. 5, 6, 7 and 8, can be understood and an approximate prediction made using G(s) in Eq. (3), K(s) in Eq. (10), and approximating the effects of the N-year averaging with the Laplace transform of a pure time delay, e ^−Ns (obtained from the Laplace transform of $\tilde{y}(t)=y(t-N)$).

However, more accurate calculations of the frequency response requires taking into account that updates of solar forcing are only made at discrete time-intervals, not as a continuous function of time. The feedback system including this detail is shown in Fig. 14, where the block G(s) describes the continuous-time evolution of the climate response to forcing as before, A(s) represents the averaging of the output over the past N years, which is then sampled every N years, and Z(s) is a “zero-order hold” that describes the assumption that the solar reduction computed at every N-year decision point is held constant over the subsequent N years. The discrete-time PI control law

$$ u(k)=k_py(k)+k_i\sum_{n=0}^{n=k}y(n) $$

(24)

is represented by its z-transform, K(z). Analysis details can be found in any discrete-time controls textbook (e.g. Franklin et al. 1997); here we simply provide the required formulae used in computing the results herein.

Fig. 14

Block diagram of geoengineering feedback, as in Fig. 2, but with additional detail required for accurately predicting dynamics. The response of the climate system G(s) is averaged over the previous N years [A(s)], sampled, and the actual feedback law implemented in discrete-time [K(z)] rather than continuous-time. The desired SRM forcing at each discrete decision point in time is assumed to be held constant for the next N years, until the next sample is made. The system within the dashed box is sampled, resulting in aliasing

For frequencies less than the Nyquist frequency (half the sampling rate), then the Laplace transform of the discrete-time control law K(z) can be obtained by setting z = e ^Ns, yielding

$$ K(s)=k_p+k_i\frac{N}{1-e^{-Ns}} $$

(25)

The Laplace transform of the N-year averaging process is

$$ A(s)=\frac{1-e^{-Ns}}{Ns} $$

(26)

which is used in all calculations here, and at frequencies small compared to 1/N, behaves similarly to a pure time delay of N/2 years. Maintaining a constant value of the applied radiative forcing for N years (a zero-order-hold) yields Z(s) = A(s), so that A(s)Z(s) has an effect similar to that of an N-year time delay.

Finally, note that sampling the continuous-time system G _az (s) = A(s)G(s)Z(s) at N-year intervals results in aliasing. That is, temperature variations with frequency f and variations at frequency 1/N − f are indistinguishable in the sampled signal. (There are an infinite sequence of indistinguishable frequencies, but only the first is significant in predicting the response.) Thus at frequencies below the Nyquist frequency, the system G _s (s) within the dashed lines of Fig. 14 is approximately

$$ G_s(i\omega)=G_{az}(i\omega)+G_{az}(2\pi/N-i\omega) $$

(27)

$$ =G_{az}(i\omega)+G_{az}^*(i\omega-2\pi/N) $$

(28)

with $(\cdot)^*$ denoting complex-conjugate. The loop transfer function in Figs. 3 and 4 and the subsequent calculations of the sensitivity function are obtained using K(s) in (25) and G _s (s) in (28), where the latter depends not only on G(s) in (3) but also on A(s) and Z(s) in (26).