1 Introduction

Decisions relating to either mitigation of or adaptation to climate change have to consider both the magnitude and the timescale of the climate response to anthropogenic forcing, in addition to the spatial distribution of this response. Although controversial, consideration of both magnitude and timescale forms an important aspect of the definition and use of global warming potentials (e.g. Caldera and Kasting 1993). Climate sensitivity, S (K), or the global mean surface temperature change for a doubling in atmospheric CO2 concentration, has emerged as a common currency for communicating the potential magnitude of the global temperature response to a given radiative forcing (Cubasch et al. 2001). Due to the significant amount of lag in the climate system, a feature determined in the first instance by the thermal inertia of the oceans (Stouffer 2004), specifying the timescale(s) applicable to any particular definition of S becomes as important as specifying S itself. For example, if the predominant components of S are associated with ‘short’ timescales (say <102 years) then clearly climate change will be an immediate issue, whereas if it were predominantly associated with ‘long’ timescales (say >103 years) then perhaps it is less so.

To date, two timescales have been widely discussed in connection with S. The first is the equilibrium timescale of the climate system to perturbations, τ ∞, which is implicitly associated with the now familiar equilibrium climate sensitivity, S ∞ . The thermal inertia of the oceans alone places a lower limit on τ ∞ of the order of 103 years (e.g. Hoffert et al. 1980; Stouffer and Manabe 1999; Stouffer 2004). The combination of this inertia allied to the generally non-stationary nature of radiative forcing means climate data seldom reflect the equilibrium case, making observation based estimation of S ∞ difficult (Wigley et al. 1997; although see Kuntti and Hegerl 2008). As a result, atmospheric–ocean general circulation model (AOGCM) experiments have been the preferred tool for specifying S ∞ . However, given the computational expense of running these models, allied to the very long runs required for full equilibration (Stouffer and Manabe 1999; Stouffer 2004; see later), S ∞ is invariably estimated either from slab ocean AOGCMs (Stainforth et al. 2005; Danabasoglu and Gent 2009), or the partially equilibrated full AOGCM response using simpler global energy balance models (e.g. Watterson 2000; Raper et al. 2002; Meinshausen et al. 2008). More recently, earth system models of intercomplexity (EMICs) have been specially designed for long-run simulations over millennia such that S ∞ can be obtained directly (e.g. Claussen et al. 2002; Petoukhov et al. 2005; see also Cubasch et al. 2001 Figure 9.24).

Stouffer and Manabe (1999) and Stouffer (2004) report the equilibrium temperature of a full AOGCM run to steady state following both doubling or quadrupling of the atmospheric CO2 boundary condition. Here they show the time taken for various regions of this model to reach a given fraction (70%) of the equilibrium response. Although useful as an approximate measure of τ ∞, the time taken to attain a fixed fraction of a response is only representative of a system timescale when the response is first order (i.e. characterised by one time constant or e-folding time) and the system is subject to a step change in forcing. Given it is highly unlikely climate models can be characterised in this way alternative methods for specifying τ ∞ (and its components) are required.

In addition to the equilibrium characteristics of the climate system, several studies have sort to characterise the transient climate response and its associated sensitivity S (e.g. Hansen et al. 1985; Murphy 1995; Gregory and Forster 2008). It appears from the use of this term that two timescales are applicable to S. The first is the timescale for the equilibration of the atmospheric and land surface energy balance, τ a which is of the order of <100 years, reflecting the low thermal inertia of these elements of the climate system. The second is the equilibration timescale of the ocean mixed layer, τ m , which is of the order of <101 years. This timescale is discussed by Hansen et al. (1985) and in detail by Watts et al. (1994) and later by Dickinson and Schaudt (1998). These studies derive various analytical solutions for 1d global energy balance models (GEBM) in order to point out that, given the distinction between the well-mixed surface ocean layer and the remaining poorly-mixed fraction of the oceans, τ m should be a discrete characteristic of the climate to perturbations in radiative forcing, rightly characterised by a single time constant. Also, because of the low thermal inertia of the atmosphere and the land, allied to the strong coupling of atmospheric and surface temperatures, S relates more closely to τ m than τ a .

Watts et al. (1994) define two further timescales for ocean heat uptake kinetics from the GEBM; the thermocline timescale τ t , which they predicted was of the order 102 years depending on the thickness of the thermocline; and the upwelling timescale τ u , which they predicted was in the range 102–103 years and related to the time taken to balance upwelling and diffusive heat fluxes in the deep ocean. The existence of intermediate timescales in the climate response in the range 101–103 years such as those identified by Watts et al. (1994) could be important in a decision making context because, if expressed with their associated fractional contribution to S ∞ , these might be helpful for communicating the temporal dimension of the climate response in a more meaningful manner than S ∞ alone, given τ ∞ is somewhat off the political radar. More specifically, this would allow the relative importance of different timescales to be weighed in decision making processes so that the appropriate balance between near-term and long-term can be considered (Toth and Mwandosya 2001).

It was clear however, from the analysis of Watts et al. (1994) that, unlike τ m , τ t and τ u were not discrete timescales of the climate response to which fractions of S ∞ could be attributed. Instead, they acted as physical markers on the continuum of timescales associated with the GEBM they analysed. Indeed, Watts et al. (1994) point out that because GEBMs express a continuum of timescale responses, it is not possible to represent this behaviour using discrete timescale metrics such as time constants or e-folding times. This is seen in the analysis of MacKay and Ko (1997) who used an eigenvalue method to summarise the step response of the GEBM of Harvey and Schneider (1985) and found that anywhere between 4 and 20 first order modes with associated time constants provided possible descriptors of the response. Therefore, if one wishes to discuss the timescale of surface temperature in GEBMs then they must be treated as time varying properties dependent on, for example, the evolution of ocean heat feedbacks (Hansen et al. 1985).

The representation of ocean heat dynamics has evolved since the analysis of Watts et al. (1994) in one important aspect. To account for the effects of large-scale ocean circulation such as that associated with meridional overturning circulation (MOC) (and to fit AOGCM responses; Raper et al. 2001; Wigley et al. 2005; Meinshausen et al. 2008), GEBMs explicitly relay a portion of the surface ocean heat directly into the deep ocean upwelling. This apparently simple feature means that these models are no longer pure advection–dispersion systems, but instead are advection–dispersion systems allied to large-scale circulatory feedbacks. Such feedbacks have the potential to significantly redistribute the relationship between S and timescale of these models, not least because there are two quite different oceanic heat uptake mechanisms operating. Indeed, if the circulation rate of heat increased, in the limit this system will to tend toward a well mixed state represented by the single timescale of the equivalent well mixed box ocean. Although large-scale ocean circulation of heat is never parameterised to this extreme, the introduction of oceanic heat circulation into climate models will promote this tendency and hence the emergence of discrete timescale effects; a feature that could facilitate the specification of a partitioning for S ∞ across a limited number of identifiable timescales.

1.1 The timescale–gain relationship of the climate system

Although S is in widespread use in the climate literature it is clearly context specific given it relates to an arbitrary double CO2 forcing scenario. A more reasonable measure of magnitude is the climate system response to unit forcing. This too is often referred to as sensitivity in the climate literature, so to avoid any confusion we have elected to follow the systems literature and refer to this quantity as the gain of the system. If g ∞ is the equilibrium gain of a stable, fully damped climate system H, relating perturbations in radiative forcing ΔQ to global surface temperature ΔT, then S ∞  = g ∞ \( \Updelta Q_{{2 \times{\text{CO}}_{2} }} \) where \( \Updelta Q_{{2 \times{\text{CO}}_{2} }} \) is the radiative forcing associated with doubling in atmospheric CO2. As discussed above, in addition to its equilibrium properties, H will also have a range of transient properties and as a result we are concerned with the partitioning of g ∞ according to the timescales of these transients.

When empirical response functions are used to describe the transient dynamics of AOGCMs it appears the behaviour of H for these high order models can often be captured by the sum of a relatively small number of discrete first order terms, each with an associated time constant τ i and component gain g i. Footnote 1 For example, Hasselmann et al. (1993, 1997) found that the 2×CO2 forcing of ECHAM3 was captured by the sum of just three first order exponential terms whilst Hooss (2001) and Lowe (2003) found that the 4×CO2 forcing of ECHAM3 and HadCM3 were captured by the sum of two first order exponential terms. Grieser and Schönwiese (2001) and Li and Jarvis (2009) re-analysed the same responses and provided additional justification for identifying them to be predominantly third order. However, the significance of these results with respect to providing useful timescales for partitioning g ∞ and hence S ∞ appears to have been overlooked, probably because it is felt that response functions do not reflect meaningful elements within the climate response; a criticism often levelled at the specification of global warming potentials (Enting 2007). However, model reductions such as these are often observed in fluid dynamics where there can be a clustering of the system eigenvalues about a subset of eigenmodes. In avionics for example, this model reduction property is exploited in order to derive robust reduced order models amenable to control design and analysis (e.g. Dowell 1996; Tang et al. 2001). If similar behaviour were observed in global climate models then this would go some way to explaining the success of response function analysis of AOGCMs and might in turn provide a foundation for the partitioning g ∞ and hence S ∞ across an appropriate range timescales.

In this paper, we present an analysis of various climate models which attempts to reveal the composition of H in terms of the relationship between the timescales τ i and their associated component gains g i as expressed in the equilibration of ΔT to ΔQ. To start with, we investigate the relationship between g i and τ i , g(τ), of the simple GEBM discussed in Watts et al. (1994) in order to see whether the introduction of large scale circulation of heat does indeed result in a tendency for discrete timescale effects in the response. We then investigate the relationship g(τ) of an EMIC and two AOGCMs to demonstrate this phenomenon in credible 3-D climate models driven to equilibrium. Because timescale is clearly an important component of this analysis, the AOGCM equilibration runs investigated here are for full, as opposed to slab, ocean models given slab ocean models are clearly designed to omit ocean heat equilibration dynamics.

2 Methods

2.1 Climate models and radiative forcing runs

The preliminary data analyzed here are produced using the 1-D GEBM detailed in appendix A of Eickhout et al. (2004), which is a streamlined version of MAGICC and based on the earlier work of Harvey and Schneider (1985). We have omitted the iterative land component to further streamline the model because this has no bearing on our analysis given its lack of inertia. The surface temperature feedback gain λ is normalised to 1 W m−2 K−1 so that g ∞ = λ −1 = 1 K W−1 m2. The model is forced using a ΔQ = 1 W m−2 step forcing under two different parameterisation scenarios for large scale circulation; π = 0 (no surface ocean heat entering MOC) and π > 0 (surface ocean heat entering MOC). For both simulations, the mixed layer depth d m is 90 m, the effective oceanic diffusivity for heat k is 1 cm2 s−1 and the upwelling rate w is 4 m year−1 (Eickhout et al. 2004). The two responses of ΔT are shown in Fig. 1a.

Fig. 1
figure 1

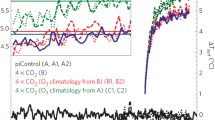
The left hand panels show the global surface temperature response (ΔT) of six climate models along with the associated radiative forcing (ΔQ) (dashed). The right hand panels show the gains g of a range of additive first order responses with time constants τ required to account for the response shown in the left hand panels. The bars are the individual gains, the lines are the cumulative gains

Full size image

In addition to the GEBM we also analyse three further fully equilibrated climate model responses to a ramped forcing input, one EMIC and two AOGCMs. Figure 1c shows 1% compound, 4×CO2 forcing of the University of Victoria Earth System Climate Model (UVicESCM) EMIC (Weaver et al. 2001). \( \Updelta Q_{{2 \times{\text{CO}}_{2} }} \) for this model is given as 4 W m−2 (Weaver et al. 2001). The AOGCMs we investigate are GFDLR15a (Manabe et al. 1991) and CCSM3 (Danabasoglu and Gent 2009). Figure 1c shows the 1% compound, 2×CO2 forcing of CCSM3 (for details see Danabasoglu and Gent 2009). \( \Updelta Q_{{2 \times{\text{CO}}_{2} }} \) for this model is given as 1.928 W m−2 (Danabasoglu and Gent 2009). Figure 1e shows the 1% compound 2×CO2 and 4×CO2 forcings of GFDLR15a (for details see Stouffer and Manabe 1994). \( \Updelta Q_{{2 \times{\text{CO}}_{2} }} \) for this model is assumed to be 3.7 W m−2 (Myhre et al. 1998) in the absence of any direct estimate.

2.2 Timescale-gain analysis

Ideally, we would derive the relationship g(τ) for H analytically from the state equations of the climate model in question. Unfortunately, this is a formidable task to conduct on high order models (Prather 1996; MacKay and Ko 1997) and hence is only practicable for very simple models. Alternatively, traditional frequency domain methods to characterise timescale (frequency)–gain (amplitude) relationships could be exploited here. However, we believe frequency−1 is a somewhat unhelpful characterisation of timescale in this particular application because the simulations being investigated tend not to be periodic. Therefore, we propose the following approach: Firstly, because we know the climate models in question are high order, we assume the dynamic response of a given climate model can be represented by the sum of a very large number (N > 100) of discrete linear first order terms i.e.

$$ \Updelta T\left( t \right) = \sum\limits_{i = 1}^{N} {\left( {a_{i} \Updelta T_{i} \left( {t - \Updelta t} \right) + b_{i} \Updelta Q\left( t \right)} \right)} $$
(1)

where ∆t (years) is the annual sample interval; ∆T i (t) is the temperature response of the ith first order element; g i  = b i /(1 − a i ) (K W−1 m−2) in the gain of the ith first order element; and τ i  = −∆t/ln(a i ) (years) is the time constant of the ith first order element which is taken as the appropriate measure of timescale in this study. Because each first order element is additive, g ∞ = g 1 + g 2 + … + g N ; and for any given timescale the cumulative gain at that timescale is g τ  = g 1  + g 2  + … +g n where n is the increment number of the timescale in question. g τ is analogous to the effective climate sensitivity ∆T/∆Q (Gregory et al. 2002) but defined relative to the timescale τ rather than time.

The values of τ i are pre-specified in 10 year increments spanning the dynamic range of the model response we are investigating. For example, if the model is seen to equilibrate with ∆Q within 3,000 years then τ i  = 0, 10, 20,…, 2,990, 3,000 years. This guarantees coverage of the dynamic response of the model because the 3,000 year time constant will only have expressed some 63% of its response by then. Having specified τ i this gives the corresponding values of a i in Eq. 1; a i  = exp(−1/τ i ). Having specified a i we then attempt to estimate g(τ) and hence b(a) by searching for the values of g i which provide the least squares fit of Eq. 1 to the ∆T(t) of the climate model in question. The 10 year increments for τ i was found to be an adequate trade off between on the one hand capturing the subtleties of g(τ) whilst on the other being coarse enough to make the estimation of g(τ) manageable.

Despite being a constrained linear problem (sum of gains) it is also heavily over parameterised (N > 100). In addition, any large collection of first order responses can always be approximated by a smaller subset of first order responses (see later). Because of this, direct search methods for g(τ), such as gradient search, tend to gravitate on low order approximations and not on the ‘true’ relationship (see e.g. MacKay and Ko 1997). To address this we have elected to use slow cool simulated annealing to search for g(τ) because this method is unable to exploit any covariance between the individual estimates of g i and hence avoids gravitating on unwanted low order approximations. The simulated annealing should also provide an (approximate) estimate of the global optimum solution. g i is also estimated under the constraint g i  > 0; i.e. only positive gains are considered given this is consistent with all the responses investigated here.

The annealing conditions we found to be appropriate were 106 iteration and a cooling rate of 10−6 K per iteration. Because each annealing result is corrupted by random perturbations, the results we present are the average of 100 individual annealing runs. The estimation was done using a vectorized annealing algorithm adapted from Yang et al. (2005) run in Matlab™ 7.0, which on a 2.83 GHz Intel Core 2 Quad machine took approximately 20 h for each 100 member ensemble. These conditions were found to provide reasonable results when recovering pre-specified g(τ) relationships.

3 Results

3.1 GEBM

Figure 1a shows the two responses of the global energy balance model for the π = 0 and π = 0.4 cases. The corresponding relationships for g(τ) are shown in Fig. 1b. For the π = 0 case, g is inversely related to τ as expected for this model (Kreft and Zuber 1978; see also Hansen et al. 1985 Eq. 5). Because of the continuous scaling between g and τ in this case it is clearly inappropriate to consider discrete partitioning of g ∞ with timescale (Watts et al. 1994). However, it is also inappropriate to stress the equal importance of all timescales because the shorter the timescale the greater the contribution to g ∞. Figure 1b also shows how the cumulative gain g τ increases with τ in this response, approaching g ∞ asymptotically. In contrast, for the π = 0.4 case we see that the introduction of the MOC heat uptake mechanism makes the relationship g(τ) distinctly bi-modal with a partitioning of 0.66g ∞ for τ < 250 years and 0.34g ∞ for τ > 250 (see Table 1).

Table 1 Parameter values derived from the time constant gain relationships shown in Fig. 1 (see text for explanation)
Full size table

3.2 UVicESCM EMIC

One could argue that the results shown in Fig. 1 were a product of the simple structure of the global energy balance model and not relevant to ‘more realistic’ climate models with 2-D and 3-D oceanic circulation. Figure 1d shows the results from the same timescale-gain analysis applied to the 4×CO2 forcing temperature response of UVicESCM shown in Fig. 1c. Although there is less separation between the two modes than for the π = 0.4 response of the GEBM, the same bimodal relationship is evident. The resultant partitioning of g ∞ is 0.67g ∞ for τ < 250 years and 0.33g ∞ for τ > 250 years (see Table 1) where g ∞ = 0.9723 K W−1 m2.

3.3 CCSM3v3 AOGCM

Figure 1d also shows the results of the same analysis applied to the instantaneous 2×CO2 forcing of CCSM3v3 shown in Fig. 1c. Again, we see a similar bimodal distribution of g(τ) although in this case there is a very large separation between the two modes. Furthermore, we see that the fast mode of the response is associated with a very limited range of timescales. As a result, the partitioning of g ∞ is 0.64g ∞ for τ < 100 years and 0.34g ∞ for τ > 800 years (see Table 1) where g ∞ = 1.2984 K W−1 m2.

3.4 GFDLR15a AOGCM

Figure 1f shows the same analysis applied to the GFDLR15a 2×CO2 and 4×CO2 forcing experiments in Fig. 1e. Again, both responses are clearly bimodal, although the 4×CO2 response is less so given there is less separation between modes and there remains some residual gain over the intervening timescales. For the 2×CO2 response g ∞ = 1.2000 K W−1 m2 and is partitioned 0.55g ∞ for τ < 100 years and 0.45g ∞ for τ > 500 years (see Table 1). For the 4×CO2 response g ∞ = 1.0704 K W−1 m2 and partitions 0.69g ∞ for τ < 100 years and 0.31g ∞ for τ > 500 years (see Table 1).

4 Discussion and conclusions

From the analysis of the GEBM it is clear that, in the absence of a MOC ocean heat uptake mechanism, a single oceanic heat uptake pathway via widespread diffusion leads to a broad spectrum of timescales being relevant to the equilibration dynamics of surface temperature, with this diffusive mechanism giving rise to an inverse relationship between g i and τ i as expected (Watts et al. 1994). However, the addition of a MOC heat uptake mechanism results in a clear partitioning of climate system gain between relatively fast diffusive ocean heat equilibration and relatively slow MOC ocean heat equilibration. Unlike the diffusive heat uptake dynamics, for circulatory heat uptake g i has a symmetric relationship to τ i . This feature was observed for both the EMIC and AOGCM model responses investigated here and facilitated a partitioning of g ∞ between both ‘fast’ and ‘slow’ timescales. This partitioning was relatively consistent between the various models at approximately 65% fast and 35% slow, the GFDL 2×CO2 response being a notable exception to this.

The relationship g(τ) for the GFDLR15a AOGCM 2×CO2 and 4×CO2 forcing experiments shown in Fig. 1f are markedly different. Therefore, despite producing remarkably linear dynamics for a given forcing, the behaviour of this AOGCM is itself dependent on the pattern and magnitude of the forcing (Stouffer and Manabe 1999). The higher level of forcing is associated with a greater levels of thermohaline shut down in this (and other) AOGCM (Stouffer and Manabe 2003). Thermohaline shut down is equivalent to π and or w reducing over time in the GEBM (Raper et al. 2001) with the consequence that the system tends toward a more diffusive ocean heat uptake regime. This would be enhanced by increased thermal stratification of the oceans associated with the greater warming in the 4×CO2 simulation. The results in Fig. 1f are consistent with this pattern, with the two discrete g(τ) relationships in the 2×CO2 case becoming less distinct in the 4×CO2 case and the relative contribution of the longer timescales to g ∞ falling from 45 to 31% (see Table 1). Figure 7 of Stouffer and Manabe (2003) shows near full recovery of the thermohaline circulation in the 4×CO2 case after approximately 1,500 years of this simulation. This is equivalent to significant non-stationarity in the g(τ) relationship in our linear analysis, highlighting an important limitation of the current approach. This implies that g(τ) depends on the forcing scenario for this model and hence cannot be simply predicted for an arbitrary anthropogenic forcing scenario without predicting the changes in circulation induced by that forcing. The thermohaline circulation is far more stable in the 2×CO2 run (Stouffer and Manabe 2003) hence the greater distinction between the components of g(τ).

If a component of g(τ) is near symmetrical its behaviour is fully summarised by the first moment with respect to τ i and the net gain with respect to g i . Because the MOC component of g(τ) appears to behave in this way for the models in Fig. 1 this would suggest that MOC dynamics can be accurately summarised using the first moment τ c and net gain g c . Why MOC behaves in this way in all the models investigated here is unclear and merits further investigation. The shorter timescale component of g(τ) has two components. First there is the mixed layer dynamic with associated time constant τ m and gain g m (Hansen et al. 1985; Watts et al. 1994). From the results in Fig. 1 we can see that this component is indistinguishable from the diffusive ocean heat uptake dynamics which retain an inverse relationship between g i and τ i for all models. However, MOC heat uptake causes the diffusive response to become concentrated on a limited range of τ i meaning it too may be approximated by a single time constant τ d and net gain g d . These observations explain the results of the various studies that have successfully captured high order climate model dynamics using low order response function frameworks (Hasselmann et al. 1993, 1997; Hooss 2001; Lowe 2003; Grieser and Schönwiese 2001; Li and Jarvis 2009). Clearly this does not apply in the absence of MOC as seen in the results of MacKay and Ko (1997).

Because g ∞ = g m  + g d  + g c , despite being a semi-empirical description of the associated processes, this simple framework provides a reasonable foundation for partitioning of g ∞ according to the mixed layer, diffusive and circulatory heat uptake timescales τ m , τ d and τ c . Although under specific conditions there may be simple box model interpretations for these response functions (Grieser and Schönwiese 2001; Hooss 2001; Li and Jarvis 2009), these properties are better viewed as the emergent dynamic characteristics of these models. However, given τ m and τ d are indistinct from a policy perspective partitioning with respect to τ d and τ c appears appropriate, although for interrogating model behaviour all three components are clearly relevant. The values of g d , g c , τ d and τ c are given in Table 1.

Figure 2 shows the effect of varying both π and k in the GEBM on g c and τ c . From this we see that increasing π and hence MOC heat uptake increases both τ c and g c in this model as expected, with commensurate reductions in g d . τ d remains relatively unaffected. When π < 0.1 then it becomes difficult to differentiate the components of g(τ) as the system tends toward predominately diffusion driven dynamics. Increasing k also results in an increase in g c and commensurate reductions in g d . At first sight this might appear counter intuitive as one might expect g d to increase with diffusive heat uptake. However, k is a component of the feedback gain for surface to ocean heat uptake (Hansen et al. 1985) whilst g d is a component of the closed loop gain for surface temperature and hence g d α k −1. From Fig. 2 we also see that, although increasing both π and k have the same effect of increasing g c , they have opposing effects on the timescale τ c , which increases with π and decreases with k.

Fig. 2
figure 2

The effect of varying the effective diffusivity k and MOC heat uptake efficiency π on the median time constant τ c and net gain g c of the long timescale component of the global energy balance model detailed in Eickhout et al. 2001 and used in this study (see Fig. 1b). g c is expressed relative to the full equilibrium gain g ∞

Full size image

Randall et al. (2007) present a suite of estimates of S ∞ for a family of AOGCMs. These estimates were derived from a GEBM (MAGICCv6) calibrated to each AOGCM (Meinshausen et al. 2008). Although Meinshausen et al. (2008) used a more complex circulation architecture than used here in the GEBM analysis, the parameterisation of MOC in their framework is still likely to result in the same discrete timescale phenomena, not least to capture the effect oceanic circulation in the AOGCMs they wish to emulate (Raper et al. 2001). As a consequence, there must be a corresponding partitioning of their estimates of S ∞ across the timescales τ d and τ c . Somewhat surprisingly π is not calibrated in Meinshausen et al.’s analysis but rather a fixed value of π = 0.2 (albeit with depth dependent entrainment) is assumed. The distribution of S ∞ with timescale is then implicitly calibrated through adjusting k in their analysis. From Fig. 2 we can see that adjusting k is effective in determining the partitioning between g d and g c but at the cost of an inaccurate account of τ c . Because their calibration is explicitly designed to operate using short run (<250 years) AOGCM response data it is not surprising that π is assumed a priori because one would require runs of the order of >1,000 years for such a calibration (see Fig. 2). Given long run, full AOGCM data sets are rare the approach taken by Meinshausen et al. is understandable, although more use of EMICs could be made in this area.

Table S8.1 in Randall et al. (2007) gives the calibrated values of k = 1.8989 ± 1.0201 cm2 s−1 for 19 AOGCM models. Assuming some equivalence between the dynamics of Meinshausen et al.’s and Eickhout et al.’s versions of the MAGICC GEBM and taking π = 0.2 then the results in Table S8.1 of Randall et al. (2007) partition as follows: g d  = 0.51 (±0.23)g ∞ with a timescale τ d  = 20 years; g c  = 0.49 (±0.24)g ∞ with a timescale τ c  = 580 (±30) years. From the preceding arguments we would conclude that an approximate 50:50 partitioning of g ∞ between long and short timescales is probably a reliable summary of Meinshausen et al.’s results. The small sample of models analysed here would indicate this is nearer 60:40 (see Table 1). However, despite the 20 year timescale probably being a fair reflection of τ d , the 580 year estimate of τ c is likely to be much more variable than this for the AOGCM ensamble because fixing π at 0.2 is an unrealistic reflection of the between model variability with respect to MOC (Raper et al. 2001). That said, from Table 1 τ c  = 716 (±155) years, which is not significantly different to the 580 (±30) year estimate derived from Meinshausen et al.’s results, especially if one considers this is one of the most uncertain traits of a climate model response (Baker and Roe 2009).

Whether the split of g ∞ is 50:50 or 60:40 between τ d and τ c it appears that a significant proportion of the equilibrium climate sensitivity in these models is associated with both short (decades) and long (centuries) timescales, highlighting the need to consider both when directing mitigation actions. Similarly, if one is attempting to estimate S ∞ from partially equilibrated data then there is a genuine risk of significant underestimation because, as can be seen from Fig. 1, once the decade timescale response has equilibrated the system could appear to be approaching equilibrium when in fact there is still a significant oceanic heat uptake still in play (Gregory and Forster 2008). This ocean heat equilibration represents a feedback on surface energy balance in these models. For process studies clearly it would be useful to express g(τ) in terms of these feedbacks i.e. the estimation of the corresponding feedback gain–timescale relationship. This need not be restricted to global energy balance. Because low order response functions appear to have been used successfully to capture the dynamics of global carbon cycle models (e.g. Maier-Reimer and Hasselmann 1987; Caldera and Kasting 1993) one might imagine that this analysis could be extended to consider CO2 as well if, like heat, large scale circulation affected the associated g(τ) relationship similarly.

Finally, we have seen that the introduction of circulation into a system like a model ocean causes a shift from the timescale independence of a purely diffusive regime toward the emergence of particular timescales dominating the equilibration dynamics of the partially mixed system. In the limit, increasing the circulation of heat will give rise to a single well mixed system characterised by a single gain and time constant, although clearly oceanic heat distribution is never parameterised in this way. However, we would argue that frameworks for understanding and indeed modelling partially mixed systems could be developed out of this methodology. This would not only have applications in the distribution of heat and CO2 in the global oceans, but would also have wider applications in many areas of environmental systems where imperfect mixing is important.