1 Introduction

The operational global weather forecast models routinely used in the 1980's were well-known to suffer from serious biases in the representation of the northern hemisphere (NH) winter mid-latitude synoptic and planetary atmospheric disturbances (Tibaldi 1986). In particular, it was confirmed in a number of studies that such models on the average featured a large overestimation of the baroclinic synoptic waves (e.g. Sumi and Kanamitsu 1984; Klinker and Capaldo 1986; Siegmund 1995) and a large underestimation of the planetary waves (e.g. Wallace et al. 1983), with biases sometimes of the same size as the average climatology of the observations and analyzed atmospheric fields. In many cases, such forecasting models constitute the base of the atmospheric components presently adopted in up-to-date global climate models (GCMs). Some brief notes on the history of atmospheric modeling can be found at http://www.aip.org/history/sloan/gcm/intro.htm. Such biases may have a relatively minor impact on reanalysis systems, since observations are used to correct the autonomous evolution of the atmospheric models. Instead, since synoptic and planetary waves provide a relevant contribution to the meridional transport of energy and momentum in the mid-latitudes, the physical processes driving such phenomena are sensible ingredients for the characterization of the climate system (Speranza 1983; Peixoto and Oort 1992), and discrepancies may be critical when interpreting the results of unconstrained climate models, possibly reducing the significance of the resulting simulations of past and future climatic conditions.

In view of the above remarks, we compare the performances of 19 GCMs, which contribute to the development of the scientific basis of the IPCC 4th Assessment Report (henceforth, IPCC-4AR), in the description of the NH mid-latitudes winter atmospheric disturbances. We do this by analysing in detail the statistical properties of the modelled 500 hPa geopotential height fields. We analyze the self-consistency of the climate models and we assess their realism by comparing their statistics with those of the NCEP-NCAR and ECMWF global reanalyses, which have been analyzed in detail elsewhere (Dell’Aquila et al. 2005). The 500 hPa geopotential height is a very powerful and widely used proxy for characterizing atmospheric variability on a wide range of spatial and temporal scales (Blackmon 1976). We perform for all models a space-time spectral analysis devised along the way of Hayashi (1971, 1979), which allows the definition of the spectral densities of different types of atmospheric disturbances as well as the separation of the spectral densities describing statistically standing and propagating waves. May (1999) has provided an example of application of Hayashi spectra techniques for the assessment of the performance of climate models. The synoptic travelling waves can be represented as high-frequency high-wavenumber (HFHW) eastward propagating spectral features, characterized by periods of order 2–7 days and by spatial scales of a few thousands of kilometers. These waves can be associated with the release of available energy driven by conventional baroclinic conversion (Blackmon 1976; Speranza 1983; Wallace et al. 1988), so that they are often referred to as baroclinic waves. On the other hand, planetary waves, which interact with orography (Charney and DeVore 1979; Charney and Straus 1980; Buzzi et al. 1984; Benzi et al. 1986) and are catalyzed by the sub-tropical jet (Benzi and Speranza 1989; Ruti et al. 2006), play a dominant role in the low-frequency low-wavenumber (LFLW) spectral region of standing waves, whose characteristic time and space scales are in the interval 10–45 days and 7,000–15,000 km, respectively (Hansen and Sutera 1986).

To support the tantalizing aim of planning practical strategies for the improvement of numerical climate models, the project for climate model diagnostics and intercomparison (PCMDI: http://www. pcmdi.llnl.gov) has gathered the output of climate models produced worldwide into a single server and solicited the provision of simple scalar metrics of model performances. We underline the possibility of distinguishing two distinct, albeit related, kinds of metrics.

The comparison of bulk thermodynamic quantities defining the climate state, such as the tropospheric average temperature, tropospheric average specific humidity, variance of geopotential height, allows the definition of global metrics which may be considered as robust diagnostic tools which are representative of the overall properties of the system. Nevertheless, such an approach does not allow for the disentanglement of the role of each one of the vast range of distinct physical processes. In order to capture the differences in the representation of specific physical processes, it is necessary to use specialized diagnostic tools—that we may call process-oriented metrics—as indexes for model reliability. This approach may be helpful in clarifying the distinction between the performance of the models in reproducing diagnostic and prognostic variables of the atmospheric system.

In the present analysis, we introduce the global and process oriented metrics by defining ad hoc integral measures over different spectral sub-domains of the computed Hayashi spectral densities. The estimate of the total wave variability of the field is chosen as a global scalar metric assessing the overall statistical properties of different types of atmospheric disturbances. The estimate of the variability pertaining to the eastward propagating HFHW waves and to the standing LFLW waves are taken as scalar metrics, accounting for the model representation of specific physical processes and specifically related to the capability in describing the travelling baroclinic waves and planetary waves, respectively. We maintain that by applying this method, the reliability of GCMs in the simulation of some basic climatic processes can be critically addressed.

This paper is organized as follows. In Sect. 2 we describe the datasets and sketch the method employed for analysis. In Sect. 3 we compare the model performances in specific sub-regions of the full space-temporal spectrum; the conclusions are drawn in Sect. 4.

2 Data and methods

The 19 IPCC models considered in this study are listed in Table 1 along with their main features. Although the analysis is applied to an atmospheric variable, we report also a few details about the ocean component in order to stress that the results are representative of the response of a complex system which can not be reduced to the behavior of its single components (Lucarini 2002). Indeed, we will see that for some models (e.g. the GISS model), the same atmosphere over different oceans results in substantially different atmospheric variability. The PCMDI datasets consists of various simulations of different scenarios, including the reconstruction of past and present climate, control runs with fixed atmospheric compositions, and future climate projections. In this work we consider the 20th century simulations, where the time frame considered is 1962–2000. The output data of the INGV-SXG model have been obtained directly from the INGV modeling group, since unfortunately up to September 2006 they have not been available from the PCMDI server. All models attempt the simulation of the climate of this period by setting as time-varying input the observed concentrations of trace gases, such as co2 and ozone.

Table 1 An overview of the IPCC models
Full size table

The IPCC models output for 1962–2000 is compared with observations by considering two major reanalysis datasets: the reanalysis produced by the National Center for Environmental Prediction (NCEP), in collaboration with the National Center for Atmospheric Research (NCAR) (Kistler et al. 2001), and one released by the European Center for Mid-Range Weather Forecast (ECMWF) (Simmons and Gibson 2000).

2.1 Geostrophic approximation and latitudinal averaging

Since the goal of this study is to diagnose the mid-latitude winter atmospheric variability of GCMs, along the lines of Dell’Aquila et al. (2005), we should use the December–January–February (DJF) daily values of geopotential height at 500 hPa data averaged over the latitudinal belt 30°N–75°N, where the bulk of mid-latitude atmospheric waves activity is observed (Blackmon 1976; Speranza 1983).

Unfortunately, this field is not one of the standard daily three dimensional (3D) field outputs of the IPCC models, which comprise only zonal and meridional wind speed, air temperature and specific humidity. In principle, the geopotential height could be rigorously computed from temperature and specific humidity using the hydrostatic relation and the equation of state for air. Such an approach requires, however, knowledge of two time-varying 3D fields, namely temperature and specific humidity. Also the knowledge of boundary terms such as the constant 2D field of surface height and the time-varying 2D field of surface pressure is needed. The latter field is not readily available in the IPCC-4AR dataset, but could be reconstructed with suitable interpolations from the available sea-level pressure data.

In view of the large computational resources needed and the uncertainties on the surface boundary term, we have instead retrieved the 500 hPa meridional wind speed. In fact, in the geostrophic approximation, the meridional wind is related to the zonal gradient of the geopotential height by:

$$ f{\left(\phi\right)}v{\left({p,\phi,\lambda,t} \right)} =\frac{g}{R\cos{\left(\phi\right)}}\frac{\partial z{\left( {p,\phi,\lambda,t} \right)}}{\partial \lambda} $$
(1)

where t is time, p, ϕ, and λ, respectively, the pressure, the latitude and the longitude, \({f{\left( \phi\right)} = 2\Omega\sin{\left(\phi\right)}, v}\) indicates the meridional component of the wind velocity vector, g is the gravity acceleration, R is the radius of the Earth, and z is the geopotential height. This approach requires much smaller computer resources, has a simple model-independent implementation, and is local in the sense that it involves only the relevant p = 500 hPa level. Of course the geostrophic relation is only an order Rossby number (about 0.05–0.10 in our case) approximation, but is well suited for the mid-latitudes (Peixoto and Oort 1992; Holton 1992), where we restrict our analysis. Finally, since, geostrophy justifies the possibility of extracting information about the dynamics from the geopotential height field, such an approach is consistent with the goal of this study.

We can then obtain the following relation between the longitudinal derivative of the zonally averaged geopotential height and the meridional velocity (Peixoto and Oort 1992):

$$ \frac{{\partial{\left\langle{z{\left({p,\phi,\lambda,t} \right)}} \right\rangle}^{{\phi_{2}}}_{{\phi_{1}}}}}{{\partial \lambda}} = \frac{R}{g}{\left\langle{f{\left(\phi\right)}v{\left( {p,\phi,\lambda,t} \right)}\cos{\left(\phi\right)}} \right\rangle}^{{\phi_{2}}}_{{\phi_{1}}} $$
(2)

where the area-weighted latitudinal average of the generic function ψ(p,ϕ,λ,t ) is defined as follows:

$$ {\left\langle {\psi {\left({p,\phi,\lambda,t} \right)}} \right\rangle}^{{\phi _{2}}}_{{\phi _{1}}} = \frac{{{\int\limits_{\phi _{1}}^{\phi _{2}} {\psi {\left({p,\phi,\lambda,t} \right)}\cos {\left(\phi \right)}{\rm d}\phi}}}} {{{\int\limits_{\phi _{1}}^{\phi _{2}} {\cos {\left(\phi \right)}{\rm d}\phi}}}} $$
(3)

We rename the function \({{\left\langle{z{\left({p,\phi,\lambda,t} \right)}} \right\rangle}^{{\phi_{2}}}_{{\phi_{1}}}}\) as Z(p, λ, t ) and the function \({R/g{\left\langle{f{\left( \phi\right)}v{\left({p,\phi,\lambda,t} \right)}\cos{\left(\phi\right)}} \right\rangle}^{{\phi_{2}}}_{{\phi_{1}}}}\) as V(p, λ, t ). We then have:

$$ \frac{{\partial Z{\left({p,\lambda,t} \right)}}}{{\partial \lambda}} = V{\left({p,\lambda,t} \right)}, $$
(4)

which constitutes the baseline of the later described spectral approach.

2.2 Hayashi spectra

The variability of a 1D + 1D (space-time) field in terms of waves of different periods and zonal wavenumbers can be effectively described by means of the space-time Fourier decomposition introduced by Hayashi (1971, 1979). Straightforward space-time decomposition will not distinguish between standing and travelling waves: a standing wave will give two spectral peaks corresponding to travelling waves moving eastward and westward at the same speed and with the same phase. The problem can only be circumvented by making assumptions regarding the nature of the wave. One approach relies on assuming complete statistical coherence between the eastward and westward components of standing waves and on attributing the incoherent part of the spectra to real travelling waves (Fraedrich and Bottger 1978; Hayashi 1979). By computing the cross-spectra and the coherence of the signal, the method allows for separating statistically the propagating and the standing components of the atmospheric waves. We then adopt a very similar procedure to that described in Dell’Aquila et al. (2005) to compute the Hayashi spectra H n a (k j , ω m ), where the index n refers to the year; the subscript a can take the values of T, S, E, W, corresponding to the total (T), standing (S), eastward propagating (E), and westward propagating (W) components of the spectrum; (k j  = 2πj, ω m  = 2πm/τ) represent the discrete set of wavelengths and frequencies over which the spectrum is computed, and τ = 90d is the length of the winter. We emphasize that customarily, in our terms, Hayashi spectra are represented by plotting the quantity k j ω m  2π/τ H n a (k j ,ω m ), so that equal geometrical areas represent equal variance in log–log plots. With this definition, the Hayashi spectra presented in this paper are expressed in m2, as done in Blackmon (1976) and Speranza (1983), and can be compared to those given in Dell’Aquila et al. (2005) after a multiplication by 1/8 × 86400 s.

By considering the basic properties of transformation of the Fourier series with respect to the derivation, we have the following relations between the Hayashi spectra of the function Z(p,λ,t ) and of the function V(p,λ,t ):

$$ \left.H_{a} {\left({k_{j}, \omega_{m}} \right)} \right|_{Z}= k^{2}_{j} H_{a} {\left({k_{j}, \omega_{m}} \right)}|_{V}. $$
(5)

Therefore, in this work, for each dataset, we first compute the Hayashi space-time spectra of the quantity \({V{\left({p,\lambda,t} \right)} =R/g{\left\langle {f{\left(\phi \right)} v{\left({p,\phi,\lambda,t} \right)} \cos {\left(\phi \right)}} \right\rangle}^{{\phi _{2}}}_{{\phi _{1}}} }\) with p =  500 hPa, φ1 and φ2 set to the grid-points closest to 30°N and 75°N, respectively, and then obtain the Hayashi spectra of the corresponding latitudinally averaged geopotential height by using Eq.  5.

In order to evaluate the model performances in different spectral sub domains, we introduce the following integral quantity:

$$ E^{n}_{a} {\left(\Omega \right)} = {\sum\limits_{m = m_{1}, j = j_{1}}^{m = m_{2}, j = j_{2}} {H_{a}^{n} {\left({k_{j}, \omega _{m}} \right)}}}, $$
(6)

where a = T,S,E,W, n indicates the winter; the integration extremes, m 1,2 and j 1,2, determine the spectral region of interest, with \({\Omega={\left[ {\omega _{{m_{1}}}, \omega _{{m_{2}}}} \right]} \times {\left[ {k_{{j_{1}}}, k_{{j_{2}}}} \right]}.}\) The quantity E n a (Ω) introduced in Eq. 6 represents the portion of variance of the spectrum associated with a given subdomain Ω and with a given winter n and is expressed in units of m 2. The averaging process defined in Eq. 6 overcomes the well-known instability of the direct Fourier transform, in particular in describing small scale spectral features. Moreover, the intercomparison of the statistical properties of quantities such as those defined in Eq. 6 obtained for various models allow us to test the models agreement for the waves occurring on the subdomain Ω. Following basic statistical arguments, we estimate the average intra-seasonal atmospheric variability in the spectral subdomain Ω as:

$$ \bar{E}_{a} {\left(\Omega \right)} = \frac{1} {N}{\sum\limits_{n = 1}^N {E^{n}_{a} {\left(\Omega \right)}}}, $$
(7)

where N is the number of years in the averaging process. The interannual variability of the signal E n t (Ω) is described in terms of its standard deviation:

$$ \sigma _{{E_{a} {\left(\Omega \right)}}} = {\sqrt {\frac{1} {{N - 1}}{\sum\limits_{n = 1}^N {{\left({E^{n}_{a} {\left(\Omega \right)} -\bar{E}_{a} {\left(\Omega \right)}} \right)}^{2}}}}}. $$
(8)

The two quantities \({\bar{E}_{a}{\left(\Omega\right)}}\) and \({\sigma_{E_{a}} {\left(\Omega\right)}}\) characterize the climatology of the atmospheric waves occurring in the spectral subdomain Ω. If, for a given Ω, the confidence interval of two models, defined e.g. by \({{\left[ {\bar{E}_{a} {\left(\Omega \right)} - 2\sigma _{{E_{a} {\left(\Omega \right)}}} ,\ifmmode\expandafter\bar\else\expandafter\=\fi{E}_{a} {\left(\Omega \right)} + 2\sigma _{{E_{a} {\left(\Omega \right)}}}} \right]} }\) do not overlap, we can say that the two time series of the corresponding waves are not statistically consistent.

It is possible to test the reliability of the Hayashi spectra of the reconstructed geopotential height and to estimate the essentially model-independent biases introduced by the geostrophic approximation by including in this study the analysis of the variability of the readily available 500 hPa geopotential height of the NCEP-NCAR and ECMWF reanalyses, thoroughly studied in Dell’Aquila et al. (2005).

All computations are implemented in a MATLAB® routine available at http://www. clima.casaccia.enea.it/staff/calmanti/ipcc_hayashi_v.m.

3 Results

The space-time spectra are computed for each of the 39 winters included in our datasets spanning the time frame 1962–2000. Figure 1a–d shows the various components of the 39-winters averages of the spectra computed in each DJF period from the geostrophically reconstructed 500 hPa geopotential height for the NCEP reanalysis dataset averaged over the latitudinal band 30°N–75°N. Figure 1a shows the total power spectrum; Fig. 1b shows the power spectrum related to standing waves; Fig. 1c shows the power spectrum related to eastward propagating waves; Fig. 1d shows the spectrum of the westward propagating waves. The average spectrum for the eastward propagating waves has a sloping lobe which is the possible signature of a dispersion relation ω = ω(k) defining the kinematic properties of the— mainly—baroclinic waves. Note that the spectral width of the lobe is mainly related to the fact that we actually observe waves that are characterized by a life-cycle including growth and decay besides simple propagation. We will deal elsewhere with a better spectral characterization of this type of signal. In contrast, the average spectrum of westward propagating variance, mainly due to long and low-frequency waves, does not feature a similarly clean and legible structure, suggesting that specific phenomena with well-defined propagation properties, such as the Branstator–Kushnir waves (Branstator 1987; Kushnir 1987; Branstator and Held 1995), may not be distinguished by this method.

Fig. 1
figure 1

Climatological average over 39 winters of Hayashi spectra for the geostrophically reconstructed 500 hPa geopotential height (relative to the latitudinal belt 30°N–75°N) from NCEP data. The Hayashi spectra have been obtained multiplying the spectra by \({k\omega \cdot \tau \mathord{\left/ {\vphantom {\tau {2\pi}}} \right. \kern-\nulldelimiterspace} {2\pi}.}\) The units are m 2

Full size image

For comparison, we show in Fig. 2 the Hayashi spectra computed with the 500 hPa geopotential height for the NCEP reanalysis dataset averaged over the latitudinal band 30°N–75°N. A similar figure, related to the time-frame 1958–2002, has been already shown and discussed in Dell’Aquila et al. (2005). The Hayashi spectra of the 500 hPa geopotential height (Fig. 2) have consistently slightly higher values than those computed with the reconstructed field, thus suggesting that the geostrophic reconstruction filters out some atmospheric variability, as can be reasonably expected. We obtain similar results by reconstructing geopotential height field from ERA40 reanalysis. However, the qualitative structure of the spectra is maintained. Since the effect of adopting the geostrophic approximation is essentially model-independent, we assume our approach to be reasonable and consider the Hayashi spectra of the latitudinally averaged and geostrophically reconstructed 500 hPa geopotential height fields of the various models as good estimates for the spectra of the exact fields.

Fig. 2
figure 2

Climatological average over 39 winters of Hayashi spectra for the 30°N–75°N averaged 500 hPa geopotential height from NCEP data. The Hayashi spectra have been obtained multiplying the spectra by \({{k\omega \cdot \tau} \mathord{\left/ {\vphantom {{k\omega \tau} {2\pi}}} \right. \kern-\nulldelimiterspace} {2\pi}.}\) The units are m 2

Full size image

The 39 year-average of the winter Hayashi spectra of the IPCC GCMs reported in Table 1 are presented in Figs. 3, 4, 5 and 6.

Fig. 3
figure 3

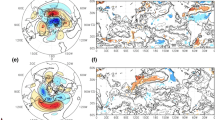
Climatological averages over 39 winters of the total Hayashi spectra for the geostrophically reconstructed 30°N–75°N averaged 500 hPa geopotential height from the ERA40 reanalysis and the 19 GCMs, as indicated in the panels. Hayashi spectra are multiplied by \({{k\omega \cdot \tau} \mathord{\left/ {\vphantom {{k\omega \tau} {2\pi}}} \right. \kern-\nulldelimiterspace} {2\pi}}\) for representation purposes (see text). Darker shades of grey denote higher values and isolines intervals are 200 m2. Period (in days) in abscissas and wavenumber in ordinates

Full size image

At first glance, all models spectra are qualitatively similar to those of the NCEP and ERA40 datasets. In particular, a large portion of the total variance is concentrated in the LFLW domain, and can be related mostly to standing waves and to westward propagating waves. The HFHW domain, corresponding mainly to synoptic disturbances, contains a smaller portion of the total variance, and is almost exclusively related to eastward propagating waves.

Discrepancies stem from a closer comparison of Fig. 1 and Figs.  3, 4, 5 and 6. For example, some models, such as ECHAM5/MPI-OM and FGOALS-g1.0, tend to overestimate the atmospheric variability for the eastward propagating waves (Fig. 4). Other models [e.g. CGCM3.1 (T42), the CNRM-CM3, the CSIRO-Mk3.0, the ECHO-G, the entire family of GISS GCMs, the MRI-CGCM2.3.2 models)] underestimate the power spectrum of the atmospheric signal for the standing and westward propagating waves at most time and space scales (Figs. 5, 6). Focusing on the standing waves (Fig. 5) and looking in more detail at the spectra, we find that only the IPSL-CM4, MIROC, and CGCM3.1(T63) models feature a peak at wavenumber 4 and period of about 20 days, as the two reanalyses. This feature is not in agreement with the common wisdom, coming from the linear Rossby wave theory, that the low-frequency resonant wave has wavenumber 3, thus suggesting the inadequacy of such a simple conceptual model when climatic properties are considered (Holton 1992). Of course, a rigorous statistical assessment of the significance of such spectral feature is required in order to draw more robust conclusions (see discussion below), but nevertheless it has to be noted that, since the geometrical domain is truly periodic, the assessment of the wavenumber decomposition of the field is more reliable than the frequency analysis.

Fig. 4
figure 4

As in Fig. 3 but for the eastward propagating component

Full size image
Fig. 5
figure 5

As in Fig. 3 but for the westward propagating component

Full size image
Fig. 6
figure 6

As in Fig. 3 but for the standing component

Full size image

It is clear that visual inspection of the Hayashi spectra, though instructive and useful, is not a viable way for objectively intercomparing the models and auditing their performances with respect to the reanalyses. For any nonparametric distribution, it is in general a hard task to deconvolve in a statistically rigorous way real signal (if any) from noise for a given 2D spectral density, i.e. to assess the significance of single peaks and dips, and it is still harder to assess whether two densities are statistically consistent. Note that for the computation of the space-time spectra shown in Figs. 1, 2, 3, 4, 5 and 6, some general hypothesis have been formulated as to the contribution of noise o the observed signal (Hayashi 1979). A possible strategy for assessing the robustness of the observed spectral features has been discussed by Hansen et al. (1989), who compared different spectral decompositions and pointed out relevant discrepancies only for the standing component of the spectrum. Nevertheless, in this study, instead of focusing on the details of the spectra, we adopt a coarse grain approach and degrade the retrieved information contained in the Hayashi spectra by suitable averages, obtaining, as a trade-off, the possibility of objectively interpreting and statistically assessing the results. We choose this approach in order to fulfill one of the main requests of PCMDI, which is the provision of simple scalar metrics for the evaluation of model performances.

In the following sections, we summarize the most relevant information contained in each panel of Figs. 3, 4, 5 and 6 into a few well-defined numbers more robustly characterizing the skill of each model. We then consider the averaging procedure defined in Eq. 6, and we introduce two different but complementary approaches, the first one evaluating the overall performances of the various models at all time and space scales (global metrics), the second one assessing the abilities of the models in reproducing the correct features of the baroclinic and planetary waves (process oriented metrics).

3.1 Global metric

A global scalar metrics can be introduced by integrating power spectrum corresponding to each one of the 39 winter seasons over the full frequency–wavenumber domain. We then consider the quantity E n T (Ω) introduced in Eq. 6 where Ω is set to be the full frequency–wavenumber domain and n is the index running over the winters.

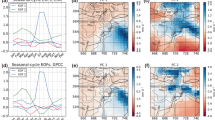
In Fig. 7 we show the climatological average \({\bar{E}_{T}{\left( \Omega\right)}}\) of the integral of the full spectrum versus its interannual variability \({\sigma_{{E_{T} {\left(\Omega\right)}}},}\) estimated according to Eqs. 7 and 8, respectively. Note that NAO effects are automatically included in the evaluation of the variability and should not be considered as special in any sense, for the purposes of this study. In this scatter diagram the abscissa represents the model average intra-seasonal variability, while the ordinate represents the interannual variability of the model intra-seasonal variability. The models ensemble average is also shown. In general, similar scatter diagrams, relating the two most relevant statistical moments of any chosen variable, are the simplest representation of a given climate. All of the time series E n T (Ω) from which we derive the statistical moments reported in Fig. 7 are compatible with the null hypotheses of white noise, featuring values of the lagged correlation smaller than 0.3 for all time lags equal or greater than 1 year. Therefore, for each model the confidence interval for the estimate of the climatological mean is centered on the quantity \({\bar{E}_{T}{\left( \Omega \right)}}\) (the estimator can be assumed to be unbiased) and its half-width can be approximated as \({2{\sigma _{{E_{T} {\left(\Omega \right)}}}} \mathord{\left/{\vphantom {{\sigma _{{E_{T} {\left(\Omega \right)}}}} {{\sqrt N}}}} \right. \kern-\nulldelimiterspace}{{\sqrt N}} \approx 0.32\sigma _{{E_{T} {\left(\Omega \right)}}},}\) thus being proportional to the ordinate of the corresponding representative point. If the confidence intervals of two models do not overlap, we can say that their climatological means are not statistically consistent. Note that if we had longer runs, we could restrict progressively the confidence interval of the climatological mean. Whereas the length of the considered simulations allows for a reliable statistical interpretation of the model dicrepancies in the description of intra-seasonal variability (the x-axis of the scatter diagram), the same is not true for the interannual variability. In Fig. 7 we do not show the vertical error bar, because that would make the scatter diagram unreadable. However, by treating the variance of \({\bar{E}_{T}{\left(\Omega\right)}}\) as a χ2-distributed random variable with N − 1 degrees of freedom (N  =  39  is the length of the time series) and by choosing a confidence level of 95%, we obtain a confidence interval spanning around 30% of the variance itself. Therefore, the length of the time series is not enough for a statistical assesment of the models discrepancies in the description of midlatitude interannual variability.

Fig. 7
figure 7

Mean value \({\bar{E}_{T}{\left( \Omega\right)}}\) and interannual standard deviation variance \({\sigma_{{E_{a} {\left(\Omega\right)}}}}\) of the total spectrum integrated over the whole spectral domain for the 2 reanalyses and the 19 GCMs. The letters indicate the data computed from the NCEP-NCAR reanalysis (N), from the ERA40 reanalysis (E). The shaded areas represent the dispersion of data: the center of the ellipses is the ensemble average; the semi-axes of the inner ellipse are equal to the variance of data in the corresponding direction; the semi-axes of the outer ellipse correspond to twice the variance. For each dot, the horizontal error bars represent the 95% confidence intervals of the estimate \({\bar{E}_{T}{\left( \Omega\right)}}\) and half-width is \({ {2\sigma _{{E_{a} {\left(\Omega \right)}}}} \mathord{\left/ {\vphantom {{2\sigma _{{E_{a} {\left(\Omega \right)}}}} {{\sqrt n}}}} \right. \kern-\nulldelimiterspace} {{\sqrt n}},}\) where n = 39. The vertical error bar is not reported to maintain the readibility of the figure. See Sect. 3.1 for a discussion of the statistical significance of the variance at 95% confidence level

Full size image

The reconstructed latitudinally averaged 500 hPa geopotential height fields of the two reanalyses have similar intra-seasonal variability. If we consider the observed 500 hPa geopotential height fields (here not shown), in agreement with what results from the visual inspection of the Hayashi spectra, we have that in both cases the intraseasonal and interannual atmospheric variability is increased by a constant factor around 10%. The reliability of the approach of considering a geostrophically balanced reconstruction of the 500 hPa geopotential height field is then confirmed.

Apparently, if we consider the model ensemble (centre of the ellipses in Fig. 7), we have a good agreement with observations: both reanalyses lie well within 1 SD (inner ellipsis) from the ensemble average. However, the models are widely spread over the plane space spanned by the two variables, with a typical bias of about 15% with respect to the reanalyses.

In general, the biases on the intraseasonal and interannual variability are positively linearly correlated: for larger average signals the variability tends to be larger, so that the model spread in Fig. 7 is definitely not isotropic.

The models that are statistically consistent with the reanalyses in terms of the total wave activity are the high-resolution version of the MIROC, the GFDL-CM2.1 and the INM3.0 model. The T63 version of the CGCM3.2 also performs well, featuring a slightly too large intraseasonal variability. Some models, such as FGOALS1.0 and ECHAM5/MPI-OM, feature very large positive biases ranging over 20% for the intra-seasonal variability. Some other models, usually of relatively low-resolution, such as CNRM-CM3 GISS-ER, ECHO-G and MRI-CGCM2.3.2, feature over 20% negative biases. The GISS-EH model has a very high value of interannual variability. Although the statistical significance is low (see discussion above) it is likely that this model has serious flaws in describing the atmospheric interannual variability at mid-latitudes correctly.

In some cases, it is possible to track the improvements occurring between different versions or set-ups of the same climate model. Thus, e.g. the GISS-EH model (which includes an isopycnal ocean component) has a better representation of the intra-seasonal atmospheric with respect to the GISS-ER which has a z-coordinate ocean model. However, the two models have considerably different interannual variability, which is in both cases different from that of the reanalysis. The CGCM3.1 model is presented in two versions which are identical except for the horizontal resolution (T47, corresponding to about 3.75° resolution, and T63 corresponding to about 2.8° resolution). The CGCM3.1(T63) improves the representation of both the intra-seasonal variability and of the interannual variability with respect to CGCM3.1(T47), although the improvements concerning the interannual variability are not statistically significant. Similar improvements are observed between MIROC(hires) and MIROC(medres) and between GFDL-CM2.1 and GFDL-CM2.0. The MIROC model is presented with two different horizontal as well as vertical resolutions (T42L20 for the medres version and T106L56 for the hires version). The medres version shows already quite good performances and is among the best models. However, a substantial improvement is observed when switching to higher resolution. The GFDL-CM2.0 and GFDL-CM2.1 models are very similar. In particular they share the same horizontal as well as vertical resolution, but in the GFDL-CM2.1 model some numerical techniques are improved with respect to GFDL-CM2.0. For example, CM2.0 uses centred spatial differencing in the horizontal, whereas in CM2.1 the horizontal discretisation is performed with a flux-form semi-Lagrangian method. Finally, let us note that the models with a better representation of the intraseasonal variability and with the values of \({\sigma_{{E_{T} {\left(\Omega\right)}}}}\) closer to those of the reanalyses display also the most realistic ENSO variability as shown in Van Oldenburg et al. (2005). It is then likely that longer model simulations would not alter substantially the general picture sketched in Fig. 7, although they would allow for a more robust statistical assessment of the results concerning the models interannual variability.

We underline that for each dataset the time-series E n T (Ω) summarizes the combined effect of all types of atmospheric disturbances acting on all time and space scales in the winter n. Therefore, a metric based on the statistical properties of E n T (Ω) cannot distinguish between noise and the contributions of waves of different natures due to different physical processes, and plain noise and merely gives (thanks to Parseval’s theorem, essentially) the total variability (or energy) of the signal Z (p =  500 hPa,λ,t). In order to gain more insight into how well the various models perform, the results presented in Fig. 7 must then be supplemented with the information provided by more specific and detailed (in a spectral sense) measures of the wave signal.

3.2 Process-oriented metrics

In order to construct process-oriented metrics, i.e. those pointing at the diagnosis of specific dynamical processes, we consider a decomposition of the frequency–wave number domain based on the known phenomenology of planetary scale atmospheric perturbations. Following Dell’Aquila et al. (2005), we consider two spectral subdomains, presented in Table 2.

Table 2 Definition of four regions in the Hayashi spectra of the winter atmospheric variability; the symbol d is used as shorthand for ‘day’
Full size table

The first is the HFHW subdomain, which includes periods from 2 to 7 days (13 ≤m≤ 45) and zonal wavenumbers j ≥  6 (length scales ranging from a few hundreds of kilometres to 5,000 km). These spectral components can be associated with the release of available energy driven by conventional baroclinic conversion (Blackmon 1976; Speranza 1983; Wallace et al. 1988), so that they are often referred to as baroclinic waves.

The second is the LFLW subdomain, which includes periods from 10 to 45 days (2 ≤m≤ 9) and zonal wavenumbers 2 ≤j≤4 (length scales larger than 7,000 km). These waves are mostly generated by the flow interaction with orography (Charney and DeVore 1979; Charney and Straus 1980; Buzzi et al. 1984; Benzi et al. 1986) and are catalyzed by the sub-tropical jet (Benzi and Speranza 1989; Ruti et al. 2006). Note that the selection of the range of zonal wavenumbers corresponds to the definition of the Wave Amplitude Indicator (WAI), which has been used as a proxy for the analysis of the low frequency variability of the atmosphere (Benzi et al. 1986; Benzi and Speranza 1989; Ruti et al. 2006). The WAI provides a synthetic picture of the ultra-long planetary waves and includes the wavelengths that are suitable for orographic resonance, since an approximate mode of zero phase velocity (resonance) is around 3 (Malguzzi and Speranza 1981).

For each year of a given dataset, we then provide a bulk measure of the planetary standing waves and of the eastward propagating baroclinic waves by computing the quantities E n E (ΩHFHW) and E n S (ΩLFLW) as defined in Eq. 6, respectively, where the two Ω -domains are prescribed as above, n is the index running over the winters, and the lower indexes S and E refer to standing and eastward propagating components, respectively. The quantities E n E (ΩHFHW) and E n S (ΩLFLW) can then be used to characterize the capabilities of each model of correctly describing two different dynamical processes of the atmosphere. Note that, starting from the analysis of the physical processes of the real atmosphere, the spectral subdomain employed for the definition of the scalar metric have been selected once for all models, in order assess how well the models compare to the reference provided by the two reanalyses.

We focus on the average (climatological) description provided by each model of the planetary standing variance and of the baroclinic eastward propagating variance. We then consider for each model the mean quantities \({\bar{E}_{E}{\left( {\Omega_{{\rm HFHW}}} \right)}}\) and \({\bar{E}_{S}{\left({\Omega_{{\rm LFLW}}} \right)}.}\) Similar to the case of the global metric, the time series E n E (ΩHFHW) and E n S (ΩLFLW) are statistically consistent with a white noise model (no significant internannual lagged correlation) for all models as well for the two reanalyses. Therefore, the standard error associated with the respective metrics, i.e. the quantities \({{\sigma _{{E_{E} {\left({\Omega _{{\rm HFHW}}} \right)}}}} \mathord{\left/ {\vphantom {{\sigma _{{E_{E} {\left({\Omega _{{\rm HFHW}}} \right)}}}} {{\sqrt N}}}} \right. \kern-\nulldelimiterspace} {{\sqrt N}}}\) and \({ {\sigma _{{E_{S} {\left({\Omega _{{\rm LFLW}}} \right)}}}} \mathord{\left/ {\vphantom {{\sigma _{{E_{S} {\left({\Omega _{{\rm LFLW}}} \right)}}}} {{\sqrt N}}}} \right. \kern-\nulldelimiterspace} {{\sqrt N}},}\) is a good estimate for the uncertainty associated with the climatological mean of the corresponding atmospheric variance.

For all models and for the reanalyses the cross-correlation of the time series E n E (ΩHFHW) and E n S (ΩLFLW) is not significantly different from zero, so that they can be considered, at least approximately, as independent variables. Moreover, for all datasets, we have that the two time series E n E (ΩHFHW) and E n T (Ω) are essentially uncorrelated, while E n S (ΩLFLW) and E n T (Ω) have statistically significant positive correlation whose value is around 0.5. This implies that, for all models, whereas a certain signature of the total wave activity signal is time-wise retained in the standing variance the contribution of the baroclinic high-frequency variance seems to be somehow decoupled.

In Fig. 8 we show for all datasets the climatological average \({\bar{E}_{S}{\left( {\Omega_{{\rm LFLW}}} \right)}}\) versus the climatological average \({\bar{E}_{E}{\left( {\Omega_{{\rm HFHW}}} \right)},}\) and indicate for both directions the corresponding standard error.

Fig. 8
figure 8

Scatter plot of \({\bar{E}_{S}{\left( \Omega_{\rm LFLW} \right)},}\) mean value of the integral over the low-frequency low-wavenumber spectral subdomain of the standing waves (abscissas), versus \({\bar{E}_{E} {\left( {\Omega_{{\rm HFHW}}} \right)},}\) mean value of the integral over the high-frequency high-wavenumber subdomain (ordinates) of the eastward propagating waves. For each dot the horizontal (vertical) error bar gives the 95% confidence level of the estimate \({{2\sigma _{{E_{S} {\left({\Omega _{{\rm LFLW}}} \right)}}}}}/\sqrt{n}\) where n=39. Shading is analogous to Fig. 7

Full size image

When considering the ERA40 and NCEP renalayses datasets, we observe that the two reanalyses are virtually indistinguishable, within the confidence level provided by the error bars, and they could be brought into even closer agreement by dropping the pre-satellite period (Dell’Aquila et al. 2005). However, the discrepancies among IPCC models by far exceed the discrepancies between the two different dynamical interpolations of the available observations.

Such a process oriented metrics is complementary to the global metrics presented in the previous subsection, since it is less prone to the limitation that the errors originating in different regions of the spectrum may average out and hide major model deficiencies. Instead, considering the process oriented metrics, it is easier to bring the models biases into light.

A general (with very few exceptions) occurrence for all IPCC models is that they overestimate the variability in the HFHW subdomain. Regarding the LFLW subdomain, more than half of the models tend to underestimate the corresponding variability. As an overall result, the model ensemble (center of the ellipses in Fig. 8) overestimates the HFHW variability and underestimates the LFLW variability. This closely resembles the results of many diagnostic studies performed in the past on global weather forecast models (Tibaldi 1986), which are the ancestors of the atmospheric components of GCMs.

Moreover, if we consider the confidence intervals of the statistical estimator of the climatological means we again have that very few models are statistically consistent with the reanalyses with a reasonable significance. The models that are closer to the reanalyses are the MIROC (hires and medres) model and the GFDL2.1 model. In these cases, the error bars have relevant overlaps with the area defined by the error bars of the NCEP and ERA40 reanalyses. It is rather interesting to note that not only the MIROC(hires) model and the GFDL2.1 model are the best in both the global and the process-oriented metrics, but they are also the only two with similar performances in both metrics: some models that perform well in the global metric perform poorly in the process-oriented ones, and vice versa.

By using the process-oriented metrics, the models having the worst performances are the CNRM-CM3 model, which underestimates both the low frequency and the high frequency, the FGOALS model, which overestimates the variability in both spectral sub-domains, and the BCCR-BCM model, which seriously underestimates the high-frequency variability.

We also underline that the results of the process-oriented metrics are quite robust with respect to slightly changing the spectral subdomain, so that when perturbing the boundaries of ΩHFHW and ΩLFLW, the resulting picture is similar to Fig. 8. This rules out the possibility that our results might be strongly affected by noisy boundary effects in the spectral filtering.

Unfortunately, there is no unique way to attribute the biases of LFLW and HFHW variability to specific features that are common to a class of models. Instead, it is interesting to compare the relative changes in the performances of models presented with different configuration. This might help in the identification of specific strategies for model improvements.

In the case of the CGCM3.1 models, an increased horizontal resolution (T63) leads to a better statistics of planetary-scale standing waves. However, the performance on small scale disturbances is better in the low resolution version (T47). Thus, increasing the horizontal resolution alone leads to no automatic overall substantial improvement of the model performance. A further example in the same direction is the comparison of the models ECHAM5/MPI-OM and INGV-SXG, that share the same atmospheric component with different horizontal and vertical resolution. In this case, the model with higher horizontal resolution (INGV-SXG, T106 instead of T63) but lower vertical resolution (L19 instead of L31), has worse performance with regard to eastward propagating baroclinic waves, while retaining similar performance with regard to standing planetary waves.

As mentioned above, two of the versions of the GISS model share the same atmosphere component over different oceans. In this case, the use of vertical density coordinates (GISS-EH) appears to improve the statistics of the standing waves, whose level is too low in the case of z-coordinates (GISS-ER). Instead, the performance with regard to eastward propagating waves is worse.

In the case of the MIROC model, increased resolution alone improves the model performance, but in this case both the horizontal and the vertical resolutions are increased.

Also in the context of the process-oriented metrics, the improvement from GFDL-CM2.0 to GFDL-CM2.1 is substantial, with the latter in good agreement with the reanalyses. The experience with the GFDL models demonstrates how the increase of computer power (i.e. of resolution) may not be the only pathway to model improvements. Instead, the employment of more accurate discretisation techniques may make a substantial contribution.

4 Conclusions

This study wishes to propose possible strategies and actual tools for auditing climate models. In particular, we have focused on assessing the degree of agreement with the reanalyses, and the degree of mutual coherence, of some of the most well-known coupled GCMs in the description of the statistical properties of the atmospheric disturbances in the mid-troposphere. We maintain that such an analysis provides more insight into the performances of the coupled GCMs than the comparison of properties such as surface temperature, because the internal mechanisms of the atmosphere are taken into consideration.

We have considered the variability of the 500 hPa geopotential height field, derived from the NCEP and ERA40 reanalyses for the time frame 1962–2000 and in the twenteeth century control run of the IPCC GCMs. We compute the Hayashi spectra of the 500 hPa geopotential height fields and introduce an integral measure of the variability observed in the NH on different spectral sub-domains. The total wave variability is taken as a global metric describing the overall performance of each model, while the variability related to the eastward propagating baroclinic waves and to the standing planetary waves are taken as process-oriented metrics, aimed at measuring the model capability of describing the corresponding physical process.

In such a context, we obtain the striking result that large biases, in most cases larger than 15%, are found in the metrics between the atmospheric waves climatology of most IPCC models and the reanalyses. In all cases, the span of the climatologies of the various models is around 50% of the climatology of the reanalyses. In particular, when considering the total variability of the wave fields of the GCMs, we find that the biases on the intraseasonal and interannual variability are positively linearly correlated, i.e. for larger average signals the variability tends to be larger. When considering the process-oriented metrics, we have the confirmation that the baroclinic waves are typically overestimated by the climate models, while the planetary waves are usually underestimated. This closely resembles the results of many diagnostic studies performed in the past on global weather forecast models (Tibaldi 1986). The model ensemble obtained by arithmetic averaging the results of all models is, for both the global and process oriented metrics, biased with respect to the reanalyses, but is comparable to the best 5 models. Nevertheless, the models results do not cluster around their ensemble mean. Only for two models—GFDL-CM2.1 and MIROC(hires)—the climatologies of the wave activity are statistically consistent with those of the reanalyses, both for the global and process-oriented metrics. The fact that these two models are the only two performing well in both metrics suggest that they outperform the other models in the representation of the mid-latitude winter atmospheric dynamics of the NH. The span of performance of the GCMs in the representation of the tropospheric waves is a rather relevant issue, particularly because all models are expected to agree reasonably in other diagnostics such as the average vertical temperature profiles, average surface temperature, precipitation and so on (see e.g. the results presented in the TAR).

The general pictures obtained with the global and the process-oriented metrics, are essentially different, as most of the models showing good agreement with reanalyses for one metric do not perform similarly well for the other one.

In particular, the substantial improvement detected in the global metric for a higher resolution version of a given model may indeed mask the minor improvements (if any) in describing a specific process, as in the case of the two CGCM3.1 GCMs. Also, the INM-CM3.0 model, which seems rather close to observations when using the global metric, fails to correctly describe both the LFLW and HFHW regions of the spectrum of mid-latitude atmospheric variability. The two models ECHAM5/MPI-OM and INGV-SXG share the same atmospheric component with different horizontal and vertical resolution. In this case, on the other hand, the model with higher horizontal resolution (INGV-SXG, T106 instead of T63) but lower vertical resolution (L19 instead of L31), has worse performances on eastward propagating baroclinic waves, while retaining a similar performance on standing planetary waves, but is largely better for the global metrics.

The outputs of the process-oriented metrics may suggest some of the priorities for planning strategies for model improvements. From this perspective, we find that the increase of horizontal resolution alone has no substantial effect on our estimate of model performances, while the increase of horizontal and vertical resolution brings (e.g. MIROC(hires)) into rather close agreement with observations. An increased vertical resolution could be useful to better mimic the vertical structure of the ultra-long waves, in particular the orographic baroclinic standing perturbations (Buzzi et al. 1984). The numerical scheme improvement also has a positive impact on model performance (GFDL models). In particular, the use of semi-Lagrangian advection schemes for tracers seems to be an important requirement for model reliability.

Somewhat unexpectedly, in the case of the GISS-ER and GISS-EH models, the characteristics of the adopted ocean model also seems to play a critical role in determining the bulk of the atmospheric variability. We may guess that what could be relevant in this case might be the differences in the representation of the surface ocean temperature in the Northern Atlantic region, which delicately depends on the representation of the thermohaline circulation. Among the three GISS models, GISS-AOM displays superior performances.

In order to obtain more detailed information regarding the representation of the physical processes occurring in the different spectral regions, the process-oriented metrics proposed in this work should be complemented with a careful investigation in the space-time domain. Such an analysis should look at large scale horizontal spatial structures and wave source regions, wave dynamics, and may determine that, for example, a model populates correctly a considered spectral subdomain, but for the wrong physical reasons. The statistics of mid-latitude cyclones occurrences and intensities is a good example of this kind of dual analysis with respect to what is proposed in this paper.

Moreover, since the adopted approach requires a latitudinal averaging operation, such that all the latitudinal features of the fields are lost, we foresee the necessity of a more detailed—more differentiated in latitude - analysis in order to more thoroughly evaluate the models.

This study, although preliminary, suggests caveats concerning the ability of most of the presently available climate models in describing the statistical properties of the global scale atmospheric dynamics of the present climate and, a fortiori, in the perspective of climate change. One of the possible outcomes of this study may be the provision of quantitative information needed to weight model reliability when considering models ensemble results, e.g. in the context of the IPCC reports. A positive result of this study is that, in spite of all the (sometimes rather large) biases between the datasets in the climatological means of the signals E n E (ΩHFHW), E n S (ΩLFLW), and E n T (Ω), corresponding to the activity of the respective class of waves, some statistical properties are well represented in all models. In particular, for all models we have that all the signals considered have rather weak time-lagged self-correlation, that the cross-correlation of E n E (ΩHFHW) and E n S (ΩLFLW) is rather weak, and that, whereas the correlation of E n S (ΩLFLW) and E n T (Ω) is positive and statistically significant, the correlation of E n E (ΩHFHW) and E n T (Ω) is rather weak, so that the baroclinic waves have, as opposed to the planetary standing waves, a very weak signature in terms of the total wave activity.

On the other hand, the GFDL-CM2.1 and MIROC(hires) models, being able to reproduce with some degree of confidence the statistical properties of wave activity in the atmosphere, seem to be the best candidates for more detailed studies on atmospheric circulation regimes (Ruti et al. 2006), which will be the subject of future study. Among the several other in-depth analyses which can follow from the results presented here, we would like to mention three future paths. In the context of the global properties of the atmosphere, it seems relevant to study the links between the degree of the models mutual coherence and realism in the description of the mid-latitudes atmospheric variability, and in the representation of ENSO (Van Oldenburg et al. 2005), which seems critical in the set-up of the regimes of the low-frequency mid-latitudes planetary waves (Ruti et al. 2006). In the context of the understanding of climate change, it seems relevant to study the mutual coherence of the GCMs with regard to the statistics of the atmospheric waves considered in the present analysis in their sensitivity to CO2 doubling. We also wish to mention that performing a similar analysis of the Southern Hemisphere mid-latitudes faces the problem of the large disagreement between the two reanalyses (Dell’Aquila et al. 2006).

A further, more comprehensive, thermodynamically oriented, intercomparison study can be performed, along some of the lines proposed in the WCRP/WGNE Workshop on the Second Phase of the Atmospheric Model Intercomparison Project (Gleckler 2004), by analyzing the Lorenz cycle and estimating the efficiency of the conversion of the available potential energy of the atmosphere in the various climate models. We believe that this might be a physically robust diagnostic to be used in the study of the climate machine and in the climate models quality-check.

The computations described in this paper are implemented in a MATLAB® routine available at http://www. clima.casaccia.enea.it/staff/calmanti/ipcc_hayashi_v.m.