Uncertainties due to transport-parameter sensitivity in an efficient 3-D ocean-climate model

Abstract

A simplified climate model is presented which includes a fully 3-D, frictional geostrophic (FG) ocean component but retains an integration efficiency considerably greater than extant climate models with 3-D, primitive-equation ocean representations (20 kyears of integration can be completed in about a day on a PC). The model also includes an Energy and Moisture Balance atmosphere and a dynamic and thermodynamic sea-ice model. Using a semi-random ensemble of 1,000 simulations, we address both the inverse problem of parameter estimation, and the direct problem of quantifying the uncertainty due to mixing and transport parameters. Our results represent a first attempt at tuning a 3-D climate model by a strictly defined procedure, which nevertheless considers the whole of the appropriate parameter space. Model estimates of meridional overturning and Atlantic heat transport are well reproduced, while errors are reduced only moderately by a doubling of resolution. Model parameters are only weakly constrained by data, while strong correlations between mean error and parameter values are mostly found to be an artefact of single-parameter studies, not indicative of global model behaviour. Single-parameter sensitivity studies can therefore be misleading. Given a single, illustrative scenario of CO₂ increase and fixing the polynomial coefficients governing the extremely simple radiation parameterisation, the spread of model predictions for global mean warming due solely to the transport parameters is around one degree after 100 years forcing, although in a typical 4,000-year ensemble-member simulation, the peak rate of warming in the deep Pacific occurs 400 years after the onset of the forcing. The corresponding uncertainty in Atlantic overturning after 100 years is around 5 Sv, with a small, but non-negligible, probability of a collapse in the long term.

1 Introduction

Climate models incorporate a number of adjustable parameters whose values are not always well constrained by theoretical or observational studies of the relevant processes. Even the nature of the processes may be unclear and dependent upon resolution, as sub-grid scale mixing parameterizations, particularly for coarse resolution models, may represent a wide variety of different physical processes (eddies and unresolved motions, double-diffusive interleaving, inertia-gravity waves, tides, etc.). In such cases parameter values would ideally be chosen by optimising the fit of model predictions to observational data. This would naturally entail searching for optimal, quasi-steady solutions in the multi-dimensional space of all the model parameters. Using basic Monte-Carlo random walk techniques, tens or hundreds of thousands of quasi-steady integrations would be required. For the intensively studied models of high or moderate resolution, such as HadCM3 (Gordon et al. 2000) and CCSM (Boville and Gent 1998), the computational demands of even a single such integration can be prohibitive. Instead, large models are usually tuned by a sequence of studies looking in detail at single parameterzations. The interdependence of parameters will almost certainly mean that even the order in which such studies are conducted will affect the final result, and hence the model predictions. Efficient models have the potential to perform large numbers of integrations and hence explore larger regions of their parameter space. Where the parameters have clear physical interpretations or close equivalents in higher resolution models, the results may be of more general relevance. Efficient models are also essential for the understanding of very long-term natural climate variability, in which case the optimal inter-component balance of model complexity may depend on the timescale range of interest.

In a recent paper Knutti et al. (2002) derive probabilistic constraints on future climate change using ensembles of order 10⁴ runs of 3,000 years using the Bern 2.5-D model. This model is based on 2-D representations of the flow in each of the major ocean basins following Wright and Stocker (1991), as in the Potsdam-based model “CLIMBER” (Petoukhov et al. 2000). Models with fully 3-D representations of the world ocean, on the other hand, can much more readily be compared with higher-resolution models and with data. Furthermore, 3-D ocean models benefit from the ability to represent directly the fundamental geostrophic momentum balance; the ability to represent horizontal gyre circulations and the ability to represent topographic and geometrical effects, such as changes in the location of deep sinking and ice formation. In 2-D models all these important effects can only be parameterised. Interactions with other components of the climate system are much more readily represented as a result of the 2-D ocean surface and in addition, errors due to low resolution are much more easily quantifiable in 3-D models than corresponding errors due to reduced dimensionality.

Efficient models with 3-D ocean components include the model of Weaver et al. (2001), FORTE (Sinha and Smith 2002) and ECBILT-CLIO (Goosse et al. 2001), which use low-resolution versions of primitive-equation Bryan-Cox type ocean models. These models are considerably less efficient than the Bern 2.5-D model and are not yet capable of performing ensembles of runs representing hundreds of thousands of years of total integration. Coupled models using quasi-geostrophic (QG) ocean dynamics exist (Hogg et al. 2003) but have so far been focused on high-resolution integrations. More general than QG dynamics, and thus applicable with arbitrary bottom topography in a global setting, but significantly simpler than the primitive equation dynamics, are frictional geostrophic (FG) ocean models such as that described by Edwards and Shepherd (2002). In this paper we describe the extension of the latter model by the addition of an energy and moisture balance (EMBM) atmosphere and a zero-thickness dynamic and thermodynamic sea-ice model. At a very low resolution of 36×36 cells in the horizontal, and given the extremely simple representation of the atmosphere, the resulting coupled model is highly efficient.

After a brief description of the model physics, we perform an initial investigation of the space generated by the simultaneous variation of model parameters by analysing a set of 1,000 model runs. We do not attempt to produce well-converged statistical analyses, rather we aim to bridge the gap between the large ensembles of runs which are possible with dimensionally reduced models and the very limited numbers of runs available from high-resolution 3-D models. Our aim is to investigate the extent to which both model parameters and model predictions of global change are constrained by quantitative comparison with data. Thus we commence our analysis in Sects. 3 and 4 by defining and applying an objective measure of model error. Next, in Sect. 5, we discuss the modelled climate in the low-error runs. Then, in Sect. 6, we consider the model behaviour in a global warming scenario, weighting our solutions according to the mean error measure to define appropriate probability distributions. We conclude with a discussion in Sect. 7.

2 Model description

2.1 Ocean

The frictional geostrophic ocean model is based on that used by Edwards and Shepherd (2002) (henceforth referred to as ES) for which the principal governing equations are given by Edwards et al. (1998). Dynamically, the ocean is therefore similar to classical GCM’s, with the neglect of momentum advection and acceleration. The present version, however, differs significantly from that of ES in that the horizontal and vertical diffusion of ocean tracers is replaced by an isopycnal diffusion and eddy-induced advection parameterisation in which a considerable simplification is obtained by setting the isoneutral diffusivity equal to the skew diffusivity representing eddy-induced advection, as suggested by Griffies (1998).

In FG dynamics, barotropic flow around islands, and hence through straits, can be calculated from the solution of a set of linear constraints arising from the integration of the depth-averaged momentum equations around each island. A form of the constraint for one island is given by ES for the special case where topographic variation around the island vanishes. Here we use the general form for the ACC but neglect barotropic flow through the other straits unless otherwise stated. A further modification to the ocean model of ES is the inclusion of a variable upstream weighting for advection.

The velocity under-relaxation parameter of Edwards and Shepherd (2001) is set to 0.9. Note that velocity relaxation alters the dynamics of an equatorial pseudo-Kelvin wave which is already present in the FG system (contrary to the comment by Edwards and Shepherd 2001) see Killworth (2003) for details.

In the vertical there are normally eight depth levels on a uniformly logarithmically stretched grid with vertical spacing increasing with depth from 175 m to 1,420 m. The maximum depth is set to 5 km. The horizontal grid is uniform in the (ϕ, s), longitude sin(latitude) coordinates giving boxes of equal area in physical space. The horizontal resolution is normally 36×36 cells.

2.2 Atmosphere and land surface

We use an Energy and Moisture Balance Model (EMBM) of the atmosphere, similar to that described in Weaver et al. (2001). The prognostic variables are surface air temperature T_a and surface specific humidity q for which the governing equations can be written as

$$ \rho _{\text{a}} h_{\text{t}} C_{{\text{pa}}} \left( {\frac{{\partial T_{\text{a}} }} {{\partial t}} + \nabla .\left( {\beta _{\text{T}} {\mathbf{u}}T_{\text{a}} } \right) - \nabla .\left( {\kappa _{\text{T}} \nabla T_{\text{a}} } \right)} \right) = Q_{{\text{SW}}} C_A + Q_{{\text{LW}}} - Q_{{\text{PLW}}} + Q_{{\text{SH}}} + Q_{{\text{LH}}} , $$

(1)

$$ \rho _{\text{a}} h_{\text{q}} \left( {\frac{{\partial q}} {{\partial t}} + \nabla .\left( {\beta _{\text{q}} {\mathbf{u}}q} \right) - \nabla .\left( {\kappa _{\text{q}} \nabla q} \right)} \right) = \rho _{\text{o}} \left( {E - P} \right), $$

(2)

where h_t and h_q are the atmospheric boundary layer depths for heat and moisture, respectively, κ_T and κ_q are the eddy diffusivities for heat and moisture respectively, E is the evaporation or sublimation rate, P is the precipitation rate, ρ_a is air density, and ρ_o is the density of water. C_pa is the specific heat of air at constant pressure. The parameters β_T, β_q allow for a linear scaling of the advective transport term. This may be necessary as a result of the overly simplistic, one-layer representation of the atmosphere, particularly if surface velocity data are used in place of vertically averaged data, as in our standard runs. Weaver et al. (2001) use the values β_T=0, β_q=0.4 or 0. We allow β_T≠ 0 but only for zonal advection, while β_q takes the same value for zonal and meridional advection. In view of the convergence of the grid, winds in the two gridpoints nearest each pole are averaged zonally to give smoother results in these regions.

In contrast to Weaver et al. (2001) the short-wave solar radiative forcing is temporally constant, representing annually averaged conditions. In a further departure from that model, the relevant planetary albedo is given by a simple cosine function of latitude. Over sea ice the albedo is temperature dependent (see below). The constant C _A parameterizes heat absorption by water vapour, dust, ozone, clouds, etc.

The diffusivity κ_T, in our case, is given by a simple exponential function with specified magnitude, slope and width,

$$ \kappa _{\text{T}} = k_{\text{T}} \left( {S_{\text{a}} \frac{{2\theta + \pi }} {\pi } + \left( {1 - S_{\text{d}} } \right)\frac{{\exp \left( { - \left( {\theta /l_{\text{d}} } \right)^2 } \right) - c}} {{1 - c}}} \right), $$

(3)

where θ is the latitude (in radians) and the constant c is given by

$$ c = \exp \left( { - \left( {\frac{\pi } {{2l_{\text{d}} }}} \right)^2 } \right). $$

(4)

For width parameter l_d=1 and slope parameter s_d=0.1, this function is close to that used by Weaver et al. (2001) when β_q≠0. In our model, κ_q is always constant.

The remaining heat sources and sinks are as given by Weaver et al. (2001): Q_LW is the long-wave imbalance at the surface; Q_PLW, the planetary long-wave radiation to space, is given by the polynomial function derived from observations by Thompson and Warren (1982), cubic in temperature T_a and quadratic in relative humidity r=q/q_s, where q_s is the saturation-specific humidity, exponential in the surface temperature. For anthropogenically forced experiments, a greenhouse warming term is added which is proportional to the log of the relative increase in carbon dioxide (CO₂) concentration C as compared to an arbitrary reference value C₀.

The sensible heat flux Q_SH depends on the air-surface temperature difference and the surface wind speed (derived from the ocean wind-stress data), and the latent heat release Q_LH is proportional to the precipitation rate P, as in Weaver et al. (2001). In a departure from that model, however, precipitated moisture is removed instantaneously, as in standard oceanic convection routines, so that the relative humidity r never exceeds its threshold value r_max.

This has significant implications as it means that the relative humidity is always equal to r_max wherever precipitation is non-zero, effectively giving q the character of a diagnostic parameter. Here, since the model is used to represent very long-term average states, regions of zero precipitation only exist as a result of oversimplified representation of surface processes on large landmasses.

To improve the efficiency, we use an implicit scheme to integrate the atmospheric dynamical Eqs. 1 and 2. The scheme comprises an iterative, semi-implicit predictor step (Shepherd, submitted) followed by a corrector step which renders the scheme exactly conservative. Changes per timestep are typically small, thus a small number of iterations of the predictor provides adequate convergence.

The model has no dynamical land-surface scheme. The land-surface temperature is assumed to equal the atmospheric temperature T_a, and evaporation is set to zero, thus the atmospheric heat source is simplified over land as the terms Q_LW=Q_SH=Q_LH=0. Precipitation over land is added to appropriate coastal ocean gridcells according to a prescribed runoff map.

2.3 Sea ice and the coupling of model components

The fraction of the ocean surface covered by sea ice in any given region is denoted by A. Dynamical equations are solved for A and for the average height H of sea ice. In addition a diagnostic equation is solved for the surface temperature T _i of the ice. Following Semtner (1976) and Hibler (1979), thermodynamic growth or decay of sea ice in the model depends on the net heat flux into the ice from the ocean and atmosphere. Sea-ice dynamics simply consist of advection by surface currents and Laplacian diffusion with constant coefficient κ_hi.

The sea-ice module acts as a coupling module between ocean and atmosphere and great care is taken to ensure an exact conservation of heat and fresh water between the three components. The resulting scheme differs from the more complicated scheme of Weaver et al. (2001) and is described fully in the Appendix.

Coupling is asynchronous in that the single timestep used for the ocean, sea-ice and surface flux calculation can be an integer multiple of the atmospheric timestep. Typically, we use an atmospheric timestep of around a day and an ocean/sea-ice timestep of a few days. The fluxes between components are all calculated at the same notional instant to guarantee conservation, but are formulated in terms of values at the previous timestep, thus avoiding the complications of implicit coupling. All components share the same finite-difference grid.

2.4 Topography and runoff catchment areas

The topography is based on a Fourier-filtered interpolation of ETOPO5 observationally derived data. A consequence of the rigid-lid ocean formulation is that there is no mechanism for equilibriation of salinity in enclosed seas which must therefore be ignored or connected to the ocean. In our basic topography the depth of the Bering Strait is a single level (175 m), thus it is open only to barotropic flow, which we usually ignore, and diffusive transport, while the Gibralter Strait is two cells deep and thus permits baroclinic exchange flow. Realistic barotropic flow through Bering would require local modification of the drag to compensate for the unrealistic width of the channel. In a single experiment with default drag parameters and barotropic throughflow enabled, the model calculated a transport of 4.5 Sv out of the Pacific at steady state.

Equivalently filtered data over land were used—along with depictions of major drainage basins in Weaver et al. (2001) and the Atlantic/Indo-Pacific runoff catchment divide of Zaucker and Broecker (1992)—to guide the subjective construction of a simple runoff mask. At higher resolution, it becomes a practical necessity to automate the intial stages of this procedure. Thus the runoff mask for the 72×72 grid is constructed by applying a simple, steepest-descent algorithm to the filtered topographic data, followed by a minimum of modifications to ensure that all runoff reaches the ocean.

2.5 Default parameters and forcing fields

In principle, values used for oceanic isopycnal and diapycnal diffusivities, κ_h and κ_v and possibly momentum drag (Rayleigh friction) coefficient λ may need to be larger at low than at high resolution to represent a range of unresolved transport processes. In FG dynamics, the wind-driven component of the ciculation tends to be unrealistically weak for moderate or large values of the frictional drag parameter λ, for reasons discussed by Killworth (2003), while for low drag unrealistically strong flows appear close to the equator and topographic features. This problem is alleviated by allowing the drag λ to be variable in space. By default, drag increases by a factor of three at each of the two gridpoints nearest the equator or to an upper-level topographic feature. In addition, we introduce a constant scaling factor W which multiplies the observed wind stresses in order to obtain stronger and more realistic wind-driven gyres. For 1<W<3, it is possible to obtain a wind-driven circulation with a reasonable pattern and amplitude. Annual mean wind-stress data for ocean forcing come from the the SOC climatology (Josey et al. 1998). Wind fields used for atmospheric advection are long-term (1948–2002) annually averaged 10 m wind data derived from NCEP/NCAR reanalysis. Using upper-level winds was not found to improve model simulations. Parameters and ranges, where appropriate, are given in Tables 1 and 2.

Table 1 Ranges of model parameter values for the initial ensemble together with the ranges obtained in the subset of low-error simulations described in the text. The value given for drag, λ, is the minimum value in the ocean interior

Table 2 Further default parameter values. The full specification of variable drag, ocean density, isoneutral and eddy-induced mixing, surface fluxes, outgoing longwave radiation, specific humidity and freezing temperature involves about another 50 parameters, values for which are given or referred to in the text. ΔF₂=4/ln 2

2.6 Freshwater flux redistribution

The single-layer atmosphere described above generates only around 0.03 Sv moisture transfer from the Atlantic to the Pacific, whereas Oort (1983) estimated a value of 0.32 Sv from observations. This typically leads to very weak deep sinking in the north Atlantic in the model unless the moisture flux from the Atlantic to the Pacific is artificially boosted by a constant additional redistribution of surface freshwater flux. Oort’s estimated transfer flux was subdivided into three latitudinal bands: −0.03 Sv south of 20°S (to the Atlantic/Southern Ocean boundary); 0.17 Sv in the tropical zone 20°S to 24°N, and 0.18 Sv north of 24°N. Following Oort, we transfer fresh water at a net rate F_a, subdivided into these latitude bands in these proportions. Note that although this adjustment, and the wind scaling described above, are forms of flux correction, they serve to adjust steady-state behaviour rather than prevent climate drift. Climate drift in higher-resolution models typically arises because the models are too costly to integrate to equilibrium.

3 A semi-random set of runs

Fixing the distribution of drag, we have a set of 10 model parameters related to mixing and transport, κ_h, κ_v, λ, W, κ_hi, F_a, k_T, κ_q, β_T, β_q, augmented to 12 if we allow for variation of the width and slope l_d and s_d of the atmospheric diffusivity. If we vary these parameters individually, as in conventional, single parameter studies, we visit only a very restricted region of parameter space. We therefore allow all 12 parameters to vary at once within specified ranges, which are given in Table 1. We also consider the single parameter approach for comparison. Extreme values are chosen to cover, or exceed, a range of reasonable choices of appropriate values for such a model. We consider the effect of restricting these ranges in Sect. 7. In the case of drag λ, physically reasonable solutions are obtained only within a fairly narrow range. The wind scaling factor, suggested qualitatively by the analysis of Killworth (2003), is allowed to vary from 1 (no scaling) to 3, while the freshwater adjustment factor is varied between 0 and twice the observation estimate of 0.32 Sv. Note that it may be appropriate to use larger values of frictional and diffusive parameters than in higher-resolution models.

In our semi-random approach, we generate an ensemble by uniformly spanning the range of each individual parameter, but choose combinations of parameters at random. This is equivalent to an equal subdivision of probability space (as in Latin Hypercube sampling) if the probability distributions for the parameters are uniform. Thus with M runs and N parameters, each parameter takes M, uniformly (or logarithmically) spaced values between its two extrema, but the order in which these values are taken is defined by a random permutation. Where the minimum value is zero, the values chosen are uniformly spaced between the extrema, otherwise they are uniformly logarithmically spaced. Each run is a separate, 2,000-year integration from a uniform state of rest under constant forcing. For the purposes of this paper, we collate the results of three such sets, one with M=200 and two with M=400, making 1,000 runs in total (recall that N=12). Within each set every run is necessarily unique. Between the sets a given run could be repeated, but the probability of this happening is vanishingly small.

As discussed by ES, the final quasi-steady state may not be unique for a given set of parameters. Other quasi-steady states may be obtained using different initial conditions, in particular different initial ocean temperatures. However, in the present paper, we are primarily concerned with the effects of variations of model parameters, thus we fix the initial ocean temperature at 20°C unless otherwise stated. This results in a rapid, convectively driven start to the oceanic adjustment process.

To process the results of such a large number of runs, we have to define an objective measure of model error. To do so we use a weighted root mean square error over the set of all dynamical variables in the ocean and atmosphere, as compared to interpolated observational datasets, namely NCEP surface (1,000 mb) atmospheric temperature and specific humidity, averaged over the period 1948–2002, and Levitus et al. (1998) temperature and salinity. Quantitative comparison of the sea-ice variables with data would be over-ambitious at this resolution. Thus the error $\mathcal{E}$ is defined by

$$ \varepsilon ^2 = \sum\limits_{i = 1}^n {w_i \left( {X_i - D_i } \right)^2 } $$

(5)

where the vectors X _i and D _i represent the model and data variables, respectively, indexed by the subscript i, and the values w _i are weights which depend on the quantity (atmospheric or oceanic temperature, humidity or salinity) but not the position. For each of the four quantities the weight w _i =(n σ ²_q )⁻¹, where n is the total number of variables and σ ²_q is the variance of the relevant observationally derived quantity in the model coordinates. The values of σ ²_q are 41.5C² for ocean temperature, 162 C² for atmospheric temperature, 0.282 psu² for salinity and 2.94×10⁻⁵ for relative humidity, respectively, n=15,012. Since the weight depends explicitly only on the data variance, the contributions of ocean and atmosphere errors are effectively weighted by the density of gridpoints in each submodel. This weighting gives a useful test of model performance which is potentially sensitive to subtle changes in ocean dynamics as well as changes in the very basic representation of the atmosphere. A value of unity for $\mathcal{E}$ would be given by globally uniform model fields with the exact value of the mean of the data. Although the mean may not be accurately predicted, this should be offset by some skill in predicting spatial variation, and values for $\mathcal{E}$ somewhat less than one are obtained for reasonable simulations. At this stage, we can assume that model errors are likely to dominate observed long-term trends in the observational data. We also make use of an alternative error function $\mathcal{E}_{\text{A}}$ in which the sum in Eq. 5 is taken exclusively over points in the atmosphere (considering only ocean points provides little additional information).

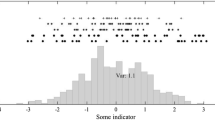
The range of $\mathcal{E}$ over the complete set of 1,000 runs (of which 785 successfully reached completion) is from 0.61 to 2.8. Figures 1 and 2 show the error at the end of each run as a function of each of the parameters in turn for all the runs with mean error less than 1. There is very little correlation between any of the parameters and the mean error. The atmospheric moisture and heat diffusivity amplitudes have correlation coefficients, across the whole range, of 0.39 and −0.32 with the mean error but no other parameters have correlation coefficients larger than 0.3 in magnitude.

Fig. 1

Mean model error $\mathcal{E}$ after 2,000 years for a set of 1,000 runs with randomly chosen parameters, as a function of each of the parameters in turn. Each data value, denoted by a cross, is the value at the end of an individual run. Circled crosses denote runs in the set $\mathcal{S}$ which have low mean and low atmospheric errors. The continuous lines give the error dependence for separate sequences of runs increasing and then decreasing a single control parameter in each case. The parameters are; κ_h, κ_v, λ, W, κ_hi, F_a. Results are shown only where $\mathcal{E} < 1.$

Fig. 2

As previous figure for the remaining parameters; k_T, κ_q, l_d (diffwid), s_d (difflin), β_T, β_q

Also shown in Figs. 1 and 2 are the results of sequences of runs in which we vary a single (control) parameter at once, changing its value in small increments between runs and initialising each run with the final state of the previous run. We start each sequence with a run of 4,000 years at the minimum value of the control parameter. Subsequent runs, first increasing to a maximum and then decreasing the control parameter, are terminated after 1,000 years. Since the variations in parameters between runs are small, the model climate remains close to equilibrium throughout the procedure unless the ocean circulation undergoes a major structural bifurcation. The mean error at the end of each individual run is plotted as a function of the control parameter in Figs. 1 and 2 (continuous lines). The two curves corresponding to the increasing and decreasing branches should pass very close to the minimum error value for the random ensemble, since the parameters of this run were used as pivotal values for the single-parameter sequences. Small differences in error between random ensemble results and outward and return branches of the single-parameter sequences are the result of residual unsteadiness in ocean temperatures and salinities. Large differences between branches (hysteresis), in the case of moisture diffusivity κ_q and moisture flux F_a, indicate the existence of multiple stable steady states. In the cases of freshwater flux adjustment and moisture diffusivity, the circulation undergoes a bifurcation in which the Atlantic overturning collapses. In simplified geometries such a change often indicates a switch between dominantly single and double-cell overturning structures, as in ES, but in this case the deep sinking in the north Atlantic is completely absent in the collapsed state.

Variations of mean error found in these single-parameter experiments can generally be understood in terms of fundamantal ocean thermohaline circulation behaviour (Edwards et al. 1998) and the atmospheric transport of heat and moisture. For the principal ocean diffusivities, for example, the mean error is closely related to the mean ocean temperature. However, we do not discuss these single-parameter experiments in detail here. They are included essentially to demonstrate that although variations of single parameters can show very clear correlations between mean error and parameter values, it can be a serious mistake to assume that these correlations apply in general, ie. when other parameters are not held fixed. For almost all parameters, runs from the random ensemble with both low and high error occur almost across the entire range of the parameter, as a result of different combinations of the other parameters. Clearly the mean error provides only a weak constraint on the possible values of model parameters.

One result of the single-parameter studies, which is worthy of note, is the asymptotic behaviour of mean error with diapycnal mixing coefficient κ_v. Below a value of around 5×10⁻⁵ m² s⁻¹, changes in mean error are insignificant. Atlantic overturning asymptotes to a minimum of 16.5 Sv, without radical changes in circulation structure, indicating that numerical leakage replaces explicit diapycnal mixing below this value. The fact that this asymptotic state is only obtained for κ_v<5×10⁻⁵ m² s⁻¹ is an important, if circumstantial, indicator that spurious diapycnal leakage is genuinely low, despite the very coarse resolution.

4 A subset of acceptable runs

The question now arises of which simulations should be deemed acceptable? If we base our decision on $\mathcal{E}$, we need to define an acceptable range $\Delta \mathcal{E}$ of error $\mathcal{E}$. There are at least three reasons for allowing $\Delta \mathcal{E} > 0,$ first there may be uncertainty in the observational data we are attempting to fit, second there may be variability in the model, and third there are processes omitted from the model which lead to inevitable errors. Since the data are based on multi-decadal averages, and the statistics are globally averaged, the component of variability due to short-term fluctuations in the data should be small, however, there has been significant global warming during the period of the data observations, which is likely to be at least comparable to expected natural variability over these timescales. Neglecting the contributions of the other fields, a uniform atmospheric warming of 1 degree would give a change in $\mathcal{E}$ of order 1/σ, where σ²=161C² is the variance of the atmospheric temperature data set, giving a contribution to the error range $\Delta \mathcal{E}$ of order 0.1. A proven source of model variability is the existence of multiple steady states for given parameters. From Figs. 1 and 2, this can result in a contribution to the error range $\Delta \mathcal{E}$ of up to around 0.1 in regions of hysteresis. No other form of internal variability in the model has appeared in the present series of experiments, although ocean-only versions often produce variability in certain regimes (Edwards et al. 1998). For deliberately simple models such as ours, the dominant source of model error is likely to be the oversimplified representation, or in many cases complete neglect, of a large range of physical processes. We term these errors representation errors. Examples include the lack of boundary current separation and poor atmospheric temperatures and humidities over land. Neglected processes should lead to systematic errors. Within the range of these errors, improved mean fit to data may not necessarily imply better model predictions. For instance, if we were to obtain the correct global average temperature while neglecting a certain positive temperature feedback effect, this would imply too great a sensitivity to those processes which are actually modelled. Representation errors are particularly difficult to estimate, although we must infer that they account for most of $\mathcal{E}$.

In summary it seems reasonable to accept simulations within an error range $\Delta \mathcal{E}$ of order 0.1 of our lowest-error simulations, thus allowing for an unavoidable minimum error plus a range of additional error stemming from some combination (not strictly additive) of the three models and physical error sources discussed above. Inevitably, this selection relies heavily on our choice of error weighting. The atmospheric error function $\mathcal{E}_{\text{A}}$ would lead to a different selection of “acceptable” simulations. In fact $\mathcal{E}$ and $\mathcal{E}_{\text{A}}$ have an overall correlation of only 0.47. A low mean error $\mathcal{E}$ places only a relatively weak constraint on the atmospheric error. Amongst the simulations with $\mathcal{E} < 0.75,$ for example, are seven simulations with $\mathcal{E}_{\text{A}} > 0.7$ rather more than the minimum value of $\mathcal{E}_{\text{A}} = 0.36.$ A low atmospheric error provides even less constraint on the mean error $\mathcal{E}$. To generate a subset of acceptable simulations, we therefore combine both of these measures and start by rejecting all simulations with high values of either. Allowing a fairly generous limit of $\Delta \mathcal{E}$ in each case we initially accept only simulations with $\mathcal{E} < 0.75$ and $\mathcal{E}_{\text{A}} < 0.5.$ Constraining both mean (ocean-dominated) and atmospheric errors in this way results in a subset of 22 runs. One of these is highly unsteady at 2,000 years, with the Atlantic circulation starting to collapse, thus we rule out this unstable simulation and restrict attention to the resulting set $\mathcal{S}$ of 21 runs, all of which remain stable for at least a further 2,000 years. The range of parameter values amongst the subset $\mathcal{S}$ remains almost as large as the range across the initial ensemble, further confirmation that parameter values are only weakly constrained by mean error, even amongst the most realistic simulations. Both ranges are indicated in Table 1.

5 The modelled climate

5.1 Ocean

We now consider in a little more detail the extent to which our automatic critera have been successful in generating a set of reasonable climate simulations. The barotropic streamfunction at 2,000 years, averaged across the set $\mathcal{S}$, is shown in Fig. 3. For these simulations, barotropic flow through the Bering Strait is neglected. With the observationally derived wind stresses scaled up, as described above, by an average factor of 2.1 the subtropical gyres in the North Pacific and North Atlantic achieve maxima of 32 and 19 Sv, respectively, while the Antarctic circumpolar current (ACC) has a barotropic transport of 28 Sv. The wind-driven flow therefore remains weak even with this scaling. With our low resolution and reduced ocean dynamics, the north Pacific and north Atlantic boundary currents fail to separate from the coasts, leading to errors in sea-surface temperature (SST) of up to 10°C or 15°C in these regions. Modelled SST is also too high in eastern boundary upwelling regions and in the southern ocean. Model SST averaged over the set $\mathcal{S}$ is shown in Fig. 4 and the SST error compared to Levitus et al. (1998) annually averaged observational data is plotted in Fig. 5. Surface values here are taken to be those in the uppermost grid cell. The data are always interpolated to the corresponding vertical model level.

Fig. 3

Model barotropic streamfunction in Sv after 2,000 years in model grid coordinates averaged over the set $\mathcal{S}$ of low-error simulations. The contour interval is 10 Sv, continents are shaded

Fig. 4

SST in degree centigrade averaged over the set $\mathcal{S}$ of low-error simulations. Continents are shaded

Fig. 5

Errors in averaged SST compared to observed long-term annual mean SST field in degree centigrade from Levitus et al. (1998)

The variance of SST across $\mathcal{S}$ is shown in Fig. 6. The largest values occur in the tropical Atlantic and Pacific and south of Greenland, all regions of large error averaged across the set. Elsewhere the variance of SST across the set is relatively small. The magnitude and general pattern of errors is relatively consistent across the set.

Fig. 6

Variance of SST in C² across the set $\mathcal{S}$ of low-error simulations. Continents are shaded

A significant contribution to the error comes from the deep ocean temperature, which is generally around 2°C too high (but see below) while at mid-depth the Indian and parts of the North Atlantic are too cold. The upper ocean is too warm in the Gulf Stream and Kuroshio separation regions, as noted earlier, and too warm in the Eastern tropical Atlantic and Pacific, although Atlantic SST is mostly too low. Surface salinity is typically too low at low and mid-latitudes and too high at high latitudes. At mid-depth parts of the north Indian and western North Atlantic are too fresh, while deep salinities are everywhere too high, especially in the North Atlantic, where the error is up to 0.5 psu.

The meridional overturning streamfunctions for the model Atlantic and for the global domain, averaged over the set $\mathcal{S}$, are shown in Fig. 7. The average Atlantic overturning has a maximum of 19.4 Sv. The maximum overturning values in the Atlantic range from 11 Sv to 32 Sv with two values below 16 Sv and three above 25 Sv. At 25°N, there is just under 19 Sv of overturning, cf. Hall and Bryden’s 1982 estimate of 19.3 Sv (Jia 2003 quotes a range of observational estimates from 16 Sv to 19 Sv at this latitude). Although our extremes values are well outside the range of observations, the range is not dissimilar to that found in the Coupled Model Intercomparison Project (CMIP) by Jia (2003).

Fig. 7

Model meridional overturning streamfunctions for the globe (upper panel) and the Atlantic (lower panel) in Sv averaged over the set $\mathcal{S}$ of low-error simulations

Figures 8 and 9 show the temperature and salinity, respectively, in a north–south, vertical section through the model Atlantic at 25°W averaged over the set $\mathcal{S}$, along with Levitus et al. (1998) data for the same section. The deep water is around 2°C too warm, while the surface and vertical salinity gradients are too weak (absolute salinity values include an arbitrary scaling factor) this is related to weak forcing as will be seen below. On the other hand the tongue of intermediate water extending northwards from the South Atlantic is a persistent feature of the model simulations which is present in the data.

Fig. 8

Model temperature in degree centigrade in a north–south, vertical section through the Atlantic at 25°W averaged over the set $\mathcal{S}$ of low-error simulations, upper panel; and Levitus data for the same section, lower panel

Fig. 9

Model salinity in psu in a north–south, vertical section through the Atlantic at 25°W averaged over the set $\mathcal{S}$ of low-error simulations, upper panel; and Levitus data for the same section, lower panel. The contour interval is 0.2 psu

Deep temperature errors are a ubiquitous problem in climate models, as shown by Fig. 10 reproduced from Jia (2003), which shows the temperatures in the upper and lower branches of the overturning cell near 25°N for the models participating in CMIP, along with estimates from data. Temperatures are calculated as heat transport divided by volume transport. For set $\mathcal{S},$ we obtain upper and lower temperatures of 16°C and 5.4°C, relatively close to the observational estimates in Fig. 10, although the mean ocean temperature in our interpolated observational dataset, at 3.9°C, is 1.8°C lower than the average value of 5.7°C across the set $\mathcal{S}$. Average ocean temperatures range from 2.3°C to 7.6°C at 2,000 years across the set $\mathcal{S}$, by comparison deep Atlantic temperatures in the CMIP models range from 3.4°C to 11.6°C, with estimates from data being around 3.0°C. It is relevant to note that high resolution models are often initialised with observational values and then integrated for 1,000 years or less, thus the equilibrium deep temperatures for some of these models may be even higher. In our simulations the deep water is hot in the initial condition and still cooling significantly in most cases, at least in the Pacific, at 2,000 years. If we continue the simulations in set $\mathcal{S}$ for a further 2,000 years the average ocean temperature drops to 5.2°C, although the mean errors are only very slightly lower. In our lowest-error run the mean temperature is 4.3°C at 4,000 years, 0.4°C above the observational value. Changes in deep temperatures after 2,000 years are greatest in the Pacific.

Fig. 10

Average temperatures of the upper and lower branches of the overturning near 25°N in the Atlantic in the CMIP climate models (circles) and DYNAMO ocean models (crosses) with observational estimates from Hall and Bryden (1982) and Roemmich and Wunsch (1985). The lines indicate fixed temperature differences of 10°C and 15°C between the upper and lower branches. Figure reproduced from Jia (2003). By comparison, average upper and lower temperatures in the 21 “best” simulations of our set $\mathcal{S}$ are 16°C and 5.4°C

Upper ocean errors, in particular, may stem from poor atmospheric forcing as well as simplified ocean dynamics. Errors in deep-ocean values are likely to be related to errors in the ocean forcing at high latitudes by exchanges with the atmosphere and sea ice. The fact that this problem afflicts many of the CMIP models suggests that deficiencies in the atmosphere are not the only cause. Another likely cause is that convection and slope flow are poorly represented in our ocean model, in common with all widely used climate models at present.

5.2 Atmosphere and sea ice

Atmospheric temperature errors are largest in polar regions, where they take both signs, and over Eurasia, where model temperatures are around 10°C too low. The model atmosphere is generally too wet over south America and too dry over north Africa and Australia. The zonal averages of atmospheric temperature and humidity, T_a and q, for the ensemble average of $\mathcal{S}$ are shown in Fig. 11 along with the equivalent averages for the NCEP data. Also indicated are the maximum and minimum values of the zonal averages across the ensemble. Averaged values stay relatively close to observed distributions, although the model results are persistently too cool and dry in the tropics. Tropical wetness is reproduced over the ocean but not over land, where precipitation is absent in some regions, although the model correctly predicts enhanced precipitation over the Gulf Stream and Kuroshio regions.

Fig. 11

Zonally averaged atmospheric temperature, upper panel, and specific humidity, lower panel, averaged over the set $\mathcal{S}$ of low-error simulations, thin line, along with data from NCEP, thick line. The maximum and minimum zonally averaged values within the set $\mathcal{S}$ are indicated by dashed lines

Sea ice in these simulations is almost ubiquitous in the northernmost grid row, which represents the model Arctic ocean. In around half of the simulations in set $\mathcal{S}$ the sea ice extends to the second most northerly grid cell and in around a quarter there is sea ice in the southern hemisphere. On average the sea ice reaches a maximum height of 18 m and a minimum temperature of −16°C. The areal fraction is usually almost exactly 0 or 1, thus the sophistication of the fractional area representation has limited effect on the steady state at this resolution. In simulations with time-varying forcing (not discussed here) sea-ice dynamics play a more significant role.

5.3 Heat and freshwater fluxes

Zonally integrated northward heat transports for the ensemble average of $\mathcal{S}$ are shown for the Atlantic ocean and for the global atmosphere in Fig. 12 along with the maximum and minimum values of the zonal averages across the ensemble. Northward transport of heat in the Atlantic peaks at 0.9 PW, whereas Hall and Bryden (1982) estimated a value of 1.2 PW from hydrographic data. By comparison, northward heat transport in the Atlantic at this latitude in the CMIP models was found by Jia (2003) to vary between 0.38 PW and 1.3 PW, with only three models reaching a smooth transport exceeding 1 PW. Atmospheric heat transport, averaged across the set $\mathcal{S}$, reaches 5.3 PW at northern subtropical latitudes. By comparison, Trenberth and Caron (2001) quote maximum values around 5 PW from ECMWF and NCEP reanalysis, with seasonal variation of the northern hemisphere maximum between 2 PW and 8 PW.

Fig. 12

Northward heat transports in PW averaged over the set $\mathcal{S}$ of low-error simulations, thin line. The maximum and minimum zonally averaged values within the set $\mathcal{S}$ are indicated by dashed lines. Upper panel; oceanic heat transport in the Atlantic, Lower panel, global atmospheric transport. Atlantic values are defined only in the enclosed part of the basin

Zonally averaged oceanic precipitation, P, evaporation, E, and their difference, P−E, for the ensemble average of $\mathcal{S}$ are shown in Fig. 13 along with observationally derived estimates from the SOC climatology. The equatorial peak of precipitation is not captured by the model, while tropical evaporation is underestimated, leading to somewhat weak latitudinal variations in zonally averaged ocean-atmosphere freshwater exchange E−P in many of the simulations. This is a likely cause of the weak oceanic salinity gradients.

Fig. 13

Zonally averaged oceanic freshwater fluxes averaged over the set $\mathcal{S}$ of low-error simulations, thin line, along with observational estimates from the SOC climatology, thick line. The maximum and minimum zonally averaged values within the set $\mathcal{S}$ are indicated by dashed lines. Upper panel; precipitation P, central panel; evaporation E; lower panel, P−E

In summary, although the set $\mathcal{S}$ was defined by applying simple criteria to a randomly generated set, we have found a range of simulations of modern climate which appears reasonable in comparison with the range of CMIP model results found by Jia (2003). In the next section we consider the range of predictions of climate change generated by this subset of simulations, and by the original ensemble.

6 A global warming experiment

We now investigate the behaviour of the model in a global warming scenario. To this end we generate an ensemble of simulations corresponding to the continuation of our initial ensemble. During an initial, forced warming phase the CO₂ concentration is made to increase exponentially at a fixed rate of about 1% per year. In our simple radiation parameterisation, the resulting change in outgoing longwave radiation is − ΔF₂ ln (C/C₀), where C/C₀ is the relative change in CO₂ concentration. Thus we are imposing a constant rate of decrease of outgoing planetary longwave radiation. Over the 100-year forcing period the CO₂ concentration rises by a factor of 2.7 from its initial value. In all cases we keep the value of ΔF₂ fixed at 4/ln 2 corresponding to a direct CO₂ forcing of 4 W m⁻² per doubling of CO₂. We are interested in the extent to which resulting changes in the model climate vary across the ensemble purely as a result of the variation of the model’s mixing and transport parameters. In a further set of runs, we consider the long-term response of the model climate by continuing the ensemble integration for a further period of 2,000 years with the CO₂ concentration remaining fixed throughout. This abrupt stabilisation scenario may be unrealistic, but is appropriate to investigate the long-term, qualitative behaviour of the system. For the purposes of this latter experiment, it is sufficient to consider only the lower-error simulations, thus we continue only the 200 or so runs with $\mathcal{E} < 0.9.$

The ranges of variation of various predicted diagnostic quantities are given in Table 3. The values in the table correspond to the changes over the 100-year forced warming period and to changes across the whole 2,100-year period including the 2,000-year equilibriation period. For the purposes of Table 3, we consider only the runs corresponding to the continuation of the low-error runs in the set $\mathcal{S}$. The quantities referred to in the table are the mean surface-air temperature (SAT) the average equator-to-pole air temperature difference in the northern and southern hemispheres, ΔT_N and ΔT_S, respectively, the maximum height of sea ice, h_max and the minimum (i.e. maximum negative) and maximum of the meridional overturning streamfunctions in the Pacific and Atlantic, Ψ_P and Ψ_A. These are all quantites which are controlled or heavily influenced by the large-scale behaviour of the global ocean circulation in the model, thus they are quantities which it seems reasonable to use the model to predict. It must be emphasised, however, that we have not considered the uncertainty in the parameter ΔF₂, corresponding to the climate sensitivity of the atmosphere, and that the atmospheric response contributing, in particular, to the prediction of the equator-to-pole temperature differences is very crude compared to atmospheric GCMs. These temperature differences are principally of interest because they may affect the average winds, but we do not attempt to parameterise any feedback on the wind field in our model.

Table 3 Ranges of changes in various predicted quantities during 100 years of forced warming and during the complete 2,100-year period including a further 2,000-year equilibriation period. All values are derived from the 21 lowest-error simulations of a 1,000-run random set

A significant part of the warming, and of all the associated changes documented in the table, occurs after the initial, forced period, although most of this change occurs in the following 100 years (see Fig. 14). Since we have ignored variations in atmospheric climate sensitivity, and the uncertainty regarding future greenhouse gas concentrations (which in our parameterisation is an equivalent uncertainty) the actual value of the change in SAT can only be considered to be the response to particular, chosen values for these variables. It is thus the range of predictions that is of most interest. The same comment must also apply to the other quantities in the table; the mean of the predicted change is the response to a particular warming scenario. It is of interest, however, that the model ensemble predicts a drop of 4.4 Sv in the maximum Atlantic overturning over 100 years, followed by a substantial recovery in the following 2,000 years. The range of the response is from −2.3 Sv to −7.3 Sv over the first 100 years, but drastically more uncertain in the long term as the overturning in some simulations collapse.

Fig. 14

Average temperatures during spin-up, forced warming and equilibriation periods for set $\mathcal{S}$ of low-error simulations, upper panel; atmosphere, lower panel; deep Pacific

Changes in the atmosphere are substantial in the 100 years following the forced warming period but relatively small thereafter. This is not the case in the ocean, as can be seen from Fig. 14, which shows average temperatures during the entire forced warming plus equilibriation period for every member of the set $\mathcal{S}$. In addition to the SAT we plot the temperature in the deep Pacific, where deep refers to the lower half of the computational domain, below about 1,000 m. Upper-ocean temperatures (not shown) converge slightly more slowly than air temperature in these runs, but deep ocean values take very much longer to converge. Averaged across the set the peak rate of warming in the deep Pacific occurs 400 years after the onset of the forcing and the rate of warming remains significant after 2,000 years. Many of the simulations respond much more slowly than this, for example in the lowest-error solution warming peaks 750 years after the onset of forcing. These long response times are related to low diapycnal diffusivities. For a diffusivity of 10⁻⁵ m² s⁻¹ and a depth of 5 km the timescale D²/κ_v for diffusion to the ocean floor is around 80,000 years. Although circulation may accelerate communication, the diffusive timescale is likely to be significant for equilibriation. Indeed these long equilibriation times mean that many of the simulations are still cooling at the start of the forced warming period in reponse to the initial condition at t=0. While this initial unsteadiness will delay the onset of warming in the deep, it should have only a small effect on the time at which warming is most rapid.

6.1 Probabilistic interpretation

In principle, it should be possible to derive more statistical information on the distribution of predicted quantities from our results, given the size of our initial ensemble, although strictly speaking if we use a discrete cutoff value $\mathcal{E}_c$ as in the selection of the set $\mathcal{S}$, accepting, with equal probability, all results with $\mathcal{E}_c$ any resulting pdfs which we generate will be biased. A more statistically sound procedure is to weight all our results according to the likelihood of the data given the model, which we can reasonably assume to be Gaussian. Using a Gaussian function centred close to our minimum error, with a decay scale equal to our assumed scale $\Delta \mathcal{E}$ for acceptable variation of error, can be broadly justified in terms of the theory of representation error (J.D. Annan, pers. comm.). We can apply this weighting to derive estimates of probability density functions for the quantities considered in Table 3. Thus we assign to each run a probability $P = \exp \left[ { - {{\left( {\mathcal{E} - \mathcal{E}_0 } \right)^2 } \mathord{\left/ {\vphantom {{\left( {\mathcal{E} - \mathcal{E}_0 } \right)^2 } {\left( {2\Delta \mathcal{E}^2 } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\Delta \mathcal{E}^2 } \right)}}} \right]$ and sum the total probability in equal bins between the extreme parameter values. The results (normalised) shown in Fig. 15 were derived using the scale value $\Delta \mathcal{E} = 0.1$ and the offset $\mathcal{E}_0 = 0.6$ but the forms of the distributions are essentially unchanged across a range of reasonable values for $\Delta \mathcal{E}$. Similarly, results are robust to changes in $\mathcal{E}_0$ as long as $\Delta \mathcal{E}$ is adjusted simultaneously so that a reasonable number of simulations have non-negligible weight in the sum. Larger values of $\Delta \mathcal{E}$ lead to smoother distribution functions and smaller values give more spiky distributions but there is no major change in form. This suggests that the very lowest-error solutions do not have a grossly different behaviour in respect of these measures than solutions with mean error $\mathcal{E}$ up to 1.0 or more. Unfortunately we cannot derive meaningful distributions in the same way from the set $\mathcal{S}$, because it has too few members. In Fig. 15 we are effectively including, with varying weight, simulations which failed our selection criteria on the basis of atmospheric error or mean error. However, the forms of the distributions are broadly consistent with the very rough view of the range of predictions seen in Table 3 for the 21 “best” simulations. Figure 15 also shows the corresponding graphs for the changes over the whole period. We infer from these distributions that an uncertainty in model predictions of global warming of around 1° due purely to uncertain model transport and mixing parameters is a fairly robust result, which is not greatly influenced by careful elimination of unreasonable simulations beyond our basic, automatic sorting of simulations on the basis of mean error. A similar uncertainty is predicted for the equator-to-pole temperature differences. For the Atlantic overturning, again the pdfs in Fig. 15 are consistent with the results in Table 3; a decrease of a few Sv after 100 years, with an uncertainty of around 5 Sv, and the bulk of the probability at 2,100 years indicating a partial recovery, with a small, secondary maximum at around −15 Sv showing a low, but non-negligible, probability of a collapse of the overturning in the north Atlantic. A decrease is predicted in the northern-sinking overturning cell in the Pacific, and a decrease in maximum sea-ice height.

Fig. 15

Probability distributions, based on mean error weights, for the changes in various mean quantities during a 100-year global warming experiment; continuous, and for the entire 2,100-year period including equilibriation phase; dashed. SAT denotes the average surface air temperature; ΔT North the average equator to pole northern hemisphere, surface air temperature difference; ΔT South the corresponding value for the southern hemisphere; Ψ min and max Pac. and Atl. the respective minimum and maximum overturning streamfunction values in the Pacific and Atlantic. Distributions were obtained with $\Delta \mathcal{E} = 0.1$ and $\mathcal{E}_0 = 0.6.$

Given the bimodel distribution for Atlantic overturning, we can proceed to calculate the resulting atmospheric temperature changes over a 4×5 grid-cell area roughly representing Europe. The resulting distributions are similar to those for global SAT change, with the addition of a tail containing a few percent of the total probability in the long-term distribution, where the warming is between 0° and 3°. This result should be treated with caution, however, bearing in mind the low resolution and reduced dynamics of our atmosphere and land surface.

Similar distributions are found using the atmospheric error $\mathcal{E}_{\text{A}}$ in place of $\mathcal{E}$, although with somewhat greater spread for the oceanic quantities, which are only indirectly controlled by $\mathcal{E}_{\text{A}}$. The bimodal distribution of change in Atlantic overturning is still visible, thus the possibility of collapse remains when we bias our predictions strongly toward the best atmospheric simulations.

It is straightforward to test the effect of the prior ranges of parameters on the forms of the pdfs in Fig. 15 by restricting the range of simulations considered. Unfortunately restricting several parameters at once in this way would drastically reduce the number of available runs and prevent us from deriving smooth results but it is possible to restrict parameters one or two at once. As an example we have repeated the 100-year predictions using only approximately the middle third of the (logarithmic) range of the atmospheric heat flux amplitude, 2×10⁶<k_T<5×10⁶ m² s⁻¹, hence around one-third of the simulations. Differences in the forms of the pdfs (not shown) are very slight, suggesting that the results are not heavily dependent on the initial ranges of parameters. A similar experiment restricting both of the principal atmospheric freshwater flux parameters simultaneously, 2×10⁵<κ_q<10⁶ m² s⁻¹, 0.21<F_a<0.42 Sv, gave more noisy, but otherwise similar distributions to those seen above.

7 Discussion and conclusions

Our principal aim has been to present and investigate a new efficient climate model. The model features a fully 3-D ocean but retains an integration efficiency considerably greater than extant climate models with 3-D, primitive-equation ocean representations (20 kyears of integration can be completed in about a day on a PC). Inevitably, this efficiency is attained at a cost: the model atmosphere has no vertical structure and is extremely basic compared to standard GCMs. Dynamical atmospheric feedbacks are poorly represented and atmospheric temperature errors are large over continents and polar regions. An additional, fixed atmospheric moisture transport is included to compensate for the weakness of the resolved transport. Winds are fixed, and observed wind stresses are artificially enhanced to compensate for strong momentum damping in the physically simplified ocean. The model is hence best suited to computationally demanding problems of climate change in which the large-scale ocean circulation plays a major role, in particular large ensemble studies and long-timescale variability. Work is in progress to develop a complete Earth system model based on the model described here.

By analysing a randomly generated set of 1,000 runs, each 2,000 years in length, we have considered the uncertainty in 12 mixing and transport parameters. Constructing a quantitative measure for the model error allowed us to address both the inverse problem of estimation of model parameters, and the direct problem of model predictions. Our results represent a first attempt at tuning a 3-D climate model by a strictly defined procedure which nevertheless considers the whole of the appropriate parameter space.

Our modelling philosophy is thus to match model outputs to observations while model inputs (parameters) are initially only weakly constrained. Weaknesses in large-scale transports have been addressed by including the two explicit adjustment parameters mentioned above, inter-basin freshwater transfer and wind scaling, so that their effects can easily be assessed and their values adjusted where necessary in altered climate states. Our approach differs from that used in GCM development where the tuning process usually involves a more detailed, but necessarily more restricted view of the model parameter space. It is common practice, for example, to alter the geometry of (unresolvable) ocean sills to improve the representation of the circulation. Any attempt to tune a model towards observations may be introducing a subtle bias towards climatic states which happen to have been observed. Further, any tuning towards observations is liable to lead to a systematic misrepresentation of included processes to compensate for the effects of missing processes. Whether such tuning is beneficial may therefore depend on the relative importance of model state quantities, such as deep-water temperature, compared to process strengths, such as atmospheric diffusivity. Our approach may therefore not suit all applications, but the important and novel feature of it is that the whole tuning process is easily definable and therefore open to analysis.

We addressed the uncertainty in model predictions in two separate ways, firstly by considering the spread of predictions across a subset $\mathcal{S}$ of roughly equally believable models and secondly by the more statistically sound procedure of weighting all the simulations according to mean error $\mathcal{E}$. Lower $\mathcal{E}$ “probably” implies better simulations and therefore, if model dynamics are reliable, better predictions, within an uncertainty of order $\Delta \mathcal{E}$. The definition of $\mathcal{E}$ is clearly an important part of this process. More sophisticated definitions than ours, using pattern-recognising algorithms or deliberately focusing on known systematic errors, may be more appropriate for more sophisticated or highly developed models. Our choice of an acceptable range of $\mathcal{E}$ was essentially heuristic, but the derivation of approximate probability density functions (pdfs) was not found to be sensitive to this choice. We also tested the effect of adding a term to our error function proportional to the departure of the maximum atmospheric heat flux from the observational estimate of 5 PW. This results in a different top set of runs with a narrower spread of maximum atmospheric heat flux values but the pdfs for greenhouse warming-induced changes were essentially unchanged. There remains the problem that we have effectively applied a sharp cutoff to the prior distribution of parameter values used to generate the ensemble. This has an indirect effect on the resulting pdfs which is difficult to account for in complete generality, but appears from our sensitivity tests to be small.

Model parameters were found to be only very weakly constrained by mean model error. For almost all parameters, runs with both low and high error occurred across almost the entire range of the parameter, as a result of different combinations of the other parameters. Although the range of parameter values across the subset $\mathcal{S}$ is slightly smaller than the initial range for the whole ensemble (see Table 1), the scatter of values made it impossible to derive pdfs for the parameter values. However, the results of Hargreaves et al. (2005) suggest that parameters can be estimated an order of magnitude more efficiently in our model using the ensemble Kalman filter technique of Annan et al. (2005). Where there are sufficient data, parameters can also be constrained. Our weak constraint of parameters therefore appears to be partly due to the limited size of our ensemble.

Generally, the fit of the best simulations to data can be expected to degrade with decreasing ensemble size, while random variation will become more pronounced. To quantify this effect properly would require the construction of the complete pdf of model behaviour as a function of the assumed pdfs of parameters. However, the fact that the pdfs derived in the previous section were relatively insensitive to reducing the parameter ranges (giving a reduced ensemble size) and to changes in the error scale $\Delta \mathcal{E}$ suggests that smaller ensembles may give useful results, but may simply indicate that the low mean error solutions behave in a physically similar way to the majority of the other solutions.

Given the efficiency and simplicity of the model, its simulation of modern climate is reasonable. In particular, zonally averaged properties and fluxes are relatively well reproduced, including meridional overturning and Atlantic heat transport, which reproduce observed values as closely as the majority of the more complex CMIP models. An intrinsic problem with FG dynamics is that the wind-driven circulation tends to be weak. The fact that wind-scaling values between 1.2 and 2.9 were found for the lowest-error simulations partially vindicates our approach to this problem, scaling up the wind forcing and using variable drag, at least within the modelling philosophy outlined above. The deep ocean in most of our best simulations is one or two degrees too warm. This is a persistent problem for all the CMIP models, caused partly by the difficulty of parameterising convection and slope flow. More sophisticated tuning, however, can eliminate this problem (Hargreaves et al. 2005). The values found here are within the range found in CMIP. Errors in atmospheric temperature are largest in polar regions, where they take both signs, and over continents, where model temperatures are several degrees too low. The model atmosphere is generally too dry over continents. Given 1,000 model runs and 12 degrees of freedom it is, perhaps, not surprising that a small set of runs can be found that fit a limited set of observations as well as a sample of GCMs. Naturally the data we chose for the tuning procedure was limited to quantities that the model can predict. Because of the very limited representation of polar oceans, for instance, we did not attempt to fit sea-ice data.

Experiments with varying diapycnal diffusivity tentatively suggest that the level of spurious diffusivity is around 5× 10⁻⁵ m² s⁻¹ at most, although more detailed investigation is required to verify this. Single-parameter sensitivity studies revealed regions of hysteresis under variation of atmospheric freshwater flux parameters. This effect is studied more intensively in our model by Marsh et al. (2005) but, in general, we find that that the strong correlations between mean error and parameter values found in single-parameter sensitivity studies can be highly misleading as an overall predictor of model behaviour across the whole of parameter space.

It is of some interest to ask how model errors depend on spatial resolution. The question is complicated by the fact that the optimal choices of parameter values will change with resolution. However, mean errors in suitably paired, 2,000-year simulations were found to decrease by 0.06 and 0.11 on doubling vertical or horizontal resolution, respectively, indicating that resolution in itself is not a dominant source of error (recall that our lowest-error simulation had $\mathcal{E} = 0.61.$ A similar experiment gave a comparable value, 0.06, for the reduction in mean error already achieved by incorporating isopycnal and eddy-induced mixing. These results suggest that further dynamical improvements may be worthwhile. A variety of such measures are currently planned or already completed, including upper and lower ocean boundary layers, seasonality of radiative forcing and incorporation of dynamical land-surface processes.

Our measured spread of climatic responses to 100 years’ global warming (for surface-air temperature a spread of around one degree) is substantial given that it represents the range of predictions arising purely from variation of mixing and transport parameters in the model. All atmospheric radiative properties were kept constant, and a large number of feedbacks ignored, including atmospheric dynamical and carbon cycle feedbacks, as well as the large uncertainties in anthropogenic emissions themselves. The results of Fig. 15 and Table 3 must be interpreted as the response to a particular scenario of greenhouse gas concentration and a particular value of the direct radiative forcing parameter ΔF₂. With our single-layer atmosphere this is not an appropriate model to study the uncertainty connected with atmospheric dynamics and radiative parameters. On the other hand, the model is a particularly useful tool for studying the thermohaline circulation (THC). The THC is intrinsically three dimensional, but with existing 3-D models it is difficult to adequately investigate parameter space.

Appendix, the sea-ice model

Ocean surface fluxes are everywhere partitioned between ocean- and ice-covered fractions, the total heat flux Q_t into the ocean or ice surface being

$$ Q_{\text{t}} = \left( {1 - C_A } \right)Q_{{\text{SW}}} - Q_{{\text{LW}}} - Q_{{\text{SH}}} - \rho _{\text{o}} LE, $$

(6)

where E is the rate of evaporation or sublimation, calculated as in Weaver et al. (2001), L is the latent heat of evaporation L_v, or sublimation L_s, over ocean or ice respectively and the planetary albedo over sea ice is assumed to decrease linearly with air temperature within a given range following Holland et al. (1993):

$$ \alpha = \max \left( {0.20,\min \left( {0.7,0.40 - 0.04T_{\text{a}} } \right)} \right). $$

(7)

The sea ice has no heat capacity, thus the heat flux Q_t from the atmosphere is assumed to be equal to the vertical heat flux through the ice given by

$$ Q_{\text{t}} = - \frac{{v_i }} {H}\left( {T_{\text{f}} - T_i } \right), $$

(8)

where ν _i is the vertical conductivity of heat within the sea ice and T_f is the local salinity-dependent freezing temperature of sea water, assumed to be the temperature at the base of the sea ice, given by

$$ T_{\text{f}} = {}_{\gamma 1}S + {}_{\gamma 2}S^{3/2} + {}_{\gamma 3}S^2 , $$

(9)

where the values for the constants γ _i , i=1,2,3, are as given by Millero (1978). From Eqs. 6 and 8 we obtain a single equation, Φ(T _i )=0, say, for the ice-surface temperature T _i , which is solved by the Newton–Raphson iteration.

Having obtained the ice-surface temperature, and hence the heat flux from atmosphere to sea ice, we calculate the heat flux from the sea ice into the ocean (normally negative) as

$$ Q_{\text{b}} = \frac{{\rho _i C_{{\text{pi}}} \Delta z}} {{\tau _i }}\left( {T_{\text{f}} - T_{\text{o}} } \right), $$

(10)

where T_o is the temperature at the ocean surface; in the model T_o is the temperature of the uppermost (mixed) layer, Δz is the thickness of this layer, C_pi is the specific heat of sea ice at constant pressure, ρ _i its density and τ _i is a timescale for the relaxation of the ocean surface temperature to the freezing temperature. McPhee (1992) suggests a physical value for the ratio Q_b/(T_f− T_o) although the most appropriate value is liable to depend on model temporal and spatial resolution. However, we retain the value of 17.5 days for τ _i implied by McPhee’s parameterisation with the present value of Δz.

We are now in a position to calculate the growth rate G _i of sea-ice height in the ice-covered ocean fraction, which is given by the deficit of heat fluxes into and out of the sea ice, minus the latent heat loss of sublimation. Snow is not considered in the model, and all the precipitation over the ocean or sea ice is added directly to the ocean surface layer. Thus

$$ G_i = \frac{{Q_{\text{b}} - Q_{\text{t}} }} {{\rho _i L_{\text{f}} }} - E\frac{{\rho _{\text{o}} }} {{\rho _i }}, $$

(11)

where L _f is the latent heat of fusion of ice. In the open-ocean fraction we take −Q_b, from Eq. 7, to be the largest possible heat flux out of the ocean. Thus if the ocean-to-atmosphere heat flux is greater than this, the deficit leads to ice growth in the open water fraction. In general the growth rate of sea ice in the open-ocean fraction is

$$ G_{\text{o}} = \max \left( {0,\frac{{Q_{\text{b}} - Q_{\text{t}} }} {{\rho _i L_{\text{f}} }}} \right). $$

(12)

We can thus calculate the net growth rate G and the rate of change of the average sea-ice height H, which is also subject to advection by the surface ocean velocity and a diffusive term, which takes the place of a detailed representation of unresolved sea-ice advection and rheological processes. Note that H represents the height of sea ice averaged over both open ocean and ice-covered fractions.

$$ \frac{{DA}} {{Dt}} - \kappa _{{\text{hi}}} \nabla _{\text{h}}^2 H = AG_i + \left( {1 - A} \right)G_{\text{o}} = G, $$

(13)

where κ_hi is a horizontal diffusivity.

The rate of change of sea-ice area A is given by

$$ \frac{{DA}} {{Dt}} - \kappa _{{\text{hi}}} \nabla _{\text{h}}^2 A = \max \left( {0,\left( {1 - A} \right)\frac{{G_{\text{o}} }} {{H_{\text{o}} }}} \right) + \min \left( {0,AG_i \frac{A} {{2H}}} \right). $$

(14)

The first term on the right-hand side parameterizes the possible growth of ice over open water. The effect of this term is that, if G_o is positive, the open water fraction decays exponentially at the rate G_o/H₀, where H₀ is a minimum resolved sea-ice height. The second term parameterizes the possible melting of sea ice and corresponds (by simple geometry) to the rate at which A would decrease if all the sea ice were uniformly distributed in height between 0 and 2H/A over the sea-ice fraction A. Note that this represents a small modification to the original sea ice-area equation proposed by Hibler (1979) in that the decay term is proportional to the (negative) growth rate AG _i over the sea-ice fraction as opposed to the total (negative) growth rate G. The two formulations differ only if sea ice is forming in the open water fraction and simultaneously melting in the ice-covered fraction, in which case using the total growth rate means that melting affects both terms; a form of “double counting”. This is not as unlikely as it sounds since the ice fraction is normally much colder than the water fraction, thus the heat flux deficit causing sea-ice growth in the model is normally smaller over sea ice and can easily be of opposite sign to the deficit over open water.

We can now define the flux of heat into the ocean as

$$ Q_\theta = \left( {1 - A} \right)\max \left( {Q_{\text{b}} ,Q_{\text{t}} } \right) + AQ_{\text{b}} . $$

(15)

The flux of fresh water into the ocean is given by

$$ F_W = P + R - \left( {1 - A} \right)E_{\text{e}} - G\frac{{\rho _i }} {{\rho _{\text{o}} }} - AE_{\text{s}} . $$

(16)

The first two terms represent precipitation and runoff, the third term evaporation, E_e, over open water and the last two ice melting and freezing. The net fresh water source due to melting being proportional to the sink of average sea-ice height minus the net rate of sublimation, denoted E_s here for clarity. The flux of salinity into the ocean is simply taken to be F _S =-S₀F _W , where S₀ is a constant reference salinity (using the local salinity would complicate the calculation of the global freshwater budget).

Finally, we have to ensure, at each timestep, that the calculated sea-ice height H is positive. In practice we ignore the presence of thin ice and set H=0 whenever the calculated value of H is less than H₀. This means that the heat and freshwater fluxes must be modified accordingly for consistency. For positive or negative H, if H is set to zero, the corresponding amount of heat to be added to the ocean is −Hρ _i L_f, while the corresponding amount of fresh water to be added is Hρ _i /ρ_o. In addition, we have to ensure that numerical truncation error does not result in unphysical values of A, A<0 or A>1, but these latter adjustments carry no further implications for the conservation of heat and fresh water.