1 Introduction

Traditional modeling systems can generate complex objects, however, they take too much time for novice users to learn. As one of the most intuitive and simplest ways, drawing is usually one of the best choices for such users. Moreover, it is desirable to express the ideas and visions of designers at the earliest possible stages. Therefore, a lot of sketch-based modeling systems have been developed recently [11, 17, 24, 27, 31].

Rotund objects are usually expected for sketch-based systems. Therefore, convolution surfaces are a good choice for sketch-based modeling because of its pleasing superposition property. A convolution surface is defined by convolving a skeleton with a three-dimensional low-pass filter kernel. The skeletal elements can be points, polylines, polygons, and even volumes. As skeletons are natural abstractions for shapes, convolution surfaces offer a new means for sketch-based surface modeling [1, 2, 27]. In the sketch-based modeling system, constructing a 3D shape based on the 2D silhouette is the most important tool to create new objects [11]. In the convolution surface-based ConvMo system [27], Tai et al. approximate the medial axis of a given silhouette curve as a set of line segments, and create a convolution surface by convolving a linearly weighted kernel along each segment. Later, Alexe et al. perform extraction of a graph of branching polylines and polygons from silhouette contours [2]. The polygons in the graph have to be further triangulated to create the convolution surface of the graph. Unlike these systems, we use the sketched silhouette as a new type of skeleton and compute its convolution surface on the GPU. By converting the double integral over a planar polygon into a simple integration along the contour of the polygon based on Green’s theorem, the triangulation process for the planar polygon, and hence the redundant computations involved are avoided. As a result, our approach allows for parallel computation on the GPU.

The majority of previously available sketch-based modelling systems relying on implicit surfaces used the iso-surface mesh extraction algorithms. However, details may be lost because of the sampling resolution of the polygonization process. This motivates us to render the resulting surface using ray-casting because it allows us to produce high-quality images. As ray-casting convolution surfaces is usually computational intensive, we try to use GPU and the natural bounding volumes of the skeletons to accelerate the ray/surface intersection so that ray-casting can be performed interactively.

The main contributions of the paper are the derivation of closed-form solutions for convolving planar polygon skeletons and its practical use in a prototype sketch-based modeling system on the GPU. We calculate the fields of all the sketched skeletons on the GPU. For a sketched silhouette curve, we convert it into a closed planar polygon and then calculate its field. By transforming the double integral of the polygon into a line integral using Green’s theorem, our solution is both analytical and efficient. A fast ray-casting method is also presented to render high-quality sketched convolution surfaces by making use of parallel computation on the GPU.

The remainder of this paper is organized as follows. After introducing the related work in Sect. 2, we derive the closed-form convolution surface solutions for planar polygon skeletons with both the quartic polynomial kernel (with finite support) and the Cauchy kernel (with infinite support) in Sect. 3. In Sect. 4, a prototype modeling system using the closed-form solutions is presented. The implementation details and some modeling results with our system are discussed in Sect. 5, and our paper ends with the conclusion section.

2 Related work

Different from traditional 3D modeling software packages, sketch-based modeling can be used to create 3D shapes conveniently by novice users without professional skills. Convolution surfaces are often used in such systems because of their smooth blending behavior and automatic changes of topology defined by the underlying skeletons. In this section, we will introduce the related work on convolution surfaces and sketch-based modeling using implicit surfaces.

Convolution surfaces. Implicit surfaces are conveniently adopted to model complex objects, such as tree branches, liquids, and organic shapes. The reason is that the field-based implicit surfaces can easily deal with smooth deformable shapes with varying topologies. Skeleton-based implicit surfaces, including metaballs, distance surfaces, and convolution surfaces, are quite suitable for animation because the skeletons can be directly used for skeleton-based animation. A convolution surface is defined as convolving geometric skeletons (e.g., lines, curves and polygons) with Gaussian kernel functions [5]. Later, many different kernels are introduced. These kernels can be classified into infinite support kernels (e.g., Cauchy kernel [22]) and finite support kernels (e.g., quartic polynomial kernel [15]). For finite support kernels, the field falls to zero when the distance from the point in question to the skeleton is greater than the effective radius of the kernel. For infinite support kernels, the field never falls to zero even the point in question is quite far from the skeleton. Theoretically, any geometric primitive can be used as a skeleton to create convolution surfaces. However, closed-form solutions for convolution surfaces depend on both the kernel functions and the skeleton primitives. Researches show that analytical convolution solutions exist for skeletons such as line segments, planes, triangles, arcs, and quadratic spline curves [12–14, 22, 26]. Before the closed-form solutions for convolving triangle skeletons with quartic polynomial kernels is introduced [15], the analytical convolution solutions for triangle skeletons with Cauchy kernels were presented by McCormack and Sherstyuk [22], which allows the authors of the sketch-based system to create models with planar surfaces [2]. Angelidis et al. [3] model convolution surfaces based on subdivision curves and subdivision surfaces. Another application of closed-form solutions for line skeletons is introduced by Kravtsov et al. [20]. They simulate the interaction of viscous objects with meshes in which a convolution surface is embedded. Recently, Hubert [10] independently derived similar analytical solutions for convolving planar polygon skeletons by applying Green’s theorem.

Sketch-based modeling using implicit surfaces. As implicit surfaces can be merged together naturally and easily, lots of researches adopt implicit surfaces as modeling primitives. These systems include BlobTrees [29, 30], RBF-based [18], and level set-based [7]. Compared to the explicit surface-based sketching modeling system, implicit surface-based methods can design smooth models with complex topology easily. Karpenko et al. [18] propose a sketch-based system using RBF, in which the input sketches are used to generate the 3D constraint points. However, with the increase of the number of constraint points, the system slows down rapidly because of the linear system involved. Moreover, the linear system must be recalculated if a point of the model is modified. BlobTree [30] extends the CSG operations by allowing intuitive global and local operations; it is a tree-based shape representation and has been successfully used in the sketch-based ShapeShop [23, 24] system. As a skeleton-based modeling tool [5], convolution surfaces were naturally introduced into sketch-based modeling [27]. The sketch-based system in [1] extracts the point skeletons of the sketched outlines, and then utilizes spherical implicit functions to construct the blobby 3D models. In order to model complex objects such as cylindrical and planar surfaces, too many point-skeletons are needed to avoid bumps. Cylindrical surfaces can be easily modeled using line skeletons [2, 4, 27], as convolution solutions for line skeletons can be obtained analytically [12–14, 26]. The triangle skeletons are also adopted by the system in [2] to construct the palm component of a hand model where an extracted polygon has to be triangulated in order to allow for the evaluation of its field values.

3 Field value calculation for planar polygon skeletons

In this section, after giving a brief introduction to convolution surfaces, we deduce analytical solutions for planar polygon skeletons with different kernels using a curve integral method. Our approach allows us to efficiently evaluate the field value at any point analytically.

3.1 Convolution surfaces

A convolution surface is an iso-surface defined in an implicit scalar field whose values are evaluated by accumulating contributions from 3D points of a skeleton. The contribution usually decreases rapidly when the distance between a point in space and a skeleton is increased. Here, we adopt the convolution surface definition by McCormack and Sherstyuk [22]. Let p(x,y,z) be a space point in ℜ3, and g:ℜ3→ℜ be a geometric function representing a modeling skeleton V:

$$ g( \mathbf{p} ) = \left\{\begin{array}{l@{\quad }l}1, &\mathbf{p} \in\ \text{skeleton}\ V \\0, &\text{otherwise} \\\end{array}. \right.$$
(1)

Let f:ℜ3→ℜ be a potential function which defines the field with a single point in the skeleton V, and let q be a point in V. Then the total field value contributed by the skeleton at point p is the convolution of functions f and g:

$$ F( \mathbf{p} ) = \int_V g( \mathbf{q} )f( \mathbf{p} - \mathbf{q} )\,dV = ( f \otimes g )(\mathbf{p} ).$$
(2)

f is also called the convolution kernel function. Theoretically, any geometric primitive can be used as a skeleton. However, closed-form solutions depend on both the kernel and the skeleton.

3.2 Curve integral for planar polygon skeletons

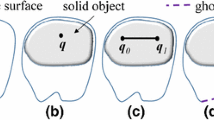
Let K(v 0 v 1 v 2⋯v n v 0) be a planar polygon skeleton, the field value at a point p for this skeleton is computed by a double integral according to (2). For a kernel function with infinite support, the integration is evaluated on the entire polygon. However, for a finite support kernel function, the valid skeletons are areas in the clipping sphere centered at p, as shown in Fig. 1(a). Generally, the intersecting area is a polygon or multiple polygons whose boundaries consist of arcs and line segments. It is difficult to perform the integration on the intersecting area directly. One solution is to decompose the polygon into triangle segments and chord segments, and then evaluate the convolution integral for each type [15], as shown in Fig. 1(b). However, such a solution is not suitable for GPU implementation because GPU branching is usually slow. Here, we present a closed-form solution by converting the double integral into a curve integral using Green’s theorem. As the integral computation can be performed for each edge one by one, we can make better use of the GPU’s enormous floating point computing capacity.

Fig. 1
figure 1

The regions for the convolution integral. The valid polygon skeleton for finite support kernels is shadowed in (a). Illustration in (b) triangulates the polygon before using closed-form convolution surface solutions for triangle skeletons. (c) shows our clipping between a general polygon and the clipping sphere

Full size image

The field value at point p for a planar polygon skeleton can be computed directly without the polygon triangulation. With the integration domain D and its boundary l, the field value at point p is:

$$ F(\mathbf{p}) = \iint_D f(r)\,dx\,dy,$$
(3)

where r=∥p−q∥ denotes the Euclidean distance between points p and q, q∈D. This double integral can be computed by converting it into a curve integration using Green’s theorem [28]:

$$ \iint_D \biggl( \frac{\partial Q}{\partial x} - \frac {\partial P}{\partial y} \biggr)\,dx\,dy = \oint_l P\,dx + Q\,dy,$$
(4)

where P and Q are functions with continuous first-order derivatives. In order to satisfy (4), P and Q must be designed elaborately. Here, we set P=0 and rewrite (4) as follows:

$$ \iint_D \biggl( \frac{\partial Q}{\partial x} - \frac {\partial P}{\partial y} \biggr)\,dx\,dy = \iint_D \frac {\partial Q}{\partial x}\,dx\,dy = \oint_l Q\,dy.$$
(5)

In our case, the boundary l consists of arcs and line segments. Taking Fig. 1(a) as an example, the boundary of the integration domain D includes an arc and five line segments. The field contribution at P is the sum of the integrals along each boundary primitive:

(6)

Once the kernel function is chosen, the continuous function Q can be determined. In the next three subsections, we will deduce the analytical field functions for two commonly used field functions which are adopted in our system.

3.3 Evaluation of a valid skeleton for planar polygons

In this section, we will discuss how to compute the valid skeleton for a planar polygon skeleton. As we convert the double integral into a line integral, the valid skeleton for infinite support kernels is just the union of the edges of the polygon. However, for finite support kernels, a key step is to determine the valid skeletons which have field contribution.

For a 3D point p, let R be the effective radius of the finite support kernel, we define the sphere centered at p with radius R as the clipping sphere. We compute the valid skeleton by adopting an approach similar to the Weiler–Atherton polygon clipping algorithm [6]. In our case, the clipping window is a clipping circle. The circle is the intersection of the clipping sphere and the plane the polygon lies. Given a polygon K(v 0 v 1 v 2⋯v n v 0) (here, we take n=9 as an example in Fig. 1(c)) and a circle C, the boundary of the intersection consists of some boundaries from K and C. Connecting the intersection points forms the boundary. The intersection points are classified into income point at which the boundary of K comes into the circle and outcome point.

We use Algorithm 1 to describe the clipping algorithm. After applying the clipping algorithm to the given polygon, a set of vertices are obtained. They are intersection points and some polygon vertices. Two adjacent vertices form a path of our convolution integral. The path is either a line segment or an arc. For two adjacent vertices, if one of them is a vertex of the polygon, then the path is a line segment. Otherwise, both of them are intersection points. In this case, if the first vertex is an income point, then the path is a line segment; otherwise, the path is an arc. Taking Fig. 1(c) as an example, after performing the intersection calculation, we create a vertex list L K of the given polygon K(v 0 v 1 v 2⋯v 9 v 0) and a list L C for the clipping circle. The intersection points \(\mathbf{v}'_{1}\), \(\mathbf {v}'_{2}\), \(\mathbf{v}'_{3}\), \(\mathbf{v}'_{4}\), \(\mathbf{v}'_{5}\), \(\mathbf{v}'_{6}\) will be inserted into two lists L K and L C , and a double pointer will be created at each intersection point between two lists, as shown in Fig. 2(a). In the clipping procedure, we choose an intersection point with an income point flag as the start point for tracing. As shown in Fig. 2(b), \(\mathbf{v}'_{2}\) is the start point which is flagged with a small red triangle. By tracing two lists, a set of resulting points, L r,1 is obtained. The second tracing is shown in Fig. 2(c). After clipping, there are two subpolygons stored in the resulting lists L r,1 and L r,2.

Algorithm 1
figure 2

Skeleton clipping

Full size image
Fig. 2
figure 3

The polygon clipping procedure. The intersection points were inserted into Lists L K and L C with a double link in (a). Two new sub-polygons were created in (b) and (c)

Full size image

However, it will consume a lot of GPU memory if we store list L K for each thread on the GPU. We solve this problem by performing the convolution integral as soon as a valid line skeleton is available. In this way, we need not store L K at all. The list L C for valid arc skeletons is created by inserting the intersection point with flag income point or outcome point. As the list L C is usually not too long, we can store it in the local memory of each thread. A list of sixteen intersection points is empirically enough in our implementation. Taking Fig. 1(c) as an example, as soon as a clipped line segment (\(\mathbf{v}'_{2}\mathbf{v}_{1}, \mathbf {v}_{1}\mathbf{v}'_{1}, \mathbf{v}'_{4}\mathbf{v}_{8}, \mathbf{v}_{8}\mathbf {v}'_{5}\), or \(\mathbf{v}'_{6}\mathbf{v}'_{3}\)) between the clipping sphere and the planar polygon skeleton is obtained, we calculate its integral. In the meantime, we store the intersection points (\(\mathbf{v}'_{2},\mathbf{v}'_{1}, \mathbf{v}'_{4}, \mathbf{v}'_{5}, \mathbf{v}'_{6}\), and \(\mathbf{v}'_{3}\)) in list L C . Then we calculate the algebraic sum of integrals along the clipped arcs.

3.4 Finite support kernel functions

If we take the following quartic polynomial as the kernel function:

$$ f(r) = \left\{\begin{array}{l@{\quad }l}(1 - \frac{r^2}{R^2 })^2 , & r \le R \\0, & r > R \\\end{array}, \right.$$
(7)

where R is the effective radius of the kernel, the analytic solution of (5) can be obtained by using the curve integral method:

$$ \iint_D \frac{\partial Q}{\partial x}\,dx\,dy = \oint_l \biggl( \int{\frac{\partial Q}{\partial x}\,dx} \biggr)\,dy.$$
(8)

To deduce the solution conveniently, in polygon K, we set up a local coordinate system whose origin is the projection point of p on the polygon. Two coordinate axes x and y are any two orthogonal vectors. Here, we set the x-axis parallel with one edge of the polygon and the y-axis perpendicular with x-axis, then the z-axis is the cross product of x and y. In Fig. 1, the x-axis and edge v 1 v 2 are parallel. In the new coordinate system, p=(0,0,z 0), where z 0 is the distance from p to the plane where polygon K lies. From (7) and (8), we can get the following equation:

(9)

where \(r_{0}^{2} = R^{2} - z_{0}^{2}\), and \(M = \frac{x^{5} }{5} - \frac{2}{3}x^{3}( r_{0}^{2} - y^{2} ) + x( r_{0}^{2} - y^{2} )^{2}\). By calculating the integrals along arcs and line segments respectively, we can obtain the field for p.

  1. (1)

    The integration along an arc c i

    Let (x,y)=(r 0cosθ,r 0sinθ), and (dx,dy)=(−r 0sinθ, r 0cosθ)dθ, from (9) we can obtain

    (10)

    where θ 1,θ 2 are corresponding angles of the start point and the end point of arc c i .

  2. (2)

    The integration along a line segment l j

    A line segment from v j (x j ,y j ) to v j+1(x j+1,y j+1) can be represented in a parametric form as following:

    $$ \left\{\begin{array}{l}x = x_j + (x_{j + 1} - x_j )t = x_j + at \\y = y_j + (y_{j + 1} - y_j )t = y_j + bt \\\end{array} \right.,\quad 0 \le t \le1.$$
    (11)

    It is easy to know that dx=(x j+1−x j )dt=adt, dy=(y j+1−y j )dt=bdt, where a=x j+1−x j , b=y j+1−y j . Then we can obtain:

    (12)

    where

3.5 Infinite support kernel functions

Infinite support kernel functions, such as Gaussian kernel, Cauchy kernel and power inverse kernel, are also well adopted in convolution surface modeling. For such kernels, skeletons impose contributions to any point in question even if its distance to the skeleton is large.

Here, we take the Cauchy kernel function as an example to deduce the analytical field function:

$$ f( r ) = \frac{1}{( 1 + s^2 r^2 )^2 },$$
(13)

where s is a parameter to control the width of the kernel.

The field for point p can be computed according to (3), (5):

(14)

where \(m = z_{0}^{2} + \frac{1}{s^{2} }\), and

$$M = \frac{x}{2( m +y^2 )( m + x^2 + y^2 )} + \frac{\arctan(\frac{x}{\sqrt{m + y^2 } } )}{2(m + y^2 )^{3/2} }.$$

As the Cauchy kernel function is infinite support, the boundary of the integration domain must be the line segments of planar polygon skeletons. Then the curve integral can be rewritten as:

$$ \oint_l M\,dy = \sum_i \int_{l_i } M\,dy.$$
(15)

For each line segment, we also use its parametric representation as shown in (11). The integral over a line segment l i (v i v i+1) can be computed as:

(16)

where

4 Prototype modeling system

In this section, we introduce a prototype modeling system which employs the analytical solutions. To accelerate the ray-casting of the resulting surface, we make full use of the bounding volumes of the skeletons. As a result, the ray-casting of the created shapes can be performed in an interactive way.

4.1 Modeling framework

The input to our prototype modeling system is a set of sketched skeletons, including points, polylines and polygons. Their geometry can be modified interactively. Our system outputs a polygonal mesh generated by the marching cubes algorithm implemented on the GPU. High-quality images of the created surfaces are rendered interactively using a ray-casting algorithm on the GPU. The framework for our modeling system is illustrated in Fig. 3, which we describe further in the text.

Fig. 3
figure 4

The modeling framework. The model in (a) is a sketched silhouette which is used to create the convolution surface in (b). The figures in (c) and (d) illustrate the added components and edition of the component respectively. The overall skeletons can be seen in (e), and the final shape is rendered using marching cubes (f) and ray-casting (g)

Full size image

Step 1. The user draws a 2D shape (or points, polylines) as the skeleton on a projection plane. Here, the sketched silhouette polygon is used for surface modeling in Step 2 directly. This step is performed on the CPU.

Step 2. The system generates a rotund generic convolution surface model using analytical field computation solutions (Sect. 3). Polynomial weighted distributions are employed for polyline skeletons [12]. For finite support kernels, the system calculates the valid part of the skeleton. A skeleton clipping algorithm is presented for finite support kernels (Sect. 3.3). The valid skeleton calculation and the field value computation are both performed on the GPU. A GPU version of marching cubes algorithm [9, 21] is provided to visualize the modeling surface.

Step 3. The user performs further editing operations on existing skeletons, such as editing the skeleton geometry, the weighting of parameters, and the kernel functions.

Step 4. In order to design complex shapes, the user rotates the partially designed shape to obtain a new projection plane, and repeats steps 1–3 to design another surface component, which can be merged smoothly with existing components.

Step 5. After the user finishes the design, an accurate visualizing result can be rendered interactively with a ray-casting algorithm for convolution surfaces (Sect. 4.2). This step is also performed on the GPU.

In this framework, step 1, step 3, and step 4 are common steps for a sketch-based modeling system using implicit surfaces. Our paper focuses on step 2 and step 5.

4.2 Ray-casting convolution surfaces on the GPU

Generally, there are mainly two methods to render implicit surfaces: ray-casting and polygonization. Polygonization is an indirect method which tessellates implicit surfaces into polygons within a given tolerance. On the contrary, ray-casting is an important direct rendering method. Compared to polygonization, it provides an accurate rendering method for visualizing implicit surfaces although it is slow. In our sketch-based modeling system, both interactive polygonization and ray-casting are supported. The sketched models with high resolution can be interactively generated with marching cubes on the GPU in our system, so the updated shape can be rendered interactively with new sketches.

As the intersection between a ray and the convolution surface is difficult to obtain analytically, iterative algorithms, such as the interval algorithm, Bezier clipping, the secant method, and the bisection method, are frequently adopted. Here, we use the bisection method. To provide interactive feedback, we use GPU and the bounding volumes of the skeletons to accelerate the rendering process. Our rendering can be made even faster if we employ advanced ray-casting techniques [8, 16, 19].

4.2.1 Bounding volume construction

The intersection point can be efficiently calculated if we can obtain the interval containing only the first intersection point. Similar to [25], we employ the bounding volume of the skeleton to isolate the domain which contains the ray/surface intersections. This will accelerate the intersection calculation significantly. The construction of bounding volumes for different primitives are illustrated in Table 1. Figure 4 shows a group of sketched skeletons and their corresponding bounding volumes.

Fig. 4
figure 5

Sketched skeletons (left) and bounding volume (right) of a chair

Full size image
Table 1 Bounding volumes of primitives
Full size table

4.2.2 Offset distance for computing the bounding volume

For a finite support kernel function, its corresponding offset distance d used for computing the bounding volume is just its effective radius. For the Cauchy kernel, as an unbounded plane has the following field function [22]:

(17)

we calculate d so that it satisfies the following equation:

$$ \frac{\pi}{s^2 ( 1 + s^2 d^2 )} = \frac{T}{N},$$
(18)

where T is the threshold of the resulting implicit surface and N is the maximum number of skeletons within a clipping sphere. It is easy to follow that:

$$ d = \frac{1}{s}\sqrt{\frac{N\pi}{Ts^2 } - 1}.$$
(19)

4.2.3 Finding the intersection point

In general, it is hard to determine the suitable step-size for searching an intersection point. In our case, as the intersection point is isolated within the bounding volume of the skeleton, we set the initial step-size for marching forward as half the bounding radius. In this way, it is not easy to miss the first intersection even if the step-size is longer than needed. That is, if the first intersection is lost, we can detect it with the negative derivative D f along the ray, and then step backwards with half the step-size and so forth. As illustrated in Fig. 5, points P 1 and P 2 are outside of the convolution surface and their derivatives along the ray are positive, so we step forwards with the current step-size to point P 3. P 3 is outside of the surface, and the derivative at P 3 is negative, so it is necessary to step backward with half the step-size to Q 1 which is within the surface. Then we can perform the bisection/secant/regula falsi algorithm between point P 2 and Q 1 until a point is found which is close enough to the convolution surface within the prescribed tolerance.

Fig. 5
figure 6

Adaptive bisection marching

Full size image

Our ray-casting is performed on GPU using a thread for each pixel. The vertices of the sketched planar polygons are stored as textures on GPU (Fig. 6).

Fig. 6
figure 7

Skeletons of a chair (left), ray-casting images with Cauchy kernel (middle) and quartic polynomial kernel (right)

Full size image

5 Results

Our prototype system is tested on a PC with a 2.67 GHz Intel Core 2 Quad 9400 CPU (only 1 core is used) with 3 GB main memory, and an NVIDIA GeForce GTX 260 GPU (with 27 stream multiprocessors) with 896 MB graphics memory. For such a sketched modeling system, surface creation and visualization are the bottlenecks as they involve massive field computation. In our approach, after transferring the skeletal data into the graphics card, the evaluation of the field is performed on the GPU, which allows us to create and visualize convolution surfaces interactively. The results (Fig. 3, Fig. 6, Fig. 7) in this paper are all interactively sketched with our system. The resolution for marching cubes algorithm is 128×128×128, and the screen resolution for ray-casting convolution surfaces is 512×512.

Fig. 7
figure 8

The leftmost column shows the sketched skeletons. The second and the third columns show results rendered with marching cubes and ray-casting respectively using the quartic polynomial kernel. The last two columns show results rendered with marching cubes and ray-casting respectively using the Cauchy kernel

Full size image

A user interface similar to ShapeShop [23] is developed in our system. The user can add, delete, and modify skeletons. With the analytical solutions and the adoption of GPU, the reextraction of the updated iso-surface can be performed interactively without any special data structure. In addition, various skeletons are supported in our system, such as points, lines, and planar polygon skeletons. Our system is convenient for modeling complex objects with arbitrary topology. Multiple components can be fused together smoothly and trivially. Figure 7 shows some sketched models with their skeletons, rendered with marching cubes and ray-casting.

To test the efficiency of our novel analytical solution for planar polygon skeletons, we have compared three different strategies to calculate the potential field values. (1) DIT: Convolution with double integral based on the triangulated polygon; (2) CIT: Convolution with curve integral based on the triangulated polygon; (3) CI: Convolution with curve integral based on the polygon (ours). The statistical results for two examples shown in Fig. 8 are listed in Table 2. The time listed in Table 2 is the total time to calculate the potential field values for all the vertices of cubes (with the resolution 128×128×128). We label the calculation time in the form of “α_β_γ”, where α represents the kernel type (quartic polynomial kernel or Cauchy kernel), β represents the processor (CPU or GPU), and γ represents the integration type (DIT, CIT or CI). The results show that our method has the best performance both on CPU and GPU. For the triangulation strategies, we have not counted in the consumed time for triangulation and the additional time and memory to transfer the triangles to GPU.

Fig. 8
figure 9

The figure on the left and the figure on the right show Ex1 and Ex2, respectively, for comparing calculation time

Full size image
Table 2 Comparison of calculation time (s)
Full size table

6 Conclusions and discussions

We have derived analytical convolution solutions for the planar polygon skeletons which are commonly used to model 3D objects. Our solution proves to be more efficient than the brute-force based triangulation method. Furthermore, we have presented a sketch-based prototype modeling system using closed-form solutions for convolution surfaces on the GPU. Since skeletons are good abstractions for 3D objects and convolution surface is a skeleton driven modeling tool, our approach can create many aesthetically pleasing models with complex topology easily.

Compared to existing sketched-based modeling systems using convolution surfaces, our approach is easy to create flat surfaces (as shown in Fig. 3, Fig. 6, and Fig. 7), which are difficult to create using ConvMo [27]. On the other hand, this can be considered as a limitation of our approach because the result is different from the inflation operation in Teddy [11]. A set of functions provided by our prototype system is not as complete as in other sketch-based modeling systems. Currently, our system can ray-cast convolution surfaces with about twenty skeletons (each of which has about twenty vertices) interactively. For more complex skeletons, we plan to employ advanced ray-casting acceleration solutions [8, 16, 19].