A cubic B-spline quasi-interpolation algorithm to capture the pattern formation of coupled reaction-diffusion models

Abstract

Diffusion plays a significant role in complex pattern formulations occurred in biological and chemical reactions. In this work, the authors study the effect of diffusion in coupled reaction-diffusion systems named the Gray-Scott model for complex pattern formation with the help of cubic B-spline quasi-interpolation (CBSQI) method and capture various formates of these patterns. The idea of Kronecker product is used first time with CBSQI method for 2D problems. Linear stability analysis of the reaction-diffusion system as well as stability of the proposed method is studied. Four test problems are considered to check the accuracy and efficiency of the method and found the stable patterns.

1 Introduction

Turing patterns [1] play a significant role in characterizing the biological and chemical reactions. Mathematical modeling, in the form of biological and chemical phenomena is a very important tool to study a variety of patterns of chemical species. The reaction-diffusion system illustrates the effect of some special types of two chemical species V and W. Let variables v and w are the concentration of these chemicals respectively. So as usual, both chemicals react with each other and then diffusion takes place in the medium and over the time passes concentration of V and W also change at every position. In this model, simultaneously two reactions take place with different rates throughout the medium

$$\begin{aligned} \left\{ \begin{array}{l} V+2W \rightarrow 3W \\ \\ W \rightarrow {\mathbb {P}} \end{array}, \right. \end{aligned}$$

where ${\mathbb {P}}$ is the inert product. For the simplicity of this work, it is assumed that reverse reaction does not take place.

The complete nature of the system described by the following model [2,3,4]

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial v}{\partial t}=d_1 \nabla ^2 v- vw^2+\gamma (1-v) \\ \\ \dfrac{\partial w}{\partial t}=d_2 \nabla^2 w+vw^2-(\gamma +\kappa )w, \end{array} \right. \end{aligned}$$

(1)

where $d_1$ and $d_2$ represent diffusion coefficients for velocities v and w, and $\nabla ^2$ represent the Laplace operator. The first term of the equation $\nabla ^2 v$ is the diffusion term. It is well known that if the concentration of V is less in its neighboring areas then $\nabla ^2 v$ will be negative and so v decreases. On the other hand, if the concentration is high in its neighboring areas then v will increase. The second term $-vw^2$ is called the reaction rate. It is clear from the above equations that the quantity of w increases in the same proportion as the quantity of v decreases. However, there is no constraint on reaction terms, but the relative concentration of the remaining terms can be balanced by constants $d_1, d_2,\gamma$ and $\kappa$. The third term $\gamma (1-v)$ is called the replenishment term. In this reaction, the quantity of v decreases eventually up to the level of refill it again and then generates w. The replenishing term says that v will be grown up in proportional to the difference between the current level and 1. Therefore, even if there is no other term then v will take the maximum value 1. The main difference between the above equations is in the third term, i.e., $\gamma (1-v)$ in first and $-(\gamma +\kappa )$ in second. The term $-(\gamma +\kappa )$ is called diminishing term because in the absence of this term w is increased drastically. Further, it diffuses out of the system at the same rate as it generates a new supply of v.

In this work, the authors attempt to capture a variety of patterns for different values of parameters $d_1, d_2, \gamma$ and $\kappa$ in nonlinear time-dependent coupled reaction-diffusion model (1) in one and two-dimensional formats with the following initial and boundary conditions

For 1-D problems

$$\begin{aligned}&v(x,0)=g_1(x),\qquad \qquad w(x,0)=g_2(x), \qquad \nonumber \\&\quad x\in \varOmega =[l_1,l_2] \end{aligned}$$

(2)

$$\begin{aligned}&v(l_1,t)=h_1(t),\, v(l_2,t)=h_2(t),\; w(l_1,t)=h_3(t),\,\nonumber \\&\quad w(l_2,t)=h_4(t),\;\, t\in (0,T].\;\;\, \end{aligned}$$

(3)

For 2-D problems

$$\begin{aligned}&v(x,y,0)=f_1(x,y),\quad w(x,y,0)=f_2(x,y), \nonumber \\&\quad (x,y)\in {\bar{\varOmega }}=[\alpha ,\beta ]\times [\gamma ,\delta ]\;\; \end{aligned}$$

(4)

$$\begin{aligned}&\dfrac{\partial v(x,y,t)}{\partial n}=\dfrac{\partial w(x,y,t)}{\partial n}=0. \nonumber \\&\quad (x,y,t)\in \partial {\bar{\varOmega }}\times [0,T]. \end{aligned}$$

(5)

The recent study of pattern formation in epidemic model has been studied by [5]. The amplitude equation for reversible Sel’kov has been studied in [6]. A specific type of reaction-diffusion model called cherite iodide malonic acid (CIMA) is used by Lee and Cho [7]. Some rigorous biological models and their pattern formation presented by [8]. The cross-diffusion phenomena, in which the concentration of one chemical species affects the other species has been proposed in [9,10,11]. Othmer and Scriven [12] presented the dynamical instability and its Turing pattern in the cellular networks. For the random network system, the Turing patterns have been studied in [13,14,15]. They have also compared their model with the classical models. The stability of the nonlinear dynamical models has been studied in [16, 17]. Also, the problems related to the stochastic control have attracted the researchers [18,19,20]. Hole et al. [21] discussed a 1-D Gray-Scott system and captured its nontrivial stationary Turing patterns. Kolokolnikov et al. [22] presented the solution of the 2-D Gray-Scott system and discussed its instability of equilibrium stripe in two different ways. Zheng et al. [23] studied the pattern formation of the reaction-diffusion immune system and also discuss its controllability over to the different patterns. Sayama [3] studied many complex structures and analyze their pattern and stability. Mittal and Rohila [4] proposed a differential quadrature scheme to solved some reaction-diffusion models. Jiwari et al. [2] captured the Turing pattern formation of nonlinear coupled reaction-diffusion systems. The solutions of the 2-D Gray-Scott model and their nonuniform Turing studied by Castelli [24]. McGough and Riley [25] studied the complex Turing pattern in Gray-Scott model. Yadav and Jiwari [26] solved the Brusselator model by finite element and studied its pattern formation. The artificial and biological immune system has many applications such as in homeostasis, adaptability and immunity are discussed in [27,28,29,30].

To begin with, we present some of the most relevant and substantial works that are fundamental to the proposed study. To approximate a function and its first-order derivative, a pioneer work was proposed by Sablonnière [31, 32], which deployed a discrete univariate B-spline quasi-interpolation technique. The claims of the author were ascertained by verifying the first-order derivative of a certain class of functions by the proposed method. In addition to this, the work even superseded the earlier known method of approximating the derivatives by finite difference method. The author observed the convergence of order $O(h^4)$ for approximating the first-order derivate of a certain class of functions using cubic spline interpolation. Based on this fundamental work, the research community has since then proposed efficient numerical schemes for solving partial differential equations. The application of the algorithm was seen in the works of Zhu and Kang [33, 34], in which they solved hyperbolic conservation laws. Quadratic and cubic B-spline technique was proposed by Kumar and Baskar [35] in which the numerical schemes of higher order were developed for solving 1-D Sobolov type equations.

Analyzing the aforementioned work, we inferred that, majority of the work done in numerically solving these PDEs has been limited to 1-D space, and apart from Mittal et al. [36] that solve a 2-D advection-diffusion problem, scarcely can one find these techniques being applied for higher-order dimensions. In the proposed work, we put forth a numerical scheme based on CBSQI for solving 1-D and 2-D reaction-diffusion equations. The 2-D partial order derivatives are approximated using the Kronecker product and 1-D coefficient matrices of derivatives. Also, we have discussed the linear stability of the given system. However, for the non-linear dynamical system, linear stability analysis doesn’t give the complete detail about its asymptotic behaviour at large. But, for many applications, it is very important, especially where the main interest is how the system sustains its state at or around its equilibrium point.

2 Linear stability investigation of reaction-diffusion system

It is well known that linear-stability of continuous field models (without reaction term) produces a strong condition analytically such that a spatial system loses stability of its homogeneous equilibrium state and immediately forms a non-homogeneous spatial pattern. Here, dealing with homogeneous equilibrium state means along a line or curve that covers the considered domain.

However, for the reaction-diffusion system we can’t find such stability condition analytically. So, we used idea of Jacobian matrix for its stability and then conclude by analyzing its eigenvalues.

Now, consider the following standard reaction-diffusion system to investigate the linear stability:

$$\begin{aligned} \dfrac{\partial v_1}{\partial t}= &\, {} d_1\nabla ^2 v_1 +\mathfrak {R}_1(v_1,v_2) \end{aligned}$$

(6)

$$\begin{aligned} \dfrac{\partial v_2}{\partial t}= &\, {} d_2\nabla ^2 v_2 +\mathfrak {R}_2(v_1,v_2). \end{aligned}$$

(7)

For equilibrium state $v_{{i{\text {eq}}}}$ no longer depend on space or time, so $(v_{{1{\text {eq}}}}, v_{{2{\text {eq}}}})$, is a solution of the following equations:

$$\begin{aligned} 0= &\, {} \mathfrak {R}_1(v_{{1{\text {eq}}}},v_{{2{\text {eq}}}}) \end{aligned}$$

(8)

$$\begin{aligned} 0= &\, {} \mathfrak {R}_2(v_{{1{\text {eq}}}},v_{{2{\text {eq}}}}). \end{aligned}$$

(9)

Now, we perturb the original state variables by introducing the equilibrium state as follows:

$$\begin{aligned}&v_i(x,t)\Rightarrow v_{{i{\text {eq}}}}+\varDelta v_i(x,t)=v_{{i{\text {eq}}}}\\&\quad +\sin (\omega x+\psi )\varDelta v_i(x,t) \quad \text {for all} \,i. \end{aligned}$$

Using these replacement, dynamical equations can be rewrite as

$$\begin{aligned}&\sin (\omega x+\psi )\dfrac{\partial \varDelta v_1}{\partial t}\\&\quad =\mathfrak {R}_1(v_{{1{\text {eq}}}}+\sin (\omega x+\psi )\varDelta v_1,v_{{2{\text {eq}}}}+\sin (\omega x+\psi )\varDelta v_2)\\&\qquad -d_1\omega ^2\sin (\omega x+\psi )\varDelta v_1 \\&\sin (\omega x+\psi )\dfrac{\partial \varDelta v_2}{\partial t}\\&\quad =\mathfrak {R}_1(v_{{1{\text {eq}}}}+\sin (\omega x+\psi )\varDelta v_1,v_{{2{\text {eq}}}}+\sin (\omega x+\psi )\varDelta v_2)\\&\qquad -d_2\omega ^2\sin (\omega x+\psi )\varDelta v_2. \end{aligned}$$

These equations can be summarized in a single vector form about $\varDelta V$

$$\begin{aligned} \sin (\omega x+\psi )\dfrac{\partial \varDelta V}{\partial t}= &\, {} \mathfrak {R}(V_{{{\text {eq}}}}+\sin (\omega x+\psi )\varDelta V)\nonumber \\&-d\omega ^2\sin (\omega x+\psi )\varDelta V, \quad \end{aligned}$$

(10)

where vector $\mathfrak {R}$ represents the reaction terms and d denotes the diagonal matrix whose diagonal entries are $d_i$ at ith place. Now, it is well known that except reaction term all the terms have been simplified easily. So the remaining task is to linearize the reaction term. Therefore, the Jacobian matrix is introduced for the linearization of the reaction term. If there is no spatial operator in reaction terms then these terms are local. Now, we use the idea of linear stability i.e., rewrite the dynamics by adding a small perturbation at equilibrium state. Therefore the vector function $\mathfrak {R}(V_{{{\text {eq}}}}+\sin (\omega x+\psi )\varDelta V)$ can be linearly approximated as follows:

$$\begin{aligned}&\mathfrak {R}(V_{{{\text {eq}}}}+\sin (\omega x+\psi )\varDelta V) \nonumber \\&\quad \approx \mathfrak {R}(V_{{{\text {eq}}}})+ \begin{pmatrix} \dfrac{\partial \mathfrak {R}_1}{\partial v_1} &{}\dfrac{\partial \mathfrak {R}_1}{\partial v_2} \\ \dfrac{\partial \mathfrak {R}_2}{\partial v_1} &{}\dfrac{\partial \mathfrak {R}_2}{\partial v_2} \end{pmatrix}\Bigg |_{V=V_{eq}} \sin (\omega x+\psi )\varDelta V \nonumber \\&\quad =\sin (\omega x+\psi ) \begin{pmatrix} \dfrac{\partial \mathfrak {R}_1}{\partial v_1} &{}\dfrac{\partial \mathfrak {R}_1}{\partial v_2} \\ \dfrac{\partial \mathfrak {R}_2}{\partial v_1} &{}\dfrac{\partial \mathfrak {R}_2}{\partial v_2} \end{pmatrix}\Bigg |_{V=V_{{{\text {eq}}}}} \varDelta V, \end{aligned}$$

(11)

from Eqs. (8) to (9), $\mathfrak {R}(V_{{{\text {eq}}}})$ become zero. Therefore Eq. (10) can be write as

$$\begin{aligned} \sin (\omega x+\psi )\dfrac{\partial \varDelta V}{\partial t}= &\, {} \sin (\omega x+\psi ) J\big |_{V=V_{{{\text {eq}}}}}\varDelta V\nonumber \\&-d\omega ^2\sin (\omega x+\psi ) \varDelta V\nonumber \\ \dfrac{\partial \varDelta V}{\partial t}= &\, {} \big (J-d \omega ^2\big )\big |_{V=V_{{{\text {eq}}}}} \varDelta V, \end{aligned}$$

(12)

where J denotes the Jacobian matrix of reaction terms and $\omega$ is representing the spatial frequency of perturbation. Hence, the stability of the system can be described by evaluating its eigenvalues at its homogeneous state.

This simple result for linear stability can be obtained because of the clear separation of diffusion and reaction terms in reaction-diffusion systems.

We can now apply the above result to the following system:

$$\begin{aligned} \left. \begin{array}{l} \dfrac{\partial v}{\partial t}=\alpha _1(v-h_1)+\beta _1(w-k_1)+d_1 \nabla^2 v, \\ \\ \dfrac{\partial w}{\partial t}=\alpha _2(v-h_1)+\beta _2(w-k_1)+d_2 \nabla^2 w \end{array} \right\} . \end{aligned}$$

(13)

Using the discussed result, we get

$$\begin{aligned}&\Bigg (\begin{pmatrix} \alpha _1 &{}\beta _1 \\ \alpha _2 &{}\beta _2 \end{pmatrix}- \begin{pmatrix} d_1 &{}0 \\ 0 &{}d_2 \end{pmatrix}\omega ^2\Bigg )\Bigg |_{(v,w)=(h_1,k_1)}\nonumber \\&\quad =\begin{pmatrix} \alpha _1-d_1\omega ^2 &{}\beta _1 \\ \alpha _2 &{}\beta _2-d_2\omega ^2 \end{pmatrix}. \end{aligned}$$

(14)

It is a well-known result for the stability of a matrix that, the trace must be negative and determinant must be positive. Therefore, this system with its the homogeneous equilibrium state is stable if the following two inequalities are true for all real values of $\omega$:

$$\begin{aligned}&(\alpha _1-d_1\omega ^2)(\beta _2-d_2\omega ^2)-\alpha _2\beta _1>0 \end{aligned}$$

(15)

$$\begin{aligned}&\alpha _1-d_1\omega ^2+\beta _2-d_2\omega ^2<0, \end{aligned}$$

(16)

for simplification we use $\text {det}({\mathbb {A}})$ and $\text {Tr}({\mathbb {A}})$ of a matrix $\begin{pmatrix} \alpha _1 &{}\beta _1 \\ \alpha _2 &{}\beta _2 \end{pmatrix}$, now above Eqs. (15)–(16) can rewritten as:

$$\begin{aligned}&\alpha _1d_2\omega ^2 +\beta _2d_1\omega ^2-d_1d_2\omega ^4< \text {det}({\mathbb {A}}) \end{aligned}$$

(17)

$$\begin{aligned}&d_1\omega ^2+d_2\omega ^2>\text {Tr}({\mathbb {A}}). \end{aligned}$$

(18)

Let us assume that the model was stable without diffusion terms, i.e., $\text {det}({\mathbb {A}})>0$ and $\text {Tr}({\mathbb {A}})<0$. Now, we try to find out the possibilities for the system becoming destabilized by itself by introducing the diffusion term to it.

As it is clear from the second inequality that the left-hand side is always positive. So for the negative $-\text {Tr}({\mathbb {A}})$, second inequality is always true. But, the first-inequality can be violated, if the following equation have a positive value for $z>0$.

$$\begin{aligned}&g(z)=-d_1d_2z^2+(\alpha _1d_2+\beta _2 d_1)z-\text {det}({\mathbb {A}}), \nonumber \\&\quad \text {where} \,z=\omega ^2 \end{aligned}$$

(19)

or

$$\begin{aligned} g(z)= &\, {} -d_1d_2\Big (z-\dfrac{\alpha _1d_2+\beta _2d_1}{2d_1d_2}\Big )^2\nonumber \\&+\dfrac{(\alpha _1d_2+\beta _2 d_1)^2}{4d_1d_2}z-\text {det}({\mathbb {A}}). \end{aligned}$$

(20)

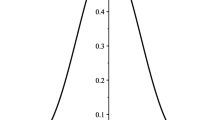
There are two possibilities for the above polynomial that can give positive value for some $z>0$, as shown in Fig. 1.

Fig. 1

Possible cases for g(z) in which it can give positive value

Case-1 If the peak of g(z) is in the positive side of z, e.i., $(\alpha _1d_2+\beta _2 d_1)>0$ Fig. 1a, then the condition is that the peak should stick out above the z-axis

$$\begin{aligned} \dfrac{(\alpha _1d_2+\beta _2 d_1)^2}{4d_1d_2}z-\text {det}({\mathbb {A}})>0. \end{aligned}$$

(21)

Case-2 If peak of g(z) is in the negative side of z, i.e., $(\alpha _1d_2+\beta _2 d_1)<0$ Fig. 1b, then the condition is that the intercept of g(z) should be positive, i.e.,

$$\begin{aligned} g(0)=-\text {det}({\mathbb {A}})>0, \end{aligned}$$

(22)

which is not true for the originally stable non-spatial model. Therefore, the only possibility of remain is case-1 for diffusion to destabilized the model otherwise it is stable. Which can be simplified further as

$$\begin{aligned} (\alpha _1d_2+\beta _2 d_1)>2\sqrt{d_1d_2\text {det}({\mathbb {A}})}. \end{aligned}$$

(23)

For example let’s apply the above results to the actual Turing models. Let $(\alpha _1,\beta _1,\alpha _2,\beta _2)=(1,-1,2,-1.5)$ and $(d_1,d_2)=(10^{-4}, 6\times 10^{-4})$, using there parameters $\text {det}({\mathbb {A}})=0.5>0$ and $\text {Tr}({\mathbb {A}})=-0.5<0$, so the system is stable without diffusion terms. However,

$$\begin{aligned} \alpha _1d_2+\beta _2 d_1= &\, {} 6\times 10^{-4}-1.5\times 10^{-4}=4.5\times 10^{-4}, \end{aligned}$$

(24)

$$\begin{aligned} 2\sqrt{d_1d_2\text {det}({\mathbb {A}})}= &\, {} 2 \sqrt{10^{-4}\times 6\times 10^{-4}}\approx 3.464\times 10^{-4}, \end{aligned}$$

(25)

inequality (23) holds.

It is clear that without diffusion term system has only one equilibrium point $(v_{{{\text {eq}}}},w_{{{\text {eq}}}})=(h_1,k_1)$. There are so many choices for the parameters $\alpha _{1}$, $\beta _{1}$, $\alpha _{2}$ and $\beta _{2}$ for which this equilibrium point remains stable. So, the most interesting fact about Turing’s is that by introducing the diffusion term and spatial dimension to the equation these stable equilibrium points may be destabilized, and then the system immediately produces a non-homogeneous pattern. This is called Turing’s instability.

There are some shortcut results available, which are helpful to predict the Turing pattern formation in the considered model. Let’s continue the above discussion. We can evaluate the eigenvalue of the matrix $(J-d\, \omega ^2)$.

$$\begin{aligned}&\begin{vmatrix} 1-10^{-4}\omega ^2-\lambda&-1 \\ \\ 2&-1.5-6\times 10^{-4}\omega ^2-\lambda \end{vmatrix} = 0 \nonumber \\&\lambda =\dfrac{1}{2}\Big (-(0.5+7\times 10^{-4}\omega ^2)\nonumber \\&\quad \pm \sqrt{2.5\times 10^{-7}\omega ^4+2.5\times 10^{-3}\omega ^2-1.75} \Big ). \end{aligned}$$

(26)

First, we find the value of $\omega$ for the dominant eigenfunction $\sin (\omega x+\psi )$ then we select that $\omega$ which gives the largest value of the positive real part of eigenvalue $\lambda$, as this $\lambda$ produces most visible patterns.

3 B-spline quasi-interpolants

In the CBSQI method, the approximation is achieved by writing it as a linear combination of cubic B-spline functions for the considered space domain. Let $X_n=\{x_i=\alpha +ih:i=0,1,\ldots ,n\},$ be the uniform partition for the considered interval $[\alpha , \beta ]$, where $h=(\beta -\alpha )/n$. Let the set $\{B_i^d: i=1,2,\ldots ,n+d\}$ form a basis for space of splines of degree d, which can be derived from de Boor-Cox [37]. Since for a B-spline $B_i^d,$ support lie within the interval $[x_{i-d-1}, x_i],$ therefore, for this purpose we need to add $d+1$ knots at each endpoint to the interval, i.e.,to the left of $\alpha$ and right of $\beta$. This extension is performed as follows

$$\begin{aligned} x_{-d}= &\, {} x_{-d+1}=\cdots =x_{-1}=x_{0}=\alpha , \nonumber \\ \beta= &\, {} x_n=x_{n+1}=\cdots =x_{n+d}. \end{aligned}$$

(27)

For a function w, the B-spline quasi-interpolant (BSQI) of degree d can be defined as [32]

$$\begin{aligned} Q_dw(x)=\sum _{i=1}^{n+d}\mu _i(w)B_i^d(x), \end{aligned}$$

(28)

where $\mu _i$ are the unknown coefficients to be calculated, which depend on the two versions of local support property of B-spline : (1) the B-spline $B_i^d$ remains non-zero within the interval $[x_{i-d-1}, x_i]$, and (2) there are only $d+1$ B-splines in $B^d(X_n)$ which are non-zero on $[x_{\eta }, x_{\eta +1}]$. Besides this, another condition is also imposed so that quasi-interpolant $Q_dw$ is exact on ${\mathbb {P}}_n^d$, i.e., $Q_dw=w$ for all $w\in {\mathbb {P}}_n^d$, where ${\mathbb {P}}_n^d$ is the polynomial space of degree at most d. This procedure is named as discrete quasi-interpolant presented by Sablonnière [38]. We also discuss that derivatives of a function approximated by the corresponding B-spline function. The flexibility and simplicity are the main advantages of BSQI.

3.1 CBSQI method

For a certain function w cubic B-spline quasi-interpolant can be defined from (28) by taking d=3 and is given by

$$\begin{aligned} Q_3w(x)=\sum _{i=1}^{n+3}\mu _i(w)B_i^3(x), \end{aligned}$$

(29)

where all nodes are taken to be same as knots, i.e., $\xi _i=x_i$ $(i=0,1,\ldots ,n)$ and the coefficients $\mu _i(w)$ are computed in terms of values $w_i$ for $(i=1,2,\ldots ,n+3)$ as follows

$$\begin{aligned} \left. \begin{array}{l} \mu _1(w)=w_0, \qquad \; \mu _2(w)=\dfrac{1}{18}\Big [7w_0+18w_1-9w_2+2w_3\Big ],\\ \\ \mu _i(w)=\;\dfrac{1}{6}\Big [-w_{i-3}+8w_{i-2}-w_{i-1}\Big ],\quad \text {for}\; 3\le {i}\le (n+1)\\ \\ \mu _{n+2}(w)=\dfrac{1}{18}\Big [2w_{n-3}-9w_{n-2}+18w_{n-1}+7w_n\Big ],\quad \mu _{n+3}(w)=w_n, \end{array} \right\} \end{aligned}$$

(30)

and the related B-spline basis functions are as follows

$$\begin{aligned} B_i^3(\xi )= \left\{ \begin{array}{ll} \dfrac{(\xi -x_{i-4})^3}{(x_{i-3}-x_{i-4})(x_{i-2}-x_{i-4})(x_{i-1}-x_{i-4})}, &{} \text {if}\; x_{i-4}<{\xi }\le {x_{i-3}}, \\ \dfrac{(\xi -x_{i-4})^2(x_{i-2}-\xi )}{(x_{i-2}-x_{i-4})(x_{i-2} -x_{i-3})(x_{i-1}-x_{i-4})}\\ +\dfrac{(\xi -x_{i-4})(x_{i-1}-\xi )(\xi -x_{i-3})}{(x_{i-1}-x_{i-4}) (x_{i-1}-x_{i-3})(x_{i-2}-x_{i-3})} \\ +\dfrac{(x_{i}-\xi )(\xi -x_{i-3})^2}{(x_{i}-x_{i-3})(x_{i-1}-x_{i-3}) (x_{i-2}-x_{i-3})},&{}\text {if}\; x_{i-3}<{\xi }\le {x_{i-2}} \\ \dfrac{(\xi -x_{i-4})(x_{i-1}-\xi )^2}{(x_{i-1}-x_{i-4})(x_{i-1} -x_{i-3})(x_{i-1}-x_{i-2})}\\ +\dfrac{(\xi -x_{i-3})(x_{i-1}-\xi )(x_i-\xi )}{(x_{i-1}-x_{i-3}) (x_{i-1}-x_{i-2})(x_i-x_{i-3})}\\ + \dfrac{(x_i-\xi )^2(\xi -x_{i-2})}{(x_{i}-x_{i-3})(x_{i}-x_{i-2})(x_{i-1}-x_{i-2})}, &{}\text {if}\; x_{i-2}<{\xi }\le {x_{i-1}},\\ \dfrac{(x_i-\xi )^3}{(x_i-x_{i-3})(x_i-x_{i-2})(x_i-x_{i-1})}, &{}\text {if}\; x_{i-1}<{\xi }\le {x_{i}}\\ 0,&{} \text {otherwise} \end{array} \right. \end{aligned}$$

(31)

The derivatives of $Q_3w$ are computed as follows.

$$\begin{aligned} (Q_3w)'(x)=\sum _{i=1}^{n+3}\mu _i(w){(B_i^3)}'(x), \end{aligned}$$

(32)

and

$$\begin{aligned} (Q_3w)''(x)=\sum _{i=1}^{n+3}\mu _i(w){(B_i^3)}''(x), \end{aligned}$$

(33)

where $(B_i^3)'$ and $(B_i^3)''$ can be obtained from (31).

$$\begin{aligned} \left. \begin{array}{l} (Q_3w)'(\xi _0)=\dfrac{1}{h}\Big [-\dfrac{11}{6}w_0+3w_1-\dfrac{3}{2}w_2 +\dfrac{1}{3}w_3\Big ],\\ \\ (Q_3w)'(\xi _1)=\dfrac{1}{h}\Big [-\dfrac{1}{3}w_0-\dfrac{1}{2}w_1+w_2 -\dfrac{1}{6}w_3\Big ],\\ \\ (Q_3w)'(\xi _{n-1})=\dfrac{1}{h}\Big [\dfrac{1}{6}w_{n-3}-w_{n-2}+\dfrac{1}{2}w_{n-1} +\dfrac{1}{3}w_{n}\Big ],\\ \\ (Q_3w)'(\xi _{n})=\dfrac{1}{h}\Big [-\dfrac{1}{3}w_{n-3}+\dfrac{3}{2}w_{n-2} -3w_{n-1}+\dfrac{11}{6}w_{n}\Big ], \end{array} \right\} \end{aligned}$$

(34)

and

$$\begin{aligned}&(Q_3w)'(\xi _i)=\dfrac{1}{h}\Big [\dfrac{1}{12}w_{i-2}-\dfrac{2}{3}w_{i-1} +\dfrac{2}{3}w_{i+1}-\dfrac{1}{12}w_{i+2}\Big ],\quad \nonumber \\&\quad 2\le {i}\le (n-2). \end{aligned}$$

(35)

The above expression can be written in the form of a matrix as

$$\begin{aligned} (Q_3w)'=\dfrac{1}{h}{\mathfrak {D}}^{(1)}w, \end{aligned}$$

(36)

where ${\mathfrak {D}}^{(1)}$ represent the coefficient matrix of order $(n+1)\times (n+1)$, which is obtained from Eqs. (34)–(35), and $w=(w_0,w_1,\ldots ,w_n)^T$.

For the second derivative, we have

$$\begin{aligned} \left. \begin{array}{l} (Q_3w)''(\xi _0)=\dfrac{1}{h^2}\Big [2w_0-5w_1+4w_2-w_3\Big ],\\ \\ (Q_3w)''(\xi _1)=\dfrac{1}{h^2}\Big [w_0-2w_1+w_2\Big ],\\ \\ (Q_3w)''(\xi _{n-1})=\dfrac{1}{h^2}\Big [w_{n-2}-2w_{n-1}+w_n\Big ],\\ \\ (Q_3w)''(\xi _{n})=\dfrac{1}{h^2}\Big [-w_{n-3}+4w_{n-2}-5w_{n-1}+2w_{n}\Big ], \end{array} \right\} \end{aligned}$$

(37)

and

$$\begin{aligned}&(Q_3w)''(\xi _i)\nonumber \\&\quad =\dfrac{1}{h^2}\Big [-\dfrac{1}{6}w_{i-2}+\dfrac{5}{3}w_{i-1} -3w_i+\dfrac{5}{3}w_{i+1}-\dfrac{1}{6}w_{i+2}\Big ],\quad \nonumber \\&\qquad 2\le {i}\le (n-2). \end{aligned}$$

(38)

Similarly, the above expression can be written in the form of a matrix as

$$\begin{aligned} (Q_3w)''=\dfrac{1}{h^2}{\mathfrak {D}}^{(2)}w, \end{aligned}$$

(39)

where ${\mathfrak {D}}^{(2)}$ represent the coefficient matrix of order $(n+1)\times (n+1)$, which is obtained from Eqs. (37)–(38).

4 Implementation of the method

Now, we apply the CBSQI method to the 1-D model, discretized the time derivative in the usual finite difference way

$$\begin{aligned} \left. \begin{array}{l} v^{m+1}=v^m+ d_1 \dfrac{{\varDelta t}}{h^2}{\mathfrak {D}}^{(2)}v^m + \phi _1(v^m,w^m) \varDelta t \\ \\ w^{m+1}=w^m+ d_2 \dfrac{{\varDelta t}}{h^2}{\mathfrak {D}}^{(2)}w^m+\phi _2(v^m,w^m) \varDelta t \end{array} \right\} , \end{aligned}$$

(40)

where ${\mathfrak {D}}^{(2)}$ is $(n+1)\times (n+1)$ matrix as given in (39), $\phi _1(v_i^m,w_i^m)=(-v^m_i(w^2_i)^m+\gamma (1-v^m_i))$ and $\phi _2(v_i^m,w_i^m)=(v^m_i(w^2_i)^m-(\gamma +\kappa )w_i^m)$ are column vectors for $i=0,1,\ldots ,n$. The dependent variables ${\varvec{v}}^m=(v_1^m,v_2^m,\ldots ,v_{n+1}^m)^T$ and ${\varvec{w}}^m=(w_1^m,w_2^m,\ldots ,w_{n+1}^m)^T$ are the column vectors. When $m=0$, the vectors ${\varvec{v}}^0$ and ${\varvec{w}}^0$ are obtained from the initial conditions and solutions of (1) at time $t=m+1$ can be calculated from explicit scheme (40) if the solution at $t=m$ is known.

Now, we extended the proposed method for two-dimensional problems, for which we introduce the idea of the Kronecker product [39].

Let for the domain $\varOmega =[\alpha ,\beta ]\times [\gamma ,\delta ]$, the uniform mesh is $\{(x_i,y_j): x_i=\alpha +ih_x:i=0,1,\ldots ,n,\; y_j=\gamma +jh_y:j=0,1,\ldots ,m\},$ where $h_x=(\beta -\alpha )/n$ and $h_y=(\delta -\gamma )/m$. Before further discussion of the proposed method, we state an important theory.

Kronecker product: For solving the higher-dimensional PDEs, the Kronecker product approach is currently very famous. For any matrices $R=[\alpha _{ij}]\in {\mathbb {F}}^{p\times q}$ and $S=[\beta _{ij}]\in {\mathbb {F}}^{r\times s}$, where their Kronecker product is defined as

$$\begin{aligned} R\otimes S=\begin{pmatrix} \alpha _{11}S &{}\alpha _{12}S &{}\cdots &{}\alpha _{1n}S\\ \alpha _{21}S &{}\alpha _{22}S &{}\cdots &{}\alpha _{2n}S\\ \vdots &{}\vdots &{}\vdots &{}\vdots \\ \alpha _{m1}S &{}\alpha _{m2}S &{}\cdots &{}\alpha _{mn}S\\ \end{pmatrix} \in {\mathbb {F}}^{(pr)\times (qs)}, \end{aligned}$$

where ${\mathbb {F}}$ is a field (${\mathbb {R}}$ or ${\mathbb {C}}$). Some essential properties and results also presented by Zhang and ding [40].

As we have discussed, the approximation of first and second-order derivatives in Eqs. (36) and (39). So, we used these 1-D differentiated matrices and Kronecker products to approximate the 2-D partial derivatives [36]. The first-order derivatives of w in 2-D w. r. t. x and y are approximate by $({\mathfrak {D}}_x^{(1)}\otimes I_y)$ and $(I_x\otimes {\mathfrak {D}}_y^{(1)})$, respectively, where ${\mathfrak {D}}_x^{(1)}$ and ${\mathfrak {D}}_y^{(1)}$ represent the 1-D first-order differentiated matrices of w in x and y directions. Similarly, we can define the for second-order derivatives.

So, after implementing the above scheme to the system, i.e., Eq. (1), we get

$$\begin{aligned}&\left. \begin{array}{l} \frac{d}{{{\text {d}}t}}v(x_i,y_j,t)=d_1\Big [({\mathfrak {D}}_x^{(2)}\otimes I_y)+(I_x\otimes {\mathfrak {D}}_y^{(2)})\Big ]v(x_i,y_j,t)\\ \quad -v(x_i,y_j,t)w^2(x_i,y_j,t) +\gamma (1-v(x_i,y_j,t))+(\hat{b_1}\otimes \hat{I_y}),\\ \qquad \text {for} \; i=1,2,\ldots ,n-1, \; j=1,2,\ldots ,m-1 \end{array} \right\} \quad \; \end{aligned}$$

(41)

$$\begin{aligned}&\left. \begin{array}{l} \frac{d}{{{\text {d}}t}}w(x_i,y_j,t)=d_2\Big [({\mathfrak {D}}_x^{(2)}\otimes I_y)+(I_x\otimes {\mathfrak {D}}_y^{(2)})\Big ]w(x_i,y_j,t)\\ \quad +v(x_i,y_j,t)w^2(x_i,y_j,t)-(\gamma +\kappa )w(x_i,y_j,t) +(\hat{b_2}\otimes \hat{I_y}), \\ \qquad \text {for} \; i=1,2,\ldots ,n-1, \; j=1,2,\ldots ,m-1, \end{array} \right\} \end{aligned}$$

(42)

where $({\mathfrak {D}}_x^{(2)}\otimes I_y)$ and $(I_x\otimes {\mathfrak {D}}_y^{(2)})$ are matrices of order $(n-1)(m-1)\times (n-1)(m-1)$. $(\hat{b_1}\otimes \hat{I_y})$ and $(\hat{b_2}\otimes \hat{I_y})$ are $(n-1)(m-1)\times 1$ column vector containing boundary values, where $\hat{I_y}$ denotes the column vector with all entries unity. The dependent variables $v(x_i,y_j,t)$ and $w(x_i,y_j,t)$ are $(n-1)(m-1)\times 1$ column vectors. All the terms are defined as follows:

$$\begin{aligned} {\mathfrak {D}}_x^{(2)}\otimes I_y= &\, {} \begin{pmatrix} \dfrac{-2}{3}I &{}\dfrac{2}{3}I &{}0 &{}0 &{}0 &{}0 &{}\cdots &{}0\\ \dfrac{13}{9}I &{}\dfrac{-53}{18}I &{}\dfrac{5}{3}I &{}\dfrac{-1}{6}I &{}0 &{}0 &{}\cdots &{}0\\ \dfrac{-1}{6}I &{}\dfrac{5}{3}I &{}-3I &{}\dfrac{5}{3}I &{}\dfrac{-1}{6}I &{}0 &{}\cdots &{}0 \\ 0 &{}\dfrac{-1}{6}I &{}\dfrac{5}{3}I &{}-3I &{}\dfrac{5}{3}I &{}\dfrac{-1}{6}I &{}\cdots &{}0 \\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ 0 &{}\cdots &{}\dfrac{-1}{6}I &{}\dfrac{5}{3}I &{}-3I &{}\dfrac{5}{3}I &{}\dfrac{-1}{6}I &{}0 \\ 0 &{}\cdots &{}0 &{}\dfrac{-1}{6}I &{}\dfrac{5}{3}I &{}-3 &{}\dfrac{5}{3}I &{}\dfrac{-1}{6}I\\ 0 &{}\cdots &{}0 &{}0 &{}\dfrac{-1}{6}I &{}\dfrac{5}{3}I &{}\dfrac{-53}{18}I &{}\dfrac{13}{9}I\\ 0 &{}\cdots &{}0 &{}0 &{}0 &{}0 &{}\dfrac{2}{3}I &{}\dfrac{-2}{3}I \end{pmatrix}, \;\\ I_x\otimes {\mathfrak {D}}_y^{(2)}= &\, {} \begin{pmatrix} {\mathfrak {D}}_y^{(2)} &{}0 &{}\cdots &{}0\\ 0 &{}{\mathfrak {D}}_y^{(2)} &{}\cdots &{}0\\ \vdots &{}\vdots &{}\vdots &{}\vdots \\ 0 &{}0 &{}\cdots &{}{\mathfrak {D}}_y^{(2)}\\ \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} {\mathfrak {D}}_y^{(2)}= &\, {} \begin{pmatrix} \dfrac{-2}{3} &{}\dfrac{2}{3} &{}0 &{}0 &{}0 &{}0 &{}\cdots &{}0\\ \dfrac{13}{9} &{}\dfrac{-53}{18} &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}0 &{}0 &{}\cdots &{}0 \\ \dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}0 &{}\cdots &{}0 \\ 0 &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}\cdots &{}0 \\ \vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots &{}\vdots \\ 0 &{}\cdots &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} &{}0 \\ 0 &{}\cdots &{}0 &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}-3 &{}\dfrac{5}{3} &{}\dfrac{-1}{6} \\ 0 &{}\cdots &{}0 &{}0 &{}\dfrac{-1}{6} &{}\dfrac{5}{3} &{}\dfrac{-53}{18} &{}\dfrac{13}{9} \\ 0 &{}\cdots &{}0 &{}0 &{}0 &{}0 &{}\dfrac{2}{3} &{}\dfrac{-2}{3} \\ \end{pmatrix}_{(m-1)\times (m-1)}\, ,\\ \hat{b_1}= &\, {} \begin{pmatrix} -\dfrac{2}{3h}v'(x_0)\\ \dfrac{1}{9h}v'(x_0)\\ 0\\ \vdots \\ \vdots \\ 0\\ -\dfrac{1}{9h}v'(x_n)\\ \dfrac{2}{3h}v'(x_n) \end{pmatrix}, \qquad \hat{b_2}=\begin{pmatrix} -\dfrac{2}{3h}w'(x_0)\\ \dfrac{1}{9h}w'(x_0)\\ 0\\ \vdots \\ \vdots \\ 0\\ -\dfrac{1}{9h}w'(x_n)\\ \dfrac{2}{3h}w'(x_n), \end{pmatrix} \end{aligned}$$

where $v'(x_0), v'(x_n), w'(x_0)$ and $w'(x_n)$ are represents the boundaries for variables v and w respectively. The above matrices can be obtained by using the approximations from Eq. (39) and Neumann boundary conditions. For Neumann boundary condition, we have derived the following results:

Neumann boundary conditions: If the Neumann’s boundary conditions are given, then from Taylor’s expansion we have

$$\begin{aligned} w(x_0+h,y)= &\, {} w(x_0,y)+h\dfrac{\partial w}{\partial x}(x_0,y)+\dfrac{h^2}{2!}\dfrac{\partial ^2 w}{\partial x^2}(x_0,y)+\cdots \end{aligned}$$

(43)

$$\begin{aligned} w(x_0+2h,y)= &\, {} w(x_0,y)+2h\dfrac{\partial w}{\partial x}(x_0,y)+\dfrac{4h^2}{2!}\dfrac{\partial ^2 w}{\partial x^2}(x_0,y)+\cdots \end{aligned}$$

(44)

On multiplying (43) by 4 and subtracting to (44), we get

$$\begin{aligned} \dfrac{\partial w}{\partial x}(x_0,y)=\dfrac{1}{2h}\Big (-w_2+4w_1-3w_0\Big )+o(h^2). \end{aligned}$$

(45)

Similarly,

$$\begin{aligned} w(x_n-h,y)= &\, {} w(x_n)-h\dfrac{\partial w}{\partial x}(x_n,y)+\dfrac{h^2}{2!}\dfrac{\partial ^2 w}{\partial x^2}(x_n,y)+\cdots \nonumber \\ w(x_n-2h,y)= &\, {} w(x_n)-2h\dfrac{\partial w}{\partial x}(x_n,y)+\dfrac{4h^2}{2!}\dfrac{\partial ^2 w}{\partial x^2}(x_n,y)+\cdots \nonumber \\ \dfrac{\partial w}{\partial x}(x_n,y)= &\, {} \dfrac{1}{2h}\Big (3w_n-4w_{n-1}+w_{n-2}\Big )+o(h^2), \end{aligned}$$

(46)

similarly, we can derive the expression for $\dfrac{\partial w}{\partial y}(x,y)$

By using the initial conditions and boundary conditions. Now system (41)–(42) can be written as

$$\begin{aligned} \left. \begin{array}{l} \frac{d}{{{\text {d}}t}}v(x_i,y_j,t)={\mathbb {M}}v(x_i,y_j,t)-v(x_i,y_j,t)w^2(x_i,y_j,t)\\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad +\gamma (1-v(x_i,y_j,t)) \\ \frac{d}{{{\text {d}}t}}w(x_i,y_j,t)={\mathbb {N}}v(x_i,y_j,t)+v(x_i,y_j,t)w^2(x_i,y_j,t)\\ \qquad \qquad \qquad \qquad \qquad \qquad \qquad -(\gamma +\kappa )w(x_i,y_j,t) \end{array} \right\} \nonumber \\ \text {for}\;i=1,\ldots ,n-1,\, j=1,\ldots ,m-1, \end{aligned}$$

(47)

where ${\mathbb {M}}$ and ${\mathbb {N}}$ are the combined matrices containing boundary values and the coefficient matrices. The system (47) can be rewritten into a set of ODE in time, i.e. for each $i=1,2,\ldots ,n-1$, $j=1,2,\ldots ,m-1$, we have

$$\begin{aligned} \frac{{d{\mathbb {W}}_{{i,j}} }}{{{\text {d}}t}}={\mathbb {G}}({\mathbb {W}}_{i,j}), \end{aligned}$$

(48)

where ${\mathbb {W}}=[v\; w]^T$ and ${\mathbb {G}}$ denotes a differential operator. The system of ODE (48) is solved by the strong stability preserving time stepping Runge–Kutta scheme (SSP-RK-43), because of its numerous advantages. Hence, we get the final solution after applying the following algorithm.

$$\begin{aligned} {\mathbb {W}}^{(1)}= &\, {} {\mathbb {W}}^m+\dfrac{\varDelta t}{2}{\mathbb {G}}({\mathbb {W}}^m) \\ {\mathbb {W}}^{(2)}= &\, {} {\mathbb {W}}^{(1)}+\dfrac{\varDelta t}{2}{\mathbb {G}}({\mathbb {W}}^{(1)}) \\ {\mathbb {W}}^{(3)}= &\, {} \dfrac{2}{3}{\mathbb {W}}^m+\dfrac{{\mathbb {W}}^{(2)}}{3}+\dfrac{\varDelta t}{6}{\mathbb {G}}({\mathbb {W}}^{(2)}) \\ {\mathbb {W}}^{m+1}= &\, {} {\mathbb {W}}^{(3)}+\dfrac{\varDelta t}{2}{\mathbb {G}}({\mathbb {W}}^{(3)}). \end{aligned}$$

5 Stability of CBSQI scheme

For the stability analysis of the presented scheme, we have the following results:

Definition

Consider the autonomous system of ordinary differential equation of the form

$$\begin{aligned} \frac{d}{{{\text {d}}t}}=g(x), \end{aligned}$$

(49)

i.e., the variable t does not appear explicitly in the above Eq. (49). Then, $x_0$ is called the critical point of the above system (49), if $g(x_0)=0$.

Theorem 5.1

Let $\dfrac{dV}{dt}={\mathbb {M}}V+G(V)$ be a non-linear system and $\dfrac{dV}{dt}={\mathbb {M}}V$ be the corresponding linear system. Let (0, 0) be a simple critical point of the non-linear system and

$$\begin{aligned} \lim \limits _{V\rightarrow 0}\dfrac{G(V)}{\parallel {V}\parallel }=0. \end{aligned}$$

(50)

According to the Lyapunov theory, an asymptotically stable critical point (0, 0) of the linear system, remains asymptotically stable for the original non-linear system also.

Proof

The complete proof and other details available in [41]. Now, consider the Gray-scott model

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial v}{\partial t}=d_1 \nabla^2 v- vw^2+\gamma (1-v), \\ \\ \dfrac{\partial w}{\partial t}=d_2 \nabla^2 w+vw^2-(\gamma +\kappa )w. \end{array} \right. \end{aligned}$$

(51)

The critical point of the above system is $(v,w)=(1,0)$ using this ${\text {d}}v/{\text {d}}t = {\text {d}}w/{\text {d}}t = 0$ with no flux. To simplify the system, we use the following transformation:

$$\begin{aligned} V= &\, {} v-1,\qquad \qquad W=w \nonumber \\ \dfrac{\partial V}{\partial t}= &\, {} d_1\nabla ^2 V- (V+1)W^2-\gamma V, \nonumber \\ \dfrac{\partial W}{\partial t}= &\, {} d_2\nabla ^2 W+(V+1)W^2-(\gamma +\kappa )W. \end{aligned}$$

(52)

Now, the above system (52) is discretized by CBSQI method and then written as follows

$$\begin{aligned} \dfrac{\partial \tau }{\partial t}={\mathbb {M}}\tau +G(\tau ), \end{aligned}$$

(53)

where ${\mathbb {M}}= \left[ {\begin{array}{cc} A_1 &{} 0\\ 0 &{} A_2 \end{array}}\right] ,$

$$\begin{aligned} \tau =[V_{00}\,V_{01}\,...\,V_{0n}\,...\, V_{m0}\,V_{m1}\,...\,V_{mn} \; W_{00}\,W_{01}\,...\,W_{0n}\,...\, W_{m0}\,W_{m1}\,...\,W_{mn}]^T,\\ G(\tau )=[g_{00}(\tau ) \,...\,g_{0n}(\tau )\,....\,g_{m0}(\tau ) \,...\,g_{mn}(\tau ) \;h_{00}(\tau )\,...\,h_{0n}(\tau )\,....\,h_{m0}(\tau ) \,...\,h_{mn}(\tau )]^T \\ -g_{ij}(\tau )=h_{ij}(\tau )=(V(x_i,y_j,t)+1)W^2(V(x_i,y_j,t)),\quad \;i=0,1,\ldots ,n,\, j=0,1,\ldots ,m \end{aligned}$$

and

$$\begin{aligned} A_1= &\, {} \big [-\gamma \big (I\otimes I\big )+d_1\big ({\mathfrak {D}}_x^{(2)}\otimes I_y+I_x\otimes {\mathfrak {D}}_y^{(2)}\big )\big ],\\ A_2= &\, {} \big [-(\gamma +\kappa )\big (I\otimes I\big )+d_2 \big ({\mathfrak {D}}_x^{(2)}\otimes I_y+I_x\otimes {\mathfrak {D}}_y^{(2)}\big )\big ], \end{aligned}$$

where the matrix ${\mathfrak {D}}_x^{(2)}$ is taken from Eq. (39).

So by the above theorem’s (5.1) statement, the stability and instability of the non-linear system depend upon the corresponding linear system. For this purpose, we have the following condition.

$$\begin{aligned} \lim _{\tau \rightarrow \infty } \dfrac{g_{ij}(\tau )}{\sqrt{V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00} +W^2_{01}+\cdots +W^2_{mn}}}=0 \end{aligned}$$

(54)

Since, $-g_{ij}(\tau )=h_{ij}(\tau ), \;\forall i=0,1,\ldots ,n,\, j=0,1,\ldots ,m$, so we proved it only for $g_{ij}$. Using the non linear term of Eqs. (53) in (54), we have

$$\begin{aligned}&\left| {\dfrac{(V_{ij}+1)W^2_{ij}}{\sqrt{V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00}+W^2_{01}+\cdots +W^2_{mn}}} }-0\right| ,\; i=0,\ldots ,n,\, j=0,\ldots ,m \\&\quad \le \left| {\dfrac{V^2_{00}W^2_{00}+V^2_{01}W^2_{01}+\cdots +V^2_{mn}W^2_{mn}}{\sqrt{V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00}+W^2_{01}+\cdots +W^2_{mn}}} }\right| \\&\quad \le \left| {\dfrac{V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00}+W^2_{01}+\cdots +W^2_{mn}}{\sqrt{V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00}+W^2_{01}+\cdots +W^2_{mn}}} } \right| \\&\quad \le \left| \sqrt{V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00}+W^2_{01}+\cdots +W^2_{mn}} \right| \\&\quad \le \left| V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00}+W^2_{01}+\cdots +W^2_{mn} \right| <\epsilon . \end{aligned}$$

Therefore for each $\epsilon >0$ there exist a $\delta ^2=\epsilon$ such that

$$\begin{aligned}&\left| {\dfrac{g_{ij}(\tau )}{\sqrt{V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00}+W^2_{01} +\cdots +W^2_{mn}}} }-0\right|<\epsilon \qquad \text {whenever}\nonumber \\&\left| V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00}+W^2_{01}+\cdots +W^2_{mn} \right| <\delta ^2. \end{aligned}$$

(55)

Hence

$$\begin{aligned} \left. \begin{array}{l} \lim _{\tau \rightarrow \infty } \dfrac{g_{ij}(\tau )}{\sqrt{V^2_{00}+V^2_{01}+\cdots +V^2_{mn}+W^2_{00} +W^2_{01}+\cdots +W^2_{mn}}}=0,\\ \qquad \qquad \qquad \qquad \qquad \qquad i=0,1,\ldots ,n,\, j=0,1,\ldots ,m. \end{array} \right\} \end{aligned}$$

(56)

Therefore, we conclude that the non linear system (53) is stable or unstable as the corresponding linear system is stable or unstable.

$$\begin{aligned} \dfrac{\partial \tau }{\partial t}={\mathbb {M}}\tau . \end{aligned}$$

(57)

There are numerous methods available in the literature to study the stability of the linear system. Here. we use simple matrix method to calculate the eigenvalues of the linear system. As we know that, system is stable or asymptotically stable as real part of it’s eigenvalues are non-positive or negative respectively. In numerical examples, we have computed eigenvalues of the matrix ${\mathbb {M}}$ and found to be non-positive as shown in Figs. 3 and 6. Hence, proposed algorithm is stable. $\square$

6 Numerical experiments

To check the performance of the proposed scheme, we implement it to some test problems and discuss the obtained results in detail.

Problem 1

We consider the 1-D Gray-Scott model

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial v}{\partial t}=d_1 \nabla ^2 v- vw^2+\gamma (1-v), \\ \\ \dfrac{\partial w}{\partial t}=d_2 \nabla ^2 w+vw^2-(\gamma +\kappa )w \end{array}. \right. \end{aligned}$$

(58)

The domain of consideration for 1-D model is $x\in [-50, 50]$. The values of the parameters are taken as $d_1=1.0, d_2=0.01, \gamma = 0.02$ and $\kappa =0.066$. For both chemical component v and w the initial conditions and boundary condition are as follows

Fig. 2

Growth of dynamic pulses at $t=0.0, 40, 200, 500, 750, 1000, 1200, 1500, 2050, 2200, 2900$ and 3500

$$\begin{aligned} v(x,0)= &\, {} 1-0.5\,\sin ^{100}(\pi (x-50)),\qquad \\ w(x,0)= &\, {} 0.25\,\sin ^{100}(\pi (x-50)) \\ v(-50,t)= &\, {} v(50,t)=1, \qquad \qquad \qquad \quad \\ w(-50,t)= &\, {} w(50,t)=0. \end{aligned}$$

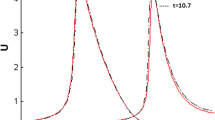
The pattern formed by the Gray-Scott model present in natural living things such as Leopard, Zebra, Fish and butterfly wings, etc. We clearly observed that the growth of Turing pattern formation over time increases. In Fig. 2 at time $t=500$ the Turing pulse split and then as time increase new pulses have been formed. We determined the eigenvalues of the matrix corresponding to problem (1). Fig. 3 shows the region of eigenvalues.

Fig. 3

Eigenvalues for the problem 1 with parameters $d_1=8 \;10^{-5}, d_1=4 \,10^{-5}, \gamma = 0.024$ and $\kappa =0.06$

Problem 2

We consider the 2-D Gray Scott model (1)

The domain of consideration is $(x,y)\in [0, 2.5]\times [0, 2.5]$. The values of the parameters are taken as $d_1=8 \;10^{-5}, d_2=4 \;10^{-5}, \gamma = 0.024$ and $\kappa =0.06$. For both chemical component v and w zero Neumann condition is imposed at the boundaries. The initial conditions are as follows

$$\begin{aligned} v(x,y,0)= &\, {} 1-2w(x,y,0), \\ w(x,y,0)= &\, {} \left\{ \begin{array}{ll} \dfrac{1}{4}\sin ^2(4\pi x) \sin ^2(4\pi y) &\quad \text {if} \le x,y\le 1.5, \\ \\ 0 & \quad \text {elsewhere} \end{array}. \right. \end{aligned}$$

Fig. 4

Pattern formation for w component with increasing time in Gray-Scott model

Initially, only four spots have been reported for component w in the center of the considered domain. As time increases, at $t=500$ these spots diffuse in eight spots see Fig. 4. Thus, this Turing pattern grows over the time.

Problem 3

Consider the 2-D reaction-diffusion model in the following form

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial v}{\partial t}=d_1 \nabla ^2 v+\kappa (a-v+v^2w), \\ \\ \dfrac{\partial w}{\partial t}=d_2 \nabla ^2 w+\kappa (b-v^2w). \end{array} \right. \end{aligned}$$

(59)

The domain of consideration is $(x,y)\in [0, 1]\times [0, 1]$. The values of the parameters are taken as $d_1=0.05, d_2=1, a=0.1305, b=0.7695$ and $\kappa =100$. For both chemical component v and w zero Neumann condition is imposed at boundaries. The initial conditions are as follows

$$\begin{aligned} v(x,y,0)= &\, {} a+b+10^{-3}\text {exp}\left(-100(x-\frac{1}{3})^2+\left(y-\frac{1}{2}\right)^2\right) \\ w(x,y,0)= &\, {} b/(a+b)^2. \end{aligned}$$

Initially, over the equilibrium state ($v\equiv 0.90, w\equiv 0.95$) the chemical shows a small Gaussian perturbation. Therefore, because of diffusion and reaction, this initial perturbation is grown and then split. In Fig. 5, the contour plot of component v is shown at time levels $t=0.5,1.0$ and 2.0. We determined the eigenvalues of the matrix corresponding to the problem (3). Figure 6 shows the region of eigenvalues.

Fig. 5

v component growth with time increasing in reaction-diffusion model

Fig. 6

Eigenvalues for the problem (3) with parameters $d_1=4 \;10^{-5}, d_1=2 \,10^{-5}, \gamma = 0.024$ and $\kappa =0.06$

Problem 4

We consider the 2-D Gray Scott model. (1)

The domain of consideration is $\varOmega = [0, 2.5]\times [0, 2.5]$. For both chemical component v and w zero Neumann boundary conditions are imposed. The initial conditions are taken as follows:

$$\begin{aligned} v(x,y,0)= &\, {} \left\{ \begin{array}{l} 1 \quad \text {if} \quad (x,y)\in \varOmega \backslash \delta , \\ \\ 0 \quad \text {if} \quad (x,y)\in \delta . \end{array} \right. \\ w(x,y,0)= &\, {} \left\{ \begin{array}{l} 0 \quad \text {if} \quad (x,y)\in \varOmega \backslash \delta , \\ \\ 1 \quad \text {if} \quad (x,y)\in \delta , \end{array} \right. \end{aligned}$$

where $\delta$ is the small square chosen at the center of the considered domain. For different values of parameters $\gamma$ and $\kappa$, we get different patterns. In all cases, initially, only a small square has been reported for component w in the center of the considered domain. As time increases it starts to split more and more in a symmetrical fashion. Therefore, we get very beautiful patterns, which are presented in many biological and chemical species.

Case-1. The parameters are taken as $d_1=4 \;10^{-5}, d_2=2\;10^{-5}, \gamma = 0.037$ and $\kappa =0.06$. We obtain patterns presented in Fig. 7.

Fig. 7

Contour plots of pattern formation at different time levels for case-1 in problem 4

Case-2. The parameters are taken as $d_1=4 \;10^{-5}, d_2=2\;10^{-5}, \gamma = 0.03$ and $\kappa =0.062$. We obtain patterns presented in Fig. 8.

Fig. 8

Contour plots of pattern formation at different time levels for case-2 in problem (4)

Case-3. The parameters are taken as $d_1=4 \;10^{-5}, d_2=2\;10^{-5}, \gamma = 0.04$ and $\kappa =0.06$. We obtain patterns presented in Fig. 9.

Fig. 9

Contour plots of pattern formation at different time levels for case-3 in problem (4)

Case-4. The parameters are taken as $d_1=4 \;10^{-5}, d_2=2\;10^{-5}, \gamma = 0.025$ and $\kappa =0.06$. We obtain patterns presented in Fig. 10.

Fig. 10

Contour plots of pattern formation at different time levels for case-4 in problem (4)

7 Conclusions

In this work, the authors proposed a numerical algorithm based on CBSQI to simulate 1-D and 2-D Gray-Scott reaction-diffusion models. In the proposed algorithm, 2-D problems are numerically solved using a combination of Kronecker product and 1-D differential matrix. The scheme is validated against four benchmark problems. The main outcomes of the work are as follows

• 1. To the best of the authors’ knowledge, this is the first application of the CBSQI in solving the 2-D reaction-diffusion equation. The major highlights of

  this method is its better accuracy, efficacy in solving these equations, and its ease of implementation.

• 2. The linear stability analysis of the system as well as stability of the proposed method is discussed.

• 3. The obtained Turing patterns of the Gray-Scott model are very similar to the available literature [2,3,4, 42].

• 4. The proposed algorithm is capable to simulate the models for large time t = 15,000. However for comparison purpose, results are reported for t = 10,000.

• 5. The proposed algorithm can be extend to higher dimensional problems with some modifications.