A practical ANN model for predicting the PSS of two-way reinforced concrete slabs

Abstract

This paper aims to develop a practical artificial neural network (ANN) model for predicting the punching shear strength (PSS) of two-way reinforced concrete slabs. In this regard, a total of 218 test results collected from the literature were used to develop the ANN models. Accordingly, the slab thickness, the width of the column section, the effective depth of the slab, the reinforcement ratio, the compressive strength of concrete, and the yield strength of reinforcement were considered as input variables. Meanwhile, the PSS was considered as the output variable. Several ANN models were developed, but the best model with the highest coefficient of determination (R²) and the smallest root mean square errors was retained. The performance of the best ANN model was compared with multiple linear regression and existing design code equations. The comparative results showed that the proposed ANN model was provided the most accurate prediction of PSS of two-way reinforced concrete slabs. The parametric study was carried out using the proposed ANN model to assess the effect of each input parameter on the PSS of two-way reinforced concrete slabs. Finally, a graphical user interface was developed to apply for practical design of PSS of two-way reinforced concrete slabs.

1 Introduction

The two-way reinforced concrete slab is an essential part of engineering structures. The use of such slab systems in reinforced concrete construction is widespread because, not only enhances architectural flexibility and leads to more clear space, but also requires less form-work, increases the number of storeys for a given building height and simplifies construction, thus leading to a reduction in the completion time and the cost of construction. However, high shear and bending stress are emerged in the slab when it is subjected to punching shear force. This phenomenon usually exists in the vicinity of slab-column connections associated with the diagonal cracks following the surface of a truncated cone around the column. Notably, the punching shear failure happens without warning and may lead to a progressive collapse of the structure [1].

In the analysis and design of two-way reinforced concrete slabs, the punching shear strength (PSS) is an important parameter. However, determination of the PSS is a difficult task owing to the influence of numerous factors involved. In the past, there were many researches based on the development of experimental studies to identify the key factors affecting the PSS. Among of them, the tests on reinforced concrete slabs conducted by Elstner and Hognestad [2], Moe [3], Mowrer and Vanderbilt [4], Regan [5], Guandalini et al. [6], Sagaseta et al. [7], Marzouk and Hussein [8], Lips et al. [9], Theodorakopoulos and Swamy [10], Metwally et al. [11], Ozden et al. [12], Birkle and Dilger [13], Hegger et al. [14], and Rizk et al. [15] were worth mentioning, where different geometric and mechanical parameters affecting on the punching shear failure were addressed. These testing programs focused on determining the impact of multiple parameters on the punching shear behavior of reinforced concrete slabs including compressive strength of concrete, yield strength of reinforcement, reinforcing ratio, column size, slab size, support and load conditions, reinforcement layout, openings in the slab, boundary restraint and size of the loaded area. They were not only provide insight into the behavior of reinforced concrete slabs under punching shear force but also create a great source of data for researchers to continue using to develop and verify new models.

For design purpose, several empirical equations have been proposed in design codes, such as ACI 318-14 [16], BS-8110-97 [17], Model Code 2010 [18], and Euro-Code 2 [19] to predict the PSS of two-way reinforced concrete slabs. These equations are generally easy to use due to the few parameters involved. However, most of the punching shear resistance equations specified in the current concrete codes are found to be empirical approaches, based on the experimental results conducted during the time of development of such equations. Hence, the results obtained from these equations for same problem reveals some differences and some of them are not able to determine the PSS of two-way reinforced concrete slabs with good precision. Questions have, therefore, been raised concerning the reliability of these equations for precise prediction of the PSS, particularly for slabs having different properties.

Nowadays, new models that are easier, convenient, and more accurate than the existing ones can be developed on account of the recent advances in data analysis techniques. In addition, exploiting the experimental data conducted by others integrating with advance computational technique can help researchers to develop a new empirical model for design applications. Soft computing techniques are becoming even more popular and particularly amenable to model the complex behaviors of most engineering problems since they have demonstrated superior predictive capacity compared to the traditional methods [20,21,22,23]. Artificial neural network (ANN) is one of the most rapidly growing research fields, attracting attentions from a wide variety of engineering field [24,25,26,27,28]. The main concept behind the use of ANN approach is that it learns adaptively from experience and extracts various functions each appropriate for its purpose. ANN has the ability to operate on large quantities of data and learns complex model functions from examples by training on a set of inputs and the corresponding output. The greatest advantage of ANN over the traditional modeling techniques is their ability to capture a nonlinear and complex interaction between variables of a system without having to assume the form of the relationship between the input and the output variables. Recently some researchers have used ANN to predict PSS of reinforced concrete slabs. Hoang [29] used sequential piecewise multiple linear regression and artificial neural network to estimate the punching shear capacity of steel fibre reinforced concrete slabs. The results showed that both models were superior to other empirical design equations in predicting the PSS. However, no explicit equation was presented to use ANN model for practical design. Akbarpour and Akbarpour [30] collected test results of two-way reinforced concrete slabs to develop artificial neural network and adaptive neuro-fuzzy inference system models for predicting the PSS. The results indicated that two models can accurately predict the PSS of two-way reinforced concrete slabs. Although this study provided the final values of weights and bias of the ANN model, however, it is difficult to use these values as no explicit explanation was showed. Therefore, it is still a “black-box” for practical use to predict the PSS of two-way reinforced concrete slabs. Other applications of ANN for one-way reinforced concrete slabs [31] and two-way reinforced concrete slabs with FRP bars [32] proved that ANN is potential approach, much simpler and cost-efficient for predicting the PSS of reinforced concrete slabs.

Although the PSS of reinforced concrete slabs has been studied with experimental and theoretical methods by numerous researchers over the past several decades. This phenomenon needs further study to get insight into the punching shear behavior and to develop better prediction formula for practical design. This paper aims to develop a practical ANN model for predicting the PSS of two-way reinforced concrete slabs by using a large of test results available in the open literature. The performance of the proposed ANN model was compared to the existing design codes and traditional multiple linear regression techniques. A parametric study was carried out to investigate the influence of input parameters on the PSS of two-way reinforced concrete slabs and show the generalization capability of the proposed ANN model. Based on the validated ANN model, a Graphical User Interface (GUI) was developed to easily apply for practical design the PSS of two-way reinforced concrete slabs. This study can provide an implementation for structural design and make some effort towards fulfilling the application of two-way reinforced concrete slabs subjected to shear punching force.

2 Punching shear failure mode

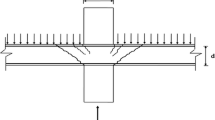
Punching failure happens due to formation of a shear cone comprising a truncated pyramid of concrete cracks encircling the column and causing the column to be pushed out of the slab [33]. Figure 1 shows typical failure pattern of punching shear failure in flat slab structures.

Fig. 1

Punching failure mode in flat slab

Punching shear failure is a three-dimensional state of stress failure that comes from the concentration of the high shear stresses in concrete around the slab-column connection. It is described by the slab fracturing along critical planes extending from the slab-column connection from compression to tension surfaces through the slab depth in an oblique direction away from the column [34]. Shear failure of concrete two-way slabs in the vicinity of concentrated loads may be due to beam action or two-way action. In case of the beam action, the slab behaves as a wide beam and the failure surface extends along the entire width of the slab. This type of failure occurs rarely in flat slab system. In case o f two-way action, the slab fails in a local area around the concentrated load.

Figure 2 shows a typical symmetric punching shear failure. When the load is applied to the slab, the first crack to form is a roughly circular tangential crack around the perimeter of the loaded area due to the negative bending moments in the radial direction. Radial cracks, due to negative bending moments in the tangential direction, then extend from that perimeter.

Fig. 2

Typical symmetric punching shear failure around an interior column

Because the radial moment decreases rapidly away from the loaded area, a significant increase in load is necessary before tangential cracks form around the load area some distance out in the slab. The diagonal tension cracks that developed in the slab tend to originate near mid-depth and therefore more similar to web-shear cracks than to flexural-shear cracks [35]. In most cases, only radial cracks were observed in the slab portion situated outside the shear crack. At higher loads some tangential cracks forming circles around the column develop. The final punching failure occurs suddenly as a result of the propagation of the outermost tangential crack.

3 Data collection

In this study, a total of 218 experimental data of two-way reinforced concrete flat slabs under punching force were collected from the literature [2,3,4, 8, 13, 36,37,38,39,40,41,42,43,44,45,46,47,48,49,50]. Based on these experimental results, the PSS of two-way reinforced concrete slabs is found to be significantly affected by the slab thickness, the width of the column section, the effective depth of the slab, the reinforcement ratio, the compressive strength of concrete, and the yield strength of reinforcement. Therefore, these factors were selected to be the influencing parameters for developing the ANN models. In this database, the slab thickness ($h$) varies from 46.0 to 550.0 mm, the width of the column section ($C$) varies from 80.0 to 520.0 mm, the effective depth of the slab ($d$) varies from 35.0 to 500 mm, the reinforcement ratio ($\rho$) varies from 0.25 to 5.01%, the compressive strength of concrete ($f_{\text{c}}^{'}$) varies from 12.3 to 119.0 MPa, and the yield strength of steel ($f_{y}$) varies from 294.0 to 720 MPa. These considered parameters are illustrated in Fig. 3.

Fig. 3

Schematic of a two-way reinforced concrete slab

The details of test specimens including their sources are presented in Appendix A. All specimens were reinforced concrete flat slab-column connections without drop panels, column capital or any type of shear reinforcement. Specimens cast with lightweight concrete were excluded. The database included square and circular columns. The summary of the statistical parameters for these variables is presented in Table 1. Figure 4 shows the distribution of each parameter in the database. Additionally, the relationship between the PSS and six input parameters by the correlation matrix plot is shown in Fig. 5, from which it can be observed the pairwise relationship between parameters with corresponding correlation coefficients for each indicator. It can be concluded that all parameters have a relatively good/meaningful correlation with one another. Some pairs of parameters have relatively satisfactory correlations is obtained. As shown in Fig. 5, the parameters $h$, $C$, $d$, and $f_{\text{c}}^{'}$ are highly correlated with $V_{\text{n}}$, whereas the parameters $\rho$ and $f_{y}$ are lowly correlated with $V_{\text{n}}$.

Table 1 Descriptive statistics for the experimental data

Fig. 4

Distribution of data information

Fig. 5

Correlation matrix plot of the database

4 Existing design code equations

This section of the paper evaluates the PSS of two-way reinforced concrete slabs by using the existing design code equations, such as ACI 318-14 [16], BS-8110-97 [17], Model-Code-2010 [18], and Euro-Code 2 [19]. These design code equations and main explanations are listed in Table 2. For a reasonable comparison, the safety factors were set as one in the design code equations.

Table 2 Different design code equations for determine the PSS

5 Multiple linear regression technique

Multiple linear regression can be used to define a mapping between one or more independent and dependent variables. The general form of a regression model is given as

$$y = a_{0} + a_{1} z_{1} + a_{2} z_{2} + \cdots + a_{m} z_{m} + e = ZA + e,$$

(5)

where $z_{1}$, $z_{2}$, $z_{m}$ are basis functions, which can be linear or higher-order with or without mixed term polynomials, while $a_{0}$, $a_{1}$, $a_{2}$, $a_{m}$ are the regression coefficients and $e$ is the residual [51].

The vector $A$ is determined in such a way that the mean squared difference between the values of the linear regression predictions and the actual experimental data is minimized. The least-square estimate of $\hat{A}$ is given by [52]

$$\hat{A} = [[Z]^{\text{T}} [Z]]\{ [Z]^{\text{T}} [Y]\} .$$

(6)

In this study, the data sets were used to fit linear, quadratic, and quadratic with mixed terms regression models. Table 3 summarizes the regression coefficients of three regression models.

Table 3 The evaluated coefficients of the linear regression models

6 Artificial neural networks

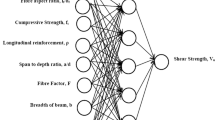
An ANN model is a mathematical tool for imitating human brain functions like learning, reasoning, and performing heavy parallel computations. In an ANN model, the smallest unit is called a neuron which is developed in three different layers including the input layer, the hidden layer, and the output layer.

The calculations that were carried out inside the ANN network include summation process of weighted input values with the bias of the input layer, as in Eq. (10), and then the results passed into the hidden layer neurons. Inside neurons, the process of tang-sigmoid function was performed as that in Eq. (11). Another linear process, using the purelin function, was carried out by summing the weighted output from the hidden layer neurons with the bias of the hidden layer as in Eq. (12):

$${\text{net}}_{j} = \sum\limits_{i = 1}^{n} {w_{ij} x_{i} + {\text{bias}}_{j} } ,$$

(10)

$$y_{j} = f({\text{net}}_{j} ) = \left( {1 + \exp^{{ - (2{\text{net}}_{j} )}} } \right) - 1,$$

(11)

$$y_{k} = {\text{purelin}}\left( {\sum\limits_{j = 1}^{m} {w_{jk} y_{j} + {\text{bias}}_{k} } } \right),$$

(12)

where ${\text{net}}_{j}$ is the weighted sum generated at the $j{\text{th}}$ hidden neuron; $x_{i}$ is the input value from the $i{\text{th}}$ input neuron; $w_{ij}$ and $w_{jk}$ are the weights added to the hidden layer and the output layer neurons, respectively; ${\text{bias}}_{j}$ and ${\text{bias}}_{k}$ are the biases added to the hidden layer and the output layer neurons, respectively; $y_{j}$ is the processed output from the $j{\text{th}}$ hidden neuron; $y_{k}$ is the processed output from the $k{\text{th}}$ output neuron; and $n$ is the number of input neurons, and $m$ is the number of neurons in the hidden layer.

The number of input and output variables in the data defines the number of neurons in input and output layers, respectively. In this study, there are six neurons in the input layer representing the six input parameters ($h,C,d,\rho ,f_{\text{c}}^{'} ,f_{y}$) and one neuron in the output layer for $V_{\text{n}}$. To classify the interval of values that are different to the same scale, it is recommended to scale the databases in a range of (− 1, 1) by a normalization procedure before the training process. It clear that normalization allows orthogonalizing the components of the input vectors in order to avoid correlation with one another and to get a faster convergence in the training process [53], which is shown in the following equation:

$$X_{\text{n}} = 2 \times \frac{{(X - X_{\text{min} } )}}{{(X_{\text{max} } - X_{\text{min} } )}} - 1,$$

(13)

where $X$ is the data sample, $X_{\text{n}}$ is the normalized data sample, $X_{\text{min} }$ and $X_{\text{max} }$ is the minimum and maximum values of the data for the interested parameter.

Input and output vectors were divided randomly into three sets including training, test and validation for constructing networks. In this paper, 70%, 15%, and 15% of the database were used for training, testing, and validating the network, respectively. The statistical analysis of the total, training, test, and validation data sets are presented in Table 1. The training set was utilized to adjusted connection weights and biases. The validation data monitored network over-training. When over-training occurs, the error in validation data begins to rise. Finally the testing data was used to measure the network performance after the training process.

There are many numerical optimization techniques which have been successfully used to speed up the convergence of the back-propagation learning algorithm. However, the Levenberg–Marquardt (LM) algorithm is the standard nonlinear least squares optimization algorithm, and was showed how to be incorporated into the back-propagation algorithm [54]. In addition, the LM algorithm has been found to be very efficient for ANN modeling by various investigators [55,56,57]. Moreover, in many cases the LM algorithm converged when the conjugate gradient and variable learning rate algorithms failed to converge. In other words, the convergence rate, generalization performance, and precision of LM is more than other algorithms and less iterations (epochs) would be required to achieve a low error. In general, on function approximation problems, for networks that contain up to a few hundred weights, the LM algorithm will have the fastest convergence.

Another crucial factor in ANN training is the number of neurons in the hidden layer. The network with too few neurons cannot sufficiently predict the data. Similarly, a network with too many neurons gives a poor performance and an over-training phenomenon may occur. In this study, a sensitivity analysis was conducted to find the best ANN model for current experimental data. Accordingly, eleven learning algorithms (‘trainlm’, ‘trainscg’, ‘traingdm’, ‘traingda’, ‘traingdx’, ‘trainrp’, ‘traincgf’, ‘traincgb’, ‘trainbfg’, ‘traincgp’, ‘trainoss’ denote 1st–11th, respectively) and number neurons in the hidden layer changed from 5 to 20 were performed to get the best ANN model for available data. For comparison, the value of best training performance (best_perf), best testing performance (best_tperf), and best validation performance (best_vperf) were evaluated. The final results are listed in Tables 4, 5 and 6. In these tables, the bold numbers of 6.2e-04, 1.3e-03, and 7.7e-04 indicate the best values of the best_perf, best_tperf, and best_vperf, respectively.

Table 4 Best training performance of different learning algorithm

Table 5 Best testing performance of different learning algorithm

Table 6 Best validation performance of different learning algorithm

It can be seen that the LM algorithm (trainlm) with 10 neurons in the hidden layer shows the best performance in the testing and validation process. The final ANN model with six inputs, one output (target), and ten neurons in the hidden layers was used, which is shown in Fig. 6.

Fig. 6

Structure of the proposed ANN model

7 Results and discussions

7.1 Performance of proposed ANN model

Figure 7 shows the performance of the proposed ANN model. This figure shows the training, testing, and validation processes of the ANN model starting at a large value and decreasing to a smaller one. The best training performance was obtained as 0.0007732 at the 11th epoch. A minimum value of mean square error defines a good ANN model.

Fig. 7

Performance of proposed ANN model

Figures 8, 9, 10 and 11 show the statistical description of training, test, validation, and all data of the proposed ANN model. As shown in the figure, the root mean square error of the training, testing, validation, and entire datasets are 0.024995, 0.03545, 0.027807, and 0.027256, respectively. Moreover, the mean and standard deviation errors are very small for training, testing, as well. The histogram plots show that most of the errors are close to the zero value.

Fig. 8

Training data performance

Fig. 9

Testing data performance

Fig. 10

Validation data performance

Fig. 11

All data performance

The values of coefficient of determination for training, test, and validation, and all data were found to be 0.9956, 0.9926, 0.9929, and 0.9947, respectively, as shown in Fig. 12. The overall response with R² close to 1 verifies that the proposed ANN model has produced the optimal results. Obviously, the proposed ANN model has acceptable performance for estimating the PSS of two-way reinforced concrete slabs. After successful training using the training data sets, the ANN model can be frozen. The network is then capable of computing the output values associated with new input data.

Fig. 12

Regression of the proposed ANN model

7.2 Comparison between the proposed ANN model and other models

The comparison was made in terms of different performance indicators, in particular, root mean square error (RMSE), mean absolute percentage error (MAPE), coefficient of determination (R²), and Pearson correlation coefficient (r). They are expressed in Eqs. (14)–(17). The value of the RMSE describes the average size of errors in giving more weight to large errors, while the value of MAPE can apply for strictly positive values and allows a measure of the prediction accuracy of the predictive model. The value of R², however, measures the degree of association between observed and predicted values to justify the importance of the relationship under study. Finally, the value of r expresses the strength of the linear relationship between two variables. When r is closer to 1 it indicates a strong positive relationship, a value of 0 indicates that there is no relationship, and a values close to − 1 signal a strong negative relationship between the two variables:

$${\text{RMSE}} = \sqrt {\left( {\frac{1}{n}} \right)\sum\limits_{i = 1}^{n} {(t_{i} - o_{i} )^{2} } } ,$$

(14)

$${\text{MAPE}} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {\left| {\frac{{o_{i} - t_{i} }}{{o_{i} }}} \right| \times 100} \right)} ,$$

(15)

$$R^{2} = 1 - \left( {\frac{{\sum\nolimits_{i = 1}^{n} {(t_{i} - o_{i} )^{2} } }}{{\sum\nolimits_{i = 1}^{n} {o_{i}^{2} } }}} \right),$$

(16)

$$r = \frac{{n\left( {\sum {t_{i} o_{i} } } \right) - \left( {\sum {t_{i} } } \right)\left( {\sum {o_{i} } } \right)}}{{\sqrt {\left( {n\sum {t_{i}^{2} - \left( {\sum {t_{i} } } \right)^{2} } } \right)\left( {[n\sum {o_{i}^{2} - \left( {\sum {o_{i} } } \right)^{2} } } \right)} }},$$

(17)

where t_i is the target value of ith sample, o_i is the output value of ith sample, and n is the number of samples.

Table 7 and Fig. 13 show the different values of these indicators in accordance with different models. According to these results, it is clear that the ANN model is significantly more efficient and accurate than the existing models.

Table 7 Performance of different indicators

Fig. 13

Statistical results of the studied models

In addition, the ratio $V_{\text{n,pre}} /V_{\text{n,exp}}$ of ANN model to existing equations based on the experimental database was used. Herein, $V_{\text{n,pre}}$ and $V_{\text{n,exp}}$ are the PSS based on the prediction models and experimental results, respectively. The statistical measurements of these models are listed in Table 8. The mean value for the proposed ANN model for predicting the experimental results is equal to 1.02 while the mean value for the other models including ACI 318-14, BS-8110-97, Model Code 2010, Euro-Code 2, MLR1, MLR2, and MLR3 are 0.87, 0.65, 0.76, 1.03, 0.8, 0.93, 1.03, respectively. Moreover, the standard deviation (SD) is small indicating that the proposed ANN network has a good ability to generalize the information.

Table 8 Statistical results of different models

The coefficient of variation (CoV) shows the extent of the variability in relation to mean value. A smaller CoV indicates a minimized amount of scatters in the results. Figure 14 shows the correlations between the predicted and experimental values. Obviously, the proposed ANN model has the highest correlations compared to others.

Fig. 14

Comparison between the proposed ANN and other models

7.3 Parametric study

A parametric study was conducted on the proposed ANN model to investigate the influence of the input parameters on the PSS of two-way reinforced concrete slabs. For this purpose, each input parameter was divided into five sets, L, ML, M, MH, and H, and varied from the lowest (L) to highest (H) values, in which M is mean value, ML is the midpoint between L and M, and MH is the midpoint between M and H. The value of these parameters is listed in Table 9. In the parametric study, each input parameter varied from its L to H value, while the other parameters remained constant at their midpoint values. It is worthy to note that the ANN model cannot properly predict the ACC for input parameters outside the range of training data. However, it is strongly noted that the obtained prediction results in this study were valid (no zero or negative value) with considered data range. This indicates that the proposed ANN model successfully predicts the PSS of two-way reinforced concrete slabs.

Table 9 The quantities regarding each input parameter

7.3.1 Effect of the slab thickness

The influence of the slab thickness, $h$ of slabs on punching shear strength is presented in Fig. 15. The ANN simulation indicates that the PSS is almost increased when the slab thickness increases. However, the effects of the slab thickness combined with the effective depth, $d$ and the reinforcement ratio, $\rho$ are more sensitive than other parameters. Additionally, the PSS increases when the slab thickness combined with in increasing of the effective depth, the width of the column section, the effective depth of the slab, the reinforcement ratio, the compressive strength of concrete, but it decreases when slab thickness combined with the yield strength of steel.

Fig. 15

Effects of the slab thickness

7.3.2 Effect of the width of the column section

The loaded section effect represented by the total perimeter of the supported area, regardless of the loaded section shape on the punching shear strength was studied using the proposed ANN model. Previous researchers represented the loaded area differently by considering a one side dimension of the loaded section, for example the width of loaded area. However, currently there is no code takes into account the influence of the loaded section size in the punching shear strength calculation. Figure 16 shows the effect of the column section width, $C$ of supported area on the PSS. For combination with the slab thickness and the effective depth of the slab, the PSS slightly increase as these parameters increase. The PSS increases when the column section width increase combined with the reinforcement ratio increases from 0.25 to 2.63%, but the PSS of this combination decreases when the reinforcement ratio increases from 2.63 to 5.01%. The PSS decreases when combining with the small the compressive strength of concrete and the yield strength of steel, but it increase when two parameters increase.

Fig. 16

Effects of the width of the column section

7.3.3 Effect of the effective depth of the slab

The influence of the effective depth, $d$ of slabs on punching shear strength is presented in Fig. 17. The ANN simulation indicates that the punching shear strength is almost increased when the effective depth increases. However, the effects of the effective depth combined with the slab thickness, $h$ and the reinforcement ratio are more sensitive than other parameters. Additionally, the PSS increases when the effective depth combined within an increasing of the slab thickness, the width of the column section, the effective depth of the slab, the reinforcement ratio, and the compressive strength of concrete, but it decreases when the effective depth combined with the yield strength of steel.

Fig. 17

Effects of the effective depth of the slab

7.3.4 Effect of the reinforcement ratio

Dilger et al. [58] explained the effect of reinforcement ratio, type, and grade of steel on punching shear resistance of slabs. The punching shear strength decreased as the reinforcement ratio decreased. Figure 18 shows the effect of reinforcement ratio, $\rho$ on the PSS. The PSS significantly increases as the reinforcement ratio increases from 0.25 to 2.63%. However, the combination with the slab thickness and the effective depth of the slab show the same trend, the PSS decreases when the reinforcement ratio increases from 2.63 to 5.01%. The combination with the width of the column section, the compressive strength of concrete, and the yield strength of steel, the PSS is nearly stable when the reinforcement ratio increases from 2.63 to 5.01%.

Fig. 18

Effects of the reinforcement ratio

7.3.5 Effect of concrete compressive strength

Metwally et al. [11] presented that an increasing in the compressive strength of concrete enhanced the PSS of slabs. Bazant et al. [59] investigated the size effect on PSS of nine RC flat slabs. The results described that nominal shear stresses at failure decreased as the column size increased. In addition, the behavior of flat slabs changed while the thickness increased. The punching shear behavior of the thin slabs was closer to plasticity, and that of the thick slabs was closer to a linear elastic fracture. Figure 19 shows the results of the punching shear strength predicted by the proposed ANN when compressive strength, $f_{\text{c}}^{'}$ is increased. The PSS increases when concrete compressive strength increases.

Fig. 19

Effects of the compressive strength of concrete

7.3.6 Effect of yield strength of steel

The sensitivity of the PSS to the yield strength of reinforcement is presented in Fig. 20. In general, the PSS decreases as $f_{y}$ increases. The reason may be due to the brittle failure in the vicinity concrete region of the connection between column and slab. However, it can be seen that ANN predicted a slight decrease in PSS with increasing yield strength combined with $h$, $d$, and $\rho$, but significantly with $C$ and $f_{\text{c}}^{'}$.

Fig. 20

Effects of the yield strength of reinforcement

8 ANN model-based user interface development

8.1 ANN-based formula

Based on observations from the previous section, the proposed ANN model can very excellently predict the PSS of two-way reinforced concrete slabs. Due to the difficulty of analytical solutions, the ease of use of the current ANN model should be exploited to derive an explicit empirical formulation in the practical design. Considering the PSS as the output response, the procedures presented in the previous sections were adopted herein. The explicit formulation of the PSS was obtained directly from the proposed ANN model by using their activation functions and parameters (weights, biases, and normalization factors). Based on the proposed ANN model, the normalized value of the PSS ($V_{n,N}$) was a function of considered parameters illustrated as Fig. 6, which is expressed as

$$V_{n,N} = h_{0} + \sum\limits_{i = 1}^{n} {h_{i} H_{i} } ,$$

(18)

$$H_{i} = \tanh (c_{i0} + c_{i1} X_{1} + c_{i2} X_{2} + c_{i3} X_{3} + c_{i4} X_{4} + c_{i5} X_{5} + c_{i6} X_{6} ),$$

(19)

where $n = 10$ is the number of neurons in the hidden layer of developed ANN model. The other coefficients: $h_{0}$ to $h_{n}$, and $c_{i0}$ to $c_{i6}$ are presented in the matrix form as follows:

$$h_{0} = \left[ {0.594} \right],$$

$$h_{i} = \left[ {\begin{array}{*{20}r} \hfill {0.538} \\ \hfill { - 0.842} \\ \hfill {0.087} \\ \hfill {0.617} \\ \hfill {0.927} \\ \hfill {0.191} \\ \hfill {0.121} \\ \hfill {0.483} \\ \hfill {0.206} \\ \hfill { - 0.540} \\ \end{array} } \right],$$

$$c_{i0} = \left[ {\begin{array}{*{20}r} \hfill { - 2.189} \\ \hfill { - 1.315} \\ \hfill {1.242} \\ \hfill {0.290} \\ \hfill { - 0.483} \\ \hfill {0.467} \\ \hfill { - 1.095} \\ \hfill {0.976} \\ \hfill {1.937} \\ \hfill {1.949} \\ \end{array} } \right],$$

$$c_{i,1 - 6} = \left[ {\begin{array}{*{20}r} \hfill {1.279} & \hfill { - 1.009} & \hfill {0.758} & \hfill {0.824} & \hfill {0.195} & \hfill { - 0.620} \\ \hfill {0.360} & \hfill {0.341} & \hfill {0.543} & \hfill { - 2.382} & \hfill { - 0.488} & \hfill { - 0.126} \\ \hfill { - 0.671} & \hfill {0.784} & \hfill {1.185} & \hfill { - 1.254} & \hfill {0.823} & \hfill {0.928} \\ \hfill {2.006} & \hfill { - 0.263} & \hfill {1.128} & \hfill {1.339} & \hfill {0.437} & \hfill { - 0.157} \\ \hfill {0.615} & \hfill {0.390} & \hfill {0.772} & \hfill { - 1.954} & \hfill { - 0.345} & \hfill { - 0.191} \\ \hfill { - 0.584} & \hfill { - 0.840} & \hfill {1.357} & \hfill {1.836} & \hfill {0.042} & \hfill {0.216} \\ \hfill { - 0.623} & \hfill { - 0.159} & \hfill {0.934} & \hfill {0.755} & \hfill { - 0.044} & \hfill {1.662} \\ \hfill {0.102} & \hfill {1.018} & \hfill { - 0.438} & \hfill { - 1.011} & \hfill {0.965} & \hfill { - 0.665} \\ \hfill {1.709} & \hfill { - 0.026} & \hfill {0.285} & \hfill {1.653} & \hfill { - 0.036} & \hfill {0.205} \\ \hfill {1.156} & \hfill {0.712} & \hfill { - 0.679} & \hfill { - 0.012} & \hfill {0.891} & \hfill { - 0.356} \\ \end{array} } \right],$$

It is worth mentioning that the output in Eq. (18) of the PSS was a normalized value between − 1 and 1, which should be converted into the real value. Finally, the PSS in kN of two-way reinforced concrete slabs is expressed as

$$V_{n} = 1326.0 \times (V_{n,N} + 1) + 29.0,$$

(20)

where $V_{\text{n}}$ and $V_{\text{n,N}}$ are real and normalized value of the PSS, respectively.

8.2 ANN interactive graphical user interface

Nowadays, structural designers are focusing on developing software that is more robust and user-friendly, resulting in a wider applicability. Indeed, considerable effort has gone into ensuring that the system developed in this study is useful and practical. Moreover, for ease of use, a graphical user interface (GUI) has been implemented in Matlab. Figure 21 shows the main user interface, which is simple and extremely easy to use. As shown in this figure, good computer software encourages the user to ask for the required parameters. User can enter numeric values for the slab thickness, the column section width, the effective depth of the slab, the reinforcement ratio, the compressive strength of concrete, and the yield strength of steel. Lastly, the PSS of two-way reinforced concrete slabs is displayed directly by clicking the Start Predict button.

Fig. 21

ANN interactive graphical user interface

9 Conclusions

A total of 218 experimental data sets collected from the literature has been used to develop the ANN models for predicting the punching shear strength (PSS) of two-way reinforced concrete slabs. To develop the ANN models, 152, 33, and 33 data sets were used for the training, test, and validation, respectively. In the proposed ANN model, the slab thickness, the width of the column section, the effective depth of the slab, the reinforcement ratio, the compressive strength of concrete, and the yield strength of steel were considered as input variables, meanwhile, punching shear strength was considered as output variable. The main findings of the present study can be summarized as follows:

• 1. In this study, an optimal artificial neural network (ANN) model was determined to accurately predict the PSS of two-way reinforced concrete slabs. The proposed ANN model provided better performance with strong relationship among PSS and selected independent variables compared to multiple linear regression and design code (ACI 318-14, BS-8110-97, Model Code 2010, and Euro-Code 2) models. R² value for the proposed ANN model was 0.995, while it was 0.840, 0.582, 0.805, 0.958, 0.880, 0.924 and 0.954 for the current design codes and the multiple linear regression (MLR1, MLR2, MLR3) models, respectively. In addition, the average and variation coefficient of the ratio of the computed PSS of the proposed ANN model to the tests were 1.02 and 0.1, respectively.

• 2. A parametric study was conducted to investigate the influence of the input parameters on the PSS of two-way reinforced concrete slabs. It was verified that the proposed ANN model has a good generalization capability in predicting the PSS of two-way reinforced concrete slabs.

• 3. This study provides a new GUI that can easily use to predict the PSS of two-way reinforced concrete slabs. This tool has been proven to be very successful, exhibiting very reliable predictions. Otherwise, it is idealistic to have some initial estimates of the outcomes before performing any extensive laboratory or fieldwork.

• 4. It should be stressed that the proposed ANN model can be reliably applied for new data ranging between the lowest and highest values of each parameter, as presented in Table 1. It will be not prudent to extrapolate beyond the data used in this study. However, the proposed ANN model can continuously retrain new data, so that it can conveniently adapt to new data in order to expand the range of suitability of the ANN. Therefore, future research may focus on enrich the experimental data with more potential input factors and number of data sets by conducting the tests or updating the database from the literature.