Idealized models for FEA derived from generative modeling processes based on extrusion primitives

Abstract

Shape idealization transformations are very common operations when adapting a CAD component to FEA requirements. Here, an idealization approach is proposed that is based on generative shape processes used to decompose an initial B-Rep solid, i.e., extrusion processes with material addition are used to segment a solid. The corresponding extrusion primitives form the basis of candidate sub-domains for idealization and their connections conveyed through the generative processes they belong to, bringing robustness to set up the appropriate connections between idealized sub-domains. This is made possible because the connections between extrusion primitives have an explicit geometric representation and can be used to bound the connections between idealized sub-domains. Taking advantage of an existing construction tree as available in a CAD software does not help much because it may be complicated to use it for idealization processes because this tree structure is not unique. Using generative processes attached to an object that is no longer reduced to a single construction tree but to a graph containing all non-trivial construction trees, is more useful for the engineer to evaluate variants of idealization. From this automated decomposition, each primitive is subjected to a morphological analysis to define whether it can idealized or not. Subsequently, geometric interfaces between primitives form also a graph that can be used to process the connections between the idealized sub-domains generated from the primitives. These interfaces are taken into account to determine more precisely the idealizable sub-domains and their contours when primitives are incrementally merged to come back to produce the global morphological analysis of the initial object. A user-defined threshold is used to tune the morphological analysis with respect to further user parameters. Finally, the idealizable sub-domains and their connections are processed to locate the mid-surfaces and connect them using generic criteria that the user can tune locally using complementary criteria.

1 Introduction

Using CAD models for FEA preprocessing often requires the applications of shape transformations to conform to the simulation objectives of engineers. Among these transformations, some of them are required when the engineer aims at describing a rather global mechanical behavior that falls into one of the reference categories described by the beam, plate, shell, or membranes theories. Considering the example of plate or shell models, they require the description of a geometric domain where they take place as a surface domain since the thickness parameter of these models becomes a FE parameter. Consequently, the volume sub-domain of the initial CAD model needs to be transformed into a surface sub-domain. This is a transformation falling into the category of idealization transformations that is addressed here.

Processing complex objects and determining their idealizable areas in a robust manner are still an issue when transforming CAD volumes for FEA and most contributions concentrate on identifying idealizable areas. These areas are subjected to morphological criteria that reflect the local plate or shell shape. If it is commonly agreed that a plate model is such that two independent dimensions are ten times greater than the plate thickness, this morphology is often adapted by the engineer to meet some simulation objectives. Therefore, these morphological criteria may need to be tuned by the engineer. Producing simple connections between idealized sub-domains remains also an issue to obtain FE models that efficiently represent some global mechanical behavior of the initial CAD model. These connections are also subjected to various criteria to simplify the FE model and ease its mesh generation phase, e.g., rather than preserving parallel and disconnected idealized sub-domains derived from mid-surfaces that are produced by adjacent volume sub-domains of variable thickness, these mid-surfaces can be moved to a common position and connected together. The previous criterion avoids setting up kinematic boundary conditions between the two disconnected sub-domains to describe the mechanical model of the continuum medium physically represented by the two adjacent volume sub-domains. Such criteria may need to be locally modified by the engineer to meet his, resp. her, simulation objectives.

Here, the purpose is to focus on the idealization of solid models where plate and shell mechanical models may be applicable on some areas of the input solid. It is not the purpose of the present contribution to address the interactions between the idealization transformations and the FE mesh generation phase. This is left for future work. Also, the mechanical engineering components cover a wide range of shapes containing common geometric features such as extrusions, revolutions, blends, chamfers, etc. In a first place, it is considered that blends and chamfers have been removed using de-featuring algorithms as available in commercial software like CADFix, SolidWorks, CATIA, etc. to concentrate on the segmentation of the input solid to identify idealizable areas and analyze them morphologically.

Modeling processes can be a good basis to identify idealizable areas but are difficult to acquire because they are internal to CAD modelers and not available through neutral files exchange (STEP, etc.). Additionally, they are not unique, i.e., different users may generate different construction trees for the same final shape, and furthermore, these trees may not be suited to define idealized areas. Using generative processes to decompose an object shape independently of any CAD modeler is a means to obtain a description that is intrinsic to each object [9] while they stand for a set of modeling actions that can be used to identify idealizable sub-domains. Representing explicitly and processing the geometric interfaces between these sub-domains enable the aggregation of sub-domains and help updating idealizable sub-domains. This process can be conducted robustly using the interface graph when decomposing the initial object into extrusion primitives. The review of prior work in these areas is the purpose of the next section. Then, Sect. 3 describes the major steps of the segmentation approach used to extract extrusion primitives from the input solid. In Sect. 5, the morphological analysis of the extrusion primitives is conducted on a standalone basis and then, propagated to the whole solid through the connections between these primitives. Finally, the explicit geometric models of the connections between extrusion primitives are used to analyze the mid-surfaces and set up connections between these surfaces as described in Sect. 6.3. Results obtained with the proposed approach are inserted in each of the sections referenced previously.

2 Prior work

Different approaches have been proposed to generate automatically idealized models for CAE. Among them, the face pairing [17, 22] works from nearly parallel faces of CAD models, which produce robust results on a reduced set of configurations, and medial axis transform (MAT) methods work on mesh models, which are more generic, but produce complex geometry in connection areas. More recently, Robinson et al. [18] used the MAT to identify thin regions candidate to idealization. A first step uses a 3D MAT to identify potential volume regions. Then, the MAT of these regions is analyzed by a second 2D MAT to determine the inner sub-regions which fully meet an aspect ratio between local thickness and MAT dimensions. With this approach, the authors take into account the dimensions associated to the local object thickness. Chong et al. [3] proposes operators to decompose solid models based on concavity shape properties prior to the mid-surface extraction that reduces the model dimension. However, the solid model decomposition algorithm detects thin configurations if edge pairs exist in the initial model and match an absolute thickness tolerance value. Some volume regions remain not idealized because of the nonexistence of edge pairs on the initial object.

To reduce the complexity of detection of dimensional reduction areas, Robinson et al. [19] use preliminary CAD information to identify 2D sketches used to generate revolving or sweepable volumes in construction trees. These sketches are analyzed by MAT to determine thin and thick areas. However, in industry, even if the construction tree information exists in a native CAD model, the selected features depend on the designer’s modeling choices, which does not ensure to obtain maximal sketches mandatory to get efficient results. Generating construction trees from solid models has been proposed when converting B-rep models into CSG ones [21] using Boolean operations to find one CSG tree but this tree may not produce directly suitable features for idealization. To reduce the complexity of assembly models, Kim et al. [7] propose a multi-resolution decomposition of an initial B-Rep assembly model. These operators simplify the parts by detecting and removing small features and idealize thin volume regions using face pairing. The obtained features are structured in a feature tree depending on the level of simplification. This work shows, with three operators, the many possible feature combinations creating multi-resolution models but these model abstractions do not meet idealization requirements. Li et al. [11] look for design intents based on recovering symmetries from shape properties. This work is closely related to our method because it iteratively analyses an object but their algorithm produces a unique tree and favors negative features over positive ones. The wrap-around operation proposed by Seo et al. [20] also proposes a multi-step operator but is restricted to concave features only. Our objective is to favor positive extrusion features to reduce the complexity of the analysis determining idealizable areas.

Our approach is also related to previous work in feature recognition and suppression. Different application domain requirements lead to a wide variety of feature definitions. In CAE applications, the focus has been set on removing detail features to simplify models before meshing [4, 8]. A particular domain, mostly studied in the 80–90s, is the recognition of machining features. These methods are efficient to recognize and classify negative features as holes, slots, or pockets [6]. Han et al. [5] give an overview of the state-of-the-art in manufacturing features recognition. Derived from these approaches, Woo [24] proposes a volume decomposition combined with mid-surface abstraction based on face pairing. The principle of the volume decomposition shows an improvement in the management of connections between mid-surfaces but the volume decomposition is restricted to convex volumes. Additionally, the volume decomposition obtained does not ensure that the volume left from the initial object is also simple and can be used for mid-surfacing. Automatic blend features removal, and more precisely finding sequences of blend features in an initial shape, is relevant to FE preprocessing. Regarding blends removal, Zhu and Menq [25] and Venkataraman et al. [23] detect and classify filet/round features to create a suppression order and remove them from a CAD model. In FEM, automatic decomposition of mechanical parts into hex meshable sub-regions creates positive feature decompositions. The methods of Lu et al. [14] or Liu and Gadh [13] use edge loops to find convex and sweepable sub-volumes for hex meshing, and more recently, the one proposed by Makem et al. [15] to identify automatically long, slender regions is also close to our work. However, these segmentation algorithms do not aim at producing a construction tree and the features found are extrusions for [15] only. For others, the sub-domains may not be extrusions because they should be suited for hex meshing only.

Our work focuses on additive generative processes using extrusion primitives to identify and generate idealized sub-domains. Extrusion primitives are taken as a first step to evaluate the segmentation approach proposed as well as the morphological analysis. Previous methods have shown the possibility of generating modeling processes from an original CAD model. However, the processes generated are unique for a component and often not suited for idealization due to the configurations focusing on particular application areas. In this paper, we propose to generate a construction graph adapted to idealization from extrusion primitives corresponding to material addition processes. Sections 3 and 4 describe the main phases of the construction graph generation.

3 Construction graph generation

3.1 Modeling context

As a first step, the focus is placed on a category of mechanical components as modeled using solid modelers that produce B-Rep models. Looking at solid modeling functions in industrial CAD systems, extrusion and revolve operations combined with the addition or removal behavior of a volume domain cover the major range of modeling operations. As a complement, blending radii or chamfers derive from configurations where some of them can be inserted in extrusions or revolutions, i.e., they can be inserted into sketched contours used in extrusion or revolution primitives (see Fig. 1a). However, some blends and chamfers require specific modeling operations, hence they are complementary to the previous operations.

Fig. 1

a Set of basic volume modeling operators, b sketch defining an extrusion primitive in a

Still as a first step, we consider the set of modeling functions that incorporate a sketch phase set in a plane to define at least one closed contour and this contour is reduced to line segments and arcs of circles. These functions cover extrusions and revolutions and this does not restrict significantly the range of mechanical components that can be addressed (see Fig. 1b). Combining extrusions and revolutions in a construction tree, i.e., extrusion and pocket form features on the one hand and revolution and notch form features on the other hand, is equivalent to Boolean operations of type union or subtraction. To start processing engineering components, we focus on extrusion primitives to reduce the complexity of the description of the proposed approach. Revolve features have not been addressed in this paper apart from cylindrical primitives that can be regarded as extrusions as well as revolutions. Consequently, the range of solids used to illustrate the proposed approach is such that each of them can be decomposed into extrusion primitives. Solids outside this range would be processed partially where extrusions can be extracted. We assume that the object $M$ analyzed for shape decomposition is free of blending radii and chamfers that cannot be incorporated into sketched contours, as mentioned in the Sect. sec:intro. Prior work in this field [12] can be used to derive $M$ from the initial object $M_I$, possibly with user’s interactions.

3.2 Decomposing an object into sets of extrusion primitives

Given a target object $M$ to be analyzed, independently of the modeling context stated above, $M$ can be considered as obtained through a set of primitives combined together to add or remove material. The B-Rep of $M$ can be seen as the memory of generative processes where primitives are sequentially combined [9].

Current CAD modelers are based on strictly sequential processes because the user can hardly generate simultaneous primitives without looking at intermediate results to see how they combine/interact together. Consequently, B-Rep operators in CAD modelers are reduced to binary operators combining the latest primitive generated to the existing shape of $M$ at a stage $t$ of a construction process. Indeed, the decomposition $\mathcal {D}$ of $M$ into extrusion primitives is not bound to a single construction tree, but produces a construction graph $G_D$ that contains all possible non-trivial construction trees of $M$. To this end, the major concepts and features of $\mathcal {D}$ can be listed as follows. $G_D$ is iteratively generated from $M$, ‘backward in time’, by removing all possible primitives $P_i$ until either a single or a set of disconnected extrusion primitive(s) is reached. This termination holds whenever $M$ is effectively decomposable into a set of extrusion primitives. Otherwise, $\mathcal {D}$ is only partial and its termination produces either one or a set of volume partitions describing the simplest objects $\mathcal {D}$ can reach. Figure 2 summarizes this process. When generating $G_D$, we refer to $M=M_0$ and evolutions of it, $M_{-j}$, backward at the $j$th step of $\mathcal {D}$.

Fig. 2

Overall scheme to obtain construction trees. $M'$ designates the successive evolutions of $M$, i.e., $M_{-j}$

$G_D$ is an oriented graph where each node contains a set of extrusion primitives $P_i$ and arcs are regularized Boolean unions, in our current case. Only such unions are considered presently, not only for simplification purposes but also because these unions are better suited to idealization processes rather than subtractive operators. Indeed, studying the morphology of each $P_i$ is sufficient to decide whether a sub-domain is idealizable or not, independently of the other steps in $G_D$. This independence no longer holds when subtractions take place between $P_i$s. Anyhow, the idealization process must favor a decomposition of $M$ that minimizes the number of subtractions. Using only regularized unions to propagate idealized $P_i$ is the topic addressed in Sect. 5.3. Incorporating regularized subtractions and unions is left for future work. Figure 3 gives an example of graph obtained on a rather complex object. One can notice that the first steps of the generation of $G_D$ of $M$ contain effectively a set of primitives $P_i$, each. This is more compact than referring to the combinatorial combinations of dyadic unions as prescribed by industrial CAD modelers. $G_D$ is generated automatically with a software application based on Open Cascade software.

Fig. 3

$G_D$ of a component. Orange sub-domains indicate the removed primitives $P_i$ at each node of $G_D$. Label $M_{{-j}_k}$ indicates the step number $j$ when ‘going back in time’ and the existence of variants $k$, if any. Arrows describe the successive steps of $\mathcal {D}$. Arcs of $G_D$ are obtained by reversing these arrows to produce construction trees. Steps $M_{{-6}_1}$ and $M_{{-6}_2}$ differ because of distinct lengths $L_1$ and $L_2$

Also, this figure highlights the graph structure inherent to the shape of $M$ with the two construction variants taking place between $M_{-4}$ and $M_{-7}$.

Often, the number of possible generative processes producing $M$ can be very large, e.g., even a cube can be obtained from an arbitrary large number of extrusions of arbitrary small extent combined together with a union operator. Here, we refer to the concept of maximal primitives so that the number of primitives is as small as possible for $M$. As an example, Fig. 1a is obtained from three maximal primitives after removing the two blends with variable radii. Maximal primitives mean that the contour of a sketch can be arbitrary complex and the extrusion length of each $P_i$ is as large as possible.

To converge, $\mathcal {D}$ is subjected to two major criteria:

• when a set of primitives $P_i$ is removed from $M_{-j}$ to produce $M_{-(j+1)}$, the shape of $M_{-(j+1)}$ must be simpler than that of $M_{-j}$. This is characterized by the fact that the number of faces bounding $M_{-(j+1)}$ must be strictly smaller than the number of faces bounding $M_{-j}$;

• each primitive $P_i$ removed from $M_{-j}$ to produce $M_{-(j+1)}$ must be as simple as possible. Because $P_i$ contains necessarily two faces containing the sketched contour, the simplicity of $P_i$ reduces to the number of geometric entities defining the sketch, i.e., lines and arcs.

Each of these criteria is tightly related to the concept of maximal faces and edges of $\partial M_{-j}$, the boundary of $M_{-j}$. The concept of maximal faces and edges derives from the fact that there is an infinite number of decompositions of $\partial M_{-j}$ that do not change the shape of $M_{-j}$, which is expressed by the Euler’s theorem [16]. The concept of maximal faces and edges is mandatory to avoid the side effects of the designer’s modeling process, the topological constraints inherent to geometric modelers, and some consequences of the parameterization of curves and surfaces describing $\partial M_{-j}$ (see [1, 10] for more details about the generation of maximal faces and edges). Generating maximal faces and edges is achieved with a merging operator applied when adjacent faces are supported by identical surfaces. The outcome of this process is a unique boundary decomposition of $\partial M_{-j}$ that is intrinsic to the shape of $M_{-j}$. Therefore, the convergence criteria mentioned previously can rely on the maximal faces and edges of $M_{-j}$ and $P_i$ to characterize simple shapes.

Based on the generation principle of $G_D$ described previously, the core step of its generation process is the identification of each $P_i$ that can be extracted from $M_{-j}$ to produce $M_{-(j+1)}$. This is the purpose of the next section.

4 Identifying extrusion primitives in an object

Starting with the object $M_{-j}$, each $P_i$ is identified through two phases:

• $P_i$ is visible in $M_{-j}$, i.e., at least one base face and one lateral edge of $P_i$ exist in $M_{-j}$ (see Fig. 4a);

• $P_i$ is valid in $M_{-j}$, i.e., the visibility of $P_i$ in $M_{-j}$ is invariant w.r.t. the extrusion distance of $P_i$ and the geometric interface $I_G$ between $P_i$ and $M_{-(j+1)}$ is minimal. This refers to the attachment of $P_i$ to $M_{-(j+1)}$.

Before addressing the concepts of visibility and attachment, let us first describe the major entities of an extrusion primitive. In an extrusion $P_i$ there are two base faces, $Fb_1$ and $Fb_2$, that are planar and contain the same sketched contour where the extrusion takes place. Considering extrusions that add volume to a pre-existing solid, the edges of $Fb_i$ are called contour edges and are convex. A convex edge is such that the normals at its adjacent faces define an angle $\alpha$ such that: $0 < \alpha < \pi$. When $P_i$ belongs to $M_{-j}$, the contour edges along which $P_i$ is attached to $M_{-j}$ can be either convex or concave depending on the neighborhood of $P_i$ in $M_{-j}$ (see Fig. 4a).

In the direction $\mathbf d$ of the extrusion, all the edges are straight line segments parallel to each other and orthogonal to $Fb_i$. These edges are named lateral edges. Faces adjacent to $Fb_i$ are called lateral faces. They are bounded by four edges, two of them being lateral edges. Lateral edges can be fictive lateral edges when a lateral face coincides with a face of $M_{-j}$ adjacent to $P_i$ (see Fig. 4a). When lateral faces of $P_i$ coincide with adjacent faces in $M_{-j}$, there cannot be edges separating $P_i$ from $M_{-(j+1)}$ because of the definition of maximal faces. Such a configuration refers to fictive base edges (see Fig. 5 with the identification of primitive $P_1$).

Fig. 4

a Entities involved in an extrusion primitive. Visible extrusion feature with its two identical base faces $Fb_1$ and $Fb_2$. b Visible extrusion feature with its two different base faces $Fb_1$ and $Fb_2$. c Visible extrusion feature with a unique base face $Fb_1$. d Example of geometric interface $I_G$ of type volume between $P_i$ and $M_{-(j+1)}$

Fig. 5

An example illustrating the major steps for identifying a primitive $P_i$ and removing it from the current model $M_{-j}$. Steps 1 and 2 illustrate the influence of the validity of candidate primitives. Step 3 illustrates the effect of the primitive simplicity criterion on $P_1$

Visibility The concept of visibility of $P_i$ in $M_{-j}$ refers to the faces of $\partial M_{-j}$ that belong either partly of entirely to $\partial P_i$. An extrusion primitive $P_i$ can be visible in different ways depending on its insertion in a current object $M_{-j}$. The simplest visibility is obtained when $P_i$’s base faces $Fb_i$ in $M_{-j}$ exist and when at least one lateral edge connects $Fb_i$ in $M_{-j}$ [see Figs. 4a, 5 (step 1)].

More generally, the contour of $Fb_1$ and $Fb_2$ may differ from each other (see Fig. 4b) or $P_i$ may have only one base face $Fb_1$ visible in $M_{-j}$ together with one existing lateral edge that defines the minimal extrusion distance of $Fb_1$ (see Fig. 4c). Our two hypotheses on extrusion visibility thus state as follows. First, at least one base face is visible in $M_{-j}$, i.e., the contour of either $Fb_1$ or $Fb_2$ coincides with a subset of the attachment contour of $P_i$ in $M_{-j}$. Second, one lateral edge exists that connects $Fb_i$ in $M_{-j}$. This edge is shared by two lateral faces and one of its extreme vertices is shared by $Fb_i$. $P_i$ is entirely defined by $Fb_i$ and the extrusion length is obtained from the maximum length of the generatrix of $P_i$ extracted from its lateral faces partly or entirely visible in $M_{-j}$. The lateral edge used to define the extrusion distance may be partially visible in $M_{-j}$. However, to reduce the complexity of the description of the proposed approach, the lateral edges of extracted primitives must be totally visible in $M_{-j}$. Even with this restriction, numerous primitives are generated based on all the existing lateral edges.

Attachment An extrusion primitive $P_i$ is attached to $M_{-j}$ in accordance to its visibility in $M_{-j}$. The attachment defines a geometric interface, $I_G$, between $P_i$ and $M_{-(j+1)}$, i.e., $I_G = P_i \cap M_{-(j+1)}$. This interface can be a surface or a volume or both, i.e., a non-manifold model. One of the simplest attachments occurs when $P_i$ has its base faces $Fb_1$ and $Fb_2$ visible. This means that $P_i$ is connected to $M_{-(j+1)}$ through lateral faces only. Consequently, $I_G$ is a surface defined by the set of lateral faces not visible in $P_i$. Figure 4a illustrates such a type of interface ($I_G$ contains two faces depicted in yellow).

A simple example of attachment involving a volume interface $I_G$ between $P_i$ and $M_{-(j+1)}$ is given in Fig. 4d. This occurs when base faces $Fb_1$ and $Fb_2$ differ from each other. The removal operator, removing $P_i$ from $M_{-(j)}$, minimizes the surfaces filling the gaps in $M_{-(j+1)}$ derived from $P_i$’s removal. The principle is to get am $M_{-(j+1)}$ object as simple as possible by extending existing surfaces in $M_{-(j+1)}$. Therefore, a volume interface occurs when $P_i$ penetrates $M_{-(j+1)}$. It represents the ‘invisible’ part of $P_i$ lying inside $M_{-(j)}$. Notice that in Fig. 4d the interface between $P_i$ and $M_{-(j+1)}$ contains also a surface interface that is not highlighted.

Whatever the category of interface, once $P_i$ is identified and its parameters are set (contour and extrusion distance), it is necessary to validate it prior to define its interface. Let $P_i$ designates the volume of the reference primitive, i.e., the entire extrusion $P_i$. To ensure that $P_i$ is indeed a primitive of $M_{-j}$, let the necessary condition formally be expressed with regularized Boolean operators between these two volumes (see Fig. 5 step 2):

$$\begin{aligned} (M_{-j} \cup ^* P_i) -^* M_{-j} = \phi . \end{aligned}$$

(1)

This equation states that $P_i$ intersects $M_{-j}$ only along the edge loops forming its attachment to $M_{-(j+1)}$, i.e., $P_i$ does not cross the boundary of $M_{-j}$ at other location than its attachment. The regularized Boolean subtraction states that limit configurations producing common points, curve segments or surface areas between $P_i$ and $M_{-j}$ at any other location than the attachment of $P_i$ are acceptable. This condition strongly reduces the number of valid primitives over time.

The next step is to generate $M_{-(j+1)}$ once $P_i$ has been identified and removed from $M_{-j}$. Depending of the type of $I_G$, some faces of $P_i$ may be added to ensure that $M_{-(j+1)}$ is a volume (see Fig. 5 steps 3 and 4).

If, in a general setting, there exists several variants of $I_G$ to define $M_{-(j+1)}$, these variants always produce a realizable volume, which differs from the halfspace decomposition approaches studied in [2, 21] where complements to the halfspaces derived from their initial boundary were needed to produce a realizable volume. Anyhow, all variants of valid $I_G$ are processed so that simplest $P_i$ and simplest versions of $M_{-(j+1)}$ can be obtained without loosing construction variants of $M$. Simplest $P_i$ ensuring that $M_{-(j+1)}$ gets simpler over the successive graph generation steps, is related to the generation of shapes reducing the number of faces bounding $P_i$ and $M_{-(j+1)}$. Other, though less important criteria, can be found in [1] to help classify variants of $M$ that can be of interest for applications differing from idealization.

As a result of this first phase, $M$ is segmented into a set of extrusion primitives $P_i$ and the geometric interfaces $I_G$ between $P_i$s are explicitly defined. This is an automated process that provides the engineer with the appropriate input for the morphological analysis of $M$ and this segmentation is independent of any CAD software.

5 Performing idealizations from a construction graph

The purpose of this section is to illustrate how a construction graph $G_D$ obtained with the algorithm described at Sect. 3.2 can be used in shape idealization processes. In fact, idealization processes are high-level operations that interact with the concept of detail because the idealization of sub-domains, i.e., $P_i$ obtained from $G_D$, triggers their dimensional reduction, which, in turn, influences the shape of areas around $I_G$, the geometric interfaces between these sub-domains. Here, the proposed approach is purely morphological, i.e., it does not depend on discretization parameters like FE sizes. It is divided into two steps. Firstly, each $P_i$ of $G_D$ is evaluated with respect to an idealization criterion. Secondly, according to $I_G$s between $P_i$s, the ‘idealizability’ of each $P_i$ is propagated in $G_D$ through construction trees up to the shape of $M$. As a result, an engineer can evaluate effective idealizable areas. Also, it will be shown how variants of construction trees in $G_D$ can influence an idealization process. Because the idealization process of an object is strongly depending on the engineer’s know-how (see the Sect. 1), it is the principle of the proposed approach to give the engineer access to the whole range of idealization variants. Finally, some shape details will appear subsequently to the idealization process when the engineer will define FE sizes to mesh the idealized representation of $M$.

5.1 Evaluating sub-domains for idealization

The primitives extracted from $G_D$ are subjected to a morphological analysis to evaluate their adequacy for idealization transformations into plates or shells. Because the primitives are all extrusions and add material, analyzing their morphology can be performed with the MAT [15, 19, 22]. MAT is particularly suited to extrusion primitives having constant thickness since it can be applied in 2D. Further, it can be used to decide whether sub-domains can be assigned a plate or shell mechanical behavior. In the present case, the extrusion primitives obtained lead to two distinct configurations (see Fig. 6). Figure 6a shows a configuration with a thin extrusion, i.e., the maximal diameter $\varPhi$ obtained with the MAT from $P_i$’s contour is much larger than $P_i$’s thickness defined by the extrusion distance $d$. Then, the idealized sub-domain would be a surface parallel to the base face having $P_i$’s contour. Figure 6b shows a configuration where the morphology of the sub-domain leads to an idealization that would be based on the content of the MAT because $d$ is much larger than $\varPhi$.

Fig. 6

Indication of idealization direction of extrusion primitives with 2D MAT applied to their contour

To idealize a sub-domain in mechanics, a commonly accepted reference proportion used to decide whether a sub-domain is idealizable or not is a ratio of ten between the in-plane dimensions of the sub-domain and its thickness, i.e., $x_r =10$. Here, this can be formalized with the morphological analysis of the sub-domain obtained from the MAT using: $x= \max ( ({\max \varPhi }/{d}), ({d}/{\max \varPhi }))$. Consequently, the ratio $x$ is applicable for all morphologies of extrusion sub-domains.

Fig. 7

Idealization analysis of components, the decomposition of one of them is shown at Fig. 3. Components a–c are new components whose decomposition results reduce to a single-tree structure in $G_D$. T and B indicate top and bottom views of the component, respectively. The decompositions of a and b are shown in Fig. 9. Violet indicates sub-domains that cannot be idealized as plates or shells, green ones can be idealized and yellow ones can be subjected to user decision

Because idealization processes are heavily know-how dependent, using this reference ratio as unique threshold does not seem sufficient to help an engineer analyze sub-domains, at least because $x_r$ does take precisely into account the morphology of the sub-domain’s contour. To let the engineer tune the morphological analysis and decide when sub-domains can/cannot be idealized a second, user-defined threshold, $x_u < x_r$, is introduced that lies in the interval $]0, x_r[$. Figure 6b illustrates a configuration where the morphological analysis does not produce a ratio $x > x_r$ though a user might idealize the sub-domain as a plate.

Let $x_u =3$ be this user-defined value, Fig. 7 shows the result of the interactive analysis the user can perform from the graphs $G_D$ obtained with the components analyzed in Figs. 7a–c and 3. Interpretation of colors is given in the figure caption. It has to be mentioned that the analysis is applied to $G_D$ rather than to a single construction tree structure so that the engineer can evaluate the influence of $\mathcal {D}$ with respect to the idealization processes. However, the result obtained on component of Fig. 3 shows that the variants in $G_D$ have no influence with respect to the morphological analysis criterion, in the present case. Consequently, Fig. 7 displays the morphological analysis obtained from the variant ${M_{-j}}_2$ of Fig. 3. Results on components of Figs. 3 and 7a, c also show a limit of this criterion because some non-idealizable sub-domains (see indications on Fig. 7 regarding violet sub-domains) are indeed well proportioned to be idealized with beams. Such configurations are clearly calling for complementary criteria that are part of our future work.

These results are already helpful for an engineer but it is up to him or her to evaluate the mechanical effect of $I_G$s between primitives $P_i$. Because $x_u$ is a user-defined parameter, the engineer can adjust this parameter to evaluate its influence over idealizable (yellow areas) and non-idealizable areas (violet areas). To help the engineer process the stiffening effects of $I_G$s, the morphological analysis is extended with a second step as follows.

5.2 Processing connections between ‘idealizable’ sub-domains

The morphological analysis of standalone primitives $P_i$ is the first application of $G_D$. Also, the decomposition obtained can be used to take into account the stiffening effect of interfaces $I_G$ between $P_i$ when $P_i$ are iteratively merged together along their $I_G$ up to obtain the whole object $M$. As a result, new sub-domains will be derived from the primitives $P_i$ and the morphological analysis will be available on $M$ as a whole, which will be easier to understand for the engineer. To this end, a taxonomy of connections between extrusion sub-domains is mandatory and summarized in Fig. 8a. This taxonomy refers to parallel and orthogonal configurations for simplicity but these configurations can be extended to process a larger range of angles, i.e., if Fig. 8 refers to interfaces of surface type, these configurations can be extended to interfaces of volume type when the sub-domains $S_1$ and $S_2$ are rotated w.r.t. each other. More specifically, it can be noticed that the configuration where $I_G$ is simultaneously orthogonal to the mid-surfaces of $S_1$ and $S_2$ is lacking of robust solutions [17, 22] and other connections can require deviation from mid-surface location to improve the mesh quality. Figure 13b illustrates such configurations and further details will be given in Sect. 6.2.

Fig. 8

a Taxonomy of connections between extrusion sub-domains. b Decomposition of configurations (1) and (4) into sub-domains showing that the decomposition produced reduces to configurations (2) only. c Example configurations of types (1) and (4) where $S_1$ and $S_2$ have arbitrary angular positions that generate volume interfaces $I_G$ where base faces $F_{b1_{S1}}$ and $F_{b1_{S2}}$ are intersection free in configuration (1) and $F_{b1_{S2}}$ only is intersection free in configuration (4)

Figure 8 describes all the valid configurations of $I_G$ between two sub-domains $S_1$ and $S_2$ when a thickness parameter can be attached to each sub-domain, which is presently the case with extrusion primitives. (a) The four valid configurations can be structured into two groups: (1) and (4) form $C_1$ and (2) and (3) form $C_2$. (b) The effect of the decomposition of configurations (1) and (4) that produces configurations (2) only.

Configuration (1) of $C_1$ is such that the thicknesses $e_1$ and $e_2$ of $S_1$ and $S_2$, respectively, are influenced by $I_G$, i.e., their overlapping area acts as a thickness increase that stiffens each of them. This stiffening effect can be important to be incorporated into a FE model as a thickness variation to better fit the real behavior of the corresponding structure. Their overlapping area can be assigned to either $S_1$ or $S_2$ or form an independent sub-domain with a thickness $(e_1 + e_2)$. If $S_1$ and $S_2$ are rotated w.r.t. each other and generate a volume $I_G$, the overlapping area still exists but behaves with a varying thickness. Whatever the solution chosen, the sub-domains $S_1$ and $S_2$ get modified and need to be decomposed. The extent of $S_2$ is reduced to produce $S'_2$ now bounded by $I'_G$. Similarly, the extent of $S_1$ is reduced to $S'_1$ now bounded by another interface $I'_G$. A new sub-domain $S'_3$ is created that contains $I_G$ and relates to the thickness $(e_1 + e_2)$ (see Fig. 8b). Indeed, with this new decomposition, $I_G$ is no longer of interest and the new interfaces $I'_G$ between the sub-domains $S'_i$ produce configurations of type (2) only.

Similarly, configuration (4) is such that $S_2$ can be stiffened by $S_1$ depending on the thickness of $S_1$ and/or the 2D shape of $I_G$ (see examples in Fig. 9). In this case, the stiffening effect on $S_2$ can partition $S_2$ into smaller sub-domains and its $I_G$ produces a configuration of type (2) with interfaces $I'_G$ when $S_2$ is cut by $S_1$. The corresponding decomposition is illustrated in Fig. 8b. This time, $I_G$ is still contributing to the decomposition of $S_1$ and $S_2$ but $S_2$ can be decomposed in several ways (${S'}_{2_1}$, $S'_{2_2}$) or ($S''_{2_1}$, $S''_{2_2}$) producing interfaces $I'_G$. Whatever, the decomposition selected, the key point is that $I'_G$ located on the resulting decomposition are all of same type that corresponds to configuration (2).

Configuration (1) reduces the areas of $S_1$ and $S_2$ of constant thicknesses $e_1$ and $e_2$, which can influence their ‘idealizability’. Configuration (4) reduces the area of $S_2$ of thickness $e_2$ but that of $S_1$ is not reducing, which influences the ‘idealizability’ of $S_2$ only. As a result, it can be observed that processing configurations in $C_1$ produce new configurations that always belong to $C_2$. Now, considering configurations in $C_2$, none of them is producing stiffening effects as $C_1$. Consequently, the set of configurations in Fig. 8a is a closed set under the decomposition process producing the interfaces $I'_G$. More precisely, there is no additional processing needed for $C_2$ and processing all configurations in $C_1$ produces configurations in $C_2$, which outlines the algorithm for processing iteratively interfaces between $P_i$ and shows that the algorithm always terminates.

Figure 8a and b refers to interfaces $I_G$ of surface type. Indeed, $\mathcal {D}$ can produce interfaces of volume type between $P_i$. This is equivalent to configurations where $S_1$ and $S_2$ depart from parallel or orthogonal settings as depicted in Fig. 8. Such general configurations can fit into either set $C_1$ or $C_2$ as follows. In the 2D representations of Fig. 8a, b, the outlines of $S_1$ and $S_2$ define the base faces $F_{b1}$ and $F_{b2}$ of each $P_i$. What distinguishes $C_1$ from $C_2$ is the fact that configurations (1) and (4) each contains at least $S_2$ such that one of its base face ($F_{b1_{S2}}$ in Fig. 8c) does not intersect $S_1$ and this observation applies also for $S_1$ in configuration (1) ($F_{b1_{S1}}$ in Fig. 8c). When configurations differ from orthogonal and parallel ones, a first subset of configurations can be classified into one of the four configurations using the distinction observed, i.e., if a base face of either $S_1$ or $S_2$ does not intersect a base face of its connected sub-domain, this configuration belongs to $C_1$ and if this property holds for sub-domains $S_1$ and $S_2$ both, the corresponding configuration is of type (1). Some other configurations of type (4) exist but are not detailed here.

As depicted in Fig. 8c, if $S_1$ and $S_2$ depart from parallel or orthogonal settings, generating their connection through a simple extension of their mid-surface may not be always appropriate. Indeed, this connection may lie far away from the interface $I_G$ between $S_1$ and $S_2$ depending on the relative angle between them. Such configurations may need specific connection schemes and this connection schemes may influence the mechanical behavior of the model. This is not further detailed here and is left for future work.

5.3 Extending morphological analyses of sub-domains to the whole object

Now, the purpose is to use the stiffening influence of some connections as analyzed in Sect. 5.2 to process all the $I_G$ between $P_i$ to be able to propagate and update the ‘idealizability’ of each $P_i$ when merging $P_i$s. This process ends up with a subdivision of some $P_i$ as described in the previous section and a decomposition of $M$ into sub-domains, each of them having an evaluation of its ‘idealizability’ so that the engineer can evaluate more easily the sub-domains he or she wants to effectively idealize.

The corresponding algorithm can be synthesized as follows (see Algorithm 1). The principle of this algorithm is to classify $I_G$ between two $P_i$ such that if $I_G$ belongs to $C_1$ (configurations 1 and 4 in Algorithm 1), it must be processed to produce new interface(s) $I'_G$ and new sub-domains that must be evaluated for idealization (procedure propagate morphology analysis). Depending on the connection configuration between the two primitives $P_i$, one of them or both are cut along the contour of $I_G$ to produce the new sub-domains. Then, the MAT is applied to these new sub-domains to update their morphology parameter (procedure MA morphology analysis) that reflects the effect of the corresponding merging operation taking place between the two $P_i$ along $I_G$ that stiffens some areas of the two primitives $P_i$ involved. The algorithm terminates when all configurations of $C_1$ have been processed.

Fig. 9

Propagation of the morphology analysis on $P_i$ to the whole object $M$. a–c $G_D$ of objects, a and b were depicted in Fig. 7a, b, respectively. d–f illustrate the influence of the morphology analysis propagation over the each object b, a, and c, respectively, when their sub-domains are iteratively connected together to form the initial object

Among the key features of the algorithm, it has to be observed that the influence of the primitive neighbor $P_{ngh}$ of $P_i$ is taken into account with the update of $P_i$ that becomes $P_r$. Indeed, $P_r$ can contain several volume partitions, when $Card(P_r) > 1$, depending on the shapes of $P_i$ and $P_{ngh}$. Each partition $P'$ of $P_r$ may exhibit a different morphology than that of $P_i$, which is a more precise idealization indication for the engineer. In case of configuration 1, the overlapping area between $P_{ngh}$ and $P_i$ must be analyzed too, as well as its influence over $P_{ngh}$ that becomes $P_{r_{ngh}}$. Here again, $P_{r_{ngh}}$ may exhibit several partitions, i.e., $Card(P_{r_{ngh}} \ge 1)$, and the morphology of each partition $P'_{ngh}$ must be analyzed. If the common volume of $P'_{ngh}$ and $P'$ is not idealizable, it is merged with either of the stiffest sub-domains $P_{ngh}$ or $P_i$ to preserve the sub-domain the most suited for idealization. In case a partition $P'$ of $P_r$ is not idealizable in configuration 4, this partition can be merged with $P_{ngh}$ if it has a similar morphological status.

Examples of the extension of the morphological analysis to the whole object $M$, using the interfaces $I_G$ between the primitives of $G_D$, are given in Fig. 9. Figure 9a–c depicts the construction graphs $G_D$ of Fig. 7a, b. In the present case, each of these graphs reduces to a single-tree structure. Then, Fig. 9d–f shows the sub-domain decomposition obtained after processing the interfaces $I_G$ between primitives $P_i$ of each object $M$. The same figures illustrate also the update of the morphology criterion on each of these sub-domains when they are iteratively merged through Algorithm 1 to form their initial object $M$. Areas A and B show the stiffening effect of configurations of category (1) on the morphology of sub-domains of $M$. Areas C and D are examples of the subdivision produced with configurations of type (4) and the stiffening effects obtained that are characterized by changes in the morphology criterion values.

It has to be pointed out that the propagation process of the morphological analysis is performed automatically. However, the engineer still has the possibility to adjust the $x_u$ parameter to evaluate its influence over idealizable or non-idealizable areas and adjust the idealization process to his, resp. her, simulation objectives.

After applying Algorithm 1, one can notice that every sub-domain strictly bounded by one interface $I_G$ of $C_2$ or by one interface $I'_G$ produced by this algorithm gives a precise idealization information about an area of $M$. Areas exhibiting connections of type (1) on one or two opposite faces of a sub-domain give also precise information, which is the case for examples of Fig. 9. However, if there are more piled up configurations of type (1), further analysis is required and will be addressed in the future.

6 Idealization processes

Having decomposed $M$ into extrusion primitives $P_i$, the locations of interfaces $I_G$ between $P_i$s are explicitly identified and the morphological analysis determines the $P_i$s that can be subjected to the idealization process. Then, given the type of connection between each idealizable $P_i$ and its neighborhood, criteria can be used to monitor the deviations needed from mid-surfaces to improve the idealization process and take into account the engineer’s know-how when preparing a FE model so that the FE mesh generation phase can be improved as mentioned in the Sect. 1.

Each extrusion primitive to be idealized with a medial surface is generated with a mid-surface such that:

• 1. Offsetting a base face of the primitive to the middle of the extrusion. This occurs when the extrusion distance is much lower than the maximum inscribed circle of the 2D MAT applied to the extrusion contour (see Fig 6a);

• 2. extruding medial edges of the 2D MAT applied to the extrusion contour. This occurs when the extrusion distance is much higher than the maximum inscribed circle of the 2D MAT applied to the extrusion contour (see Fig 6b).

6.1 Relating geometric interfaces to extrusion information

From the construction graph $G_D$ and the geometric interfaces $I_G$ between its primitives $P_i$, the interface graph $G_I$ can be derived. In $G_I$, the nodes are primitives $P_i$ and arcs are geometric interfaces between any two primitives. In a first step, the interface graph $G_I$ is enriched with the imprints of the boundary of $I_G$s on each couple of primitives $(P_i, P_j)$ that defines an $I_G$. These boundaries of $I_G$ w.r.t. a primitive $P_i$ are noted $C_{m(P_i)}$. A direct relationship can be established between $C_{m(P_i)}$ and the information related to the extrusion property of the primitives. The interface boundaries $C_{m(P_i)}$ are classified in accordance with their location over $\partial P_i$. To this end, each node $N_i$ of $G_D$ representing $P_i$ is subdivided into three distinct subsets: $N_i(F_{b1})$, $N_i(F_{b2})$, $N_i(F_{l})$, that designates its base face $F_{b1}$, its base face $F_{b2}$ and its lateral faces $F_{l}$, respectively. Then, $C_{m(P_i)}$ is assigned to the appropriate subsets of $N_i$. As an example, if $C_{m(P_i)}$ has its contours located on the base face $Fb_1$ of $P_i$, it is assigned to $N_i(F_{b1})$, or if $C_{m(P_i)}$ belongs to one of the lateral faces $F_{l}$, it is assigned to $N_i(F_{l})$. Figure 10 illustrates the enrichment of the interface graph $G_I$ of a simple model containing three primitives $P_1$, $P_2$ and $P_3$. For example, the boundary $C_{1(P_1)}$, resulting from the interaction between $P_1$ and $P_2$, is assigned to $Fb_1$ of $P_1$. Respectively, the equivalent $C_{1(P_3)}$ refers to a lateral face of $P_2$.

Fig. 10

An interface cycle between primitives $P_1$, $P_2$ and $P_3$

The following step determines potential interactions of $C_{m(P_i)}$s over a same primitive. When a pair of $C_m(P_i)$s share a common geometric area, i.e., their Boolean intersection is not null: $C_{m(P_i)} \cap C_{n(P_i)} \ne \phi$, the resulting intersection produces common points or curve segments that are defined as an interface between the pair of interfaces $(C_{m(P_i)}, C_{n(P_i)})$ and it is noted $IDi_{C_m/C_n}$. Three interfaces between $C_m(P_i)$ have been identified on the example of Fig. 10, e.g., $ID1_{C_1/C_2}$ represents the common edge interaction between $C_1(P_1)$ and $C_2(P_1)$. These new relations between $C_{m(P_i)}$s generate a graph structure $G_{ID}$ where the nodes represent the boundary $C_{m(P_i)}$ and the arcs define the interface $IDi_{C_m/C_n}$. The graph structure $G_{ID}$ is strictly nested into the nodes of $G_I$.

6.2 Analysis of interface graphs to generate idealized models

The graph structure $G_{ID}$ derived from the relations between the boundaries of interfaces $I_G$ can be merged with the interface graph $G_I$ between primitives $P_i$s. Using this new enriched graph, algorithms may be applied to identify specific configurations of connections between idealized primitives. These algorithms correspond to the current industrial practices of idealized FEM generation from B-Rep models. Specific configurations of interface connections can be determined automatically while allowing the user to locally modify the proposed results. This another stage of the idealization process where the engineer can locally modify the general criteria implemented to switch to other possible connections better suited to meet his, or her, simulation objectives. To generate a fully idealized model, i.e., a model where the medial surfaces are connected, three algorithms have been developed to identify interface cycles, groups of parallel medial surfaces and boundary primitives configurations. Each of them is now shortly described and this full set of algorithms is a first step to define criteria that may simplify the mesh generation process while expressing correctly the mechanical behavior of the connection between idealized sub-domains.

6.2.1 Interface cycles

Cycles of interfaces are of particular interest to robustly generate connections among idealized sub-domains. To shorten their description, the focus is placed on a common configuration where all the interfaces between primitives are of type (4). To define a cycle of interfaces of type (4), it is mandatory, in a first step, to identify a cycle in $G_I$ from primitive nodes connections. In a second step, the structure of connections between $P_i$s, as defined in $G_{ID}$, must contain themselves a path between their interface boundaries $C_{m(P_i)}$ that extend the cycle in $G_I$ to a cycle in $G_I \cup G_{ID}$. An example of such a cycle is illustrated on Fig. 10. This level of description of interfaces among sub-domains indicates dependencies between boundaries of medial surfaces. Indeed, such a cycle is a key information to the surface extension operator to connect the set of medial surfaces simultaneously. The medial surfaces perpendicular to their interfaces $I_G$ ($P_3$ in Fig. 10) have to be extended not only to the medial surfaces parallel to their interfaces ($P_1$ and $P_2$ in Fig. 10), but they have to be extended also in accordance with the extrusion directions of their adjacent primitives. For example, to generate a fully idealized model of the three primitives of Fig. 10, the corner point of the medial surface of $P_3$, corresponding to the $ID3_{C_1/C_2}$ edge, has to be extended to intersect the medial surface of $P_1$ as well as the medial surface of $P_2$. As described, the information available in an interface cycle enables a precise and robust generation of connections among idealized sub-domains.

6.2.2 Groups of parallel medial surfaces

Connections of parallel mid-surfaces can be handled with mid-surface repositioning (see $P_1$ and $P_2$ on Fig. 13b) and a corresponding adjustment of the material thickness on both sides of the idealized surface to generate a mechanical model consistent with the shape of $M$. This current practice in linear analysis has been advantageously implemented using the relative position of extrusion primitives. These groups of parallel medial surfaces can be identified in the graph $G_I$ as the set of connected paths containing edges of type (2) only. As a default processing of these paths, the corresponding parallel medial surfaces are offset to a common average position of the medial surfaces weighted by their respective areas. However, the user can also snap a mid-surface to the outer or inner skins of an extrusion primitive whenever this prescription is compatible with all the primitives involved in the path. Alternatively, the engineer may even specify a particular offset position.

6.2.3 Shifting medial surfaces

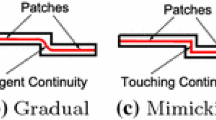
When processing an interface of type (4) in $G_I$, if an interface boundary $C_{m(P_i)}$ is located either on or close to the boundary of the primitive which is parallel to the interface (see $P_2$ and $P_3$ on Fig. 13b), the mid-surfaces need to be relocated to avoid meshing narrow areas along one of the sub-domain boundaries (here $P_3$ is moved according to $d_3$). If this configuration refers to mesh generation issues, which have not been addressed yet, configurations where a subset of $C_{m(P_i)}$ coincides with the boundary of a connected primitive (see $P_2$ in Fig. 13b) can be processed unambiguously without mesh generation parameters. Processing configurations where $C_{m(P_i)}$ is only close to a primitive contour requires mesh parameters handling and is left for future work. This configuration can be processed using the precise location of $I_G$ so that the medial surface repositioning operated can stay into $I_G$ to ensure the consistency of the idealized model.

The locations of medial surfaces are described here with orthogonal or parallel properties. It can be generalized to arbitrary angular positions as described in the previous Sect. 5.2.

Fig. 11

Example of a volume detail configuration lying on an idealized primitive

Fig. 12

Idealization process from the extraction of shape modeling processes to the generation of idealized surfaces. The idealization is detailed on two interface configurations of type (2) and (4)

The relationships between extrusion information and primitive interfaces may also be combined to analyze the behavior of standalone primitives such as small protrusions that can be considered as details. As an example, Fig. 11 shows the interaction between a primitive $P_1$, which can be idealized as a surface, and a primitive $P_2$ morphologically not idealizable. The enriched interface graph with $G_{ID}$ indicates that the boundary $C_{1(P_1)}$ lies on a base face, $Fb_1$, of $P_1$ that is used as boundary to idealize $P_1$. Then, if the morphological analysis of the face $F = (Fb_1 -* F_{C_{1(P_1)}})$ shows that $F$ is still idealizable, this means that $P_2$ has no morphological influence relatively to $P_1$, even though $P_2$ is not idealizable. As a result, $P_2$ may be potentially considered as a detail of $P_1$ and processed accordingly when generating the mesh. This example illustrates also further analyses that can be derived from these graph structures.

6.3 Generation of idealized models

To illustrate the benefits of the interface graph analysis, which has been used to identify specific configurations with the algorithms shortly described in the previous Sect. 6.2, an operator connecting the medial surfaces has been developed. Once the groups of parallel medial surfaces have been correctly aligned, the medial surfaces involved in interfaces of type (4) are connected using an extension operator. Because the precise locations of the interfaces between primitives are known through their geometric imprint $C_{m(P_i)}$ on primitives, the surface requiring extension is bounded by the imprint of $C_{m(P_i)}$ on the adjacent medial surface. The availability of explicit and detailed interface information in $G_I$ and $G_{ID}$ increases the robustness of the connection operator and prevents the generation of inconsistent surfaces located outside interface areas. Figure 12 illustrates the idealization process benefiting from the explicit geometric definition of interfaces between primitives. Two interface connections are shown corresponding to interface of type (2) and type (4). The type (2) interface processed uses an offset to align the mid-surfaces adjacent to this connection, as described in the previous section. Similarly, the type (4) interface processed uses the shifting process described in the previous section.

Figure 13a illustrates a component with its decomposition through the generative process graph and the corresponding interfaces between its extrusion primitives. This decomposition contains a set of primitive connections of categories discussed in Sect, 8 and Fig. 13b shows the repositioning of mid-surfaces among $P_1$, $P_2$ and $P_3$ that improves their connections and the overall idealization process. Figure 13c shows the resulting idealized model and its corresponding FE mesh.

Fig. 13

Idealization process of a component taking advantage of its generative process graph, its corresponding primitives as well as the geometric interfaces between these primitives

Finally, the complete idealization process is illustrated in Fig. 14. The initial CAD model is segmented using the construction graph generation of Sect. 3.2. It produces a set of volume primitives with interfaces between them. A morphological analysis is applied on each primitive as described in Sect. 5.1. Here, the user has applied a threshold ratio $x_u = 2$ and an idealized ratio $x_r = 10$. Using these values, all the primitives are considered to be idealized as surfaces and lines. The final CAD idealized model is generated with the algorithms proposed in Sect. 6 and exported to a CAE mesh environment. In addition to the medial surfaces, the interfaces between them are also exported to ensure the mesh connectivity between medial surfaces in the CAE environment , i.e., constraints to ensure that the mesh obtained is conform. This interface information is also important for meshing non-idealizable regions which must be constrained at their boundary with neighboring domains. Indeed, this interface information is a mandatory input to the mesh generation process, whether the sub-domains have been idealizable or not. Initially, the medial surfaces are located at the mid-thickness of the primitive. However, the user can specify a particular position for medial surfaces. Then, the interface graph is used to update the neighboring surfaces and generate a new idealized model. This functionality allows the user to access variants of idealization. Finally, the preprocessing time using manual transformations, currently made by engineers in industry, has been initially estimated to one man.hour for each simple component of Fig 9 and one man.day for the complex component of Fig 3. The proposed automatic idealization process allows the user to highly reduce this preprocessing time to 10 min for each component. The user may be punctually involved regarding the morphology of primitives close to the allowed threshold or regarding the connection choice between medial surfaces which depends on the simulation objective.

Fig. 14

Successive phases of the idealization process (please read from left to right on each of the three rows forming the entire sequence)

7 Conclusion and future work

The previous sections have described the main features of a construction graph generation as a backward process to decompose an object into a set of extrusion primitives corresponding to material addition processes. This graph is unique and intrinsic to each object shape because it overcomes modeling, surfaces and topological constraints inherent to current CAD modelers. The properties of this graph bring meaningful primitives that can be used as a first step of a morphological analysis. This morphological analysis forms the basis of an analysis of ‘idealizability’ of primitives. This analysis takes advantage of geometric interfaces between primitives to evaluate stiffening effects that propagate or not across the primitives when they are iteratively merged to regenerate the initial object and locate idealizable sub-domains over this object. Though the idealization addressed concentrates on shell and plates, it has been observed that extensions of the morphological analysis can be achieved to derive beam idealizations from primitives. The graph structures derived for geometric interfaces among primitives has proved its adequacy to bring a detailed description of the interfaces among primitives that can be used to improve the generation of idealized models.

The morphological analysis relies on a user-defined threshold that can be used by an engineer to tune the idealization process to his, resp. her, simulation objectives.

Overall, the construction graph lets the engineer access non-trivial variants of the shape decomposition into primitives, which can be useful to evaluate variants of idealizations of an object. Then, it has been shown how this decomposition into sub-domains and their geometric interfaces can be used to effectively idealize sub-domains and take into account some general-purpose mesh generation constraints that ensure better-quality meshes. The graph structures of interfaces combined with the morphological analysis of primitives have illustrated how a concept of shape detail can be related to the idealization process.

The work described is a first step and needs to be further developed to address a larger range of object shapes as well as more complex construction processes including volume removal operators that may be mandatory to model some components. Further developments are also required to extend the range of shapes with robust identification of idealizable sub-domains and addressing symmetry properties in one next step in that direction. These are targets for future work.