1 Introduction

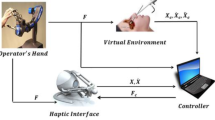
A haptic device is a computer-controlled actuated mechanical device that provides a physical interface between human sense of touch, and computer-generated virtual or remote environment. Based on manipulation and interaction with objects within the virtual or remote environment, these devices provide force and torque feedback to the user. Applications of haptic devices are increasing in many fields, particularly in medicine, telerobotics, engineering design, and entertainment [1]. Current trends in mechanical design of haptic devices have targeted the lightweight design in order to achieve high dynamic performance with relatively small actuators and low energy consumption [2]. This motivates using advanced kinematical architectures, high strength and light-weight materials, as well as minimization of cross sections of all critical elements. The primary constraint for such a minimization is the mechanical stiffness of the manipulator, which is directly related with the manipulator accuracy defined by the design specifications. A stiff and light-weight mechanism is needed to increase the bandwidth of frequency response. The low mass, size, and force capacity are beneficial in terms of safety aspects and human-friendliness [3]. In addition, lightweight mechanical design requires no active force feedback control to provide a good back drivability [3].

Stiffness is an essential performance measure since it is directly related to the positioning accuracy and payload capability. Stiffness can be defined as the capacity of a mechanical system to sustain loads without excessive changes of its geometry, or these produced changes in geometry due to the applied forces are known as deformations or compliant displacements [4]. Compliant displacements in a robotic system produce negative effects on static and fatigue strength, wear resistance, efficiency (friction losses), accuracy, and dynamic stability (vibration).

Mechanical stiffness is one of the most important indicators in performance evaluation of robotic systems [5–7]. In particular, for industrial robots where the primary target is the precise manipulation of a technological tool, the manipulator stiffness defines the positioning errors due to the external loading arising during the workpiece processing. Similarly, in industrial pick and place applications, which are intended for simple but fast manipulations, the stiffness defines admissible velocity/acceleration while approaching the target point, in order to avoid undesirable displacements due to inertial forces [8]. Other examples include large robotic manipulators for a patient positioning in medical treatment, where elastic deformations of mechanical components of the task load (and under own link weight) are the primary source of positioning errors [9]. It is obvious that in all of these cases, the desired stiffness should be high enough to meet the requirements of the relevant application.

The stiffness analysis is becoming a critical issue in design optimization and elastic deformation compensation in real time. A stiffness model should be compact, which can be effectively used for design optimization or hardware in a loop, acting as an elastic deformation compensator for positioning errors in real time.

Although many researchers have developed stiffness models, still there is a research gap, how to improve the stiffness analysis in order to have a better match between analytical, finite element method and experimental results [10]. This aspect would require the development of more precise stiffness models. This motivates the development of a dedicated stiffness analysis methodology for a compact and accurate generalized stiffness model for a parallel/serial/hybrid manipulator.

The paper is organized as follows: Sect. 2 summarizes a literature review on stiffness analysis of 6-DOF manipulators, and Sect. 3 presents the stiffness modeling methodology. Section 4 validates the presented methodology with an illustrative example. Section 5 concludes the presented work, while Sect. 6 presents future work and discussion.

2 Related work

Stiffness analysis has been widely investigated in the literature. Several methods exist for computation of the stiffness matrix: the virtual joint method (VJM), that is often called the lumped modeling [11–15], finite element analysis (FEA) [15–17] and matrix structural analysis (MSA) [18–22].

The first of them, the virtual joint method is based on the calculation of the Jacobian matrix that relates the joint displacement in joint space to the tool center point (TCP) deflection in Cartesian space. In this method, a lumped model is defined in which the elastic elements are converted into rigid elements with an equivalent stiffness in the active joints. The main limitation of this approach is the differential nature of the Jacobian matrix, the moment induced by the deformation must be in the rank of small deformations, since they have to be compatible with kinematic constrain to use Jacobian matrix [23].

Finite element analysis is reliable for calculating the stiffness of components with arbitrary shape and complex contact interactions between components in a system. For example, the FEA model is adopted to characterize robot static rigidity and natural frequencies in [24], and it has been used to validate an analytical model in [25]. However, FEA does not provide any analytical relationship between stiffness and structure dimensions of the mechanism. Therefore, it is not considered to be suitable for any multi-objective optimization procedure in which the performance index such as a stiffness index, most likely is to be represented as a function of design parameters. Furthermore, this method is more suitable during the detail design stage because of the high computational expenses required for the repeated re-meshing of a complex structure.

The third of them, MSA incorporates the main ideas of FEA, but operates with rather large elements and flexible beams to describe the manipulator structure but does not consider the bending of links. This technique consists of defining the stiffness matrix of each compliant element in local coordinates and then transforming into reference coordinate. The stiffness matrices in reference coordinate are assembled to calculate the total stiffness of the system [18–22]. Clinton et al. [26] have used MSA to develop a stiffness model for a Stewart platform-based milling machine, in which they derived stiffness matrix for each element and assembled them to calculate the total stiffness of the system.

In addition to these three main groups of methods for modeling the stiffness matrix, Uchiyama et al. [27] has derived an analytical model for the stiffness of a compact 6-DOF haptic device based on static elastic deformation of compliance elements. The total stiffness was calculated using the serial to parallel transformation, assuming the platform to be rigid, while modeling the elastic elements as beam elements and considering the radial stiffness of the bearings.

Moreover, in order to obtain a more realistic stiffness model the existing stiffness models should be integrated with more complex effects such as joint stiffness that also degrade the positioning accuracy. When it comes to the compliance of joints, these are mostly modeled as a constant stiffness and applied only for active joints. Bonnemains et al. [28] e.g. has considered the stiffness of spherical joints in the stiffness computation and identification of kinematic machine tools.

Here, we find a need for an improved analytical modeling approach where the stiffness of both active and passive joints are included and thus using a more accurate way than a constant stiffness. The assumption that we make is that adding the stiffness of passive joints as well as the actuation system significantly will improve the accuracy of the stiffness model.

Common to all the described modeling methods is that they all need a practical validation by means of experimental testing on a prototype. Charles Pinto et al. [23] has evaluated static stiffness mapping of a lower mobility parallel manipulator by considering preload for experimental evaluation by removing backlash in the system. In experimental testing [29], the static behavior evaluation of a robot was analyzed by norms e.g. ANSI/RIA R15.05- 1-1990 [30], ISO 9283:1998 [31], which were established for serial manipulators. Other norms that can be used are the ASME norm for CNC machining [32, 33]. Clinton et al. [26] has used standard deviation for stiffness measurement of Stewart platform-based milling machine.

3 Stiffness modeling and validation methodology

In this section, a systematic procedure is proposed to develop a generalized stiffness model within the workspace of the manipulator and its evaluation with virtual (FEM analysis) and physical experiments. To develop this methodology, a work procedure defined by the flowchart in Fig. 1 is presented. The procedure established by this chart is as follows: The approach used in this methodology is to start with a simplified analytical model. This is compared (verified) by a simplified FEM model in an iterative way until these two models give the same result. Thereafter, a simplified physical experiment is made to validate the analytical model. If the difference between the analytical and the experimental results is not acceptable, i.e., it does not validate the analytical model, a more detailed analytical model has to be developed.

Fig. 1
figure 1

Stiffness modeling methodology

Full size image

For the detailed analytical model also the passive joints and actuation system are included. This is then verified with a detailed FEM model with corresponding detailing level in the same way as for the simplified model. Thereafter, this detailed analytical model is validated by means of a detailed physical experiment.After validating the proposed model, a sensitivity analysis is performed to map the variation of static stiffness in the workspace. In these maps, the mechanical stiffness is visualized as a function of the generalized coordinates of the workspace. The proposed steps for creating the mechanical stiffness model and for validating it are described in the coming sections.

3.1 Simplified modeling

The basic idea of the simplified model is that the stiffness of the end-effector of a robotic structure can be obtained from the individual stiffness properties of its links using basic principles of force and displacement transformation between coordinates. It is assumed that platform and joints are rigid, also the stiffness of the actuation system is not considered in the simplified model. The approach used can be summarized as follows.

3.1.1 Simplified analytical modeling

The simplified model is developed based on resolving forces and moments acting on the end effector into individual link forces and moment, and then compute the individual link deflections from the link stiffness properties. Finally, all these deformations are transformed from the individual link to the end effector and added to obtain the total stiffness matrix of the system.

3.1.2 Simplified FEM modeling

A parametric model can be used to develop a simplified FEM model of the mechanical structure without the actuation system with the assumptions that passive joints are rigid. In this case, a FEM tool like the Ansys parametric design language (APDL) [34] can be used to position and orient the TCP by using either inverse or forward kinematics. Beam, shell and solid elements can be used to model flexible links; similarly the multi-point constraint (MPC) equations can be used for compatibility between different elements. The stiffness (force and deflection relation) can be evaluated for each configuration.

3.1.3 Simplified physical experiments

To complement and validate the results from analytical and FEM models, the following structured physical experiment is proposed. In this case, a simplified model with the actuation system mechanically locked is experimentally tested. The proposed experimental steps are:

  1. 1.

    Position and orientation of the TCP of a platform of a manipulator at the given position and orientation within the workspace.

  2. 2.

    Applying boundary conditions to constrain the motion of active links by a manual locking mechanism.

  3. 3.

    Identification of preload P Ti to eliminate the joint clearance and backlash due to manufacturing errors in each direction (i = x, y and z) of the applied load.

  4. 4.

    At each test configuration the deflection should be calculated based on the average of measurements to minimize measurement errors.

  5. 5.

    At each configuration first identify the deflection δ i due to preload P Ti .

  6. 6.

    For full loading the preload identified in step 4 is added with the total load P T , and the total displacement δ T is measured; the stiffness K i in each direction is calculated as in Eq. (1):

    $$ K_{i} =\frac{{P_{T} -P_{Ti} }}{ {\delta _{T} -\delta _{Ti} }}. $$
    (1)

3.1.4 Evaluation of simplified modeling

The simplified modeling is verified first by evaluating the results from simplified analytical model and simplified FEM model to ascertain whether the models are correct or, on the contrary, it is necessary to refine the models. After assuring the proposed model, both models should be correlated with the simplified physical experiments to validate the models. A validation criterion based on percentage relative error and mean values is used to validate the proposed models.

3.2 Detailed modeling

In the detailed modeling, we also need to consider the stiffness of the passive joints and actuation system. Here, the contact stiffness of passive joints like spherical and universal joints are proposed based on Hertzian springs [35], and the stiffness of the actuation system is based on axial and torsional stiffness of transmission system and actuator, respectively.

3.2.1 Detailed analytical modeling

In the detailed model, additionally the stiffness of passive joints is considered. The nominal point contact model and line contact models are proposed to calculate the contact stiffness of the spherical and universal joint, respectively, while the bending stiffness of the universal joint can be calculated based on the assumptions that two axis act like a simply supported beam. The stiffness of the actuation system depends on stiffness of actuator and transmission system. For the case of linear actuation, the stiffness of the transmission system depends on the axial stiffness of cable, while actuator stiffness depends on torsional stiffness of the motor shaft. The total stiffness of the actuation system is the sum of actuator and transmission system stiffness.

3.2.2 Detailed FEM modeling

It is not computationally efficient to simulate the static behavior with a full FEM model at different configurations in the workspace. A more efficient method is to model the complete system with a 3D CAD system, such as Pro Wildfire [36], which has a kinematic modeling and motion analysis module, such as Pro Mechanism. In the CAD kinematics module, the TCP can be fixed at the required position in the workspace by motion analysis, and the geometry at the required configuration can be exported to a FEM tool, such as Ansys Workbench [34]. The stiffness (force and deflection relation) can be then evaluated for each configuration.

3.2.3 Detailed physical experiments

In the detailed physical experiment, the complete system should be experimentally tested with the actuation system by locking the actuation system using position control for positioning of the active joints at the required pose configuration for each test. The steps proposed for the simplified physical experiments can also be used to perform these tests.

3.2.4 Evaluation of detailed modeling

The detailed modeling is verified by the same procedure, as the one proposed for simplified modeling using the results from detailed analytical model and detailed FEM model to ascertain whether the models are correct or, on the contrary, it is necessary to refine the models. After assuring the proposed models, both models should be correlated with the detailed physical experiments to validate the models. A validation criterion based on percentage relative error and mean values is used to validate the proposed models.

For a given design of a manipulator, the stiffness varies with the variation of the manipulator configurations within its workspace as well as the direction of the applied force/torque. Once the stiffness model is obtained, it is desired to predict its stiffness characteristics over the workspace in order to assess whether the design fulfills the stiffness requirements.

4 Case study: a haptic device

In the following section, the methodology described in Sect. 3 will be applied to a haptic device based on a parallel mechanism in the form of a modified version of the JP Merlet kinematic structure [37, 38]. The structure consists of a fixed base, a moving platform and six identical kinematic chains connecting the platform to the base as shown in Fig. 2. Each kinematic chain consists of an active actuator fixed to the base to actuate a linear guideway of length L 1 using cable-based transmissions to provide linear motion to each linear guideways, a spherical joint, a constant length proximal link of length L 2, and a universal joint. The joint attachment point pairs are symmetrically separated by 120°, and lie on a circle, both on the base and platform. The platform attachment points are rotated 60° clockwise from the base attachment points. The 6-PSU (active prismatic, passive spherical and universal) joint’s configuration is used to get 6-DOF motion at TCP. Its stiffness is determined by the stiffness of each kinematic chain. We assume the base and platform to be rigid.

Fig. 2
figure 2

A schematic of 6-DOF haptic device

Full size image

4.1 Simplified analytical model

To apply the proposed methodology on the selected structure, the force/moment acting on the TCP of the platform is transformed into force/moment acting at connection point C for each kinematic chain. In this methodology, the forces and moment’s action at the tip of the kinematic chain is transformed into individual link forces and moments. Thereafter, deflections for linear guideways and proximal links are calculated, transformed to the platform coordinates and added, giving the total deflection at point C for each kinematic chain.

To calculate the stiffness of flexible links i.e the linear guideway and proximal link, we have used the following procedure: first, we transformed the force acting on the TCP of the platform into individual link forces, then we computed the individual link deflections from the link stiffness properties, and finally, we transformed and added all these displacements to obtain the final compliance matrix. The stiffness matrix is then calculated from the inverse of the compliance matrix. The stiffness of the linear guideway and proximal link can be calculated by transformation of forces and moments from coordinate C to B. A single kinematic chain can be modeled as shown in Fig. 3, where the stiffness model of each compliant element is given in the coming sections.

Fig. 3
figure 3

Simple kinematic chain

Full size image

4.1.1 Force/moment transformation

Considering a force/torque vector (C F , C M )T, expressed in coordinate C. To express this in coordinate B, we need to know how C is oriented with respect to B. This information is typically specified by a rotation matrix \(^{B} R_{C} \in R^{3\times 3} \) where the first, second and third columns of \(^{B} R_{C}\) are unit vectors describing the orientation of x, y and z axes of coordinate C expressed in coordinate B.

The required force/moment transformation is given in Eq. (2):

$$ \left[\begin{array}{c} {^{B}F} \\ {^{B}M} \end{array}\right]={^{B}J_{C}} \left[\begin{array}{c} {^{C}F} \\ {^{C}M} \end{array}\right] $$
(2)

where \({^{B} J_{C}} =\left[\begin{array}{cc} {^{B} R_{C} } & {0} \\ {0} & {^{B} R_{C} } \end{array}\right]\)

Using the force and moment balance of the proximal link the force and moment \(\left({^{U} F_{B}} ,{^{U} M_{B}} \right)^{T} \) at point B can be calculated using force and moment balance. The force balance equation results in Eq. (3):

$$ ^{U} F_{B} ={^{U}F_{C}}. $$
(3)

While taking moments about point C yields the moment balance Eq. (4):

$$ {^{U} M_{B}} ={^{U} M_{C}} +({^{U}R_{B}}{^{B}P_{C}} )\times {^{U}F_{C}} $$
(4)

where B P C is the position vector from B to C expressed in coordinate B. Equations (3) and (4) can be combined to a more compact matrix form of Eq. (5):

$$ \left[\begin{array}{c} {^{U} F_{B} } \\ {^{U} M_{B} } \end{array}\right]=\underbrace{\left[\begin{array}{cc} {I} & {0} \\ {\left\lfloor ({^{U}R_{B}}{^{B}P_{C}} )\times \right\rfloor } & {I} \end{array}\right]}_{_{B}^{U} J_{C,force} }\left[\begin{array}{c} {^{U} F_{C} } \\ {^{U} M_{C} } \end{array}\right]. $$
(5)

The notation \(\left\lfloor p\times \right\rfloor \in \Re ^{3\times 3}\) in Eq. (5) represents the linear transformation of a cross product with a vector \(p\in \Re ^{3}, \)where

$$ \left\lfloor p\times \right\rfloor =\left[\begin{array}{ccc} {0} & {-p_{z} } & {p_{y} } \\ {p_{z} } & {0} & {-p_{x} } \\ {-p_{y} } & {p_{x} } & {0} \end{array}\right]. $$
(6)

\(_{B}^{U} J_{C,force} \in \Re ^{6\times 6} \) is the force transformation Jacobian matrix which transforms the coordinate of application of the force vector from coordinate C to coordinate B in reference coordinate U. U B J C,force involves the relative orientation between coordinate B and coordinate U as well as the position vector describing the origin of coordinate C in coordinate B.

4.1.2 Displacement transformation

Similarly, Fig. 3 can be used for displacement transformation by considering infinitesimal displacements using velocity transformation, by assuming coordinates B and C to be moving instantaneously with respect to coordinate U. The linear and angular velocities \(\left({^{U} v_{B}} ,{^{U} \omega _{B}} \in \Re ^{3} \right),\) respectively, of coordinate B may be computed from the velocities of coordinate C using:

$$ {^{U} v_{B}} ={^{U}v_{C}} +{^{U} \omega _{C}} \times \left({^{U} R_{B}}{^{B} P_{C}} \right) $$
(7)
$$ {^{U} \omega _{B}} ={^{U} \omega _{C}} $$
(8)

The velocities in (7) and (8) may be replaced with the infinitesimal displacements \(^{U} d_{B}\) and Uθ B , and combined to the following compact matrix form in Eq. (9):

$$ \left[\begin{array}{c} {^{U} d_{B} } \\ {^{U} \theta _{B} } \end{array}\right]=\underbrace{\left[\begin{array}{cc} {I} & {\left\lfloor ({^{U}R_{B}}{^{B} P_{C}} )\times \right\rfloor } \\ {0} & {I} \end{array}\right]}_{_{B}^{U} J_{C,disp} }\left[\begin{array}{c} {^{U} d_{C} } \\ {^{U} \theta _{C} } \end{array}\right].$$
(9)

\(_{B}^{U} J_{C,disp} \in \Re ^{6\times 6} \) is referred as the displacement (or velocity) transformation Jacobian which transforms the coordinates of frame C into frame B. Coordinates of B and C can be viewed as instantaneously attached to the same proximal link, and the transformation involves determining the motion of coordinate B due to the motion of coordinate C in coordinate U. U B J C,disp involves the relative orientation between coordinates B and C as well as the position vector describing the origin of coordinate C in coordinate B. The force experience at coordinate B can be expressed in coordinate U using Eq. (5), as given in Eq. (10):

$$ \left[\matrix{ {^{U} F_{B} } \cr {^{U} M_{B} } \cr}\right]\,=\,_{B}^{U} J_{C,force} \left[\matrix{ {^{U} F_{C} } \cr {^{U} M_{C} } \cr}\right]. $$
(10)

4.1.3 Transformation of stiffness and compliance matrices

The stiffness matrix of a compliant element in reference coordinate U can be obtained from the local stiffness matrix L K from the knowledge of rotating matrix \( {^{U}J_{L}} \in R^{6\times 6}\) in Eq. (2). So forces/moments and translational/rotational displacements are related by:

$$ \left[\matrix{ {^{U} F} \cr {^{U} M} \cr}\right]={^{U}J_{L}} \left[\matrix{ {^{L} F} \cr {^{L} M} \cr}\right] \quad {\hbox{and}} \quad \left[\matrix{ {^{U}d_{L}} \cr {^{U} \theta _{L} } \cr}\right]={^{U}J_{L}} \left[\matrix{ {^{L} d} \cr {^{L} \theta } \cr}\right] $$

and from the definition of the stiffness matrices:

$$ \left[\matrix{ {^{U} F} \cr {^{U} M} \cr}\right]={^{U} K}\left[\matrix{ {^{U} d} \cr {^{U} \theta } \cr}\right] \quad {\hbox{and}} \quad \left[\matrix{ {^{L} F} \cr {^{L} M} \cr}\right]={^{L}K}\left[\matrix{ {^{U} d} \cr {^{U} \theta } \cr}\right]. $$

U K is obtained from L K using the same transformation matrix U J L and its transpose

$$ {^{U} J_{L}}^{T} =\,^{L} J_{U} ={^{U}J_{L}}^{-1} $$
$$ {^{U}K}={^{U}J_{L}}{^{L}K}{{^{U}J_{L}^{T}}}. $$
(11)

Similarly, from the definition of the compliance matrices U S and L S, i.e., being the inverse of the stiffness matrices:

$$ \left[\matrix{ {^{U} d} \cr {^{U} \theta } \cr}\right]={^{U}S}\left[\matrix{ {^{U} F} \cr {^{U} M} \cr}\right]\quad {\hbox{and}}\quad \left[\matrix{ {^{L} d} \cr {^{L} \theta } \cr}\right]={^{L}S}\left[\matrix{ {^{L} F} \cr {^{L} M} \cr}\right].$$

So we have

$$ {^{U}S}={^{U}J_{L}}{^{L}S}{{^{U}J}_{L}^{T}}.$$
(12)

The methods that have been used to calculate the stiffness of each kinematic chain is described in the next sections.

4.1.4 Displacement due to linear guideway

From the local compliance matrix of the linear guideways, we transform the compliance matrix to the reference coordinate U using Eq. (12):

$$ {^{U}S_{B}} ={^{U}J_{A}}{^{A}S_{B}}{^{U}J_{A}^{T}} $$
(13)
$$ ^{A} S_{B} =\left[\matrix{ {\frac{{E_{i} S_{i} }}{ {L_{i} }} } & {0} & {0} & {0} & {0} & {0} \cr {0} & {\frac{{12E_{i} I_{zi} }}{ {L_{_{i} }^{3} }} } & {0} & {0} & {0} & {\frac{{-6E_{i} I_{zi} }}{ {L_{_{i} }^{3} }} } \cr {0} & {0} & {\frac{{12E_{i} I_{yi} }}{ {L_{_{i} }^{3} }} } & {0} & {\frac{{6E_{i} I_{yi} }}{ {L_{_{i} }^{2} }} } & {0} \cr {0} & {0} & {0} & {\frac{{G_{i} J_{i} }}{ {L_{i} }} } & {0} & {0} \cr {0} & {0} & {\frac{{6E_{i} I_{yi} }}{ {L_{_{i} }^{2} }} } & {0} & {\frac{{6E_{i} I_{yi} }}{ {L_{i} }} } & {0} \cr {0} & {\frac{{-6E_{i} I_{zi} }}{ {L_{_{i} }^{2} }} } & {0} & {0} & {0} & {\frac{{4E_{i} I_{zi} }}{ {L_{i} }} } \cr}\right]^{-1} $$
(14)

A S B is the stiffness matrix of the linear guideways. The displacement cause by the force acting on B is then:

$$ d_{B} =\left[\matrix{ {^{U} d_{B} } \cr {^{U} \theta _{B} } \cr}\right]={^{U}S_{B}} \left[\matrix{ {^{U} F_{B} } \cr {^{U} M_{B} } \cr}\right]={^{U}J_{A}}{^{A}S_{B}}{^{U}J_{A}^{T}} \left[\matrix{ {^{U} F_{B} } \cr {^{U} M_{B} } \cr}\right].$$
(15)

The displacement d B is the contribution of the flexibility of the linear guideways. The effect of this displacement on C is computed using Eq. (9), and transforming the local compliance matrix of the beam to the reference coordinate U using

$$ \left[\matrix{ {{}^{U} d_{C} } \cr {{}^{U} \theta _{C} }}\right]_{LG} = {}_{C}^{U} J_{B,\rm{disp}} \left[\matrix{ {{}^{U} d_{B} } \cr {{}^{U} \theta _{B} }}\right] = {}_{C}^{U} J_{B,\rm{disp}} {}^{U} S_{B} \left[\matrix{ {{}^{U} F_{B} } \cr {{}^{U} M_{B} }}\right] ={}_{C}^{U} J_{B,\rm{disp}} ({}^{U} J_{A} {}^{A}S_{B} {}^{U} J_{A}^{T} ){}_{B}^{U} J_{C,\rm{force}} \left[\matrix{ {{}^{U} F_{C} } \cr {{}^{U} M_{C} }}\right] $$
(16)

where

$$ _{C}^{U} J_{B,\rm{disp}} =\left[\matrix{ {I} & {\left\lfloor (^{U} R_{B}^{B} P_{C} )\times \right\rfloor } \cr {0} & {I} \cr}\right] $$
$$ _{B}^{U} J_{C,\rm{force}} =\left[\matrix{ {I} & {0} \cr {\left\lfloor (^{U} R_{B}^{B} P_{C} )\times \right\rfloor } & {I} \cr}\right].$$

4.1.5 Displacement due to proximal link

From the local flexibility matrix of the proximal link B S C , we compute the displacement caused by U F C due to the flexibility of proximal link only:

$$ \left[\matrix{ {^{B} d_{C} } \cr {^{B} \theta _{C} } \cr}\right]={^{B}S_{C}} \left[\matrix{ {^{B}F_{C} } \cr {^{B}M_{C} } \cr}\right] $$
(17)

where

$$ ^{B} S_{C} =\left[\matrix{ {\frac{{12E_{i} I_{yi} }}{ {L_{_{i} }^{3} }} } & {0} & {0} & {0} & {\frac{{-6E_{i} I_{y} }}{ {L_{_{i} }^{2} }} } & {0} \cr {0} & {\frac{{12E_{i} I_{xi} }}{ {L_{_{i} }^{3} }} } & {0} & {\frac{{6E_{i} I_{xi} }}{ {L_{_{i} }^{2} }} } & {0} & {0} \cr {0} & {0} & {\frac{{\pi r^{2} }}{{L_{i} }} } & {0} & {0} & {0} \cr {0} & {\frac{{6E_{i} I_{xi} }}{ {L_{_{i} }^{2} }} } & {0} & {\frac{{4I_{xi} }}{ {L_{i} }} } & {0} & {0} \cr {\frac{{-6E_{i} I_{yi} }}{{L_{_{i} }^{2} }} } & {0} & {0} & {0} & {\frac{{4E_{i} I_{yi} }}{ {L_{i} }} } & {0} \cr {0} & {0} & {0} & {0} & {0} & {\frac{{G_{i} J_{iz} }}{{L_{i} }} } \cr}\right]^{-1}.$$

Next we express the force and moment vector acting on C in coordinate B using Eq. (2) to yield:

$$ \left[\matrix{ {^{B} F_{C} } \cr {^{B} M_{C} } \cr}\right]={^{B}J_{U}} \left[\matrix{ {^{U} F_{C} } \cr {^{U} M_{C} } \cr}\right] $$
(18)

where B J U is the rotation matrix for proximal link from B to U, as given by Eq. (19):

$$ ^{B} J_{U} =\left[\matrix{ {^{B} R_{U} } & {0} \cr {0} & {^{B} R_{U} } \cr}\right].$$
(19)

B R U is the unit vector describing the orientation of x, y and z axes of coordinate B expressed in coordinate U. From the local coordinate B of proximal link, the equations for rotation matrix \(^{B} R_{U}\) can be derived as:

$$ Z_{pli} =\left[\matrix{ {\frac{{L_{2ix} }}{ {L_{2} }} } & {\frac{{L_{2iy} }}{ {L_{2} }} } & {\frac{{L_{2iz} }}{ {L_{2} }} } \cr}\right]^{T} $$
$$ X_{pli} =\left[\matrix{ {-\frac{{L_{2iy} }}{ {\sqrt{L_{2ix}^{2} +L_{2iy}^{2} } }} } & {\frac{{L_{2ix} }}{ {\sqrt{L_{2ix}^{2} +L_{2iy}^{2} } }} } & {0} \cr}\right]^{T} $$

and Y pli  = Z pli  × X pli .

Finally, the rotation matrix for proximal link is given by Eq. (20):

$$ ^{B} R_{U} =\left[\matrix{ {X_{pli} } & {Y_{pli} } & {Z_{pli} } \cr}\right].$$
(20)

The displacement of point C due to the flexibility of the proximal link is expressed in the reference coordinate U using Eq. (18):

$$ \left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]_{prox} ={^{U}J_{B}} \left[\matrix{ {^{B} d_{C} } \cr {^{B} \theta _{C} } \cr}\right].$$
(21)

Substituting Eq. (17) and (18) in (21) yields:

$$ \left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]_{prox} ={^{U}J_{B}}{^{B}S_{C}}{^{B}J_{_{U}} } \left[\matrix{ {^{U} F_{C} } \cr {^{U} M_{C} } \cr}\right].$$
(22)

4.1.6 Total compliance due to linear guideways and proximal links

The total displacement of C due to the flexibility of linear guideways and proximal link is the sum of the individual displacements expressed in the reference coordinate U:

$$ \left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} }}\right]=\left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} }}\right]_{LG} +\left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} }}\right]_{prox} =\left[_{C}^{U} J_{B,disp} ({^{U}J_{A}}{^{A} S_{B}}{^{U}J_{A}^{T}} )_{B}^{U} J_{C,force} + {^{U}J_{B}}{^{B}S_{C}}{^{B}J_{U}}\right] \left[\matrix{ {^{U} F_{C} } \cr {^{U} M_{C} }}\right].$$
(23)

From the definition of the compliance matrix we therefore have:

$$ {^{U}S_{C}} =_{C}^{U} J_{B,disp} ({^{U}J_{A}}{^{A}S_{B}}{^{U}J_{A}^{T}} ){_{B}^{U} J_{C,force}} + {^{U}J_{B}}{^{B}S_{C}}{^{B}J_{U}} $$
(24)

and the overall stiffness matrix of linear guideways and proximal link is then

$$ K_{\rm{chain}} =K_{C} =^{U} K_{C} =\left(_{C}^{U} J_{B,\rm{disp}} ({^{U}J_{A}}{^{A}S_{B}}{^{U}J_{A}^{T}})_{B}^{U} J_{C,\rm{force}} +^{U} J_{B}^{B} S_{C}^{B} J_{U} \right)^{-1} $$
(25)

so the overall stiffness of the Stewart platform is given in Eq. (26):

$$ K_{\rm{Total}} =\sum _{i}^{6} K_{\rm{chain}_{i} }.$$
(26)

4.2 Simplified FEM model

In order to verify the simplified analytical model, a simplified parametric model was developed in Ansys APDL. To verify the analytical model at different configurations in the workspace, the TCP was positioned at the center (point 0, nominal position) and at eight, corner points 1–8 of a cube of 50 × 50 × 50 mm, within the reachable workspace of the haptic device, as show in Fig. 4.

Fig. 4
figure 4

Points of experiment in workspace

Full size image

The inverse kinematic method developed by Khan et al. [37] was used to calculate the length of linear guideways at different configurations of the TCP. The lower end of the linear guideways was constrained in x, y and z direction. Linear guideways and proximal links were modeled as solid and beam elements, respectively, while multi-point constraint (MPC) equations were used to satisfy the compatibility condition between joints (both spherical and universal) and links (linear guideways and proximal links). At each of the above-mentioned configurations, a maximum load of 50 N was applied in each x, y and z directions, and the corresponding deformation was measured. Table 1 shows the design parameters and material properties used for the FEM model. Figure 5 shows the resulting deflections when the FEM model was loaded with 50 N in z direction i.e perpendicular to the platform.

Table 1 Design parameters
Full size table
Fig. 5
figure 5

FEM Model

Full size image

The results of simplified analytical model were compared with simplified FEM model, which are shown in Figs. 9, 10 and 11. The results show that there is a good agreement between simplified analytical model and simplified FEM model.

4.3 Simplified physical experiments

To validate the results from both simplified analytical and FEM models, a physical prototype of the selected test case was tested experimentally.

A set of guidelines, how to experimentally evaluate the stiffness parameters are presented here. The stiffness measuring method requires common metrology devices, such as a 0.01 mm resolution dial indicator, a vernier caliper and weights. These were calibrated and specified according to standards. Their working temperature range is [−10 °C, +60 °C]. Test laboratory conditions were approximately 1 atm and 25 °C. The experimental setup is shown in Fig. 6.

Fig. 6
figure 6

Experimental setup

Full size image

4.3.1 Position of TCP

The inverse kinematics was used to find the lengths of linear guideways for the given positions of TCP of the platform. In this experiment the TCP were positioned and analyzed at nine points of cube of 50 × 50 × 50 mm within the workspace as shown in Fig. 4. The nominal position of TCP is at the center of the cube (point 0). The length of linear guideways were measured by a vernier caliper and were constrained in x, y and z direction by a locking mechanism as shown in Fig. 7.

Fig. 7
figure 7

Locking mechanism

Full size image

4.3.2 Preload identification

During manufacturing of different parts and later their assembly in the form of prototype, certain errors are introduced as a consequence of the tolerances and adjustments, that give rise to clearances between the parts of prototype. For this reason, displacement nonlinearities can be produced in the realization of the experimental test. In order to avoid these undesirable displacements, a preload is applied in the system so that measurements represent the resistant behavior of the system in a realistic way. Since the methodology was applied on a 6-DOF haptic device, and due to the limitation in the experimental setup, the loading (3 axial forces, 3 torques) was reduced to axial forces in x, y and z directions, so the preload was identified in three directions. To identify the preload the device was fixed at the nominal position.

The required preload has to be ascertained experimentally and is defined as the smallest value that makes the ratios \(\left[\frac{{F_{x_{0} } }}{ {\delta x_{0} }} ,\frac{{F_{y_{0} } }}{ {\delta y_{0} }} ,\frac{{F_{z_{0} } }}{{\delta z_{0} }} \right]\) constant. The prototype was fixed at the nominal position, and successive experimental tests were made to determine the optimal value of the preload. In each direction (x, y and z), a set of three tests was performed to find an average deformation in each direction. Each test consists of loading the platform with lumped values of the load from 5 to 30 N with a load step of 5 N, and measuring the resulting displacements in each direction. The results of the experimental test for preload are shown in Fig. 8. The stiffness is not constant for the lowest values of the preload due to the small rigid solid movements caused by gaps and friction due to assembling and manufacturing errors.

Fig. 8
figure 8

Pre-load identification at the nominal position

Full size image

4.3.3 Simplified experimental test

In the simplified physical experiment, the physical prototype was tested at maximum force of 50 N with additional force of 15 N for preload. In this experiment the linear guideways were locked by the locking mechanism of Fig. 7 in order to keep the TCP at the required position. In this experiment initially a preload of 15 N was applied at the required position of TCP, and then the corresponding displacements \((\Updelta x_{p}, \Updelta y_{p}, \Updelta z_{p})\) of TCP in x, y and z directions were measured. Finally a total force of 65 N was applied at the selected configuration, and the corresponding displacements \((\Updelta x_{t}, \Updelta y_{t}, \Updelta z_{t})\) of TCP were measured. Here subscripts p and t are used for preload and total load. The actual displacements due the maximum force of 50 N are (\(\Updelta x =\Updelta x_{t}-\Updelta x_{p}, \Updelta y =\Updelta y_{t}-\Updelta y_{p}\) and \(\Updelta z =\Updelta z_{t}-\Updelta z_{p}\)). The same procedure was used at the nine points of experiment of Fig. 4, and the displacements for each loading sequence were measured and recorded.

4.3.4 Results correlation and evaluation

To validate the simplified analytical and FEM model, the computed deflections at the nine test points were compared with those from the simplified experiments. The deflections in x, y and z directions were compared, as in Figs. 9, 10 and 11. The results show that there is a good agreement between simplified analytical model and simplified FEM, but a small difference with the physical experiments.

Fig. 9
figure 9

Deflection of platform in x direction

Full size image
Fig. 10
figure 10

Deflection of platform in y direction

Full size image
Fig. 11
figure 11

Deflection of platform in z direction

Full size image

The relative error between the simplified analytical model and the simplified physical experiments is given in Table 2. This shows a maximum error of 79, 51 and 84 % and an average error of 38, 31 and 80 % in x, y and z directions, respectively. These deviations from the experimental results are not acceptable, which motivate us to develop a more detailed model.

Table 2 Relative error between simplified analytical model and simplified physical experiments
Full size table

4.4 Detailed analytical model

In the detailed modeling, additionally the stiffness of passive joints and actuation system are considered.

4.4.1 Stiffness of passive joints

The contact stiffness of the spherical and universal joint is calculated based on the Hertzian contact model. The nominal point contact model was used for spherical joint and nominal line contact model was used for universal joint, while the bending stiffness of the universal joint is calculated based on the assumption that two axis act like a simply supported beam. The torsional stiffness of passive joints is not considered.

Nominal point contact model The contact stiffness of the spherical joint can be found by Hertzian theory. The nominal point contact can be considered between a sphere with radius R, and a plane loaded by force F as shown in Fig. 12. The radius r of the circular contact area thus formed is given by the equation proposed by Hertz (Timoshenko and Goodier [39], Johnson [40]),

$$ r=\left(3F\frac{R'}{ {E'}} \right)^{\frac{{1}}{ {3}} } $$
(27)

where F is the maximum force at coordinate B, E′ is the effective modulus of elasticity and R′ is the effective radius. F is calculated by Eq. (28):

$$ F=max\left(_{B}^{U} J_{C,\rm{force}} R_{P} \left[\matrix{ {^{U} F_{P} } \cr {^{U} M_{P} } \cr}\right]\right) $$
(28)

where \(\left[\matrix{ {^{U} F_{P} } & {^{U} M_{P} } \cr}\right]^{T} \) is the force and moment at TCP of platform, while E′ is defined by (29), and R′, the effective radius, is related to the individual components by (31):

$$ \frac{{1}}{{E'}} =\frac{{1-v_{1}^{2} }}{ {2E_{1} }} +\frac{{1-v_{2}^{2} }}{ {2E_{2} }} $$
(29)
$$ \frac{{1}}{ {R'}} =\frac{{1}}{ {R'_{x} }} +\frac{{1}}{ {R'_{y} }} $$
(30)

where \( \frac{{1}}{ {R'_{x} }}=\frac{{1}}{ {r_{1,x} }} +\frac{{1}}{ {r_{2,x} }}\) and \( \frac{{1}}{ {R'_{y} }} =\frac{{1}}{ {r_{1,y} }} +\frac{{1}}{ {r_{2,y} }}.\)

Fig. 12
figure 12

Contact model of spherical and universal joint

Full size image

The relation between contact radius and the indentation depth δ is given by Johnson [40]:

$$ r\,=\,\left(2R'\delta \right)^{\frac{{1}}{ {2}} }.$$
(31)

Substituting Eq. (27) into Eq. (31) results in contact stiffness K sp of spherical joint

$$ F={\left(\frac{{8}}{{9}} R'\right)}^{\frac{{1}}{ {2}} } E'\delta ^{\frac{{3}}{ {2}} } $$
(32)
$$ K_{sp} =\frac{{dF}}{ {d\delta }} =E'(2R'\delta )^{\frac{{1}}{{2}} } $$
(33)

so the displacement \(\left[\matrix{ {^{U} d_{C} } & {^{U} \theta _{C} } \cr}\right]\) due to flexibility of spherical joint is given in Eq. (34):

$$ \left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]_{SP} =\,_{C}^{U} J_{B,\rm{disp}} S_{\rm{sp}} \left[\matrix{ {^{U} F_{C} } \cr {^{U} M_{C} } \cr}\right] $$
(34)
$$ S_{\rm{sp}} ={\rm{diag}}\left(\frac{{1}}{ {K_{sx} }} ,\frac{{1}}{ {K_{sy} }} ,\frac{{1}}{ {K_{sz} }} ,0,0,0\right) $$
(35)

where K sx  = K sy  = K sz  = K sp .

Nominal line contact model Stiffness of the universal joint is calculated from bending and contact stiffness. The contact stiffness is based on the Hertzian contact model for line contact, while the bending stiffness is calculated based on the assumptions that two axes of the joint act as a simply supported beam. The line contact is shown in Fig. 12, the semi-axis b of a nominal line contact is derived by Hertz theory,

$$ b=2\sqrt{\frac{{2FR'}}{{\pi lE'}} }.$$
(36)

The relation between contact radius and the indentation depth δ is given by Johnson [40]:

$$ b=\left(2R'\delta \right)^{\frac{{1}}{ {2}} } $$
(37)

where E′ and R′ are defined in Eq. (29) and (30). If we compare both the Eqs. (36) and (37), we get the contact stiffness K UC of the universal joint as:

$$ F=\frac{{\pi lE'\delta }}{ {4}} ,\; K_{UC} =\frac{{dF}}{ {d\delta }} =\frac{{\pi lE'}}{ {4}}.$$
(38)

The general expression for the deflection of a simply supported beam with length L u is given as

$$ \delta _{ujoint} =\frac{{PL_{u}^{3} }}{ {48EI}} $$
(39)

so the bending stiffness K UB of the universal joint is

$$K_{UB} =\frac{{48EI}}{ {L^{3} }} $$
(40)

and the displacement \(\left[\matrix{ {^{U} d_{C} } & {^{U} \theta _{C} } \cr}\right]\) due to flexibility of universal joint is

$$ \left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]_{U} =S_{U} \left[\matrix{ {^{U} F_{C} } \cr {^{U} M_{C} } \cr}\right] $$
(41)
$$ S_{U} ={\rm{diag}}\left(\frac{{1}}{ {K_{ux} }} ,\frac{{1}}{{K_{uy} }} ,\frac{{1}}{ {K_{uz} }} ,0,0,0\right) $$
(42)

where K ux  = K uy  = K UC and K uz  = K UB .

4.4.2 Stiffness of actuation system

The stiffness of the actuation system depends on stiffness of actuator and transmission system. The stiffness of the actuation system can be calculated by force and displacement transformation. The stiffness of the actuator can be calculated based on torsional stiffness, which is given in Eq. (44):

$$ K_{\rm{rotor}} =\frac{{J_{\rm{act}} G}}{ {L_{r} }} $$
(43)

where J act is the polar moment of inertia, G modulus of rigidity and L r is the length of motor shaft.

The stiffness of the transmission system depends on the intended application of the manipulator. Different types of transmission systems, like cable-based linear transmission, cable-based rotational transmission, and timing belt transmission have been studied in Ahmad et al. [41], but in this test case only a cable-based transmission has been used.

4.4.3 Stiffness of transmission system

The cable-based transmission system consists of cable-based linear actuator driven by a DC motor as shown in Fig. 13. The stiffness coefficient, K cable of a cable with length l and pretension τ, that is statically balance with the force F e , can be approximated by Eq. (44):

$$ K_{\rm{Trans}} =K_{\rm{cable}} =\frac{{AE}}{ {l}} $$
(44)
Fig. 13
figure 13

Cable-based linear actuator system

Full size image

where A is the cross-sectional area and E is the young's modulus of the cable.

So the displacement \(\left[\matrix{ {^{U} d_{A} } & {^{U} \theta _{A} } \cr}\right]\) due to flexibility of actuation and transmission system in the reference coordinate U using Eq. (13):

$$ \left[\matrix{ {^{U} d_{A} } \cr {^{U} \theta _{A} } \cr}\right]_{Tr} ={^{U}J_{A}}{^{A}S_{Tr}} {^{U} J_{A}^{T}} \left[\matrix{ {^{U} F_{A} } \cr {^{U} M_{A} } \cr}\right] $$
(45)
$$ S_{Tr} ={\rm{diag}}\left(0,0,\frac{{1}}{{K_{\rm{Trans}} }} ,\frac{{1}}{{K_{\rm{rotor}}}} ,0,0\right) $$
(46)

where K ux  = K uy  = K UC and K uz  = K UB , so the displacement \(\left[\matrix{ {^{U} d_{C} } & {^{U} \theta _{C} } \cr}\right]\) due to actuation and transmission system using (5) and (10):

$$ \left[\matrix{ {{}^{U} d_{C} } \cr {{}^{U} \theta _{C} } \cr}\right]_{Tr} =\, [{}_{C}^{U} J_{B,\rm{disp}} {}_{B}^{U} J_{A,\rm{disp}} ({}^{U} J_{A} {}^{A} S_{Tr} {}^{U} J_{A}^{T} ){}_{A}^{U} J_{B,\rm{force}} {}_{B}^{U} J_{C,\rm{force}}]\left[\matrix{ {{}^{U} F_{C} } \cr {{}^{U} M_{C} } \cr}\right].$$
(47)

4.4.4 Total compliance of the system

The total displacement of C due to the flexibility of linear guideways, proximal link, passive joints and actuation system is the sum of the individual displacement expressed in the reference coordinate U:

$$ \left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]=\left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]_{LG} +\left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]_{prox}+ \left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]_{U} + \left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]_{SP}+\left[\matrix{ {^{U} d_{C} } \cr {^{U} \theta _{C} } \cr}\right]_{Tr} $$
(48)

using Eqs. (16), (22), (34), (41) and (47), the deflection at point C is given in Eq. (49):

$$ \left[\matrix{ {{}^{U} d_{C} } {{}^{U} \theta _{C} } \cr}\right] = [{_{C}^{U} J_{B,\rm{disp}}}({^{U}J_{A}}{^{A}S_{B}}{^{U} J_{A}^{T}})_{B}^{U} J_{C,\rm{force}} + {^{U}J_{B}}{^{B}S_{C}}{^{B}J_{U}}+S_{U} +_{C}^{U} J_{B,\rm{disp}} S_{sp} + {}_{C}^{U} J_{B,\rm{disp}} {}_{B}^{U} J_{A,\rm{disp}}({}^{U} J_{A} {}^{A} S_{Tr} {}^{U} J_{A}^{T} ){}_{A}^{U} J_{B,\rm{force}}{}_{B}^{U} J_{C,\rm{force}}]\left[\matrix{ {{}^{U} F_{C} } \cr {{}^{U} M_{C} } \cr}\right] $$
(49)

so the overall compliance matrix S C of a single kinematic chain at point C is given in Eq. (50)

$$ S_{C}={_{C}^{U}J_{B,\rm{disp}}} ({^{U}J_{A}}{^{A}S_{B}}{^{U}J_{A}^{T}})_{B}^{U} J_{C,\rm{force}}+ {^{U}J_{B}}{^{B}S_{C}}{^{B}J_{U}}+S_{U}+_{C}^{U} J_{B,\rm{disp}} S_{sp}+{}_{C}^{U} J_{B,\rm{disp}} {}_{B}^{U} J_{A,\rm{disp}}{}{A}^{U} J_{B,\rm{force}}{}_{B}^{U} J_{C,\rm{force}}({}^{U} J_{A} {}^{A} S_{Tr} {}^{U} J_{A}^{T}) $$
(50)

and the overall stiffness matrix of a kinematic chain is

$$ K_{\rm{chain}} =K_{C} =(S_{C} )^{-1} $$
(51)

so the overall stiffness for the 6-DOF haptic device is

$$ K_{\rm{Total}} =\sum _{i}^{6} K_{\rm{chain}_{i} }.$$
(52)

This method can be used to compute the stiffness and compliance matrices of N number of serially connected compliant links and joints. The end-effector stiffness expressed in the reference coordinate of N joints is a function of the N, local stiffness matrices and the position and orientation of each compliant element as described by their respective orientation transformation matrices. The stiffness of one kinematic chain with N number of compliant elements is given in Eq. (53),

$$ \begin{aligned} {^{O} K_{N} }&=^{O} J_{N-1} ^{N-1} S_{N} ^{N-1} J_{0} \\ &\quad +\cdots {}_{N}^{0} J_{N-1,{\rm{disp}}} (^{O} J_{N-2} ^{N-2} S_{N-1} ^{N-2} J_{0} )_{N}^{0} J_{N-1,{\rm{force}}} \\ &\quad +\cdots +_{N}^{0} J_{i,{\rm{disp}}} (^{O} J_{i-1} ^{i-1} S_{i} ^{i-1} J_{0} )_{0}^{i} J_{N,{\rm{force}}} \\ &\quad +\cdots +_{N}^{0} J_{1,{\rm{disp}}} (^{O} J_{1} ^{O} S_{1} ^{1} J_{0} )_{1}^{0} J_{1,{\rm{disp}}} \end{aligned}$$
(53)

4.5 Detailed FEM model

To create a detailed FEM model, the complete system was modeled in the CAD-software Pro Wildfire [36]. Using the Pro Mechanism CAD module, the TCP was fixed at the required positions of Fig. 4 in the workspace by motion analysis, and the geometry was then exported to the Ansys FEM software [34]. A motion analysis with the Pro Mechanism model is shown in Fig. 14, while the FEM-analyzed model in Ansys workbench is shown in Fig. 15.

Fig. 14
figure 14

Pro mechanism model

Full size image
Fig. 15
figure 15

Deflection analysis in Ansys workbench

Full size image

4.6 Detailed physical experiments

In the detailed physical experiment, due to the limitation of maximum current saturation of the motors, the physical prototype was tested at maximum force of 15 N with an additional force of 5 N for preload. The same procedure as described for the simplified physical experiment was used to identify a preload of 5 N.

The experimental setup consist of a 6-DOF haptic device connected to a personal computer using a dSpace 1103 board [42]. In this experiment, in order to keep the TCP at the required position, position control was implemented in dSpace environment to actuate six DC motors for the linear guideways motion, as shown in the schematic of Fig. 16.

Fig. 16
figure 16

Schematic of detailed experimental setup

Full size image

The same procedure as the one described for simplified physical experiment was used by measuring displacements \((\Updelta x_{p}, \Updelta y_{p}, \Updelta z_{p})\) and \((\Updelta x_{t}, \Updelta y_{t}, \Updelta z_{t})\) of TCP in x, y and z directions for preload and total load. The actual displacements (\(\Updelta x =\Updelta x_{t}-\Updelta x_{p}, \Updelta y =\Updelta y_{t}-\Updelta y_{p}\) and \(\Updelta z =\Updelta z_{t}-\Updelta z_{p}\)) due the maximum force of 15 N were recorded. The procedure described above was used at all nine points of experiment of Fig. 4, and the displacements for each loading sequence were measured and recorded.

4.6.1 Results correlation

To validate the detailed modeling, the three models, detailed analytical model, detailed FEM model and detailed physical experiments were tested at nine test points in the workspace, and deformations in x, y and z directions due to loading at TCP in the corresponding directions were compared, which are shown in Figs. 17, 18 and 19. The result shows that there is a good agreement between detailed analytical and detailed FEM models, and detailed physical experiments.

Fig. 17
figure 17

Deflection of platform in x direction

Full size image
Fig. 18
figure 18

Deflection of platform in y direction

Full size image
Fig. 19
figure 19

Deflection of platform in z direction

Full size image

The relative error between detailed analytical model and detailed physical experiments is given in Table 3. This shows a maximum relative error of 8, 15 and 16 % in x, y and z directions while the average relative error is 5, 8 and 9 % in x, y and z directions. This shows that considering the stiffness of passive joints and transmission system significantly has improved the accuracy of the analytical model.

Table 3 Relative error between detailed analytical model and detailed physical experiments
Full size table

4.7 Sensitivity analysis

To check the validity of the mathematical model developed, the TCP of the platform was traversed in the workspace at z = 25 mm from the nominal position within the workspace. The stiffness was calculated in a number of grid points.

To evaluate stiffness in a particular direction, first the compliance matrix was calculated, and then the stiffness in a particular direction was calculated from the inverse of compliance in a particular direction.

The analysis described in the previous section has now been used to calculate stiffness maps. The variations of stiffness in x, y and z directions are shown in Figs. 20, 21 and 22, respectively. The square in the figures shows the required workspace of 50 × 50 × 50 mm.

Fig. 20
figure 20

Stiffness variation in x direction

Full size image
Fig. 21
figure 21

Stiffness variation in y direction

Full size image
Fig. 22
figure 22

Stiffness variation in z direction

Full size image

In this simulation, we have simulated the developed model on nine points in the workspace. The average contribution of all the compliant elements of the stiffness model is shown in Fig. 23, which shows that the contributions are 32, 29, 5, 7 and 27 % for linear guide way, proximal link, universal joint, spherical joint and actuation system, respectively.

Fig. 23
figure 23

Contributions of all compliant elements

Full size image

5 Conclusions

In this paper, a new systematic method to create a generalized, highly compact and computationally efficient analytical stiffness model of parallel, serial and hybrid manipulators has been proposed. The proposed model is obtained by step by step modeling from a simplified model by considering the stiffness of all compliant elements in the system. The proposed model takes into account the stiffness of the actuation system, linear guideways, proximal links, and passive joints. The force acing at the TCP of the platform is decomposed into individual link forces, then the individual link deflections are computed from the link stiffness properties. Finally, all these displacements are transformed and added to obtain the final global compliance matrix. The stiffness matrix is then calculated from the inverse of the compliance matrix. Another systems modeling approach covered by the proposed methodology is the introduction of the Hertzian contact model for both spherical and universal passive joints and a simply supported beam model for the universal joint. The proposed modeling method is exemplified with a 6-DOF haptic device based on a modified JP Merlet kinematic structure, and validated with quasi-static FEM-based simulations and physical experiments. A comparative analysis between the simplified modeling and detailed modeling were made, which shows that by considering the stiffness of passive joints, and actuation system reduce the relative error between analytical and experimental results from 84 to 16 % and the average error from 80 to 9 %. A comparison of contributions of compliant elements was made, which shows the stiffness of passive joints has a considerable effect on accuracy of the model.

6 Discussion and future work

The presented modeling method enables and supports development and engineering of a kinetostatic control algorithm, which has the potential to compensate position errors caused by elastic deformation in links and joints due to external loading, and thus to improve the position accuracy compared to the classical kinematic control approach. There are still some unsolved challenges related to the quality and robustness of the systems stiffness model. The quality or accuracy aspect requires a thorough investigation of nonlinear phenomena such as friction and backlash. The robustness aspect is concerned with deviations in the dynamic behavior caused by variations in the physical parameters, e.g. due to manufacturing tolerances and variations in the material properties.