Controlling a system with redundant degrees of freedom: II. Solution of the force distribution problem without a body model

Abstract

What strategies may insects use when controlling redundant degrees of freedom? We investigate this question in standing stick insects. Specifically, the question is addressed how the changes of the torques are coordinated that are produced by the 18 leg joints in a still standing animal. Using a generalization of the principal component analysis, three coordination rules have been identified. These rules are sufficient to describe more than half of the variation observed in the data. To move from a descriptive approach to hypotheses on how the neuronal system may be structured, two simulation approaches are proposed. In both cases, torques are decreased by randomly selected values. In the first simulation, the coordination rules derived from the principal components are used to produce changes in torques. In the second simulation, the individual joint torques are modified using a simple local approach. In both approaches, the resulting torques are re-adjusted by Integral controllers applied in each joint. The results show that the torque distribution problem can be solved by a local approach without requiring a body model.

Introduction

A fundamental problem in brain science concerns the question of how brains are able to deal with the control of redundant degrees of freedom (DoFs). It is generally accepted that the nervous system adopts strategies that reduce the complexity of this problem. The classical proposal based on synergies (Bernstein 1967) assumed that joints are coupled via fixed rules, which reduces the effective number of DoFs. Such rules between joints can be identified by searching for regularities in movements that are not specified by the task. As for example in human arms, Morasso (1983) showed a bell-shaped velocity profile for reaching movements. Lacquaniti et al. (1983) found that in irregular movements tangential velocity and instantaneous curvature are strongly related. Gottlieb et al. (1996) provided evidence that the dynamic torque produced at each moving joint over the duration of a movement is a linear function of a single-template torque function. In human motor control such rules were found not only in arm movements but also in many different kinds of movements. Once such rules are identified, they can be used to infer the structure of the underlying motor control system.

The problem of redundant DoFs is not only relevant for the control of movement, but also already exists for “simple” static situations: if a hexapedal insect is standing on the ground with all six legs, its central nervous system has to control 18 DoFs, as each leg typically contains three joints. Because body position in space is determined by six DoFs (three for translation and three for rotation), there are 12 extra DoFs to be determined for a given body position. Therefore, the task is underdetermined and the central nervous system has to decide how to cope with these extra DoFs.

In this work, we concentrate on the investigation of how a standing insect, Carausius morosus, distributes its 18 torques. The stick insect is well suited for such an experiment because, being a nocturnal animal, under light conditions it may keep a fixed body position for hours. It maintains or resumes its body position even after considerable disturbances. However, as reaction to such stimuli or based on a spontaneous decision, the animal may change the torques applied at the different leg joints (Lévy and Cruse 2008). Furthermore, it has been shown that a torque distribution that consists of individual torques having high absolute values converges over time and appears to approach some “minimum” (Lévy Cruse 2008).

When the torques of individual joints change, but the position of the whole animal remains constant, the changes of torques of different joints necessarily have to be coupled to compensate the torque change of an individual joint. How this is done exactly addresses the question of cooperation between legs and joints, i.e., between redundant DoFs. To address this question, the data analysis has been divided into two sections. Whereas in the companion paper (Lévy and Cruse 2008) we concentrate on correlations that are based on long time periods in the order of 360 to 4,590 s, in this paper, we concentrate on the analysis of torque changes within a short time window, i.e., in the order of 10 s.

In this paper, it is shown that torque changes do not happen at random, but follow some correlation rules. Furthermore, it will be shown that the observed torque minimization process as reported in the companion paper (Lévy and Cruse 2008) can be simulated using a very simple local approach.

Methods

Experimental set-up

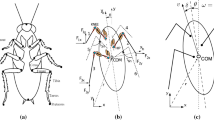
Six three-dimensional-force transducers were disposed parallel to each other in two rows (Fig. 1). The animal, an adult female stick insect Carausius morosus, was placed to stand with each leg on one force transducer. In this way 18 force signals can be simultaneously recorded. Mirrors were placed on both sides of the animal. A digital camera was fixed to record the body and leg position from above and via the mirrors from both sides.

Fig. 1

a Three-dimensional force transducer (front and side views), strain gauges are numbered. b Experimental set-up (top view from the camera and front view)

The forces are first measured in an absolute coordinate system and later transformed in a body fixed coordinate system x, y, z for each leg (Fig. 2). The origin for each leg is given by the basis of the coxa. Figure 2 also shows the rotational axis of the body (roll, pitch, yaw). The angle values describing the position of the rotational axis of the thoracic-coxal joint (ψ, φ) are taken from Cruse and Bartling (1995). The arrangement of the rotational axes of the thoracic-coxal joint (α), coxa-trochanter joint (β) and femur-tibia joint (γ) are shown for a left leg in Fig. 2. The rotational axis for right legs is the same as for the left legs in the cases of coxa-trochanter joint (β) and femur-tibia joint (γ). To simplify interpretations, the directions of rotation of the thoracic-coxal joint (α) for right legs were inverted differing from the conventions used in robotics. In this way, torques produced by retractor muscles are positive in both right and left legs.

Fig. 2

Right leg of a stick insect. 3D-view of force directions and rotational axis of joint angles

For a specific time period, varying from 360 to 4,590 s, the ground reaction forces developed by the animal have been measured. In most experiments, the animal was slightly disturbed. Disturbances were applied 360, 600, 900 or 1,200 s after the start of the experiment. Disturbances are given by either touching the animal with a brush at the body or the antennae or by applying a small lateral force to the side of the body between front and middle leg coxa or between middle and hind leg coxa. Note that the animal may change body position during the disturbance but then remains at this new position during the following experimental period.

N = 15 animals have been investigated. From these animals 59 experiments could be evaluated. The experiments with disturbance were split for the analysis into distinct datasets separated by the disturbances. Therefore, from the 15 animals 133 sets have been evaluated.

Data manipulation

Data representing the forces in absolute coordinates were measured with a rate of 100 Hz, amplified, transmitted to a computer and imported into Matlab7.0. The measurements in volts were transformed in newtons and averaged for each 10-s interval. An offset was determined channelwise and subtracted.

The spatial positions of the body and of the legs have been registered every 30 s using a digital camera. Using Matlab 7.0 the body fixed coordinate system of the stick insect was determined and the corrected forces were transposed into the body fixed coordinate system. Using the previously measured size of the stick insect’s body, the digital picture and the body fixed coordinate system, the α-, β-, and γ- angles (Fig. 2) , of each leg were calculated. With the body geometry and the force components, the torque for each joint was determined. The resulting relative error was estimated to be less than 10%.

Further details concerning experimental procedures and data manipulation could be found in the companion paper (Lévy and Cruse 2008)

Theoretical background

Principal component analysis

Methods like principal component analysis (PCA) (Manly 2004) are methods for data-reduction and -bundling. The aim of PCA is to find a limited number of components, which represent unobserved new variables that are constructed from the observed variables in such a way that they capture most of the information contained in the observed variables. Mathematically, the procedure corresponds to searching the minimum described by

$$ \begin{aligned} \hbox{min} &\sum_{i=1}^{I}\sum _{j=1}^{J}\left(x_{ij} -\sum _{q=1}^{Q}a_{iq} b_{jq} \right)^{2}\\ X&=\left[ \begin{array}{lll} x_{11}&\cdots&x_{1J}\\ \vdots&\ddots&\vdots\\ x_{I1}&\cdots&{x_{IJ}}\\ \end{array} \right],\\ A&=\left[ \begin{array}{lll} a_{11}&\cdots&a_{1Q}\\ \vdots&\ddots&\vdots\\ a_{I1}&\cdots&a_{IQ}\\ \end{array} \right], \quad B=\left[ \begin{array}{lll} b_{11}&\cdots&b_{1Q}\\ \vdots&\ddots&\vdots\\ b_{J1}&\cdots&b_{JQ}\\ \end{array} \right] \end{aligned} $$

‘X’ is the matrix containing the original data, with i = 1,…, I observations and j = 1,…, J variables. ‘A’ is a weight matrix, also called score matrix, and ‘B’ is the principal component (PC)-matrix, containing q = 1,…, Q PCs.

The principal components (PCs) are linear combinations of the original variables. Their main attribute is to represent an orthogonal transformation of the original variables into a set of uncorrelated variables.

When calculating a PCA, several methods are proposed to choose the best number of PCs. The most common rule is to take each PC with an eigenvalue greater than 1, because they represent components with a greater variance than that of the standardized original data.

Parallel factor analysis (PARAFAC)

The so-called three-way component analysis techniques are designed for descriptive analysis of three-way data, i.e., data that can be arranged in a three-dimensional array. The mainly used techniques are PARAFAC proposed by Harshman (1970) and Carroll and Chang (1970), and three-mode factor analysis proposed by Tucker (1963, 1966), further elaborated by Kroonenberg and DeLeeuw (1980), who renamed the method “three-mode PCA”.

The aim of three-way component analysis techniques, hence, of PARAFAC is the same as the aim of PCA: to find a limited number of components, which are unobserved new variables that are constructed from the observed variables in such a way that they capture most of the information contained in the observed variables. However, PARAFAC allows to weight differently each component in different situations. In other words, using this method, interactions can be considered between two factors influencing the use of the PCs.

From a mathematical point of view, PARAFAC is only an extension of PCA and corresponds to finding the following minimum:

$$ \begin{aligned} \hbox{min} &\sum _{i=1}^{I}\sum _{k=1}^{K}\sum _{j=1}^{J}\left(x_{ijk} -\sum _{q=1}^{Q}a_{iq} c_{kq} b_{jq} \right)^{2}\\ &\underline{X}=\left[\left[ \begin{array}{lll} x_{111}&\cdots&x_{1J1}\\ \vdots&\ddots&\vdots\\ x_{I11}&\cdots&x_{IJ1}\\ \end{array} \right] \right.,\cdots ,\left.\left[ \begin{array}{lll} x_{11K}&\cdots&x_{1JK}\\ \vdots&\ddots&\vdots\\ x_{I1K}&\cdots&x_{IJK}\\ \end{array} \right]\right],\\ &A=\left[ \begin{array}{lll} a_{11}&\cdots&a_{1Q}\\ \vdots&\ddots&\vdots\\ a_{I1}&\cdots&a_{IQ}\\ \end{array} \right], \quad B=\left[ \begin{array}{lll} b_{11}&\cdots&b_{1Q}\\ \vdots&\ddots&\vdots\\ b_{J1}&\cdots&b_{JQ}\\ \end{array} \right],\\ &C=\left[ \begin{array}{lll} c_{11}&\cdots&c_{1Q}\\ \vdots&\ddots&\vdots\\ c_{K1}&\cdots&c_{KQ}\\ \end{array} \right] \end{aligned} $$

$`\underline{X}\hbox{'}$ is a tensor (a three-dimensional matrix) containing the original data, with i = 1,…, I observations, j = 1,…, J variables and k = 1,…, K situations. ‘A’ and ‘C’ are weight matrices, also called score matrices, and ‘B’ is the principal component (PC)-matrix, containing q = 1,…, Q PCs.

As shown above, the PCs are linear combinations of the original variables. An important difference between PCs resulting from the PCA analysis and PCs resulting from the PARAFAC analysis is that the PARAFAC model is not nested. This means that the PCs of a q-component model do not equal the PCs of a (q – 1)-component model plus one additional component. The reason for this is that the components are not required to be orthogonal; hence, they are not independent.

It is difficult to determine the best number of PCs for the PARAFAC model. For this purpose Bro and Kiers (2003) developed a new approach called “core consistency diagnostic” (CORCONDIA). This method calculated a “core consistency”-coefficient, which gives an idea about the appropriate number of PCs. For valid models the coefficient will be close to 100, if too many components are used the coefficient will fall to 0.

Results

In the companion paper (Lévy and Cruse 2008), we have shown that after the insect has been placed on the force transducers, the values of the individual torques change over time. Some torques increase, while others decrease, but in a manner that causes the sum of all absolute torques to decrease over time. During a disturbance, the torques may increase, but again start to relax after the disturbance is finished. This torque decrement can be roughly approximated by a two-term exponential equation. As insects do not move their body during the relaxation period, these torque changes have to be coordinated somehow to maintain body position and to produce the observed exponential decrement of overall torques. In the companion paper (Lévy and Cruse 2008), the correlation between static torque values has been considered. In contrast, we here concentrate on the changes of the torques, i.e., on how the torque distribution changes on a short-term time scale. To study these torque changes for each joint and each experiment, the changes of the torques between two consecutive time steps (10 s interval) have been computed.

Correlation between torques

Long- and short-term correlation between torques

In the companion paper (Lévy and Cruse 2008), the correlations between static torques have been investigated in detail. We show that torques can neither be predicted by the position of body and legs only nor be traced back on correlation between torques. Furthermore, no obvious rule to coordinate torques could be detected. Analysis of torque change provides different results. Figure 3, a representative example, illustrates the difference between both approaches. It shows the temporal development of the torques of the α-joint and of the γ-joint of the left hind leg. As a general trend, both torques show a positive slope, which leads to a high and positive correlation (r = 0.78). However, on a “short” time scale both torques show changes with opposite sign. This is indicated for each interval in Fig. 3 by the signs showing the slope for each time step. From the 15 intervals, signs correspond with three cases only. Consequently, correlation between torque changes is high but negative (r = −0.66, in this example). Furthermore, comparison of the tables showing the correlations between torques (Lévy and Cruse 2008) and the torque changes (see below) show that correlation coefficients for the same experiment do not match.

Fig. 3

Torques of the α-joint (upper panel) and of the γ-joint (lower panel) of the left hind leg over time for the same experiment. Correlation of torques = 0.78, correlation of torque changes = −0.66. + and – stand for the positive or negative slope of the torque changes

Correlation between individual torques

As mentioned earlier, after the animal has been placed on the platform, torques start with high absolute values but in general decrease over time. Any change in a single torque has to be compensated by changes in other torques. A straightforward solution to this problem would be, for example, that some fixed linear relations exist between specific torque changes. The correlation coefficient indicates the strength and the direction of a linear relationship between two variables. Therefore, the calculation of the correlation between torque changes may provide hints concerning the rules that control the coordination of different torques.

In many individual experiments, an obvious coupling between torques of different legs on a short-term scale can be observed (recall that the position of the animal remains constant throughout the experiment). This coupling is not only found between joints of one leg but also between joints of different legs as for example of α-joint of the left front leg and β-joint of the right hind leg (Fig. 4). However, individual correlation coefficients between torque changes, both between different animals and within one animal vary considerably, and can from case to case be positive, negative or about zero. Therefore, the averages of most individual correlations are low (not shown). Even high positive/negative correlations in the first part of an experiment might get smaller or even change sign after the disturbance although body position has not changed. As a representative example, the results of one experiment are shown in Table 1 (before disturbance) and in Table 2 (after disturbance). For example the correlation between torque changes in the α-joint of the right hind leg and in the β-joint of the left hind leg changed from 0.83 before disturbance to −0.46 after. Another example is the correlation between torque changes in the α-joint of the right middle leg and in the γ-joint of the left hind leg changing from 0.56 to −0.63. Nevertheless, a few structures are more consistent (Tables 1, 2). Torque changes of joints within the same leg are often highly correlated. β- and γ- joint mostly show positive correlation, α-joints mainly show negative correlation for hind legs and positive correlation for front legs. Torque changes between γ-joints of different legs are often highly correlated.

Fig. 4

Distribution of correlation coefficients (n = 133) between the torque changes of the α-joint of the left front leg and the β-joint of the right hind leg

Table 1 Correlations of torque changes between every pair of joints during one experiment before disturbance (same experiment as shown in Table 2)

Table 2 Correlations of torque changes between every pair of joints during one experiment after disturbance (same experiment as shown in Table 1)

Correlation between legs

The analysis presented in the companion paper (Lévy and Cruse 2008) has shown that consideration of complete legs might be more informative than of individual joints. Therefore, in addition to correlation between single joints, the correlation between legs was calculated. This was done by application of the concor-method (Lafosse 1989; Lafosse and TenBerge 2005), a generalized canonical correlation analysis for k different tables with n _k -variables. This method allows to calculate the correlation between k groups of variables (here k = 6 legs) with n _k -variables (here n = 3 components: α-, β- and γ-joints).

For each experiment, there are high (up to 0.99) and low (down to 0.00) canonical correlation coefficients, but the leg combinations with high/low coefficients fluctuate considerably. On average, canonical correlation coefficients vary between 0.40 and 0.57 (Table 3). These values are not very high and indicate that no fixed correlation rules between the legs exist. Instead, the animal can apparently exploit varying combination of torque changes.

Table 3 Average canonical correlation coefficient between legs (n = 42, canonical correlation coefficients are defined between 0 and 1)

Principal component analysis

Principal component analysis for single datasets

Even though the animal can exploit different possibilities to change the torque distribution, some basic rules may exist. Therefore, PCA was calculated individually for each of the 133 datasets of torque changes.

In 10 datasets, three PCs have an eigenvalue of greater than one. In 60 datasets, the eigenvalues of the first four PCs are greater than one. In 53 datasets, five PCs have an eigenvalue of greater than one. In the remaining 10 cases, six eigenvalues are greater than one. The PCs with an eigenvalue of greater than one stand for at least 71% of the data dispersion.

This result means that the torque changes do not appear totally at random. There appear to exist four or five basic rules the animal follows to change its torque distribution and the first four to five PCs represent these rules. The capacity of these PCs to describe the data can be tested by reconstructing the data using the PCs obtained of each individual experiment. As an example, Fig. 5 shows, for the first 120 s of one representative experiment, a comparison between the original torque values (continuous line) and the reconstructed values using the four PCs obtained from this experiment (open circles). Note that the PCA was made on the torque changes, whereas Fig. 5 shows the torques values, reconstructed with the estimated torque changes. Therefore, small errors in the estimation of torque changes have a cumulative effect over time on the torque path.

Fig. 5

Reconstructed torques (mNmm) using the PCs during the first 120 s of one experiment. The continuous line shows the original torque path; open circles show the reconstruction using the four PCs of the PCA obtained for this dataset; stars show the reconstruction using the six PCs of the PCA obtained for all 133 datasets. Left column torques of α-joints; middle column torques of β-joints; right column torques of γ-joints. Rows show from top to bottom. RH right hind leg; LH left hind leg, RM right middle leg, LM left middle leg; RF right front leg, LF left front leg

Principal component analysis for all datasets taken together

When, instead of computing the PCA for each of the 133 datasets separately, PCA is calculated for all 133 datasets together, the results show that six PCs had an eigenvalue of greater than one, which describe 68% of the data dispersion. The first three PCs are the most important ones. Together they describe 51% of the whole data dispersion, while the three other PCs are less important and stand together for 17% of the data dispersion. Figure 5 shows the data reconstruction of the torques using these six PCs (marked by a star). The results show that it is possible to reduce the data dimensionality from 18 to 6, without losing a lot of information concerning the torque changes.

The fact that, taken all datasets together, a lot of PCs resulting from the PCA have high eigenvalues, together with the fact that these PCs stand for a relatively low goodness of fit, indicates that one or more unknown factors might influence the PCs. This assumption is supported by the observation that comparison of the first PCs calculated for the various experiments do not match well although the PCs are able to describe very well the corresponding original data.

Two factors are varying between the datasets and might be possible candidates: the standing position of the animal that may vary from one experiment to the next and the animal itself. Interaction between these factors and the PCs are plausible and may explain the discrepancy between the PCs. Another possible explanation for this discrepancy might be the capability of animals to use different strategies for reducing their torques, i.e., the capability to use different sets of PCs in different experiments. Therefore, the PCs resulting from the PCA obtained from all datasets together can be seen as the average PCs of the average position of all experiments on an average animal. In the following, these aspects will be studied by first performing a PARAFAC analysis followed by an ANOVA.

Parallel factor analysis

Calculus of the model

Before being able to perform the PARAFAC-analysis, the data have to be arranged as tensor, i.e., as a cube. Each slice of the cube represents a different situation (a different dataset) with, for each situation, J variables (torques) and I observations. Due to the experimental design (see “Data manipulation” section), datasets have different length, i.e., different numbers of observations. Therefore, the PARAFAC analysis cannot be made on all data. From the 133 datasets, 72 were recorded for 900 s or longer; thus, 72 dataset have 90 or more observations. This represents about 85% of all data. Therefore, the analysis was made with the first 90 observations of all datasets recorded for 900 s or longer. Consequently, the PARAFAC analysis was made on a tensor with I = 90, J = 18 and K = 72. Using CORCONDIA (see “Theoretical background” section), a model with three PCs appears to be the best one. Therefore, a three-component PARAFAC model was calculated.

The fit of the PARAFAC model is not comparable to the fit of the PCA model. This is because of the way the entities of the score matrix ‘A’, standing for the time, are calculated. In the PARAFAC model the matrix ‘A’ is identical for each dataset. This implies that the time structure, regarding the use of the PCs, is identical for each dataset. In contrast, in the PCA model the matrix ‘A’ is different for each dataset. This implies that the time structure, regarding the use of the PCs, is different for each dataset. In our case this second assumption is the better one, as animals may show different time structures. Hence, the matrix ‘A’ was re-estimated for each dataset using the least-squares method (assuming that the best fitting curve is the curve that has the minimal sum of the squared deviations from a given set of data).

The three-component PARAFAC model with a re-estimated ‘A’-matrix provides a fit of 52%. This fit is comparable to the fit of the three-component PCA model, which amounts 55% using the same data as used for the PARAFAC. Figure 6 shows, for the first 120 s of one experiment, a comparison between the original torque values (continuous line), the reconstructed values using the three PCs obtained from the PARAFAC analysis (marked by a cross) and the PCA analysis (marked by a star). Note that PARAFAC and PCA were made on the torque changes and that Fig. 6 shows the torques values, reconstructed with the estimated torque changes. Therefore, small errors in the estimation of torque changes have a cumulative effect over time on the torque path.

Fig. 6

Reconstructed torques (mNmm) using the PCs during the first 120 s of one experiment (same experiment as shown in Fig. 6). Continuous lines show the original torque path; crosses show the reconstruction using the three PCs of the PARAFAC; stars show the reconstruction using the three first PCs of the PCA obtained for all 133 datasets. Left column torques of α-joints; middle column torques of β-joints; right column: torques of γ-joints. Rows show from top to bottom. RH right hind leg, LH left hind leg, RM right middle leg, LM left middle leg, RF right front leg, LF left front leg

Interpretation of the model

The PARAFAC shows that it is possible to reduce the data dimensionality from 18 to 3, without loosing a lot of information concerning the torque changes. This means that there are three basic rules the animal follows to change its torque distribution and the three PCs (matrix ‘B’) stand for them. The way these rules are used, differs from dataset to dataset. This dataset-relative effect is represented by the matrix ‘C’.

Concerning the interpretation of the effect represented by the matrix ‘C’ three possible assumptions have been mentioned in “Principal component analysis for all datasets taken together” section. These assumptions are (i) that the standing position of the insect interacts with the PCs, (ii) that the insect itself interacts with the PCs and (iii) that the insect uses different strategies. Using the analysis of variance (ANOVA), these assumptions can now be tested. ANOVA is a statistical method that measures the amount of variability induced in measurements that comes from the measurement itself, and compares it to the total variability observed in a set of factors to determine the variability of the measurements. Table 4 shows the percentage of variation which can be explained for each component by one of the three assumptions. The influence of the body position on each of the three PCs corresponds to about a quarter of the whole variability. Nonetheless, the influence of the body position was tested as not significantly influencing any PCs. The influence of the animal on the first PC is significant. This observation indicates that all insects cannot be taken as equal, although this is implicitly assumed in many studies. The two other PCs are independent from the animal. The remaining variability described by the matrix ‘C’ is high and cannot be explained by any measured variables. Even though this variability might be interpreted as a different strategy, the animal could use to reduce its torques.

Table 4 Percentage of influence of various factors on the PCs (ANOVA)

Figure 7 illustrates the three PCs revealed by the PARAFAC. To interpret the significance of a PC it is sensible to look at the size of its entries. As each entry corresponds to a variable, it is possible to conclude that, relating to this PC, variables with similar entries are positively correlated and variables with inverse entries are negatively correlated. Furthermore, variables with high absolute entries are highly influenced by the component, while variables with a low absolute entry are influenced just a little.

Fig. 7

Entries of the PCs. a First PC, b second PC and c third PC. Torques corresponding to the entries of the PC are ordered by leg. RH right hind leg, LH left hind leg, RM right middle leg, LM left middle leg, RF right front leg, LF left front leg and abbreviated for the joints by their letters, α, β and γ

For the first PC the result can be summarized as follows (Fig. 7a). β- and γ-torques are all positively correlated with each other. α-torques of hind and middle legs are positively correlated with each other and negatively correlated with all other torques, including α-torques of front legs. This means, for example, that when a torque in a γ-joint is extended a bit, the torques of all other γ-joints will also be extended. At the same time, torques in all β-joints will elicit an elevation, in the α-joints of a front leg a retraction and in all α-joints of the middle and hind legs a protraction. The first PC can be illustrated as a vertical movement of the body, i.e., a translation along the z-axis of the body (Fig. 2).

For the second PC, the results can be summarized as follows (Fig. 7b). β- and γ-torques of the same side of the animal are positively correlated with each other and negatively correlated with β- and γ-torques of the other side. α-torques of hind and middle legs of the same side of the animal are positively correlated with each other and negatively correlated with all other torques of the same side, including the α-torque of the front legs. Therefore, α-torques of hind and middle legs of the same side of the animal are positively correlated with β- and γ-torques of all three contralateral legs and with the α-torque of the contralateral front leg. This means, for example, that when the torque in the γ-joint of the left side of the animal is extended a bit, the other torques in γ-joints of left legs will also be extended, while torques in γ-joints of right legs will be flexed. At the same time, torques in α-joints of the hind and middle left leg as well as in the right front leg will elicit a protraction, while the α-joints of the right hind and middle leg as well as the left front leg will elicit a retraction. The second PC can be illustrated as to produce a horizontal movement of the body, more precisely a rotation around the z- and the x-axis of the body (Fig. 2). In this case, the origin of the coordinate system is situated between middle and front legs.

The properties of the third PC are very similar to the properties obtained for the second one. It can be summarized as follows (Fig. 7c). All torques of the same side of the animal, apart from the α-torques of the hind legs, are positively correlated with each other and negatively correlated with the torques of the other side. Hence, α-torques of hind legs are positively correlated with torques of the other side of the animal and negatively correlated with torques of the same side. This means, for example, that when the torque in a γ-joint of the left side of the animal is extended a bit, the other torques in γ-joints of left legs will also be extended. At the same time, the torques of all β-joints of left legs will elicit an elevation, the α-joints of front and middle left legs will elicit a retraction and the α-joint of the left hind leg will elicit a protraction. Consequently, on the right side of the animal, torques of γ-joints will elicit a flexion, in β-joints a depression, in α-joints a protraction in front and middle leg and a retraction in the hind leg. The third PC can be illustrated as to elicit a horizontal movement of the body, more precisely a rotation around the z- and the x-axis of the body (Fig. 2). In this case, the origin of the coordinate system is situated between hind and middle leg. Therefore, second and third PCs differ in the position of the origin of the coordinate system, leading to different rotation of the body.

Simulation

Using correlation analyses alone does not provide direct information concerning the neuronal mechanisms that may underlie the observed behaviour. To investigate the feasibility of two hypotheses concerning these mechanisms, two dynamic simulations have been developed. In the simulation we test two hypotheses concerning the structure of the controller, which allows a decrease of the absolute torques as observed in the experiments while keeping the position of body and legs constant. The assumption, common to both hypotheses, is that each joint is subject to integral position control, and that there is, for each joint, a randomly selected decrease of its torque value. The coordination between each joint is only due to the mechanical coupling via body segments and the substrate. As explained in the Appendix, the two hypotheses differ in the manner in which values are determined when the torques are changed. However, both procedures produce data which resemble those produced by a real stick insect.

Procedure 1: application of PCs

The first procedure that is applied to change the torques is based on the PARAFAC and the correlation structure observed during the torque minimization process. The three PCs represent three rules insects are assumed to use to reduce their absolute sum of torques. Correctly weighted and added, the PCs correspond to a decrement of torques between the two time steps. In the simulation, weights are taken at random and using the weighted PCs, the set of torques is changed. For more details, see Appendix.

Applying this simulation procedure, results have been obtained as shown in Fig. 8 as a representative example. This figure shows the originally observed paths of torque decrements for one experiment and two corresponding simulated paths. Both simulated paths differ due to the stochastic effects.

Fig. 8

Two simulated torque (mNmm) changes shown for the first 48 iterations (1 iteration process correspond to 10 s real time). Stars show the original torque path; Continuous lines show two simulated paths using the first procedure based on the PCs. Left column torques of α-joints; middle column torques of β-joints; right column torques of γ-joints. Rows show from top to bottom. RH right hind leg, LH left hind leg, RM right middle leg, LM left middle leg, RF right front leg, LF left front leg

As can be seen in the example shown in Fig. 8 on a qualitative level, given the noisy structure of both experiment and simulation, there is no obvious disagreement between both results. Is there a way for a more quantitative comparison? The basic problem is that we can investigate the behaviour resulting from the random effect in the simulation, but only indirectly in the experiments, because only the former can easily be repeated using the same starting situation. The experiment can only be described by the three-component PARAFAC model which allows to fit the experimental measurements by 52% (see “Parallel factor analysis” section). The remaining 48% are not explained yet. The hypothesis tested in the simulation is that these remaining 48% result from the “disturbing” influence of the PID controllers only. If this hypothesis was correct, the simulation based on the three PCs plus the PID controllers should produce results 52% of which could be explained by the three PCs found in the experiments. If the PID controller would play no essential role, and the 48% would result from any other effects, which are however not implemented in our simulation, the three PCs should explain up to 100% of the simulated results. The reconstruction of the simulated data provides a fit of around 70%. This means that only 70−52 = 18% can be explained by the effect of the PID controllers and about 30% leave to be explained by other unknown effects. A part of this difference can be explained by the accuracy of measurement, as the relative error was estimated to be about 10% (see “Data manipulation” section). However, about 20% still remain unexplained.

Procedure 2: application of a local rule

The second procedure represents a local rule, which is not based on the PCs. In this simulation, each torque is reduced between two time steps proportionally to its actual size. The reduction factors are not fixed, but determined following a stochastic procedure that depends on the absolute sum of all torques. For more details, see Appendix.

This second procedure shows a high variation in the simulated paths but the latter are always similar to the original ones, i.e., paths observed in the experiments are situated in-between various simulated paths. Similar to the experiments, individual paths may show changes in sign of the torque as well as changes in sign of the slope. As a representative example, Fig. 9 shows an experimentally observed path of the β-torques for the left middle leg (marked by stars) as well as various simulated paths corresponding to this experiment. Another representative example is shown in Fig. 10, where the observed path of the absolute sum of the torques (marked by stars) is plotted as well as various simulated paths.

Fig. 9

Torque of the β-joint for the left middle leg over time for 14 different simulations (continuous line) using the second procedure and for the experimentally observed data from the corresponding experiment (stars)

Fig. 10

Absolute sum of all torques over time for 14 different simulations (continuous line) using the second procedure and for the experimentally observed data from the corresponding experiment (stars)

To receive a measure for the quality of these results, we tested how well the simulation results can be explained by the three PCs of the PARAFAC that were used to describe the torque changes in the experiments. To this end, the simulated data were approximated using the PCs of the PARAFAC. This was possible with a goodness of fit between simulated and reconstructed values varying around 55%. This is the same size as the goodness of fit of the three-component PARAFAC-model with a re-estimated ‘A’-matrix on the experimental measurements. Therefore, the simulation appears to apply the same three correlation rules as the animals do. Moreover, the simulation applies these rules with approximately the same size as the animals do. Note that the PCs are not used for this simulation. The parameters used for the decrease of the torques as shown in Table 5 are later compared with the corresponding data of the experiments. The trend was the same but the variances were smaller in the experiments. This means that, apart from the global factor “sum of absolute torques”, which loosely might correspond to a measure of total energy consumption, this procedure can explain the behaviour using only local procedures acting on the level of the single joint controllers.

Table 5 Parameters of the second minimization procedure. Depending on the absolute sum of all torques, denoted by τ, the reduction factors ${\hat{p}_{t_{i} j}}$ are taken for each time step t _i from a normal distribution with the parameters $\hat{\mu}{{_{p}}}_{\tau}$ and ${\hat{\sigma}{{_{p}}}_{\tau}}^{2}$

We also tested other ways to select the torques which should be decreased and other ways to reduce torques, all being less successful in describing the experimental data. Among these approaches, we tried to decrease torques in only hind, middle or front legs, or alternatively in only one single leg. We also tried to decrease torques in only the leg with the highest absolute sum of torques, in only both legs with the highest absolute sum of torques, etc. In further tests, all joints were reduced by the same constant mean value, all joints were multiplied by the same constant mean value. For different types of joints, different factors have been applied, which was based on the assumption that joints that generally provide higher torques, as are the β-joints, may decrease less than the torques of the other joints.

Discussion

Correlation rules describing the behaviour

Results presented in this article and in the companion paper (Lévy and Cruse 2008) show that correlations between torques of a standing insects on a long time scale are different from correlations on a short time scale. This implies that animals are able to control changes in torques on at least two different levels. The objective of changing torques appears to be the convergence to a torque distribution, where the overall sum of all 18 absolute torques approaches some kind of minimum (Lévy and Cruse 2008). Therefore, on a "long" time scale most torques with the same sign are positively correlated, while torques with inverse sign are negatively correlated. However, to reach a distribution with a low overall sum of all 18 absolute torques, the animal has to change some torques on a short-time scale. To maintain the same body position, other torques may then have to be readjusted in a way that opposes the direction of the long-time trend.

To analyse the data, we applied a specific extension of PCA called PARAFAC. In studies concerning human motor control PCA is often applied to reduce dimensionality of the data and thus to restrict redundancy. PCA has been performed for various tasks on different sets of parameters. Each of these sets, representing a redundancy problem, stands for another conception of motor control. The analysed parameters represent the parameters the central nervous system has to control to fulfil a task. When looking for example at arm movements, Sanger (2000) applied PCA on spatial coordinates of hand and elbow, Shemmell et al. (2007) applied PCA on muscle torque data and Bockemühl et al. (2008a) chose to apply PCA on joint angle values. Concerning body and trunk movement as another example, Alexandrov et al. (1998) chose to perform the analysis on joint angle values, while Wang et al. (2006) used electromyographic data. In the present paper, the analysis was made on torques based on the assumption that minimization is not based on forces but, if at all, on torques (Lévy and Cruse 2008). Furthermore, as already mentioned, the PCA was replaced by the PARAFAC analysis because it allows the consideration of a third mode. This means that, instead of one factor, two factors can be considered that influence the use of the PCs.

Results presented here have shown that more than half of the variation in torque changes can be described by three PCs. These three PCs stand for three dimensions of correlation between the joints and correspond to three basic rules. By weighing these three dimensions differently, a whole set of possible combinations of torque changes is determined that the stick insect may use. The three PCs show strong correlation structures within and between legs. These correlation structures are different for each PC. The only structure shown in all PCs is the positive correlation between β- (levation) and γ-torque (extension) within a leg. How could these PCs be interpreted? The first PC represents a vertical movement of the body, the second and the third PCs represent rotations of the body. The way insects may use these rules, i.e., how the PCs are weighted, is open. There is obviously a small effect related to the individual animal but no significant effect due to the body position. Unfortunately, most of the variability (Table 4) concerning the way stick insects use these rules is not explained (see below for further discussion).

Neuronal mechanisms underlying the behaviour

Simulation approaches are presented to reproduce experimental data and to introduce hypotheses concerning the neuronal mechanisms that may underlie the behaviour observed. Concerning for example the human arm, two different concepts have been proposed. In one concept, a separation between planning and execution is assumed. The equilibrium point hypothesis (Feldman 1966a,b) is a central hypothesis of this concept. It assumes that the joint angles given by the end position are specified in advance and each joint independently moves from its actual angle to this final angle value. Another hypothesis of this concept is the minimum jerk hypotheses (Flash and Hogan 1985). According to this proposal, movement is performed in such a way that the sum of the third derivate over the complete movement is minimized. According to the alternative concept, planning and execution are not separated. Todorov and Jordan (2002) and Todorov et al. (2005) proposed a control approach based on continuous feedback where only such deviations from the average trajectory are corrected that interfere with the task performance. Rosenbaum et al. (1991) and Vaughan et al. (1996) proposed that the contribution of an individual limb segment depends on its ability to perform the task when it acts alone. Similarly, Bockemühl et al. (2008b) analysed human hand movements while avoiding obstacles and proposed a model based on local mechanisms.

In this article, two simulations are presented based on continuous feedback, i.e., following the second concept and the general idea of Todorov and Jordan (2002). As has been shown in Cruse et al. (2004) standing stick insects use an Integral position controller to regulate joint position (for detailed simulation see Schneider et al. (2007a, b). Therefore, both simulation approaches use a PID position controller to govern the joint angles but apply different procedures to change torques. If any torque is changed, this in general leads to a torque distribution that changes the position. As a consequence, the PID controllers will re-adjust all 18 torques to reach a new stable torque distribution that suffices the constraint not to move any joint. How are torques changed in the first place? In most experiments, stick insects appear not to change their torques arbitrarily, but in a way to reduce the absolute sum of all their torques. Two different procedures are investigated that elicit changes of torques before the PID controllers are activated to re-adjust the effects of this change.

The first procedure is based on the PCs and uses the observed correlation rules to reproduce the experimentally observed torque paths. Such an approach may be termed a global approach because there is one central controller knowing the correlation rules. This central controller generates the change of torques. In the second procedure, the correlation structure represented by the PCs is replaced by a simpler rule, forming a local approach. According to this second procedure, the torque of each single joint is changed by more or less the same factor taken at random from a normal distribution. The specification of the normal distribution depends on the sum of all absolute torques. This approach is a local one because each change in a torque occurs independently from the other ones. However, each local controller is still supervised by a system that, based on the overall sum of torques, specifies the parameters (mean and standard deviation) of the normal distribution that is used for the random selection of the torque changes. The PCs determined from the biological results can describe the results obtained in the second simulation by about the same quality. Therefore, the PCs might reflect some kinematics constraints of the system.

Application to robots

These simulation approaches based on experimental results are not only interesting for the biologist but may also be applied in robotics to solve the problem of force distribution in standing robots. Due to its technical simplicity, this may be particularly true for the local version. In contrast to earlier proposals these solutions are based on torques rather than on forces and apply local position controllers rather than a complicated numerical function.

The results described in this article refer to the control of standing but not yet on the problem of walking. No experimental results from biological solution are yet available for the latter problem, but it might be solved using a solution based on the one proposed here for the standing animal. Assume that the animal or the robot has adopted a certain torque distribution and now decides to start walking. Thus, the robot will change the position of one or more legs. In this situation, the same procedure as discussed for the standing animal may be applied, the main difference being that the adaptation procedure has to be much faster. A drastic decrease of time constants when changing from standing to walking have indeed be observed in Cruse and Pflüger (1981) and Cruse and Schmitz (1983) which support this idea.

Appendix

Modelling the body and position control

For the simulation using the Matlab interface Simulink, the animal was represented using measurements for masses and lengths taken from Ekeberg et al. (2004). The animal is represented by a rigid body with a mass concentrated at the center of gravity between middle leg coxae. It has three translational (body fixed coordinates) and three rotational (yaw, pitch and roll angles) degrees of freedom. Each one of the 18 leg joints is represented by a joint with one rotational degree of freedom, i.e., is considered as hinge joint. α-joints are connected to the body after being rotated using the values of the ψ and φ-angles. Coxa, femur and tibia are defined as rigid body segments with a mass concentrated at their center of gravity. Each leg is connected to the ground via a joint with three rotational degrees of freedom. These joints ensure that leg endpoints remain at fixed positions, but do not affect the workspace of the insect. Gravity force was set to act on the body.

α- β-, and γ-joints are supplied with a position controller that controls the size of the angle values. The P- (Proportional), I- (Integral), and D- (Derivative) components of the negative feedback controller were set manually. The P- and the D- parts are small. The I-part is large. The reason for this setting is to guarantee that the size of the individual joint angles and therefore the position of the insect remains constant during the complete simulation as was observed in the experiments.

Minimization of torques

Before starting the simulation run, the body model was given the position the insect has chosen in the experiment to be simulated. These 18 angle values are given as reference values to the PID joint controllers. At the beginning, the joint motors are provided with the torque values measured at the beginning of this experiment. Due to errors in the measurements these torque values do not exactly produce the position introduced. Therefore, torques were allowed to relax to a torque distribution that fits to the body position given. This torque distribution is determined by the PID controllers and is similar to the original torques values. After a stable situation is reached, i.e., a situation where torques match the given position, the actual simulation is started.

The simulation consists of a repetition of the following iteration process. First the torques are changed following one of the two given procedures as explained below. In general, the changed torques do not match the position constraint. Therefore, governed by the PID controller, the torque values are allowed to relax for 1,300 iterations until a new torque distribution is found that matches the angular reference values, i.e., the given body position. This is illustrated by Fig. 11, which shows two consecutive iteration procedures for one selected joint. As mentioned earlier, at the beginning of the first iteration process, torques are given a value (left upper panel, circle, about −45.68 mNmm). As the torques (in combination with the other 17 torques values and the rigid connection via the body and leg segments) do not match the desired body position which is maintained via the PID position controllers, the torque relaxes to adopt a new value (also the other 17 torques), in this example relaxes to −45.87 mNmm. After relaxation, in a next time step, the torque is changed again according one of the two procedures explained below (11, right upper panel, circle, new torque value is about −45.55 mNmm). Again the torques do not fit the position, and are allowed to relax during the iteration process. The two lower panels of Fig. 11 show the time courses of the deviation from the angular reference value, i.e., the error signal received by the PID controller, which approximate zero during the relaxation. Note that the deviations are very small in absolute terms.

Fig. 11

Two consecutive iteration processes of a simulation (from left to right). The upper panel shows the time course of the torque. The lower panel shows the corresponding error signals used by the negative feedback controller. The starting values are marked by circles

In the following, the two procedures are explained that are used to simulate the minimization of torques.

Procedure 1: application of PCs

The first procedure that is applied to change the torques is based on the PARAFAC and on the correlation structure observed during the torque minimization process. Correctly weighted and added, the PCs correspond to a decrement of torques between the two time steps t _i and t _i+1. In the simulation, weights are taken at random from normal distributions whose parameters $({\mu}_{a_{q}} ,{\sigma}_{a_{q}}^{2} ,{\mu}_{c_{q}} ,{\sigma}_{c_{q}}^{2})$ were estimated from the experimental data. Using the weighted PCs, the set of torques obtained at the end of an iteration process is changed and the new set of torques is used for the initiation of the new iteration. The minimization process between the two time steps t _i and t _i+1 is illustrated as follows:

$$ \begin{aligned} x_{t_{i+1} j} &=x_{t_{i} j} -\sum_{q=1}^{3} a_{t_{i} q} c_{q} b_{jq}\\ X&=\left[ \begin{array}{lll} x_{t_{i} 1}&\cdots&x_{t_{i} 18}\\ x_{t_{i+1} 1}&\cdots&x_{t_{i+1} 18}\\ \end{array} \right], B=\left[ \begin{array}{lll} b_{1,1}&b_{1,2}&b_{1,3}\\ \vdots&\vdots&\vdots\\ b_{18,1}&b_{18,2}&b_{18,3}\\ \end{array} \right],\\ A&=\left[ a_{t_{i} 1} a_{t_{i} 2} a_{t_{i} 3} \right], a_{t_{i} q} \sim N(\mu _{a_{q}} ,\sigma _{a_{q}}^{2}),\\ C&=\left[ c_{1} c_{2} c_{3}\right], c_{q} \sim N(\mu _{c_{q}} ,\sigma _{c_{q}}^{2}) \end{aligned} $$

‘X’ is the matrix containing the set of torques. ‘B’ is the PC-matrix, containing the three PCs calculated from the PARAFAC analysis and is the same for each simulation. ‘A’ is a score matrix whose entries are taken at random from a normal distribution for each time step t _i . ‘C’ is another score matrix whose entries are taken at random from a normal distribution at the beginning of each simulation and stays the same for each time step.

Procedure 2: application of a local rule

The second procedure represents a local rule, which is not based on the PCs. In this simulation, each torque is reduced between two iteration processes proportionally to its actual size. These reduction factors $({\hat{p}_{t_{i} j}})$ are not fixed, but, for each time step t _i taken at random from normal distributions whose parameters $(\hat{\mu}{{_{p}}}_{\tau},{\hat{\sigma}{{_{p}}}_{\tau}}^{2})$ depend on the absolute sum of all torques, denoted by τ in Table 5. The minimization process between the two time steps t _i and t _i+1 is illustrated as follows:

$$ x_{t_{i+1} j} =x_{t_{i} j}{\hat{p}_{t_{i} j}} , {\hat{p}_{t_{i} j}} \sim N(\hat{\mu}{{_{p}}}_{\tau},{\hat{\sigma}{{_{p}}}_{\tau}}^{2}) $$

The parameters $\hat{\mu}{{_{p}}}_{\tau}$ and ${\hat{\sigma}{{_{p}}}_{\tau}}^{2}$ were estimated in a way that the amount of torque decrease and variation was large for a high sum of absolute torques but became smaller when the sum of absolute torques decreases.