Effects of roughness on a turbulent boundary layer in hypersonic flow

Abstract

Particle image velocimetry experiments were performed to study the effects of surface roughness on a hypersonic ($M \approx 7.3$), flat-plate turbulent boundary layer. Diamond mesh and square bars of different heights were used to form the roughness. No significant compressibility effects were apparent in the flow response in that the behavior of the mean velocity and streamwise turbulence profiles was in general accord with similar experiments in incompressible flows. The effects of the roughness extended to about one roughness height above the roughness itself and Townsend’s hypothesis were confirmed. Outside of this region, the streamwise lengthscale and the inclination of the spatial correlation contours also showed good agreement with observations on smooth-wall and incompressible flow experiments.

Graphical abstract

1 Introduction

The present study is part of a continuing effort at Princeton University to investigate the behavior of hypersonic turbulent boundary layers using particle image velocimetry (PIV). The canonical case of a smooth, flat-plate, turbulent boundary layer with a freestream Mach number $Ma_e = 7.5$ was reported recently by Williams et al. (2018), and a study of two shock/turbulent boundary-layer interactions at Mach 7.2 was given by Schreyer et al. (2018). Here, we report measurements on the effects of roughness using both two-dimensional square bar roughness and three-dimensional diamond mesh roughness, for three different roughness heights, with $0.06 \le k/\delta \le 0.18$ and $30 \le k^+ \le 112$. Here, k is the height of the roughness elements, $\delta$ is the boundary-layer thickness at the measurement location and $k^+=ku_\tau /\nu _w$, where $u_\tau =\sqrt{(\tau _w/\rho _w)}$, in which $\tau _w$ is the shear stress at the wall, and $\nu _w$ and $\rho _w$ are the kinematic viscosity and the density at the wall temperature, respectively. Preliminary measurements were recorded by Sahoo et al. (2010), and the results reported here make use of additional datasets and take into account the filtering effects due to the limitations on particle response as outlined by Williams et al. (2015).

For the Mach 7.5 flow over a smooth, flat plate, Williams et al. (2018) found few, if any, dynamic effects due to compressibility. The mean and fluctuating streamwise velocities in the outer layer were similar to incompressible flows at comparable Reynolds numbers when scaled according to van Driest (1956) and Morkovin (1961). In addition, correlation lengths and structure angles based on velocity statistics were found to be less sensitive to compressibility than indicated by previous studies based on density fields or mass-weighted statistics.

As to the effects of roughness on high-speed boundary layers, only four relatively complete sets of experiments have been reported previously. The study by Berg (1977) includes mean and fluctuating measurements for sudden changes in surface roughness, from smooth to rough and from rough to smooth. The freestream Mach number was approximately 6, and the wall was near adiabatic. The roughness was formed by square bars, with a pitch-to-height ratio $\lambda /k=4$. The roughness heights varied from $k/\delta =0.012$, 0.025 and 0.04, with $k^+=ku_\tau /\nu _w=7.1$, 14.9 and 33.8, respectively, in the “equilibrium” rough regime far downstream of the step change in roughness. The effective origin of the profiles below the crest of the roughness element was found to be about 0.5k. The case of $k^+=33.8$ was considered to be fully rough, and here, the equivalent sand grain roughness $k_s$ was 1.3k, which was about half the value found in subsonic investigations of similar roughness.

The group headed by Bowersox has reported a number of experiments to study the effects of large-scale roughness on a Mach 2.86, high Reynolds number boundary layer ($Re_\theta \approx 60,000$) on an adiabatic wall. Their earlier work used a variety of roughnesses with $k^+$ ranging from 104 to 571, including three kinds of sand grain roughened plates, a two-dimensional square bar roughness and a three-dimensional square block roughness (both with $\lambda =3.9$) Latin (1998, 2000 and 2002). In their later work, diamond mesh and square block ($\lambda /k=2$) roughness geometries were used Ekoto et al. (2008 and 2009). For the mesh roughness, the flow was aligned with the long dimension of the diamond. The mesh roughness produced a pattern of oblique shocks and expansion waves leading to strong local distortions which had a significant effect on the mean and turbulent flow structure throughout the boundary layer. By comparison, the effects of the local distortions caused by the square block roughness were much less significant. The results showed that if roughness-induced localized distortions were weak, the classic inner-scaling captured the effects of the roughness on the turbulence without the use of Morkovin scaling. The equivalent sand grain roughness $k_s$ for the square block geometry was found to be 0.73k, but the diamond mesh results were strongly affected by the local disturbances produced by the mesh and only tentative conclusions could be made regarding $k_s$.

In a closely related experiment, Kocher et al. (2018) used PIV to explore the effects of different roughness topologies on a Mach 2 boundary layer at high Reynolds number. Diamond-shaped crosshatch roughness as well as a random roughness pattern were used ($k^+=270$ and 240, with $k/\delta =0.03$ and 0.04, respectively). The roughness elements resembled an inverted mesh-type roughness where the diamond sections were raised rather than inset. Generally, their mean and turbulent statistics compared well to other results such as those obtained by Ekoto et al. (2009) when scaled by the roughness friction velocity.

To investigate the response at higher Mach numbers, Peltier et al. (2016) investigated the effects of periodic crosshatch roughness ($k^+ = 160$) on a Mach 4.9 turbulent boundary layer ($Re_\theta$ = 63 000) using PIV. The roughness elements generated a series of alternating shock and expansion waves that spanned the entire boundary layer, causing significant (up to +50% and -30%) variations in the Reynolds shear stress field. They also noted a change in the organized motions due to roughness, where the hairpin vortices that make up the vortex packets or large-scale motions (LSM) lean farther away from the wall, become more spatially compact, and altering their populations. They suggested that this may be a result of either an increase in the strength of the rough-wall hairpins, or the effects of the mean arrangement of shock waves and expansion fans generated by the roughness elements.

Here, we report experiments at Mach 7.3 on two kinds of diamond mesh roughness and three kinds of two-dimensional square bar roughness. The Mach number is higher than in any previous investigation on roughness, and it is expected to be a severe test of the kinds of similarities seen at lower Mach numbers. PIV is used to measure the mean and turbulent velocities. The Reynolds number is relatively low so that the flow is amenable to DNS.

2 Experimental Facilities

The experiments were conducted on a flat plate mounted in the Mach 8 Hypersonic Boundary Layer Facility at the Princeton Gas Dynamics Laboratory. The working fluid is air, and the maximum stagnation temperature is limited to about 800$^\circ$ K, so that the air always behaves as a perfect gas. The test section is circular with an internal diameter of 229 mm, and the flat plate was mounted so that its upper surface was on the tunnel centerline. The flat-plate model is made of brass, 152 mm wide, 476 mm long and 12 mm thick. When the working section is empty, the Mach number is $8.0 \pm 0.1$ over the central 80% of the cross-sectional area Baumgartner (1997), Magruder (1997), Etz (1998), and with the flat plate installed, the freestream Mach number is in the range 7.2 to 7.5 at the measurement location, depending on the configuration. The surface roughness of the smooth plate has been estimated to be $\le 2\mu$m ($ku_\tau /\nu _w \approx 0.10$) Baumgartner (1997), so that it is assumed to be hydrodynamically smooth. The mean test conditions are summarized in Table 1. The smooth-wall data correspond to Case 2 reported by Williams et al. (2018), where more details on the facility and its instrumentation are given.

Table 1 Mean test conditions. The standard deviations are always less than 2%. The smooth-wall data correspond to Case 2 reported by Williams et al. (2018)

The roughness elements covered the entire plate, from leading edge to trailing edge. For the first type of roughness, three rectangular plates were machined to produce two-dimensional square bar roughnesses of three different heights. For the second type of roughness, three titanium diamond-shaped meshes were used with three different heights. The roughness geometries are illustrated in Fig. 1 for the roughnesses of height $k=1.65$ mm. The specific details of all roughness geometries used in this study are given in Table 2. Here, $\ell _x$ and $\ell _z$ are the streamwise and cross-stream dimensions of the diamond-shaped roughness, respectively (6.37 mm and 12.7 mm for $k=$ 1.65 mm, as shown in Fig. 1). Also, $\lambda$ is the characteristic streamwise wavelength of the roughness elements. For the square bar roughness, it is measured from the front face of one element to the front face of an adjacent element. For the mesh roughness, it is taken to be equal to $\ell _x$ (this assumption will be discussed in more detail in results section). The solidity $\lambda _s$ is the total projected frontal roughness area per unit wall-parallel projected area. For the square bar roughness $\lambda _s = k/\lambda$, and for the mesh roughness $\lambda _s = k/\ell _x$. The parameter $\lambda _s$ is sometimes called the frontal solidity Placidi and Ganapathisubramani (2018), to distinguish it from the plan solidity $\lambda _p$ which is the ratio between the plan area and the unit wall-parallel area. Note that all roughnesses are likely to be in the k-type roughness regime according to Perry et al. (1969). Furthermore, all roughnesses tested here have large blockage ratios $k/\delta$ according to Jiménez (2004). Flows with higher blockage ratios retain few of the mechanisms of normal wall turbulence and may be better described as flows over obstacles. They are also known to be very dependent on the roughness geometry Jiménez (2004).

Fig. 1

Left Three-dimensional diamond mesh-type roughness geometry (k=1.65 mm). Right Two-dimensional square bar roughness geometry (k=1.65 mm). All dimensions are in mm

Table 2 Roughness geometrical parameters. $\ell _x$ and $\ell _z$ are the streamwise and cross-stream dimensions of the diamond-shaped roughness, respectively (6.37 mm and 12.7 mm for $k=$ 1.65 mm, as shown in Fig. 1

3 Particle Image Velocimetry

The velocity data were obtained using particle image velocimetry (PIV). A New Wave Tempest and Gemini PIV dual-head Nd:YAG laser system was used as the laser source. Each laser delivered 100 mJ energy per pulse at a wavelength of 532 nm. The laser pulses have a pulse width of 3–5 ns and a jitter of $\pm 0.5$ ns. A PCO Cooke 1600 camera (1600 – 1200 pixels) with a 100-mm lens was used to acquire PIV images. Camware V2.1 was used to acquire the images. The region for the PIV measurements started approximately 380 mm from the leading edge. While the hardware was identical for all cases (including the previously published smooth-wall Case 2 of Williams et al. (2018)), the size of the interrogation region, calibration and interframe times varied somewhat, resulting in freestream particle displacements between 18.1 and 25.8 pixels for different rough-wall cases. The imaged region was approximately 16 x 16 mm on average. See Table 3 for further acquisition setting details for each case.

Table 3 PIV setup and post-processing parameters. All data use a single run

Seeding the flow presents significant challenges in performing accurate PIV experiments in hypersonic flow. $\hbox {TiO}_2$ particles were used due to their temperature stability. To minimize the flow disturbance, the seeding particles were introduced in the settling chamber upstream of the throat. In the present system, the $\hbox {TiO}_2$ particles were first suspended in a fluidized bed where high-pressure air (typically 10 bar above the tunnel stagnation pressure) was fed from below. A heating tape was used to heat the bottom part of the bed to help reduce particle agglomeration. The air-entrained particles then passed into the stagnation chamber of the tunnel through a 12.7-mm tube facing downstream. The end of the tube was approximately 450 mm upstream of the nozzle throat and was located on the centerline of the settling chamber. Further details are given by Sahoo et al. (2009).

The in situ response of $\hbox {TiO}_2$ particles in this facility was measured by Williams et al. (2015) using two shocks of different strengths in the freestream flow to estimate the particle size, density and response time $\tau _p$. The variation in Stokes number across the boundary layer was thus estimated for a small velocity disturbance $(<5\% U_\infty )$, accounting for changes in density and viscosity across the layer. The resulting Stokes number variation $St = \tau _p/\tau _f$ is O(1) in the near-wall region for the smooth-wall case, where $\tau _f = 10\delta /U_\infty$Williams et al. (2018). An estimate taken from Samimy and Lele (xxx) suggests that slip velocities in this region could therefore be upward of 10% of the local instantaneous velocity. However, previous studies in this facility have indicated that particle frequency responses of this magnitude appear to have little filtering effect on the streamwise fluctuations while significantly reducing the measured wall-normal turbulence Williams et al. (2015, 2018). The particle frequency response of the rough-wall cases presented in this study is expected to be similar to Williams et al. (2015) due to our concordance with the smooth-wall measurements of Sahoo et al. (2009) acquired at a similar time, and the use of heating to prevent particle agglomeration. Subsequent work by Williams et al. significantly improved the seeding homogeneity and duration, while particle sizes are believed to be similar. Due to particle response limitations that limit our ability to resolve the wall-normal velocity component, as discussed by Williams et al. (2018), only results based on the streamwise component will be presented in this paper.

The PIV image processing closely followed that of Williams et al. (2018), aiming to maximize accuracy and data yield from images with inhomogenous or intermittent seeding. All image and vector processing routines were conducted using DaVis 10.1 from LaVision. First, prior to cross-correlation, the wall position and roughness element locations were normalized to the nearest pixel, accounting for plate vibration and thermal expansion. The edges were then trimmed. Velocity fields were computed using a multi-grid, multi-pass cross-correlation method with iterative image deformation (Huang et al. 1993; Jambunathan et al. 1995; Nogueira et al. 1999; Scarano xxx). Four passes were employed beginning with 128x128 pixel interrogation regions. Final passes employed Gaussian windowing of 48x48 pixel interrogation regions with 75% overlap, resulting in an inner-scaled resolution $r^+=r u_\tau /\nu _w= 36$-55 as shown in Table 3. All vectors with normalized correlation of less than 0.5 were removed, and expected particle displacement ranges were also enforced ($k=$ 0.75mm: $V_x = -6$ to +26, $V_y = -2$ to +3 pixels; $k=$ 1.27mm: $V_x = -4$ to +20, $V_y = -2$ to +3 pixels; $k=$ 1.65mm: $V_x = -5$ to +27, $V_y = -2$ to +3 pixels). Vectors were further validated using a normalized median vector validation filter with a residual cutoff of 2.5 and a 5x5 vector neighborhood. All vector groups with a population less than five were also removed. All vector fields with greater than a specified percentage of missing vectors (“% Cut” in Table 5) were eliminated from the dataset, to help ensure the validity of the normalized median filter. The cutoff was set as low as possible while still ensuring sufficient data remained for statistical examination.

Multiple experiments were conducted for each roughness element, and a number of these replicates were discarded due to observed evolution of the near-wall velocity profile in time, likely due to the accumulation of particles within the roughness elements during an experiment. A number of experiments have also been removed due to observed statistical inhomogeneity in the streamwise direction due to particle deposition on the imaging window. When multiple replicates remained, a final test run was selected that was consistent with as many other runs as possible. Statistical profiles presented here were derived from that final test run.

The sampling uncertainties of the streamwise mean velocity and rms were determined to be approximately $\pm 0.5\%$ and $\pm 7\%$ or better, respectively, for the 0.75-mm and 1.27-mm roughness cases. This calculation assumed a 95% confidence interval and that the data were uncorrelated for distances greater than half the boundary-layer thickness (see Benedict and Gould (1996)). For the 1.65-mm cases, the sampling uncertainties were $\pm 2\%$ and $\pm 20\%$ for the streamwise mean velocity and rms, respectively.

4 Flow visualization

Schlieren visualizations of the flow near the wall are shown in Fig. 2 for the three square bar cases and the $k=$ 1.27 mm mesh case. Likewise, figure 3 displays some PIV visualizations of the mean velocity and the streamwise Reynolds stress $\overline{{u^2}^+}= \overline{u^2}/u_\tau ^2$ for the 1.27-mm square bar case. The shock structure generated by the square bar roughness is clearly visible in the schlieren visualizations and is echoed in the distributions of the streamwise Reynolds stress. These features are similar to that seen in studies of raised diamond roughness Kocher et al. (2018), Peltier et al. (2016). In the mean flow fields, we see a flow deflection toward the cavity before it rises to meet the next roughness element. For the $k=$ 1.27-mm case where $\lambda /k=10.63$, we observe a reattachment shock located within the cavity, but this feature appears to be absent for the other two cases where $\lambda /k = 8.33$-5. In contrast to the square bar visualizations, the mesh roughness flow field does not display any particular disturbances. Although we defined the $\lambda =\ell _x$ for the mesh roughness, it would seem that there is a strong sheltering effect in place for this roughness which would imply that the effective wavelength is considerably smaller than $\ell _x$.

Fig. 2

Schlieren visualizations. Flow is from left to right. (a) Square bar, $k=0.75$ mm. (b) Square bar, $k=1.27$ mm. (c) Square bar, $k=1.65$ mm. (d) Mesh, $k=1.27$ mm ($k^+=93$) (Ghassen 2010)

Fig. 3

(a) Mean streamwise velocity $U/U_\infty$ and (b) streamwise Reynolds stress $\overline{{u^2}^+}= \overline{u^2}/u_\tau ^2$ in proximity to the 1.27-mm square bar roughness elements

5 Mean Flow Results

Fig. 4

Mean velocity profiles, where $y_T$ is measured from the top of the roughness elements. Symbols as in Table 4

Table 4 Boundary-layer parameters. All dimensions are in mm or m/s

The boundary-layer parameters for all profiles are summarized in Table 4. The mean velocity profiles themselves are shown in Fig. 4. Here, the wall-normal coordinate $y_T$ is measured from the top of the roughness elements. We see a strong flow retardation due to roughness throughout the profile, with the square bars having the stronger influence. Near the wall, the enhanced mixing due to the roughness elements causes the flow to become more uniform in velocity, especially for the larger roughness elements.

The data were transformed using the van Driest transformation van Driest (1951), assuming Walz’s form of the temperature profile (Smits and Dussauge 2005), and the friction velocity was determined by the Clauser chart method. Here, we assumed the log-law applied for $y^+>30$ and $y/\delta <0.15$, where

$$\begin{aligned} \frac{U_{VD}}{u_\tau } ={1 \over \kappa } \ln {y^+} + B \end{aligned}$$

(1)

where $\kappa =0.4$ is von Kármán’s constant $B=5.1$. The velocity profile for the smooth plate is in good agreement with the incompressible law-of-the-wall correlation, as shown in Fig. 5 and the measurements by Owen et al. (1975) at approximately the same Mach number (not shown here).

For a rough wall, the origin of the boundary layer will not necessarily coincide with either the top of the roughness elements, or the bottom. The (positive) offset in the virtual origin below the top of the roughness elements is $\epsilon$. In the present investigation, neither $\epsilon$ nor $u_\tau$ is known a priori and must be found by iteration. Here, we followed the procedure first outlined by Perry and Joubert (1963). Hence, for the incompressible flow over a rough wall, including the Coles wake function $\Pi$

$$\begin{aligned} {U_{VD} \over u_\tau } ={1 \over \kappa } \ln {y^+} + B -\Delta \left( {U_{VD}/ u_\tau } \right) + {{2\Pi } \over \kappa }\sin ^2{\left( {\pi \over 2}{y \over \delta } \right) } \end{aligned}$$

(2)

where $y=y_T+\epsilon$, $y_T$ is the wall-normal distance measured from the tops of the roughness elements, and $\Delta ( {U/ u_\tau } )$ is the Hama’s roughness function (the amount the velocity profile on a rough wall is shifted below the standard log-law by the effects of roughness). We will assume that this representation applies to compressible flows when using the van Driest transformation.

The mean velocity profiles for all cases are shown in Fig. 5 transformed according to van Driest and plotted in semi-log coordinates. The profiles demonstrate the expected effects of surface roughness, whereby the profiles are shifted below the standard log-law by $\Delta ( {U/ u_\tau } )$. This is somewhat surprising because all roughness heights employed here exceed the “small” roughness rule of $k/\delta <0.02$ identified by (Jiménez 2004) and the limit of applicability of Townsend’s hypothesis for incompressible flows ($\delta /k_s\ge 40$) as suggested by Flack et al. (2005). This shift is seen to be similar for both roughness types for the same value of k, suggesting that the coherence of the disturbances introduced by the 2D roughness may not a significant influence in this case.

Fig. 5

Mean velocity profiles for the smooth and rough surfaces (transformed according to van Driest). The log-law is given by Eq.1. Symbols as in Table 4

The profiles in van Driest outer-layer scaling are shown in Fig. 6. According to Coles,

$$\begin{aligned} {{U_e-U}_{VD} \over u_\tau } =- {1 \over \kappa } \ln {\left( {y \over \delta } \right) } + {{2\Pi } \over \kappa } \left( 1-\sin ^2{\left( {\pi \over 2}{y \over \delta }\right) } \right) \end{aligned}$$

(3)

for incompressible boundary layers. Here, we assume that this correlation still applies when the velocity transformed according to van Driest and when $\delta$ is measured from the virtual origin of the velocity profile. The smooth- and rough-wall profiles correspond very closely throughout the layer, deviating only near the wall. These results thus support the applicability of Townsend’s hypothesis at high Mach numbers, despite the relatively large roughness elements employed in this study. They also, indirectly, support our estimates for the friction velocity made on the basis of the logarithmic profiles.

Fig. 6

Wake profiles for the smooth and rough surfaces (transformed according to van Driest). Symbols as in Table 4

Bettermann (1966) considered low-speed flow over square bars and developed the correlation shown in Fig. 7 for $\lambda /k < 5$. Dvorak (1969) extended this to larger values of $\lambda /k > 5$, and the two correlations agree well with the data available from incompressible flow. They also capture the compressible cases well, except for our $k=$ 0.75-mm square bar and mesh roughness results, which are clearly anomalous.

Fig. 7

Roughness correlations based on $\lambda /k$, the characteristic wavelength of the roughness elements divided by their height. Figure adapted from (Dvorak 1969)

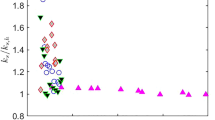
A different correlation based on the solidity $\lambda _s$ was suggested by (Jiménez 2004), as shown in Fig. 8. The vertical axis shows the ratio of the sand grain roughness height to the geometric height, divided by the drag coefficient of the roughness element, $C_D$. Here, we have assumed $C_D=1.25$ for all roughnesses tested. None of the compressible flow results seem to follow this general scaling well, but again we note that the data for the $k=$ 0.75 mm roughnesses are far removed from the other results.

Fig. 8

Roughness correlations based on the solidity $\lambda _S$, the ratio of the roughness frontal area to the total surface area. Figure adapted from (Jiménez 2004), with references given therein

6 Turbulence results

Fig. 9

Streamwise velocity fluctuations for all cases, scaled with $u_\tau$. Symbols as in Table 4. Dashed line for incompressible flow experiment at $Re_\theta =5200$ from (DeGraaff and Eaton 2000)

Fig. 10

Streamwise velocity fluctuations for all cases, scaled with $u_* = u_\tau \sqrt{\rho /\rho _w}$. Symbols as in Table 4. Solid line for direct numerical simulations at $Ma=7.2$ at $Re_\theta =3300$ (Priebe and Martin 2011)

The rms turbulent intensities for the mesh and square bar roughness are shown in Fig. 9 using classic scaling (that is, with the friction velocity $u_\tau$) and in Fig.10 using Morkovin scaling (that is, with the velocity $u_* = u_\tau \sqrt{\rho /\rho _w}$). These results represent averages over the streamwise field of view.

In classic scaling, the profiles near the wall show the strong influence of the roughness, but for $y/\delta >0.3$ the profiles show a high level of agreement, with the exception of the 1.65-mm mesh which has an effect out to $y/\delta =0.4$ and the 1.65-mm square bar which shows some deviations for $0.4< y/\delta < 0.9$. However, in Morkovin scaling the profiles show much more scatter, and it would seem that this scaling is not appropriate for rough walls, as concluded earlier by (Ekoto et al. 2008 and 2009) at $Ma=$ 2.86 when the roughness-induced localized distortions were weak. It appears that this conclusion extends to the cases considered here where the roughness-induced effects are substantial.

These current results run counter to the hot wire data of (Berg 1977) at Mach 6 that showed that, in the equilibrium region well downstream of the smooth to rough transition, his largest square bar roughness (where $k^+=33.8$, assumed to be fully rough) amplified the rms mass-flux fluctuations by a factor of about two near $y/\delta =0.5$, but actually showed some damping for $y/\delta <0.1$. It is clear that we need further information on the velocity and density fields in order to understand this behavior more fully.

7 Spatial correlations

The spatial structure of the streamwise velocity fluctuation field was investigated using the two-dimensional spatial correlation function, $R_{uu}$, defined by

$$\begin{aligned} R_{uu}\left( \Delta x, y, y_{ref}\right) = \frac{\overline{u'\left( x, y_{ref}\right) u' \left( x+\Delta x, y\right) }}{ \tilde{u} \left( y_{ref}\right) \tilde{u} \left( y\right) }, \end{aligned}$$

(4)

where $y_{ref}$ is the distance from the wall at which the correlation is computed and $\Delta x$ is the in-plane streamwise separation.

Fig. 11

Correlations of streamwise velocity fluctuations for 1.27-mm 2D square bar roughness. Contours are shown between 0.2 and 0.7. (a) $y/\delta = 0.075$ (b) $y/\delta = 0.15$ (c) $y/\delta = 0.4$ (c) $y/\delta = 0.6$

Contours of $R_{uu}$ are shown in Fig. 11 for four wall-normal locations. Here, we only consider the 1.27-mm square bar roughness as a representative case. For the two correlation maps closest to the wall, a slight periodicity is indicated corresponding to the roughness wavelength; however, this is subtle (see disturbances to correlation contours centered on $|\Delta x|/\delta \approx 1$). Away from the wall, the contours indicate a well-defined structure inclined at a shallow angle to the streamwise direction, similar to the smooth-wall cases of Williams et al. (2018) at the same Mach number.

Fig. 12

(a) Wall-normal variation of mean streamwise lengthscale, $L_x^u$, for $\square$ $R_{uu}=0.3$, $\triangleleft$ $R_{uu}=0.4$ and $\triangle$ $R_{uu}=0.5$ contours for 1.27 mm 2D roughness. (b) $L_x^u$ for $R_{uu}=0.5$ contour. $\times$Volino et al. (2007), [Ma = 0, $Re_{\delta 2} = 6000$, $0.1< y/\delta < 0.5$], $\triangleleft$Ganapathisubramani (2007) [$Ma = 2$, $Re_{\delta 2} = 11,500$, $0.3< y/\delta < 0.7$], $+$ Duan et al. (2011a) [Ma = 0-12, $Re_{\delta 2} = 1500$, $y/\delta = 0.1$] $\triangle$ Smooth, $\blacktriangle$, Rough, Peltier et al. (2016) [Ma = 4.9, $Re_{\delta 2} = 11,200$, $y/\delta = 0.1,0.2$] $\bigcirc ,\triangleright ,$ Williams et al. (2018) Cases 2-4 [$Ma =$ 7.3-7.6, $Re_{\delta 2} = 800-1300$, $0.3< y/\delta < 0.7$]. Other symbols for current dataset, as in Table 4. Error bars indicate variability for indicated range of wall-normal locations

The variation in streamwise lengthscale $L_x^u$ with wall-normal distance is shown in Fig. 12a for the $R_{uu}=0.3-0.5$ contours. $L_x^u$ is defined as the width of a given $R_{uu}$ contour at wall-normal position, $y_{ref}$. This streamwise lengthscale is seen to increase with distance from the wall for each of the contour levels chosen, with its shallowest slope in the middle of the layer. Near-wall lengthscales are thus smaller than seen in corresponding smooth-wall experiments, which demonstrated a maximum streamwise coherence in this region. While this lengthscale can be sensitive to measurement noise, this result is consistent with the study of Peltier et al. (2016) who also observed shorter coherence lengths in the near wall region for compressible rough walls at $Ma=$ 4.9.

To further compare the current results with previous velocity correlation data, $L_x^u$ is averaged for the $R_{uu}=0.5$ contour between $0.3< y/\delta < 0.7$ as in (Williams et al. 2018). Figure 12b shows the mean of $L_x^u$ over this wall-normal range for 0.75-mm and 1.27-mm square bar roughnesses as well as 0.75-mm mesh roughness. The largest roughnesses are excluded from this analysis due to reduced data yield. Error bars indicate the variability of $L_x^u$ across this range of wall-normal positions, when available. In this outer region of the flow, the mean lengthscale compares quite favorably with the smooth-wall data for the 2D roughness, but with greater variation. The lengthscale is greatly reduced for the 3D mesh roughness. As previously indicated, the sensitivity of this lengthscale to measurement noise may be playing a role.

Fig. 13

Inclination angle of the streamwise velocity correlation contours. (a) Variation with wall normal distance for Case 4 and $0.2<R_{uu}<0.5$. Symbols as in Fig. 12a. (b) Inclination of the $R_{uu} = 0.5$ contour from a range of studies. The shaded region indicates a range of incompressible results from Volino et al. (2007). For this figure, the smooth- and rough-walled Peltier et al. (2016) data represent an average for $y/\delta = 0.3-0.6$, where the inclination angle was approximately constant. Other symbols and wall-normal locations as in Fig. 12b. Error bars indicate variability for indicated range of wall-normal locations

The angle of inclination of the correlation contours is also examined by fitting an ellipse to a given contour, centered on the origin of the correlation. Here, we define $\alpha$ as the angle of the semi-major axis of the ellipse. The variation of $\alpha$ with wall-normal position is shown in Fig. 13a for $R_{uu} = 0.2-0.5$. While more noisy, the variation and magnitude of the angles in this figure mimic those of the smooth wall (detailed in (Williams et al. 2018)). The average angle in the outer layer $(0.3<y/\delta <0.7)$ for $R_{uu} = 0.5$ contour is compared with previous results in Fig. 13b. The error bars in each of these cases indicate the range of angles observed over the given range of wall-normal locations. All three new rough-wall results lie very close to the smooth-wall result and the previous data of Peltier et al. (2016), while acknowledging the variability of this indicator in the present case.

8 Conclusions

PIV experiments were conducted to study the effects of surface roughness on a Mach 7.3 turbulent boundary layer, using both diamond mesh and square roughness geometries. The mean flow results conformed to Townsends hypothesis for all roughnesses despite the relatively large roughness elements and the relatively low Reynolds number employed. The downward shift in the mean velocity profile due to roughness was also in reasonable accord with correlations suggested for incompressible flows, except for the smallest roughnesses. However, correlations based on the solidity did not reveal any particular agreement with previous incompressible flow results.

As to the streamwise turbulence intensities, Morkovin’s hypothesis does not seem to be appropriate for scaling the rough-wall data, in agreement with earlier studies at Mach 2.86 Ekoto et al. (2008). Conventional scaling with the friction velocity works well, and it makes clear that the roughness effects are confined to a region above the roughness that is comparable to the roughness height itself.

The spatial velocity field correlations indicated a reduction in lengthscale near the wall due to roughness, as found by Peltier et al. at Mach 4.9 Peltier et al. (2016), but the outer-layer lengthscales were similar to those seen for smooth walls. Streamwise lengthscales may be smaller in the outer layer for the diamond mesh, but the results may have been influenced by data yield and seeding quality.

The spatial correlations were also used to infer the characteristic inclination of the large-scale motions, and the results mostly followed the smooth-wall pattern with perhaps slightly reduced values in the core of the flow.

In general, few differences were identified between 2D and 3D roughness elements, despite obvious differences in the coherence of the near-wall disturbances, as seen with schlieren and PIV flow fields.