1 Introduction

Droplet breakage is commonly seen in a variety of scientific and engineering applications such as liquid drops splashing on the solid substrate (Geppert et al. 2017), fuel atomization and spray in combustion engines (Shanmugadas et al. 2018), coating production (Mashayek and Ashgriz 1998) and so on. Generally, it is a process of fragmenting liquid particles under interplay of multiphase interfacial forces. In an internal combustion engine nozzle, for instance, fuel liquid jet or droplet is subjected to the surrounding airflow moving at a relative velocity, which generates external drag forces on the liquid–gas interface to cause it to deform and breakup (Guildenbecher et al. 2009). Emulsification, or immiscible liquids dispersion, is another paramount process widely carried out in foods (Galus and Kadzińska 2015), pharmacy (Pouton 1997), energy (Kumar et al. 2009) industries, where droplet breakage is essential both in laminar (Bremond and Bibette 2012; Zhao and Middelberg 2011) and turbulent flows (Chen and Middleman 1967; Walstra 1993; Andersson and Andersson 2006). As the efficiency, stability and quality of emulsion are dependent on droplet breakage, considerable progress has been made to characterize the dynamics of a single droplet immersed in another fluid phase.

Rayleigh (1878) firstly studied the conditions governing the breaking up of a jet of one fluid projected into another, showing the effect of surface tension in making cylindrical liquid thread unstable and breaking into drops further. Taylor (1932) gave the analytical solution of the largest size of the drop which can keep spherical geometry in a simple shear flow and pointed out that the drops tend to breakup when the rate of distortion of the fluid is great enough. To extend the understanding of the drop morphology, Taylor (1934) deduced the expression to predict the distortion degree of the drop in defined two-dimensional linear viscous flows. Later, Grace (1982) systematically discussed the correlations of single drop deformation and breakup in rotational and extensional shear flow fields. Reviewing work done by Rallison (1984) and Stone (1994) on drop dynamics in the viscous flows at low Reynolds number showed that the effects of the flow and material parameters on fragmenting drops in defined laminar flow fields have already been well characterized.

It is no doubt that getting a deep insight of drop deformation and breakup processes at low Reynolds number contributes to the understanding of drop dynamics from the fundamental perspective. However, in many practical industrial applications, liquid–liquid dispersions are required to be implemented at turbulent flow conditions. This is the case for massive productions processed at high throughput, such as oil–water emulsion preparation by means of stirring (Ohtake et al. 1987), statically mixing (Theron and Le Sauze 2011), and impinging jets (Siddiqui 2014; Tsaoulidis and Angeli 2017). Going back to earlier studies, Kolmogorov and Hinze (Kolmogorov 1949; Hinze 1955) laid foundation by proposing scaling theory of dispersion breaking up into emulsion droplets at turbulent flow conditions, stating that energy cascade inside the flow contributes the most. Dependent on hydrodynamic condition of the surrounding fluid and droplet itself characteristics, Liao and Lucas (2009) summarized and classified the breakup mechanism in the turbulent flows into four main categories: (1) turbulent fluctuation and eddy collision; (2) viscous shear stress; (3) shearing-off process; (4) interfacial instability. Particularly, mechanism (1) is assumed to be the dominant one in most turbulent flow cases. It is also reviewed and elaborated later by Solsvik et al. (2013). Unlike the low Reynolds flow cases, what characterizes the drop breakup within turbulent flow fields is the rapidity of the phenomenon and also its irregularity. The fragmentation of the dispersed phase into the continuous one leads to a size distribution of droplets. Except for characterizing in detail single drop deformation and breakup morphology, research focusing on quantity outcomes of a breakup event, including daughter drop size distributions, number of daughter drops, breakage time and so on, is also imperative.

Then, in the following sub-sections, different aspects discussed in the literature are briefly reviewed; they are respectively: (i) the development of a balance equation for droplets population, (ii) the study of the behavior of a single droplet (breakup or no breakup) and (iii) drop dynamics in microfluidic emulsifiers. As a final part of the introduction, we will expose the objectives of the present work.

1.1 Population balance equation

Population Balance Equation (PBE) (Solsvik and Jakobsen 2015a) is used to describe the temporal variation of dispersed phase size in turbulent flows. Here, dispersed phase is treated as an assembly of particles:

$$\frac{\partial f({D}_{{\rm p}})}{\partial t}={\dot{Q}}_{{\rm b}}({D}_{{\rm p}})- {\dot{Q}}_{{\rm c}}({D}_{{\rm p}})$$
(1)

where \({\dot{Q}}_{{\rm b}}\) and \({\dot{Q}}_{{\rm c}}\) are breakage and coalescence terms respectively. For the breakage term, it can be modeled as:

$${\dot{Q}}_{{\rm b}}({D}_{{\rm p}})={\int }_{{D}_{{\rm p}}}^{{D}_{{\rm p}, {\rm max}}}n ({D}_{0}){\beta ({D}_{{\rm p}},{D}_{0})k}_{{\rm b}} ({D}_{0})f ({D}_{0},t)d{D}_{0}-{k}_{{\rm b}} ({D}_{{\rm p}})f ({D}_{{\rm p}},t)$$
(2)

The first term at the right hand of the equation describes the birth rate from the breakup process and the second one is the death rate. To be specific, \(n ({D}_{0})\) is the number of daughter drops resulting from the fragmentation of the mother drop with the size of \({D}_{0}\). \(\beta ({D}_{{\rm p}},{D}_{0})\) denotes to the size distribution and \({k}_{{\rm b}} ({D}_{0})\) represents the breakage rate. Considerable studies have been performed on modeling them (Lasheras et al. 2002; Liao and Lucas 2009) by various theoretical or statistical means. Taking the daughter drop size distribution (DDSD), \(\beta ({D}_{{\rm p}},{D}_{0})\), as the example, bunch of the models have been proposed and tested (Saijadi et al. 2013). Overall, two groups of models are involved, namely, phenomenological and statistical models. Phenomenological models are extracted from empirical observations of breakup phenomenon or mechanism (1–4) mentioned in the above section and built on the basis of some assumptions. On the other hand, statistical models treat DDSD as a random variable.

It was pointed out by Solsvik and Jakobsen (2016) that most of the present studies handle the drop breakup in the inertial subrange. However, for flows with finite Reynolds number, the inertial subrange might even disappear. The existing breakup models limited to the inertial subrange of turbulence should thus be extended and made consistent with the entire spectrum of turbulence. Karimi and Andersson (2018) showed the advantages of the extension models enhancing the predictive capability. Razzaghi and Shahraki (2016) developed generalized phonological models based on the theories of probability and isotropic turbulence for multiple breakup liquid particles in the turbulent flow. Breakup models developed based on different mechanisms and assumptions may not be sufficiently reliable to predict the breakage behavior accurately since the liquid–liquid dispersion phenomena are quite complex, varying from system to system. Single drop experiment is thus extremely necessary to investigate the droplet breakup dynamics for validating and improving models.

1.2 Experimental investigations on single drop breakup

First experimental measurement on single drop breakage was attempted by Konno et al. (1983) in geometrically similar stirred-mixing systems. The mean numbers of daughter drops were found to be varied from 2.6–4.4, then ternary breakage was thus incorporated into the corrected model for number of daughter drops. However, the number and distribution of daughter drops were not correlated with the mother drop size. Moreover, the number of data was not relevant on a statistical point of view (less than 100 breakage events for most of the tested conditions).

Realizing this, Hančil and Rod (1988) tested breakup dynamics of a single drop with controlled size in a stirred tank; they indicated that the number of daughter drops increases with the mother drop size and presents to be a random variable over 2 by averaging. Similar conclusion was made by Bahmanyar and Slater (1991) from the observations in a rotating contact disc system, reporting that two to three child drops are commonly produced, with five drops at the most. A second parameter, the viscosity ratio between the dispersed phase, i.e. drop, to the continuous one influences the resulting number of daughter drops greatly. Kuriyama et al. (1995) have highlighted that this number is in a correlation of \(n\propto {({\mu }_{{\rm d}}/{\mu }_{{\rm c}})}^{1/2}\). Maaß et al. (2007) developed a single drop breakup test bench consisting of a rectangular channel with a fixed blade representing for a section of stirring turbine. In such device and based on high-speed photography and image analysis, the number of daughter drops and its distribution, as well as the breakage rate (Maaß et al. 2011; Maaß and Kraume, 2012), were investigated. The results show that the possibility of binary breakup reaches as high as 60%, especially for small mother drops. The fact that the binary-breakup probability increases with reducing the mother drop size is also stated by another study in the stirred tank (Solsvik and Jakobsen 2015b). Regarding the breakup rate, they found that parameters for breakage time terms in PBE in the literature are at least one magnitude higher than values from experimental observations. Hence, the new model taking elongation and turbulent pressure fluctuations into account were built and validated.

Most of the above studies focus on the initial mother drop status or physical properties of the dispersed and continuous phases by assuming the turbulence is quasi-homogenous. However, in realistic engineering systems, turbulent flow is far from being isotropic. Hydrodynamic conditions, which may vary spatially, highly determine the breakup behavior. In the case of a turbulent flow in a pipe downstream of an abrupt restriction, Galinat et al. (2005, 2007) have managed to correlate the breakup probability and number of daughter droplets with Weber number. The Weber number (\(\text{We}=\Delta {p}_{{\rm max}}D/\sigma\)) is a global parameter considering the combined effects of the turbulence level as well as the mother drop size. It was indicated that asymmetrical fragmentation tends to be triggered at low and moderate \(\text{We}\) (lower turbulence and smaller mother droplet), while symmetrical breakage into multiple child droplets in equal size occurs at higher \(\text{We}\) (higher turbulence or larger drop). Similar scaling strategy using \(\text{We}\) number to identify different breakup behaviors was performed by Ashar et al. (2018) in a custom-built rotor–stator mixer. The authors argue that taking either a binary breakup or a fixed larger number of daughter drops into consideration for modeling breakup kernels is apparently not sufficient to well describe the breakup phenomenon in complex turbulent flow condition. Solsvik and Jakobsen (2015b) investigated breakage of mother drops with diameters ranging from 0.6 to 4 mm in a stirred liquid–liquid tank, showing that the value of the breakup time gets high uncertainty, which can be resulting from the non-uniformity of local turbulent characteristics, e.g., energy dissipation rate.

To conclude with, the literature on drop breakage studies points out that results (number of daughter drops, breakage time and breakage probability) vary to a great extent. Based on that, it is not hard to summarize that a general model applied to all liquid–liquid systems may be pseudo-proposition. It means that the implementation of single drop breakup experimental work is essential when a new emulsification device is designed.

1.3 Drop dynamics in microfluidic emulsifier

Emulsification via microfluidics or porous membranes (Nakashima and Shimizu 1988) has attracted plenty of focus in the last several decades because of its superior performances in terms of controlling droplets size distribution. The biggest advantage of these micro systems is the possibility of achieving monodispersed emulsion (Bremond and Bibette 2012; Zhao and Middelberg 2011). Cross flowing (Thorsen et al. 2001), flow focusing (Anna et al. 2003) and co-flowing (Cramer et al. 2004) are three main categories of geometry used to generate a regular droplet train. Unlike liquid–liquid dispersion in the stirring tank working in the turbulent flows, conventional microfluidic devices can only handle limited flow rate cases, corresponding to low Re regime. The droplet morphology and breakage mechanism have been widely and well disclosed in previous studies. Determined by the flowrates, or normalized in non-dimensional way, Capillary number of continuous and dispersed flows (\({\text{Ca}}_{{\rm c}}\) and \({{\text{Ca}}}_{{\rm d}}\)) weighs a lot in terms of the breakup pattern including five typical modes: squeezing, dripping, jetting, tip streaming and tip-multi-breaking (Zhu and Wang 2017). The latter four modes correlate with the capillary instability and the squeezing mode is significantly influenced by the channel confinement.

The main concern is that the possible flow rate that can be treated within these types of microfluidic devices is quite small, which drastically limits their industrial usage. The microsystem proposed in the present study uses head-on impinging configuration and is designed to operate at high flow rates (typically more than 100 mL/min). Water-in-oil emulsification has been investigated by Belkadi et al. (2015) using it. The results reveal that the high-throughput head-on collision microfluidic can work at much higher capillary number (3–14) than traditional ones. Enhanced viscous shear and elongational forces are thus expected to counter-balance the cohesion of filaments of water due to interfacial tension. The finely dispersed droplets in W/O emulsion are consequently produced in the emulsion. Further modifications were made by placing 90° bend at outlet channels (Belkadi et al. 2018) or arranging two impinging microsystems in series (Belkadi et al. 2016) to produce emulsified biofuel with finer water dispersed droplets. Most recently, Ji et al. (2020) reported oil-in-water emulsification process in this microsystem by characterizing the flow patterns and droplet size, emphasizing the advantage of two jets impinging configuration in the microchannel on transporting great kinetic energy to disrupt dispersed phase fluids. As said, the flow rate inside the channels is at mL/min level, which is, according to the literature, two or three orders of magnitude higher than most of those implemented in microfluidics; this leads to flow conditions in the transient or turbulent flow regime. Most of the single drop breakup experiments in the turbulent liquid–liquid dispersion systems, such as agitated tank, pipe flow or rotor–stator mixer, investigate mother drops sizing in the millimeter level. The relative size between the confinement and drop to be burst is often much larger than in the case of micro-channels. Based on this difference, existing knowledge in terms of droplet dynamics may not fully apply to the presently studied microsystem. In this context, single drop breakup behavior inside the proposed cross-slot microchannel requires to be studied for deeply understanding its working principle.

To sum up, the objective of this work is to characterize the drop breakage in microsystems based on head-on impingement for emulsifying at high throughput. Therefore, it is intended and necessary to analyze hundreds of breakup events to characterize the breakage probability, number of daughter drops and breakage time. Besides, two configurations are compared in this work. One is designed as off-axis for the inlet channels, due to their different sizes, to generate macro swirl motion of flow in the impingement region for enhancing mixing intensity. The other one, used as a reference, consists in a simple traditional cross-slot geometry, i.e., inlet channels have equal dimensions. By comparison, the role of swirl flow is expected to be demonstrated, knowing that emulsions with finer droplets can be obtained using the configuration based on off-axis for the inlet channels.

2 Experimental methodology

The experimental setup used to investigate drop breakage within the head-on impinging microfluidic facility is diagramed in Fig. 1. Water and oil-in-water raw emulsion are supplied into the emulsification device by two AP TRIX 500 pumps (Armen, France) (possible flowrate up to 500 mL/min). Using a raw and dilute emulsion (water carrying oil drops) allows to admit optically separated drops at one entrance and then to study their respective behaviors in the device. The o/w raw emulsion is prepared by stirring rapeseed oil (5% v/v) and water with 1% w.t. of Tween 20. The pressure measured at the pump inlet can reach up to 200 bar, making fluids possible to flow at flowrate up to 500 mL/min. Two weighing scales (Sartorius-MSE 2203) with a mass accuracy of 0.001 g are used to measure flowrates of water (\(\dot{{m}_{{\rm w}}}\)) and emulsion (\(\dot{{m}_{{\rm e}}}\)) by connecting to a NI DAQ module (USB-6009 analog to digital). The sampling rate for the mass flow rate acquisition is 1 Hz.

Fig. 1
figure 1

Experimental system for drop breakup observation

Full size image

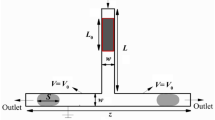
The two microfluidic devices tested in this work and respectively denoted as 600–300 and 600–600 are shown in Fig. 2. 600–300 presents an off-axis of the two inlets channels; it is designed for enhancing emulsification utilizing impingement configuration in the case of two streams with different flow rates. The narrower inlet channel is used to admit the dispersed phase; its smaller cross section allows enhancing the kinetic energy of the fluid. 600–600 has a classical cross-slot geometry. Figure 2a depicts the 3D layout of the device. The whole facility is mainly made of two transparent PMMA slabs considering accessibility for optical measurements. One slab is mechanically grooved with square inlet and outlet channels in micro scale, and they are arranged in a crossroad format. The other slab covers over it with several bolts and nuts tightened. A rubber gasket is inserted between them to avoid leakage.

Fig. 2
figure 2

Microchannel system: a microfluidic device; b 600–600 system; c 600–300 system; d XZ-plane of 600–300 system; e XZ plane of 600–600 system

Full size image

The flow visualization in the region of interest is carried out using a Photron fast speed camera (FASTCAME SA-X2 1080K M4), whose maximum frame rate is 1080 kHz. To balance the spatial and temporal resolutions, the shooting frame rate is selected to be 300 kHz, hence the exposure time is adjusted to be the longest available (1/583,784 in seconds) for enhancing the light intensity of the recorded signals. To watch the fluid at the micrometer scale in the microfluidic facility, a Lavision high magnification (12 ×) zoom lens is assembled. The focus of the lens is adjusted in the channel depth. Because of high speed capturing images with so large zoom lens at so short exposure time, external strong light source is necessary to illuminate the microchannel crossroad for ensuring high-intensity signal recorded by camera. A 50 W Halogen lamp is located at the opposite side and facing the camera beyond the transparent microchannel so as to enhance the brightness to a great extent. Attention is paid on the fact that the use of the lamp does not warm up the fluid flowing through the studied microsystem. Preliminary tests have shown that, in each system, the flow pattern and breakup events are similar in each of the two outlet channels, therefore the observation of droplets is focused in the area presented in Fig. 3, i.e. in a single channel. This is necessary to benefit from the best available resolution on the observed droplets. Typically, the size resolution is 2.2 μm/pixel.

Fig. 3
figure 3

Illustration of the typical behaviour of a droplet during breakup evolution

Full size image

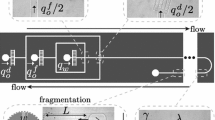
During the experiments, the breakup process of an isolated drop follows the sequential stages shown in Fig. 3. The mother drop with a diameter of \({D}_{0}\) dispersed in the water arrives from the raw emulsion inlet; it enters into the crossing impingement region at the initial time (\({t}_{{\mathrm{o}}}\)). It then starts to deform at the \({t}_{{\mathrm{d}}}\) time, due to the exerted stress. Further, the drop continues to be greatly elongated and fragmentation will be trigged at a given location when conditions are such that external force is over cohesive force exposed on the drop. This breakage starting time is denoted as \({t}_{{\mathrm{b}}\_0}\). In the last stage, the drop may go through cascade breakup and finally be teared into several daughter drops. If no further fragmentation occurrence is observed anymore, the breakup is considered as finished at this moment (\({t}_{{\mathrm{b}}\_f}\)), and number of child drops in the final population will then be counted. Breakage time, \({t}_{{\mathrm{b}}}\), interpreted as the starting period from deformation to breakup completion (\({t}_{{\mathrm{b}}\_{\mathrm{f}}}-{t}_{{\mathrm{d}}}\)), is calculated for assessing breakup duration at different hydrodynamic conditions. Basically, the breakup event is defined according to what Solsvik et al. (2016) suggested in their study. They firstly stated the importance of an adequate definition of the drop breakup event. A single drop breakup represented by the initial breakup and the breakup cascade gets the great difference in terms of breakup time, daughter droplets number and daughter drops size distributions. The breakup cascade should not only be considered as a series of binary breakup because the successive breakages are dependent on the previous ones and the difference in energy states for different breakage events within the cascade. The whole breakup cascade should be considered as a single breakup event. Herø et al. (2019) also stressed the significance of breakup event definition and the advantage of choosing the cascade breakage for quantifying number and size of each daughter drops.

Six testing cases (shown in Table 1) are designed to evaluate both hydrodynamic and geometric (600–300 system vs. 600–600 system) effects on the drop dynamics. Particularly, in the 600–300 system, macro swirl flow is intended to be generated because of the off-axis inlet jets impinging. Swirl strength index (SSI) is determined to estimate the swirling intensity caused by this particular off-axis geometric effect with global parameters. As seen in Fig. 4, water and raw O/W emulsion collide in the impinging cell (Fig. 4a), where they carry a momentum flux, \(\dot{{m}_{{\rm w}}}{\bar{U}}_{{\rm w}}^{2}\) and \(\dot{{m}_{{\rm e}}}{\bar{U}}_{{\rm e}}^{2}\) respectively. They encounter and then flow towards the two side outlets. Resulting from the offset of the flow core in the X direction, rotating motion of the fluid will be triggered. The exert force for this rotation is simply viewed to be in a positive correlation with the sum of the momentum of the two jets acting on the corresponding distance (\({d}_{{\rm w}}\) and \({d}_{{\rm e}}\)), which is \(\dot{{m}_{{\rm w}}}{\bar{U}}_{{\rm w}}^{2}{d}_{{\rm w}}+\dot{{m}_{{\rm e}}}{\bar{U}}_{{\rm e}}^{2}{d}_{{\rm e}}\). The swirl will be stronger if this value is higher. In addition, the swirl strength is also dependent on the mass magnitude (\({\rho }_{{\rm o}}{\bar{U}}_{{\rm o}}\)) of fluid to be rotated. To obtain a dimensionless indicator, SSI is obtained as:

$${\mathrm{SSI}}=\frac{\dot{{m}_{{\rm w}}}{\bar{U}}_{{\rm w}}^{2}\frac{{\bar{U}}_{{\rm w}}}{({\bar{U}}_{{\rm w}}+{\bar{U}}_{{\rm e}})}d+\dot{{m}_{{\rm e}}}{\bar{U}}_{{\rm e}}^{2}\frac{{\bar{U}}_{{\rm e}}}{({\bar{U}}_{{\rm w}}+{\bar{U}}_{{\rm e}})}d}{\dot{{m}_{{\rm o}}}{\bar{U}}_{{\rm o}}^{2}H}$$
(3)

\(d\) is the offset distance between the streams axis and H is the height of collision cell in Z direction. Since the inlet flow cores are co-axial in the 600–600 system (\(d\) = 0), SSI is regarded as zero there. Attention should be paid that this SSI is proposed to characterize the off-axis geometry inducing swirl, not for the swirl generated by the hydrodynamic instability. In other words, in the 600–600 system, interaction between streams may trigger swirl flow pattern, but it is relatively much weaker than that in the 600–300 at the same flow conditions. Certainly, detail flow field obtained by experimental implements, i.e., micro-PIV, could provide more accurate evaluation of the swirl strength inside the channel. However, it is planned for a prospective work, rather than in the scope of the present study.

Table 1 Test conditions
Full size table
Fig. 4
figure 4

Definition of swirl strength index (SSI)

Full size image

In energy consumption systems, the energy dissipation rate (\(\varepsilon\)) is normally used to describe the mixing intensity level. In the confined head-on collision configuration, \(\varepsilon\) can be estimated as follows (Johnson and Prud’homme 2003; Siddiqui et al. 2009):

$$\varepsilon = \left(\frac{\dot{{m}_{{\rm w}}}{\bar{U}}_{{\rm w}}^{2}}{2}+\frac{\dot{{m}_{{\rm e}}}{\bar{U}}_{{\rm e}}^{2}}{2}-\frac{\dot{{m}_{{\rm o}}}{\bar{U}}_{{\rm o}}^{2}}{2}\right)/{\rho }_{{\rm o}}{V}_{{\rm m}}$$
(4)

where \({\rho }_{{\rm o}}\) and \({V}_{{\rm m}}\) denote to outflow density and mixing volume, respectively. Here we assume the mixing is undergoing in the whole length (40 mm) of the outlet flow channels. Water flow rate is set as 50 and 100 mL/min for low and high energy dissipation rate conditions, the corresponding velocity is 2.3 m/s and 4.6 m/s. The flow rate for raw emulsion flow is varied from 6.3 to 25 mL/min to meet the velocity ratio of two channels reaching 1:1 and 2:1. Case 5 and 6 are arranged for the 600–600 system to compare with the 600–300 system (Case 1 and Case 3) at low and high energy dissipation rate cases respectively, which is mainly designed to discover the effect of the macro swirl flow on motion drop breakup behavior. The values of the Reynolds number in the two outlet channels (\({{\rm Re}}_{{\rm O}}\)) range from 850 to 1880, which is considered to be in the laminar flow regime for fully developed pipe flow referred to classic fluid dynamics theory. However, the interaction due to the two streams head on impact inside the cross-slot region induces great instability and thus high energy dissipation rate. Flow in the collision region can reach transient or turbulent regime locally. The detail hydrodynamic parameters are listed in Table 1.

For each case, around 200 breakup events (\({N}_{\mathrm{b}}\)) were captured and stored by high-speed camera. Meanwhile, about 100 non-broken drops (\({N}_{\mathrm{s}}\)) were also recorded to assess size dispersion of stable droplets in the channel. Therefore, nearly 1800 drops were analyzed in total. Since the raw emulsion is prepared by mechanically mixing, a size dispersion of initial oil drops (\({D}_{0}\)) to be fragmented is observed, which is in the range of 30–200 μm.

3 Results and discussion

3.1 Breakage probability

A breakage probability (Eq. 5) can be calculated which needs to integrate the total number of observed mother drops, thus submitted or not to a breakage, as well as the number of mother drops submitted to a breakage, in different ranges \([{D}_{0,{{\rm max}}}; {D}_{0,{{\mathrm{min}}}}]\) of initial droplets size. Intervals of 10 μm are presently considered:

$$P[{D}_{0, {{\mathrm{max}}}}; {D}_{0,{\mathrm{min}}}]=\frac{{\sum }_{{D}_{0,{\mathrm{ min}}}}^{{D}_{0, {\mathrm{max}}}}{N}_{\mathrm{b}}}{{\sum }_{{D}_{0, {\mathrm{min}}}}^{{D}_{0, {\mathrm{max}}}}({N}_{\mathrm{b}}+{N}_{\mathrm{s}})}$$
(5)

The variation of \([{D}_{0, {\mathrm{max}}}; {D}_{0, {\mathrm{min}}}]\) is shown in Fig. 5 at low and high energy dissipation rates, respectively.

Fig. 5
figure 5

Breakage probability at low and high \(\varepsilon\) conditions

Full size image

Generally, the breakage probability increases rapidly when the mother drop goes beyond a critical size. This critical size \({D}_{{\mathrm{crit}}}\) denotes to the diameter of the drop under which it is not possible to break it in the current emulsifier. It corresponds to a physical cut-off threshold below which forces from flow energy dissipation cannot overcome interfacial ones. At higher energy dissipation rate cases tested here (Fig. 5b), \({D}_{{\mathrm{crit}}}\) is around 25 μm for both microchannels. For much less energy dissipation rates (Fig. 5a), the critical size is spread between 30 and 50 µm, depending on specific hydrodynamic conditions. So, the maximum possible size (\({D}_{{\mathrm{max}}}\)) of drop which can sustain in different systems depends on energy dissipation rate. This size can be visualized in Fig. 5; it corresponds to the upper limit of the last interval before \(P[{D}_{0, {\mathrm{max}}}; {D}_{0, {\mathrm{min}}}]\) reaches 100%. It shows that higher \(\varepsilon\) is, smaller \({D}_{{\mathrm{max}}}\) will be. The value of \({D}_{{\mathrm{max}}}\) is more sensitive to \(\varepsilon\) at low energy dissipation rate conditions. From the perspective of \({D}_{{\mathrm{max}}}\), it is straightforward that at similar flow conditions (600–300 system, \(\varepsilon\) = 105 m2/s3 vs. 600–600 system, \(\varepsilon\) = 100 m2/s3 in Fig. 5a; 600–300 system, \(\varepsilon\) = 838 m2/s3 vs. 600–600 system, \(\varepsilon\) = 802 m2/s3 in Fig. 5b), the 600–300 system tends to be more effective in tearing smaller drop into much more smaller particles while the 600–600 system can retain some larger drop from being fragmented.

To model the breakage probability, Coulaloglou and Tavlarides (1977) attributed the event of a drop breakup in the turbulent flow to the fact that turbulent kinetic energy of the particle exceeds the critical value and then proposed the following equation for characterizing the breakup rate (\({k}_{{\rm b}}\)):

$${k}_{{\rm b}}=\frac{P}{{t}_{{\rm b}}}={c}_{1,b}\frac{{\varepsilon }^{1/3}}{{D}_{0}^{2/3}}{\mathrm{exp}}\left(-\frac{{c}_{2,b}\sigma }{\rho {\varepsilon }^{2/3}{D}_{0}^{5/3}}\right)$$
(6)

The breakage probability is further defined as:

$$P={\mathrm{exp}}\left(-\frac{{c}_{2,b}\sigma }{\rho {\varepsilon }^{2/3}{D}_{0}^{5/3}}\right)$$
(7)

Hence, it can be seen that the breakage probability is correlated with energy dissipation rate and mother drop diameter as a synthetic factor, \({\varepsilon }^{-2/3}{D}_{0}^{-5/3}\). In addition, deduced from the classic Kolmogorov and Hinze theory on turbulent emulsification (Kolmogorov 1949; Hinze 1955), \({\text{We}}_{{\rm t}}\) number is the criteria to evaluate the ratio of the disruptive external stress exerted on the drop to the cohesive stress resisting breakage in the turbulent system. \({\text{We}}_{{\rm t}}\) can be estimated as:

$${\text{We}}_{{\rm t}}=C\frac{{\rho }_{{\rm c}}{\varepsilon }^{2/3}{D}_{0}^{5/3}}{\sigma }$$
(8)

where \({\text{We}}_{{\rm t}}\) is proportional to \({\varepsilon }^{2/3}{D}_{0}^{5/3}\). The value of the scaling constant \(C\) depends on the considered turbulent system and is hard to determine precisely. Even though the test conditions of the present study are not in fully turbulent regime (Reo ∈ [850–1880]), strong instability is generated by the two-streams collision, associated to a great amount of energy dissipated there. Thus, the idea of referring to the concept of turbulent We number is reasonable to inspect the data obtained in this study. Based on these considerations, a dimensionless, \({\text{We}}^{\boldsymbol{*}}\), excluding the scaling influence, is used here to elaborate the drop breakup outcomes:

$${\text{We}}^{\boldsymbol{*}}=\frac{{\rho }_{{\rm c}}{\varepsilon }^{2/3}{D}_{0}^{5/3}}{\sigma }$$
(9)

Similarly, Galinat et al. (2005) correlated the breakup probability and number of daughter drops with specifically defined Weber number (\({\text{We}}_{D}=\Delta {p}_{{\mathrm{max}}}{D}_{0}/\sigma\), \(\Delta {p}_{{\mathrm{max}}}\) represents the maximum pressure drop across the orifice) in the turbulent pipe flow with an abrupt restriction in the upstream, considering the combined effects of the energy dissipation rate level as well as the mother drop size. These authors have proposed to model the breakage probability in their system according to the following equation:

$$P={\text{We}}_{D}^{a}{\mathrm{exp}}\left(-\frac{A}{{\text{We}}_{D}}\right)$$
(10)

Experimental data and prediction of different models are presented in Fig. 6 for the 600–300 and the 600–600 systems separately. Adopting the concept of \({\text{We}}^{\boldsymbol{*}}\) allows the fusion of the sets of data obtained with the two different systems. For the 600–300 system, as shown in Fig. 6a, the model proposed by Coulaloglou and Tavlarides (1977) over predicts the breakage probability when \({\text{We}}^{\boldsymbol{*}}\) is large. Moreover, it predicts a breakage probability above 100% for higher \({\text{We}}^{\boldsymbol{*}}\). On the other hand, the model of Galinat et al. (2005) underestimates the breakage probability when \({\text{We}}^{\boldsymbol{*}}\) is over 0.5, but overestimates it when \({\text{We}}^{\boldsymbol{*}}\) is smaller than 0.5.

Fig. 6
figure 6

Modeling of the breakage probability. a 600–300 system, Coulaloglou and Tavlarides (1977) model: \({c}_{2,b}=0.071\); Galinat et al. (2005) model: a = 1.1, A = \(0.035\); Own model: B = 0.0068, b = 2.4. b 600–600 system, Coulaloglou and Tavlarides (1977) model: \({c}_{2,b}=0.094\); Galinat et al. (2005) model: a = 0.09546, A = \(0.038\); Own model: B = 0.056, b = 1.2

Full size image

Therefore, the following corrected model is proposed:

$$P={\mathrm{exp}}\left(-\frac{B}{{{(\text{We}}^{\boldsymbol{*}})}^{b}}\right)$$
(11)

This model includes two adaptative parameters, B and b. It is applied and found to fit well experimental data (Fig. 6). The breakage probability increases more drastically with \({\text{We}}^{\boldsymbol{*}}\) in the 600–300 system than the 600–600 system. In other words, it corresponds to the fact that a large drop gets a higher possibility to burst into small daughter drops in the 600–300 system. This could be attributed to the particular swirl flow structure formation associated with a higher energy dissipation rate in it.

3.2 Breakage time

Breakage time (\({t}_{\mathrm{b}}\)) is another paramount parameter to evaluate the drop breakage efficiency. Figure 7 presents \({t}_{\mathrm{b}}\) at all tested conditions. As same as the breakage probability, the breakage time is also strongly dependent on the size of the mother drop. Larger mother drops take longer time to break up, which is more evident at lower energy dissipation rate cases (Fig. 7a–c). A duration of about 5 ms is recorded for some drops in the 600–300 system corresponding to their whole breakage process (Fig. 7b). If the energy dissipation rate is boosted, the breakage time is statistically shortened and its dispersion is slightly reduced. It doesn’t exceed 2 ms for the higher energy dissipation rate group (Fig. 7d–f)). Due to the comparatively higher dissipated energy and smaller mother drops investigated in the present microchannel setup, the breakage time scale is relatively lower than that in conventional emulsifiers, as summarized in Table 2.

Fig. 7
figure 7

Breakage time at all tested conditions

Full size image
Table 2 Comparisons of single drop experiment in different devices
Full size table

There is a great variance in the breakup time measured, especially for the larger mother drop. This variance could be caused by the different initial status of mother drop, including its velocity and location. Moreover, it is possible for larger drops to experience several generations of breakup, which aggravates the variability and uncertainty of the breakage time. Solsvik and Jakobsen (2015b) also noticed a variance of the breakage time in the stirred tank for single drop breakup experiments. They attributed this uncertainty to space and temporal resolution limitations as well as to the difficulty of determining breakup time when the mother drop undergoes multiple breakage.

It is noteworthy that strong swirl flow in the 600–300 microchannel can delay the breakup process, which can be explained, as mentioned, by the flow characteristics inside it. To be specific, it is recalled that in the 600–300 system two jets collide off-axis resulting in a vortex flow with a relatively lower pressure region in the vortices core. Towards to the downstream, the pressure increases gradually. So, a fraction of the fluid can probably flow reversely to the upstream in the central region, due to the development of a reverse pressure gradient when the swirl strength is strong enough. Figures 8 and 9 provide illustrations on the motion path followed by some unbroken small drops in the 600–300 system; the trajectory has been retraced sequentially in 2D. In Fig. 8, after entering in the system a small drop moves helically in the outflow channel. Some small drops, especially at more intensified swirl cases, can be trapped in the impingement region. Trapping phenomenon of a representative small drop is depicted in Fig. 9. The drop is firstly carried by the flow into the two-stream collision region. Then, it moves towards an outlet channel but a little after it is thrown back to the impinging region due to a reversed flow structure located inside the channel near this impinging region. Several back and forth movements of the drop can be observed in the trapping region, giving the illusion that the drop is dancing. Concerning the drop followed in Fig. 9, the duration of its trapping is 5 ms, but it finally only takes 1.25 ms to move towards downstream and out of the region of interest. The existence of an adverse pressure gradient and this mechanism of backflow observed in the core of vortices that dominates in the trapping region were also reported by Vigolo et al. (2014) in common T junction flow networks with 3D numerical and experimental study. Parent drops can be trapped into the collision region initially, i.e. before breakage, or occasionally. Some daughter drops can be entrained after the first breakup back to the trapping region and then can undergo a secondary break up or a breakup cascade, which undisputedly induces in this case a longer breakage time. Moreover, the higher the swirl strength is, the stronger the trapping ability will be.

Fig. 8
figure 8

Example of a small drop motion path following the swirl flow

Full size image
Fig. 9
figure 9

Example of the path of a small drop trapped in the swirl flow before being released (to be read from the right to the left)

Full size image

Marked as red-cross symbols in Fig. 7, the implementation of 600–300 system together with the most intense swirl tested (SSI = 0.48) corresponds to the highest chance to trap the drops to burst. This explains why its breakage time (Fig. 7b) is comparatively higher than with the other two cases. For the same 600–300 configuration, comparison between Fig. 7a, b proves the credibility of swirl strength index definition suggested in the present study, since the case with higher SSI leads to more trapping events. At higher energy dissipation rate conditions (Fig. 7d–f), the detrimental effect of this trapping on extending breakage duration is weakened and balanced by the effectiveness of the high energy dissipation rate, favoring diminishing breakage time.

Another noticeable finding is that the 600–600 system also shows trapping capability in some cases, although the swirl strength index is zero as characterized in this study. This is not surprising because two impinging jets will form a stagnation point in the center of the region where they encounter and develop into the extensional flow at the downstream. This mechanism is utilized to capture drops firstly in a four-mill apparatus proposed by Taylor (1934) and then used to develop hydrodynamic trapping devices (Akbaridoust et al. 2018; Tanyeri et al. 2010). Zhang et al. (2019) also observed a swirl flow structure and vortex breakdown in a device based on symmetrically impinging micro-channels, like the 600–600 system. But the swirl strength in a device favoring collision of symmetrical jets configuration is smaller than that in a setup with off-axis layout generating initially a macro-swirl flow.

Modeling of averaged breakage time is performed even though the breakage time shows great uncertainty for the larger drops. From the perspective of statistics analysis, the trend is reasonable and can be predicted. As introduced in the ahead section on modeling breakage rate by Coulaloglou and Tavlarides (1977), breakage time is assumed to be modeled as:

$${{t}_{{\rm b}}=c}_{1,b}\frac{{\varepsilon }^{1/3}}{{D}_{0}^{2/3}}$$
(12)

\({c}_{1,b}\) is the parameter fitted with experimental data. This model is validated by a lot of prior studies and proves to give well prediction performance. Hence, it is also applied to the current measurements. The comparison between the model and experimental results is given in Fig. 10.

Fig. 10
figure 10

Modeling of averaged breakage time. a Low \(\varepsilon\) case: \({c}_{1,b}=0.073\) for 600–600 system; \({c}_{1,b}=0.052\) for 600–300 system, SSI = 0.32; \({c}_{1,b}=0.085\) for 600–300 system, SSI = 0.48. b High \(\varepsilon\) case: \({c}_{1,b}=0.050\) for 600–600 system; \({c}_{1,b}=0.029\) for 600–300 system, SSI = 0.32; \({c}_{1,b}=0.043\) for 600–300 system, SSI = 0.48

Full size image

It can be told that the averaged breakage time still reserves some extent of uncertainty when parent drop to be broken is large, notably in the 600–300 system. Higher swirl strength aggravates this variation. Model of \({t}_{{\rm b}} \sim {D}_{0}^{-2/3}\) gives fair predicting outcome for the 600–600 system and the 600–300 system with conditions of relatively lower swirl strength (SSI = 0.32). Concerning the 600–300 system working at high swirl intensity, it would be difficult to conclude that this general model predicts the breakage time precisely. The overall trend between three sets of experimental results indicates that it takes longer time for the 600–300 system with higher swirl intensity than the 600–600 system to fragment a drop with a given size when energy dissipation rate is not high enough (Fig. 10a). The situation reverses in the more unstable flow conditions (Fig. 10b). Furthermore, the 600–300 microchannel with moderate swirling strength (SSI = 0.32) always performs to be superior at both low and high energy dissipation rates, suggesting that there could be an optimal swirl intensity for the 600–300 system in terms of accelerating the drop breakup.

3.3 Number of daughter drops

The final key parameter to be investigated is the number of daughter drops generated by the breakup event. Although mother drops in the raw emulsion can’t be strictly controlled in size, it instead provides the convenience to investigate the number of child drops obtained as a function of the mother drop diameter. The most straightforward message conveyed by the results, as shown in Fig. 11, is that more fragments can be produced from the breakage events in our micro-systems compared with previous breakage studies in other systems (Table 2), even though the size of mother drop is relatively smaller in our work. For example (Fig. 11d), at the highest energy dissipation rate condition imposed in the 600–300 system, up to 56 children's drops are captured after breaking a mother drop with a diameter of 118 μm. It has to be mentioned that the limitation of the spatial resolution of the camera induces a cut-off in the size of droplets that can be accurately measured; presently drops with a diameter of less than 20 μm are difficult to be recognized accurately. Then, the daughter drop with the size less than 20 μm is not inventoried in the current study. Just like for the breakage probability and breakage time, the number of the daughter drops is also highly dependent on the energy dissipation rate and mother drop diameter. Overall, larger mother drops at any energy dissipation rate situation or any drops at high energy dissipation rate situation tend to burst into a larger number of daughter droplets.

Fig. 11
figure 11

Number of daughter drops at all test conditions

Full size image

Binary breakup, namely, the event for which parent drop disintegrates into two equal or unequal drops, is characterized as the typical breakup mode at most low Reynolds number flow conditions, and incorporated into the modeling of the number of the child drops for the single drop behavior. It is also observed in this study for both 600–300 and 600–600 systems, particularly at lower impact intensity cases, as drop breakage sequences are shown in Fig. 12. In this figure, two droplets are followed from their arrival (first picture) in the impinging area, till their breakup occurring in the outflow channel in which they are carried along. The main direction of flow is shown with an arrow. Initial drop deforms first along with the motion following the outlet flow. Then mass accumulates towards to the two ends with a narrow connection between them (snapshots at t = 0.83 ms in the 600–300 system and at t = 1.05 ms in the 600–600 system). As deformation continues, the elongated filament gets thinner and drop is finally pinched off into two particles. The binary breakup behavior in the current microchannels is very similar to that in the low Reynolds number flows as the pattern of “end pinching”, which is also addressed by Eastwood et al. (2004) and Galinat et al. (2005) in their turbulent systems. “End pinching” breakup mode was firstly proposed by Stone et al. (1986) from the observation of the time-dependent dynamics of drop motion, which is featured as a relatively rapid formation of bulbs at the two ends of the drop. It is followed by break-off of the ends, from the central portion of the drop, at the condition that Capillary number excesses the critical value (\({\text{Ca}}\ge {{\text{Ca}}}_{{\mathrm{crit}}}\)). As the capillary number increases furtherly (\({\text{Ca}}\ge {2{\text{Ca}}}_{{\mathrm{crit}}}\)), the capillary instability driven breakup mechanism shows up (Stone and Leal 1989), which presents to be in a spatial-periodic “end-pinching” pattern with forming more satellite and sub-satellite drops between two ends of the elongated drop (Tjahjadi et al. 1992). Recent numerical work on drop breakup in the confined channel performed by Barai and Mandal (2016) found that drop can undergo different breakup modes as “mid-point pinching”, “edge breakup” and “homogenous breakup” under the synthetic effect of confinement degree, capillary number and viscosity ratio.

Fig. 12
figure 12

Binary breakup in the studied micro-channels. a Binary breakup is achieved between 0.95 and 1.07 ms. b Binary breakup is achieved between 1.05 and 1.20 ms

Full size image

Although binary breakup phenomenon shows up at some cases, especially at the case either the mother drop is small or the energy input is not enough, multiple breakages are more frequently observed in the current microchannel devices. Figure 13 compares the probability of multiple breakage (\({P}_{{\mathrm{m}}}\)) at all test conditions for low and high energy dissipation rate groups in different mother drop size ranges with an interval of 50 μm. It indicates that multiple breakup possibility is statistically increased with the mother drop size. For example, in the range of [0–50 μm], multiple breakage probability for the 600–300 system at \(\varepsilon\)=118 m2/s3 condition is 60%, it gradually increases to 100% in the range of [150–200 μm]. It means that a drop with a diameter over 150 μm will no longer undergo binary breakage. As the energy dissipation rate intensity grows, this increasing rate of multiple breakage probability is more aggressive. Specifically, at higher energy dissipation conditions, mother drop with the diameter below 50 μm owns 80% possibility mostly to be burst into multiple pieces, and the possibility reaches 100% when the mother drop diameter is larger than 100 μm. The contrast of results at different levels of energy dissipation rate clearly shows that the probability of multiple breakage is very sensitive to the kinetic energy input on the drops, just like the above discussion on the general breakage probability.

Fig. 13
figure 13

Probability of multiple breakages in the micro-systems

Full size image

Regarding the distinction between the two systems, it is found that swirl flow in the 600–300 system enhances the probability of multiple breakage. That is, a mother drop with a given size will fragment into less daughter drops in the 600–600 system than in the 600–300 one. When energy dissipation rate is low (Fig. 11b vs. c), number of daughter drops in the 600–600 system collapses between 2 and 15, and it shows a weaker correlation with the mother drop size. However, a clear tendency is observed for the 600–300 system, with which the largest parent drop (\({D}_{0}\) ~ 200 μm) produces 27 child drops. From the perspective of multiple breakage probability shown in Fig. 13, the same conclusion can be reached. The disparity of the multiple breakage ability between two micro-systems is more evident when the energy dissipation rate is comparatively lower.

As demonstrated, the number of subsequent fragmentations after the drop breakup is highly related to mother drop size and dissipated energy level. As what has been verified for the breakage possibility, the same parameter, \({\text{We}}^{\boldsymbol{*}}\), is applied to correlate the experimental data set of the arithmetic mean of the child drops number, as shown in Fig. 14. It turns out that \({\bar{n}}\) is linearly increasing with \({\text{We}}^{\boldsymbol{*}}\) for both systems. Considering the 600–300 configuration with two respective values of the swirl intensity (SSI = 0.32 and 0.48) proceeded by imposing different flow rates of raw emulsion and keeping the same amount of the pure water, a similar trend is observed in terms of the mean number of daughter drops at the same corresponding \({\text{We}}^{\boldsymbol{*}}\). However, in the 600–600 system whose nominal swirl strength is zero, the slope of the linear relation is lower, showing that a drop will be broken into less small ones than that in the 600–300 system. This is attributed to the benefit of swirl flow generated in the particular off-axis head-on impinging configuration. Thus, if \({\text{We}}^{\boldsymbol{*}}\) increases, the gap of \({\bar{n}}\) between two systems yawns, stressing the great advantages of the specific designed geometry (600–300 system) at higher flow rate conditions. Based on this comparison, it can be concluded that the microchannel with enhanced swirl flow is more efficient in terms of producing more daughter drops and then finer emulsion dispersions, which could result from the less isotropic unstable flow conditions in the 600–300 system. The mechanism is discussed hereafter.

Fig. 14
figure 14

Mean of the number of daughter drops after the breakage

Full size image

3.4 Breakage mechanism and effectiveness

As mentioned before, although binary breakup occurs at both systems, multiple breakage is the most dominant dynamics for the drop behavior, as shown in Fig. 15. The breakup sequences of a small (Fig. 15a) and big drop (Fig. 15b) are demonstrated here in the 600–300 systems at low energy dissipation rate conditions. For the small drop, it deforms and winds around the vortex (swirl structure). A few of knots are formed during the observed corrugated elongation process (\(t\) = 0.91 ms) and the drop is finally nipped off in the thin portions connecting nodes, like for the pinching-off process in the binary breakup mode. The number of daughter drops is shown to be equal to the number of nodes generated in the deformation stage. Some of the fragments can stay in the trapping region for a while (\(t\) = 1.27 ms) and then undergo another breakage or just move out of the channel. This is similar to a typical multiple breakup mode of fluid particles in the turbulent jet flow experimentally studied by Eastwood et al. (2004). They pointed out that the capillary effects-driven breakup mechanism occurs at low Weber number, which is analogous to that in the low Reynolds number flows. To be specific, prior to the breakup, the liquid particle starts to elongate significantly and rotates with eddies at the first stage, and then accumulate at the ends and knots along the elongation length. Finally, it is pinched off at the locations in the thinning region between ends and knots. This multiple-knots pinching mechanism was also reported by Galinat et al. (2005) in the turbulent pipe flow downstream of an abrupt restriction and Andersson and Andersson (2006) in a static mixer. In the 600–600 system, most of the drops are also fragmented in this way.

Fig. 15
figure 15

Examples of multiple drop breakage at low energy dissipation rate in 600–300 system

Full size image

Different from other systems, the typical mechanism of drop breakage in the present microfluidics is the swirl assisted breakup. Although swirl induced breakup of liquid drops in the gas environment has already been well characterized in the literature, mainly on the object of swirl nozzle (Saha et al. 2012), here the difference is that the swirl flow structure is generated in a highly compact confined space. As shown in Fig. 15b, the large drop can be trapped into the impinging region and deformed simultaneously. Driven by the swirl flow near the impinging region, the whole drop starts to rotate initially. In the second stage \((t\) = 1.68 ms), one head of the drop is pinned in the trapping region. Away from the trapping region, the continuous phase fluid flowing towards the outlet direction exerts a considerable dragging force on the drop, making it highly stretched in a spiral pattern. At a certain point, the local balance between exerted stress and cohesive stress is broken, breakage then takes place \((t\) = 2.10 ms). Likewise, child drops gets captured in the trapping region again after the first breakage, and then a secondary breakage and more sequential breakup cascades continue to occur. In this example, the whole breakage process lasts 3.78 ms in total, which testifies the fact it takes a long time to breakup in the 600–300 systems with high swirl strength for some large drops (Fig. 7b). Miniature and microfluidic devices based on a design with opposed jets in a simple cross-slot have been widely investigated for hydrodynamic trapping (Hudson et al. 2004; Narayan et al. 2020). It is generally concluded that the trapping mechanism is induced by the stagnation point flow developed in the intersection (Akbaridoust et al. 2018). Deformation and breakup mode of particles entrained is similar to that in the extensional flow. The droplet is trapped in the cross road and elongated afterward along with the outlet flow (Janssen et al. 1997). Whether it gets breakage or not depends on the operating flowrates. It is apparently distinct from the swirl induced trapping-breakage mode in the studied 600–300 system.

As the flow rate of the two impinging jets is increased, the kinetic energy dissipated in the microsystem increases drastically. Figure 16 illustrates this situation in the two systems at higher energy dissipation rate conditions. As displayed in Fig. 16a, the drop breakage behavior in the 600–300 system at high energy dissipation rate conditions is generally similar to that at the low energy dissipation rate conditions. However, the elongated filament is much thinner and it is not along a specific direction away from the collision region. In the 600–600 system, the drop is firstly and quickly stretched in a more limited area. The swirling flow being less intense and of different nature, the drop is not trapped and consequently less elongated in the main direction of flow than it is in the 600–300 system. So, the drop enters into the channel and deforms in highly elongated 3-dimensional thin filaments winding around eddies; then it explodes suddenly in every direction into a great number of small drops. This drop breakage dynamics can be attributed to the more isotropic characteristics of the flow when the energy dissipation rate is enhanced. To be concluded, the merit of the swirl flow lies in that non-isotropic flow releases a great potential of instability in the collision region. This in turn brings a large fluctuation in flow and dissipates energy into the interacting drops, leading to their fragmentation. Also, by trapping the drop, kinetic energy input into this region is utilized as much as possible, with less chances for relaxation. Although it may take relatively longer time to transport the energy to the final assembly of drops, a greater number of daughter droplets is obtained from the specific energy consumption.

Fig. 16
figure 16

Drop breakage behavior at high energy dissipation rate conditions

Full size image

To finish with, breakage efficiency of the two micro-systems is assessed using a set of key indicators previously defined (\(P, n, {t}_{{\mathrm{b}}}\)). The efficiency of the single drop breakage is denoted as \({\bar{n}}*P/\bar{{t}_{{\mathrm{b}}}}\), representing how many possible fragments a drop with certain size will be burst into in the unit of breakage time duration at the fixed energy input. As defined, it includes the influence of breakage probability, number of daughter drops and breakage time.

As shown in Fig. 17, drop breakage effectiveness increases with \({\text{We}}^{\boldsymbol{*}}\) for both systems. The effectiveness is always higher in the 600–300 system than the 600–600 one, meaning that the specifically designed cross-slot device with off-axis head-on impinging configuration shows great advantages over the conventional one, based on equal-size feeding channels, like the 600–600 system. Additionally, the growth of breakage effectiveness versus \({\text{We}}^{\boldsymbol{*}}\) is the lowest for the 600–600 system. Concerning the role of the swirl, Fig. 17 gives the hint that the effectiveness grows rapidly with \({\text{We}}^{\boldsymbol{*}}\) at moderate intensity condition (SSI = 0.32), which signifies that it may be possible to reach best drop breakage efficiency by an adequate selection of imposed hydrodynamic conditions. Regardless of the system used and, if applicable, the SSI conditions imposed, the data indicate that the efficiency tends towards a limit value when \({\text{We}}^{\boldsymbol{*}}\) is greater than 0.7.

Fig. 17
figure 17

Drop breakage effectiveness of different microsystems

Full size image

4 Conclusions

Single drop breakup experiments were performed by the present study in the microchannel utilizing head-on impinging configurations. Breakage probability, breakage time and number of daughter drops were statistically analyzed on thousands of drops to characterize their breakup behavior. Different geometries of microchannels, namely the 600–600 system and the 600–300 system, were compared to disclose the influence of the swirl flow structure generated by an off-axial layout of the two impinging streams. Breakup mechanisms in the cross-slot microchannels are then elucidated.

Analysis of experiments points out that a drop entering in the studied microchannel device has a very high probability of breakup. This is particularly true for the larger drops subject to high energy dissipation rate conditions. Modeling based on the defined parameter, \({\text{We}}^{\boldsymbol{*}}\), incorporating mother drop size and energy dissipation rate is proposed and found to fit the experimental data well. A drop entering in the 600–300 system is more likely to breakup compared with the 600–600 system, at the same hydrodynamic conditions. This is explained by the higher mixing intensity induced by the swirl flow.

Because of the great instability of flow interaction between the two streams, head-on impinging microchannel system exhibits greater variance in terms of breakage time, especially when the mother drop is larger. In addition, it takes relatively longer time for the drop to break in the 600–300 system compared to the 600–600 system. The main reason is that swirl flow can form low-pressure center in the impingement region, which further triggers a “dead zone” and make the drop trapped into it or even regress from the downstream. Besides, trapping of daughter drops produced from the initial breakup and subsequent breakage cascades also lead to a relatively longer breakage time in the 600–300 system, with higher swirling strength at low energy dissipation cases. As energy dissipation rate increases, the detrimental effect of swirl flow on prolonging the breakage duration weakens.

Multiple breakage, rather than binary breakage, occurs more frequently in the current micro-systems. The number of daughter drops increases greatly with the mother drop size, which stresses that breakage models assuming constant number of daughter drop may not be enough accurate for the studied microfluidic device. As for the comparison of two micro-systems, the swirl flow enhanced in the 600–300 microchannel favors the mother drop to breakup into a larger number of daughter drops than in the 600–600 system.

Binary breakup mode in the studied cross-slot impinging jets microchannels is similar to that observed in existing single drop studies, represented as the “pinched-off” mechanism. Although binary breakup occurs from time to time, multiple breakage is the most dominant pattern. In the 600–600 system, the drop is highly deformed around vortex or eddies inside flow before breakage. For the 600–300 system, where swirl flow is triggered inside the confined channel, drop tends to be trapped into the impingement region firstly. One end is then pinned in the dead zone with the drop elongated along the flow direction in a helical way. After breakup, re-trapping and sequential breakup cascades could occur. At higher energy dissipation rate conditions, much thinner filaments wind around and the drop burst into all directions. Including all three key indicators, i.e. breakage probability, breakage time and number of daughter drops, fragmentation efficiency is finally evaluated to characterize the breakage capability of the two systems investigated. The 600–300 system presents an absolute advantage over 600–600 system, especially at medium swirling strength conditions.