Dynamical aspects of a backward-facing step flow at large Reynolds numbers

Abstract

A contribution to the study of separating and reattaching flows over a backward-facing step configuration is reported. Simultaneous unsteady wall-pressure and velocity field measurements are made to investigate the dynamical aspects of the separated flow field at high Reynolds numbers, up to 182,600. An array of 25 unsteady pressure sensors in the streamwise direction coupled with PIV velocity fields is used to analyze the statistical properties as well as the streamwise time–space characteristics of the separated flow. A comparison with some previous studies is done to highlight the expansion ratio influence and dependency on the main separation flow. Emphasis is placed on the dynamical aspects of turbulent flows at a wide range of Reynolds numbers, specifically in the convective motion of the vortical flow structures. Unsteady pressure spectra show, even for high Reynolds numbers, the relative dominance of low-frequency flapping motion over high-frequency modes of the large-scale vortical structure. The latter shows a ‘waked mode’ behavior, where these large-scale coherent structures grow in place and further accelerate in the downstream direction. The ability to understand the flow field unsteadiness will lead future investigations to develop active and/or passive flow control techniques in separating and reattaching flows.

1 Introduction

Separating and reattaching flows can be found in many practical engineering applications. More recently, control strategies to improve performance in these flows have been actively researched. The ability to understand the flow field can lead to the development of active or passive flow control techniques. According to the linear evolution of perturbations in space and time (Huerre and Rossi 1998), these unstable flows can be classified into two distinct classes: hydrodynamic oscillators (absolutely unstable) and noise amplifiers (absolutely stable, but convectively unstable). In hydrodynamic oscillators, instabilities grow in situ and survive for all time. They display an intrinsic dynamic at a well-defined frequency and do not depend on external noise, e.g., flow past a cylinder or cavity flow. For amplifier flows, the basic flow carries growing perturbations away in the downstream direction, and the system eventually returns to its unperturbed state. The former are very sensitive to external perturbations and their characteristics determine the type of waves amplifying the flow (Pier and Huerre 2001).

One of the most commonly amplifier configurations is the backward-facing step. The flow over a backward-facing step (BFs) represents a geometrically simple canonical flow situation exhibiting both separation and reattachment. Although these flows have been extensively studied for several years, the dynamics of the fluid motions, regarding external perturbations, are still not fully understood, particularly Reynolds number dependency. Although many studies have been conducted at very low Reynolds numbers $Re_h=10^4$ (Chung and Sung 1996; Nadge and Govardhan 2014; Hudy et al. 2007) and only few of them have been carried out at moderate and high Reynolds numbers (Heenan and Morrison 1998), what remains to determine is the dependency of the Reynolds number to external parameters (e.g., expending ratio ER and boundary layer $\delta /h$) and the nature of the flow for turbulent flows, especially at $Re_h>10^4$. Most practical flows are turbulent, and are furthermore complicated by strong large-scale vortices or recirculation. Practical real-time estimation is a tool to accurately estimate the velocity field of an unsteady, complex flow given a set of measurements such as velocity, pressure and wall gradient (Nguyen et al. 2010).

The proper orthogonal decomposition (POD) estimation approach is used in the present study to analyse the dynamical aspect of the flow fields. Lumley (1967) proposed the proper orthogonal decomposition as an unbiased technique for studying coherent structures in turbulent flows. POD is a logical way to build basis functions that capture the most energetic features of the flow. The inner product $(\mathbf {u},\mathbf {v})$ and the norm $\Vert \mathbf {u}\Vert =(\mathbf {u},\mathbf {u})^{1/2}$ are considered as:

$$\begin{aligned} (\mathbf {u},\mathbf {v})= \sum _{i=1}^{2} \int _\Omega u_i(\mathbf {x})v_i(\mathbf {x})\mathrm{{d}}\mathbf {x}, \end{aligned}$$

(1)

where $u_i (\mathbf {x},t)$ is the ith component of the fluctuating velocity field $\mathbf {u}(\mathbf {x},t)$ at point $\varvec{x}$ of the spatio-temporal domain $\Omega$. The POD modes are obtained by searching the function $\varvec{\Phi }(\mathbf {x})$ that has the largest mean square projection of $\mathbf {u}(\mathbf {x},t)$. This maximization problem leads to the well-known Fredholm integral problem, where the kernel is the two-point correlation tensor $R_{ij}(\mathbf {x},\mathbf {x}+\Delta \mathbf {x})=<u_i(\mathbf {x},t)u_j(\mathbf {x}+\Delta \mathbf {x},t)>$, in which angle brackets is the time-average operator. The integral equation has a discrete set of solutions $\varvec{\Phi }^{(n)}(\mathbf {x})$ and $\lambda ^{(n)}$ where n is the mode order of the orthogonal decomposition. The eigenfunction is orthonormal, e.g., $(\varvec{\Phi }^{(n)}(\mathbf {x}), \varvec{\Phi }^{(p)}(\mathbf {x}))=\delta _{np}$. Then the fluctuating velocity field can be decomposed as follows:

$$\begin{aligned} \mathbf {u}(\mathbf {x},t) = \sum _{n=1}^{n_m} a_{n}(t)\varvec{\Phi }^{(n)}(\mathbf {x}), \end{aligned}$$

(2)

where $n_m$ is the total mode number. The temporal coefficients $a_{n}(t)=(\mathbf {u}(\mathbf {x},t),\varvec{\Phi }^{(n)}(\mathbf {x}))$ are uncorrelated, e.g., $<a_{n}a_{p}>=\lambda ^{(n)}\delta _{np}$.

To resolve the entire flow field, a linear stochastic estimation (LSE) is first used to estimate velocity information using a conditional averaging scheme applied to the measured locations (Tinney et al. 2008). LSE was first introduced by Adrian (1977) as a mean to approximate the conditional average of the fluctuating velocity vector field given the occurrence of an event vector and can be expanded in a Taylor series of the event. In general, $\mathbf {u}(\mathbf {x},t)$ indicates the velocity fluctuation, since the mean flow is known and does not need to be estimated. As shown by Naguib et al. (2001), and Picard and Delville (2000), a condition average of the fluctuating velocity, $\varvec{u}(\mathbf {x},t)$, can be formulated using the j time-dependent wall-pressure events, $p_j(t)$, as the condition to yield an estimated velocity field, $\tilde{\varvec{u}} (\mathbf {x},t)$:

$$\begin{aligned} \tilde{\varvec{u}} (\mathbf {x},t) =\,<\varvec{u}(\mathbf {x},t)|p_j(t)>, \qquad j=1,\,\ldots ,\,n_s \end{aligned}$$

(3)

The conditional average can be estimated by a power series as shown by Guezennec (1998):

$$\begin{aligned} \tilde{\varvec{u}} (\mathbf {x},t) = \sum _{j=1}^{n_s} \varvec{b}_{j}(\mathbf {x})p_j(t)+\sum _{j=1}^{n_s} \sum _{k=1}^{n_s} \varvec{c}_{jk}(\mathbf {x})p_j(t)p_k(t), \end{aligned}$$

(4)

where $p_j(t)$ is the value of the fluctuating pressure probe $p(\mathbf {x}_j,t)$ at point $\mathbf {x}_j$ of the boundary spatio-temporal domain $\partial \Omega$. $n_s$ is the number of fluctuating pressure probes.The coefficients $\varvec{b}_{j}$ and $\varvec{c}_{jk}$ are obtained from unconditional statistics, i.e., two-point correlations, which result from a minimum square error procedure. Then, given these considerations, the LSE correspond to the linear truncated expansion of the conditional average and the QSE to the quadratic one. Since the n temporal POD coefficients, $a_n(t_s)$, are obtained through the integration over all space, they contain the global knowledge of the flow field. However, they are also a function of the discrete time step, $t_s$, of the measured velocity PIV data, which are generally not time resolved. To temporally resolve these coefficients, the stochastic estimation techniques have been frequently applied together with the POD (Tinney et al. 2008; Lasagna et al. 2013). The MLSE complementary technique, introduced by Bonnet et al. (1994), allows the estimation of the temporal dependence of the first POD coefficients, providing a temporally resolved low-dimensional estimate of the flow state. This technique has also been used to define efficient closed-loop feedback control (Pinier et al. 2007). One advantage of the approach is that POD coefficients are scalar quantities which are independent of the spatial location. In the present study, MLSE/MQSE complementary techniques, see (Taylor and Glauser 2004; Murray and Ukeiley 2007; Baars and Tinney 2014), were used to obtain an estimation of the full flow field dynamics from the classical PIV and the unsteady pressure measurements to investigate the low-frequency flapping contributions. The MLSE/MQSE complementary approaches consist of estimating the temporal POD coefficients of velocity fields by a conditional average associated with the j wall-pressure events denoted by $p_j(t)$, i.e., the time-resolved pressure along the line of wall points in Fig. 1. This can be written as

$$\begin{aligned} \tilde{a}_n (t)\;=\; <a_n(t_s)|p_j(t)> \qquad n=1,\,\ldots ,\,n_r, \end{aligned}$$

(5)

where the subscript n denotes the POD mode, from the first to the $n_r$ mode retained for the low-order estimation. The new time-resolved estimated MQSE coefficients can be expressed as a power series expansion truncated at the quadratic terms as follows:

$$\begin{aligned} \tilde{a}_n (t) = \sum _{j=1}^{n_s} b_{nj}p_j(t)+\sum _{j=1}^{n_s} \sum _{k=1}^{n_s} c_{njk}p_j(t)p_k(t), \end{aligned}$$

(6)

while in MLSE-POD it is truncated at the linear term. As an example, the linear term $b_{nj}$ is obtained by solving the mean square error minimization leading to the linear system of $n_s$ equations,

$$\begin{aligned} \sum _{j=1}^{n_s} b_{nj}<p_j(t_s)p_k(t_s)>\;=\; <a_n(t_s)p_k(t_s)>.\end{aligned}$$

(7)

Once the time-resolved estimated MQSE coefficients have been determined, they can then be projected onto the eigenfunctions obtained from the discretely measured flow field to reconstruct the following time-resolved estimate of the flow field,

$$\begin{aligned} \tilde{\varvec{u}} (\mathbf {x},t) = \sum _{n=1}^{n_r} \tilde{a}_n (t)\varvec{\Phi }^{(n)}(\mathbf {x}). \end{aligned}$$

(8)

This estimate of the velocity field was used to estimate power spectra as previously seen in the literature (Tinney et al. 2008).

The present study aims to clarify the main separate dependencies of the flow over a wide range of Reynolds numbers regarding downstream external parameters (e.g., expending ratio ER and boundary layer $\delta /h$). The recirculation length and the secondary separation point, as well as the statistics of the velocity fields and the surface pressure, were analyzed and compared to previous studies. This comparison was done to understand the influence of incoming boundary layer thickness and wall-bounded effect associated with high expanding ratio. This paper is organized as follows: Sect. 2 presents the experimental apparatus with the backward-facing step model. Section 3 is divided into four subsections: (1) a preliminary investigation to define the mean backward-facing step flow structure and the parameters used for further scaling; (2) a discussion of the experimental results, including the separation/reattachment lengths, velocity and pressure one-point statistics regarding external parameters; (3) a study of the spatial characteristics in the streamwise direction and (4) the time evolution and frequency analysis to better understand the coherent structure in separated flows and the effect of unsteady wakes. Section 4 deeply investigates the dynamical aspects of the flow fields using POD techniques, providing an insight into the flow structures.

2 Experimental apparatus

2.1 Facility and backward-facing step model

Fig. 1

Experimental setup with a sketch of the expected topology of a backward-facing step flow and reference system

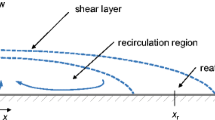
Experiments took place in an optically accessible closed-loop wind tunnel with a 2 m $\times$ 2 m $\times$ 10 m test section. The air is conditioned in a settling chamber to minimize free stream turbulence through a contoured converging nozzle. The facility can be operated in the velocity range 0.5–60 m/s. The model is mounted in the middle of the test section and exactly fits spanwise. The step height of the backward-facing step is 83 mm and corresponds to an expansion ratio of 1.04, i.e., negligible inference of the upper wall. An effectively nominally two-dimensional flow is provided by the large span of 2000 mm yielding an aspect ratio of 24 (De Brederode and Bradshaw 1978). The free stream flow velocity was measured by a Pitot tube 5 h downstream of the step edge. Measurements were performed at various free stream velocities in the range of $U_\infty = 5.7{-}33.0$ m/s corresponding to a Reynolds number range of $Re_h=$31,500–182,600, the latter based on the step height and the free stream velocity. The origin of the co-ordinate system is located at the edge of the step. The abscissa axis x represents the streamwise flow direction, the ordinate axis y is the normal direction of the flow and the third axis z corresponds to the spanwise or cross-stream flow. To represent the exposed parts described above, a 3D view is shown in Fig. 1.

2.2 Surface pressure and velocity measurements

A set of 25 static pressure taps was distributed upstream of the back-facing step in the streamwise flow direction and 0.2 h from the mid-span in the spanwise direction. Probes were placed starting at 25–1225 mm every 50 mm ($x_i/h=0.6$) as shown in Fig. 1. In addition, a second set of 25 sub-miniature piezo-resistive Kulite XCQ-062 sensors, with a nominal measurement range of 35kPa, was also used. Flush-mounted Kulite transducers are placed at the same $x_i$ location as the static ones, but in the mid-span. The 25 sensor array extends up to 14.75 h. The velocity flow fields are obtained using a standard two-component TSI particle image velocimetry (PIV) system. The flow is seeded with oil particles using a jet atomizer upstream of the stagnation chamber. This location allows homogenous dispersion of the particles throughout the test section. The system consists of a double-pulse laser system generating the light sheet and two cameras ($2000\times 2000$ pixels charge-coupled-device Powerview with a 50 mm optical lens) recording the light scattered by the tracer particles. The frequency-doubled laser (Q-switched Nd:YAG operating at 532 nm; dual-head BigSky) emits laser pulses with a maximum energy of 200 mJ. The dynamic range was approximately 30 pixels and the interrogation window size was 16 $\times$ 16 pixels with an overlap of 50%. The PIV domain was about 7.3 h $\times$ 1.8 h on the x–y plane passing through center of the backward-facing step. The resolution is 19.2 pixels/mm for the cameras used. For every Reynolds test cases, 2000 double-frame pictures are recorded to assure the velocity fields statistics convergence. The PIV time-uncorrelated snapshots were recorded with a repetition rate of 7Hz. For a dynamical aspect purpose, unsteady pressure time histories need to be recorded simultaneously with the PIV measurements. To achieve the synchronization, the Q-switch signal of the laser B was recorded simultaneously with the 25 pressure transducer signals using a 32-channel A/D converter Dewesoft data acquisition system, at a sampling frequency of 10kHz and a cutoff filtered at 3kHz as shown in Fig. 1.

3 Flow statistics and dependencies

3.1 Mean flow structure and main parameters

Fig. 2

Non-dimensional, mean vorticity $\Omega _z \cdot h/U_\infty$ and associate streamlines for $Re_h=64,200$. The dark line denotes that the streamline originated at the step edge, i.e., x = 0, y = h

The main flow characteristics were first investigated for seven Reynolds numbers (Table 1). For all cases studied, the mean flow fields showed a classical backward-facing step flow topology. As an example, the non-dimensional mean vorticity field in the x–y plane, $\Omega _z \cdot h/U_\infty$, with associated streamlines for $Re_h=$ 64,200, is plotted in Fig. 2. The contour map of the mean spanwise vorticity underlines the boundary layer separation at the edge of the step. The formed shear layer is detached from the step, increasing in width throughout the streamwise direction. The transformation of this turbulent boundary layer on the free shear layer produces a separated flow (impingement point of the shear layer). The shear layer is distributed predominantly around the mean separation streamline and is globally represented in Fig. 2 as the negative vorticity region. The mean separation streamline, which originated at the step edge, i.e., x = 0, y = h, and denoted as a dark line in Fig. 2, impacts the surface at the mean reattachment point. Beneath the shear layer, a primary recirculating region and a secondary recirculation bubble (closer to the step corner) are also observed.

On separating and reattaching flows, one of the most important values is the mean reattachment length $L_r$, due to its use as a scaling parameter. Simpson (1996) introduced two different methods to obtain the detachment/reattachment length. Detachment (D) is the point where the time-averaged wall shear stress (or the time-averaged velocity at the vicinity of the wall) is equal to zero. Transitory detachment/reattachment (TD) estimates the point where the forward flow probability FFP reaches a value of 50%. Simpson states that D and TD are at the same x-location. These two methods are illustrated in Figs. 3 and 4 for $Re_h=$ 64,200. To experimentally estimate the mean reattachment length $L_r$, the first methodology extracts the near-wall velocity profile (Fig. 3b) from the mean normalized streamwise velocity field (Fig. 3a), while the second one extracts the near wall FFP (Fig. 4b) from the FFP field (Fig. 4a). Blue areas correspond to the recirculation region and solid lines represent the zero streamwise velocity and the 50% FFP values for mean and transitory detachment length, respectively. Both cases showed a similar recirculation length of around $L_r\approx 5.3,$ corroborating Simpson’s statement. Spazzini et al. (2001) used the same methodology to calculate this length for lower Reynolds numbers. Another important parameter, normally not taken into account in previous investigations, is the mean secondary separation location ($X_r$). To deduce the position of this point, both previous approaches were used; see + symbols in Figs. 3b, 4b. Hereafter, results obtained from the TD methodology have been used. Table. 1 summarizes both $L_r$ and $X_r$ values, with the respective boundary layers (calculated as $\delta /h=99\%U_{\infty }$), for all Reynolds numbers studied.

Table 1 Mean flow parameters. Expansion ratio (ER=1.04)

Fig. 3

a Normalized streamwise velocity field; solid line denotes the zero streamwise velocity value. b Velocity profile extracted from (a) at $y/h=0.07$ for $Re_h=$ 64,200

Fig. 4

a Forward flow probability field; the solid line denotes the 50% value of the FFP. b FFP profile extracted from (a) at $y/h=0.07$ for $Re_h=$ 64,200

Table 2 Mean flow parameters for various authors

3.2 Flow statistics of external parameters’ dependencies

As previously explained, the backward-facing step configuration is a noise amplifier class; thus, it is very sensitive to upstream perturbations. The separated flow structure can be particularly influenced by the inflow conditions. In this framework, planar backward-facing step flow has been the subject of numerous experimental investigations. However, there is a considerable scatter among the values reported in the literature, more specifically the mean length of the recirculation or the mean and rms pressure coefficients. The experimental investigations described herein address some of these unsolved discrepancies, in particular the backward-facing step flow as a function of the Reynolds number and the expanding ratio (ER). Durst and Tropea (1981) and more recently Nadge and Govardhan (2014) reported numerous investigations concerning the mean recirculation length dependencies for moderate Reynolds numbers. The authors concluded that both parameters, $Re_h$ and ER, significantly influence the mean velocity field behind the step. The measurements of (Adams and Johnston 1988), at a fixed ER, showed that several parameters, such as the state of the separating boundary layer and the ratio between the boundary layer thickness and height, can affect the reattachment length. But, the main critical variable was clearly the ER. Nadge and Govardhan (2014) underlined that for low Reynolds number ($Re_h\le 10^4$), significant variations of the mean reattachment length can be observed. Once the Reynolds number is sufficiently high, a constant reattachment length appears. Figure 5 shows a compilation of some of the previous works reported in Table 2. Most of these works refer to moderate Reynolds numbers and only a few of them cover high Reynolds numbers ($Re_h\ge 10^5$). Heenan and Morrison (1998) studied the backward-facing step flow at $Re_h=$ 190,000 with an $Er=1.1$. The reattachment length at this expansion ratio is slightly lower than the saturation threshold given by Nadge and Govardhan (2014). The present results, reported in Fig. 5, also showed a decrease of the mean reattachment length when the Reynolds number increased; in other words, for high Reynolds numbers, there is no constant trend as stated by Nadge and Govardhan (2014), but a decrease of the recirculation length due to another parameter. For higher Reynolds numbers, the reattachment length dependency with the Reynolds number disappears, but the expansion ratio becomes relevant in the determination of this length.

In the same way, the mean pressure coefficients found in literature show strong variations. This coefficient is defined as $Cp=(P-P_\mathrm{{ref}})/(1/2\rho U_\infty ^2)$ , with P the pressure measured along the surface of the model and $P_\mathrm{{ref}}$, a reference pressure measured with a static-pressure tap located upstream the step edge. Figure 6 compares the present mean pressure coefficients with those obtained from similar previous configurations. For the present results, the mean pressure distributions show a classical, backward-facing step, pressure profile. Immediately downstream of the step, no strong variations are seen in the Cp, but a positive peak is clearly seen at 7h. All the amplitudes studied from the mean pressure coefficients are similar, and only small variations around the separation point can be observed. The present results are in agreement with those obtained by Heenan and Morrison (1998). However, some differences appear when a comparison is made with other references, e.g., the data of Driver and Seegmiller (1985) ($Re_h=$ 37,420 and $Er=1.12$, black circles) and Chung and Sung (1996) ($Re_h=$ 33,000 and $Er=1.5$, black squares), presented in Fig. 6, show discrepancies in the mean pressure coefficient graphic due to an expansion ratio effect, corroborating the flow dependency on the latter.

Fig. 5

Recirculation lengths against $Re_h$ for various ER values. The authors from Table 2 are also reported

Fig. 6

Mean pressure coefficients from the present and previous studies reported in Table 2

Fig. 7

Rms pressure coefficients from the present and previous studies reported in Table 2 for ER bteween 1.10 and 1.15

Fig. 8

Countour map of the streamwise rms velocity $({\mathrm{u}}_{\mathrm{{rms}}/{\mathrm{U}}_{\infty })}$ for $Re_h=$ 64,200 with associated streamlines. Black cross symbol denotes the maximum rms velocity location

Similar differences also appeared for the rms pressure coefficient. The present and previous rms pressure coefficients, defined as $Cp_\mathrm{{rms}}=p_\mathrm{{rms}}/(1/2\rho U_{\infty }^2),$ are shown in Fig. 7 as a function of $x/L_r$. The global behavior of the rms pressure distribution, obtained in the present work, is consistent with the findings of Castro and Haque (1987) and Hudy et al. (2007). A peak in the rms pressure distribution is clearly observed for both the past and present studies. However, the maximum values are not located at the same $x/L_r$. This discrepancy could be related to the variations in the $\delta /h$ values being compared. Nevertheless, for the same ER ($\approx 1{-}1.1$) studied, the locations of the peaks are similar and are situated near the reattachment point ($X/L_r=1)$. For higher ER, these locations are found to be around $0.8L_r$. In addition, the location of the maximum rms pressure coefficient is strongly linked to the maximum streamwise rms velocity, as denoted in Fig. 8 with a cross symbol. This near-wall interdependence, reattaching shear layer structure and wall rms pressure in the reattachment region, is due to shear layer structures convecting downstream and producing an increasingly strong wall-pressure signature. This signature reaches a maximum level near the location where the flow “impinges” onto the wall, as described by Farabee and Casarella (1986).

Fig. 9

A series of time delay cross-correlation of the wall-pressure fluctuations at a reference point located near the reattachment length (sensor 9, $x/L_r=0.95$) for $Re_h=$ 64,200

Fig. 10

Contour map of the wall-pressure time delay cross-correlation for a reference position close to the reattachment point ($x/L_r=0.95$) for $Re_h=$ 64,200

Fig. 11

Convection velocities from wall-pressure measurements for all the Reynolds numbers studied. Results are compared with the data of (Heenan and Morrison 1998; Hudy et al. 2007)

3.3 Spatial characteristics in the streamwise direction

To better understand the coherent structure in separate flows and to globally observe the effect of unsteady wakes, the time delay cross-correlation of the wall-pressure fluctuations was calculated in the streamwise direction and defined as:

$$\begin{aligned} R_\mathrm{{pp}}(x_0, \xi , t+\tau )=\frac{<p(x_0,t) \cdot p(x_0+\xi , t+\tau )>}{p_\mathrm{{rms}}(x_0,t) \cdot p_\mathrm{{rms}}(x_0+\xi ,t)}, \end{aligned}$$

(9)

where $x_0$ is the reference position. An example of a series of time delay cross-correlation of the wall-pressure fluctuations are plotted in Fig. 9 for $Re_h=$ 64,200. The reference point $x_0$ (sensor 09, $x/L_r=0.95$) is located near the reattachment region. For the sensors upstream of the reference point (sensor 07 and 08, dashed line), the cross-correlation reaches a positive peak for a negative time delay ($\tau U\infty /h<0$) and then dramatically decreases, arriving at a negative peak for a positive time delay ($\tau U\infty /h>0$). The opposite behavior is observed for the sensors downstream of the reference point (sensor 10 and 11, pointed line), where the negative peak is seen at the negative time delay and the positive one is reached at the positive time delay. Positive cross-correlation peaks are higher than the negative ones. Therefore, The negative–positive peaks, obtained from cross-correlation, confirm the intermittent motion of the vortices in both (positive and negative) streamwise directions, but more frequently in the positive direction. This behavior is also known as the dual dynamic mode.

To underline the behavior of the flow structures and especially their velocity propagation (convection), a contour map of all the time delay cross-correlation of the wall-pressure fluctuations was plotted in Fig. 10. The normalized cross-correlation time delay ($\tau U_\infty /h$) was plotted against the normalized streamwise coordinate where the correlation was obtained ($X/L_r$). The contour bar represents the magnitude of the cross-correlation coefficient (Rpp). A main positive peak section (red area) and two negative peak ones (blue areas) on either side of the main positive peak section are clearly seen. The main peak is centered around the time-shifted value obtained at the largest positive correlation between the wall-pressure signal, at this x location, and the reference point (near the reattachment length). Open circles represent the maximum positive correlation for the main peak at each x location.The relation between these maximum positive correlations can be used to obtain an average of the convection velocity of the flow structures, which are dominant in the generation of surface pressure fluctuations. This convection velocity, of the dominant wall-pressure generated flow structures, was calculated from the second-order fit (shown as a dashed line in Fig. 10) of the maximum positive cross-correlation peaks (open circles) following the procedure proposed by Hudy et al. (2007). The convection velocities obtained for all the Reynolds numbers studied and deduced from wall-pressure space–time correlations are seen in Fig. 11. Results show a decrease of the convection velocities from $0.6\approx U_\infty$, near the step edge, to $0.4U_{\infty }$, at $x=0.8L_r$; after this point, the values increase almost linearly. For the present case, the convection velocities appear to reach a minimum value near the position where the mean pressure coefficient is equal to zero $x=5h$. A good qualitative agreement between the previous results of Heenan and Morrison (1998) and Hudy et al. (2007) was observed, regardless of the Reynolds numbers. Nevertheless, the data from Heenan and Morrison (1998) and Hudy et al. (2007) seem to reach minimum values lower than those obtained in the present study.

3.4 Time evolution and frequency analysis

The space–time contour plots of instantaneous wall-pressure fluctuations normalized by the rms pressure $p/p_\mathrm{{rms}}$ is shown in Fig. 12 for all the pressure sensors. The time sequence is clearly representative of the full time history of the instantaneous pressure signal. The downstream convective feature, denoted by a positive slope contour pattern is observed, especially for $x>L_r$ (over the dashed line) where a downstream evolution of these large-scale vortices can be clearly seen. This behavior was also reported by Lee and Sung (2002), Lee and Sung (2001). The instantaneous negative peaks (blue area) in the wall-pressure fluctuations are associated with the passage of large-scale vortices Lee and Sung (2001). On the contrary, the region inside the recirculation bubble ($x<L_r$ and under the dashed line) shows high-pressure fluctuations, scatter in the pattern and some upstream motions, negative slope contour pattern, e.g., $t \cdot U_\infty /h\approx 35$ in Fig. 12. It is also interesting to observe that the measurements presented here appear to confirm the dual dynamical mode highlighted by the cross-correlation of the wall-pressure fluctuations.

Fig. 12

Space–time contour plots of instantaneous wall-pressure fluctuations normalized by the rms pressure $p/p_\mathrm{{rms}}$ for $Re_h=$ 64,200. The dashed line denotes the reattachment point

Fig. 13

Power spectra of wall-pressure fluctuations for different x / h locations at $Re_h=$ 64,200

Figure 13 shows a log–log plot of the pressure fluctuations spectra at several x/h locations downstream of the step at $Re_h=$ 64,200. The dynamical behaviors change as a function of the probe position. Four different regions can be identified and showed the global behavior of the flow downstream the backward-facing step. The first region, situated downstream of the step edge up to $x/h\approx 1.5$ ($x/L_r<0.3$), shows low-pressure fluctuations where the spectra are dominated by both low- and high-frequency fluctuations. A second region shows that a transition occurs from the previous frequency peaks, at $x/h\approx 1.5$ ($x/L_r\approx 0.3$), to a merged frequency value, at $x/h\approx 4.5$ ($x/L_r<0.8$). The third one corresponds to the recirculation region from $x/h\approx$ 4.5–6.5, where the pressure fluctuations are strong and high energy levels are clearly visible; this behavior is consistent with the pressure coefficient results in Fig. 7. The last region represents the reattached zone where the behavior approaches a typical turbulent boundary layer spectrum. This global mechanism is also reported for the same configuration, but for low Reynolds numbers by Spazzini et al. (2001).

Fig. 14

Non-dimensional premultiplied power spectra of fluctuating wall pressure measured at $x/h=1.5$ for the various Reynolds numbers studied. premultiplied power spectra are defined as $E(f) \cdot f/p_\mathrm{{rms}}^2$

In the literature (Lee and Sung 2001; Kiya and Sasaki 1985; Cherry et al. 1984), it is generally accepted, for low Strouhal numbers that a high frequency corresponds to vortex formation and shedding, while a lower one is related to the flapping motion of the whole flow field. To analyze the behavior of the low frequencies in the flow field and their Reynolds number dependency, premultiplied pressure fluctuation power spectra were evaluated at $x/h=1.5$ from the step edge, where the flow is clearly dominated by low frequencies. Several observations have been previously reported for backward-facing step flows at low Reynolds numbers: Li and Naguib (2005) found frequency peaks at 0.1 and 0.65 and Spazzini et al. (2001) found 0.08 and 1.0, respectively. Peak frequencies of 0.11 and 0.50 were found by Lee and Sung (2001) and of 0.18 and 0.6 by Driver et al. (1987). The present results are shown in Fig. 14 for all Reynolds numbers studied. Two frequency peaks can be observed. The first one $f \cdot L_r/U_\infty =0.12$ corresponds to a classical well-defined flapping frequency and a higher one at around $f \cdot L_r/U_\infty =1$.

4 Flow field dynamics

Fig. 15

Non-dimensional, fluctuating velocity fields for $Re_h=$ 64,200 at various snapshot instants a #100 ; b #101 ; c #102. Contour bar indicates the magnitude of the normalized fluctuating vorticity, $\omega _z \cdot h/U_{\infty },$ illustrating vortical structures in the shear layer. Vorticity levels at $-\;0.8$ (gray line) and 0.8 (black line) were plotted as contour plot and enhanced the visibility of the dominant features in the flow field

4.1 Instantaneous flow structures

Once the power spectra reveal the key frequency peaks, it is important to determine which type of vorticity structures are present in the flow. Instantaneous structures play an important role in the dynamics of the flow and are largely responsible for the shear layer growth and momentum transfer across the shear layer. Separated flows are at the origin of strong vortices (Lee and Sung 2002) and backward-facing flow presents isolated, spanwise vortical structures in the shear layer. These structures originate from Kelvin–Helmholtz instabilities leading to the growth of waves that eventually roll up into discrete vortical structures. These vortices can be seen in the fluctuating velocity fields obtained from PIV. Consecutive fluctuating snapshots $\#100$ to $\#102$ are presented in Fig. 15a–c, respectively. Some complex interaction phenomena can be qualitatively seen before the reattachment. Following classical literature, it is known that at the step edge, the turbulent boundary layer separates and forms a thin shear layer. Due to Kelvin–Helmholtz instability, the shear layer rolls up to form small vortices with a size equivalent to the thickness of the shear layer. An array of these vortices can be observed close to the separation point; Fig. 15c. However, Hudy et al. (2007) propose a new scenario for flow structure development; they introduce the concept of “wake mode”, in place of the classical “shear layer mode”. Instead of growing inside the shear layer and continuously moving downstream, this new concept assumes that flow structures grow in place. The fluctuating velocity PIV in Fig. 15a shows a strong structure transition close to $x/h=2$, corroborating their statement. In the region between the step edge and $x/h=2$, small structures, driven by the shear layer, are observed (e.g., Fig. 15c). But, after $x/h=2$, most of the flow structures show an important spatial correlation leading to large flow structure features as seen in Fig. 15a, b. Also, for $x/h>2$ and more specifically near the mean reattachment point, the flow structures are strongly linked to the wall-pressure footprint as illustrated in Fig. 16. The normalized streamwise velocity and pressure correlation coefficient shows, in Fig. 16a, a strong elongated positive level as a result of flow structure convection. A negative peak is also observed at approximately 1.5 h. This peak underlines the vortical velocity behavior also seen by the normalized normal velocity and pressure correlation coefficient in Fig. 16b. This behavior is similar for all the other sensors and Reynolds numbers studied. This high degree of correlation allows using stochastic approaches to deeply understand the flow dynamic and describe the velocity/vorticity fluctuations.

Fig. 16

Pressure/velocity correlation coefficient for sensor 10 and $Re_h=$ 64,200, a normalized streamwise velocity and pressure correlation coefficient, b normalized normal velocity and pressure correlation coefficient. Correlation levels between 0.1 and 0.1 were set at zero to minimize noise in the contour plots and enhance the visibility of the dominant correlations

Fig. 17

Cumulative energy from the POD decomposition of the velocity fields for $Re_h=$ 64,200. Red square symbols denote the normalized mean square energy

Fig. 18

Low-order POD velocity modes: a mode 1, b mode 2, c mode 3, d mode 4 and e mode 5. The contour map shows the vorticity calculated from the corresponding POD velocity basis function and normalized with the step height, $\omega _z \cdot h$. Vorticity levels between − 0.5 and 0.5 were set at zero to minimize noise in the contour plots and enhance the visibility of the dominant feature of the modes

Fig. 19

Contour map of the normalized mean square estimation error, $\epsilon$ from MLSE and MQSE, for n = 200 POD modes across the whole domain

4.2 POD and stochastic results

PIV is able to capture 2000 instantaneous two-component velocity fields. The volume of these PIV measurements is sufficient to perform a POD analysis to reveal the statistically dominant structures of the flow. Figure 17 shows the cumulative energy of the first 15 velocity modes with the corresponding normalized mean square energy, defined as $\lambda _u^{(n)}/\sum _{i}{\lambda _u^{(i)}}$. The energy fraction of the first and the second POD modes were found to contain almost 20% of the total flow energy, the first 15 modes comprise 50% and the 200 first modes constitute up to 90%. Therefore, since the first 200 modes include most of the flow energy, modes up to this value were taken into account. Ma et al. (2003) also indicated that the experimental modes above the fifth were contaminated by noise. Figure 18 shows the low-order POD velocity modes (for n = 1–5) with corresponding vorticity modes. The POD basis functions are non-dimensional and the vorticity calculated from the POD mode $\omega _z$ is normalized with the step height h. These modes represent the most common events being developed in the fluctuating velocity/vorticity fields. Modes 1–5, from the vorticity decomposition shown in Fig. 18, contribute to approximately 30% of the total energy. This small energy contribution, compared to the total fluctuating kinetic energy in the flow, suggests a greater diversity of the flow structures. Typical patterns in the POD spatial modes are clearly seen: the two first modes present elongated vorticity regions, while the others show uniformly shaped vortical structures (either positive or negative). The round and regular shape in the streamwise direction and the relatively small degree of elongation evidence a strong organization of vortical structures in space Kostas et al. (2002).

Whereas the preceding discussion was devoted to the analysis of the instantaneous large-scale vortical structures, based on PIV snapshots, the unsteady aspects of the flapping motion will now be studied. To further examine the relation between the flapping motion and wall-pressure fluctuation in the frequency domain, the previously described MLSE/MQSE complementary techniques were used. In the present case, the conditional average and its approximations via stochastic approach were not able to accurately describe the velocity fluctuations, as mentioned by Murray and Ukeiley (2007). They found that the MQSE can successfully estimate the structure of the complex cavity flow field using few wall-pressure measurements. However, previous studies (Tinney et al. 2008; Hudy et al. 2007) suggest that the QSE might be less efficient than the LSE. The selection of the estimation approach will depend on how thorough the large-scale structures will be analyzed. To evaluate the accuracy of the two different approximations, MLSE/MQSE, local estimation errors defined as $\epsilon \;=\;<(u(t)-\tilde{u}(t))^2>/<u^2>$ were computed. The parameter $\epsilon$ describes the fraction of the original variance in u(t),  which has not been recovered by the estimated $\tilde{u}(t)$. Furthermore, $\epsilon$ is bound between [0, 1]. The estimation accuracy of both the MLSE/MQSE, complementary approaches is presented in Fig. 19 by the contour map of the $\epsilon$ distribution. The quadratic form technique MQSE was chosen as it guarantees a satisfying reconstruction of the whole flow field investigated and strongly highlights the reattachment region, as shown in Fig. 19b. To further emphasize the ability of the quadratic complementary technique to reconstruct the flow field, the original PIV and both estimation snapshots of the five first temporal coefficient time histories, obtained from POD, are shown in Fig. 20. Even though a short part of the time histories is compared with those estimated, an overall agreement is observed. It can be seen from Fig. 20 that the quadratic reconstruction MQSE (blue line) fits better to the original PIV (diamond shape) than the linear estimation MLSE (red line).

Fig. 20

Comparisons between the original ($\diamondsuit$) and estimated MLSE (red line) and MQSE (blue line) temporal coefficients for the POD modes 1–5

Fig. 21

Non-dimensional premultiplied power spectra of the estimated MLSE temporal coefficients for modes 1–5 compared to the non-dimensional premultiplied power spectra of the fluctuating wall pressure measured at $x/h=1.5$ for $Re_h=$ 64,200

Fig. 22

Correlation between the fluctuating wall pressure $p_j$ and the estimated MQSE temporal coefficients for mode 1 (black), 5 (red) and 200 (blue)

Fig. 23

a Reconstruction MQSE modes 1 and 2; b reconstruction MQSE modes 3 200

The non-dimensional premultiplied power spectra of the estimated MQSE temporal coefficients for modes 1–5 are plotted in Fig. 21 and compared to the non-dimensional premultiplied power spectra of the fluctuating wall pressure measured at $x/h=1.5$ for $Re_h=64,200$. It is clearly seen from the figure that the two first modes exhibit a dominant peak at $f \cdot L_r/U_\infty =0.12,$ corresponding to the flapping frequency. The other modes highlight a transitioning and increasing peak associated with the shedding frequency. The peak variation throughout the frequency range might be due to the fact the shedding phenomenon is known as a quasi-periodic instability (broadband phenomenon) or as a consequence of experimental data error (commonly exhibted for high energetic modes). This result suggests that the first two modes could be retained if the interest is focused in the low-frequency large-scale dynamics of the recirculation region which, intrinsically, is closely related to the flapping mode, as previously observed by Fadla et al. (2016).

The causality relationship between wall-pressure sensors and temporal POD coefficients was investigated. Correlations $<\tilde{a}_i \cdot p_j>$ between the fluctuating wall pressure $p_j$ and the temporal POD coefficients (1st, 5th and 200th) are shown in Fig. 22. A high positive correlation between the wall pressure and the first POD mode for $x/h<2$ and a strong negative peak around $x/h\approx 6{-}7$ are observed in Fig. 22 (black line).

These high peaks highlight that a strong correlation of the flapping phenomena, linked to the first POD mode, is presented close to the step edge and near the reattachment region, where the shear layer impinges the wall. The introduction of a time delay $\tau$ in the correlation $<\tilde{a}_i(t+\tau ) \cdot p_j(t)>$ (not shown here) evidences a phase opposition of the correlation between the pressure measured inside the recirculation area $x/h<5$ and the one measured outside $x/h>5$, positive and negative peaks, respectively. This oscillating behavior corroborates the breathing movement of the shear layer. Alternate negative and positive peaks, obtained from the correlation between the pressure and the 5${th}$ POD mode, are clearly seen from $x/h=2$ to the end of the domain. This result illustrates the shedding process, associated with POD decomposition, and emphasizes that the modes higher than 2 are sensitive to the dynamics of large-scale structures, as previously observed in the spectra analysis. The correlation between the pressure and the 200th POD mode is also plotted to confirm the low correlation level for higher-order modes.

Finally, an estimation of the normalized root mean square streamwise velocity $\tilde{u}_\mathrm{{rms}}/U_{\infty }$ is given for the two first POD modes (Fig. 23a) and for the POD modes between 3 and 200 (Fig. 23b). A strong peak of the first $\tilde{u}_\mathrm{{rms}}/U_{\infty }$ of the two modes (35% of the total ${u}_\mathrm{{rms}}/U_{\infty }$ value) was obtained close to the shear layer impact region, around $x=L_r$. The $\tilde{u}_\mathrm{{rms}}/U_{\infty }$ of the higher modes (3–200) exhibits two peaks (contributing to 50% of the global ${u}_\mathrm{{rms}}/U_{\infty }$ value), one close to the reattachment zone around $x=L_r$, as also obtained in Fig. 23a, and a secondary peak located close to the region where the large structure commonly grows in size, i.e., $x/h=3.5$. This last remark is in agreement with the results of Hudy et al. (2007), stating that there is a particular region, close to the minimum value of the reversal wall flow velocity, where the structures grow in place instead of a slow continuous formation, as classically assume in the literature.

5 Conclusion

The unsteady characteristics of the wall-pressure fluctuations and velocity field in the separating and reattaching flows over a backward-facing step have been described. Previous experimental data in a similar configuration were compared to present results, to clarify the flow dependency on external parameters, e.g., Reynolds number and expanding ratio. Only a few experiments at high Reynolds numbers ($Re_h>10^5$) have been done. In the former conditions, the recirculation length dependency on the Reynolds number disappears as stated in previous experiments. However, results show that there is no constant trend after $Re_h>10^5,$ but a decrease in the recirculation length, meaning that this reattachment point depends on other parameters. Even though discrepancies with previous authors were found, the results with close expanding ratios and Reynolds numbers showed similar values in both the pressure and root mean square pressure coefficient. Therefore, it is possible to highlight that, for high Reynolds numbers, the expanding ratio dependency becomes relevant in the determination of the recirculation length.

A study of the dynamical aspects of the flow is also presented. The spatial characteristics in the streamwise direction showed an intermittent structure motion throughout this axis, though the latter is stronger in the downstream direction. Premultiplied power spectra of the pressure fluctuations exhibit two main peaks. A reconstruction of the flow was done using POD techniques. With this procedure, the pressure fluctuation power spectra were separated in different modes. The two first modes contained a predominant peak at 0.12 corresponding to the flapping motion (low frequency of the large scale structures). The other modes (from 3 to 5) showed a transitional and increasing peak that could be related to the shedding phenomena. For the first modes, an oscillating behavior in the wall pressure and MQSE estimation correlation corroborates a breathing movement of the shear layer. Alternate peaks in the correlation with the modes higher than 2 confirm the presence of the shedding phenomena; the latter modes are sensitive to the dynamics of the large-scale structures. Finally, the results obtained in the present study, from the normalized rms streamwise velocity of the last modes (3–5) and the decrease–increase behavior of the convective velocity of the vortical structures, validate the “wake mode”™ statement presented by Hudy et al. (2007), where the large-scale coherent structures temporally grow in place and once they are large enough accelerate in the downstream direction. The knowledge of the shedding and flapping instabilities presented at high Reynolds numbers and the ability to separate them in different modes opens the door to create passive and active laws to control the flow.