Wall-drag measurements of smooth- and rough-wall turbulent boundary layers using a floating element

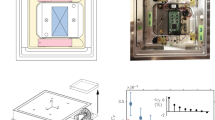
Abstract

The mean wall shear stress, $\overline{\tau }_w$, is a fundamental variable for characterizing turbulent boundary layers. Ideally, $\overline{\tau }_w$ is measured by a direct means and the use of floating elements has long been proposed. However, previous such devices have proven to be problematic due to low signal-to-noise ratios. In this paper, we present new direct measurements of $\overline{\tau }_w$ where high signal-to-noise ratios are achieved using a new design of a large-scale floating element with a surface area of 3 m (streamwise) × 1 m (spanwise). These dimensions ensure a strong measurement signal, while any error associated with an integral measurement of $\overline{\tau }_w$ is negligible in Melbourne’s large-scale turbulent boundary layer facility. Wall-drag induced by both smooth- and rough-wall zero-pressure-gradient flows are considered. Results for the smooth-wall friction coefficient, $C_f \equiv \overline{\tau }_w/q_{\infty }$, follow a Coles–Fernholz relation $C_f = \left[ 1/\kappa \ln \left( Re_{\theta }\right) + C\right] ^{-2}$ to within 3 % ($\kappa = 0.38$ and $C = 3.7$) for a momentum thickness-based Reynolds number, $Re_{\theta } > 15{,}000$. The agreement improves for higher Reynolds numbers to <1 % deviation for $Re_{\theta } > 38{,}000$. This smooth-wall benchmark verification of the experimental apparatus is critical before attempting any rough-wall studies. For a rough-wall configuration with P36 grit sandpaper, measurements were performed for $10{,}500< Re_{\theta } < 88{,}500$, for which the wall-drag indicates the anticipated trend from the transitionally to the fully rough regime .

1 Introduction

A turbulent boundary layer (TBL) forming adjacent to a surface converts the streamwise momentum of the bulk flow into a force acting on the wall, which per unit area is known as the wall shear stress (WSS), $\tau _w$. The instantaneous WSS is composed of a time-averaged mean, $\overline{\tau }_w$, and a zero-mean fluctuating component, $\tau '_w$, following $\tau _w = \overline{\tau }_w + \tau '_w$. The mean WSS may be expressed in terms of the non-dimensional friction coefficient $C_f \equiv \overline{\tau }_w/q_{\infty }$. Here, the free-stream dynamic pressure, $q_{\infty } = \rho U_{\infty }^2/2$, is used for normalization; $U_{\infty }$ is the free-stream velocity and $\rho$ is the fluid density. Intuitively, $C_f$ should be established as a function of, for instance, the momentum thickness-based Reynolds number, $Re_{\theta } \equiv \theta U_{\infty }/\nu$, where $\theta$ is the momentum thickness and $\nu$ is the kinematic viscosity. A mapping of $C_f\left( Re_{\theta }\right)$, for a given surface, is imperative for predicting frictional drag of engineering systems. Equally important, $C_f$ appears in the definition of the friction velocity, $U_{\tau } \equiv \sqrt{\overline{\tau }_w/\rho } = \sqrt{C_f/2}U_{\infty }$, which is the primary scaling parameter in near-wall turbulence.

Optimally, the WSS is assessed by way of direct force measurements on frictionless supported elements exposed to the flow, with either smooth or rough surfaces.¹ Pioneering studies, dating back more than a century, attempted such direct measurements (Schetz 1997). Due to persistent systematic error, the focus shifted primarily toward the development of techniques other than the floating element (FE) method to infer the WSS, which may be categorized as (Brown and Joubert 1969) (1) momentum techniques, (2) wall similarity techniques and (3) oil-film interferometry (OFI); the status quo is to assess $\overline{\tau }_w$ through one of these methods. Detailed descriptions of these techniques can be found in notable reviews by Haritonidis (1989), Fernholz et al. (1996), Hanratty and Campbell (1996), Schlichting and Gersten (2000) and Klewicki (2007), all of which address the necessity of a consolidation of assumptions about the structure of TBLs, as well as the need for inevitable calibration procedures. Moreover, TBLs over rough walls impose additional constraints. For rough surfaces, the wall-drag is comprised of a viscous and a pressure drag component. Since OFI only measures the former it is no longer applicable. Being able to accurately measure the rough-wall drag is invaluable, given its importance in studying rough-wall TBL flows (Raupach et al. 1991). The outer-layer similarity hypothesis of Townsend (1976), for example, predicts that the only influence of the bounding wall on the outer region of the TBL flow is to determine the velocity scale, $U_{\tau }$, and length scale, $\delta$, the boundary layer thickness, appropriate for scaling mean velocity profiles and higher-order statistics in the outer region. In this paper, we review FE devices (Sect. 2) and present the apparatus at the University of Melbourne (Sect. 3). Details of the measurements are described in Sect. 4, followed by results of the wall-drag in Sect. 5.

2 Floating element measurements of wall-drag

2.1 Configuration of floating elements

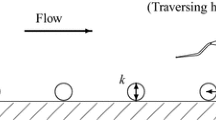
In simple terms, the FE method consists of a flush-mounted frictionless supported surface exposed to TBL flow. Surveys of WSS are performed by acquiring the reaction force necessary to sustain a zero displacement of the FE, or the element’s displacement when its motion is elastically constrained (e.g., by a spring or flexure). A rectangular FE is schematically shown in Fig. 1 with an exposed surface area of length l and width $\beta l$ (circular elements, with diameter d, are also common), and thickness t. Occasionally, the element-to-fixed-surface joint comprises a labyrinth design, resulting in an effective gap width $g_v$ (generally, $g_v$ is smaller than the wall-parallel gap size, $g_h$). The underside of the FE is often enclosed by a pressure chamber to avoid substantial pressure differences between the flow-exposed surface of the element and its underside.

Fig. 1

General principle of a floating element (FE) sensor embedded in the surface of a flow facility (random scale)

2.2 Review of floating elements

Our review of FE devices is confined to studies that were concerned with the local mean WSS. As such, studies of an integrated value of the WSS, e.g., for a flat plate (Mori et al. 2009), are not considered. Likewise, the category of microsensors that are being developed for measuring—in particular—the fluctuating WSS, relying on microelectromechanical systems (MEMS), cannot yet provide reliable measurements of the mean WSS (Löfdahl and Gad-el-Hak 1999; Naughton and Sheplak 2002). Moreover, we limit ourselves to studies of the absolute mean, $\overline{\tau }_w$, as opposed to ones presenting differential measurements. The latter generally consider a form of flow manipulation and assess the fractional drag change relative to an uncontrolled scenario.

Pioneering work on FE devices has focused on correction schemes for erroneous pressure forces and methods to make them applicable to both ZPG and non-ZPG flows. Summaries of traditional FE devices applied to low-speed flows appear in seminal reviews by Winter (1977) and Hakkinen (2004), while the reviews by Schetz (1997, 2004) focus on supersonic applications. Only very few studies achieved the acquisition of accurate wall-drag ($\overline{\tau }_w$, or expressed as $C_f$ or $U_{\tau }$), occasionally presented for a range of Reynolds numbers, which were compared to other techniques. Most notable studies are addressed here. Data of $C_f$ presented by Brown and Joubert (1969) were 4–5 % higher than friction data inferred from Preston tube measurements or Clauser’s method. Frei and Thomann (1980) and Hirt et al. (1986) documented discrepancies between their data and the Schultz-Grunow friction law within the experimental errors. Acharya et al. (1985) noted discrepancies on the order of 5 % between their direct WSS data and Preston tube data. Krogstad and Efros (2010) measured the WSS of rough-walled channel and diffuser flows. For such a higher wall-drag scenario, their direct measurements obeyed indirect methods (extrapolation of the Reynolds stress in the diffuser and the pressure gradient in the channel) to within 3 %. Sadr and Klewicki (2000) attempted measurements of $\overline{\tau }_w$ over the salt plains of Western Utah. Their WSS data agreed with sonic anemometer-based estimates to within 20 %; laboratory measurements revealed that the system provided the WSS with an accuracy of 7 %. Another application of a FE in field work is presented by Lynch and Bradley (1974). Yang et al. (2014) utilized a water channel to investigate the friction of surfaces treated with polymer-added paint. Measurements of their smooth wall $C_f$ were 15–20 % larger than empirical friction laws (Nagib et al. 2007). Various devices have also been developed to measure the bed shear stress in coastal applications. Pujara and Liu (2014) acquired the WSS under a TBL that agreed with PIV-based values to within 10 %. The aforementioned studies illustrate that, thus far, direct mean WSS measurements result in discrepancies that make them inapplicable for the fundamental study of TBLs. For instance, studying the universality and value of the von Kármán constant is exclusively scrutinized by way of other experimental techniques, such as OFI (Nagib et al. 2004; George 2006). This is not to say that FE devices are not applicable to TBLs; however, a novel approach is required to manage potentially large experimental uncertainties.

2.3 Design considerations of floating elements

A measurement of the surface-integrated WSS, $F_w$, may be affected by other forces. These erroneous contributions can be induced by the following: (1) a non-uniform static pressure acting on the area over which the WSS acts, (2) static pressure forces acting on non-parallel surfaces to the flow (such as the element’s edges), (3) flow beneath the FE, (4) cavity-induced flow asymmetries in the gap surrounding the element, and (5) misalignment of the FE (Allen 1977). Generally, contributions (2)–(4) are negligible when the FE and ZPG-TBL facility are properly designed; see for instance the analyses by Brown and Joubert (1969) and Frei and Thomann (1980). Contribution (1) may be influential, depending on the working principle. To illustrate this, we consider the schematic shown in Fig. 2a. A non-uniform static pressure acting on the FE is labeled as ‘non-ZPG’, since practically unavoidable imperfections in a ZPG facility may cause this pressure variation. When the FE is supported on a single pivot arm (Fig. 2b), the moment induced by the friction force, $F_w$, may be altered by a resultant moment of the pressure distribution. Even if a device operating according to this moment-principle is manufactured with the highest precision, it is adversely affected by such a non-ZPG. Hence, planar-supported elements are more favorable in this regard (Fig. 2c), since the wall-normal pressure forces do not yield a resultant force along the direction of the friction force (Allen 1980). How erroneous contribution (5) affects the WSS is less straightforward, although scaling arguments can be made. Misalignment and gaps disrupt the near-wall flow and may cause local separation [$g_h$ and possibly h are generally ${\mathcal {O}}\left( 10-100\right) \nu /U_{\tau }$]. Consequentially, a contaminated flow area appears in close proximity to the edges (gray-shaded region in Fig. 1) and is proportional to the circumference of the element and gap size, $g_h$, or misalignment, h. The signal-to-noise ratio (SNR) associated with these spurious effects is then proportional to the total surface area, relative to the edge-affected area, and is denoted as $\eta _A$. For the schematic in Fig. 1, $\eta _A \equiv \beta l^2/\left[ 2\alpha g_h\left( \beta l + l\right) \right]$; the constant is taken as $\alpha = 1$. Large values of $\eta _A$ are favorable for decreasing systematic error. For many FE designs $\eta _A$ is ${\mathcal {O}}\left( 10\right)$; see for example Allen (1980, $\eta _A\approx 25-250$), Brown and Joubert (1969, $\eta _A \approx 62$), Acharya et al. (1985, $\eta _A\approx 62-165$), Savill and Mumford (1988, $\eta _A\approx 75$), Sadr and Klewicki (2000, $\eta _A \approx 50$), Krogstad and Efros (2010, $\eta _A\approx 36$) and Pujara and Liu (2014, $\eta _A\approx 16$). Obtaining larger values for $\eta _A$ is practically challenging since elements are often restricted in size so that researchers can make local measurements of WSS in existing facilities. Specifically, a local measurement of $C_f$ is only credible when the variations of boundary layer parameters are negligible over the element. Here, we utilize a large-scale TBL facility at the University of Melbourne that enables us to have a larger effective surface area ($\eta _A = 375$, Sect. 3.2), without violating the ability to measure the local WSS (Sect. 3.3).

Fig. 2

a Wall-normal pressure forces acting on a FE. b FE supported by a pivot arm, and c a wall-normal suspension

Fig. 3

a Schematic of the Melbourne wind tunnel (HRNBLWT) for turbulent boundary layer studies. b Open view (sidewalls and ceiling removed) of the test section, indicating the location of the floating element assembly, centered at $x = x_F$

3 Experimental arrangement

3.1 Wind tunnel facility at Melbourne

The Melbourne wind tunnel, located in the Walter Bassett Aerodynamics Laboratory, is shown in Fig. 3a. Downstream of the plenum inlet (1), a 160 kW heat exchanger (2) facilitates a constant airflow temperature via closed-loop control. A 200 kW axial fan (3) generates the bulk flow, followed by two 90° turning vane sections (4) redirecting the flow into the conditioning section (5). The airflow then enters the 6.2-area-ratio contraction (6) and test section (7), where the boundary layer is tripped at $x = 0$, on the bottom- and sidewalls, using a 154 mm streamwise section of P40 grit sandpaper. The test section has a length of 27 m and an initial cross-sectional area of 1.89 m (width, $w_T$) × 0.92 m (height). The pressure gradient throughout the test section can be modified with an adjustable ceiling with embedded bleeding slots, while the test section width, $w_T$, is constant. The pressure coefficient, $C_p$, was constant to within ±0.87 % for our ZPG setup (Marusic et al. 2015). Free-stream turbulence intensities are nominally <0.05 % of the free-stream at $x = 0$ and remain in the range of 0.15–0.20 % at $x \approx 18$ m. The wind tunnel was designed for studying high Reynolds number TBLs, by combining a long streamwise development length with relatively low free-stream velocities ($U_{\infty } < 45\,\hbox {m}/\hbox {s}$). At $U_{\infty } = 20\,\hbox {m}/\hbox {s}$, the TBL grows to a thickness of $\delta \approx 0.360$ m at $x = 21$ m; this TBL thickness is obtained by fitting the mean velocity profile to the composite profile of Chauhan et al. (2009). The associated friction Reynolds number is $Re_{\tau } \equiv \delta U_{\tau }/\nu \approx 14{,}800$, while $Re_{\theta } \approx 38{,}200$. Note that Reynolds numbers as high as $Re_{\tau } \approx 32{,}000$ can be obtained at the extreme boundaries of the tunnel’s operating envelope.

3.2 Mechanical design of floating element

Shown in Fig. 4 is a view of the FE assembly, exploded in the vertical direction to visualize subassemblies [1] to [4]; its key components are annotated by labels (A) to (L). Subassembly [2] comprises the floating part. Its surface (D) has a streamwise length of $l_F = 3.000$ m and a width of $w_F = 1.000$ m, and is centered at $x_F = 21.0$ m; the surface area is $A_F = 3\,\hbox {m}^2$. Hence, the element’s leading and trailing edges reside at $x_L = 19.5$ m and $x_T = 22.5$ m, respectively (see Fig. 3b). Centered within the outer part of the FE surface (D) is a rectangular cutout of 2.7 × 0.7 m², where either a total of nine modular inserts (B) or a single piece of glass can be flush-mounted. These inserts can be adjusted in wall-normal direction using fine-threaded screws so that any wall-normal steps are restricted to ~0.05 mm (measured with a precision height gage). After adjusting the inserts, the seams are covered by a single layer of Scotch Magic™ tape to prevent any potential flow leakage through the FE surface. Since the viscous length scale is relatively large at $x = x_F$ (Marusic et al. 2015), the step sizes are <2–3 viscous units; hence, the surface is hydraulically smooth. The floating surface is embedded within the wind tunnel surface (A) using a labyrinth joint (qualitatively similar to the one in Fig. 1). A welded tubular steel frame (C) integrates the floating part and is supported on four air-bearing assemblies at its corners; the floating top pad of these bearings is labeled by (E). Assembly [2] is embedded in subassembly [3], whose main component is the tubular steel outer frame (J) that is connected to the tunnel. The planar-support air-bearing assemblies (H) are supported from this frame and are supplied with compressed air (K). A pressure-controlled chamber (L), subassembly [4], is mounted to the outer frame to enclose the bottom of the FE. The spanwise motion of the element is prohibited by two spanwise air bearings (G) on diagonally opposite corners. These planar bearings, oriented in the $\left( x,z\right)$-plane, are connected to a floating surface (D) and a fixed surface (A). Therefore, the only degree-of-freedom of the FE (in the streamwise direction x) is constrained by a load cell assembly at the downstream end (G) to measure force $F_w$ (Sect. 4). Since the element is an integral and permanent part of the tunnel, it can be locked in position using four locks (I) when unused. A bottom view (in z-direction) is shown in Fig. 7a for additional details and is labeled with the same annotations.

Fig. 4

Exploded view of the floating element assembly embedded in the test section of the Melbourne wind tunnel. The assembly is exploded in vertical direction (z-coordinate) in four stages in order to explicitly visualize subassemblies [1]–[4]

Regarding tolerances, the gap width is measured as $g_h \approx 2 \pm 1$ mm (see Fig. 1) at the transverse edges, and $g_h \approx 2$ mm for the longitudinal side edges, resulting in an effective surface area of $\eta _A = 375$. The labyrinth design at all four element-to-surface joints encompasses a vertical clearance of $g_v \approx 0.7$ mm. With an ohmmeter, it has been verified that no electrical current could flow from the FE to the tunnel surface, which ensured the absence of any metal-to-metal contact in the labyrinth seal over the entire FE perimeter. The floating surface is aligned with the tunnel surface to within $-0.6\,{\mathrm{mm}}< h < 0$ (the floating surface is slightly recessed), resulting in a maximum step size, relative to the boundary layer thickness, of $h/\delta = {\mathcal {O}}\left( 10^{-2}\right)$. Floating subassembly [2] has a mass of $m_F \approx 250\,\hbox {kg}$ when the nine flush-mounted wall modules are incorporated. The weight is dependent on the experimental configuration, since modules may, for instance, include control architecture for active TBL perturbation studies. This provides the unique capability of performing net-wall-drag reduction studies by measuring the parasitic drag of the entire system. All necessary control hardware can be suspended from the FE, since the floating system is designed to remain frictionless for total weights up to $m_F \approx 500\,\hbox {kg}$. Each of the four air-bearing assemblies has a planar surface of 200 × 100 mm² and is operated with an air supply pressure of around 800 kPa.

3.3 Local measurements of friction

Measuring local values of $C_f$ is viable despite the long streamwise dimension of our FE; we illustrate this using Fig. 5. A Coles–Fernholz (C–F) friction curve is shown as a function of Reynolds number in our facility, $Re_x \equiv x U_{\infty }/\nu$, for $U_{\infty } \approx 7.2\,\hbox {m}/\hbox {s}$. The C-F relation is given by $C_f = 2\left[ 1/\kappa \ln \left( Re_{\theta }\right) + C\right] ^{-2}$, with chosen constants of $\kappa = 0.38$ and $C = 3.7$; its exact validity is irrelevant for this analysis. Conversion of $Re_{\theta }$ to $Re_x$ was empirically based from a sequence of velocity profiles acquired in the Melbourne wind tunnel (“Appendix”). The leading and trailing edges of the element reside at $x_L$ and $x_T$, respectively, and the detailed variation of $C_f$ within that spatial range, $x_L< x < x_T$, is shown in the inset. The element is centered at $Re_x \approx 9.8 \times 10^6$. Figure 5 confirms that the variation in mean WSS ($C_f \propto \overline{\tau }_w$) is approximately linear for $x \in \left( x_L,x_T\right)$. Our measurements rely on this linear behavior when the obtained WSS is assumed to be affiliated with the streamwise center, $x_F = \left( x_L + x_T\right) /2$. The resultant force corresponds to the integrated friction, $\int _{x_L}^{x_T} C_f\left( Re_x\right) dRe_x$, and equals the local value of $C_f$ at $x = x_{C_F}$, slightly upstream of $x_F$. Since the latter is the actual WSS, we can deduce that our measurement, $C_f\vert _{x = x_F}$, underestimates the friction by 0.024 %. For reference, the difference in $Re_x$ between locations $x = x_F$ and $x = x_{C_f}$ is roughly 0.120 %. When measurements are performed at larger $Re_x$, by increasing $U_{\infty }$, these insignificant errors become even less.

Fig. 5

Variation of $C_f\left( Re_x\right)$ throughout the test section of the Melbourne wind tunnel, according to a Coles–Fernholz relation with $\kappa = 0.38$ and $C = 3.7$. For a free-stream velocity of $U_{\infty } \approx 7.2\,\hbox {m}/\hbox {s},$ the x-locations of the FE leading and trailing edges are indicated, as well as the location where the measurement of WSS is interpreted $\left( x_F\right)$ and the location where the integrated shear acts $\left( x_{C_F}\right)$

4 Measurement procedure

4.1 Instrumentation and uncertainty

Five independent quantities are acquired to obtain the WSS and associated free-stream velocity: the friction force, $F_w$, the free-stream dynamic pressure, $q_{\infty }$, the pressure differential over the FE, $\Delta p$ (explained in this section), and atmospheric pressure and temperature, $p_{\infty }$ and $T_{\infty }$, respectively.

Force $F_w$ is measured using a scale components LPS single-beam load cell with a full-scale range (FS) of 6 N and a combined accuracy of ~0.06 % of FS, which includes random error from nonlinearity, hysteresis, non-repeatability, creep over a loading period <20 min, and temperature variations (temperature fluctuations were found not to exceed ±1.5 °C). The combined FE and load cell system has a natural frequency of $f_n \approx 1.5\,\hbox {Hz}$ when the floating assembly weighs $m_F \approx 250\,\hbox {kg}$. The frictionless element and load cell can be modeled as a spring-mass system, which results in a spring constant of $k = m_F \left( 2 \pi f_n\right) ^2 \approx 2.2 \times 10^4\,\hbox {N}$/m. Consequentially, a friction force of 5 N (relatively high operating velocity of the wind tunnel) yields a displacement of $s \approx 0.23$ mm, which is one order of magnitude smaller than the streamwise clearance, $g_h$.

Differential pressures, $q_{\infty }$ and $\Delta p$, were acquired using two MKS Baratron pressure measurement systems (models 698A11TRA and 698A01TRC) with FS ranges equal to 10 Torr and 1 Torr, respectively. Both systems have an accuracy of 0.05 % of the reading. Regarding the setup of the pressure instrumentation, $q_{\infty }$ was measured using a Pitot-static tube mounted to a streamlined traverse system in the spanwise center of the wind tunnel. The tip of the Pitot-static tube was positioned at a wall-normal location of $z = 0.525$ m, aligned with the trailing edge of the FE. The pressure differential, $\Delta p$, was acquired to monitor the difference in static pressure between the flow-exposed surface of the FE and its underside (for reasons discussed in Sect. 4.4). For the smooth-wall configuration, the static pressure experienced by the flow-exposed surface was acquired through a static pressure tap located in the floor, approximately 0.80 m upstream of the element’s leading edge and at its spanwise center (see $p_2$ in Fig. 10). For the rough-wall measurements, a static probe is positioned at $z \approx 30$ mm and approximately 5 cm downstream of the trailing edge of the element. The static pressure on the underside of the element is equal to the static pressure in the pressure-controlled chamber, measured approximately 0.40 m beneath the FE surface ($p_1$ in Fig. 10). The hydro-static pressure difference (~5 Pa) between the two measurement locations, $p_2$ and $p_1$ in Fig. 10, was accounted for by appropriately zeroing the transducer. An absolute value of the atmospheric pressure was measured using a PCB transducer (model 144SC0811BARO) with an accuracy of 60 Pa, and the air temperature was obtained using an Omega thermistor (model 44018) accurate to within 0.20 °C. Characteristics of the transducers are summarized in Table 1.

Table 1 Specifications of the five transducers used to infer the WSS at a certain Reynolds number condition

The mean WSS is obtained via $\overline{\tau }_w = F_w/A_F$, while the air density is found from the perfect gas law, following $\rho _{\infty } = p_{\infty }/R/T_{\infty }$, where $R = 287.058\,\hbox{J}\,\hbox{kg}^{-1}\,\hbox {K}^{-1}$ is the specific gas constant. Therefore, three quantities are independently measured to assess the friction velocity: $U_{\tau } = f_1\left( F_w,T_{\infty },p_{\infty }\right)$. Measured quantities are assumed to be uncorrelated and exhibit random inaccuracies, so that the uncertainty in $U_{\tau }$ is given by

$$\delta U_{\tau } = \sqrt{\left( \delta U_{\tau }\vert _{F_w}\right) ^2 + \left( \delta U_{\tau }\vert _{T_{\infty }}\right) ^2 + \left( \delta U_{\tau }\vert _{p_{\infty }}\right) ^2},$$

(1)

where, for instance, the uncertainty related to $F_w$ is given by $\delta U_{\tau }\vert _{F_w} = {\partial f_1}/{\partial F_w} \delta F_w$; here, $\delta F_w = 3.6 \times 10^{-3}\,\hbox {N}$ is the transducer uncertainty. The relative uncertainties for $U_{\tau }$ are provided in Fig. 6. Here, we chose a standard temperature and pressure (STP) condition of $T_{\infty } = 293.15$ K and $p_{\infty } = 101{,}325$ Pa, while $U_{\tau }$ was varied over its expected measurement range by varying $F_w$. The uncertainty in $U_{\tau }$ is, particularly for low velocity settings, driven by the load cell uncertainty (1–10 % for $U_{\tau }/\nu < 1.5 \times 10^4$). Similar to the analysis for $\delta U_{\tau }$, the uncertainty in free-stream velocity is found from its dependence on three measured variables via Bernoulli’s principle, $U_{\infty } = f_2\left( q_{\infty },T_{\infty },p_{\infty }\right)$. Since the differential pressure transducer used to measure $q_{\infty }$ has a constant percentage accuracy of the reading, it yields a constant uncertainty in $U_{\infty }$ of approximately 0.06 % for all velocities. Hence, any uncertainty propagating into $C_f \equiv 2\left( U_{\tau }/U_{\infty }\right) ^2 = f_3\left( F_w,q_{\infty }\right)$ is predominantly caused by $\delta F_w$. Error bars in our results of $C_f$ (Sect. 5) follow $\delta C_f = \sqrt{\left( \delta C_f\vert _{F_w}\right) ^2 + \left( \delta C_f\vert _{q_{\infty }}\right) ^2}$.

Fig. 6

Relative uncertainty in measurements of $U_{\tau }$; the uncertainty is decomposed into contributions from each variable, while the total uncertainty is shown by $\delta _{\mathrm{sum}}$; $\nu = 1.51 \times 10^{-5}\,\hbox {m}^2/\hbox {s}$ (STP condition) is used for the top axis

4.2 Static calibration

Tunnel-off calibrations were performed prior to and after each set of measurements, denoted as pre- and post-calibrations. Our calibration setup is drawn in Fig. 7b by way of a sectional view. The inner-frame (C) encompasses a threaded rod that contacts the load cell at the force-transmitting point (F). During calibration, weights are suspended via a single string-pulley configuration. Both the load cell and pulley are attached to the outer frame (J). It was ensured that the vector of the calibration force was aligned with the center line of the tunnel. Calibration weights were measured accurately to ±0.01 g (10⁻⁴ N) using an Ohaus PA512C scale, calibrated in situ with 1–500 g F1 class calibration weights. A gravitational acceleration of $g = 9.79965\,\hbox {m}/\hbox {s}^2$ was used to convert weight to force (personal communication, Hirt et al. 2013)². Due to static friction in the string-pulley system, the applied force on the FE, $F_1$, is smaller than the force of the suspended weights, $F_2$ (see inset in Fig. 8b). This friction discrepancy may be expressed by the Capstan equation (Stuart 1961), given by $F_1/F_2 = \exp \left( \mu _s \phi \right)$, where $\phi$ is the angular displacement of the string, in radians, and $\mu _s$ is the static friction coefficient; here found via an offside procedure. First, a sequence of forces $F_2$ was applied directly to the load cell, oriented to measure forces aligned with gravity. Secondly, output voltages corresponding to the same sequence of forces were acquired, but were now induced via the string-pulley configuration (Fig. 8b); thus, $F_1$-forces were measured. Afterward, $\mu _s$ was computed via $\mu _s = \ln \left( F_1/F_2\right) \phi ^{-1}$ and is shown in Fig. 8b as a function of force $F_2$. A fifth-order polynomial fit through the measurements (gray circles) resulted in the solid black curve. Most scatter lies within the uncertainty range of the transducer, indicated by the dashed lines. Coefficient $\mu _s$ has the highest magnitude for low values of the suspended force. Indicatively, for forces $F_2 > 0.5\,\hbox {N}$, the ratio $F_1/F_2$ is below $\exp \left( -0.005 \pi /2\right) = 0.9922$, which implies a force discrepancy of <0.8 %. Because any calibration bias propagates into the WSS ($\overline{\tau }_w \propto F_w$), we correct for the static friction during all calibrations.

Fig. 7

a Bottom view of FE assembly (in z-direction) with labeled annotations described in Fig. 4. b (right) Sectional view A–A illustrating the force-transferring setup and pulley configuration employed during calibration, (left) detailed cross section of double-labyrinth seal between tunnel floor and FE surface

Fig. 8

a Pre- and post-calibration curves of force, $F_1$, applied to the element, as a function of the load cell voltage; note that the post-calibration curve is shifted by 0.5 N in the vertical direction for clarity. b Static friction coefficient $\mu _s$ of the single string-pulley configuration as a function of force $F_2$ induced by weights. The solid black curve (—) represents a fifth-order polynomial fit through the measurements and the dashed lines (- -) indicate the uncertainty range of the transducer

Pre- and post-calibration curves, acquired for WSS surveys on a smooth-wall configuration, are shown in Fig. 8a. Friction forces were expected to reside between $F_w = 0.25$ and 2.40 N. Typically, the range for calibration is extended by ~15 % and divided into a sequence of N discrete forces, $F_2$. During the course of calibration, load cell output voltages are acquired for 30 s to obtain a converged mean, after the FE device has come to static equilibrium with the beam-type load cell (see also Sect. 4.3). As an aside, the element floats naturally in the positive x-direction, against the load cell, even without suspended calibration weights. Thus, a preload exists, generated by a small inclination of the normal surface vector of the air bearings, relative to gravity; we refer the reader to Sect. 4.4 for an in-depth discussion of that inclination. For each force $F_2,\,M$ independent measurements are acquired by shifting the FE device upstream by ${\mathcal {O}}\left( 1\,{\mathrm{mm}}\right)$ in between periods of sampling; note that the streamwise clearance of the element is $\pm g_h \approx 2$ mm from its centered position. The acquisition of M samples accounts for any non-repeatability in the overall system and the way by which the device achieved static equilibrium. Additionally, unloading the load cell is known to minimize creep error of the load cell. Figure 8a presents 18 individual calibration points (typically, $N = 6$ and $M = 3$). A linear best fit (in a least-squares sense) results in pre- and post-calibration curves shown by the solid line; calibration coefficients of the fits, following $F_1 = a E + b$, are indicated adjacent to each curve (the post-calibration curve is shifted by 0.5 N in the vertical direction for clarity). The linear best fits without corrections for static friction are plotted for reference.

On-site calibrations ensured the most accurate relation between the applied force–simulating the integrated WSS—and the load cell output voltage and at the same time, served as a verification of the setup being frictionless. Any nonlinear behavior in our calibration may indicate a flaw in the assumption that the system is frictionless, as the force-to-voltage relation for this load cell is nominally linear. Potential nonlinearity can be gleaned from a quadratic least-squares fit, following $F_1 = cE^2 + dE + e$. For pre-calibration, $c = -0.00026,\,d = 0.344,\,e = 1.106$ and for post-calibration $c = -0.00077,\,d = 0.347,\,e = 1.116$. The small magnitude of c results in a negligible contribution from the nonlinear term, which verified the frictionless behavior. Repeatability tests indicated that the linear fit has to be shifted by $\pm \delta F_1 = 0.012\,\hbox {N}$ to bound all individual calibration points (note that there is a small scatter of the $M = 3$ individual calibration points per applied force in Fig. 8a). For this reason, we take several independent WSS measurements, so that any scatter can be observed. Shift $\delta F_1$ is roughly three times the absolute accuracy of the load cell, $\delta F_w = 3.6 \times 10^{-3}\,\hbox {N}$.

4.3 Measurement recordings

To ensure stationary flow conditions, the facility is operated for an extended period of time (~1 h) prior to the tunnel-off pre-calibration and WSS measurements. Depending on laboratory conditions, the heat exchanger may assist in achieving steady flow parameters. Two actions are carried out prior to each acquisition of the WSS. At first, the FE device is shifted upstream, for a duration of $\approx\! 10\,{\mathrm{s}}$, to unload the force transducer for the reasons stated in Sect. 4.2: to minimize creep error of the load cell and to obtain stochastically independent measurements. Secondly, the static pressure difference, $\Delta p$, over the FE, is controlled to be zero through the use of a centrifugal fan connected to the pressure-controlled chamber, annotated by (L) in Fig. 10; a detailed discussion is provided in Sect. 4.4. After these two procedural acts, the WSS is measured by acquiring all transducers at a sample rate of $f_s = 1$ kHz using a 16-bit Data Translation DT9836 A/D converter. A total acquisition time of $T_s = 180$ s was found to be sufficient, as this corresponds to $T U_{\infty }/\delta \approx 4\,500$ at the lower operating velocities; typically, a few thousand boundary layer turnover times are required for converged mean statistics. The aforementioned description is performed for each measurement condition, and several samples (up to 12) are taken per unit Reynolds number. Finally, a tunnel-off post-calibration is performed.

A sample time series of the measured force, $F_w$, is shown in the inset of Fig. 9 for a smooth-wall experiment at $U_{\infty }/\nu \approx 1.29 \times 10^6$ ($U_{\infty } \approx 20\,\hbox {m}/\hbox {s}$). Its associated energy spectrum, $G_{\mathrm{FF}}\left( f\right) = \vert \mathcal {F}\left[ F_w\left( t\right) \right] \vert ^2$, computed via ensemble averaging, is presented in pre-multiplied form, $G_{\mathrm{FF}}\left( f\right) \cdot f/\sigma ^2$, in Fig. 9. Here, $\sigma = 0.051\,\hbox {N}$ is the standard deviation of the force time series; the mean is $\mu = 1.439\,\hbox {N}$. As expected, the large surface area of our element (length $l_F/\delta > 9$ and width $w_F/\delta > 3$) results in excessive spatial averaging so that no meaningful WSS fluctuations can be examined. The most energetic spectral peak resides at $f_{\mathrm{max}} = 1.55\,\hbox {Hz}$, close to the natural frequency of the system. The highest resolvable streamwise frequency (neglecting any spanwise averaging) is equal to $f_{\mathrm{res}} = U_c/\left( 2 l_F\right) \approx 2.33\,\hbox {Hz}$, where $U_c = 14\,\hbox {m}/\hbox {s}$ is the convective speed of the WSS footprint (Baars et al. 2014). Seemingly, the FE resonates at $f_{\mathrm{max}}$ due to large flow features that continuously influence the FE over long timescales. This behavior does not adversely affect our results, as the near-harmonic displacement of the FE is very small. Excessive fluctuating forces of $2\sigma$ correspond to motions with an amplitude of less than $s = 2\sigma /k \approx 5\,\mu {\mathrm{m}}$. All other spectral features in Fig. 9 are believed to be electrical noise or are the result of wind tunnel vibrations. The SNR of this measurement is ${\mathrm{SNR}} \equiv \mu /\sigma \approx 28$, while the SNR for all our measurements is generally in the range $25< {\mathrm{SNR}} < 40$.

Fig. 9

Pre-multiplied spectrum of force $F_w$, corresponding to the smooth-wall experiment at a unit Reynolds number of $U_{\infty }/\nu \approx 1.29 \times 10^6$. The raw time series of $F_w$ is shown in the insert and has a mean of $\mu = 1.439$ N and a standard deviation of $\sigma = 0.051$ N

4.4 Potential errors and post-processing

Here, we start with a quantification of the manufacturing intolerance, as this plays a vital role in the understanding of potential experimental errors. The element is nominally positioned at the center of its streamwise range-of-motion. As mentioned in Sect. 4.2, the floating assembly moves naturally in the positive x-direction. Consequentially, a preload of magnitude 0.447 N exists when the floating configuration has a weight of $m_F \approx 250\,\hbox {kg}$. Small inclinations of the air-bearing surfaces, relative to a plane orientated normal to the gravity vector, cause this preload. Hence, the average bearing tilt angle is computed as $\alpha _b = \sin ^{-1}\left( 0.477/{\hbox{g}}/m_F\right) \approx 0.011^{\circ }$ and is shown in the sectional view of Fig. 10.

Fig. 10

Sectional view B–B, indicated in Fig. 7a (enlarged 2×), illustrating the air bearings, FE surface, wind tunnel floor and relevant misalignment angles. Labeled annotations are described in Fig. 4

Fig. 11

a Friction coefficient $C_f$ as a function of unit Reynolds number. Square symbols, and the fifth-order polynomial fit (dotted line), correspond to an uncontrolled $\Delta p$ ($\Delta p > 0$). Circles and curve fit (—) correspond to a controlled $\Delta p$ of zero. The insert shows the $Cp \equiv \Delta p/q_{\infty }$ (see Fig. 10, in the absence of the pressure-controlled environment); $\nu = 1.51 \times 10^{-5}\,\hbox {m}^2$/s (STP condition) is used for the top axis. b Empirically determined floating surface tilt angle, $\alpha _s$, from the two datasets presented in (a). A fifth-order polynomial fit is shown by the black solid curve (—)

Tilt of the air bearings manifests as a calibration offset. However, the flow-exposed surface of the FE must be parallel to the bearing surfaces, so that any resultant pressure force vector, $F_p$, does not affect the measurement of friction force $F_w$. A static pressure force is normally present due to a minor overpressurization of the test section, caused by a uniform-meshed grid at the wind tunnel outlet; which aids in achieving ZPG conditions. Such a pressure differential, $\Delta p = p_2-p_1$, is visualized in Fig. 10, over the FE surface that is inclined at an angle $\alpha _s$ with respect to the bearing surfaces. Values of this $\Delta p$ in the absence of the pressure-controlled environment (L) are shown in the inset of Fig. 11a in terms of the pressure coefficient, $C_p \equiv \Delta p/q_{\infty }$.

Inspection of the floating element surface tilt, using a high-precision spirit level, yielded values of $0.025^{\circ }< \alpha _s < 0.100^{\circ }$, depending on the location. We illustrate the effect of such an unavoidable misalignment (manufacturing tolerance) by considering how the pressure differential affects our WSS results. Two sets of stochastically independent WSS measurements are provided in Fig. 11a. The first set ($\Delta p > 0$) corresponds to a configuration without the controlled pressure-environment in place. When $\Delta p$ was controlled to be nominally zero, by increasing $p_1$ in the sealed environment (described in Sect. 4.3), the WSS decreased in magnitude, reflected by the $\Delta p = 0$ dataset. These data affirm that $\alpha _s > 0$, since the measured friction force is too high when a resultant pressure force acts into the plane of the FE surface. The floating surface tilt may be quantified from the data in Fig. 11a. It will follow in Sect. 5 that the $\Delta p = 0$ data yield friction values that are in close agreement to the literature. Since the only difference between the $\Delta p = 0$ and $\Delta p > 0$ datasets is the pressure differential, the dashed curve fit equals the WSS ($\overline{\tau }_w = C_f q_{\infty }$), affected by the component of the resultant pressure stress, tangential to the bearing surface: $\Delta p \sin \left( \alpha _s\right)$. For each measurement of WSS, in the $\Delta p = 0$ dataset, we can therefore infer $\alpha _s$ for which the addition of the pressure component results in an agreement with the dashed curve. Values of angle $\alpha _s$ are shown in Fig. 11b and should be constant for data residing at all $U_{\infty }/\nu$-settings due to the rigidity of the FE assembly. Generally, we retrieve $\alpha _s \approx 0.08^{\circ }$. The small variation in the empirical determination of $\alpha _s$, particularly for $U_{\infty }/\nu < 1 \times 10^6$, is attributed to the less repeatable measurements at these operating settings. It is important to realize that it is unfeasible to manufacture the large-scale element to the required precision for the pressure differential not to affect the measurements of WSS. For instance, when we consider an operating velocity of $U_{\infty } \approx 20\,\hbox {m}/\hbox {s}$, the unmodified pressure differential is $\Delta p \approx 30$ Pa, generating a pressure force of $F_p = \Delta p A_F \approx 90\,\hbox {N}$. An estimation of the friction force at this condition is $F_w \approx 1.41\,\hbox {N}$. When we demand that $F_p$ affects the magnitude of $F_w$ by <1 %, this requires $\alpha _s < 0.009^{\circ }$ (a slope of $\Delta z \approx 0.15$ mm per $\Delta x = 1$ m) which is practically unfeasible.

In theory, it is possible to correct for the effects of a nonzero pressure differential using $\alpha _s \approx 0.08^{\circ }$ and a measurement of $\Delta p$. However, some discrepancy may result from not knowing the exact value of $\alpha _s$. In order to have a minimal effect of the erroneous pressure component, we therefore control $\Delta p$ to be nominally zero during the acquisition of WSS samples, as outlined in Sect. 4.3. Our setup was adjusted so that the pressure differential was in the range $0< \Delta p < 0.5$ Pa. Measurements for which $\Delta p > 0$ are preferred over a marginal negative pressure difference ($p_2 < p_1$) as the latter may cause a flow through the labyrinth joint into the test section. In post-processing, we still correct for a nonzero $\Delta p$, by subtracting the erroneous contribution, $\Delta p A_F \sin \left( \alpha _s\right)$, from the measured friction force $F_w$; angle $\alpha _s$ is taken as 0.08°. The maximum correction is $\Delta p A_F \sin \left( \alpha _s\right) = 0.5 \cdot 3 \cdot \sin \left( 0.08^{\circ }\right) = 2.10$ mN, which, at our lowest friction force measurement, is a correction of <0.90 %. Moreover, for typical WSS measurements at $U_{\infty } \approx 20\,\hbox {m}/\hbox {s}$, the correction is <0.015 % (smooth wall). Although any drift in the output voltage of the load cell was minimal, and the time between pre- and post-calibrations was shorter than 90 min, we applied a drift correction. Using a linear interpolation with time, within the interval between pre- and post-calibrations, unique calibration coefficients were derived for each 180 s long WSS sample.

5 Wall-drag of smooth and rough walls

5.1 Smooth- and rough-wall configurations

In addition to the nominally smooth wall, we provide wall-drag results for one particular type of roughness. Characteristics of the smooth-wall setup were described earlier (Sects. 3.1, 3.2). The entire flow-exposed side of the wind tunnel floor consists of 6-mm-thick aluminum sheets that span the width of the test section and have a streamwise length of 6 m. The plates are supported by the steel frame of the wind tunnel with leveled panels of 24-mm-thick MDF wood.

The rough wall comprised P36 grit sandpaper (Awuko Abrasives), supplied as a single sheet with a width of 1.85 m and a length of 100 m. The sandpaper was laid in several sheets to allow for unrestricted movement of the FE; the arrangement is shown in Fig. 12a. Three 1 × 1 m$^2$ sheets were adhered to the FE using double-sided tape (DSPRC, Tenacious Tapes). Likewise, at either side of the FE, three 1 × 0.43 m² sheets were attached. The sheets were cut using a Worldcut 350AII CO2 laser cutter, with a position accuracy of ±0.05 mm. Two single sheets covered the remainder of the tunnel floor and were adhered using double-sided tape (AT302, Advanced Tapes) just upstream of the leading edge, $x_L$, and downstream of the trailing edge, $x_T$, respectively. The downstream sheet, number (2) in Fig. 12a, was 5 m in length and extended beyond the tunnel exit. The sheet was passed over a 10-cm-diameter, 2-m-wide PVC pipe, such that the free end of the sheet was oriented in the $\left( y,z\right)$-plane. Masses with a total weight of 40 kg were attached to the clamped end to tension the sandpaper in order to prevent any undulations in the sandpaper sheet, which were occasionally observed when it was not in tension. The 20-m-long upstream sheet, (1) in Fig. 12, passed through a rounded spanwise slot in the tunnel floor located under the BL trip, at $x \approx 0.15$ m, and was tensioned in a similar manner as the downstream sheet. The slot was covered using a small sheet of sandpaper, secured along its upstream edge. Roughness parameters were quantified by laser surface scanning a 25.4 × 25.4 mm² sample, which provided the deviation $h'$ about the mean height, $\overline{h}$. The peak-to-trough height is $k_p = h'_{\mathrm{max}} - h'_{\mathrm{min}} = 1.219$ mm and the mean amplitude is $k_a = \overline{\vert h' \vert } = 0.119$ mm, with a standard deviation of $k_{\mathrm{rms}} = \sqrt{\overline{h'^2}} = 0.150$ mm.

Fig. 12

a Arrangement of the sandgrain roughness (P36 grit sandpaper) in the vicinity of the FE. Continuous sheets of sandpaper, (1) and (2), appear upstream and downstream of the FE, respectively. Three 1 m² square sections, (3), cover the FE, while a total of six rectangular sections, (4), of 1 m × 0.43 m cover the test section on both sides of the FE. The gap affiliated with the labyrinth joint, (M), remains $g_h \approx 2$ mm. b Photographic view in positive x-direction of the roughness laid around, and on the FE. The traverse system supporting the static pressure probe, (N), is also visible

5.2 Results of wall-drag and discussion

5.2.1 Smooth-wall results

Smooth-wall surveys were performed for free-stream velocities between $U_{\infty } = 8$ and 26 m/s, with increments of 2 m/s. Three stochastically independent WSS samples were acquired for each velocity, bounded by pre- and post-calibrations. This procedure was repeated three more times (over two separate days). As such, we obtained a total of twelve stochastically independent samples for near-similar values of $U_{\infty }/\nu$. Three wall-drag samples for the rough wall were acquired at velocity settings of $U_{\infty } = 4$, 6, 10, 12, 15, 20, 24 and 30 m/s.

Fig. 13

a Friction velocity of the smooth- and rough-wall configuration at $x_F = 21.0$ m as a function of unit Reynolds number. Dimensional values of $U_{\infty }$ and $U_{\tau }$, on the top and right axes, respectively, are computed using a value of $\nu = 1.51 \times 10^{-5}\,\hbox {m}^2$/s (STP condition). b Smooth-wall friction data expressed in terms of $U^+_{\infty } = U_{\infty }/U_{\tau }$ as a function of $Re_{\theta }$; a Coles-Ferhnolz relation is shown with the solid black line (—) and bounds corresponding to ±1 % (- -). Individual WSS samples are indicated by the gray circles, while their means are represented by the black-lined circles. The vertical lines, centered on the black-lined circles, indicate the magnitude of the measurement uncertainty

Fig. 14

Skin friction coefficient $C_f$ as a function of $Re_{\theta }$ for the floating element measurements of wall-drag under a smooth- and rough-wall TBL. Larger $Re_{\theta }$ conditions are achieved by increasing the free-stream velocity. Individual samples are shown with the gray markers, while the black-lined markers reflect the mean at each flow condition. The vertical lines, centered on the black-lined circles, indicate the magnitude of the measurement uncertainty. Smooth-wall data are shown in company with a Coles–Fernholz relation (following Fig. 13), while a seventh-order polynomial is fit through the rough-wall data

Values of the friction velocity are shown in Fig. 13a as a function of the unit Reynolds number, $U_{\infty }/\nu$. The additional ordinate on the right-hand side is added to provide a qualitative magnitude of the friction force, $F_w$. As anticipated, the rough wall exhibits a larger wall-drag than that experienced by the smooth wall. Each marker reflects the mean of the stochastically independent samples. The repeatability of the measurements may be revealed by the more sensitive metric of $U^+_{\infty } = U_{\infty }/U_{\tau }$, which is shown for the smooth-wall data in Fig. 13b as a function of $Re_{\theta }$ (see “Appendix” for the $Re_x \rightarrow Re_{\theta }$ conversion). Here, gray circles represent the individual WSS samples, while their means are indicated by the black-lined circles. Superposed on each mean marker is a vertical line with a length equal to the uncertainty in the measurement (see Sect. 4.1). Generally, the scatter of the individual samples is within two-to-three times the uncertainty in the measurement; this degree of system repeatability agrees to what was found during calibration (Sect. 4.2). A small amount of static friction in the labyrinth joint may cause this scatter. Although any static friction is theoretically accounted for during calibration, it is stochastic in nature. To accommodate comparison of our data to the literature, we consider a Coles–Fernholz relation of the form

$$U_{\infty }^+ = \frac{1}{\kappa } \ln \left( Re_{\theta }\right) + C,$$

(2)

with a chosen value of the von Kármán constant, $\kappa = 0.38$ (Marusic et al. 2013). Extracting a meaningful value for $\kappa$ from a fit to data spanning less than a decade of Reynolds numbers ($15{,}500< Re_{\theta } < 48{,}500$) would require an unfeasible experimental accuracy. A fit of Eq. (2) to the mean measurement point at the highest Reynolds number ($Re_{\theta } \approx 48{,}500$) yields $C = 3.661 \approx 3.7$. Performing the fit to the highest $Re_{\theta }$ data point alone was done as the WSS signal is strongest for this high velocity setting, and as such, is least affected by measurement error. The trend line of Eq. (2), with $\kappa = 0.38$ and $C = 3.7$, is shown in Fig. 13b with the solid black line. This trend follows high-Reynolds number data to within experimental error of the technique employed, primarily OFI (Nagib et al. 2007). We present a $C_f$ friction curve in Fig. 14. Data follow the Coles–Fernholz expression to within 1 % (indicated by the two dashed lines) for $Re_{\theta } > 38{,}000$ and provides confidence in the precision of the rough-wall results. As noted previously, OFI is the well-established method to obtain the empirical constants for any friction laws (Nagib et al. 2007). Our smooth-wall scenario serves as a benchmark verification for the experimental apparatus. Any systematic discrepancy, relative to the Coles–Fernholz relation, is most pronounced at lower Reynolds numbers. For $Re_{\theta } \approx 15{,}300$, the measured $C_f$ is 3 % larger in value than what is expected from the Coles–Fernholz relation ($\kappa = 0.38$, $C = 3.7$); this equates to an absolute force discrepancy of 7.3 mN. It is challenging to find the source of discrepancy due to the low magnitude of this force. Nevertheless, two plausible contributors to our disparity are provided here.

First of all, potential forces acting on the edges of the element may affect the measured force. Although scaling arguments illustrated a favorable SNR ratio for a large scale FE (Sect. 2.3), lip forces remain present; no measurements of those could be achieved. Secondly, although the pressures between the flow-exposed surface of the FE and its underside are equalized to within $\Delta p = 0.5$ Pa (Sect. 4.4), the pressure on the flow-exposed side was measured 0.80 m upstream of the FE. Hypothetically, the ZPG condition can vary between the FE surface and the pressure tap by ±0.87 % in terms of $C_p$ (see Sect. 3.1), which may result in a pressure differential of $\Delta p = 2\cdot 0.87\%\cdot q_{\infty }$. For $Re_{\theta } \approx 15,300$, $\Delta p = 0.32$ Pa, which results in a force discrepancy of 0.6 %. We cannot correct for this pressure differential, unless the 2D pressure distribution over the FE is mapped out. Hence, a small remaining pressure force may contribute to our discrepancy seen at lower $Re_{\theta }$. For geometrically down-scaled FE devices, it is important to note that the discrepancy due to a resultant wall-normal pressure force remains equal. That is, an equal misalignment in a smaller-scale system (here $\alpha _s \approx 0.08^{\circ }$, see Fig. 11b) results in a similar influence on $C_f$ when the pressure differential is equal in terms of $C_p \equiv \Delta p/q_{\infty }$ (both pressure and friction forces act on the same surface area).

Overall, our $C_f$ values agree with the quoted Coles–Fernholz relation to within 2.50 % for $Re_{\theta } > 15{,}000$, and to within 1 % for $Re_{\theta } > 38{,}000$. For any rough wall, the wall-drag is higher compared to the smooth wall, which should result in even less systematic discrepancy.

5.2.2 Rough-wall results

When we consider the rough-wall data in Fig. 14, black-lined markers indicate the average of the three individual samples (gray squares) at each Reynolds number. Reynolds number conversions for the rough-wall data ($Re_x \rightarrow Re_{\theta }$) were performed similarly to the conversion for the smooth wall (“Appendix”). A seventh-order polynomial fit is added to aid in visualizing the trend of $C_f\left( Re_{\theta }\right)$. For an increasing $Re_{\theta }$, an initial decrease in $C_f$ appears, followed by an approach to a constant value of $C_f \approx 3.24 \times 10^{-3}$ for $Re_{\theta } > 60{,}000$. This behavior of the friction factor reflects a transition from the transitionally rough to the fully rough regime. Such an inflectional trend in the $C_f$ curve is well known for pipe flow with uniform sandgrain roughness, as observed in the renowned work by (Colebrook 1939; Moody 1944). Following the work of Nikuradse (1950), a Reynolds number invariant friction factor corresponds to an asymptotic behavior in his proposed roughness function, given by

$$\Delta U^+ = \frac{1}{\kappa } \ln \left( k_s^+\right) + A - A'_{\mathrm{FR}}.$$

(3)

Here, $\Delta U^+$ is the decrease in inner-normalized mean velocity in the logarithmic region of the TBL velocity profile, relative to a smooth-wall velocity profile at matching Reynolds numbers. The equivalent sandgrain roughness, $k_s$, is inner-normalized to form $k_s^+ \equiv k_s U_{\tau }/\nu$. Finally, constant $A'_{\mathrm{FR}}$ is taken to be 8.5 (Nikuradse 1950) and constant A is the additive constant in the smooth-wall mean velocity log-law. A fit of the roughness function to hot-wire anemometry data of $\Delta U^+$ was performed by Squire et al. (2016). An asymptotic behavior in the roughness function, at the location of our FE, appeared for $Re_{\theta } > 70{,}000$ and revealed a fully rough equivalent sandgrain roughness of $k_s = 1.96$ mm. Our rough-wall measurement at $Re_{\theta } \approx 62{,}000$ corresponds to $k_s^+ \approx 105$. In close proximity to this sandgrain Reynolds number, the $C_f\left( Re_{\theta }\right)$ curve plateaus to a constant value, which corresponds to the region where the roughness function asymptotes. A recent hot-wire anemometry study by Squire et al. (2016), above the same roughness, employed values of the friction velocity, $U_{\tau }$, for the inner-scaling of flow quantities. Mean velocity profiles, and profiles of higher-order statistics, were shown to collapse in the outer- layer of the TBL over this roughness. In the fully rough regime, this collapse is evidence for Townsend’s outer-layer similarity hypothesis.

6 Summary and conclusions

A floating element device is shown to be capable of measuring the flow-induced wall-drag of smooth- and rough-wall surfaces. Although alternative techniques exist for obtaining the wall shear stress for smooth-wall flows—most notably oil-film interferometry—they generally reside around a priori assumptions. Moreover, an accurate and reliable floating element measurement becomes invaluable when flows over rough walls, or actively perturbed TBL flows, are considered, since this is the only technique suitable to extract the wall shear stress without making assumptions.

Our floating element comprises a substantial surface area of 3 m (streamwise) × 1 m (spanwise) to achieve minimal systematic error. Despite its large size, local values of the friction coefficient are acquired due to the near linear variation of the TBL parameters over the element in the large-scale Melbourne wind tunnel. Measurements on the ZPG smooth-wall configuration revealed friction factors that are in agreement with a Coles–Fernholz relation, $C_f = \left[ 1/0.38 \ln \left( Re_{\theta }\right) + 3.7\right] ^{-2}$, to within 1 % for $Re_{\theta } > 38{,}000$, thus proving the viability of accurate measurements with our apparatus. Direct measurements of the wall-drag associated with one particular sandgrain roughness were acquired for $10{,}500< Re_{\theta } < 88{,}500$, and uncovered the transitionally to fully rough regimes in the friction curve. A narrow range of scatter appeared for independent measurements, roughly three times larger than the transducer uncertainty in the measurement. Small systematic discrepancy of the mean of stochastically independent samples was observed in the appearance of a slightly different slope of the friction curve, $C_f\left( Re_{\theta }\right)$, compared to a Coles–Fernholz relation with $\kappa = 0.38$. Plausible contributions to this discrepancy were discussed in Sect. 5.2.1 and may be related to remaining pressure forces on the edges of the element or an induced wall-normal force from a weak pressure gradient over the FE (given the small misalignment discussed in Sect. 4.4).

There is in essence no limit on the type of roughness that could be studied using our device. As long as the roughness can be laid-up seamlessly in the tunnel’s test section, and can be cut accurately around the edges of the floating element, it is feasible to examine its wall-drag. Our setup is suitable for embedding active control architecture to infer the parasitic drag of the entire system, typically encountered in studies of actively perturbed boundary layers. Our macroscale element is, of course, restricted to measurements of the local mean wall shear stress due to spatial averaging and an absence of any practical temporal resolution. However, hot-films can be embedded on the system to acquire the fluctuating wall shear stress.

Appendix

Wall-normal boundary layer profiles of the mean velocity were acquired for both the smooth- and rough-wall configurations. These data allow for an empirical conversion from $Re_{x} \equiv x_F U_{\infty }/\nu$ to $Re_{\theta } \equiv \theta U_{\infty }/\nu$, at the position in the Melbourne wind tunnel where these profiles were taken ($x \approx x_F = 21.0$ m, in the spanwise center). For the smooth-wall case, individual Pitot and static tubes were used to examine the mean velocity. The outside diameter of the Pitot tube was $d_p = 0.98$ mm and the diameter of the total pressure port was ~0.4 mm. The static tube was positioned 13.5 mm above the Pitot tube, and had an outside diameter of $d_s = 1.57$ mm, with the static pressure tab positioned 14.2 mm from the leading edge. For dynamic pressures lower than 100 Pa, a 0–1 Torr pressure gauge transducer was used (Table 1). Otherwise, a 0–10 Torr transducer was employed. A logarithmic wall-normal spacing was selected up to the geometric center of the log-region, beyond which linear spacing was used; typical profiles consisted of 60 points. Post-measurement corrections were applied following Bailey et al. (2013) to yield the wall-normal velocity profiles. Profiles above the rough wall were acquired using hot-wire anemometry (Squire et al. 2016). For each $Re_x$ condition, the momentum thickness was found via numerical integration of the velocity profiles. The obtained $Re_x \rightarrow Re_{\theta }$ conversions are presented in Fig. 15. An empirical relation of Nagib et al. (2007) is superposed to show its agreement (within experimental tolerance) with our current conversion.

Fig. 15

Reynolds number $Re_x$ versus $Re_{\theta }$ above the smooth- and rough-wall configurations at $x \approx x_F = 21.0$ m