1 Introduction

Shallow flows exist in many forms in our environment, including inland rivers, as well as coastal flows. Such flows have a free surface and a bed (bottom surface), and their horizontal dimensions are much larger than their depth h w. These flows are usually fully turbulent and, in most cases, satisfy the criterion for a fully developed turbulent flow L e /h w > 50 (Uijttewaal et al. 2001), where L e is the distance from the origin of the flow. Such a fully developed condition refers to the small-scale, three-dimensional turbulence between the free surface and the bottom surface (bed); this turbulence has a characteristic length scale L T less than or equal to the water depth L T < h w. It is, however, typically considered to have an insignificant influence on the onset and the development of large-scale instabilities and vortex formation in the horizontal plane, which are considered to be quasi-two-dimensional. Shallow flows satisfy the criterion that the wavelength λ of an instability or the characteristic diameter D of a large-scale vortical structure is much larger than the water depth h w.

Basic classes of separated shallow flows in the horizontal plane include shallow jets, mixing layers and wakes, which often have large, or practically infinite, streamwise length. A dimensionless stability parameter S determines whether a flow instability develops in the horizontal plane, thereby leading to development of a vortex (ices). This parameter S is defined as \( S = \bar{c}_{\text{f}} \delta \bar{U}/2h_{\text{w}} \Updelta U \), where \(\bar{c}_{\text{f}}\) is the bed friction coefficient, δ is the width of the transverse shear flow, \(\bar{U}\) denotes the average velocity across the shear layer, ΔU is the corresponding velocity difference across the layer, and h w is the water depth (Chu and Babarutsi 1988). The velocity difference ΔU imposes a destabilizing influence that promotes the onset of instability, whereas the friction coefficient \(\bar{c}_{\text{f}}\) tends to retard the onset of the instability, i.e., it has a stabilizing effect. In essence, the onset of the instability and the associated vortex formation can therefore occur only when the magnitude of the stability parameter S is less than the critical stability parameter value S cr.

1.1 Shallow wakes, mixing layers, jets of infinite streamwise extent

In recent decades, major contributions have been made to our understanding of shallow wakes, mixing layers and jets, involving experiments, theoretical developments, and numerical simulations. The primary emphasis has been on these classes of shallow flows having infinite streamwise extent. Representative investigations of instabilities and vortex formation in shallow wakes include the studies of Ingram and Chu (1987), Chen and Jirka (1995), and Ghidaoui et al. (2006); in shallow mixing layers by Chu and Babarutsi (1988), Chen and Jirka (1998), van Prooijen and Uijttewaal (2002); and in shallow jets by Giger et al. (1991), Dracos et al. (1992), Jirka (1994). Theoretical analyses and numerical simulations of the possible convective and absolute instabilities of shallow wakes, mixing layers and jets, and the relationship of these instabilities to eventual development of large-scale vortical structures, have been undertaken in a range of studies, including those of Chu et al. (1991), Chen and Jirka (1997), van Prooijen and Uijttewaal (2002), Socolofsky and Jirka (2004), Chan et al. (2006) and Ghidaoui et al. (2006). Kolyshkin and Ghidaoui (2003) also characterized the effects of the rigid lid assumption. Ghidaoui and Kolyshkin (1999) and Kolyshkin and Ghidaoui (2002) extensively assessed gravitational and shear instabilities of shallow flow in open channels.

1.2 Shallow mixing layers of finite length

All of the foregoing studies involve shallow flows of infinite streamwise extent. An obstacle or corner in a mixing layer produces a finite length scale in the streamwise direction. As a consequence, development of the mixing layer is influenced by the finite length scale of the instability as well as the upstream influence from the region of the impingement upon the obstacle or corner. A representative example of a shallow mixing layer having a finite length scale in the streamwise direction is the shallow flow past a cavity, which has been investigated experimentally by Weitbrecht and Jirka (2001), Kurzke et al. (2002), Wallast et al. (1999), Uijttewaal et al. (2001), and computationally by McCoy et al. (2008).

Shallow flow past a cavity can potentially give rise to excitation of an eigenmode of a gravity standing wave within the cavity, due to coupling with an inherent instability of the separated shear layer along the cavity opening. Kimura and Hosoda (1997) qualitatively visualized the formation of vortical structures along the opening of a cavity and computed the velocity field. Meile et al. (2011) experimentally determined the frequency and amplitude of periodic oscillations of the free surface in rectangular cavities along both walls of a channel. For a cavity configuration analogous to an organ pipe in air, Ekmekci and Rockwell (2007) related the coherence of vortex formation along the cavity opening to the degree of coupling with a longitudinal gravity standing wave mode within the cavity.

Wolfinger et al. (2012) considered shallow flow past a rectangular cavity and addressed the flow structure in relation to onset of a gravity standing wave. Emphasis was on the turbulence statistics at mid-depth for the progression of states associated with increasing inflow velocity: pre-lock-on; onset of lock-on; lock-on; and late lock-on. It was found that the largest magnitude Reynolds stress occurred during the locked-on state of the flow oscillation. Not yet addressed are the flow patterns as a function of elevation above the bed, including the interrelationship between topological patterns of streamlines, vorticity, Reynolds stresses, and mass exchange between the cavity and the main flow. The present investigation addresses these unresolved aspects.

1.3 Mass exchange

The mass exchange between the cavity and the mainstream has been addressed using a variety of experimental approaches. Jarrett and Sweeney (1967) used an evaporative surface technique to determine the local mass transfer coefficients of a fully submerged cavity in a non-shallow flow and Valentine and Wood (1979) used dissolved tracer to determine the effects of a sequence of small cavities along the bed (bottom surface) on longitudinal dispersion beneath the free surface. More recently, Uijttewaal et al. (2001) and Kurzke et al. (2002) visualized the flow with colored dye; variation with time of patterns of dye concentration was used to determine the mass exchange coefficients. The mass exchange coefficient was determined from planar concentration analysis (PCA). Jamieson and Gaskin (2007) used colored dye visualization and particle tracking and observed that three-dimensional flow structures have an important role in the mass exchange process. These studies concluded that the exchange between the main stream and the cavity is a first-order process, even though the flow patterns show three-dimensional characteristics. A method that does not use marker fluid was advanced by Weitbrecht et al. (2008), who used (free-) surface particle image velocimetry, in order to determine the mass exchange coefficient in terms of the cross-stream velocity fluctuation along the opening of a cavity formed by adjacent groynes. Computations of McCoy et al. (2007) and Constantinescu et al. (2009) have yielded insight into the mass exchange process between the cavities formed by neighboring groynes and the main channel flow. In their simulations, the free surface of the water is treated as rigid, corresponding to the rigid lid assumption.

1.4 Unresolved issues

Shallow flow past a cavity can give rise to vortex formation in the separated shear layer along the cavity opening. This vortex formation may be highly coherent if coupling occurs between the separated layer and a gravity wave mode within the cavity. Due to the fundamentally different boundary conditions at the bed (bottom surface) and the free surface above the bed, it is anticipated that the flow structure with and without gravity wave coupling will exhibit variations with depth. The nature of, and correlation between, the flow patterns in the bed and free-surface regions, as well as the regions between them, has not been addressed. Complementary representations of the flow structure, involving streamlines, vorticity contours and contours of constant velocity components, can provide a basis for interpretation of the flow physics as a function of elevation above the bed (bottom surface). Use of topological concepts allows identification of critical points of the streamline patterns, in relation to patterns of vorticity and velocity, thereby providing insight into the degree to which the imprint of highly coherent vortex formation above the bed exists adjacent to the bed. These aspects have not yet been pursued.

Significant turbulent stresses, that is, Reynolds normal and shear stresses, are expected to occur in the separated shear layer along the cavity opening. Enhanced turbulent shear stress in the separated shear layer would increase the entrainment from the cavity into the separated shear layer, thereby altering the flow patterns within the cavity. These normal and shear stresses may also have significant magnitudes along the impingement (trailing) wall of the cavity, as well as in the interior of the cavity. All of these features involving turbulent stresses have not been characterized in relation to elevation above the bed, for cases with and without coupling with a gravity wave mode of the cavity. The mass exchange between the cavity and the main stream is a function of the turbulence characteristics of the separated shear layer along the cavity opening. The manner in which the structure of the separated layer varies with elevation above the bed, and its relation to the effectiveness of the mass exchange between the cavity and the main stream, has not been determined.

2 Experimental system and techniques

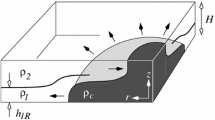
Experiments were performed in a large-scale recirculating, free-surface water channel that has low free-stream turbulence intensity (0.2 %). The main test section of this channel has an adjustable depth of 610 mm, a length of 4,877 mm and a width of 927 mm. A primary objective of the present study is to determine the structure of a shallow, unsteady shear layer along the mouth of a cavity. Specifically, both non-coupled and fully coupled shear layer oscillations with the gravity wave mode of the cavity are of interest. A test section was designed to control the cavity dimensions, water depth and flow velocity. Full details of the experimental system are given by Wolfinger et al. (2012). A side view of the experimental system is given in Fig. 1. Upstream of the test section, the flow passed through a settling chamber with flow conditioning in the form of honeycombs and screens, followed by a contraction. In addition, a contraction is located upstream of the leading edge of the cavity, as indicated in the plan view of Fig. 1 of Wolfinger et al. (2012). This contraction reduces the width of the test section from 927 mm to W e = 470 mm. The width and streamwise length of the channel located downstream of the contraction are, respectively, W e = 470 mm and L e = 1,384 mm.

Fig. 1
figure 1

Schematic of experimental facility (after Wolfinger et al. 2012)

Full size image

The cavity width W, cavity length L and water depth h w were varied in order to attain non-coupled and fully coupled states. The test section includes a long acrylic (transparent) plate of 12.7 mm thickness to elevate the floor of the channel to a height of 165 mm as indicated in Fig. 1. The shallow water flow was therefore generated along the upper surface of the plate. The streamwise length of the shallow water layer, that is the distance from the leading edge of the acrylic plate to the leading corner of the cavity, is L i = 1,905 mm. The ratio of the inflow length L i to water depth h w is L i /h w = 50.1 which satisfies the criterion of L i /h w > 50 of Uijttewaal et al. (2001) for attainment of a fully evolved turbulent shallow layer. The cavity section has a length L = 305 mm and a width W = 457 mm. All of these acrylic components have a height h a = 102 mm. Boundary layer trips of 1.6 mm thickness and a length of 13 mm are located at the marked positions on the top wall of the raised plate and the vertical surface of the inflow channel, at a location immediately downstream of the contraction. By using this arrangement, it was possible to produce rapid onset of a turbulent boundary layer and attainment of a fully turbulent boundary layer at the leading edge of the cavity. The water level h w could be adjusted to an arbitrary value, as shown in the side view of Fig. 1. A value of h w = 38.1 mm was employed in the present experiments; it was associated with the largest amplitude of the resonant-coupled oscillations of the free surface within the cavity. The amplitude of the gravity standing wave was h d = 3 mm which is shown in the plan view (section A–A) in Fig. 2. This peak amplitude corresponds to a ratio of wave amplitude h d to the water depth h w of h d /h w = 0.08.

Fig. 2
figure 2

Schematic of experimental test section and quantitative imaging system. Also illustrated are unstable shear layer along opening of cavity and deformation of free surface due to gravity standing wave within the cavity

Full size image

The eigenfrequencies of the eigenmodes of the gravity standing wave in the cavity aligned in the streamwise direction are given by Kimura and Hosoda (1997) and Naudascher and Rockwell (1994):

$$f_{n} = \frac{{n\,\sqrt {gh} }}{2L}\quad n = 1,2,3 \ldots$$
(1)

in which L is the cavity length, h w is the water depth, g is the gravitational acceleration, and n and f n are the mode and frequency of the oscillation. The first mode of the standing wave corresponds to n = 1, for which the wavelength of the standing gravity wave is twice the cavity length. This mode is represented by the schematic of Fig. 2 (section A–A). The predicted frequency according to Eq. (1) is f 1 = 1.0 Hz, which compares with the experimentally determined value of f 1 = 1.02 Hz. When the frequency f n of the gravity standing wave mode within the cavity approaches and matches the most instable frequency f s of the separated shear layer, a coupled, self-sustained oscillation occurs. Lock-on exists when the frequency of the coupled oscillation remains at f s /f n  = 1 as the reduced velocity U/f n L is varied. Within this range, the fully coupled maximum amplitude of oscillation is attained; it is of primary interest herein, and is attained at a value of depth-averaged inflow velocity of U = 433 mm/s. The representative non-coupled state involving insignificant amplitude of the coherent oscillation occurs at a U = 236 mm/s. The velocity variation with depth follows the one-seventh power law, in accord with the fully turbulent nature of the shallow water layer. At each elevation z L /h w above the bed (bottom surface), the local velocity U in the main stream was employed for normalization of velocity components, turbulence statistics and vorticity.

To characterize analogous systems involving coupling between a flow instability and a resonator, the reduced velocity U r = U/f n L (inverse of Strouhal number) is employed (Naudascher and Rockwell 1994). The two aforementioned states of the flow occur at U/f n L = 0.78 for the non-coupled state and U/f n L = 1.44 for the coupled state. For shallow flow having a free surface (air–water interface), in absence of an adjacent resonator, the Froude number U/(gh w)1/2 is used to define the onset of both gravitational and hydrodynamic instabilities, as described by Ghidaoui and Kolyshkin (1999). The corresponding values of Froude number based on the depth-averaged inflow velocity and water depth are Fr = U/(gh w)1/2 = 0.39 for the uncoupled state and 0.71 for the coupled state. In order to investigate the flow structure as a function of depth, elevations above the bed of z L /h w = 0.033, 0.067, 0.167, 0.333, 0.500, 0.667 and 0.833 were considered. The values of Reynolds number, based on the width W of the inflow channel, for values of U/f n L = 0.78 and 1.44, were, respectively, Re w = 110,431 and Re w = 202,613; based on water depth h w, \(Re_{{h_{\text{w}} }}\) = 8,956 and \(Re_{{h_{\text{w}} }}\) = 16,432.

The stability parameter S was computed using the standard definition \(S = \bar{c}_{\text{f}} \delta \bar{U}/2h_{\text{w}} \Updelta U.\) Velocity field data obtained from digital particle image velocimetry were used to determine the shear layer thickness δ, and \(\bar{c}_{\text{f}}\) was determined using the correlation \(\frac{1}{{\bar{c}_{\text{f}}^{.5} }} = - 4\log \left( {\frac{1.25}{{Re*\bar{c}_{\text{f}}^{5} }}} \right)\), also employed by Chu and Babarutsi (1988). The values of stability parameter S determined herein, S = 0.002 for the non-coupled state and S = 0.003 for the coupled state, are of the same order as those determined in the investigations of Chu and Babarutsi (1988), and Kolyshkin and Ghidaoui (2002). Kolyshkin and Ghidaoui (2002) address both shear and gravitational instabilities in shallow water flows in compound channels. Even though the present configuration is a constant depth channel, it is desirable to consider limiting values for onset of an instability. Bed friction does not stabilize the flow below values of the stability parameter S cr of the order S cr = 0.01–0.1 (Kolyshkin and Ghidaoui 2002). That is, below these critical values of S cr, instabilities occur due to the destabilizing effect of the velocity difference ΔU across the shear layer; in the present study, the values of the stability parameter are S = 0.002 and S = 0.003. Kolyshkin and Ghidaoui (2002) also provide insight into the effects of channel width on the stability of the shallow flows. Using the terminology herein, the dimensionless channel width is defined as W d = W e /h w, where h w is the water depth and W e is the width of the channel. In present study, the dimensionless width of the channel is W d = 12.3. By considering the wavenumber of the instability k = 0.4 and comparing with computations of Kolyshkin and Ghidaoui (2002, Fig. 5), the growth rate of the instability does not vary significantly for values of the dimensionless channel width W = 10 to ∞. One can therefore conclude that an increase in channel width in the present experiment would not affect the instability of the flow.

The frequency and amplitude of both shear layer and gravity standing wave oscillations were determined with PCB piezoelectric pressure transducers (model number 106B50). The pressure transducers were located at the impingement corner of the cavity (p a ) and within the cavity (p b ) at a location 229 mm from the impingement corner. Both transducers p a and p b are located at an elevation of h p = 13 mm from the bed (bottom surface). Transducer p b was employed as a phase reference for phase-averaging of images. This series of transducers has a nominal sensitivity of 72.5 mV/kPa. They were connected to a PCB Piezotronics signal conditioner (model number 480E09). The conditioned pressure signals were transmitted to ports on a National Instrument Data Acquisition Board (model PCI-MIO-16E-4). A low-pass digital filter was employed during signal processing; it had a cutoff frequency of 5 Hz. The pressure signal is sampled with 20 Hz which was well above the Nyquist frequency. Sampling was conducted over a time span of 102.4 s, corresponding to a total of 2,048 samples. Ten of these time records were acquired for each inflow velocity and then transformed into the frequency domain and averaged.

The flow patterns of the non-coupled and fully coupled oscillations were characterized with high-image-density digital particle image velocimetry (DPIV). The main components of this system are indicated in Figs. 1 and 2. The double-pulsed Nd:YAG laser, which illuminated the tracer particles with an approximately 1-mm-thick horizontal sheet of laser light, had a maximum energy output of 90 mJ/pulse; the repetition rate was 15 Hz. In order to avoid a large number of spurious vectors and to allow optimal evaluation of the particle image patterns, the time delay between the two pulses of the laser was varied from 2.5 to 3.5 ms depending on the inflow velocity. The elevation of the laser sheet z L above the bed (bottom surface), relative to the water depth h w, had values of z L /h w = 0.033, 0.067, 0.167, 0.333, 0.500, 0.667 and 0.833. The flow was seeded with metallic coated, hollow, plastic spheres having a diameter of 12 μm. The patterns of these illuminated particles were recorded with a charge-coupled device (CCD) sensor camera, which had an array of 1,600 × 1,192 pixels providing a magnification of 4.2 pixel/mm. The camera was placed below the water channel orthogonal to the horizontal plane. The aforementioned double-pulsed laser and camera were triggered by a synchronizer. The camera operated at a maximum of 30 frames per second, which gives 15 sets of image pairs per second. The patterns of images were evaluated using a Hart correlation technique with a 32 pixel × 32 pixel interrogation window and an effective overlap of 50 % in both directions in order to satisfy Nyquist criteria. This technique resulted in 7,227 vectors with an effective grid size of 3.7 mm.

For each set of PIV experiments, 200 sets of images were recorded simultaneously with the pressure signal. For each water depth, 20 sets of experiments were conducted, corresponding to 4,000 sets of images were recorded. The time-averaged flow structure and turbulence quantities were evaluated using 2,000 instantaneous velocity fields. Phase-averaging of the flow structure was also done for the fully coupled state corresponding to a reduced velocity of U/f n L = 1.44. In order to define the phase information for each velocity field, a laser trigger signal was recorded simultaneously with the digitally filtered pressure signal from the transducer p b located inside the cavity. Images were recorded at different phases of the gravity wave oscillation, and the information from the trigger signal was used to determine the phase of the each image. The phase window size for this determination was ten degrees, where the complete cycle corresponded to 360°. This method led to a minimum of 90 velocity fields per phase window which were selected from the pool of 4,000 velocity fields. These 90 velocity fields were used to evaluate the phase-averaged flow structure and turbulence specifications.

3 Identification of coupling and lock-on

In contrast to the onset of instabilities in isolated, shallow separated layers such as jets, mixing layers and wakes, the present configuration of shallow flow past a cavity can give rise to coupling between a gravity wave mode of the cavity and the inherent instability of the separated shear layer along the cavity. This coupling can lead to not only resonant response of the system, but also to lock-on of the overall oscillation frequency to the eigenfrequency of the gravity wave standing mode, that is, f/f n  = 1. This type of coupling and locked-on response has direct analogies with the cases of airflow past a deep cavity, whereby an acoustic mode of the cavity is excited, and flow past an elastically mounted cylinder, where a structural mode of the cylinder is excited (Naudascher and Rockwell 1994). If one denotes the natural frequency of a mode as f n , then the reduced velocity is typically represented in the form U/f n L, where U is the inflow velocity and L is the characteristic dimension of the deep cavity or the cylinder (L = D). In accord with this terminology, the same form of the reduced velocity will be employed herein.

The pressure response of the cavity was assessed for different flow velocities, in order to determine the level of coupling between the separated shear layer along the mouth of the cavity and the gravity standing wave within the cavity. Pressure measurements were made at the locations indicated in Fig. 2. The transducer at the impingement corner (p a ) indicates the combined influence of the unsteady shear layer along the cavity opening and the gravity standing wave, while the transducer inside the cavity (p b ) senses only the contribution from the gravity standing wave within the cavity.

The pressure fluctuation p b (t) in the cavity and the corresponding spectra are given in the upper part of Fig. 3, i.e., Fig. 3a. The difference between the non-coupled case U/f n L = 0.78 (dashed line) and the coupled case U/f n L = 1.44 (solid line) is seen clearly. In the coupled case, the signal is well defined and periodic, which is represented by a sharp peak in the spectrum. On the other hand, the spectral peak for the non-coupled case is barely detectable.

Fig. 3
figure 3

a Pressure fluctuation at two dimensionless velocities U/f n L = 0.78 (blue) and U/f n L = 1.44 (red) that represent, respectively, cases without and with a gravity standing wave. b Corresponding amplitude of spectral peak S p(f)max /(1/2ρU 2) and frequency f n of peak response

Full size image

In Fig. 3b (left plot), the magnitudes of the spectral peaks, designated as S p(f)max /(1/2ρU 2), are plotted against dimensionless inflow velocity U/f n L for the pressures p a and p b . It is clear that the magnitude of the peak is consistently higher for pressure p a at the corner of the cavity, due to the impingement of unsteady shear layer (Tang and Rockwell 1983). The magnitudes S p(f)max /(1/2ρU 2) of the spectral peaks of p a and p b rapidly increase with increasing U/f n L and reach a maximum at U/f n L = 1.44. Then, drastic decreases occur with increasing U/f n L.

In Fig. 3b (right plot), both the dimensionless frequency f/f n and the magnitude of the spectral peak S p(f)max /(1/2ρU 2) are plotted against dimensionless inflow velocity U/f n L for the pressure fluctuation p b within the cavity. The symbol f denotes the spectral peak S p(f)max /(1/2ρU 2) of the oscillation at a given value of dimensionless inflow velocity U/f n L. At low inflow velocities, f/f n increases quasi-linearly with the increasing U/f n L. Moreover, the magnitude of S p(f)max /(1/2ρU 2) is lower at low U/f n L due to the lack of sufficient coupling with the gravity wave mode of the cavity. At U/f n L = 1.1, onset of lock-on occurs represented by the line f/f n  = 1.0 and the magnitude of S p(f)max /(1/2ρU 2) starts to increase rapidly. For further details of this coupling phenomenon, the reader is referred to the investigation of Wolfinger et al. (2012).

4 Quantitative flow structure

4.1 Time-averaged flow patterns

Figure 4 shows patterns of time-averaged contours of constant velocity magnitude \(\left\langle { V} \right\rangle /U\). The images in the left column (U/f n L = 0.78) represent the case where a gravity standing wave does not occur within the cavity and the images in the right column (U/f n L = 1.44) correspond to existence of a gravity standing wave.

Fig. 4
figure 4

Contours of time-averaged velocity magnitude \(\left\langle { V} \right\rangle /U\) at two different elevations: well above the bed (z L /h w = 0.667); and near the bed (z L /h w = 0.067). Dimensionless velocities U/f n L = 0.78 (left column) and U/f n L = 1.44 (right column) correspond, respectively, to cases without and with a gravity standing wave

Full size image

Comparison of the contours of constant velocity magnitude \(\left\langle { V} \right\rangle /U\) in the right column with the corresponding contours in the left column shows the effect of coupling between the unstable shear layer along the opening of the cavity and the gravity wave mode within the cavity. At both elevations z L /h w = 0.067 and 0.667 from the bed (bottom surface), existence of the gravity standing wave is associated with an increase in the velocity magnitude \(\left\langle { V} \right\rangle /U\) within the cavity. As defined by the color bar at the bottom of the image layout, light blue and light green colors represent larger magnitudes relative to the dark blue color, which corresponds to a very low magnitude of \(\left\langle { V} \right\rangle /U\).

Figure 5 shows patterns of time-averaged streamlines \(\left\langle { \psi } \right\rangle\). Images in the left and right columns represent, respectively, cases without and with a gravity standing wave within the cavity. The successive rows of images, from top to bottom, correspond to elevations closer to the bed (bottom surface). The first two rows of images correspond to elevations well above the bed, i.e., five-sixths (z L /h w = 0.833) and two-thirds (z L /h w = 0.667) of the depth h w of the shallow water layer. At these elevations, the recirculation pattern within the cavity does not show any unusual features and, furthermore, the separation line from the leading edge of the cavity to the trailing edge is nearly straight, with very little deflection.

Fig. 5
figure 5

Patterns of time-averaged streamlines \(\left\langle { \psi } \right\rangle\) at different elevations above the bed (z L /h w = 0.033–0.833). Dimensionless velocities U/f n L = 0.78 (left column) and U/f n L = 1.44 (right column) correspond, respectively, to cases without and with a gravity standing wave

Full size image

At an elevation closer to the bed, corresponding to z L /h w = 0.167, the separation line from the leading corner of the cavity is deflected inward (downward) in the vicinity of the trailing corner. Along the trailing (downstream) wall of the cavity, an alleyway of streamlines occurs, corresponding to a layer of downward-oriented, jet like flow. Moreover, along the leading (upstream) wall of the cavity, a small-scale separation bubble forms.

The appearance of three-dimensional vortex systems in the presence of groynes in river flows has been computed by McCoy et al. (2007). They showed that a horseshoe-like vortex can be present at the base of a groyne. In the present experiment, a three-dimensional vortical structure may exist at the base of the trailing corner of the cavity; it could distort the sectional streamline pattern in that region.

Finally, in Fig. 5, at the two elevations z L /h w = 0.067 and 0.033 closest to the bottom surface (bed) of the cavity, the scale of the separation bubble adjacent to the leading (upstream) wall of the cavity is generally larger. Moreover, the streamlines along the opening of the cavity diverge substantially with increasing streamwise distance as they are deflected toward the interior of the cavity. The inward-directed, jet like flow along the trailing (downstream) wall of the cavity is pronounced. These features can be defined with topological concepts involving critical points of the flow, which are most evident at z L /h w = 0.033 (right image, with gravity standing wave). A focus F occurs near the leading (upstream) corner of the cavity; it is the center of a swirl pattern of the streamlines. A bifurcation line BL+ corresponds to very rapid divergence of the streamlines with increasing streamwise distance along the opening of the cavity; this divergence starts near the leading corner of the cavity where the streamlines are very closely spaced. Another type of bifurcation line BL− occurs near the trailing (downstream) wall of the cavity. That is, convergence of streamlines occurs along this line. Finally, a saddle point S p occurs just upstream of the trailing (downstream) corner of the cavity; it represents the upstream migration of the wall stagnation point that is evident at larger values of elevation z L /h w = 0.833, 0.667 and 0.167 of the laser sheet. Moreover, the bifurcation line BL− adjacent to the trailing (impingement) wall of the cavity is also present at z L /h w = 0.167. These critical points and unusual features are generally present in all of the streamline patterns close to the bed, that is, at 0.067 and 0.033, though certain of them are not detectable at elevations close to the free surface, that is, at 0.833 and 0.667. It is hypothesized that these unusual features close to the bottom surface (bed) are due to three-dimensional effects.

It is therefore evident that the region of flow close to the bed (bottom surface) is associated with the onset of a number of critical points, which distinguish the flow patterns from those occurring at higher elevations above the bed. In addition, a generic feature of the flow patterns close to the bed is the inward deflection of the streamlines toward the cavity, more specifically, toward the center of the overall pattern of curved streamlines. This streamline deflection, toward the origin of the radius of curvature, has been observed in quite different applications, for example, along the end wall of a turbomachine (Lakshminarayana 1996). The concept of streamline deflection is illustrated in the schematic of Fig. 6. Consider flow along the two streamlines designated as 1 and 2 in Fig. 6. The flow is assumed to be inviscid, and in the region indicated, equilibrium exists between the centrifugal and pressure forces. The pressure gradients in the normal n direction at 1 and 2 are:

$$\left.\left. {\frac{\partial p}{\partial n}} \right|_{1} = \rho \frac{{V_{1}^{2} }}{{R_{1} }}\quad\quad {\frac{\partial p}{\partial n}}\right|_{2} = \rho\frac{{V_{1}^{2} }}{{R_{2} }}$$
(2)

Assuming that the static pressure does not vary across the boundary layer:

$$\left.{\frac{\partial p}{\partial n}} \right|_{1}= \left. {\frac{\partial p}{\partial n}}\right|_{2}$$
(3)

The flow velocity decreases as the wall is approached, that is, V 2 is less than V 1. To satisfy the foregoing conditions, the radius of curvature must decrease, that is R 2 becomes smaller than R 1. So the streamline near the bed is deflected from 2 to 2′, and a corresponding radial flow occurs in the boundary layer. An equivalent explanation of the streamline deflection toward the origin of the radius of curvature is given by Einstein (1926); he explains the meandering of a river using a tea cup analogy. The centrifugal force, which varies as the square of the velocity, is smaller close to the bottom surface (bed) due to friction effects; this decreased force gives rise to an inward-oriented flow. The foregoing concepts are therefore the basis for the inward deflection of the streamlines in the region close to the bed in Fig. 5.

Fig. 6
figure 6

Illustration of the concept of radial (secondary) flow due to streamline curvature. Streamline (1) is located at the edge of the boundary layer. Due to the radial pressure gradient, streamline (2) within boundary layer is deflected to position (2′), giving rise to radial flow toward the center of curvature (after Lakshminarayana 1996)

Full size image

Figure 7 provides time-averaged contours of constant transverse velocity \(\left\langle {\upsilon} \right\rangle /U\). As in previous layouts, the left column of images (U/f n L = 0.78) corresponds to absence of a gravity standing wave and right column (U/f n L = 1.44) represents the case where the gravity standing wave is present. Rows of images from top to bottom correspond to successive layers closer to the bed (bottom surface). Blue contours of \(\left\langle {\upsilon} \right\rangle /U\) indicate flow in the outward direction (positive y direction) away from the cavity and red contours in the inward direction (negative y direction) toward the interior of the cavity.

Fig. 7
figure 7

Contours of time-averaged transverse velocity \(\left\langle {\upsilon} \right\rangle /U\) at different elevations z L /h w above the bed (bottom surface). Dimensionless velocities U/f n L = 0.78 (left column) and U/f n L = 1.44 (right column) correspond, respectively, to cases without and with a gravity standing wave. Red contour levels represent flow toward the interior of the cavity and blue contours represent the flow toward the exterior of the cavity

Full size image

The first general observation is that the magnitudes of the transverse velocity \(\left\langle {\upsilon} \right\rangle /U\) are larger in the right column of images (U/f n L = 1.44), corresponding to the case with the gravity standing wave. That is, the magnitudes of both the positive (blue) and negative (red) regions are larger than those in the left column of images (U/f n L = 0.78) where the gravity standing wave does not occur. It is interesting to note that in the region near the bed, corresponding to elevations of z L /h w = 0.067 and 0.033, relatively high velocity (dark red color) flow into the cavity occurs along the trailing (impingement) wall. Furthermore, high velocity (darker blue color) flow occurs out of the cavity toward the cavity opening. One can therefore conclude that coupling between the separated shear layer at the mouth of the cavity and the mode of the gravity standing wave within the cavity, which is associated with existence of the gravity standing wave, induces a global influence throughout the interior of the cavity, that is, enhanced recirculation flow, indicated by the higher levels of red and blue contours within the cavity.

In Fig. 7, within the left column of images (U/f n L = 0.78) corresponding to the case of no gravity standing wave, specifically the region near the bed, at elevations z L /h w = 0.067 and 0.033, the extended blue contours along the upper edge of the cavity indicate significant outward deflection (upward oriented arrow) of the flow in that region. On the other hand, in the corresponding images in the right column, where the gravity standing wave exists, these extended blue regions are eliminated in favor of pronounced downward flow directed toward the interior of the cavity along the entire length of the cavity opening. A common feature of these regions close to the bed, i.e., at z L /h w = 0.067 and 0.033, is a high concentration of outward-oriented (blue) flow at the trailing corner of the cavity. This concentration is associated with the saddle point of the streamline pattern shown in the image at the lower right of Fig. 5; it occurs in conjunction with a region of localized flow separation at the trailing corner.

Figure 8 gives time-averaged contours of constant vorticity \(\left\langle { \omega } \right\rangle L/U\). At elevations above the bed region, the highest levels of vorticity are attenuated more rapidly along the cavity opening when the gravity standing wave is present (right column) in comparison with absence of the gravity standing wave (left column). This comparison is made for a given green level of vorticity (\(\left\langle { \omega } \right\rangle L/U\) = −6) at the elevation z L /h w = 0.667. The length of the line indicated with an arrow is shorter in the right image than in the left image. As will be shown subsequently, this more rapid degradation of high-level vorticity in streamwise direction is associated with occurrence of larger turbulent shear and normal stresses in the separated shear layer along the cavity opening. A further trend is enhanced deflection of a region of vorticity toward the interior of the cavity, which occurs at the trailing (impingement)-corner. That is, especially at elevations close to the bed, z L /h w = 0.067 and 0.033, the layer of vorticity extending into the cavity has a relatively large width, and the extent of this region is enhanced in presence of the gravity standing wave. Comparison of the images of \(\left\langle { \omega } \right\rangle L/U\) in the right column with those in the left column shows that this inward deflection of the vorticity layer is compatible with the streamline patterns of Fig. 5, and the patterns of transverse velocity of Fig. 7, especially in the vicinity of the trailing corner of the cavity.

Fig. 8
figure 8

Contours of time-averaged vorticity \(\left\langle { \omega } \right\rangle L/U\) at different elevations z L /h w above the bed (bottom surface). Dimensionless velocities U/f n L = 0.78 (left column) and U/f n L = 1.44 (right column) correspond, respectively, to cases without and with a gravity standing wave

Full size image

Figures 9 and 10 show contours of constant root-mean-square streamwise u rms and transverse v rms velocity fluctuations. The influence of the coupled oscillation involving a gravity standing wave (right column of images, U/f n L = 1.44) is evident at all values of elevation above the bed, extending from z L /h w = 0.067 to 0.500. Magnitudes of both u rms /U and v rms /U are substantially higher at all elevations above the bed (bottom surface), and extend over a larger width in presence of the gravity standing wave.

Fig. 9
figure 9

Patterns of root-mean-square streamwise velocity fluctuation u rms /U at different elevations z L /h w above the bed (bottom surface). Dimensionless velocities U/f n L = 0.78 (left column) and U/f n L = 1.44 (right column) correspond, respectively, to cases without and with a gravity standing wave

Full size image
Fig. 10
figure 10

Patterns of root-mean-square transverse velocity fluctuation v rms /U at different elevations z L /h w above the bed (bottom surface). Dimensionless velocities U/f n L = 0.78 (left column) and U/f n L = 1.44 (right column) correspond, respectively, to cases without and with a gravity standing wave

Full size image

Figure 9 shows that large-scale, high-level clusters of u rms /U occur in the immediate vicinity of the trailing corner of the cavity as the bed is approached (z L /h w = 0.067 and 0.033). These clusters are associated with the onset of the saddle point in the vicinity of the trailing (impingement) corner, in the streamline patterns of Fig. 5. The patterns of v rms /U given in Fig. 10 show high levels of v rms /U at the trailing corner of the cavity at all elevations. In the region closest to the bed (z L /h w = 0.067), two peaks of v rms /U are evident, thereby indicating large transverse undulations at the location of the saddle point indicated in Fig. 5.

Corresponding patterns of Reynolds stress \(\left\langle { u^{\prime } \upsilon^{\prime } } \right\rangle /U^{2}\) are given in Fig. 11. In essence, the Reynolds stress represents the degree of correlation between the streamwise u′ and transverse v′ velocity fluctuations. This correlation is clearly high when the gravity standing wave exists, as shown in the top two figures in the right column of images, corresponding to elevations z L /h w = 0.500 and 0.333. As the bed region (z L /h w = 0.167 and 0.067) is approached, however, the peak value of Reynolds stress is significantly attenuated. Enhanced Reynolds stress increases the entrainment demand of the separated shear layer along the cavity. It is therefore anticipated that the mass exchange between the cavity and the free stream will be higher for the case where the standing wave occurs (right column of images, U/f n L = 1.44). Note that the magnitude of the Reynolds stress decreases as the bed is approached (z L /h w = 0.167 and 0.067). This observation suggests that the mass exchange will decrease as the bed region is approached. Detailed calculations and interpretation of mass exchange as a function of depth are addressed subsequently.

Fig. 11
figure 11

Patterns of Reynolds stress \(\left\langle { u^{\prime } \upsilon^{\prime } } \right\rangle /U^{ 2}\) at different elevations z L /h w above the bed (bottom surface). Dimensionless velocities U/f n L = 0.78 (left column) and U/f n L = 1.44 (right column) correspond, respectively, to cases without and with a gravity standing wave

Full size image

4.2 Phase-averaged flow patterns

In order to understand the effect of coupling between the separated shear layer along the mouth of the cavity and the gravity standing wave within the cavity, phase-averaging of the velocity fields (at U/f n L = 1.44) was conducted, using the pressure fluctuation within the cavity as a reference signal. Different interpretations of the flow structure were then constructed using the phase-averaged velocity fields.

Figure 12 shows patterns of phase-averaged streamlines \(\left\langle { \psi } \right\rangle_{\text{p}}\) and contours of constant velocity magnitude \(\left\langle { V} \right\rangle_{\text{p}} /U\) for three different phases (ϕ = 80°, 200°, 320°) of the oscillation cycle. The left column of images represents the region well above the bed (z L /h w = 0.667), and the right column of images corresponds to the region near the bed (z L /h w = 0.067).

Fig. 12
figure 12

Phase-averaged patterns of streamlines \(\left\langle { \psi } \right\rangle_{\text{p}}\) and contours of velocity magnitude \(\left\langle { V} \right\rangle_{\text{p}} /U\) at two different elevations: well above the bed (z L /h w = 0.667) and near the bed (z L /h w = 0.067) in presence of a gravity standing wave (U/f n L = 1.44)

Full size image

For both the regions well above the bed (z L /h w = 0.667) and at the bed (z L /h w = 0.067), flapping motion of the shear layer along the cavity mouth is evident. At z L /h w = 0.667, the recirculation pattern within the cavity does not show any abnormalities and deflection of the separation line along the cavity opening is apparent. At z L /h w = 0.067, the formation of the separation bubble along the leading (upstream) wall of the cavity is clearly evident. Furthermore, the downward-directed, jet like flow patterns along the trailing (impingement) wall of the cavity are related to formation of a saddle point, as designated in Fig. 5.

The bottom half of Fig. 12 shows contours of constant velocity magnitude \(\left\langle { V} \right\rangle_{\text{p}} /U\). In accord with the aforementioned patterns of the time-averaged velocity magnitude \(\left\langle { V} \right\rangle /U\) given in Fig. 4, the magnitudes of \(\left\langle { V} \right\rangle_{\text{p}} /U\) at the trailing (impingement) edge of the cavity are higher in the bed region (z L /h w = 0.067, right column of images), relative to the region well above the bed (z L /h w = 0.667, left column of images). Furthermore, it is evident that the interface along the cavity opening exhibits undulations at both elevations z L /h w = 0.667 and 0.067.

Figure 13 shows phase-averaged contours of constant vorticity \(\left\langle { \omega } \right\rangle_{\text{p}} L/U\) and transverse velocity \(\left\langle { \upsilon} \right\rangle_{\text{p}} /U\) for three different phases (ϕ = 80°, 200°, 320°) of the oscillation cycle. The left column of images represents the region well above the bed (z L /h w = 0.667), and the right column of images corresponds to the region near the bed (z L /h w = 0.067). At both z L /h w = 0.667 and z L /h w = 0.067, the patterns of \(\left\langle { \omega } \right\rangle_{\text{p}} L/U\) show the onset and development of a large-scale vortical structure. It moves in the downstream direction with increasing phase angle ϕ. At z L /h w = 0.667, the patterns of vorticity are highly ordered and do not show significant irregularities. On the other hand, at z L /h w = 0.067, notable distortions or irregularities occur; they are due to the decreased coherence of vortex formation along the bed region. Moreover, the cluster of vorticity that is along the trailing (impingement) wall of the cavity at z L /h w = 0.067 persists over all values of phase angle. On the other hand, this cluster of vorticity does not exist along the trailing (impingement) wall of the cavity at z L /h w = 0.667. These observations are in accord with the patterns of the time-averaged streamlines of Fig. 5.

Fig. 13
figure 13

Contours of phase-averaged vorticity \(\left\langle { \omega} \right\rangle_{\text{p}} L/U\) and transverse velocity \(\left\langle { \upsilon} \right\rangle_{\text{p}} /U\) at two different elevations: well above the bed (z L /h w = 0.667) and near the bed (z L /h w = 0.067) in presence of a gravity standing wave (U/f n L = 1.44). Red contour levels represent flow toward the interior of the cavity, and blue contours represent the flow toward the exterior of the cavity

Full size image

The bottom half of Fig. 13 shows contours of constant phase-averaged transverse velocity \(\left\langle { \upsilon} \right\rangle_{\text{p}} /U\). The red color indicates the direction of transverse velocity oriented in the negative vertical direction, that is, into the cavity, whereas blue color indicates an orientation in the positive vertical direction, that is, out of the cavity. In accord with the aforementioned patterns of the time-averaged vorticity (Fig. 8) and transverse velocity (Fig. 7), as well as patterns of phase-averaged vorticity (Fig. 13), the magnitudes of the inward-directed (red) transverse velocity at the trailing edge and outward (blue)-oriented velocity at the leading edge of the cavity are higher in the bed region at z L /h w = 0.067 (right column of images), relative to the region well above the bed z L /h w = 0.667 (left column of images).

Consider, in Fig. 13, the concentrations of \(\left\langle { \upsilon} \right\rangle_{\text{p}} /U\) along the opening of the cavity. They are labeled as a, b, and so on. In the left column of images, corresponding to the elevation z L /h w = 0.667 above the bed, the first image at ϕ = 80° shows concentrations a and b; these concentrations correspond to the vorticity \(\left\langle { \omega } \right\rangle_{\text{p}} L/U\) concentration at ϕ = 80°. At successively larger values of ϕ, these concentrations move downstream and the successor a 2 appears and increases in scale. In the right column of images, corresponding to the region of the bed z L /h w = 0.067, the arrangement of the concentrations of \(\left\langle { \upsilon} \right\rangle_{\text{p}} /U\) is more complex. A prominent feature is the occurrence of large-scale, high magnitude \(\left\langle { \upsilon} \right\rangle_{\text{p}} /U\) immediately above the trailing corner of the cavity, which is due to the predecessor of concentration b. It glides above the impingement corner, rather than impinging directly upon it. In addition, a large magnitude of \(\left\langle { \upsilon} \right\rangle_{\text{p}} /U\) occurs along the trailing (impingement) wall of the cavity; this region arises from deflection of concentration a down along the impingement wall.

4.3 Time-averaged exchange velocity patterns

A dimensionless exchange coefficient is employed, in accord with Weitbrecht et al. (2008), in order to characterize the mass exchange between the flow within and outside the cavity. Determination of this exchange coefficient requires, first of all, knowledge of the exchange velocity E. It is determined using the distribution of transverse velocity along the mouth of the cavity, which extends from the leading to the trailing corner of the cavity. At a given instant of time, fluid may either enter or leave the cavity, depending upon the streamwise distance along the cavity opening. The volume ∀ cav enclosed by the cavity boundary and a line between leading (upstream) corner and trailing (downstream) corner of the cavity is given as ∀ cav = LW. The time needed for complete flushing of the fluid from the cavity is:

$$T_{D} = \;\frac{{\forall_{w} }}{Q}\;$$
(4)

in which ∀ w is the volume of the exchanged water, Q = EL is the mass flux between the cavity and main stream, and E is the exchange velocity. During the complete flushing of fluid from the cavity, the volume of exchanged water ∀ w is twice the cavity volume ∀ cav. That is, during the time interval T D , a volume of water equal to twice the volume ∀ cav is transported across the interface between cavity and main stream. Then Eq. (1) leads to:

$$T_{D} = \;\frac{{\mathop {2{\kern 1pt} \forall }\nolimits_{\text{cav}} }}{Q}\; = \frac{{2{\kern 1pt} W}}{E}$$
(5)

The instantaneous exchange velocity E(t), spatially averaged over the cavity mouth, is given as:

$$E(t)\; = \;\frac{1}{L}\;\int\limits_{0}^{L} {\left| {\,\upsilon(t)\,} \right|\,{\text{d}}x}$$
(6)

where v(t) is the transverse (cross-stream) component of velocity. Time-averaged values \(\overline{E(t)}\) were obtained by averaging 2,000 instantaneous velocity distributions. The mass exchange coefficient k was then calculated by normalizing with the main stream velocity U and width of the cavity W to give:

$$k\; = \;\frac{{\overline{E(t)} }}{2U}\;$$
(7)

in which U is the velocity of the main stream.

Patterns of time-averaged exchange velocity \(\overline{E(t)}\) are given in Fig. 14. They were obtained by taking time averages over defined successive segments of length Δx/L = 0.1 along the opening of the cavity, then connecting the time-averaged values. The left graph shows the case of no gravity standing wave (U/f n L = 0.78), and the right graph shows the case where the gravity standing wave exists (U/f n L = 1.44). The coordinate z L /h w represents, as in preceding figures, the elevation above the bed (bottom surface), and the x/L axis shows the streamwise location along the opening of the cavity. The blue point represents the leading edge (x/L = 0) of the cavity, and red point shows the trailing edge (x/L = 1) of the cavity.

Fig. 14
figure 14

Patterns of time-averaged exchange velocity \(\overline{E(t)}\) at different elevations z L /h w above the bed (bottom surface). Dimensionless velocities U/f n L = 0.78 (left column) and U/f n L = 1.44 (right column) correspond, respectively, to cases without and with a gravity standing wave. Blue point shows the leading edge of the cavity (x/L = 0), and red point shows the trailing edge of the cavity (x/L = 1)

Full size image

It is evident that the overall magnitudes of the exchange velocity are higher for the case corresponding to the coupled oscillation associated with the gravity standing wave (U/f n L = 1.44). From Eq. (5), one can therefore deduce that the mass exchange coefficient k will be larger in presence of the gravity standing wave. Moreover, for this case, the largest values of the exchange velocity \(\overline{E(t)}\) occur at approximately z L /h w = 0.500, and the smallest values occur at z L /h w = 0.067, i.e., in the bed region. Furthermore, the largest magnitudes occur at a streamwise location of approximately x/L = 0.6.

Comparing with the patterns of time-averaged Reynolds stress \(\left\langle { u^{\prime } \upsilon^{\prime } } \right\rangle /U^{ 2}\) in Fig. 11, it is clear that regions of large Reynolds stress correspond to the largest values of exchange velocity \(\overline{E(t)}\). This correspondence between Reynolds stress \(\left\langle { u^{\prime } \upsilon^{\prime } } \right\rangle /U^{ 2}\) and exchange velocity \(\overline{E(t)}\) at z L /h w = 0.500 is illustrated in Fig. 15. The x/L axis is along the opening of the cavity, and the y/L axis is in the transverse (cross-stream) direction. The pattern of \(\left\langle { u^{\prime } \upsilon^{\prime } } \right\rangle /U^{ 2}\) is displayed along the bottom surface of this layout, and the profile of \(\overline{E(t)}\) is represented by the solid line. This line corresponds to the opening of the cavity (y/L = 0) at an elevation of z L /h w = 0.500. It is evident that \(\overline{E(t)}\) is largest where the \(\left\langle { u^{\prime } \upsilon^{\prime } } \right\rangle /U^{ 2}\) is large. A further point is that \(\overline{E(t)}\) increases in the vicinity of the trailing (impingement) corner (x/L = 1.0). This observation agrees with the study of Zhang (1995), which indicates that the fluid exchange from the cavity to the main flow occurs primarily near the trailing (impingement) corner of the cavity.

Fig. 15
figure 15

Pattern of time-averaged exchange velocity \(\overline{E(t)}\)and Reynolds stress \(\left\langle { u^{\prime } \upsilon^{\prime } } \right\rangle /U^{ 2}\) at the mouth of the cavity (y/L = 1) for the dimensionless velocity U/f n L = 1.44 corresponding to the case with gravity standing wave

Full size image

The images of Figs. 4, 5 and 7 do not provide a direct indication of the influence of potentially significant vertical velocity (v z ) within the cavity. Integration of the transverse velocity v component along the cavity opening was conducted to determine the difference between the mass flux into the cavity and out of the cavity at each of the elevations above the bed. The integration is normalized with cavity length L and free-stream velocity U at the corresponding depth z L /h w. It was found that the net mass flux\(\int {\upsilon{\kern 1pt} {\text{d}}x/LU}\) from the cavity opening at each elevation is not equal to the zero and has values between −0.007 and 0.005. This observation suggests the existence of vertical velocities v z . On the other hand, the values of the mass exchange \(\int {\left| \upsilon \right|{\kern 1pt} {\text{d}}x/LU}\) between the cavity and main stream are in the range of 0.065–0.083. The ratio of net mass flux \(\int { \upsilon {\kern 1pt} {\text{d}}x/LU}\) to the mass exchange \(\int {\left| \upsilon \right|{\kern 1pt} {\text{d}}x/LU}\) is 0.031, −0.080, 0.088, −0.084, 0.037 and 0.067 at each respective elevation above the bed z L /h w = 0.833, 0.667, 0.500, 0.333, 0.167 and 0.067. The presence of vertical velocities is suggested in the study of Jamieson and Gaskin (2007) where dye marker was ejected in the vertical (z-direction).

Profiles of the time-averaged exchange velocity \(\overline{E(t)}\) along the mouth of the cavity at different elevations z L /h w above the bed are given in the left plot of Fig. 16. The value of \(\overline{E(t)}\) at each elevation z L /h w is obtained by integrating the v along the opening (y = 0) of the cavity. The blue line represents the case where a gravity standing wave does not occur within the cavity (U/f n L = 0.78), and red line corresponds to existence of a gravity standing wave (U/f n L = 1.44). It is evident that magnitudes of \(\overline{E(t)}\) along the opening of the cavity are higher for the locked-on case (U/f n L = 1.44) at all elevations z L /h w. In accord with aforementioned patterns of \(\overline{E(t)}\) (Fig. 14), values of \(\overline{E(t)}\) in Fig. 16 decreases near the bed and become largest at z L /h w = 0.500. The mass exchange coefficient k was calculated from the information in the left plot of Fig. 16 by using Eq. (5), and is shown with respect to elevation z L /h w in the right plot of Fig. 16. Mass exchange coefficient values are 40 % higher in presence of the gravity standing wave (U/f n L = 1.44). One can therefore conclude that the mass exchange between the cavity and the main stream increases due to the coupling between the unstable shear layer along the mouth of the cavity and the gravity wave mode within the cavity. The range of the mass exchange coefficient k is from 0.026 to 0.042 for different elevations z L /h w. These values compare well with k ≈ 0.03 obtained by Weitbrecht et al. (2008).

Fig. 16
figure 16

Patterns of time-averaged exchange velocity \(\overline{E(t)}\) and mass exchange coefficient (k) at different elevations z L /h w above the bed (bottom surface). Dimensionless velocities U/f n L = 0.78 (left column) and U/f n L = 1.44 (right column) correspond, respectively, to cases without and with a gravity standing wave

Full size image

5 Concluding remarks

The aim of the present investigation is to characterize the flow structure and mass exchange due to shallow flow past a cavity, as a function of elevation above the bed (bottom surface). In addition, the effects of coupling between the unstable shear layer along the opening of the cavity and a gravity wave mode within the cavity are accounted for at successive elevations above the bed. The time- and phase-averaged flow patterns were determined via a technique of high-image-density particle image velocimetry in conjunction with pressure measurements. This approach revealed the relationship between the depthwise variations in the flow structure of the unsteady shear layer along the opening of the cavity and the recirculating flow within the cavity. The principal findings of this investigation are described in the following.

Effective coupling between the inherent instability of the separated shear layer along the opening of the cavity and the fundamental gravity standing wave mode within the cavity is a global phenomenon that persists for regions close to and well above the bed (bottom surface). Such coupling is associated with large-scale coherent vortical structures in the unstable shear layer and periodic oscillations of the free surface within the cavity. Phase-averaged patterns of vorticity show the timewise development of the undulating vorticity layer along the opening of the cavity in relation to elevation above the bed. Sufficiently far from the bed, the undulating layer evolves into a highly coherent vortex, which eventually impinges upon the corner of the cavity. Close to the bed, these overall patterns of vorticity are maintained and are synchronized with those above the bed, but the degree of coherence of the vortical structure is decreased. In addition, immediately adjacent to the bed, a layer of vorticity is ejected into the cavity along the impingement wall. Time-averaged patterns of vorticity also show this ejected layer and indicate that it becomes more extensive at elevations closer to the bed. Moreover, for all elevations above the bed, the consequence of the organized undulations of vorticity along the cavity opening is to attenuate the magnitude of time-averaged vorticity in the streamwise direction along the cavity opening.

Corresponding phase-averaged patterns of transverse velocity indicate a region of large magnitude velocity along the impingement wall of the cavity, corresponding to the aforementioned vorticity layer along the impingement wall. Moreover, along the cavity opening, the organized undulations of the separated vorticity layer are associated with corresponding concentrations of transverse velocity that are highly ordered at elevations well above the bed, and take on a more complex, but nevertheless ordered form, at elevations very close to the bed. Time-averaged patterns of transverse velocity indicate that, in presence of the gravity standing wave, and at elevations close to the bed, the flow along the cavity opening is oriented toward the interior of the cavity, over the entire streamwise extent of the cavity opening.

Patterns of both phase-averaged and time-averaged streamlines show common features, when interpreted within a framework of topological concepts using critical points. At locations well above the bed, the number of critical points is minimal, but as the bed region is approached, well-defined critical points occur in the form of a focus adjacent to the upstream (leading) wall of the cavity, a negative bifurcation line originating from the leading corner of the cavity, a saddle point immediately upstream of the trailing impingement corner of the cavity and a positive bifurcation line adjacent to the trailing impingement wall of the cavity. Moreover, the streamlines along the cavity opening, at elevations close to the bed, are deflected in a direction toward the interior of the cavity, and a physical explanation is provided in terms of secondary flow related to streamline curvature. A further, remarkable result is that the form of the time-averaged streamline pattern at a given elevation above the bed is relatively insensitive to the existence or non-existence of the gravity standing wave within the cavity.

Patterns of normal and shear turbulent Reynolds stresses are substantially enhanced in presence of the gravity standing wave. In the region close to the bed, however, the Reynolds shear stress is attenuated in the separated shear layer along the cavity opening, which is due to decreased correlation between the velocity fluctuation components in the streamwise and transverse directions.

Time-averaged exchange velocity and mass exchange coefficient, determined along the opening of the cavity, indicate substantial (40 %) enhancement in presence of the gravity standing wave. This observation is in accord with the enhanced Reynolds stresses in the separated shear layer along the opening of the cavity.