1 Introduction

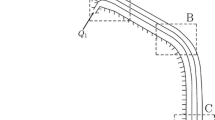
Driving a car under heavy rain can be hazardous as water droplets or films are deposited on windshields or side windows and restrict the driver visibility. Understanding the flow of such films would thus contribute to improve safety. Beyond the specific problem of windshields, film flows are ubiquitous in chemical engineering processes where complex heat transfer and physical or chemical reactions may also interfere. Although practical application may also involve counter-current flows or wetting issues, we focus here on the simplified configuration of a water film flowing under the action of gravity over an inclined plane (Fig. 1), with the aim of extracting elementary physical phenomena.

Fig. 1
figure 1

Experimental setup: (1) liquid film; (2) glass plate; (3) electroluminescent sheet; (4) injection device; (5) high-speed camera; (6) setup seen from above; (7) gear pump

Full size image

In the case of a laminar flow, the classical balance between the viscous shear stress and gravity dictates the thickness of the film as demonstrated by Nusselt (1916):

$$h_{Nu} = \left(\frac{3\nu^2}{{\rm g}\,\hbox{sin}\,\alpha}\right)^{1/3}Re^{1/3}\quad\quad\hbox{with}\quad Re=\frac{q_o}{l_p \nu},$$
(1)

where q o is the flow rate, l p the width of the plate, ν the kinematic viscosity of the liquid, g the gravity constant and α the inclination of the plate. However, such films are not always stable and surface waves may appear as the flow rate is increased. The linear stability analysis from Benjamin (1957) and Yih (1963) in the limit of long wavelengths (for which capillary effects become negligible) leads to a critical number depending on the inclination:

$$Re_{L,C}=\frac{5}{6}\hbox{cot}\,\alpha. $$
(2)

This criterion implies that a vertical configuration of the flow is always unstable. However, the wavelength of the most unstable mode in a vertical film diverges as the film thickness decreases. Kapitza and Kapitza (1949) studied the stability of the film when a controlled perturbation is applied at the inlet. As a main result, the stability of the film is dictated by the non-dimensional Kapitza number:

$$Ka=\frac{\gamma}{\rho}\left(\frac{1}{{\rm g} \nu^4}\right)^{1/3}, $$
(3)

where γ is the surface tension and ρ the density of the liquid film. Note that Ka depends solely on material properties and Ka 3/4 can be interpreted as a Reynolds number based on a the capillary length \(l_c = \sqrt{\gamma/\rho {\rm g}}\) and the velocity reached for a free fall over l c . High values of Ka lead to unstable films, which is the case for water (Ka ≃ 3,300). Conversely, the surface instabilities developed in oil films are difficult to detect (Ka ≃ 2,000 for silicone oil 20 time more viscous than water). Anshus (1972) finally performed a stability analysis in the limit of large Reynolds numbers and predicted that the wave velocity depends on Re but not on α.

Numerous experimental works (Tailby and Portalski 1962; Portalski 1963; Portalski and Clegg 1972) describe the inception and the development of waves in cylindrical and rectangular vertical geometries. These works do not put in evidence any typical distance for the inception of waves. The studies of Chu and Dukler (1974) and Takahama and Kato (1980) focus on the laminar-turbulent transition at large Reynolds numbers. These experiments rely essentially on vertical falling liquid films and local measurements of the thickness. Karapantsios and Karabelas (1995) show that the film thickness is essentially independent of the streamwise position beyond a certain distance from the injection point, for high values of Re. A recent experimental work by Drosos et al. (2004) finally compares the wave velocities observed for a vertical film with theoretical solutions from the Orr-Sommerfeld equation resolved by Anshus (1972) in the limits of large Reynolds numbers and long wavelengths. Argyriadi et al. (2004) showed that low-frequency excitation leads to the destruction of regular wave trains and to the formation of nonlinear solitary waves. However, the effect of the inclination angle was not explored in all these studies.

In the current work, we focus on the streamwise development of the instability of the flowing film as a function of the inclination angle α and the Reynolds number Re. We first present the experimental setup and technique for measuring the film profile based on light absorption. The different observations are qualitatively described, and the average film thicknesses are quantitatively compared with the stable solution from Nusselt. We finally describe the formation of surface waves and study their velocity as a function of the experimental parameters.

2 Experimental setup

The experimental apparatus consists essentially in a glass plate of variable inclination α with a slot along the upper edge from where the liquid is ejected with a flow rate q o (Fig. 1). The length of the glass plate is l p   =  300 mm, and the channel is limited by a pair of parallel borders of 10 mm high and separated by a distance l p  = 60 mm. The inclination angle α can be adjusted between 0° and 30°. The liquid is injected through a slot which has been machined at the level of the glass surface. The aperture of the slot can be varied between 0 and 3 mm (this adjustment prevents the formation of bubbles that would perturb the film flow). The setup is placed inside a collecting tank, and the liquid is recirculated through a gear pump with flow rates ranging from 0.1 to 1 l.min−1 (which corresponds to Reynolds numbers ranging from 27 to 300). We used distilled water for the main set of experiments. However, additional experiments were performed with an aqueous solution of sodium dodecyl sulfate (SDS) at 1.7 g.l−1 in order to study the effect of surface tension in the liquid film dynamics.

An electroluminescent sheet is placed underneath the glass plate and provides a uniform light. The film flow is monitored with a high-speed camera Photron APX RS set with a resolution of 1024 × 1024 pixels at 500 fps and a gray scale resolution of 10 bit (210 levels). The gray scale resolution is a crucial parameter since it determines the resolution in the measurements of the thickness described in the following section.

3 Measuring the film profile

Different techniques for measuring film thicknesses are described in the literature. For instance, laser reflection is used by Evers and Jackson (1995) and Oliveira et al. (2006) to measure locally liquid thickness between 1 and 4 mm in an annular film flow configuration through acrylic fibers. White light interferometry technique (Nohyu 2005; Wang et al. 2005) also provides very accurate measurements but is limited to thicknesses on the order of the wavelengths of light (100–600 nm).

Fluorescence techniques have also been recently developed by Hidrovo and Hart (2000, 2001), Hidrovo et al. (2004). These techniques rely on a fluorescent dye and ultraviolet lighting for dye excitation. The signal-to-noise ratio is optimized by using a pair of fluorescent dyes with different re-emission wavelengths and measuring the ratio of the corresponding signals. However, this technique requires a complex optical system, which may limit its application. We propose here to use a simple and versatile application of light absorption to monitor the film profile.

In our experiments, the difference between the intensity I 0 of the light directly emitted by the electroluminescent sheet and the intensity I 1 of the transmitted light through the liquid film of thickness h is expected to follow Beer-Lambert’s law:

$$I_h=\left(I_0-I_1 \right)=I_0\left[ 1-\hbox{exp}({-C_a\beta h}) \right] $$
(4)

where C a is the dye concentration and β the attenuation coefficient of the dye (I h thus corresponds to the light partially absorbed by the dye). In order to provide a uniform incident light, we use an electroluminescent sheet and work in a dark environment, which promotes a better contrast. However, residual spatial variations of the light intensity due to the environment or to local defects of the sheet are removed from the signal as the ratio (I 0 − I 1)/I 0 is considered. The main precaution with this technique is thus to ensure that I 0 and I 1 are measured in the same lighting conditions.

We used methylene blue aqueous solutions with a concentration of 0.1 g.l−1. The absorption coefficient β is determined with a calibration carried out with a liquid wedge obtained by tilting the plate by a narrow angle (Fig. 2a). Due to surface tension effect, the profile of the wedge is not perfectly linear in the vicinity of the edges (Fig. 2b). This profile can, however, be estimated in parallel with a micrometric gauge. In order to limit the errors due to the gauge, the calibration is carried for thicknesses larger than 500 μm and then extrapolated to thinner films.

Fig. 2
figure 2

Calibration procedure: a A liquid wedge is obtained by slightly inclining the plate. b Light intensity topography through the wedge, c Fitting of the measured intensity by Beer-Lambert’s law; red points (‘cont’): light intensity measured along the wedge; blue points (‘disct’): discrete mechanical measurements of the film thickness; green solid curve (‘fit’): Exponential fit

Full size image

The optical settings of the camera provide a spacial resolution of 55 pixel for 1 mm, while the gray scale resolution (1,024 levels) allows a typical resolution for h on the order of 5 μm.

4 Experimental results

The observations are realized at inclination angles of 5°, 10°, 15°, 20° and 30°. The flow rate is decreased by steps of 0.1 l.min−1 from 1 l.min−1 until dewetting occurs. This limit depends on the inclination and on the wetting characteristics of the plate. Ensuring good wetting properties of the glass plate is crucial for this experiment since dewetting would produce dry holes or liquid arches in the liquid film described in Podgorski et al. (1999), Rio et al. (2004) and lead to different dynamics. Glass freshly removed from a concentrated acid solution is perfectly wetted by water. Nevertheless, we used a simple commercial anti-fogging treatment (from RainX TM), which also enhances the wetting of glass by water. In these conditions,, the liquid film dewets for q o  < 0.1 l.min−1 corresponding to Re < 27, for a typical inclination α = 30°.

The development of surface waves is observed in the whole flow range investigated (Fig. 3), in agreement with Benjamin’s prediction for the flow stability (Eq. 2). Indeed, the minimum Reynolds number within our experimental range of Re is higher than different critical Reynolds numbers corresponding to the selected inclination angles. As shown in Fig. 3, the wave amplitude can, however, be very small for slight inclinations of the plate (α = 5°) and would require a long distance to reach a visible amplitude. In the other limit, we observe that the amplitudes of the waves grow and their pattern becomes scattered as the Reynolds number or the inclination angle is increased (Fig. 3).

Fig. 3
figure 3

Development of interfacial waves and evolution of the instability with α and Re L (the flow is always unstable as Re > Re L,C ). The amplitude of the waves increases as Re and α increase

Full size image
Fig. 4
figure 4

Streamwise profiles of the liquid film thickness along the centerline for different Reynolds numbers for α = 15°: The amplitude of the waves and theirs scattering increase with Re and α

Full size image

According to the work of Portalski (1963), the film is expected to be steady and laminar for Re L  < Re L,C , pseudo-laminar within the range Re L,C  < Re < 100, transitional in the range 100 < Re < 300 and finally turbulent for Re > 300. Our flows should thus lie in the pseudo-laminar regime. Moreover, Drosos et al. (2004) have observed that instabilities become three-dimensional for vertical falling films and we expect to also observe such structures in our experiments in the case Re ≫ Re L,C .

Power spectral densities extracted from the film profile confirm our qualitative observations (Fig. 5). Except at moderate Reynolds numbers (around Re = 27) where the wavelength is well defined (λ = 23 mm), the wavelength distribution is rather broad. The distributions of the wavelength are centered around 50 mm, which corresponds to gravity waves. These observations are in qualitative agreement with the data from Drosos et al. (2004) obtained for vertical falling film in an equivalent range of Re.

Fig. 5
figure 5

Power spectral density of liquid film thickness in wavelength representation for different values Re and α = 15°

Full size image

We finally observe that adding surfactant to the solution tends to attenuate the waves as was also observed by Portalski (1963) with vertical films. This effect is counter-intuitive since the addition of surfactant to water decreases the surface tension of the solution (γ = 45 mN.m−1 for our aqueous solution of SDS) and would promote the destabilization of the smooth liquid film by waves of short wavelengths. The phenomenon, also observed by Benjamin, is usually interpreted as a consequence of the peculiar rheology of the surfactant layer, which results into visco-elastic stresses on deformed surfaces (Behroozi et al. 2007).

5 Quantitative analysis

We first present in this section a quantitative description of the average film thickness of the flowing films. As we note in the previous qualitative section, these films are not stable and develop wavy patterns. We focus in the second part of this section on propagation velocity of these waves.

5.1 Mean film thickness

In the case of a steady laminar flow, we expect the film thickness to follow Nusselt law (Eq. 1) obtained by balancing gravity and viscosity: \(h_{Nu} = \left({3\nu^2}/{{\rm g}\,\hbox{sin}\,\alpha}\right)^{1/3} Re^{1/3}\). Although we have observed that our flows are not steady, the study from Portalski (1964) shows that the velocity profile remains parabolic beyond the laminar and pseudo-laminar regimes, with an interfacial velocity of the liquid film approximately equal to 3/2 of the average velocity. This observation suggests that Nusselt’s ideal configuration may remain relevant above Re L,C . In the case of turbulent liquid films, Takahama and Kato (1980) propose a description of the thickness based on Nusselt relation corrected by an empirical prefactor.

In our experiments, the film thickness is measured along the middle of the channel between 100 and 300 mm from the inlet and averaged over 2,000 video frames. We represent in Fig. 6a the variation of the average thickness h avg with Re for different values of α. We added for comparison data from Drosos et al. (2004) obtained in a vertical configuration as well as one set of experiments which was carried out with a surfactant solution. As a general trend, the fluctuations of h avg (represented as error bars in the graph) are amplified as Re increases and tend to vanish when surfactant is added. The comparison of the measured data with the ideal steady laminar situation (h avg /h Nu ) is displayed in Fig. 6b. Within the range of our experimental parameters h avg is approximately proportional to h Nu for a given inclination angle. However, the prefactor is equal to 1.8 ± 0.2 in the range 5° < α < 30° and on the order of 0.5 for the vertical films from Drosos, as well as for our experiments with surfactant solutions. Our qualitative observations suggest that the average thickness could be strongly connected to the formation of waves. The particular situation of vertical films studied by Drosos et al. (2004) may also be singular since three-dimensional wave patterns have been reported. In the case of surfactant solutions, the difference in surface tension could obviously play a role in the thinning the film. However, the main effect is probably the attenuation of surface waves in connection with the rheological properties of the surfactant layer. We were nevertheless unable to provide a rational description of these effects.

Fig. 6
figure 6

Evolution h avg as a function of Re and the comparison of measured thickness with the Nusselt prediction for different inclination angles. The data corresponding to α = 90° were extracted from Drosos et al. (2004). Data with surfactant solutions are also included (α = 15°). Error bars represent the thickness fluctuations

Full size image

5.2 Space-time analysis

We focus now on the propagation of surface waves. Measuring the film profile over the whole channel, with a high temporal resolution allows a global analysis of the waves dynamics. Space-time diagrams where the film thickness along a line parallel to the flow is plotted as a function of time reveals the downstream propagation (Fig. 7). Indeed, the succession of ridges results in oblique lines which slope directly gives the phase velocity c of the waves with a accuracy estimated to 10 %. The results obtained for the lowest flow rate Re = 27 confirms our qualitative observation: The waves are very regular with a well-defined wavelength and propagation velocity. However, the space-time diagrams corresponding to higher flow rates are more surprising since they reveal a characteristic propagation velocity out of irregular wave patterns.

Fig. 7
figure 7

Space-time diagrams of liquid film thickness: each diagram shows the time evolution of the thickness profile along the centerline of the water film

Full size image

The wave velocities extracted from similar space-time diagrams are plotted in Fig. 8 as a function of Re for different inclination angles. Measurements from Drosos et al. (2004) have been added for comparison. As a general trend, c increases with Re and with α. Again the vertical configuration is found singular and provides wave velocities similar to those obtained with slopes of 10°. One series of experiments was finally carried out with surfactant at an inclination angle of 15°, which lead to wave velocities slightly lower than measured with pure water.

Fig. 8
figure 8

Evolution of wave speed c as a function of Re and \(\overline Re (\overline Re= Re/Re_{L,C})\) for different inclination angles. Additional data obtained by Drosos et al. (2004) on vertical films and a series of measurements realized with surfactant solutions (for α = 15°). Error bars represent the fluctuations of the velocity along the channel. a C versus Re. b C versus \(\overline{Re}\). Full line: fit following relation (7)

Full size image

The stability analysis presented by Anshus (1972) leads to analytical predictions for the wave velocity. In the limit of high Reynolds and Kapitza numbers, the velocity is expected to follow the scaling:

$${c}/{u_{Nu}} - 3/2\propto Re^{-2/3}_L Ka^{2/11}, $$
(5)

where \(u_{Nu}=\left({\nu {\rm g} \,\hbox{sin}\,\alpha}/{3} \right) ^{1/3} Re^{2/3}_{L}\) is the average velocity of the liquid in the unperturbed ideal solution from Nusselt. The measured wave velocities are found to be proportional to Re 2/3, which is consistent with Anshus’s prediction: The waves are basically convected by the liquid flow. Indeed, since the product Re −2/3 L Ka 2/11 is lower than 1 for all our experiments, the expected wave velocity is given by \(c\simeq3/2\left({\nu {\rm g}\,\hbox{sin}\,\alpha}/{3} \right) ^{1/3} Re^{2/3}_{L}\). We finally note that although the addition of surfactant decreases the surface tension of water by one half, the impact in the wave velocity remains negligible in agreement with Anshus prediction.

The additional data from Drosos correspond to a vertical configuration. Although these data are in agreement with Anshus formulation, the plot corresponding to α = 90° appears not correlated to the others. We interpret this peculiar behavior of vertical films as a consequence of the development of 3D instabilities.

The data at different inclinations angles α (α ≠ 90°) collapse into the same master curve when the Reynolds number is normalized by the critical Reynolds number that characterize instability:

$$\overline{Re}= Re/Re_{L,C}. $$
(6)

From waves dynamics point of view, the main parameter of liquid film in this configuration is the normalized Reynolds number \(\overline{Re}\) and the Anshus (1972) relation can be generalized and written as followed:

$$C=\left(\frac{9}{8} \nu {\rm g}\,\hbox{sin}\,\alpha\right)^{1/3}\overline Re^{2/3}_L $$
(7)

The Fig. 8b shows the superposition of data of different inclinations and liquids into the same master curve.

6 Conclusion

A simple visualization technique based on light absorption was successfully used to study the dynamics of liquid films flowing down an inclined plane. Besides its easiness of implementation, this non-intrusive method gives the thickness profile (over a wide range depending on the dye concentration) of the whole field of view in a single image. The combination with high-speed imaging thus provides a good space-time resolution. The main precaution is to ensure stable lighting conditions and a precise calibration step. Flickering light sources may, however, be used provided a non-absorbing reference is also present in the images.

The flow dynamics of the water films were studied in the range 25 < Re < 300 (intermediate Reynolds numbers) and 5° < α < 30°. The flow of water films flowing down an incline plane at intermediate Reynolds numbers is found unstable and presents wavy patterns, in agreement with Benjamin’s theoretical prediction \((Re_{L,C}=\frac{5}{6}\hbox{cot}\,\alpha )\). In parallel to the formation of waves, the average film thickness is fairly well described as in the ideal case of a steady laminar flow determined by Nusselt, but with a prefactor equal to 1.8 ± 0.2. The narrow range of Reynolds number of flow (Re L,C  < Re < 55) is characterized by the development of periodic and regular waves which start from the injection point. However, these waves become irregular as the Reynolds number is increased, which leads to a broad range of wavelengths. However, space-time diagrams of the thickness profiles reveal well-defined phase velocities of the waves, even for the highest values of Re. The waves dynamics are well described by the analytical predictions from Anshus, where Re is replaced by a normalized Reynolds number \(\left( \overline Re = Re/Re_{L,C} \right)\). The critical Reynolds number of wave inception Re L,C   introduced by Benjamin (1957) appears as a characteristic coefficient that controls the velocity of the waves. While the critical Reynolds number is defined (α ≠ 90°), waves are found two-dimensional and previous results are applicable. For vertical inclination, Re L,C is not defined and waves quickly become 3D. This behavior confirms the singularity of the falling film flow in the vertical configuration which was studied many times in the past.

Although we were not able to clearly elucidate the amplification of the average film thickness for wavy films, this work may contribute to a better understanding of the dynamics of a liquid film flowing down an incline. Open questions still remain to be solved. Indeed, vertical flows do not follow the same trends we observed for lower angles: films are thinner, waves move slower and present three-dimensional structures. It would be interesting to bridge the gap between low angles and vertical configurations. Qualitative experiments carried out with surfactant solutions also lead to counter-intuitive wave attenuation. This situation of practical importance still remains to be fully explored. Coming back to the safety issue encountered when driving a car under rain, wind-induced shear also plays an important role in the flow of water films. We will explore the impact of wind in a future work.