1 Introduction

In its simplest form, a precessing jet refers to an axisymmetric jet flow issuing through an axisymmetric nozzle into a chamber with a geometry that generates an instability in the flow such that the jet axis rotates (precesses) about the nozzle axis. This flow differs from a swirl flow, where the jet is rotating about its own axis. Instead, the axis of the jet is rotating about the axis of the chamber in a gyroscopic-like motion. The basic configuration investigated by Nathan (1988) and Nathan et al. (1998) consists of a round nozzle of diameter d exiting into a chamber with an inner diameter D and length L through an abrupt expansion (see Fig. 1). For appropriate expansion ratios (d/D) and chamber lengths (L/D), the flow may destabilize resulting in the precessing jet flow. Otherwise, the flow expands into the chamber in an axisymmetric manner. The optimal dimensions to generate this instability have been found to be L/D = 2.75 (Nathan et al. 1998), with precession occurring over the range 2 ≤ L/D ≤ 3.5 (Newbold 1997), for an expansion ratio of D/d = 5. This flow is bistable, intermittently and chaotically switching between this precessing jet (PJ) mode and an axial jet (AJ) mode, where the jet exiting the nozzle/chamber closely resembles an axisymmetric jet. To stabilize the PJ mode, Nathan et al. (1998) introduced a center body on the axis of the chamber at the chamber exit. This was accompanied with an exit lip which directed the flow across the nozzle exit at a large angle to affect the characteristics of the downstream jet flow field.

Fig. 1
figure 1

Sectioned view of the fluidic precessing nozzle

Full size image

The main interest in this type of nozzle has been from its use in industrial installations to control mixing (Nathan et al. 2006). The velocity field decays more rapidly than its axisymmetric counterpart (Wong et al. 2003) as the momentum source rotates azimuthally away from the bulk jet flow. High-scalar gradients are maintained (Newbold 1997) as turbulent mixing is slowed. When the flow field from this type of a nozzle is used as a gas burner, the slower mixing leads to heating of the fuel and soot formation which generates a highly luminous flame while maintaining a constant flame stand-off from the nozzle up to choked flow (Newbold et al. 2000). Large vortical puffs are generated that maintain a mixing\combusting field such that complete burnout is achieved (no soot) with low levels of NO x and CO generation (Newbold et al. 2000, 2002, Nathan et al. 2006). This flow instability has found applications in large industrial processes for the production of cement and lime where radiant heat transfer is required over convection (Manias and Nathan 1994, Nathan et al. 2006). Use of precessing jet nozzles has also shown improvement in flame stability, increased burner efficiency, and decreased pollutant emissions (Newbold 1997; Nathan 1988; Nathan et al. 2006). Such installations have shown 5–20% reductions in specific fuel consumption, 5–10% increases in kiln output, and 40–70% reductions in NO x emissions (Nathan et al. 2006).

The nozzle-chamber geometry and of the mechanics driving this flow phenomenon were described by Nathan (1988) and Nathan et al. (1998) with their qualitative flow visualization of the flow within the cavity. The jet that exits the nozzle into the chamber flow separates as it passes the sudden expansion and spreads as it entrains chamber fluid. The bulk jet asymmetrically reattaches to the chamber wall and surrounding fluid is drawn into the chamber from outside of the chamber, inducing a rotating pressure field. This causes the reattaching jet flow to rotate around the inside wall of the chamber and also induces the precession of the jet as it exits the chamber into the jet mixing field. A transverse pressure gradient enhanced by an exit lip causes the jet to deflect, achieving an initial deflection of ~50° from the chamber axis, and decreasing to ~30° within z/D = 0.4 (Wong et al. 2003), where z is the axial distance from the chamber exit. The exiting jet has been shown in cross-section to be kidney-bean in shape along a plane parallel to the chamber exit and be dominated by a pair of counter-rotating vortices (Wong et al. 2008).

The characteristics of the nozzle exit condition at the entrance to the chamber have been shown to effect the probability of developing the PJ mode (Wong et al. 2004), with a smooth contraction nozzle resulting in a lower probability than nozzles made from a long pipe or an orifice. This has been attributed to the symmetry of large-scale structures being shed at the nozzle exit plane which directly influence the stability of the downstream flow field within the chamber. The presence of a lip at the chamber exit greatly increases the dominance of the PJ mode, while the addition of a center body results in a near 100% precession probability provided that the Reynolds number is sufficiently high and it is mounted upstream from the lip (Wong et al. 2004). The inlet flow condition has also been shown to influence the precession frequency of the jet (Wong et al. 2008), with the orifice nozzle producing the highest precession frequency and the long pipe the lowest.

Other studies have investigated the mechanics of this flow and effects of nozzle geometry on the instability. Guo et al. (1999) carried out numerical simulations using a k-ɛ turbulence model of the downstream flow field of an axisymmetric jet issuing through expansion ratios 3.95 ≤ D/d ≤ 6, observing both precession and an oscillatory flapping motion. The relationship between precession frequency, chamber length, and Reynolds number were studied by Mi and Nathan (2004, 2006) with pressure measurements along the nozzle axis. They found an almost linear increase of precessing frequency with chamber length and jet velocity and that downstream mixing is strongly influenced by the Strouhal number of the flow. Wong et al. (2003) performed laser Doppler anemometry measurements within and beyond the precession chamber and observed the asymmetric deflection of the jet and its reattachment to the wall of the chamber. Their methodology, however, was unable to determine entrainment of surrounding fluid back into the chamber (entrainment-into-the-chamber) due to seeding losses in the reattachment region. England et al. (2010) used particle image velocimetry (PIV) and frequency measurements to determine the effect of the density ratio of jet-to-surrounding fluid on the initial decay and spread of a precessing jet emanating from a triangular nozzle into a symmetric chamber. They showed a strong relationship between the density ratio and the deflection angle of the jet, which directly influences jet spread and decay rates. It was also observed that there is an inverse relationship between density ratio and precession frequency. Wong et al. (2008) investigated the transverse and longitudinal planes at the chamber exit to examine the flow field immediately beyond the chamber both at the center body and an exit lip. Use of a two-component PIV technique in this study reveals in-plane velocity distributions and the existence of pairs of vortical structures that were related to the center body that had been attached to the nozzle.

The mechanics of the precessing flow instability require further investigation. There are only limited studies to determine the optimal chamber length (L/D) to generate stable precession, nor is there an established relationship between Reynolds number (Re) and the probability of the PJ mode occurring. Understanding of the effect of L/D and Re on the entrainment-into-the-chamber of surrounding fluid and how it varies between AJ and PJ modes, is still needed. To address these, the three-component flow field just beyond the exit plane of a nozzle-chamber geometry for which precession can occur is investigated in a parametric study for a number of L/D and Re conditions. A more fundamental geometry that consists of an abrupt expansion and chamber is chosen to study the effects related to the chamber geometry only. The inlet nozzle has a smooth contraction to minimize pressure drop and define an inlet boundary condition that has been well documented in the literature. In addition to the probability of precession, the effect of Re and chamber length on entrainment-into-the-chamber of surrounding ambient fluid is investigated with the aim to identify its importance on the precession instability and determine the size of the jet in PJ mode.

2 Experimental method

2.1 Nozzle configuration

A schematic of the nozzle and chamber assembly used to generate the precessing flow in this study is shown in Fig. 1. It is comprised of an axisymmetric jet exiting from a smooth contraction nozzle of exit diameter d = 5.08 mm (1/5″), which issues through a sudden expansion into a chamber with diameter D = 5d. This expansion ratio has been shown by Nathan et al. (1998) to be favorable to generate precession. Seven chamber lengths are studied, with lengths L/D = 1, 2, 2.5, 2.75, 3, 3.5, and 4.5. A chamber length of L/D = 2.75 is included to match the work of Nathan (1988), Nathan et al. (1998) and Newbold (1997) who identified this as the optimum chamber length for precession and also that precession occurs over the range 2 ≤ L/D ≤ 3.5. The chamber lengths studied encompass this range, as well as chamber lengths below and above it. The jet flow is characterized with a Reynolds number \( \left( {Re = {\raise0.7ex\hbox{${W_{e} d}$} \!\mathord{\left/ {\vphantom {{W_{e} d} \nu }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\nu $}}} \right) \) based on the average exit nozzle velocity W e , calculated from the volume flow rate through the nozzle, the exit diameter of the nozzle, d and the kinematic viscosity of the fluid, ν which for this study is water. Six different Reynolds number conditions equivalent to Re = 10,000; 21,000; 32,400; 40,800; 50,700 and 61,900 are investigated to cover a range of conditions used both in industry and reported in the literature.

Similar sorts of jet flows into abrupt expansions have been studied by Mi and Nathan (2004), Nathan et al. (1998), Wong et al. (2003, 2004, and 2008). The precessing nozzle and chamber configurations used for these, however, have included a lip and center body, which have been shown to stabilize the flow and increase its probability of precession (Wong et al. 2008). The configuration used here lacks a center body and an exit lip and is appropriate for a fundamental study to investigate the effect of chamber geometry on the probability of the occurrence of the PJ mode.

2.2 The flow facility

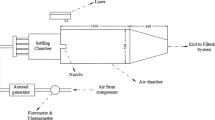
The flow facility comprises of a 240-l glass tank (1,200 mm length × 500 mm height × 400 mm width), which serves as a quiescent fluid environment into which the jet under study issues. The working fluid, water, is driven by a progressive-cavity, pulse-less pump (Model 33204, Moyno) and fluid velocity is set with a variable-speed controller (Model ID15H201-E, Baldor). A plenum was used to minimize any swirl or fluctuations in the incoming flow. Figure 2 shows a sectioned view of the plenum and highlights its components and this complete system was submerged within the tank. Flow into the plenum enters a settling chamber and passes though four flow conditioning grids. The fluid then passes through a honeycomb grid and a steel mesh before finally flowing though a smooth contraction nozzle into a 508-mm (20″) long supply pipe of internal diameter 19.05 mm (0.75″) to the precessing nozzle shown in Fig. 1.

Fig. 2
figure 2

Sectioned view of the flow plenum, showing major components

Full size image

2.3 Effects of flow the facility

The plenum and precessing jet nozzle were placed into the water tank and the water level was maintained at 400 mm so that the centerline line of the nozzle was placed on the central long axis of the tank. The end of the precessing nozzle was placed 230 mm from the end wall which equates to 46d or 9.2D. The adverse pressure gradient imparted by the wall would potentially affect the decay of jet field emerging from the precessing nozzle. Wong et al. (2003) investigated the phase average velocity field in the near region of the chamber exit (x/d < 4 from the end of the chamber) for a nozzle with a center body and exit lip. They found that the dominance of the exiting precessing jet quickly diminished. The presence of the end wall may have effects on the precession phenomenon and one of its main characteristics, the precision frequency (f p ). A study was carried out to investigate possible effects of the wall using a nozzle with a chamber of L/D = 2.75 that had a center body and exit lip for a range of Re (Babazadeh 2011). A pressure port installed in the exit lip monitored the dynamic pressure of the passing jet. An FFT analysis of 25 s of data sampled at 1,000 Hz was used to determine the peak frequency in the spectra and calculate a Strouhal number (St = f p d/W e ) for the flow. This was repeated 20 times for each Re case and a comparison of the results with those of Mi and Nathan (2006) who investigated a similar precessing jet nozzle over a similar range is shown in Fig. 3. The mean values were compared well while the bars of standard deviation show a wide range of results depicting the unsteady nature of the precession. This result indicates that the precessing jet phenomenon generated in the flow facility with the presence of the end wall is similar to that reported in the literature.

Fig. 3
figure 3

A comparison of measured St as a function of Re for a chamber of L/D = 2.75 with a center body and exit lip with the data of Mi and Nathan (2006)

Full size image

2.4 Stereo-PIV setup

The configuration of the Stereo-PIV (Prasad 2000; Raffel et al. 1998) system is shown in Fig. 4 along with the jet plenum situated within the flow facility. Typical Stereo-PIV configurations orient the light sheet so that the largest component of velocity is in-plane, which for a jet is typically the axial velocity component (Prasad 2000). Due to the rotational and chaotic nature of the precessing jet flow, neither the position of the jet within the chamber exit plane nor the angle formed between the jet and chamber axes can be anticipated. Therefore, it is not possible to orient the light sheet so that the axial component of velocity is parallel to the light sheet while ensuring that it remains in the region-of-interest. For this work, the light sheet is instead located just downstream from the chamber exit to avoid scatter off the nozzle and oriented normal to the chamber axis and the main flow direction flow. In this configuration, the entire exit plane of the chamber is visible in the field-of-view and the projection of axial velocity onto the chamber axis corresponds to the out-of-plane velocity component, w. Since the highest velocity component is no longer an in-plane velocity component, a thicker light sheet is required (van Doorne et al. 2003).

Fig. 4
figure 4

The arrangement of the Stereo-PIV system relative to the precessing jet nozzle

Full size image

The Stereo-PIV system consist of two dual-frame, 2,048 × 2,048 pixel (px), 14-bit cameras (LaVision, Imager Pro X) positioned at the same height as the nozzle and at a downstream distance from the nozzle of ~300 mm. The optical axis of the cameras form an angle of 16° to the chamber axis. A Scheimpflug adapter (LaVision) was used with each 105-mm SLR camera lens (Sigma) to ensure that the entire image plane was in focus. The recirculating water in the tank which was fed to the nozzle was seeded with 18-μm hollow glass spheres (Model 60P18, Potters Industries) with a density of 0.6 g/cc to track fluid motion. Particles images on the CCD chip were in the range of 2–4 px allowing good determination of particle displacement. Seeding of this type has been used in flow investigations of liquids (Raffel et al. 2007) due to their relatively small velocity lag and relaxation time which enables them to flow the smaller scales of the flow (Melling 1997; Raffel et al. 2007). Particle illumination was provided by a dual-cavity Nd:YAG laser (Spectra Physics, PIV-400), operating at 532 nm and 10 Hz and controlled to produce 10 ns pulses at ~250 mJ/pulse. The generated light sheet had a thickness ~3 mm and was located adjacent to the exit of the chamber for each chamber length. Time steps, Δt were selected so that particles travelled less than one-quarter of its thickness within the field-of-view. With this light sheet thickness and angle between cameras and jet axis, the particles imaged on the camera CCD plane had a sufficient pixel displacement (~8 px) for the calculation of the out-of-plane velocity component.

2.5 Calibration

The collected data was processed using commercial software (DaVis 7.4, LaVision) to produce three-component velocity vector fields. An initial calibration was achieved by imaging a three-dimensional calibration target (Type 11, LaVision) with the two cameras to locate their relative position and map both images onto a common calibration plane. This target is comprised of an array of regular sized and located dots in columns which are alternate in depth. The target is positioned so that the plane corresponding to the region-of-interest occurs between the two planes of dots. The calibration procedure defines a selected origin and orientation of the coordinate system in the images of the target from both cameras. An automated algorithm finds all dots in both images from both cameras. Comparing the position of the imaged dots to their known distances on the calibration target, a third-order polynomial mapping function is calculated, allowing for the image obtained by the cameras to be de-warped onto the calibration plane. The calibration is further refined by performing a self-calibration (Wieneke 2005), to ensure that the calibration and measurement planes (location of the laser sheet) are in the same position in space, thereby decreasing any errors introduced from the camera images not being properly overlapped. Images of particle distributions from the two cameras are cross-correlated with one another, resulting in a disparity vector map. This map shows the difference in position of the same particle in physical space when mapped from the image planes of the two cameras using their respective calibration functions back onto the calibration plane. If the initial calibration is perfect, the de-warped particle images from both cameras will overlap perfectly on the calibration plane. This is usually not the case and the disparity vector map is used to adjust the initial calibration function so that the calibration plane corresponds to the position of the light sheet. An advantage of this calibration method is that the light sheet and calibration plane do not have to be coincident; instead, the self-calibration adjusts for any offset between them.

2.6 Stereo-PIV processing

To determine the average and RMS velocity fields 1,000 image pairs were taken for each configuration of Re and chamber length. Raw images from the cameras were first preprocessed using background count subtraction and sliding background subtraction of time series (over three images), in order to remove any background intensities which may exist in sequential images, as well as to remove any intensity which remained constant, such as the image of the chamber. Background noise was reduced using sliding background subtraction with a 5 px filter size. The intensity of particles was normalized using a min–max filter with a 10 px window and the particle images were finally smoothed using a 3 × 3 linear filter. Vector fields were generated using a multi-pass correlation scheme with a decreasing window size. Five passes were used to improve the quality of the calculation of the out-of-plane vectors, which were of the most interest in this study. The correlation was performed twice with a 64 × 64 px interrogation window and then further processed with three passes of a 32 × 32 px interrogation window with 50% overlap. At this final interrogation window size, the determined velocity vector is an average over a physical region of 1.25 mm × 1.25 mm in plane by the thickness of the light sheet of ~3 mm. This resolution was selected with the aim to capture the bulk characteristics of the flow rather than the flows of fine scale turbulence. The resulting vector field from each correlation step was used as an initial particle search field for the next. This resulted in 67,804 vectors in each instantaneous vector field. Vector fields were finally treated with a median filter, to remove any spurious vectors, as well as a 3 × 3 smoothing filter. A comprehensive discussion of the image preprocessing and vector calculation can be found in Madej (2010).

2.7 Measurement uncertainties

A number of uncertainties affect the absolute value of the measurement of velocity, mostly due to the configuration of the experiment used. The cameras were arranged at an angle of 16° to the axis of the nozzle-chamber and in the same plane. This leads to an uncertainty in the out-of-plane velocity component that is 4 times the in-plane (Lawson and Wu 1997, Prasad 2000). This shallower than optimal angle between the two stereo cameras was used as a trade-off between having a large angle to minimize uncertainties in the measurement of the out-of-plane component with the restricted view at the end of the water tank and the limited movement of the Scheimpflug adapter’s that were used to keep the image in focus. The thick laser sheet used enabled the out-of-plane velocity component to be measured but degrades the measurement resolution in the out-of-plane direction. Overlap of the laser sheet with the calibration target is always a potential source of uncertainty. The use of the self-calibration deduces the uncertainty of particle locations from a normal 1–2 px to 0.1–0.2 px (Wieneke 2000) while correcting for optical distortion across the CCD array. Uncertainty in the timing of events had a time resolution of 10 ns with a jitter of <1 ns between all signals. The uncertainty in determining particle displacements with the multi-pass, window off-set Stereo-PIV algorithm used was on the order of 1/10th of a pixel.

3 Characterization of the nozzle jet

The jet entering that chamber can be characterized by its average axial velocity profile and its average axial decay. This was carried out to use a conventional Stereo-PIV approach with the light sheet oriented such that the axial component of the jet velocity was in-plane. The axial velocity profile data was collected with no chamber present and as such the flow can be described as a jet from a smooth contraction nozzle exiting into a quiescent fluid. This could also be considered as a nozzle configuration with a chamber length of L/D = 0 and as such the flow coordinate system defined in Fig. 1 will be such that the end of the chamber will overlap the end of the inlet nozzle. The end of the nozzle was placed ~120d from the end wall of the tank. Average axial velocity (W) and RMS (w′) scaled with the jet bulk inlet velocity (W e ) are shown in Fig. 5 at z/d = 1 for the range of Re investigated in this study. These are plotted by spatially scaling the position of the measurement with the nozzle diameter (d) and are compared with what would be the theoretical “top-hat” profile from a perfect smooth contraction nozzle. The profiles collapse well under this scaling with maximum turbulence levels of 20% in the axisymmetric shear layer of the jet. At this location of one diameter from the nozzle exit, initial spreading of the jet is evident. The decay of the jet’s momentum field can be characterized by the decay of the centerline axial velocity (W cl ) compared to the exit velocity of the jet (W e ). This ratio comparison can be expressed as \( \frac{{W_{e} }}{{W_{cl} }} = \frac{1}{K}\chi \) (Rajaratnam 1976) where K is the decay rate of the jet and \( \chi \equiv \frac{{z - z_{o} }}{d} \) is the dimensionless axial position in the jet corrected for the jet virtual origin, z o . The axial velocity decay of the jet is plotted in Fig. 6 and shows a potential core region (W e /W cl  = 1) up to χ ~ 6. This is followed by the decay region of the jet, which when plotted in this manner is linear. The decay rates are similar for each jet except for Re = 5,800 where K Re=5,800 = 6.07. For all other Re cases, the average decay rate is K Re≥10,000 = 6.69. This is compared to published values in the literature for smooth contraction nozzles that are in the range of K = 5.6 (Fellouah et al. 2009) to 6.7 (Weisgraber and Liepman 1998). The data presented in Figs. 5 and 6 highlight that the nozzle and the jet generated from it compare will with the expected characteristics of this type of jet and are unaffected over the range investigated by the confining environment used in the study.

Fig. 5
figure 5

Average and RMS velocity profiles of the smooth contraction nozzle at z/d = 1 for the range of Reynolds number under investigation

Full size image
Fig. 6
figure 6

Non dimensionalized centerline axial velocity of the jet exiting from the smooth contraction nozzle used in this study. Only every 20th data point is plotted for clarity

Full size image

4 Data processing for mode determination

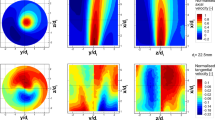
An example of the axial instantaneous velocity (w) component of the jet exiting the chamber scaled with W e is shown in a contour plot in Fig. 7a where the spatial position is scaled by the chamber radius, R = D/2. The figure highlights that the flow is highly turbulent and that both the exiting jet and entrainment-into-the-chamber of surrounding fluid can be detected. The chaotic and turbulent nature of the field however, makes it difficult to easily interpret the flow using automated computer algorithms. In Fig. 7b, a 15 × 15 linear filter is applied to the velocity data shown in Fig. 7a to emphasis the bidirectional flow regime. This is further processed in Fig. 7c to highlight only the outflow from the chamber which corresponds to the jet flow and is used to allow easy interpretation of the flow field using automated approaches. The majority of flow fields presented here have been processed in this manner with exceptions noted in the text.

Fig. 7
figure 7

A sample instantaneous axial velocity field in precessing mode (L/D = 2.75, Re = 61,900) a before smoothing, b after a 15 × 15 linear filter is applied, c after 15 × 15 linear filter and setting all negative axial velocity to zero

Full size image

Illustrative instantaneous velocity fields of the jet exiting the chamber are shown in Fig. 8 for jet conditions highlighted in each sub figure. The data for all figures in processed as in Fig. 7c. These contour plots reveal the presence of the two dominant modes of flow; PJ mode (Fig. 8a–e) and AJ mode (Fig. 8f–j) for a range of Re and chamber length ratios. There is a third mode denoted the transitioning mode (Fig. 8k–o), in which the jet is neither obviously in PJ mode nor AJ mode. In these figures, the smoothed velocity fields highlight the dominant shape and structure of the flow and minimize the presence of any turbulence or small scale structures. The nozzle in PJ mode is illustrated in Fig. 8a–e and is characterized by a high-positive axial velocity region near to the chamber wall. This flow resembles a kidney-bean in shape and occupies approximately half of the perimeter of the chamber. There is no outflow in the region around the chamber axis; instead in this region fluid is being entrained back into the chamber. As shown in Fig. 8f–j, the AJ mode resembles an axisymmetric jet flow, where the high-axial velocity is near to the chamber axis. The shape of the flow field is also reasonably symmetric about the axis. The maximum axial velocity in this mode can reach \( {w \mathord{\left/ {\vphantom {w {W_{e} \cong 0.9}}} \right. \kern-\nulldelimiterspace} {W_{e} \cong 0.9}} \) for a chamber length of L/D = 1 (Fig. 8f) which closely resembles an axisymmetric jet. Examples of the transitioning mode are shown in Fig. 8k–o. The outflowing jet is not necessarily crescent-shaped, as in PJ mode, but instead has a round shape as would be expected in AJ mode. However, the region of highest outflow, is not sufficiently close to the chamber axis for the jet to be characterized as AJ mode.

Fig. 8
figure 8

Instantaneous positive axial velocity contours for the flow field at the chamber exit in (a–e) precessing mode, (f–j) axial mode, and (k–o) transitioning mode

Full size image

In order to determine precession probability, as well as conditionally average only those instantaneous vector fields which were in PJ mode, a technique was developed to determine the flow mode based on the instantaneous axial velocity distribution. It is relatively easy to visually distinguish the two modes based on the axial velocity distribution, since the outflowing region is either kidney-bean-shaped and along the chamber wall (PJ mode), or reasonably axisymmetric and in-line with the chamber axis (AJ mode). However, due to the large volume of data collected in this study (42,000 instantaneous vector fields for all Re and chamber lengths conditions), manual mode determination relying on visual inspection of instantaneous velocity fields is not feasible.

The automated mode determination method characterizes the flow based on the instantaneous, positive axial velocity field. Due to the chaotic nature of the flow and the possibility of the jet existing in a mode which is neither obviously AJ nor PJ, as evident in Fig. 8k–o, three quantitative criteria are used to deem the flow as in either PJ or AJ mode. Then, a best two-of-three approach is used with these results, so that if two mode-finding methods find the jet to be in PJ mode while the third disagrees, it is considered to be in PJ mode. The probability of precession is defined as the ratio of the number of instantaneous axial velocity fields found to be in PJ mode (N PJ) to the total number of vector fields in a dataset (N) at a given Re and chamber length and is given as,

$$ P_{\text{PJ}} \equiv \frac{{N_{\text{PJ}} }}{N}. $$
(1)

4.1 Mode determination #1: maximum outflow velocity position

The first mode-finding method considers the position of the peak axial velocity of the issuing jet since in AJ mode the highest velocity region is near to the chamber axis, while in PJ mode the velocity peak is closer to the chamber wall. Considering that the flow is highly turbulent, the axial instantaneous velocity field is first heavily smoothed (25 × 25 linear filter) to highlight the dominant velocity distribution. Figure 9 shows a sample instantaneous positive axial velocity field before and after smoothing for the jet in both PJ and AJ modes, as well as the position of the maximum velocity, (x p , y p ). If this point is beyond a heuristically determined threshold radius, R c1 , from the axis of the nozzle, the jet is assumed to be in PJ mode. If (x p , y p ) is within the circle of radius R c1 , it is assumed to be in axial mode.

Fig. 9
figure 9

The location of the maximum outflow velocity is shown for sample velocity fields in PJ mode (L/D = 2.75, Re = 61,900) (a, b) and AJ mode (L/D = 2.75, Re = 10,000) (c, d). Instantaneous axial velocity data is heavily smoothed with a 25 × 25 linear filter (b and d), and the location of the highest velocity is shown with open diamond. The characteristic radius, R c1 is shown with dashed line

Full size image

4.2 Mode determination #2: volume flow within areas of the chamber

In its two characteristic modes, the shape of the issuing jet (the region of positive axial velocity) can be relatively circular (in AJ mode) and coaxial with the chamber axis, or kidney-bean-shaped (PJ mode), where the majority of outflow is nearer to the chamber wall than its center. Flow out of the chamber can be defined as q 1, the volume flow rate inside the radius R c2 and q 2, the volume flow rate outside radius R c2 . It is assumed that in AJ mode, there is a higher volume flow rate out of the chamber in a circular region within a radius R c2 than beyond it. For PJ mode, the opposite should hold true: there should be more volume flux in the annulus bounded by R c2 and the chamber radius. For each masked instantaneous axial-component flow field, the volume flow rates q 1 and q 2 are approximated using the following equations:

$$ q_{{_{1} }} = \sum\limits_{r = 0}^{{R_{c} }} {w\left( {x,y} \right)\delta x\delta y,} \quad r = \left( {x^{2} + y^{2} } \right)^{{\tfrac{1}{2}}} $$
(2)
$$ q_{2} = \sum\limits_{{r = R_{c} }}^{R} {w\left( {x,y} \right)\delta x\delta y,\quad r = \left( {x^{2} + y^{2} } \right)^{{\tfrac{1}{2}}} } $$
(3)

These are the sums of volume flux through finite rectangular areas of dimensions δx and δy at all data points either within R c2 or in the annulus beyond it, respectively. If q 1 ≥ q 2, the jet is considered to be in AJ mode, and if q 1 < q 2, it is considered to be in PJ mode.

4.3 Mode determination #3: centroid of volume flow rate

The third method characterizes the flow mode based on the position of the fluidic centroid of the issuing jet relative to a third cutoff radius R c3 . This centroid is weighted with the value of axial velocity and in cylindrical coordinates is:

$$ \tilde{r} = \frac{{\sum {rw\left( {r,\theta } \right)} }}{{\sum {w\left( {r,\theta } \right)} }}, $$
(4)

and

$$ \tilde{\theta } = \frac{1}{{\tilde{r}}}\frac{{\sum {r\theta w\left( {r,\theta } \right)} }}{{\sum {w\left( {r,\theta } \right)} }} $$
(5)

To calculate the centroid, the vector field is mapped into a cylindrical coordinate system and the radial distance of the centroid defines the mode. If the position of this centroid is beyond R c3 , the jet is considered to be in PJ mode and if it is within R c3 , it is considered to be in AJ mode. The mapping of coordinate systems resembles a radar sweeping out a circular area starting at an initial angle of θ 0 with the y-axis and completing a 2π-revolution about the center of the chamber. Figure 10 illustrates this method for the jet in AJ mode and PJ mode, respectively.

Fig. 10
figure 10

Illustration of centroid method for an instantaneous axial velocity field in a–c PJ mode and d–f AJ mode. Subfigures (a) and (d) show a heavily smoothed axial velocity distribution showing the position of maximum outflow (filled star), and the location opposite from it (open star) from which the sweep begins, and is shown as “dashed line”; b and e show the same unsmoothed data with the centroid marked as open diamond. Sub-figures c and f show the equivalent data mapped into a cylindrical coordinate system, with the centroid marked as open diamond and the cutoff radius as R c3 “dashed line”

Full size image

The location of the highest outflow velocity, (x p , y p ), is first found in a heavily smoothed (25 × 25) axial velocity field. The angle ϕ is formed between vector \( \vec{s} = [x_{p} ,\,y_{p} ] \), which joins the origin and (x p , y p ), and the y +-axis. Angle θ 0 is defined as the angle opposite to ϕ, formed between the y +-axis and \( \left( { - x_{p} , - y_{p} } \right) \) and serves as the angle at which the sweep begins and ends. By mapping the coordinate system with this initial offset, it guarantees that if in PJ mode the outflowing region appears continuously within the range \( \theta_{0} \le \theta < \theta_{0} + 2\pi \).

Since the data exists in positional coordinate arrays \( {\mathbf{x}} \) and \( {\mathbf{y}} \) and velocity component arrays \( {\mathbf{u}} \), \( {\mathbf{v}} \), and \( {\mathbf{w}} \) (each with size \( I \times J \)) as discrete data points, it is necessary to create new positional coordinate grids, \( {\mathbf{r}} \) and \( {\varvec{\theta}} \), containing all \( 0 < r \le R \) and \( \theta_{0} \le \theta < 2\pi + \theta_{0} \) positional coordinates. The size of these arrays has been chosen to be the same as \( {\mathbf{x}} \) and \( {\mathbf{y}} \), which results in a grid spacing of \( \delta r = {R \mathord{\left/ {\vphantom {R I}} \right. \kern-\nulldelimiterspace} I} \) and \( \delta \theta = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } J}} \right. \kern-\nulldelimiterspace} J} \). Arrays \( {\mathbf{r}} \) and \( {\varvec{\theta}} \) are filled according to:

$$ {\mathbf{R}}_{s,t} = s\delta r;\quad 1 \le s \le I,\quad 1 \le t \le J $$
(6)

and

$$ {\varvec{\theta}}_{s,t} = \theta_{0} + \left( {t - 1} \right)\delta \theta ;\quad 1 \le s \le I,\quad 1 \le t \le J, $$
(7)

where s and t are their array indices in two dimensions.

Mapping from the masked axial velocity array in the Cartesian coordinate system, \( {\mathbf{w}} \), to the new array in cylindrical coordinates, w cyl , is achieved with

$$ \begin{array}{*{20}c} {{\mathbf{w}}_{{{\mathbf{cyl}}s,t}} = {\mathbf{w}}_{i,j} \mathrel\backepsilon \left[ {\begin{array}{*{20}c} {{\mathbf{x}}_{i,j} } \\ {{\mathbf{y}}_{i,j} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {x_{c} } \\ {y_{c} } \\ \end{array} } \right] + {\mathbf{r}}_{s,t} \left[ {\begin{array}{*{20}c} {\sin \left( {{\varvec{\theta}}_{s,t} } \right)} \\ {\cos \left( {{\varvec{\theta}}_{s,t} } \right)} \\ \end{array} } \right],} & {\forall s,t} \\ \end{array} . $$
(8)

For every grid point in array w cyl with position \( \left( {r,\theta } \right) = \left( {{\mathbf{r}}_{s,t} ,{\varvec{\theta}}_{s,t} } \right) \), the corresponding point in Cartesian coordinates \( \left( {x,y} \right) = \left( {{\mathbf{x}}_{i,j} ,{\mathbf{y}}_{i,j} } \right) \) has values \( x = x_{c} + r\sin \theta \) and \( y = y_{c} + r\cos \theta \). Since the data are not continuous, any point \( \left( {x,y} \right) \) which does not fall on a grid point has its axial velocity value cubically interpolated from the surrounding grid points.

The radial component of the centroid is then calculated as

$$ \tilde{r} = \frac{{\sum\nolimits_{s = 1}^{I} {\sum\nolimits_{t = 1}^{J} {{\mathbf{r}}_{s,t} {\mathbf{w}}_{{{\mathbf{cyl}}s,t}} } } }}{{\sum\nolimits_{s = 1}^{I} {\sum\nolimits_{t = 1}^{J} {{\mathbf{w}}_{{{\mathbf{cyl}}s,t}} } } }} $$
(9)

If \( \tilde{r} > R_{c3} \), the jet is considered to be in PJ mode. Otherwise, the jet is considered to be in AJ mode. Note that all values of w cyl beyond the chamber radius have a null value.

The third mode-finding process is illustrated in Fig. 10 for a sample vector field in both PJ, (Fig. 10a–c) and AJ, (Fig. 10d–f) modes. Sub-figures (a) and (d) show the axial velocity contours after heavy smoothing. The position of the highest outflow velocity is marked with ⋆ while ☆ shows the point opposite to it. The broken line forms angle \( \theta_{0} \) with the y +-axis, and is the angular position from which the data is “swept-out”. Sub-figures (b) and (e) show the position of the determined centroid, marked with ◊, on instantaneous velocity field. This position was determined from the velocity fields mapped to cylindrical coordinates that are shown in sub-figures Fig. 10c, f.

4.4 Determining the cutoff radius

It was necessary to determine the cutoff criteria R c for the three mode determination (MD) methods outlined in the previous sections in order to determine the mode for each vector field. Of the eighteen Re and chamber length combinations studied, six were arbitrarily chosen. For each of these, the mode probability of the first one hundred vector fields was determined by visual inspection. The precession probability values found are reported in Table 1. The same one hundred images from each set were analyzed using the three mode-finding methods at different cutoff radii over the range \( 0 \le R_{c} \le R \), which resulted in a different precession probability for each method at each cutoff radius. The relationship between R c and the mode probability determined by the three methods is shown in Fig. 11.

Table 1 The cutoff radii determined from six chamber length/Reynolds number combinations
Full size table
Fig. 11
figure 11

Results of cutoff radius sensitivity testing for six chamber length and Reynolds number combinations: a L/D = 2, Re = 32,400; b L/D = 2.5, Re = 32,400; c L/D = 2.75, Re = 61,900; d L/D = 2.75, Re = 21,800; e L/D = 3, Re = 32,400; f L/D = 3.5, Re = 32,400

Full size image

For each of the six chamber length-Re combinations and for each of the mode-finding methods, the cutoff-radius value was found which resulted in the same precession probability as manually determined for that set. For example, for a chamber length of L/D = 2.75 at a Re of 61,900, the PJ mode probability determined from visual inspection of the axial velocity fields was found to be 84%. In Fig. 11d, it can be observed that in order to produce a precession probability of 84% the mode determination approach MD #1: maximum outflow velocity position, R c1  = 0.77R; for MD #2: volume flow within areas of the chamber, R c2  = 0.73R; and for MD #3: centroid of volume flow rate R c3  = 0.60R. The cutoff radii for the three methods for the six cases investigated are documented in Table 1.

For a given MD method, the appropriate cutoff radius is assumed to be the average of the cutoff radii found for the different Re and chamber length combinations for that method. It is apparent from Table 1 that the cutoff radius for a given mode is not greatly dependant on neither Re nor chamber length. This is especially true for MD #2 and MD #3, which have a standard deviation of only 0.01R between the six Re and chamber length combinations. Of the three methods, MD #1 is the most volatile, with a standard deviation of 0.04R; however, the use of a best-two-of-three approach should address the larger spread of cutoff radii with this method.

5 Conditional averaging

Due to the rotational nature of the issuing jet, its position varies throughout the chamber exit plane with time and in successive images. To obtain averages and statistical metrics of the velocity fields of the jet in PJ mode, it is necessary to include only those vector fields which are in PJ mode and rotate them in such a way that the same regions of the jet are averaged together. The fluidic centroid of the jet is chosen as a common point and instantaneous vector fields which are in PJ mode are rotated about the chamber axis so that the centroid always lies on the y +-axis. Average and RMS axial velocity distributions are then calculated.

The following steps were used to perform the conditional averaging. The mode of each vector field was first determined. If in PJ mode, the axial velocity field was mapped to cylindrical coordinates and the position of the centroid is found. The azimuthal component of the position of the centroid is found using:

$$ \tilde{\theta } = \frac{1}{{\tilde{r}}}\frac{{\sum\nolimits_{s = 1}^{I} {\sum\nolimits_{t = 1}^{J} {{\mathbf{r}}_{s,t} {\varvec{\theta}}_{s,t} {\mathbf{w}}_{{{\mathbf{cyl}}s,t}} } } }}{{\sum\nolimits_{s = 1}^{I} {\sum\nolimits_{t = 1}^{J} {{\mathbf{w}}_{{{\mathbf{cyl}}s,t}} } } }} $$
(10)

The method for rotation is based on the change of basis from an old basis \( B = \left( {\hat{x},\hat{y}} \right) \) to a new basis \( B^{\prime} = \left( {\hat{x^{\prime}},\hat{y^{\prime}}} \right) \). Here, the new basis is rotated by an angle θ from the old one (Anton and Rorres 2000) and \( \hat{x} \) and \( \hat{y} \) are unit vectors in the x and y directions, respectively. This yields a transformation matrix between the rotated and original coordinate system such that \( B^{\prime} \mapsto B \). Rotation is achieved by mapping each vector field so that the position of the centroid in the rotated axial velocity array, w rot , lies on the y +-axis. This array has the same size as its original counterpart, \( {\mathbf{w}} \). The necessary angle for rotation is \( \theta = \tilde{\theta } \), which is the azimuthal location of the fluidic centroid of the jet. If the data were continuous, the relationship between original and rotated vector fields, \( \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} \) and \( w_{rot} \), is:

$$ w_{\text{rot}} \left( {x,y} \right) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{w} \left( {x^{\prime}\cos \tilde{\theta } + y^{\prime}\sin \tilde{\theta }, - x^{\prime}\sin \tilde{\theta } + y^{\prime}\cos \tilde{\theta }} \right) $$
(11)

Since, however, the data exists in discretized arrays, it is necessary to map the value of each data point in data array \( {\mathbf{w}}_{{{\mathbf{rot}}}} \) from its corresponding position in \( {\mathbf{w}} \). In data-array notation, this would be described by:

$$ \begin{array}{*{20}c} {{\mathbf{w}}_{{{\mathbf{rot}}i^{\prime},j^{\prime}}} = {\mathbf{w}}_{i,j} \mathrel\backepsilon \left[ {\begin{array}{*{20}c} {{\mathbf{x}}_{i,j} } \\ {{\mathbf{y}}_{i,j} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \tilde{\theta }} & {\sin \tilde{\theta }} \\ { - \sin \tilde{\theta }} & {\cos \tilde{\theta }} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\mathbf{x}}_{{i^{\prime},j^{\prime}}} } \\ {{\mathbf{y}}_{{i^{\prime},j^{\prime}}} } \\ \end{array} } \right],} & {\forall i^{\prime},j^{\prime}} \\ \end{array} , $$
(12)

which assigns every position \( \left( {x^{\prime},y^{\prime}} \right) = \left( {{\mathbf{x}}_{{i^{\prime},j^{\prime}}} ,{\mathbf{y}}_{{i^{\prime},j^{\prime}}} } \right) \) in the rotated velocity array and the corresponding value of velocity from the original array at position \( \left( {x,y} \right) = \left( {{\mathbf{x}}_{i,j} ,{\mathbf{y}}_{i,j} } \right) \). Any velocity value in \( {\mathbf{w}} \) which does not lie on a grid point is cubically interpolated from the velocity values at the surrounding grid points. Figure 12 shows a sample axial velocity field before and after rotation. The axial velocity distribution in this plot is smoothed and shows only regions of positive axial velocity in order to more clearly illustrate the rotation. Vector fields undergoing this process were unsmoothed and included both positive and negative axial velocity data.

Fig. 12
figure 12

Instantaneous axial velocity field in PJ mode a before and b after rotation. The fluidic centroid is shown as open diamond

Full size image

Mapping from \( \left( {x^{\prime},y^{\prime}} \right) \mapsto \left( {x,y} \right) \) was chosen instead of the reverse, due to the discretized nature of the data. If discrete points from the original array were mapped to the rotated array, most of the points in the new array would not fall on discrete grid points. Then, assigning values to grid points in the rotated array would require solving sets of equations for each point, since axial velocity values at grid points would have to be determined by reverse interpolation from velocity values existing between them. By mapping from the rotated array to the original array, values at discrete grid points in the rotated array correspond to points which may or may not exactly lie on grid points in the original array. If they do not, their value is simply interpolated from surrounding points.

With the data mapped such that the fluidic centroid of the PJ mode jet is at the same azimuthal position on the y +-axis, a phase-averaged mean and RMS of the axial velocity fields, W and w′ can be determined using:

$$ W = \frac{1}{{N_{\text{PJ}} }}\sum\limits_{n = 1}^{{N_{\text{PJ}} }} {\left( {{\mathbf{w}}_{{{\mathbf{rot}}}} } \right)_{{\mathbf{n}}} } , $$
(13)

and

$$ w^{\prime} = \frac{1}{{N_{\text{PJ}} }}\left\{ {\sum\limits_{n = 1}^{{N_{\text{PJ}} }} {\left[ {{\mathbf{W}} - \left( {{\mathbf{w}}_{{{\mathbf{rot}}}} } \right)_{{\mathbf{n}}} } \right]^{2} } } \right\}^{\frac{1}{2}} $$
(14)

Here, \( \left( {{\mathbf{w}}_{{{\mathbf{rot}}}} } \right)_{{\mathbf{n}}} \) is the nth of N PJ rotated instantaneous vector fields in PJ mode determine from the describe mode-finding techniques.

6 Results and discussion

6.1 The probability of precession

The relationship between precession probability, P PJ, and the chamber length at various Re is shown in Fig. 13. It is apparent in this figure that the PJ mode probability trend is similar for all Re except for Re = 10,000. In this case, the jet is potentially not yet fully turbulent and for this result can be considered to be still developing. For the shortest chamber length case investigated, L/D = 1, precession was found not to occur for all Re conditions investigated. In this case, the chamber acts as a shroud around the emerging jet only. The highest precession probability occurs at a relatively short chamber length range of L/D = 2–2.75 where the probability of the jet precessing is above 50%. As the chamber length is increased, there is an abrupt decrease in P PJ in the region of L/D~3 with the probability of precession occurring falling below 30%. For chamber lengths of L/D = 3–4.5, there is a recovery in the probability of the jet being in PJ mode however, this is limited to below 50% for the chamber lengths investigated. At these longer chamber lengths, the jet is beyond the chamber length range investigated by Newbold (1997) and may not be “precessing”. However, the axial velocity field of the jet at these chamber lengths do exhibit the crescent-shaped jet with high velocity near to the chamber wall, characteristic of the PJ mode jet.

Fig. 13
figure 13

The effect of chamber length on precession probability for different Reynolds numbers. Symbols: Re = plus 10,000, open diamond 21,800, inverted open triangle 32,400, open square 40,800, open round 50,700, open triangle 61,900

Full size image

The relationship between P PJ and Re number at different chamber lengths is shown in Fig. 14. This also shows the data for the short chamber length investigated L/D = 1, for which the PJ mode was not detected. There appear to be three distinct trends in the plot. First, for chamber lengths L/D ≥ 3, the P PJ increases almost linearly with Re number, beginning with a nonzero P PJ at Re = 10,000. Second, at a chamber length of L/D = 2.75, P PJ is near-zero at the lowest Re number, and increases almost linearly with Re. This excludes the precession probability value at Re = 40,800 and potentially Re = 50,700 due to this chamber length being on the cusp of the mode switch which is better highlighted in Fig. 13. Third, in the range of chamber lengths of 2 ≤ L/D ≤ 2.5, P PJ = 0 at the lowest Re and appears to increase toward an asymptote at higher Re. In all cases, the dependence on Re reduces with increasing Re which also been observed by Nathan et al. (1998).

Fig. 14
figure 14

The effect of Reynolds number on precession probability for different chamber lengths. Symbols: L/D = asterisk 1.0, plus 2.0, open diamond 2.5, inverted open triangle 2.75, open square 3.0, open round 3.5, open triangle 4.5

Full size image

6.2 Entrainment-into-the-chamber of ambient fluid

The amount of fluid being drawn back into the chamber through the exit plane of the chamber (at an axial distance z = 0) is compared for the two flow modes for each Re and chamber length using the measured velocity data. The amount of fluid being entrained back into the chamber is characterized with the entrainment-into-the-chamber ratio, C E , which is defined as the ratio of mass flux into the chamber to the mass flux out of the chamber at the chamber exit plane, as:

$$ C_{E} \equiv \left. {\frac{{\dot{m}_{\text{in}} }}{{\dot{m}_{\text{out}} }}} \right|_{z = 0} $$
(15)

The mass fluxes in and out of the chamber are approximated as the sum of mass flux through finite rectangular regions centered at each grid point within array \( {\mathbf{w}} \) of size \( \delta x \) and \( \delta y \). Mass flux into the chamber, \( \dot{m}_{\text{in}} \), sums of all the mass flux through all of these regions where the local axial component is negative (into the chamber), while the mass flux out of the chamber, \( \dot{m}_{\text{out}} \), includes all data points where axial velocity is positive (out of the chamber). The numerical approximations for these two values are defined as:

$$ \dot{m}_{\text{in}} = \rho \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left| {{\mathbf{w}}_{i,j} } \right|\delta x\delta y,} \quad {\mathbf{w}}_{i,j} < 0} $$
(16)
$$ \dot{m}_{\text{out}} = \rho \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {{\mathbf{w}}_{i,j} \delta x\delta y,\quad } } {\mathbf{w}}_{i,j} > 0 $$
(17)

here, ρ is the fluid density with a value of ρ = 998 kg/m3 for water used in calculations. At each Re and chamber length, there are N = 1,000 vector fields. The entrainment-into-the-chamber ratio for each vector field, \( \left( {C_{E} } \right)_{n} \), is calculated and averaged with other values from the same jet mode. The entrainment-into-the-chamber ratio for each chamber length and Re for both modes is finally determined by averaging all mass flux fractions using:

$$ C_{{E({\text{PJ}})}} = \frac{1}{{N_{\text{PJ}} }}\sum\limits_{n = 1}^{{N_{\text{PJ}} }} {\left[ {\left( {C_{E} } \right)_{n} } \right]_{\text{PJ}} } $$
(18)
$$ C_{{E({\text{AJ}})}} = \frac{1}{{N_{\text{AJ}} }}\sum\limits_{n = 1}^{{N_{\text{AJ}} }} {\left[ {\left( {C_{E} } \right)_{n} } \right]_{\text{AJ}} } $$
(19)

The relationship between entrainment-into-the-chamber ratio and chamber length is shown in Fig. 15 for both PJ and AJ modes. Figure 16 shows the relationship between C E and Re also for both jet modes. It is apparent from Fig. 15 that there is a strong relationship between chamber length and C E . Entrainment-into-the-chamber ratio is highest at L/D = 2, and decreases with increasing chamber length for both modes. Figure 16 shows a weak relationship between Re and C E , except at Re = 10,000. An interesting finding shown in both plots is that there is negligible difference in C E for the two jet modes. This would indicate that the amount of surrounding fluid entrained into the jet entering the chamber is the same for both PJ and AJ modes. Increasing the chamber length limits the amount of surrounding fluid that can be entrained into the chamber as the jet expands and grows within the chamber.

Fig. 15
figure 15

The effect of chamber length on entrainment-into-the-chamber ratio for different Reynolds numbers. Symbols: Re = plus 10,000, open diamond 21,800, inverted open triangle 32,400, open square 40,800, open round 50,700, open triangle 61,900; solid line PJ mode, dashed line AJ mode

Full size image
Fig. 16
figure 16

The effect of Reynolds number on entrainment-into-the-chamber for different chamber lengths. Symbols: L/D = asterisk 1.0, plus 2.0, open diamond 2.5, inverted open triangle 2.75, open square 3.0, open round 3.5, open triangle 4.5; solid line PJ mode, dashed line AJ mode

Full size image

6.3 The axial velocity field at the chamber exit in PJ mode

The velocity field at the exit of the chamber when the jet is in PJ mode is investigated using conditional averaging. In this process, information of the in-plane components are strongly affected when determining the conditional average by any mode switching and the direction of precession which is a random process. The average out-of-plane or axial component of velocity (W) will only be marginally affected with some spatial smoothing occurring.

The average axial velocity field for several Re conditions at the exit of the chamber for the jet in PJ mode is shown in Fig. 17. The corresponding RMS field, w′ is shown in Fig. 18. The data shown is for a chamber length condition of L/D = 2.5 where precession probability is high for a range of Re conditions. A complete set of velocity fields for all chamber length and Re conditions can be found in Madej (2010). For certain Re and chamber length combinations at which P PJ is low, average and RMS axial velocity flow fields appear inconsistent and not as smooth as the others. This is due to the low number of instantaneous velocity fields used for calculating the average and RMS. For example, at L/D = 2.5 and Re = 10,000 only 1% of the observed instantaneous axial velocity fields were in PJ mode, which means that the average and RMS field for this Re and chamber length combination is calculated from 10 images. Those combinations with higher precession probability show much smoother average and RMS axial velocity fields.

Fig. 17
figure 17

Conditionally averaged mean axial velocity distribution in PJ mode at the chamber exit plane for a chamber length L/D = 2.5 at Reynolds numbers: a 10,000, b 21,800, c 32,400, d 40,800, e 50,700, f 61,900

Full size image
Fig. 18
figure 18

Conditionally averaged RMS velocity distributions in PJ mode at the chamber exit plane and a chamber length L/D = 2.5. Reynolds numbers are the same as in Fig. 17. Contours have been smoothed with 5 × 5 linear filter

Full size image

As shown in Fig. 17, all chamber lengths show a symmetrical crescent or kidney-bean-shaped region of positive axial velocity which hugs the chamber wall. Opposite this region is a negative flow back into the chamber. The highest region of axial velocity is at a radial distance of approximately r/R = 0.8. The distribution of axial velocity for a constant chamber length does not appear to be a function of Re when normalized by the nozzle inlet velocity, W e . The largest velocity fluctuations shown in Fig. 18 occur in the high-positive velocity region of axial velocity. Velocity fluctuations decrease with increasing radial and azimuthal distances from this region. The smallest velocity fluctuations occur near to the chamber wall opposite to the outflow region, at \( \left( {x,y} \right) \approx \left( {0, - R} \right) \). The distribution and magnitude of the RMS axial velocity distribution does not appear to change significantly at different Re and chamber lengths, except at those conditions for which there was a low precession probability potentially and hence low data density.

The effect of changing chamber length on the exit axial velocity profile for a constant Re = 32,400 is examined in the conditionally averaged velocity plots in Fig. 19 and the corresponding RMS plots in Fig. 20. For all chamber lengths where precession is detected (except for L/D = 4.5), there is entrainment-into-the-chamber in a round region opposite to the region of outflow. The general shape that can be resolved from the contour plots is similar as found in Figs. 17 and 18. The main difference is that by changing the chamber lengths there is a change in the strength of the exiting jet. The maximum inflow into the chamber of surrounding fluid occurs at shorter chamber lengths and this corresponds also to the conditions where maximum RMS intensity is present in the exiting jet flow. The area of inflow into the chamber decreases in size as L/D increases, disappearing completely at chamber lengths L/D ≥ 3.5. The RMS velocity intensity also decreases indicating that the entrainment-into-the-chamber of fluid into the cavity plays a role in both the intensity of the exiting jet and its RMS characteristics.

Fig. 19
figure 19

Conditionally averaged mean axial velocity distribution in precessing mode at the chamber exit plane for a Re = 32,400 with chamber lengths L/D = (a) 2.0, (b) 2.5, (c) 2.75, (d) 3.0, (e) 3.5, (f) 4.5

Full size image
Fig. 20
figure 20

Conditionally averaged RMS velocity distributions in precessing mode at the chamber exit plane. Re = 32,400 and chamber lengths are the same as in Fig. 19. Contours have been smoothed with a 5 × 5 linear filter

Full size image

A surface plot of the conditionally averaged axial velocity component is shown in Fig. 21 for the maximum jet flow case of Re = 61,900 when L/D = 2.75. The overlaid color map represents the RMS in this velocity component and shows high in the region of high-jet velocity. The plot shows that there is an axis of symmetry in the velocity profile about the x-axis. A dashed velocity line profile along this axis is included to highlight the wall jet exiting the chamber and the inflow back into the chamber. This profile can be used to characterize the effect of Re and chamber length on the shape and behavior of the flow at chamber exit plane. These profiles were taken for all chamber length and Re combinations, at which precession occurred as determined by the mode-finding technique and are shown for each chamber length in Fig. 22. The axial velocity data for each Re is scaled against bulk inlet velocity, \( W_{e} \) and all Re are presented for each chamber length.

Fig. 21
figure 21

Surface plot showing the conditionally averaged mean axial velocity distribution of the jet in PJ mode for L/D = 2.75 and Re = 61,900. Color represents the RMS component of velocity. The edge of the chamber is shown with a solid line, and a line profile through the maximum on the x-axis as a dashed line

Full size image
Fig. 22
figure 22

Conditionally averaged mean and RMS velocity profiles of the jet in PJ mode. Symbols: Re = plus 10,000, open diamond 21,800, inverted open triangle 32,400, open square 40,800, open round 50,700, open triangle 61,900. Black markers indicate mean values; green/gray markers indicate RMS values

Full size image

The average and RMS axial velocity data shown in Fig. 22 collapse well for all Re except Re = 10,000 (marked with +), which is assumed here to be the result of the jet flow not being fully turbulent. All chamber lengths show a region of positive axial velocity between the chamber center and chamber wall, which reaches a maximum at ~r/R = 0.8 which is equivalent to the location y/R = 0.8, x/R = 0 in Fig. 21. On the opposite side of the chamber centerline, the region of entrainment-into-the-chamber is apparent as a negative velocity. As the chamber length increases from L/D = 2 in Fig. 22a, both the maximum average positive axial velocity out of the chamber as well as the negative axial velocity into the chamber decrease in magnitude. At chamber lengths L/D ≥ 3.5, there is no apparent entrainment-into-the-chamber and at a chamber length of L/D = 4.5 in Fig. 22f, the axial velocity profile begins to become symmetric about the nozzle centerline. The RMS profiles of axial velocity reveal high fluctuations in the region of highest positive axial flow and low fluctuations in the region where surrounding fluid is being entrained back into the chamber.

The influence of the chamber length can be seen in a comparison plot of all chamber lengths and all Re conditions in Fig. 23. In these plots, all Re conditions (except for Re = 10,000 which is excluded) are grouped together for a single chamber length using the same plotting symbol. The conditionally averaged profiles in Fig. 23a clearly show the entrainment-into-the-chamber with a negative flow into the chamber for r/R = −1 → ~0.25 and the outflow from the chamber of the wall jet for r/R = ~0.25 → 1. There is a clear trend of increasing magnitude of the flow with decreasing chamber length. The position of the maximum outflow velocity is in a similar location of r/R~0.8 for all Re cases plotted. The RMS velocity data shown in Fig. 23b highlights that with decreasing chamber lengths there is a significant increase in axial velocity fluctuations.

Fig. 23
figure 23

Conditionally averaged a mean and b RMS axial velocity profiles for all Reynolds numbers at different chamber lengths. The condition Re = 10,000 is excluded from the plot

Full size image

The effect of Re on the maximum average axial velocity out of the chamber for different chamber lengths is shown in Fig. 24 of all Re cases with the maximum velocity, \( W_{\max } \), scaled against bulk inlet velocity, \( W_{e} \). Two trends are apparent in this figure. The first occurs at Re = 10,000, where maximum axial velocity appears to be inversely proportional to chamber length, i.e., \( {{W_{\max } } \mathord{\left/ {\vphantom {{W_{\max } } {\upsilon_{e} \propto \left( {{L \mathord{\left/ {\vphantom {L D}} \right. \kern-\nulldelimiterspace} D}} \right)}}} \right. \kern-\nulldelimiterspace} {\upsilon_{e} \propto \left( {{L \mathord{\left/ {\vphantom {L D}} \right. \kern-\nulldelimiterspace} D}} \right)}}^{ - 1} \). At all higher Re, all points collapse well with each other, indicating that Re has little effect on the scaled maximum outflow velocity compared to the effect of chamber length. For the nozzle diameter to chamber diameter ratio used in this investigation of d/D = 5, the average velocity in a long chamber that is approaching a long pipe will be 1/25th of W e or 0.04. The maximum velocity for a chamber length of at L/D = 4.5 is W max /W e  = 0.08 or double this value indicating that for this and any longer chamber lengths, the flow is approaching a symmetric velocity distribution.

Fig. 24
figure 24

Effect of chamber length on the relative maximum outflow velocity of the jet in PJ mode at the chamber exit plane for the different Re conditions investigated

Full size image

6.4 Area of the jet in PJ mode

The effect of Re and chamber length on the expansion of the jet while in precessing mode can be determined from the conditionally averaged axial velocity fields. The dimensionless area ratio, \( \gamma_{c} \), is defined as the ratio between the cross-sectional area of the jet, \( A_{j} \), and the area of the chamber exit, \( A_{c} = \pi R^{2} \) and characterizes the fraction of chamber area which is occupied by the jet and is defined as:

$$ \gamma_{c} \equiv \frac{{A_{j} }}{{A_{c} }} = \frac{{A_{j} }}{{\pi R^{2} }} $$
(20)

The jet is defined as any position in the exit plane where the average axial velocity is positive. The jet’s cross-sectional area can then be approximated as

$$ A_{j} \approx \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {{\mathbf{f}}_{i,j} \delta x\delta y,} } \quad \left\{ {\begin{array}{*{20}c} {{\mathbf{f}}_{i,j} = 1,} & {{\mathbf{w}}_{i,j} > 0} \\ {{\mathbf{f}}_{i,j} = 0,} & {{\mathbf{w}}_{i,j} \le 0} \\ \end{array} } \right. $$
(21)

This sums the areas of all finite rectangular regions of size \( \delta x \times \delta y \) centered about grid points within the averaged axial velocity array w whose axial velocity is positive. Array f is a Boolean array identical in size to w, where every grid point within it is valued at unity if the corresponding grid point in w has a positive axial velocity, and zero otherwise.

The influence of Re and chamber length on the area ratio, is presented in Fig. 25. The area ratio characterizes the relative size of the issuing jet from the chamber with respect to the chamber exit area. As γ c increases, so does the cross-sectional area of the chamber occupied by the jet. At a value of γ c  = 1, the jet occupies the entire chamber exit area and there is no entrainment-into-the-chamber of surrounding fluid. The figure shows an increase in γ c with chamber length, with the area ratios reaching unity for all Re when L/LD = 4.5. Two trends are apparent. One occurs at Re = 10,000, where γ c increases almost linearly over the range 2 ≤ L/D ≤ 3, then reaches its asymptotic value of γ c  = 1 at a chamber length beyond L/D = 3.5. For all higher Re, the area ratios are similar in value for each chamber length. The area ratio increasing in value more sharply as the chamber length increases up to L/D = 3.5, after which they converge to unity. These results highlights that the cross-sectional area of the jet and hence the length scale of the jet is only a function of the length of the chamber and not a function Re for these conditions.

Fig. 25
figure 25

Effect of chamber length on the area ratio, γ c of the jet in PJ mode at different Reynolds numbers

Full size image

7 Conclusions

A jet exiting from a smooth contraction nozzle of diameter, d into an axisymmetric chamber of length, L and diameter D = 5d has been investigated at the chamber exit for various Re and chamber lengths, L/D. This nozzle configuration differs from those previously reported in the literature in that it did not have an exit lip or center body. A Stereo-PIV approach measured the velocity field normal to the main flow direction at the exit to the chamber to capture the jet characteristics across the entire chamber exit. An axisymmetric (AJ) mode, with the jet along the nozzle axis, or a precessing jet (PJ) mode, where the jet exits the chamber as a wall jet and azimuthally rotates or precesses about the chamber axis was documented for several Re and chamber lengths. Determination of the jet exit mode allowed conditional averaging of the velocity field in PJ mode.

The probability of the jet being in PJ mode (P PJ) was found to be a strong function of the chamber length but only a weak function of Re for Re > 10,000. The highest values of P PJ were found for cavity lengths in the range of 2 < L/D < 2.75 with precession not found for L/D = 1. There is a sharp transition P PJ to lower values in the range 2.75 < L/D < 3.5 with a minimum occurring at L/D ~ 3. This range borders the chamber length of L/D = 2.75 which has often been used in the literature to investigate the precession jet phenomenon. For L/D > 3, P PJ again increased but at a slower rate compared to lower L/D ratios.

In both AJ and PJ modes, ambient surrounding fluid is entrained back into the chamber. Measurement of the mass flux ratio of inflow over outflow was used to define an entrainment-into-the-chamber ratio. This was found to not be a function of Re for a constant chamber length or the mode of the jet being either AJ or PJ. The value of entrainment-into-the-chamber was found to be a strong function for chamber length with a maximum value at L/D = 2.

Conditional averaging of the axial velocity of the flow in PJ mode showed that when scaling the field with the nozzle inlet velocity, W e there is little variation in the distribution of average axial velocity across the chamber exit with Re. Increasing L/D resulted in a reduction in the measured maximum average axial velocity for both flow out-of and into the chamber. For L/D ≥ 3.5 negative velocities are not observed in the conditionally averaged axial velocity plots. Line plots of the average axial velocity across the chamber exit and passing through the jet maximum are shown of collapse well for all Re, except Re = 10,000, when scaled with the inlet velocity, W e . The RMS field is also seen to scale in a similar manner with the highest RMS values overlapping the region of the maximum jet velocity.