Laser stripe measurements of near-wall solid fraction in channel flows of liquid-granular mixtures

Abstract

A simple, robust, and accurate imaging technique is proposed to measure granular concentration profiles in channel flows of liquid-granular mixtures. We focus on moderate to high granular concentrations (5–50%), for which optical access is restricted to regions close to a transparent wall. To measure concentrations in this range, we illuminate solid grains moving near the wall using a transverse laser light sheet. The evolving shape of the laser stripe, deformed by passing grains, is then monitored using an oblique camera. Statistics of the granular distance to wall can thus be acquired and converted to volumetric solid fraction measurements. The method is verified using fluidization cell tests and applied to open-channel sheet flow experiments. Free of any parameter adjustment, the laser stripe method is found to yield good results, and allows joint measurements of granular velocity and solid fraction profiles.

1 Introduction

Granular flows, both dry and liquid-saturated, are encountered in a variety of industrial and environmental processes. These include solids handling, sea bed dredging, river bed load transport, and torrential debris flows. We focus here on water-saturated flows of moderate to high granular concentrations (ratio of solid to total volume in the range 5–50%). The distribution of solid fraction in these flows is of great interest because it largely determines the solid transport capacity of the channel, the rheological dynamics of the sheared granular phase, and the potential for turbulence damping due to density stratification. In the laboratory, such mechanisms are often studied in transparent-walled channels, offering optical access to the flow. At moderate to high granular concentrations, access to the flow interior is hindered by occlusion effects, with near-wall particles hiding those further inside. Nevertheless, near-wall measurements have been found to provide valuable information about a variety of flow behaviors. Alternative approaches not restricted to near-wall measurements include refractive index matching (Cui and Adrian 1997), gamma ray absorption (Pugh and Wilson 1999), and magnetic resonance imaging (Bonn et al. 2008).

Focusing on the near-wall region, particle tracking techniques have been successful at obtaining detailed profiles of granular velocities. Concurrent measurements of the solid fraction profile, however, have proved more difficult to obtain by imaging techniques. When occlusion intervenes, the number density of particles per unit area, readily estimated from side view images, does not reflect their actual volumetric concentration. One must then either exploit the two-dimensional patterns formed by neighboring grains in the image plane, or collect three-dimensional information. In earlier work (Capart et al. 2002; Armanini et al. 2005), we proposed and used 2D pattern statistics to estimate near-wall granular concentration. Unfortunately, empirical relations between patterns and concentration lack robustness, because particle arrangements are flow dependent as well as concentration dependent. In Spinewine et al. (2003), we therefore turned to stereoscopic techniques, obtaining more accurate and robust concentration measurements from the measured 3D positions of near-wall grains. The painstaking experimental care and heavy computational effort required by stereo techniques, however, have until now prevented their use in practical, large-scale experimental efforts.

In this work, we propose and test a novel technique that we find to be robust, accurate, and simple to implement. Like the approach of Spinewine et al. (2003), it is based on acquiring information in the normal-to-wall direction. Instead of using a stereoscopic principle, however, the approach uses a single camera combined with a laser light sheet. The laser sheet illuminates a thin bright stripe where it intersects the wall-facing surfaces of moving grains. This stripe can then be imaged at an oblique angle by the camera to measure distances between illuminated grains and the wall. Intuitively, illuminated particles will, on average, be observed further away from the wall when the dispersion is dilute than when it is dense. To make this intuitive idea quantitative, a conversion model is required to relate distance-to-wall statistics to the volumetric granular concentration. We derive such a model by accounting for the concentration-dependent probability of occlusion as laser light travels in and out of the granular dispersion.

In the following sections, we present the proposed imaging configuration and algorithms (Sect. 2), and derive the conversion model (Sect. 3). We then verify the technique using fluidization cell tests (Sect. 4), before applying the approach to laboratory sheet flow experiments (Sect. 5). For this application, laser stripe results are compared with pattern and stereo measurements. Based on the verification and comparison results, we end with practical recommendations and conclusions (Sect. 6).

2 Image acquisition and processing

2.1 Image sequence acquisition

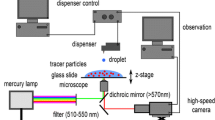
The adopted imaging configuration is illustrated in Fig. 1. The flow of a mixture of water and solid grains is observed through a transparent channel side wall. A red diode laser fitted with a special lens is used to emit a light sheet. The resulting laser-illuminated plane is oriented perpendicular to the wall and to the dominant flow direction. Through the transparent wall, the laser projects a thin stripe of bright light onto the wall-facing surfaces of the solid grains. This stripe is piecewise continuous: it is formed of a collection of short arc segments associated with distinct grains. Since moving grains are involved, the stripe shape evolves in time, likewise in a piecewise continuous manner as successive grains pass by. Depending on where near-wall grains happen to pass through the laser-illuminated plane, the short arc segments are observed at various distances y from the wall. Our objective is to acquire measurements of these distances and use them to estimate the near-wall granular concentration profile c(z). We describe in this section the image-processing steps used to measure the wall distances. In the next section, we will explain how distance-to-wall measurements can be converted to granular concentration.

Fig. 1

Imaging configuration adopted in the present work: near a transparent channel wall, the flow (F) of a liquid-granular mixture is illuminated by a transverse laser light sheet (L) and filmed using an oblique high-speed camera (C). The light sheet projects a laser stripe onto the wall-facing surfaces of the flowing grains (in red). Imaging measurements of the distance y between the laser stripe and the wall, at different elevations z, are used to determine the near-wall granular concentration profile c(z)

To measure the evolving distance-to-wall profile y(z, t), we image the laser-illuminated stripe using an off-axis high-speed camera (see Fig. 1). An oblique angle is chosen to obtain a well-resolved view of the stripe shape, while limiting the distortion due to refraction across the air–wall–water transitions. Because of the oblique angle, grains interposed between the laser-illuminated stripe and the camera cause the stripe to be partly occluded, and this will need to be accounted for in the conversion model. Various companies supply laser and camera devices that can be used to implement the proposed approach. The laser used in the present work is a Laser Components Flexpoint^® diode laser emitting red light at output power 40 mW and wavelength 660 nm. It is fitted with a special lens to obtain a light sheet of nearly uniform intensity over a fan angle of 45 degrees. By carefully focusing the laser, a narrow stripe of sub-millimetric width can be obtained at the channel wall. A Photron^® high-speed camera operated at a frequency of up to 500 frames per second is used to acquire gray scale digital images of resolution 1,024 by 1,024 pixels. The camera has a good sensitivity to light, permitting motion-induced blur to be avoided by reducing shutter opening times to 1/2,000 s. To obtain good statistics, we acquire video sequences of more than 1,000 frames for each run.

Starting from the raw image sequence, the following processing steps are needed. First, a calibrated relation between image and physical coordinates is used to transform oblique camera views into ortho-rectified images of the laser-illuminated plane. Second, bright points belonging to the projected laser stripe are identified on the ortho-rectified images, and their positions are recorded in a binning map. This map can then be used to obtain distance-to-wall statistics at different elevations. Finally, the binning map is also used to determine more precisely the position of the channel wall. The algorithms developed to carry out these steps are presented in detail in the next sub-sections.

2.2 Image calibration and ortho-rectification

The first step of the analysis is to convert distorted images acquired by the oblique camera into distortion-free, ortho-rectified images of the laser plane. The camera images are recorded as pixel arrays I[r, c], where r and c are row and column coordinates, and I is the brightness value of each pixel (taking values between 0 and 255 for gray levels going from black to white). Our objective is to convert these distorted images into ortho-rectified arrays J[i, j] = J(y _j , z _i ), where i and j are row and column indices, and the brightness values J are now sampled at regularly spaced positions (y _j , z _i ). These positions are drawn from a Cartesian mesh spanning the laser-illuminated plane.

To make the conversion, a relationship between image coordinates (c, r) and physical coordinates (x, y, z) is needed. This relation is calibrated by placing a target of known geometry inside the viewing volume (Fig. 2a). The target is a rigid aluminum plate, machined to high precision, on which is mounted an array of upright pins. Our physical coordinate system is chosen so that the mutually orthogonal laser-illuminated plane, inner channel wall, and flume floor correspond, respectively, to the planes x = 0, y = 0, and z = 0 (see Fig. 1). Prior to an experiment, the target is therefore positioned so that the plate edge and pin heads are in contact with the flume floor and wall, and the first column of pins is aligned with the laser stripe. To take into account the influence of light refraction, the target is immersed in water. The camera viewpoint, zoom, and focus settings are then frozen, and a calibration image is acquired. This is used to harvest via mouse clicks the image coordinates (c, r) of a series of reference points of known physical positions (x, y, z). Following Spinewine et al. (2003), the relation between image and physical coordinates is approximated by a central projection of the form

$$ \left( {\begin{array}{*{20}c} {\lambda c} \\ {\lambda r} \\ \lambda \\ \end{array} } \right) = {\mathbf{A}}\left( {\begin{array}{*{20}c} x \\ y \\ z \\ \end{array} } \right) + {\mathbf{b}}, $$

(1)

where λ is a scalar parameterizing the distance of each point from the center of the projection. Using at least six points of known image and physical coordinates, the nine coefficients of matrix A and the three coefficients of column vector b can be calibrated (see Spinewine et al. 2003 for details). In practice, we use least squares applied to 85 calibration points to gain better accuracy.

Fig. 2

Ortho-rectification of the video images: a image of the rigid target of known geometry used to calibrate the relation between physical coordinates (x, y, z) and image coordinates (c, r); b image of the flowing grains, highlighting the neighborhood of the laser stripe; c Cartesian mesh (0, y _j , z _i ) projected onto the video image in the neighborhood of the laser stripe (for readability, the mesh resolution has been reduced to 5 mm); d ortho-rectified image obtained for the mesh of higher resolution (Δy = Δz = 0.5 mm) used in the actual analysis. Brightness values are obtained by interpolation from the video image, then sent back to the physical plane (y, z). To improve clarity, raw images have been gamma corrected

Once the relationship is calibrated, we can process video images of the laser-illuminated grains (Fig. 2b). To convert distorted camera images into ortho-rectified images J(y _j , z _i ), target-to-source mapping is used. Points (0, y _j , z _i ) are first chosen at regularly spaced locations in the laser-illuminated plane, forming a Cartesian mesh of the desired resolution Δy = Δz = 0.5 mm. Equation 1 is then used to convert the physical coordinates of each mesh point (0, y _j , z _i ) to image coordinates (c _ij , r _ij ). This amounts to projecting the mesh onto the image plane (Fig. 2c). Finally, the brightness value J[i, j] of each mesh point is linearly interpolated from the camera image I[r, c] at the corresponding position (c _ij , r _ij ). When the resulting array J[i, j] is plotted in the physical coordinates (y _j , z _i ), an ortho-rectified image is obtained (Fig. 2d). The pixel rows and columns of image J[i, j] are aligned with physical directions y and z, and the position of each pixel center is known in metric units. Interpolation is repeated for each image of the video sequence, yielding a sequence of ortho-rectified views of the evolving laser stripe.

2.3 Stripe identification and binning

The next step of the analysis is to retrieve the evolving shape y(z, t) of the laser stripe. Using the results of the previous section, we start from a sequence of ortho-rectified images J[i, j, k]. Here, i and j are the row and column indices of the Cartesian mesh (y _j , z _i ), respectively, and index k denotes the k-th video frame acquired at time t _k . For each time t _k , we first locate the maximum brightness attained in each horizontal row i of the frame. The maximum brightness value J _max is given by

$$ J_{\max } [i,k] = \mathop {\max }\limits_{j} J[i,j,k], $$

(2)

and the corresponding location j _max is obtained from

$$ j_{\max } [i,k] = \mathop {\arg \max }\limits_{j} J[i,j,k], $$

(3)

where the operator arg max yields the argument j which maximizes J[i, j, k]. We interpret as bright spots belonging to the laser stripe only the points (i, j _max, k) for which the corresponding brightness J _max[i, k] exceeds a minimum brightness threshold J _min. To record the locations of these bright spots, we define a binning map M[i, j] counting the number of laser stripe hits at location (y _j , z _i ). The i-th row of this map is obtained by initializing M[i, j] to zero for all j, then iterating over all image frames k the statement

$$ {\text{if}}\,J_{\max } [i,k] > J_{\min } ,\quad M[i,j_{\max } [i,k]] = M[i,j_{\max } [i,k]] + 1. $$

(4)

In Fig. 3a–c, we illustrate the above steps and the resulting binning map M[i, j]. The binning map of Fig. 3c shows a clear influence of granular concentration on the pattern of recorded laser hits. In the lower part of the layer, grains are static and all laser hits are recorded in a narrow band near the wall. In the upper part of the layer, on the other hand, grains flow past the laser plane at random distances from the wall, and the map shows significant dispersion. The number of observed laser hits generally decreases with distance from the wall. This is because there is an increasing probability that laser light has already been intercepted by grains lying closer to the wall.

Fig. 3

Laser stripe identification and binning of the laser hits: a original ortho-rectified frame (without gamma correction); b locations of the points identified as belonging to the laser stripe; c binning map M[i, j] used to accumulate from 0 to 1,000 laser hits at each location over the entire video sequence, with the resulting counts color-coded according to the value of log₁₀(M[i, j] + 1); d identified channel wall position (dashed white line) superposed on the binning map M[i, j]. The line is close to, but does not coincide with the locus y = 0

For each elevation z _i , the associated i-th row of the binning map records a histogram of laser hits as a function of the distance to wall y _j . Upon normalization, this histogram approximates the probability density distribution of the observed distance to wall at level z _i :

$$ f_{i} (y_{j} ) \approx {\frac{M[i,j]}{{\sum\nolimits_{j} {M[i,j]} }}}\,{\frac{1}{\Updelta y}}, $$

(5)

where Δy is the bin width. It can also be used to estimate statistics such as the mean $\bar{y}$ and standard deviation σ of the observed distance to wall, via the expressions:

$$ \bar{y}_{i} = {\frac{{\sum\nolimits_{j} {M[i,j]y_{j} } }}{{\sum\nolimits_{j} {M[i,j]} }}} $$

(6)

$$ \sigma_{i}^{2} = {\frac{{\sum\nolimits_{j} {M[i,j](y_{j} - \bar{y}_{i} )^{2} } }}{{\sum\nolimits_{j} {M[i,j]} }}}. $$

(7)

We explain below how these can be used to estimate and check the near-wall granular concentration profile c(z). If the positions of the flume wall, laser plane, and calibration target could be perfectly aligned relative to each other, with the wall placed exactly at position y = 0 and the first column of pins perfectly aligned with the laser stripe, the above procedure would be sufficient to measure accurate distances from the wall. In practice, we are able to position and orient these elements to within a millimeter. However, this falls short of the desired sub-millimetric accuracy. We therefore use image processing to estimate a more precise wall position y ₀(z) ≠ 0. Assuming a planar wall, the inner profile of the wall is given by the straight line

$$ y_{0} (z) = y_{\min } + {\frac{{z - z_{\min } }}{{z_{\max } - z_{\min } }}}(y_{\max } - y_{\min } ), $$

(8)

where z _min, z _max are the lower and upper limits of the ortho-rectified images, and y _min, y _max are the corresponding intercepts that need to be determined to high precision. To find these intercepts, we differentiate the binning map M[i, j] in the normal-to-wall direction, and record the corresponding row maxima in a binary image B[i, j]. Coinciding with sudden jumps in the numbers of recorded laser hits, the non-zero pixels of B[i, j] cluster along a straight line associated with the wall. The line of best overlap is found by applying to B[i, j] a Hough transform (Duda and Hart 1972), constructed using the discrete delta function proposed by Smereka (2006; see Huang et al. 2008). The resulting straight line, adopted as our improved estimate of wall position, is shown in Fig. 3d. Using this refined wall position y ₀(z), we correct distance-to-wall measurements using the formula

$$ \eta (y,z) = y - y_{0} (z), $$

(9)

where η and y, respectively, denote the corrected and uncorrected distance to wall at elevation z. Corrected estimates are used for the calculations described in the next sections. By applying the above procedure separately to the upper and lower halves of height range 0 < z < 150 mm, we have also checked that the flume wall over this range is planar to a tolerance of 0.1 mm. To apply our method to flumes with less planar walls, we recommend that a piecewise linear or curved wall profile be determined instead of the linear profile of Eq. 8.

3 Conversion model

To estimate granular concentration from distance-to-wall measurements, a conversion model is needed. The model we propose is illustrated in Fig. 4. To determine the near-wall concentration c _i at elevation z _i , we restrict our attention to the plane z = z _i cut through the experimental configuration of Fig. 1. Within this plane, consider the fate of a single light ray emitted by the laser. Entering through the side, the ray will hit the solid grain nearest to the wall, illuminating a bright spot on the wall-facing surface of the grain. This bright spot will be seen by the oblique camera only if the corresponding light path out of the channel is unobstructed. The key observation underlying our conversion model is that the average distance travelled by a light ray before hitting a grain depends on the granular concentration. When grains are dilute, a ray is likely to travel a large distance before hitting a grain, and the opposite when grains are densely packed.

Fig. 4

Idealized model used to convert distance-to-wall measurements to granular concentration. The definition sketch shows a plane section through the configuration illustrated in Fig. 1. C camera; L laser; F Flow direction (other symbols are explained in the text). Camera calibration yields an equivalent camera position and angle α assuming no refraction (continuous lines). The true camera position and light path is shown in dashed lines

To derive our conversion model, we adopt a number of idealizations. The actual granular particles used in our experiments are cylindrical, not spherical, and present some size dispersion. For simplicity, however, we approximate them by spheres of identical diameter. This is reasonable in our view because concentration measurements result from large numbers of laser hits, sampled from multiple particles as they cross the laser sheet. The method thus averages over particles of different sizes and orientations, the resultant of which can be represented by a spherical particle of a single size (the equivalent spherical diameter corresponding to the average particle volume). Likewise, optical rays are assumed to have no breadth, which presumes that the laser stripe thickness and pixel size are no more than a fraction of the grain diameter. This is achieved in the experiments reported below by using a laser stripe of sub-millimeter thickness, a camera of sub-millimetric pixel resolution, and grains of diameter above 3 mm. Finally, we assume that all laser light rays penetrate the grain assembly in a direction normal to the flume wall, as would be the case if a planar collimated laser light sheet was used. In the actual experiments, the ray bundle emanates instead from a point laser, placed at elevation z _L . By restricting our attention to elevations not far from z _L , errors due to laser ray directions deviating from the wall normal can be kept small enough to have a negligible effect on distance-to-wall measurements.

Let μ denote the optical mean free path, or average distance that a light ray can travel in the liquid-granular medium before hitting a grain. We will proceed in three steps. First, we will assume that this mean free path μ is known and determine the resulting probability density distribution f(η) of observing a laser-illuminated spot at distance to wall η. Second, we will show how the mean free path μ, which is in fact unknown, can be retrieved from a measured pdf f(η). Finally, we will derive a relationship between the optical mean free path μ and the concentration c of solid particles in the medium.

Following Fraccarollo and Marion (1995) and Spinewine et al. (2003), we take the optical free path to be exponentially distributed with mean μ. This follows from assuming that a transition from liquid to solid along the ray path occurs with a constant probability per unit length (see e.g. Stirzaker 1999). The probability that a light ray entering through the sidewall will hit its first grain at a distance to wall in the range η to η + dη is then given by

$$ P_{1} = {\frac{1}{\mu }}\exp ( - \eta /\mu ){\text{d}}\eta . $$

(10)

It is not guaranteed, however, that the resulting bright spot will be observed by the oblique camera, because grains may intercept the outgoing light. This is the phenomenon of occlusion. Two types of occlusion can occur: self-occlusion and intruder occlusion. Self-occlusion occurs if the laser ray hits a portion of the grain surface at a location hidden from view of the oblique camera by other portions of the same grain. Such locations are found in a crescent-shaped sector of the sphere. Assuming that laser rays are equally likely to hit any point of the projected area of the sphere, the probability that self-occlusion does not occur is

$$ P_{2} = {\tfrac{1}{2}}(1 + \cos \alpha ), $$

(11)

where α is the viewing angle, dependent on the orientation of the oblique camera (see Fig. 4). Intruder occlusion, on the other hand, occurs if another grain intercepts the path of the outgoing light before it has a chance to reach the side wall. Assuming that grain positions are uncorrelated, and that the distance from bright spot to first grain hit along the outgoing path is again exponentially distributed, the probability that no intruder occlusion occurs is

$$ P_{3} = \exp \left( {{\frac{ - \eta /\mu }{\cos \alpha }}} \right). $$

(12)

This is equivalent to requiring that the exponentially distributed distance to first grain hit exceeds the distance η/cos α needed to reach the wall along the oblique outgoing path (see Fig. 4). Probability P ₃ decreases when the laser-illuminated spot is located further away from the wall, providing more opportunities for other grains to intrude. To estimate both self-occlusion and intruder occlusion, the angle of view α of the oblique camera must be known, and can be derived from the calibrated camera viewpoint. The optimum viewing angle depends on a variety of variables, including light refraction, particle occlusion, and camera resolution, and would be difficult to determine precisely. Fortunately, this angle may vary within certain limits without affecting the quality of the results. To avoid excessive occlusion and refractive distortion, yet measure the laser stripe deformation with sufficient resolution, we recommend angles between 25 and 35 degrees.

Finally, the probability P that a laser-illuminated spot is observed at a distance to wall in the range η to η + dn is given by the product

$$ P = P_{1} P_{2} P_{3} = {\frac{1 + \cos \alpha }{2\mu }}\exp \left( { - \left( {1 + {\frac{1}{\cos \alpha }}} \right){\frac{\eta }{\mu }}} \right){\text{d}}\eta . $$

(13)

The spot must both be located in that distance range and be seen by the oblique camera, implying the absence of occlusion. After normalizing the associated area to unity, the probability density distribution of the observed distance to wall is given by

$$ f(\eta ) = {\frac{1}{{\mu_{\text{obs}} }}}\exp ( - \eta /\mu_{\text{obs}} ), $$

(14)

where

$$ \mu_{\text{obs}} = {\frac{1}{1 + 1/\cos \alpha }}\mu . $$

(15)

Like the distribution of actual distances to wall, the distribution of observed distances to wall is exponential, but with a reduced mean μ _obs < μ. Here, self-occlusion is normalized out because it does not depend on distance to wall. Intruder occlusion does depend on distance, however, and this causes the observed mean distance to wall μ _obs to be smaller than the optical mean free path μ. Due to intruder occlusion, those laser hits that are recorded by the oblique camera tend to lie closer to the wall.

It is a simple matter to determine the mean μ _obs from the observed probability density distribution f(η). At each level z _i , a discrete version of the pdf f _i (y _j ) is obtained from the recorded binning map using Eq. 5. Upon correcting for the wall position y ₀(z) using Eq. 9, our estimate of the observed mean is therefore

$$ \mu_{\text{obs}} (z_{i} ) = \bar{y}_{i} - y_{0} (z_{i} ) = {\frac{{\sum\nolimits_{j} {M[i,j]y_{j} } }}{{\sum\nolimits_{j} {M[i,j]} }}} - y_{0} (z_{i} ), $$

(16)

where M[i, j] is the binning map obtained by imaging methods. Working backwards using first Eq. 16 then Eq. 15, we can thus estimate the optical mean free path μ based on the imaging measurements.

The third and final step is to relate the optical mean free path μ to the granular concentration c. For this purpose, consider again the laser ray shown in Fig. 4, but assume now that the ray passes straight through a series of granular particles as it goes from one side of the channel to the other. The successive distances Y _k (k = 1, 2, …) travelled between grains are exponential random variables of mean E[Y _k ] = μ. The successive distances S _k (k = 1, 2, …) travelled through solid grains, on the other hand, have expectation

$$ E[S_{k} ] = {\tfrac{2}{3}}D $$

(17)

where D is the grain diameter. This is again derived by assuming that laser rays are equally likely to hit any point of the projected area of a sphere. Summing over an infinitely long path, alternating between liquid and solid, the ratio of length travelled through solid grains to total length will attain the limiting value

$$ c_{\infty } = \mathop {\lim }\limits_{n \to \infty } {\frac{{\sum\nolimits_{k = 1}^{n} {S_{k} } }}{{\sum\nolimits_{k = 1}^{n} {(Y_{k} + S_{k} )} }}} = {\frac{{E[S_{k} ]}}{{E[Y_{k} ] + E[S_{k} ]}}} = {\frac{{{\tfrac{2}{3}}D}}{{\mu + {\tfrac{2}{3}}D}}}, $$

(18)

by virtue of the law of large numbers. Assuming that the medium is homogeneous and isotropic, the concentration given by this length ratio is equivalent to the volumetric solid concentration (Einstein 1906). This implies a linear relation

$$ e_{\infty } = {\frac{{1 - c_{\infty } }}{{c_{\infty } }}} = {\tfrac{3}{2}}{\,}{\frac{\mu }{D}}. $$

(19)

between limiting void ratio e _∞ = (1 − c _∞)/c _∞ and dimensionless optical mean free path μ/D. This dependence between μ and the limiting concentration c _∞ agrees with the result of Fraccarollo and Marion (1995) for the special case of identical spheres. Provided that the particle diameter D and mean optical free path μ are known, the limiting void ratio and granular concentration can therefore be estimated. For actual channel experiments, however, we must consider that the width W is finite instead of infinite. To take this into account, we note that a wall-to-wall path featuring n solid segments will feature n + 1 liquid segments. Replacing segment lengths by their expectations, the number of solid segments n must approximately satisfy the geometrical constraint

$$ n{\,}{\tfrac{2}{3}}D + (n + 1)\mu = W. $$

(20)

To estimate the granular concentration, on the other hand, we divide the length travelled through solid grains by the channel width

$$ c = {\frac{{n{\,}{\tfrac{2}{3}}D}}{W}}. $$

(21)

Eliminating n between these two equations, we obtain a linear relation

$$ e_{\text{corr}} = {\frac{1 - c}{{c + {\tfrac{2}{3}}D/W}}} = {\tfrac{3}{2}}{\,}\mu /D. $$

(22)

between width-corrected void ratio e _corr and the dimensionless mean optical free path μ/D. As could be expected, the correction becomes important when the flume width W is narrow relative to the grain diameter D. We encounter this situation in the fluidization cell tests presented in the next section. For the granular concentration, likewise, we obtain the corrected estimate

$$ c = {\frac{W - \mu }{W}}\,{\frac{{{\tfrac{2}{3}}D}}{{{\tfrac{2}{3}}D + \mu }}}. $$

(23)

and this is the relation we will use to convert from optical mean free path μ to granular concentration c.

4 Model verification using fluidization cell experiments

To verify and demonstrate the proposed method, we conducted tests using two laboratory devices: a fluidization cell and an inclined open channel. The granular material used in both cases is the same and consists of extruded PVC pellets. Material of the same type was previously used in experiments reported by Armanini et al. (2005), Larcher et al. (2007), and Spinewine and Zech (2007). White in color, the PVC grains contrast well with darker surrounding fluid, and are ideal for automated imaging measurements. The material has specific gravity s = ρ _S /ρ _W  = 1.51, where ρ _S and ρ _W are the densities of solid grains and water. Lighter than natural sediment (s ≈ 2.65), the grains are more readily entrained by water, and this facilitates observation. The pellets are cylindrical in shape, with height approximately equal to diameter. Their equivalent spherical diameter D, defined as the diameter of a sphere of the same volume, varies between 3 and 4 mm. For the calculations, we will use mean value D = 3.3 mm determined from the measured volume of 500 grains. This and other properties of the granular material are listed in Table 1. In this section, we present the fluidization cell tests used to verify the laser method. Application of the method to steady uniform sheet flow in an inclined channel will be presented in the next section.

Table 1 Material properties of the cylindrical PVC grains used in the experiments

To validate the proposed approach, we obtain agitated dispersions of grains of controlled concentrations c in a transparent fluidization column (Fig. 5a). The perspex-walled column has a rectangular cross section of inner dimensions B × W = 100 mm by 50 mm and is 1.6 m high. A given dry mass m _S of solid grains is inserted into the column and immersed in water. Grains are then fluidized by a steady water discharge Q _W in the vertical upward direction. The discharge is pumped from a water tank and fed through a porous bottom layer (used to make the flow more uniform) into the fluidization column. Once drag and immersed weight equilibrate, the grains in the compartment move randomly, with null steady flux at any cross section. The agitated grains occupy a well-defined volume in the lower part of the cell, of height H, within which the concentration is steady and homogeneous in the mean. This fluidized volume expands or shrinks depending on the water discharge Q _W . By adjusting the water discharge, homogenous fluidized beds of different heights H can therefore be obtained. The corresponding granular concentration c is given by

$$ c = {\frac{{m_{S} }}{{\rho_{S} AH}}} $$

(24)

where A = BW = 5,000 mm² is the cross-sectional area, and ρ _S  = 1,512 kg m⁻³ is the density of the granular material (see Table 1). This will serve as the reference concentration against which to compare the laser stripe measurements. Two distinct series of tests were carried out with different camera viewpoints. Each series explored a wide range of water discharges and solid concentration. Overall, the tests cover the concentration range 0.037≤ c ≤ 0.50. The lowest concentration c = 0.037 corresponds to the largest fluidization discharge Q _W attainable in the column. The highest concentration c = 0.50, on the other hand, corresponds to a transition in fluidization regime to a non-homogeneous bubbling state.

Fig. 5

Set-up used for the fluidization experiments: a photo of the fluidization column; b imaging configuration. The column cross section has inner dimensions B × W = 100 mm by 50 mm

Since the walls of the fluidization column are transparent, we can apply the laser stripe approach. The corresponding laser and camera configuration is illustrated in Fig. 5b. To accommodate the vertical orientation of the column, the laser plane is now horizontal, and the camera views the measurement section obliquely from below. Directions x, y, z are rotated accordingly, so that y is again the normal-to-wall distance, and z the along-wall coordinate in the laser-illuminated plane (see Fig. 5b). The calibrated camera angle is calculated to be α = 35 degrees for the first series and α = 25 degrees for the second series of tests. The image domain covers the full frontal width of the column B = 100 mm, and ortho-rectified images are obtained at resolution ∆y = 0.5 mm. The first series of tests consists in 10 runs with distinct fluidization discharges. For each of them, sequences of 3,072 frames were acquired at a rate of 500 frames per second (fps). The second series of tests consists in 28 runs that explore 15 distinct discharges: for the upper 13 discharge values, two repeat sequences of 1,536 frames were acquired at different frame rates, i.e. 250 and 60 fps, respectively; the two lowest discharge values, corresponding to the dense limit, are imaged with 1,536 frames acquired at 60 fps. The sequences of all runs from both series are processed using the methods presented in Sect. 2.

Binning maps M[i, j] obtained for the first series of tests at three different concentrations, from dilute to dense, are illustrated in Fig. 6. Because the fluidized state is close to homogeneous in all three cases, no variation is observed in the along-wall z direction, except near the column boundaries at z = 0 and z = 100 mm. To avoid perturbations due to these boundaries, in what follows we restrict our analysis to a central band of the binning maps, corresponding to the 180 rows in range 5 < z _i  < 95 mm. In the normal-to-wall y direction, observed laser hits tend to cluster closer and closer to the wall (y ≈ 0) as the granular concentration increases. At higher concentrations, laser light rays tend to hit the numerous grains located closer to the wall, and those laser hits which by chance penetrate further inside the column tend to be occluded by interposed grains. These qualitative features are in good agreement with the assumptions underlying our conversion model, presented in Sect. 3.

Fig. 6

Binning maps M[i, j] obtained from fluidization tests at three different granular concentrations: a c = 0.13; b c = 0.23; c c = 0.43

To test our assumptions quantitatively, Fig. 7 shows probability distribution results P(y) for the same three tests illustrated in Fig. 6. Experimental frequencies are obtained from

$$ P(y_{j} ) = \frac{1}{N}\sum\limits_{i} {M[i,j]} $$

(25)

where M[i, j] is the binning map recording the number of laser hits observed at each location over the full image sequence, and N = 3,072 × 180 is the total number of laser hits that would be recorded without occlusion. This is equal to the number of image frames acquired times the number of binning rows retained. The curves show the predicted distributions which would result in the absence of occlusion (dashed lines) and with occlusion taken into account (continuous lines). Disregarding occlusion, each dashed curve represents probability P(y) = P ₁(y) = μ ⁻¹exp(−y/μ)Δy (from Eq. 10). Accounting for self-occlusion and intruder occlusion, each continuous curve represents probability P(y) = P ₁ P ₂ P ₃ (from Eq. 13). Curves are calculated using the mean optical free path μ predicted by Eq. 22, based on the reference value of concentration c (determined from the height H of the fluidized bed). The curves thus represent independent predictions, without any fitting to the recorded frequency data. By taking occlusion into account (as explained in Sect. 3), good agreement is obtained between the predicted and observed frequencies. For all concentrations, the recorded data fall close to the predicted exponential distributions, indicating that our assumptions regarding optical mean free path and the effects of occlusion are good approximations of reality.

Fig. 7

Distribution of the probability $P[y_{j} - {\tfrac{1}{2}}\Updelta y \le y \le y_{j} + {\tfrac{1}{2}}\Updelta y]$ of observing a laser hit in the j-th column of the binning map M[i, j], for fluidization tests at three different concentrations: (a) c = 0.13; b c = 0.23; c c = 0.43. Dashed lines show the predicted probability P = P ₁ in the absence of any occlusion effects (see Eq. 10). Continuous lines show the predicted probability P = P ₁ P ₂ P ₃, taking into account self-occlusion and intruder occlusion (see Eq. 13). Dots show the experimentally recorded frequencies

To further check the conversion model, we plot in Fig. 8 aggregate results from the two series of tests. We check first the exponential character of the distance-to-wall distribution. For perfectly exponential probability distributions, the standard deviation σ = μ is equal to the mean. In Fig. 8a, we verify that this property is approximately satisfied by the distance-to-wall data recorded in the 38 experiments. Next, we test in Fig. 8b the linearity of the relation between the corrected void ratio e _corr and the dimensionless optical mean free path μ/D (see Eq. 22). Here, the corrected void ratio is calculated using the known reference concentration c, grain diameter D and channel width W. On the other axis, the optical mean free path μ is calculated from the laser binning map M[i, j] using Eqs. 15 and 16. Good linearity is observed, with a consistent trend for both series of tests, and the data fall close to the line of perfect agreement. Finally, we plot in Fig. 8c the concentration obtained by laser stripe imaging (c from μ, Eq. 23) against the reference concentration (c from H, Eq. 24) estimated from the height H of the fluidized bed. The two different estimates of concentration are found to closely agree with each other. We emphasize that the good agreement shown in Fig. 8 is obtained without fitting or parameter adjustment. As the conversion model includes no free parameter, the comparisons provide a rigorous check of model outcomes and assumptions.

Fig. 8

Fluidization test results used to verify the conversion model: a exponentiality check, comparing the mean and standard deviation of the observed distance-to-wall pdf; b linearity check, plotting the calculated optical mean free path μ (normalized by 2/3 times the grain diameter D) against the width-corrected void ratio e _corr (see Eq. 22); c laser estimate of concentration (c from μ) compared with a direct estimate (c from H) based on the measured thickness H of the fluidized bed. Each test is represented by a data point and error bar, denoting the mean and standard deviation of 180 values calculated from individual rows of the binning map. Circles and triangles denote results from the first and second series of tests. Diagonals are lines of perfect agreement

To gauge uncertainties, error bars in Fig. 8c are estimated by calculating μ _i separately for each binning row, evaluating the mean and standard deviation over all rows, then converting the global mean μ ± one standard deviation to concentration. The resulting error bars are acceptably narrow, except for the highest concentration c = 0.50. Deteriorating performance at high concentration can be ascribed to three factors. First, the laser imaging estimate becomes more sensitive to small errors in distance-to-wall measurements. Second, granular agitation decreases: because near-wall grains explore fewer configurations during the time of image acquisition, statistics deteriorate. Finally, the fluidization state becomes less homogeneous, with grain-free bubbles starting to appear in an otherwise dense granular dispersion. The second factor can be mitigated by adopting a slower frame rate, ensuring that the near-wall grain configurations are uncorrelated on successive frames. This explains why the second series of tests, imaged at 60 fps in the dense limit, is associated with narrower error bars than the first series, imaged at 500 fps. All three factors can be mitigated by averaging over a larger data set, here by pooling together all 180 rows of the binning map (explaining why the global mean remains accurate). In practical applications, however, profiles of variable concentration are sought, and only a limited set of data can be accumulated at each level (see next section). In those conditions, measurements at certain levels may become unreliable for lack of sufficient data.

5 Sheet flow application and comparison with particle-based techniques

5.1 Experimental set-up and imaging configuration

Application of the laser-stripe method can now be demonstrated for laboratory sheet flow experiments. The set-up is composed of an open channel and hydraulic transport system, circulating water and solid grains in a closed loop. The channel is 5 m long, 200 mm wide, and 300 mm deep, with glass side walls and a Perspex floor mounted on a rigid frame, which can be inclined at slopes ranging from 0 to 23 degrees. The channel outflow is conveyed back to the channel inlet by hydraulic transport, using a sump pump and pipeline. The pumping system is especially designed for the conveyance of slurries and can re-circulate solid–liquid mixtures up to ratios of solid to total discharge of approximately 30% by volume. The total volumetric discharge Q (water + grains) is measured using an electromagnetic flow meter mounted on the supply pipeline. The granular material used is the same as for the fluidization cell experiments: PVC grains of equivalent spherical diameter D = 3.3 mm. Other properties of the material are summarized in Table 1.

A range of flow conditions can be obtained in the channel by adjusting discharge and slope. In all the experiments reported hereafter, the water-granular mixture flows over a loose bed composed of static, but erodible PVC grains, controlled by a downstream bed stop. By adjusting the slope of the flume, a deposit of uniform thickness is obtained, over which steady uniform flows of liquid and grains are observed. Moderate slopes in the range 0.6–4.5 degrees are examined, with total volumetric discharge Q in the range 6.1–10.9 l/s. The resulting granular transport layer is many grains thick, but does not invade the entire water depth, a transport regime known as sheet flow, intense bed load or immature debris flow. The granular concentration in such flows goes from dense at the bed to dilute at the top of the transport layer, providing an interesting set of conditions to test the laser stripe technique.

For comparison, we apply to the same flows two alternative measurement techniques, proposed, respectively, by Capart et al. (2002) and Spinewine et al. (2003). Both techniques are based on identifying the positions of near-wall particles, then analyzing particle configurations using the Voronoï diagram (see e.g. Okabe et al. 1992). In the first technique, a normal axis camera is used to acquire monoscopic images. Plane particle patterns are then characterized using the two-dimensional Voronoï diagram, formed of polygonal cells surrounding each particle center. Defining cell roundness by the ratio ξ = 4πA/P ² where A is the polygon area and P its perimeter, Capart et al. (2002) found that the average Voronoï cell roundness $\bar{\xi }$ could be related to the volumetric granular concentration c by the power law correlation

$$ c = c_{\text{rcp}} \left( {{\frac{{\bar{\xi } - \xi_{\min } }}{{\xi_{\text{rcp}} - \xi_{\min } }}}} \right)^{b} $$

(26)

where subscripts rcp and min designate the state of random close packing and the dilute state, respectively. For a granular material very similar to the one used here, Capart et al. (2002) estimated parameter values ξ _min = 0.73, ξ _rcp = 0.84, c _rcp = 0.64 and b = 3.5, which are the values that will be used below.

In the second technique (Spinewine et al. 2003), two cameras are used to acquire stereoscopic images, and spatial particle configurations are analyzed using the three-dimensional Voronoï diagram. This diagram is constructed on the set of 3D particle positions, supplemented by their mirror images across the side wall, and forms a set of polyhedral cells. For low to moderate concentrations, Spinewine et al. (2003) found that the average area $\bar{a}$ of Voronoï cell faces shared with the wall could be related to the volumetric granular concentration using the relation

$$ c_{\text{stereo}} = {\frac{{\pi D^{3} }}{6}}(\chi \bar{a})^{ - 3/2} $$

(27)

where χ = 0.92 was calculated by Monte-Carlo simulations. For high concentrations, however, it was found necessary to correct this estimate using the formula

$$ c = {\frac{1}{\kappa }}\tanh^{ - 1} (\kappa c_{\text{stereo}} ), $$

(28)

where κ = 1.2 is an empirical coefficient obtained by best fit from fluidization cell experiments. Equations 26 and 28 provide two alternative ways of estimating granular concentration and will be compared with the laser-based estimate of Eq. 23.

To simultaneously apply the laser method and the Voronoï techniques to the channel flows, we use the imaging configuration shown in Fig. 9. As before, a diode laser oriented normal to the side wall is used to project a brightly illuminated stripe onto the near-wall grains (Fig. 9a). The shape of the laser-illuminated stripe is again captured using an oblique camera, of calibrated orientation α = 32 degrees. To apply particle-based techniques, a second camera is now added, having viewing axis normal to the wall (α ≈ 0). This is used to apply the 2D technique of Capart et al. (2002), and capture the plane positions of near-wall grains. Furthermore, the normal and oblique cameras are synchronized to allow stereoscopic imaging and application of the 3D technique of Spinewine et al. (2003). In addition to the laser, two flicker-free light sources illuminate the entire viewing window, making individual PVC grains visible on the oblique and normal camera images. To increase depth of field and obtain sharp images of the bright laser stripe, a smaller aperture is chosen for the oblique camera than for the normal view camera. All cameras and light sources are mounted on a rigid frame attached to the flume (Fig. 9b), allowing the channel slope to be modified without altering the imaging configuration. A local coordinate system is adopted, with the x axis parallel to the flume wall and floor, the y axis normal to the sidewall, and the origin at the intersection between floor, wall, and laser-illuminated plane.

Fig. 9

Imaging configuration for the open-channel sheet flow experiments: a imaging configuration; b photograph of the set-up. Instrumentation includes the laser (L), the oblique camera (OC), a normal view camera (NC), and two flicker-free light sources (LS). The flow direction (F) is from left to right and the channel width is W = 200 mm

5.2 Monoscopic and stereoscopic particle capture

To apply the particle-based techniques of Capart et al. (2002) and Spinewine et al. (2003), two-dimensional and three-dimensional grain positions must first be determined. Starting from the raw video images illustrated in Fig. 10a–b, we proceed in the following steps. Having calibrated the camera viewpoints as explained in Sect. 2.2, we first convert camera images to wall-projected ortho-rectified frames. For this purpose, a Cartesian mesh (x _j , 0, z _i ) of resolution Δx = Δz = 0.25 mm is defined, and images are re-sampled at mesh nodes by bilinear interpolation. This yields ortho-rectified pixel arrays in which the physical position (x _j , z _i ) of each pixel (i, j) is known (Fig. 10c–d).

Fig. 10

Particle identification on normal and oblique camera views: a raw normal view image, highlighting region (c); b oblique view image, highlighting region (d); c ortho-rectified region of the normal view image; d ortho-rectified region of the oblique view image. Crosses on (c) and (d) indicate identified particles

The next step is to identify particle positions on each frame. Whereas Capart et al. (2002) and Spinewine et al. (2003) positioned particles on raw video images; here, we apply this step to the ortho-rectified frames. This has the advantage that particle positions are directly obtained in metric coordinates (x, z). It also prevents difficulties resulting from shape and size distortion. On images acquired under an oblique viewpoint, grains adopt an ellipsoidal shape, and the apparent pixel size of each grain varies depending on distance from the camera. Although grains have approximately the same physical size, their apparent pixel diameter varies from 6 to 12 pixels between the left and right limits of raw oblique images. These difficulties are removed when ortho-rectified frames are used, and the particle positioning algorithms proposed by Capart et al. (2002) can be applied without changes. Images are first convoluted with a Laplacian-of-Gaussian filter (Jähne 1995). Particle positions are then obtained by identifying local brightness peaks to sub-pixel accuracy. The resulting sets of two-dimensional particle positions are shown in Fig. 10c–d.

Because projection onto the wall is done under different viewpoints, particle positions do not perfectly coincide on frames obtained from the oblique and normal axis cameras. Instead, an apparent displacement is observed, dependent on particle distance from the wall. This stereoscopic information can be exploited to determine three-dimensional grain positions, provided that particles can be matched between the two viewpoints. The algorithms used for this purpose were presented in Spinewine et al. (2003). For each particle on one view, match candidates on the other view are sought in the immediate vicinity of the corresponding epipolar line. A global match minimizing residual distances is then sought under the constraint that each particle on one frame can be matched with at most one particle on the other. Not all particles are matched, because particles seen under one viewpoint may be occluded under the other. Once particles are paired, their three-dimensional positions are found by seeking approximate intersections between the corresponding rays issuing from the projection centers of the two cameras. The positions obtained in this way are located along the wall-facing surfaces of the grains. To determine the positions of particle centers, an offset equal to the particle radius (D/2 = 1.65 mm) must be added in the normal-to-wall y-direction.

Applied to the images of Fig. 10, the stereoscopic method yields the three-dimensional particle positions illustrated in Fig. 11. On Fig. 11a, grains are rendered in 3D as shaded spheres, with coloring used to indicate distance from the wall. Bright and dark spheres denote grains located near the wall and away from the wall, respectively. The reconstruction is found to perform reasonably well. Despite the possibility of occlusion, most particles identified on either the normal or oblique view have been successfully matched and positioned in space. As could be expected, the lower bed region features mostly bright particles located near the wall. In the upper region of the transport layer, by contrast, darker spheres further away from the wall can be observed in greater numbers. On Fig. 11b, a point cloud is used to plot the acquired particle positions in the transverse (y, z) plane. Again, grains are seen to align with the wall in the dense bed region, and to disperse randomly in the dilute upper region of the transport layer. In the same figure, two vertical lines are used to highlight the near-wall particle alignment observed in the lower part of the flow. The solid line is the wall position y = 0. The dashed line shows the expected location of particle centers for particles touching the wall, along plane y = D/2 one radius away. Due to errors in stereoscopic matching, a few particle centers are positioned on the wrong side of the flume wall. As this is limited to 5 particles among 682, the error rate appears acceptably low.

Fig. 11

Three-dimensional positions of the granular particles identified on stereo views 10c and 10d: a 3D rendering of the grains, colored bright to dark with increasing distance from the wall; b particle centers seen in cross section normal to the wall. The solid and dashed lines indicate wall y = 0 and parallel plane y = D/2 one particle radius away

5.3 Particle tracking parallel to the wall

Although our main objective is to use the particle positions to estimate concentrations, we can also use them to determine velocities parallel to the wall. Using particle positions extracted from ortho-rectified images, particle tracking velocimetry can be used to determine granular velocities (u, w) in the (x, z) plane. The algorithms we use for this purpose are described in Huang et al. (2009), and rely on a path-regularity indicator proposed in Capart et al. (2002). For each pair of match candidates on two successive frames (at times t _k and t _k+1), the associated displacement is extrapolated backward and forward (to times t _k-1 and t _k+2). The presence of nearby particles on the corresponding frames (at times t _k-1 and t _k+2) is then used to evaluate path regularity. Candidate pairs are finally selected by seeking pairs of maximum regularity, under the assumption that true particle paths tend to be reasonably smooth. For the sheet flow application of the present work, this is found to yield better results than the method based on pattern regularity used in Armanini et al. (2005).

The procedure described above to perform particle tracking velocimetry can be performed using images from either camera. Results for the normal and oblique camera, respectively, are illustrated in Fig. 12a, b. In both cases, particle positions were extracted from ortho-rectified images, and tracked based on path regularity. Results are presented in the form of binning maps, counting the number of measurements falling in a certain velocity range at each level z _i . Although the velocity cloud extracted from the oblique camera is more noisy (seen especially in the bed region), the velocity maps extracted from normal and oblique views appear to be in good agreement. To make the comparison more precise, we plot in Fig. 12c the mean velocity profiles $\bar{u}(z_{i} )$ extracted from both maps. Profiles based on normal and oblique images are seen to be in close agreement, save for slightly reduced velocities at the top of the profile obtained from oblique views. This could be due to a weak helicoidal circulation causing transverse velocities to contaminate the longitudinal velocities inferred from the oblique camera. For this example, however, discrepancies are small, and it appears possible to use ortho-rectified images from the oblique camera to obtain a good approximation of the mean velocity profile. In practice, this suggests that a single oblique camera could be used to simultaneously monitor the laser stripe shape normal to the wall (to estimate the concentration profile) and track particles parallel to the wall (to estimate the velocity profile). We caution, however, that this may not hold true for other flow conditions.

Fig. 12

Binning maps and profiles of longitudinal velocity obtained by particle tracking velocimetry: a binning map of velocities u obtained from normal view images; b binning map of velocities u obtained from oblique view images; c mean velocity profiles $\bar{u}(z)$ obtained from normal view (line) and oblique view images (dots)

5.4 Concentration results and comparison

We are now in position to apply the different techniques and obtain concentration measurements that can be compared with each other. In Fig. 13, we show detailed results for the same run used earlier in this section to illustrate the methods. This sheet flow run was obtained at a channel slope of 1.4 degrees, under total discharge Q = 9.8 l/s. Figure 13a shows the distribution of Voronoï face areas a obtained at different levels z _i using the stereoscopic technique. Figure 13b, by contrast, shows the corresponding distribution of the distance to wall y, obtained using the laser stripe technique. Both distributions are shown as binning maps, obtained by counting individual measurements falling in each bin over the full image sequence (1,536 images acquired at 500 frames per second). Because the stereo technique gathers data from the entire viewing window (instead of just the laser-illuminated cross section), data counts are larger and the binning map can be acquired at finer resolution. Otherwise, the two maps show similar trends: both the mean and dispersion of the area and distance signals increase as the granular phase goes from dense (lower part of the layer) to dilute (upper part of the layer).

Fig. 13

Binning maps and concentration profiles obtained by near-wall imaging: a distribution of the areas a of Voronoï cell faces shared with the wall, obtained using the stereoscopic method; b distribution of the wall distances y of laser stripe hits, obtained using the laser stripe method; c concentration profiles c(z) obtained using the laser stripe method (black dots), pattern-based monoscopic method (open circles), and stereoscopic method (crosses). The dashed line indicates bed concentration c _b  = 0.66

To compare the three methods, Fig. 13c shows concentration profiles c(z) estimated, respectively, using the laser (black dots), monoscopic (open circles), and stereoscopic methods (crosses). The vertical dashed line corresponds to the expected granular concentration in the static bed (see Table 1). For the laser stripe technique, we truncate profiles at the top and bottom based on the following criteria. At the top, measurements are disregarded when data counts become lower than 500 laser hits per binning layer over the duration of recording. At the bottom, they are disregarded when particles move across the laser sheet by less than their own diameter over the duration of recording. Since these criteria intervene where either the concentration or velocity becomes very low, they do not significantly affect the volumetric solid discharge obtained by integrating the product of concentration and velocity (see Eq. 30 below).

As anticipated, the solid concentration decreases from high values in the bed to low values at the top of the transport layer. Without any coefficient adjustment, the three independent estimates show a consistent trend over the whole depth, giving confidence in their applicability. Compared with each other, the different profiles exhibit some deviations. In the flowing transport layer (z > 150 mm), the stereoscopic estimate (crosses) is consistently lower than the laser stripe estimate (black dots). The monoscopic pattern-based estimate (open circles), on the other hand, matches the laser data in the upper part, and the stereo data in the lower part of the transport layer. A possible explanation for the lower stereo estimate could involve the influence of occlusion, removing from consideration a subset of the particles needed to determine the Voronoï cell faces shared with the wall.

In the bed region, (z < 140 mm), where one would expect values close to the reference bed concentration c _b  = 0.66 (dashed vertical line), the three methods yield irregular profiles. This is because all three methods rely on averaging individual measurements over many frames and/or particles. Since bed particles are nearly motionless, data from successive frames are not independent and instead repeatedly measure the same static assembly. Ways to circumvent this limitation would be to set concentrations equal to the bed value below a certain level, or to scan the measurement instruments along some length of the bed to explore different static particle configurations. To test this second approach, we conducted additional tests in which relative motion was induced between the laser sheet and a rigid granular bed. Rather than translating the measuring instruments, it was found more practical to leave the imaging system untouched and instead slowly translate the granular bed along the flume sidewall. 5,000 images were acquired, with the laser stripe spanning about 40 particle diameters. Put together, all stripe images thus cover an aggregate stripe length of 5,000 × 40 = 200,000 particle diameters. The method was then applied to increasingly large subsets of this length, covering K = 781.25, 1,562.5, 3,125, 6,250, 12,500, 25,000, 50,000, 100,000 and 200,000 particle diameters, respectively. The resulting bed concentration estimates c are plotted in Fig. 14 as a function of the number K of particle diameters involved in the statistics (a logarithmic scale is adopted for clarity). Error bars are obtained by taking the minimum and maximum values of the concentration estimated from each tenth of the length of each subset. Encouragingly, the resulting concentration measurements fall close to each other and to the reference bed concentration value of 0.66, indicated by a dashed line in Fig. 14. By increasing the dataset size 256-fold (from 781.25 to 200,000 particle diameters), measurement uncertainties are reduced from 10 to 0.5% of the mean. As anticipated, the uncertainty decreases when larger sets of uncorrelated particle arrangements are scanned by the laser stripe. This test shows that the laser stripe method remains applicable up to the static bed concentration c _b  = 0.66, provided that relative motion occurs between the laser sheet and the granular assembly. Only when static grains are illuminated by a stationary laser sheet do the statistics deteriorate so much that no reliable concentration measurement can be obtained.

Fig. 14

Measured concentration c of a rigid granular bed translated past the laser sheet, deduced from an aggregate laser stripe length spanning an increasing number K of grain diameters. The dashed line is the reference bed concentration c _b  = 0.66

To evaluate the methods further for flowing granular mixtures of variable concentration, reference volumetric data obtained independently from the imaging techniques are needed. No such data are available for the local concentration, since (unlike the fluidization cell tests) the channel sheet flows are not homogeneous. Global data can be obtained, however, by measuring the solid discharge at the channel outlet. For each experiment, we measured this solid discharge by collecting the flume outflow over a short time T in a meshed box. After allowing water to drain, the mass m of collected material was weighed. The volumetric solid discharge can thus be calculated from

$$ Q_{S} = {\frac{m}{{\rho_{S} T}}}\,{\frac{{\rho_{S} c_{b} }}{{\rho_{S} c_{b} + \rho_{W} S_{r} }}}, $$

(29)

where the second factor is a correction for water retained by capillarity in the granular bulk. In this correction, the specific retention S _r and bed concentration c _b are used to estimate the volume fractions of wetting water and solid grains, respectively (see Table 1 for parameter values). For comparison purposes, the volumetric solid discharge can also be estimated from the imaging measurements using the formula

$$ Q_{S} = W\int_{0}^{{z_{w} }} {c(z)\bar{u}(z)} {\text{d}}z, $$

(30)

where W is the channel width, z _w is the water level, $\bar{u}(z)$ is the mean velocity profile and c(z) is the concentration profile measured by any of the three techniques (laser, monoscopic, or stereoscopic). Note that Eqs. 29 and 30 are not expected to perfectly agree, since the flow may not be uniform over the channel width. For high transport rates, especially, wall measurements extrapolated to the entire width are known to underestimate the actual solid discharge (Armanini et al. 2005; Jop et al. 2005). For lower rates, however, transport is more uniform over width; hence, near-wall and outlet estimates should at least be approximately equivalent.

Figure 15 compares imaging estimates of solid discharge with outlet measurements for a series of 12 different runs. For each run, imaging estimates of the concentration profile c(z) were obtained from sequences of 1,536 images using the three methods described earlier: the laser stripe method (dots), pattern-based monoscopic method (open circles) and stereoscopic method (crosses). The same mean velocity profile $\bar{u}(z)$, obtained by tracking particles on normal camera images, was used in all three cases. As expected, the near-wall imaging methods significantly underestimate the solid discharge at high rates of transport, but come closer to outlet values at lower transport rates. For low to moderate rates of transport, laser stripe estimates come close to the line of perfect agreement, indicating that at least in this case it is the most reliable of the three. The three imaging estimates could be brought in line with each other by tuning the calibration parameters that intervene in the monoscopic and stereoscopic conversion formulas (see Eqs. 26 and 28). Here, we have not done so and use the values as calibrated in previous work. Encouragingly, the best agreement is obtained for the method that does not involve any adjustable parameter: the new laser stripe technique.

Fig. 15

Solid discharge Q _S estimated by near-wall imaging (in ordinate) compared with values measured at the outlet (in abscissa). Black dots: laser stripe method; open circles: pattern-based monoscopic method; crosses: stereoscopic method. The diagonal line is the line of perfect agreement

6 Conclusions

In the present work, we proposed a new method for the measurement of concentration profiles in channel flows of liquid-granular mixtures. The method is based on the acquisition and analysis of images of a laser-illuminated stripe, projected on near-wall grains. In contrast with stereoscopic methods, the approach requires only images acquired from a single oblique viewpoint. The same images, moreover, can be processed by particle tracking velocimetry to determine the granular velocity profile near the wall. Using a single camera, it is therefore possible to acquire joint measurements of concentration and velocity profiles. Unlike other methods, the conversion model proposed to interpret the measurements requires only geometrical parameters (grain size, channel width, camera viewpoint, and channel wall position). These can either be measured independently, or deduced from the images themselves.

We verified the method using fluidization tests and demonstrated its application to open-channel sheet flow experiments. Using a fluidization cell, we were able to verify both the outcomes and assumptions of the conversion model. Good agreement was obtained, without any parameter adjustment. For the sheet flow experiments, we compared laser, monoscopic, and stereoscopic estimates of concentration, as well as imaging and outlet estimates of solid discharge. Discrepancies could be expected for these comparisons. First, the stereo measurements were obtained in sub-optimal conditions, the camera configuration having been designed to the requirements of the laser approach. Second, the granular flux measured near the wall may differ from the width-averaged discharge measured at the outlet. Nevertheless, a fair degree of agreement was obtained.

In light of these results, we conclude that the laser approach yields measurements of accuracy better or equivalent to the stereo approach (dependent on how stereo cameras are positioned and calibrated) at highly reduced cost. The laser approach requires only a single camera, tolerates a less precise camera viewpoint calibration, and involves image processing algorithms of much reduced complexity and running time. We therefore recommend the approach as a simple, robust, and accurate method of measuring near-wall granular concentration profiles.

Nevertheless, the method is subject to a number of requirements and limitations. For the method to work, the resolution of the camera and thickness of the laser light sheet must allow the stripe shape to be resolved to a fraction of the grain diameter. In its current version, moreover, the method is limited to moving grains of a single grain size (or a narrow size range) observed near the channel wall. These limitations, however, could be relaxed in the future. First, a preliminary analysis performed by slowly translating a rigid bed assembly with respect to a fixed laser/camera system has shown that statistics greatly improve when a larger number of particles are imaged. Concentration data for slow-moving or static grains could therefore be obtained by repeating experiments with the laser stripe positioned at different locations, by using multiple laser stripes, or by slowly scanning the laser stripe along the flume (instead of keeping it stationary). This would resemble the topographic laser scans used by Ni and Capart (2006), Spinewine et al. (2009), and Huang et al. (2010). Second, bimodal or multimodal grain size distributions could be handled by extracting more information from the images, exploiting for instance the correlation structure of the distance-to-wall signal. Finally, concentration measurements inside the flow could be obtained by illuminating and viewing grains via thin periscope or borescope devices, instead of through the sidewall. A borescopic technique was recently proposed by Cowen et al. (2010) to measure grain velocities in the sheet flow layer of a sediment-laden flow. We note that the method proposed, already in its current version, can be applied to dry granular flows as well as liquid-granular mixtures. These various avenues are suggested for further work.