1 Introduction

The relationship between the near wall structures and wall shear stress in a wall-bounded shear flow has been the subject of both computational and experimental studies for many decades. There is a consensus that streamwise or quasi-streamwise vortices dominate in the inner layer of the turbulent boundary layer, and are involved in the so-called “bursting” processes (Brooke and Hanratty 1993; Hamilton et al. 1995; Jimenez 2005; Jimenez et al. 2001; Kim et al. 1987; Robinson 1991; Schoppa and Hussain 2002, just name a few). Recently, equipped with a planar measurement technique, particle image velocimetry (PIV), several groups (e.g. Adrian et al. 2000) have studied flow structures in the logarithmic layer and concluded that hairpin structures form and travel as packets. Advances in volumetric, 3D measurement techniques, e.g. tomographic PIV (Elsinga et al. 2006), has enables characterization of vortical structures in regions extending from 15 to 47% of a supersonic turbulent boundary layer (Elsinga et al. 2007).

Most insight on buffer layer dynamics and its interaction with the wall have been obtained largely through direct numerical simulations (DNS) at low Reynolds numbers. Kravchenko et al. (1993), using a DNS database by Kim et al. (1987), found that streamwise vortices situated very close to the wall are strongly correlated with the local high skin friction. These findings have motivated numerous attempts to develop schemes for drag reduction, e.g. Kim (2003).

Experimental assessment of relationships between turbulent structures and wall stress require simultaneous measurement of both with sufficient spatial resolution. Various techniques have been developed and implemented for measuring the wall shear stress, using oil film interferometry, chemical probes, or hot-wire MEMS sensors, as summarized in several reviews (Ho and Tai 1998; Lofdahl and Gad-el-Hak 1999; Naughton and Sheplak 2002). Recently, Foucaut et al. (2006) used high resolution stereo PIV velocity measurements to obtain the mean velocity profile in the viscous sublayer, and from it, the wall shear stress in a turbulent boundary layer. However, to the best of our knowledge, we do not have simultaneous 3D experimental data on buffer layer flow structures and their resulting distributions of wall shear stress. Consequently, the aforementioned analysis of DNS data provides the only direct evidence on relationships between small structures in the inner part of the boundary layer and wall shear stresses.

In this paper, we apply a recently developed technique, in-line digital holographic microscopy (Sheng et al. 2006), to simultaneously measure both components of the instantaneous wall shear stress, and 3D velocity distribution in the 0 < y + < 100 range. The measurement resolution is equivalent to current DNS, five wall units in the stream- and span-wise directions, and about one wall unit in wall-normal direction.

2 Facility and measurement techniques

2.1 Facility

Measurements are performed in a vertical 57 × 57 mm square duct facility (Tao et al. 2000, 2002; Zhang et al. 1997), and the sample volume is situated at 3.3 m (~60 width) downstream to a honeycombed entrance. As illustrated in Fig. 1, the flow is seeded locally with 2 μm polystyrene particle through a set of five 50 μm injectors located 40 mm (~800 injector diameter) upstream to the sample volume. The seeding fluid with 1% solid concentration, i.e. ~10,000 particles/mm3, is injected at 0.05 ml/s by a motorized syringe. The mean exit velocity is 2 mm/s, i.e. 0.1% of the centerline velocity, U c = 2 m/s. At this velocity ratio, the fluid containing the particles is expected to remain close to the wall (Gopalan et al. 2004), as confirmed by the present observation. Even 75 mm downstream of the injectors, the penetration depth of particles is only about 2 mm. This low injection speed and proper distance from the sample volume insure that the effect of injection on the near-wall flow in the sample volume is negligible. Also, to prevent adverse effects of surface discontinuities, the inner surface of the wall is kept intact in the vicinity of the sample volume, i.e. the bore containing the microscope objective does not penetrate into the inner wall. The measurement volume has dimensions of 1.5 mm × 2.5 mm × 1.5 mm in streamwise, wall-normal, and spanwise directions, denoted as x, y, z, respectively, which is equivalent to 90 × 145 × 90 wall units, as determined by measurements of shear stress discussed later. The corresponding velocity components are u, v, and w.

Fig. 1
figure 1

Flow facility and digital holographic microscope setup

Full size image

2.2 Digital holographic microscopy

To perform 3D velocity measurement of a dense cloud of particle in a flow with an extended depth, we have recently introduced the application of in-line digital holographic microscope (DHM) as a means of simultaneously tracking thousands of particles located in a dense suspension (Sheng et al. 2006, 2007). As shown in Fig. 1, this method records an enlarged in-line hologram. The microscope objective focuses the hologram plane, located outside of the sample volume (dash–dot line in Fig. 1b), onto a CCD array. Thus, the image is an interference pattern between light scattered from objects located in the sample volume and the illuminating collimated reference beam. It does not contain in-focus images of these objects. As discussed in the following section, this interference pattern contains information on both the shape and location of the particles. Theoretical analysis shows that the image plane contains a magnified hologram with a phase correction that becomes unity when the magnification is sufficiently large. Reconstruction of this hologram provides a stack of 2D light intensity distributions at evenly spaced depth, which is then analyzed to obtain a magnified 3D particle field. Each 2D image at depth, z 0, is reconstructed using Fresnel diffraction formula, i.e. by convoluting the digital hologram with an impulse response function (Milgram and Li 2002; Sheng et al. 2003), giving

$$ I_{{\text{r}}} (x_{0} ,\,y_{0} ;\,z_{0} ) = \iint {I_{{\text{h}}} (\underline {x_{1} ,\,y_{1} } )}\frac{{\exp \left\{ {j\frac{{2\pi }}{{\lambda z}}\left\lfloor {\left( {x_{0} - x_{1} } \right)^{2} + (y_{0} - y_{1} )^{2} } \right\rfloor } \right\}}}{{j\lambda z_{0} }}{\text{d}}x_{1} y_{1}. $$
(1)

Here I h is the intensity distribution in the hologram, and I r(x 0, y 0; z 0 ) is the reconstructed image containing particle traces at a distance, z 0, away from the hologram. In Sheng et al. (2006), we provide detailed data on resolutions, image quality and depth of focus (DOF). As shown there, the DHM substantially reduces the “depth-of-focus (DOF)” problem, namely that reconstruction of a spherical particle creates an elongated ellipsoidal image, whose length in the depth direction is typically (in non-magnified holograms) two orders of magnitude larger than the lateral dimensions. Using a DHM, the DOF decreases with increasing magnification. For example, with a 10× objective, DHM reduces the DOF of a 2 μm particle down to 6–10 times the particle diameter, as determined from the depth at which the intensity distribution decreases to 75% of its peak value.

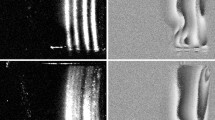
A 2 × 2 K CCD camera (Kodak ES 4.0) is used to record a pair of in-line holograms of the sample volume seeded with particles, with in-pair time interval of 80 μs. Numerical reconstruction of 2D wall-parallel planes is performed every 2 μm, totaling 1,250 planes for each hologram. Figure 2 shows a small section of a sample hologram, demonstrating the fringe patterns generated by the particles. Figure 2b–d show reconstructed pairs of particle images at two distance ranges from the wall, as well as a collapsed image of all the particles pairs seen at y + < 30 (wall unit is 17 μm, as we show later). To determine the 3D coordinates of each particle we use a 3D segmentation procedure (Sheng et al. 2003, 2006). Briefly, the reconstructed planes are initially thresholded based on the local SNR, i.e. based on \( [I(x,\,y,\,z) - \bar I_{{x \in V}} ]/\sigma _{{x \in V}} , \) where \( \bar I_{{x \in V}} \) is the mean intensity of a small volume around the particle of interest, and \( \sigma _{{x \in V}} \) is the standard deviation of intensity over this volume. Scanning through each plane, we generate a list of line segment that satisfy the intensity criterion. Neighboring line segments are then combined into 2D planar blobs. Repeating this procedure at each depth, we unite neighboring 2D segments into 3D particle traces. The location of a particle center is then estimated using the centroid of the 3D blob by intensity weighted averaging based on the original intensity distribution.

Fig. 2
figure 2

Small sample (400 × 400 μm) of recorded and reconstructed particle images. a Sample section of the digital hologram; b collapsed in-focus particle images within the 0 < y + < 30 layer; c particle image pairs within the 5 < y + < 10 layer; and d particle image pair within the 18 < y+ < 23 layer. The arrows show the particle displacements

Full size image

2.3 Velocity measurement

A flow chart of the velocity measurement procedure is presented in Fig. 3. Particle tracking is used to measure the velocity, i.e. each particle pair provides one vector. Background on 3D particle tracking methods based on images obtained using conventional photography or specialized systems, some of which involving complex analysis, can be found in Ge et al. (2006), Guasto et al. (2006) and Walpot et al. (2007). In dense particle suspensions located within an unsteady shear layer, and with only two exposures available, a tracking algorithm based on the nearest neighbor is insufficient, forcing us to develop a specialized algorithm. The guiding principle in tracking particles that we have opted for involves a trial-and-error process, which finds the most likely displacement between two exposures among all possible candidates. The possible candidates in the second exposure for a particle identified in the first exposure are selected initially among particles located within a search sphere centered on a “guess” location. The diameter of the search sphere is 0.25U 0, where U 0 is the freestream velocity. To define the guess vector and improve the efficiency and accuracy of the matching process, 2D slices of images are first collapsed into sets of 2D images, each combining all the images located within a 30 μm thick layer. Conventional (cross-correlation) planar PIV analysis is then applied to each image to obtain the volumetric two-component velocity distributions, which define the planar projection of the guess vector for the particle-tracking algorithm. Among the particles located within the search sphere, we determine the most likely displacement using the following multiple criteria:

Fig. 3
figure 3

Flow chart of procedures for calculating velocity

Full size image
  1. •

    Deviation from PIV prediction, i.e. the likelihood of being a good 3D displacement increases with decreasing deviation from the predicted PIV displacement. The maximum allowed deviation tolerance is 75% of the local velocity.

  2. •

    Similarities of (1) particle size, (2) total volume, and (3) intensity distribution within the 3D segmented volume of the two exposures, with the likelihood increasing with decreasing difference. The similarities for scalars, such as size, total volume, etc., are defined as the absolute difference of two scalar quantities normalized by their mean. In our analysis we typically allow them to range from 0 to 2, with 0 being the same quantity and 2 being the maximum allowed difference. The similarity of 3D intensity distribution of the same particle at different exposures is determined based on the difference between mean covariance of the two intensity distributions. We allow the normalized difference to vary between 0 and 1, with 0 implying highly correlated intensity distributions, and 1 indicating substantially different images.

  3. •

    Spatial smoothness of velocity distribution, i.e. continuity of velocity gradients, with likelihood increasing with decreasing spatial variance. To determine this variance, a 250 × 30 × 250 μm sub-region of 3D intensity distribution centered on the centroid of a particle in the first exposure is 3D spatially correlated with the sub-regions centered on the centroids of all the candidate particles in the second exposure. Each sub-volume contains multiple particles, and the magnitude correlation for the displacement between particle centroids is an indicator for agreement of this displacement with those of the surrounding particles. The higher this correlation coefficient is, the larger the chance that surrounding particles move in the same direction with the similar displacement.

  4. •

    Constraint on the magnitude of wall-normal gradients of streamwise velocity that varies with elevation. The mean values and range are determined based on results of prior calculations, and the likelihood is assigned assuming a Gaussian distribution.

  5. •

    Our experience indicates that the range of allowed differences in particle size, total volume, and intensity distribution depend on the local signal to noise ratio, which decreases with increasing local particle concentration. Thus, the last variable adjusts the allowed differences and assigned likelihood to be inversely proportional to the local particle concentration.

Totally, we have seven criteria for matching traces. Thus, each (not necessarily correct) displacement produces a “vector” in a 7D space with each criterion being a different axis. The vector with the highest scalar product with an “expected” vector (i.e. cosine of angle between them) is the best candidate for a matched pair. In the applied mathematics (image processing) community, this procedure is referred to as a “supported vector machine classifier” (Mavroforakis and Theodoridis 2006; Susskind et al. 2007). Initially, the likely displacements along with their assigned values based on the above criteria are examined manually. This manual checking is not performed for each 3D vector map. We perform it once for a certain dataset, i.e. a series of 200 hologram pairs recorded during the same run. For such a set, we select 2–3 holograms, e.g. at the beginning, middle and end of the series. The algorithm provides initial guesses for matched pairs, and we pick those that appear to give the correct velocity. This information is fed back to the program to initiate the rest of the analysis following the abovementioned criteria. Subsequent analysis of the selected as well as all the other holograms in the series is fully automated. At the present concentrations, we have encountered very few cases with ambiguity, and discarded them. Since the paring accuracy depends on particle density, noise level and complexity of the local flow, pairing results of the automated analysis are added into the supported vector machine. The resulting “expected” 7D vector is then recalculated, and is available while analyzing the next hologram. Once the criteria are established (and continuously updated), it takes about 5 min for the current Matlab based code to determine all the 5,000–10,000 3D vectors in one realization using a single PC processor. The reason for repeating the procedure for each dataset is uncertainty related to effects of variations in laser intensity, substantial changes in particle concentration and background noise due to, e.g. dirt on windows, etc. It is likely that once we gain sufficient experience, these criteria may become repeatable, and the initial manual examination may become unnecessary.

2.4 Accuracy and uncertainty of velocity measurement

The streamwise and spanwise resolutions are 0.7182 μm/pixel, referring to the pixel resolution of the image, corresponding to ~1 mm/s, i.e. 0.0005U c. The resolution in wall normal direction is lower due to the depth-of-focus problem. Although a great improvement over lens-less systems, one still has to determine whether it is adequate for accurately determining the wall-normal velocity. In attempting to measure this component we keep in mind that: (a) we have data on the well-resolved intensity distribution within the elongated spheroids, and (b) the shapes of traces of the same particle are very similar since they are subjected to the same recording conditions (e.g. intensity of laser and optical distortions). Previous attempts to measure the wall normal velocity from the displacement of the centroid of an elongated trace, using film based off-axis holography, are reported in Pu and Meng (2005). To determine how accurate this measurement is, we calculate the probability distributions of the normalized velocity divergence,

$$ \sigma = {{\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right)^{2} } {\left[ {\left( {\frac{{\partial u}}{{\partial x}}} \right)^{2} + \left( {\frac{{\partial v}}{{\partial y}}} \right)^{2} + \left( {\frac{{\partial w}}{{\partial z}}} \right)^{2} } \right]}}} \right. \kern-\nulldelimiterspace} {\left[ {\left( {\frac{{\partial u}}{{\partial x}}} \right)^{2} + \left( {\frac{{\partial v}}{{\partial y}}} \right)^{2} + \left( {\frac{{\partial w}}{{\partial z}}} \right)^{2} } \right]}}, $$
(2)

over 100 realizations. The average value of σ varies between 0, if the velocity distribution is divergence free, and 1 for random data (Zhang et al. 1997). Figure 4a compares the present PDF and cumulative distribution of σ to those of our previous 3D velocity distributions, obtained using two perpendicular views and complex off-axis optical setup (Sheng et al. 2003; Tao et al. 2002; Zhang et al. 1997). Clearly, the present results are substantially more divergence free than our previous data. To quantify the error in wall-normal direction, we also add random errors with standard deviation denoted as ε, to our measured wall-normal velocity component, and reevaluate the normalized divergence. As is evident, the divergence free condition deteriorates very quickly when the random error increases from ε = 1.25–2.5 mm/s. Thus, Fig. 4a suggests that our measurements have uncertainties of about 1 mm/s in all directions.

Fig. 4
figure 4

a Cumulative probability distribution of the present normalized divergence, σ (Eq. 1), in comparison with those obtained in previous measurements and when we artificially introduce random errors with standard deviation of ε. The insert is the probability density function. b Illustration of method for measuring the local wall shear stress using linear regression of velocity in the viscous sublayer

Full size image

The number of resolved vectors in individual realizations for the present data varies from 2,000 to 10,000 with a mean nearest neighbor distance of 50–100 μm, i.e. 3–8 wall units (provided later in Sect. 3.1). However, the particle are most concentrated near the wall (<1 mm), where they provide an averaged mean nearest neighbor distance in the wall normal direction of less than 15 μm (<1 wall unit, as demonstrated in Sect. 3.1), and about three wall units in streamwise and spanwise directions. This spatial resolution should not be considered as an upper limit, it is only the level achieved with the present data set.

2.5 Instantaneous wall shear distribution measurement

Instantaneous wall shear stresses, \( \tau _{{xy}} = \mu \partial u/\partial y|_{{y = 0}} \) and \( \tau _{{zy}} = \mu \partial w/\partial y|_{{y = 0}} , \) are estimated from the slope of local velocity profiles in the viscous sublayer, y < 75 μm, or y + ≤ 4.5 [following typical sign conventions: \( y^{ + } = y/\delta _{\vartheta } , \) \( \delta _{\vartheta } = \nu /u_{\tau } , \) \( u_{\tau } = (\tau _{w} /\rho )^{{0.5}} \)]. To determine this slope, we divide the viscous sublayer into sub-volumes of 150 × 75 × 150 μm, and apply linear regression over all velocity vectors measured within each volume, as illustrated by a sample in Fig. 4b. Thus, the spatial resolution of skin friction presented is 150 μm, about 9 wall units. The typical standard deviation of scatter around regression lines is ~8%. This uncertainty is well below measured spatial variations in stress, 60–300%, hence has minor consequence in interpretation of results.

2.6 Post processing

Inherently, the measured velocity fields are unstructured. To simplify subsequent analysis, the scattered velocity measurements are interpolated to the regular grids. Many data assimilation methods have been developed for interpolating unstructured data using finite element methods (Gunes and Rist 2007; Kim and Sung 2006; Vedula and Adrian 2005). In our analysis, we choose to use a simple but robust post-processing scheme based on Taylor expansion to obtain the velocity vector and velocity gradient tensor on a structured grids. For any given structured grid point, (x g, y g, z g), we locate the nearest 30 velocity measurements that are located within a search ellipsoid with a long axis of 5δ υ (~85 μm) parallel to the wall and a short axis of 2.5δ υ (~45 μm) perpendicular to the wall. Typically, such an ellipsoid contains more than 30 points near the wall. The measured velocity at (x m, y m, z m) is expanded to the 1st order Taylor expansion centered on the intended grid point using

$$ \left[ {\begin{array}{*{20}c} {u_{1} } \\ {v_{1} } \\ {w_{1} } \\ \vdots \\ {w_{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & {\Updelta x_{1} } & {\Updelta y_{1} } & \cdots & 0 \\ 0 & 1 & 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 1 & 0 & 0 & \cdots & {\Updelta z_{1} } \\ {} & {} & {} & {} & \ddots & {} & {} \\ {} & {} & {} & {} & {} & \ddots & {} \\ {} & {} & {} & {} & {} & {} & {\Updelta z_{n} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {u_{g} } \\ {v_{g} } \\ {w_{g} } \\ {{{\partial u_{g} } \mathord{\left/ {\vphantom {{\partial u_{g} } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}} \\ {{{\partial u_{g} } \mathord{\left/ {\vphantom {{\partial u_{g} } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}} \\ \vdots \\ {{{\partial w_{g} } \mathord{\left/ {\vphantom {{\partial w_{g} } {\partial z}}} \right. \kern-\nulldelimiterspace} {\partial z}}} \\ \end{array} } \right]. $$
(3)

The interpolated velocity is computed iteratively via inverse of Eq. 3 using single value decomposition (SVD, Press et al. 1992). The same interpolation method but with different number of expanding points is also used to obtain the velocity gradient tensors on the unstructured grid. The calculation of velocity and its gradients for each grid point is local and independent, i.e. we do not impose any boundary conditions, such as no slip or periodicity during the interpolation. Using this technique, the initially unstructured measured velocity map is then interpolated onto a grid with spacing of 20 × 15 × 20 μm (~1.2δ υ × 0.9δ υ × 1.2δ υ ), i.e. there is 66% overlap in the vertical direction and 76% in the horizontal direction.

3 Result

3.1 Sample data and mean scales

The present sample results are based on the first 500 3D velocity vector maps. Figure 5 shows a sample instantaneous velocity distribution, in this case at low seeding concentration, containing 1,228 vectors. A “large-scale” streamwise vortex is, nonetheless, observable in the projected y–z view.

Fig. 5
figure 5

a A sample 3D instantaneous velocity distribution with 1,228 vectors, and b end view (y–z projection) of the same flow. The location of a particle in the first exposure is marked by a dot, and in the second by an multiplication sign

Full size image

Superimposing u of all realizations, we can estimate the mean wall unit by linear regression to the velocity profile within the viscous sublayer, as illustrated by the inserts in Fig. 6a. The mean streamwise wall shear stress, \( < \tau _{{xy}} > |_{{y = 0}} \) (y = 0 will be omitted for brevity), is 3.19 N/m, i.e. the friction velocity, \( u_{\tau } = \sqrt {\tau _{{xy}} /\rho } , \) is 56.5 mm/s, the wall unit, δυ, is 17 μm. The friction Reynolds number, \( Re _{\tau } = u_{\tau } \delta /\nu, \) where δ is half channel height (δ+ = 1,500) is 1,400, and the outer variables Reynolds number, \( Re _{\delta } = U_{c} \delta /\nu, \) is 50,000. As shown in Fig. 6a, the mean streamwise velocity profile scaled with the inner variables follows the characteristic law of wall for mean streamwise velocity in the viscous sublayer, buffer layer, and lower part of the logarithmic layer. Since the present results are based on 500 realizations, the profile in the log layer is not fully converged yet. Distributions of Reynolds stresses and turbulent kinetic energy, presented in Fig. 6b, have the expected near-wall distributions, as obtained in DNS of 2D channel flow (Kim et al. 1987), but our profiles, especially in the log layer are still a bit wavy/jittery due to the limited data base. The amplitudes of these undulations clearly diminish with increasing database size (not shown). Table 1 compares the location of the peak of \( u^{{\prime 2}} \), as well as peak magnitudes of normal and shear Reynolds stresses in our measurements o the DNS results of Kim et al. (1987). In our data, \( u^{{\prime 2}} \) peaks at y + = 16.3 where \( u^{{\prime 2}} /k = 1.6. \)

In Kim et al. (1987), the corresponding values are 11.8 and 1.7. Although the actual values and location of peaks differ, trends are mostly consistent. Discrepancies may be attributed to differences in Reynolds number, geometry (square vs. 2D channel), and insufficient data especially in the outer parts of our sample volume.

Fig. 6
figure 6

a Measured mean streamwise velocity profile compared to the law of the wall. Insert: data points from 500 realizations and linear regression used for calculating u τ; b profiles of turbulence quantities, \( \left\langle {u^{2} } \right\rangle, \) \( \left\langle {v^{2} } \right\rangle, \) \( \left\langle {w^{2} } \right\rangle, \) \( \left\langle k \right\rangle \) and \( \left\langle {uv} \right\rangle \) normalized by u τ 2

Full size image
Table 1 Characteristic turbulence statistics compared to 2D Channel DNS simulation at lower Reynolds number (Kim et al. 1987)
Full size table

3.2 Statistics of wall shear stresses

Figure 7a–d shows two randomly selected but representative instantaneous wall stress distributions, the contour plot displaying \( \tau _{{xy}} (x,z), \) and the vector plots showing both components. Both have streak-like structures aligned in the streamwise direction. The vector plots reveal a divergent pattern on both sides of a stress maximum, and a convergent pattern on both sides of a minimum. Examination of the velocity distribution shows that the divergent pattern is the result of local stagnation flow by a strong sweeping event and the convergent pattern is caused by a local ejection. However, a significant fraction of the shear stress maps, ~50%, shows no streak-like distribution.

Fig. 7
figure 7

Left: sample instantaneous streamwise wall stress distributions. Right: corresponding vectors showing both components of the wall stress

Full size image

Compiled over 10,000 local wall stress measurements from the first 100 realizations, joint probability density (PDF) distribution of streamwise and spanwise wall stresses (Fig. 8) shows a symmetric distribution of the spanwise component, and a long tail of high streamwise component. Skewness and kurtosis for \( \tau _{{xy}} \) are 0.9 and 5.2, respectively, in very good agreement with wind tunnel data at comparable Reynolds numbers (Kimura et al. 1999; Miyagi et al. 2000; Ruedi et al. 2004). The PDFs of both components are compared to Gaussian distributions in Fig. 9a, b. They both display a non-Gaussian distribution at large values, as revealed in the log-linear plots, suggesting influence of intermittent large scale vortex structures (Aubry et al. 1997; Fiedler and Head 1966; Jiang and Zhang 2005; Zosimov 1996). Figure 8 also shows that the width of spanwise shear stress distribution increases with increasing streamwise shear, i.e. a large τ xy is often accompanied by a large τ zy . This relationship suggests that both are caused by the same phenomenon, e.g. near wall vortical structures.

Fig. 8
figure 8

Top left: joint PDF of streamwise and spanwise shear stress components. Right: PDF of spanwise component. Bottom left: PDF of streamwise component

Full size image
Fig. 9
figure 9

Probability density functions of wall stresses normalized by their standard deviations for a \( \left( {\tau _{{xy}} - \left\langle {\tau _{{xy}} } \right\rangle } \right)/\sigma _{{xy}} \); and b \( \left( {\tau _{{zy}} - \left\langle {\tau _{{zy}} } \right\rangle } \right)/\sigma _{{zy}}. \) Symbols: measured pdfs. Solid lines: Gaussian distributions. Inserts: Semi-log plots of corresponding pdfs

Full size image

3.3 3D buffer layer structures and associated wall stress

Simultaneous observations on near wall flow structures and wall stress provide insight on relationships between them. Spatial topologies of near-wall coherent structures can be visualized using λ2 (Jeong and Hussain 1995) or swirling strength (Adrian et al. 2000). We have found that iso-surfaces of both quantities capture similar “large-scale” flow structures, so only the λ2 distributions are presented. To highlight certain features, we also present the shapes of selected vortex lines, i.e. the stream-tracers of the vorticity field. All the displayed vortex lines (in Fig. 10) are initiated at y + = 5, x + varying from 0 to 85 with a spacing of 2.5 and z + = 75. To-date, we have carefully examined the 3D structure of only 100 3D distributions, and the brief discussion that follows, in which we classify them, is based on these observations. Although classifying structures is a subjective process, we have identified the following flow phenomena:

Fig. 10
figure 10

Instantaneous distribution of λ 2 iso-surfaces, wall shear stress and vortex lines (defined in the text): a counter-rotating vortex pair, \( {{\lambda _{2} \delta } \mathord{\left/ {\vphantom {{\lambda _{2} \delta } {u_{\tau } = - 220}}} \right. \kern-\nulldelimiterspace} {u_{\tau } = - 220}} \); b multiple streamwise vortices, \( {{\lambda _{2} \delta } \mathord{\left/ {\vphantom {{\lambda _{2} \delta } {u_{\tau } = - 350}}} \right. \kern-\nulldelimiterspace} {u_{\tau } = - 350}} \); c hairpin, \( {{\lambda _{2} \delta } \mathord{\left/ {\vphantom {{\lambda _{2} \delta } {u_{\tau } = - 240}}} \right. \kern-\nulldelimiterspace} {u_{\tau } = - 240}} \); d high lying outer-layer structure, \( {{\lambda _{2} \delta } \mathord{\left/ {\vphantom {{\lambda _{2} \delta } {u_{\tau } = - 300}}} \right. \kern-\nulldelimiterspace} {u_{\tau } = - 300}} \)

Full size image
  1. •

    Counter rotating pair of streamwise vortices with similar strength, shown in Fig. 10a, appears in 30 of the 100 realizations. These pairs of vortices are typically inclined at various angles, but frequently close to 45°, to the downstream direction. Pure streamwise alignment is rare. These vortices often seem to be originated from the wall, as in Fig. 10a, and then quickly lift off. Once extending away from the wall into the lower logarithmic layer, they tend to swerve partially towards the spanwise direction. The centers of these pairs are located in the 3 < y + < 40 range, but mostly around y + = 20, and the spacing between them is z += 50–70. Their normalized streamwise vorticity, ω x δυ/u τ, often exceed 1,000, i.e. 2/3 of the spanwise shear. Depending on the direction of rotation, the flow induced by a pair is either a downward, stagnation-like flow (“sweeping”) or “de-straining” motion away from the wall (“ejection”). During ejection, there is a stress minimum between the vortex pair (Fig. 10a). Conversely, during a sweep a stress maximum develops on the wall (not shown). The spatial variations of wall stress magnitudes associated with these structures are often large, ranging between 0.4 and \( 3\left\langle {\tau _{{xy}} } \right\rangle \).

  2. •

    Multiple quasi-streamwise vortices: we have observed 30 cases that have multiple quasi-streamwise vortices coexisting within the buffer layer, e.g. Fig. 10b. These structures are also primarily aligned in the streamwise direction, with tilting angle of less than 20°, but have much larger range of orientation in the spanwise direction compared to the counter-rotating pairs. They have a wide variety of spatial arrangements with spacing between vortices ranging from 5 to 90δυ. Their core sizes, as determined based on the magnitude of λ2, vary from 5 to 10δυ in the y + = 5–12 range, but extend to 20–40δυ in the upper parts of the buffer layer. There seems to be no preferred direction of rotation, and no correspondence in magnitude of neighboring vortices. In Fig. 10b, four streamwise vortices coexist in the sample volume, with one of them (bottom-right) situated very close to the wall, initially at y + = 5. Complex vortex–vortex interactions, i.e. vortices interlacing around each other, and vortex–wall interactions, i.e. lateral movement near the wall with significant distance from other structures, are clearly evident, even in the viscous and buffer layers. The resulting induced flow field is not as distinct as in the previous cases. Here, the values of ω x δυ/u τ ranges from −600 to +600, i.e. ±45% of mean spanwise shear. Spatial distributions of wall stresses beneath such complex flows do not display clear causal relationships, as it does for counter rotating vortex pairs. Their “footprints” on the wall stresses, nonetheless, bear some signatures when they are located close to the wall (e.g. Fig. 10b), but with little streamwise coherence. The associated stress magnitudes vary only between 0.8 and \( 1.2\left\langle {\tau _{{xy}} } \right\rangle \). However, one should not consider such events of less importance. Flows containing these types of structures contribute to ~35% of the mean wall shear stress.

  3. •

    Only outer layer structures: as illustrated in Fig. 10d, in 38 of the 100 cases, we do not see “small” buffer layer structures. In many of them there is evidences of induced motion by structures that are larger than the sample volume or located beyond the sample volume, e.g. a “large” scale sweeping flow or circular motion associated with large vortices. The associated stress magnitudes vary substantially.

  4. •

    Spanwise structures: spanwise structures forming a closed hairpin head, which reside entirely in the buffer layer are rare, two in the initial set of 100, but do exist. A clear snapshot of a newly generated hairpin is presented in Fig. 10c. Due to the limited data, we cannot attach statistical significance for this phenomenon. The “hairpin” has a shape of an “Ω“ whose legs are deeply embedded in the buffer layer, at y + = 12, whereas the head extends to y + = ~45. The legs are initially aligned with the spanwise direction, and then turn upward at an angle of 45° to the streamwise direction. The spacing between legs is ~45 δυ.

It is worth noticing that there is a spot with elevated wall shear stress in the vicinity of the kinked leg. This spot does not appear to be associated with entrainment of high momentum flow from higher elevation (as in the streamwise pairs), but may be related to the torque necessary to bend the vortex tube towards the streamwise direction from its initial spanwise orientation. At the wall, \( \rho \partial \omega _{x} /\partial x = \partial \tau _{{zy}} /\partial x \) and \( \rho \partial \omega _{y} /\partial y = \partial \tau _{{xy}} /\partial z - \partial \tau _{{zy}} /\partial x, \) i.e. spatial gradients of the wall shear stress must be involved with bending of the legs.

4 Discussion and conclusions

A DHM is used to simultaneously measure the spatial distribution of instantaneous wall shear stresses and the corresponding near-wall flows in a fully developed turbulent square duct at a moderately high Reynolds number, Re τ = 1,400. Instantaneous 3D flow fields are spatially resolved within a “microscopic” volume with size of 90 × 145 × 90 wall units. Particle tracking is used for calculating the velocity. Matching of particle pairs is perform using supported vector machine classifier based on multiple criteria including estimates of velocity using PIV analysis, size and shape of the reconstructed particle, as well as smoothness in velocity and its spatial gradients. Conservatively, we claim in the paper that the spatial resolution near the wall in streamwise and spanwise directions is 3–8 wall units (depending on seeding), and one wall unit in the wall-normal direction, mostly based on the present non-uniform seeding density. However, judging from the distributions of divergence and statistics of mean flow and fluctuating quantities, the flows in the viscous sublayer, buffer layer and low portion of logarithmic layer are resolved down to ~1 wall unit in all directions. The uncertainty in velocity is estimated to be better than 1 mm/s by comparing the statistics of normalized velocity divergence to divergence obtained by randomly adding an error of 1 mm/s to the wall normal component of our measurements.

Spatial distributions of wall shear stresses are approximated with the least square fit of velocity measurements in the viscous sublayer. The joint probability density distributions of instantaneous spanwise and streamwise wall shear stresses reveal that the streamwise component has a substantial tail towards the high stress values, whereas the spanwise component is essential symmetric with respect to zero. The distribution also reveals that large streamwise stresses are often accompanied by enhanced spanwise component. Examination of instantaneous wall stress distributions confirms the correlation between strong streamwise and spanwise components. The distributions also demonstrate the streak-like distribution for high stresses region. Thse observations suggest that the same near-wall structure is responsible for both high stress components, consistent with the model introduced by Kravchenko et al. (1993) using a DNS database. However, the strong correlation between stress components does not lead to a clear bimodal distribution for large streamwise stress, suggesting that: (1) significant portion of streamwise stress is not accounted for by a single-streamwise vortex model; in our case, only 35% of stresses measured have strong correlation between two components. (2) Significant portion of the regions with high streamwise stresses have no or small spanwise stress components. These results suggest that other mechanisms induce local stress extremes. Further discussion will be communicated by later publications using conditional averaging to distill the characteristics of responsible flow structures.

A wide variety of organized flow structures are observed in the buffer layer, some of which are deeply rooted in the viscous layer. For the present volume, the distance of the structure center from the wall ranges from 3 to 50 λυ. The characteristic size of these structures is typically 5–10 δυ in the buffer layer, but they grow to larger sizes while migrating away from the wall. Around 62 cases of first 100 measurements clearly contains coherent structures, amongst them 31 cases show counter rotating pair, 30 cases contain multiple quasi-streamwise vortices, and two cases of a baby hairpin.

Buffer layer structures leave strong “footprints” on the spatial distribution of wall shear stresses. Counter rotating vortex pairs, by far, show the strongest imprints: streak-like high and low stress regions with large amplitude. Multiple quasi-streamwise vortices, on the other hand, generate more complex stress distributions due to their combined effects, but with small amplitude modulations. When streamwise structures are located in the buffer layer, enhanced momentum exchange between outer and inner parts of the boundary layer seem to be the main mechanism for augmenting and mitigating the wall stress. Another mechanism for a local stress peak involves kinking of the the spanwise vortex tube towards (quasi) streamwise direction. The associated change in vorticity must be accompanied with spatial gradients of wall stresses, i.e. a spot-like high stress region in the vicinity of the kinks.

We have demonstrated in this paper that DHM can be applied to simultaneously obtain the 2D wall stress distribution and 3D flow structures in the buffer layer of a turbulent boundary layer. The spatial resolution of the measurements is comparable to that of DNS. Such experimental data can be used for addressing many long-lingering questions about turbulence and coherent structures in buffer layers, and their effects on wall stresses in a turbulent boundary layer. Our on-going data analysis and future publication will focus on quantifying the relationship between location, strength and orientation of buffer layer structures and occurrence of local stress extreme.