Analysis of velocity interpolation schemes for image deformation methods in PIV

Abstract

The spatial resolution of PIV can be increased significantly by using an image deformation method (IDM) and very small grid distance (i.e. the final distance between vectors), therefore, also increasing the processing time. By using an interpolation scheme with a good spectral response, in the dense predictor step of the algorithm, it is possible to increase the grid distance without decreasing the spatial resolution therefore decreasing the total processing time.

1 Introduction

The application of an image deformation method (IDM) in PIV (Huang et al. 1993; Jambunathan et al. 1995) enables to have a significantly more accurate method with respect to the classical cross-correlation approach (Utami et al. 1991; Willert and Gharib 1991). Really, a percentage that varied between about 50 to about 75% of the teams that participated to the first, second and third International PIV Challenge (Stanislas et al. 2003, 2005), held from 2001 to 2005 used an IDM for the competition. Even if this method was introduced more than 10 years ago, there is still a strong interest in a further development of the algorithm also on account to the possibility of increasing the spatial resolution of the measurements.

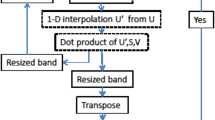
A very schematic flowchart of the algorithm is shown in Fig. 1, further details can be found in the review article by Scarano (2002). In the predictor and the correlation steps normally a cross-correlation approach with or without a weighting window is performed. The use of a weighting window to modify the spatial response for PIV applications have been introduced by Nogueira et al. (1999) and successively studied by various authors in particular the works by Nogueira et al (2005a, b) and Astarita (2007) are acknowledged. The interpolation schemes used in the image deformation step have been investigated by Astarita and Cardone (2005), and Kim and Sung (2006). The weighted average, that is a filtering step and can be placed also in other positions in the flowchart, has been investigated in the works made by Scarano and Schrijer (2005) and Astarita (2007). Clearly, the validation procedure has been the object of a significant amount of work in the past and one of the most recent papers on this subject is the one by Westerweel and Scarano (2005). In the refinement step, the dimension of the interrogation windows is reduced in the initial iterations.

Fig. 1

Schematic flowchart of a possible image deformation method for PIV

The only step of the algorithm that has not been analysed in detail in the past is the dense predictor one in which the predictor displacement field that normally is evaluated on a rather coarse grid is interpolated by using a bilinear interpolation scheme (IS) on a 1 pixel grid. Aim of this paper is to analyse the dense predictor step and propose a different approach that enables to have a better spatial response. In this way, it is possible to increase the grid distance and, as a consequence, decrease the processing time. A secondary aim is also to introduce a new interpolation scheme for the image deformation step that enables to obtain better results with respect to the classical bilinear one without increasing the processing time.

The effects of a bilinear IS in the evaluation of the dense predictor are analysed in the next section, while in the following one other interpolation schemes are proposed. The performance assessment is conducted by using synthetic images in Sect. 4 and real images in Sect. 5, and finally the conclusions are drawn.

2 Effects associated to the dense predictor interpolation scheme

In order to deform the images, when the vector grid distance W _c is larger than 1 pixel, it is needed to interpolate the predictor displacement field over each pixel of the image. Most probably also on account to the easiness of the scheme, a bilinear interpolation scheme is usually used (Scarano 2002) to build the dense predictor.

Clearly, if the grid distance W _c is small and/or only large spatial wavelengths are present in the displacement field, this kind of interpolation scheme results accurate as it is clear from Fig. 2a where the real signal is a sinewave (continuous curve) with a spatial wavelength λ of 60 pixels and W _c  = 4. The circles indicate the points used for the interpolation while the squares the interpolated ones. When the spatial frequency is higher and W _c is relatively large the bilinear IS introduces both a modulation and, in general, distorts the input signal as shown in Fig. 2b where λ = 30 and W _c  = 10.

Fig. 2

Interpolation of a sinewave with a standard bilinear interpolation scheme: a λ = 60 and W _c  = 4, b λ = 30 and W _c  = 10. The squares are the interpolated values and the circles and the continuous line is the original signal

Under the hypothesis that the PIV algorithm is correctly represented by the flowchart of Fig. 1, the effects of a simple modulation, without a phase change, on the spatial resolution of the complete IDM method can be synthesized by the formula (Astarita 2007):

$$ m^{k} = m^{{k - 1}} bc + (1 - m^{{k - 1}} c)a $$

(1)

where, a, b and c are the modulation associated to the correlation, weighted average and dense predictor steps, respectively and m ^k is the modulation at the generic k iteration.

The stability criterion is (Astarita 2007):

$$ - 1 < c(b - a) < 1. $$

(2)

Thus, in some cases a modulation in the evaluation of the dense predictor can help to stabilise the process. On the other hand, if the condition expressed by Eq. 2 is satisfied, the modulation of the complete IDM can be evaluated by the following equation (Astarita 2007):

$$ m^{\infty } = \frac{a} {{1 - c{\left( {b - a} \right)}}} $$

(3)

from which it can be seen that, since normally b > a, increasing c results in a better spatial resolution.

The modulation of the bilinear interpolation scheme is difficult to analyse on account to the distortion of the input signal but it is evident that an improvement of the IS can enhance the performance of the PIV algorithm.

3 Interpolation schemes

In this paper apart from the classical bilinear approach other three different interpolation schemes, used in the dense predictor step have been analysed. It has been chosen to use a modern approach to bilinear interpolation, the well-known B-Spline schemes and an ideal interpolator based on the FFT. The linear interpolation schemes are a natural choice to reduce the computational burden. On the other side the other two IS are, to the author knowledge, the best approximation to an ideal interpolator.¹

3.1 Shifted bilinear interpolation scheme

Blu et al. (2004) introduced a different approach to the bilinear interpolation that is essentially based on a shift of the interpolation points and for this reason will be called shifted bilinear interpolation scheme. The frequency response function is enhanced at the cost of a small phase error. This interpolation scheme can be used also in the image deformation step and enables to improve the accuracy with respect to the classical bilinear IS.

3.2 Ideal interpolation scheme

For a periodic signal, it is possible to obtain easily an ideal interpolation by first transforming the signal in the frequency domain by using a standard FFT algorithm, then increasing the length of the FFT by inserting zeros in the high frequencies and finally by performing the inverse transform. An example of the application of this technique to the example of Fig. 2b is shown in Fig. 3. Since the signal is periodic, a perfect reconstruction of the signal is achieved.

Fig. 3

Interpolation of a sinewave with an ideal interpolator λ = 30 and W _c  = 10. The squares are the interpolated values and the circles and the continuous line is the original signal

In real PIV applications the signal is, normally, non-periodic and the straight application of the described method gives rise to the Gibbs phenomenon as it is clearly evident from the graph of Fig. 4 where the real signal is a sinewave (continuous curve) with a spatial wavelength equal to 120 pixels and W _c  = 4. Furthermore, even if various FFT algorithms, accepting an arbitrary size of the input vector, exists, it is well known that sizes with small prime factors are usually less time consuming.

Fig. 4

Interpolation of a sinewave with an ideal interpolator (Gibbs phenomenon) λ = 120 and W _c  = 4. The squares are the interpolated values and the circles and the continuous line is the original signal

The Gibbs phenomenon is linked to the discontinuity between the last and first point of the input signal and can be reduced by removing the jump. A possible way to reduce this phenomenon is to subtract a continuous linear function that passes through the two extreme points, then the modified signal is interpolated and finally the linear function is added again. The main drawback of this approach is that the size of the input signal does not change. A second approach based on a continuous extension of the input signal is pursued herein.

In the present work, a third order polynomial function is used to extend the input signal in a continuous way. First, the total number of points (input plus extension signals) is chosen as the first power of 2 that enables to have an extension that is long at least 40% of the input one so that the total number of points is increased of at least 40%. This choice is made in order to have a sufficiently large extension and insure that the final number of points is a power of 2 so that an efficient FFT algorithm can be applied. Then, in order to remove the discontinuity of both the signal and its first derivative, it is imposed that the cubic passes through the last two points and that at the chosen distance also passes through the first two points of the input signal. The procedure is shown in Fig. 5 where the input signal is identical to the one of Fig. 4 and is made of 8 points so that the extension signal is also 8 points long. The cubic extension is plotted as a dashed curve and the input signal is repeated in order to better understand the periodicity. In the same figure are plotted also the interpolated values that, as expected, do not suffer from the Gibbs phenomenon. It has to be noticed that if W _c is a power of 2. The number of points used for the inverse Fourier transform is also a power of 2 otherwise others small prime numbers appear as factors.

Fig. 5

Interpolation of a sinewave with an ideal interpolator and extension of the input signal λ = 120 and W _c  = 4. The squares are the interpolated values, the circles and the continuous line are the original signal and the circles and the dashed curve the extended one

When the interrogation window spans an even number of pixels the displacement vector is evaluated on a grid that is staggered of 0.5 pixel from the one relative to the dense predictor. Thus, even for W _c  = 1 by using a bilinear interpolation scheme there is a modulation; this problem is easily solved with the ideal interpolation since it is easy to shift, of half a pixel, the interpolated values by simply applying the shift theorem in the Fourier domain.

In order to extend the ideal interpolation to two dimensions, it is possible to interpolate first all the points in the x direction and then on the y direction. It is evident that such an interpolation scheme is sensible to the noise present in all the displacement field and this is clearly a drawback of the method.

3.3 B-Spline interpolation scheme

A family of interpolation schemes that normally performs well is the one based on the B-splines (Unser 1999). Some authors use, for the image deformation step, this interpolation scheme on account of the good spectral response. For a B-spline of order 2 an interpolation stencil of 3 × 3 points is needed so also in this case a prolongation of the signal is needed and herein this is done by using a mirror boundary condition on the edges.

4 Performance assessment with synthetic images

In order to asses the performance of the proposed interpolation schemes a one-dimensional sinusoidal shear displacement, synthetic image (256 gray levels) with ten wavelengths λ varying from 16 to 160 pixels is used for the comparison. The exact vertical displacement v is plotted as a function of the x direction in Fig. 6; each wavelength (apart for the largest for which only half wavelength is used) is repeated for a varying integer number of times and extends for around 80 pixels. A particle diameter equal to 3 pixels with a maximum deviation of ± 0.5 pixels, a mean particle intensity level equal to 60 with a maximum variation of ±20 and a particle density of 0.076 particles per square pixel is used. Uniformly distributed background random noise with an amplitude equal to 80 (i.e. with a maximum standard deviation of 23 and, consequently, with a value of the ratio between the noise standard deviation and the mean particle intensity level n = 0.38) is added only to the top half part of both images. Only the lower part of the images is examined and the noise is introduced only to verify the influence of it on the global ideal interpolation. The cross-correlation is evaluated by using the classical Blackman weighting window (WW) with W _a  = 32 pixels and the weighting average step is performed by using a Top Hat WW. A sixth order B-spline will be the reference interpolation scheme for the image deformation step, while the linear interpolation scheme introduced by Blu et al. (2004) will be also used. The displacement field is validated by using the algorithm proposed by Westerweel and Scarano (2005).

Fig. 6

Imposed exact displacement v as a function of x

Both the total error δ and the modulation transfer function (MTF) evaluated with the formulae defined in Astarita (2006):

$$ \delta = {\sqrt {\frac{1} {N}{\sum\limits_{i = 1}^N {{\left( {v_{i} - v} \right)}^{2} } }} } $$

(4)

and

$$ MTF{\left( \lambda \right)} = 1 - {\sqrt {\frac{{{\sum_{i = 1}^N {{\left( {v_{i} - v} \right)}^{2} } }}} {{{\sum_{i = 1}^N {{\left( {\sin {\left( {2\pi x/\lambda } \right)}} \right)}^{2} } }}}} } $$

(5)

are used for the performance assessment.

4.1 Effects of the interpolation scheme used to build the predictor

The effect of the interpolation scheme used to build the predictor is significant only in presence of very high wavelengths that are detectable only if a small filtering window is used in the weighted average step. As an example in Fig. 7 the mean, over the y direction, dense predictor is plotted for the three couples of sine waves having λ = 32 and 26 pixels for W _b  = 2, W _c  = 8 and 40 final iterations. The continuous curve is the exact displacement, the circles indicate the displacement field at the previous iteration and the squares the interpolated displacements. The typical linear pattern of the bilinear interpolation scheme (Fig. 7a) is clearly visible in the figure for both wavelengths. In particular, it is possible to note that, accordingly to the fact that the interrogation windows have an even linear dimension, the circles are not exactly superimposed over the squares but are shifted of half pixel. The nature of the shifted bilinear interpolation scheme is clearly evident from Fig. 7b where it can also be seen that, on average, the differences between the interpolated points and the exact one are decreased with respect to the previous case.

Fig. 7

Mean (circles) and interpolated (squares) displacements for various interpolation schemes: a bilinear, b shifted bilinear, c third order B-spline and d ideal interpolation. The continuous line is the original signal

A completely different behaviour is present for both the third order B-spline (Fig. 7c) and the ideal interpolation scheme (Fig. 7d), really a quasi sinusoidal pattern is found. The better representation of the sinewave will result in an improved accuracy of the complete algorithm.

4.2 Modulation transfer function and total error

The modulation transfer function is plotted, as a function of the normalised spatial frequency ω = W _a /λ, for various values of W _c and for the tested configuration in Fig. 8. It has to be noticed that for the case W _c  = 8, the Nyquist frequency coincides with λ = 16 (ω = 2), i.e. the maximum tested spatial wavelength so in this case no reconstruction is possible. For the bilinear interpolation scheme (Fig. 8a) and small spatial frequencies the differences are very small apart for the case of W _c  = 8. Since, the formula introduced by Astarita (2006) to evaluate the MTF is also sensible to the random error, the modulation transfer function is in this case fictitiously smaller. Indeed the significant amount of random error present is transformed by Eq. 5 into a decrease of the MTF. For ω > 1, the differences became significant even when the distance between windows W _c is only two pixels; the curves collapse again for W _c  > 4. For the shifted bilinear interpolation scheme (Fig. 8b), the modulation is less pronounced at the high frequencies but the random noise increases at the smaller ones. The differences between the second and third order B-spline (for the sake of brevity the former is not plotted) are very small and the MTF (Fig. 8c) is significantly better than the previous cases. Only the curve relative to W _c  = 8 deviates from the others at the very high frequencies. A similar behaviour is found also for the ideal interpolator (Fig. 8d). The presence of noise in the upper part of the images, that is not included in the present results, is perceived in a more significant way by the IS that uses more points; accordingly the global ideal interpolator is the more affected and this explains the slightly smaller MTF with respect to the B-spline method. Really, even if not shown, by using noiseless images this result is reverted and the ideal interpolator performs better especially at the higher frequencies.

Fig. 8

MTF as a function of the normalised spatial frequency for various interpolation schemes: a bilinear, b shifted bilinear, c third order B-spline and d ideal interpolation. The numbers in the legend indicate different values of W _c

A similar behaviour is found for the total error δ plotted in Fig. 9 as a function of the spatial wavelength λ. The shifted bilinear interpolation scheme (Fig. 9b) performs better than the standard one (Fig. 9a) at the small wavelengths but introduces a significant amount of noise at the medium wavelengths. The ideal interpolator (Fig. 9d) has the smallest error at the small wavelengths but, as already said, is noisier at the higher ones. By using the third order B-spline interpolation scheme (Fig. 9c) the error is normally smaller than the one relative to the other schemes. As it is clear from the figure, in this case, the filtering effect associated to an increase of the grid distance is usually beneficial at the larger wavelengths and slightly worsen the smaller ones. As shown by Fig. 10a the only significant improvement of the third order B-spline with respect to the second order one is the capability to have a smaller error also for W _c  = 8 at the very high frequencies.

Fig. 9

Total error as a function of the wavelength for various interpolation schemes: a bilinear, b shifted bilinear, c third order B-spline and d ideal interpolation. The numbers in the legend indicate different values of W _c

Fig. 10

Total error as a function of the wavelength for the second order B-spline in the evaluation of the dense predictor and two IS in the image deformation step: a sixth order B-spline and b shifted bilinear. The numbers in the legend indicate different values of W _c

4.3 Influence of the shifted bilinear interpolation scheme in the image deformation step

The shifted bilinear interpolation scheme has not been used in the past for the image deformation step thus, it is interesting to compare the total error obtained with this IS with the one relative to the sixth order B-spline. The total error curves obtained by using a second order B-spline IS in the evaluation of the dense predictor and the shifted bilinear interpolation scheme in the image deformation step are shown in Fig. 10b. The comparison with Fig. 10a clearly shows that there is no appreciable difference between the two interpolation schemes at the high frequencies. On the other hand, even if the total error remains very small, also for the shifted bilinear IS, the differences for ideal images are appreciable at the large wavelengths.

4.4 Time performances

The analysis of time performances is a delicate point since different results can be found for different coding of the algorithm. In the present case at the first iteration, the cross correlation step is performed by using the FFT so that the complete correlation map is evaluated. In the next forty final iterations, the correlations are evaluated directly by considering only the five points needed to evaluate the Gaussian interpolation. In particular, when overlapping windows are used, since two successive cross correlation maps differs only by a small amount of data only the differences are evaluated thus, the speed of this step is significantly enhanced with respect to the FFT approach. When a maximum is not found with the direct correlation approach the software automatically evaluate the complete map; in the present conditions this normally happens for less than 1% of the total number of vectors.

The percentage time t _e needed to perform the dense predictor step is plotted as a function of the grid distance in Fig. 11a by using the sixth order B-spline in the image deformation step and in Fig. 11b by using the shifted bilinear one. Since for small values of W _c the total processing time is essentially linked to the predictor and correlation steps initially t _e is rather small for all the tested IS. For the two bilinear interpolation schemes, increasing the distance between vectors does not influence significantly t _e which is normally smaller than 5%. A completely different behaviour is found for the others IS, indeed, by using the shifted bilinear IS for the deformation of the images and the third order B-spline for the evaluation of the dense predictor, t _e reaches a maximum value a little smaller than 33%.

Fig. 11

Percentage time needed, for various IS, to perform the dense predictor step for two IS in the image deformation step: a sixth order B-spline and b shifted bilinear

By using a third order B-spline for the evaluation of the dense predictor and a sixth order B-spline IS in the image deformation step, the time needed to perform the main steps of the algorithm are shown in Table 1. In particular the worst, from the point of view of time consumption, configuration (W _c  = 1) is compared to the best one (W _c  = 8). For a grid distance equal to 1 the total time is about 10 times greater than the case W _c  = 8 but as already shown the total error only changes slightly at the high frequencies. For W _c  = 1 the correlation step is the most time consuming but at W _c  = 8 the time needed to perform both the interpolations (dense predictor plus image deformation steps) is significantly higher. Since, in real situation, the use of the shifted bilinear interpolation scheme in the image deformation step practically does not increase the error, a further reduction of the total time can be achieved.

Table 1 Distribution of computational time (s)

5 Performance assessment with real images

The effects of the interpolation scheme used in the evaluation of the dense predictor on real images will be made by using experimental data obtained from a jet in cross flow. Details about the experimental configuration and the PIV setup can be found in Carlomagno et al. (2004). In particular, in the present case, images of the symmetry plane, relative to a velocity ratio of 2 and a Reynolds number equal to 8,000, are elaborated. As already done in a previous work (Astarita 2007) the turbulent spectrum is investigated by processing five hundreds images.

The power spectra E ₂₁ of v evaluated along the same line already investigated by Astarita (2007) are plotted, as a function of the spatial frequency ω, in Fig. 12. Only the BL65-TH5 combination of WW (i.e. W _a  = 65, W _b  = 5, a Blackmann WW is used during the correlation step and a Top Hat filter is used in the weighted average step) is considered herein. The curve already shown by Astarita (2007), in which W _c  = 1, is plotted as the reference curve; all the other curves are relative to a grid distance equal to eight pixels. The curve relative to the bilinear IS begins to deviate from the other curves when the spatial frequency is greater than 0.5. The decrease of the spectrum is clearly associated to the modulation introduced in the dense predictor step. The other curves follow better the reference curve but the shifted bilinear interpolation introduces some noise especially at the high frequencies. The best result is obtained with the second order B-spline. Even if not plotted the curves relative to the ideal interpolation scheme and the higher order B-spline practically coincide with the curve relative to the second order B-spline.

Fig. 12

Power spectra E ₂₁ for a jet in cross flow for various IS used to evaluate the dense predictor

By using W _c  = 8 the time needed to process the images is reduced by a little less than one order of magnitude. It has to be pointed out that since in the evaluation of the reference curve it has been used a B-spline of tenth order also in the new results the same IS scheme has been used. By using a shifted bilinear IS for the image deformation step the spectra virtually does not change but the time needed to perform all the processing is reduced of another 33%.

6 Conclusions

The effect of the interpolation scheme used in the dense predictor step has been examined. In this step of the algorithm, the predictor displacement field that is evaluated on a rather coarse grid is interpolated on a 1-pixel grid, normally, by using a bilinear interpolation scheme. In particular, the application of the shifted bilinear, B-spline based and ideal interpolation schemes has been also considered. The performance assessment has been made by using both real and synthetic images with particles of Gaussian shape and a sinusoidal displacement field. The modulation transfer function and the total error have been analysed.

The use of a bilinear interpolation scheme yields a rough discretization of the displacement field producing a decrease of the accuracy at the high frequencies. On the other hand the use of a shifted bilinear IS enables to have better accuracy at the high frequencies but introduces some noise at the smaller ones. The global nature of the ideal interpolation scheme has the disadvantage of being sensible also to distant points. The best accuracy is obtained with the B-spline interpolation scheme; a second order appears to be sufficient for most practical situation. Similar results are obtained by comparing the turbulent spectrum obtained from real images of a jet in cross flow.

Clearly, the time performances of the more accurate interpolation schemes are significantly worst with respect to the standard bilinear IS and can reach 33% of the total processing time. On the other hand the better spectral response enables to use larger distances between the vectors thus reducing the total time even of one order of magnitude. Moreover, the use of the shifted bilinear interpolation scheme in the image deformation step enables to have fairly accurate results with a further decrease in time.