Fluid dynamics of self-propelled microorganisms, from individuals to concentrated populations

Abstract

Nearly close-packed populations of the swimming bacterium Bacillus subtilis form a collective phase, the “Zooming BioNematic” (ZBN). This state exhibits large-scale orientational coherence, analogous to the molecular alignment of nematic liquid crystals, coupled with remarkable spatial and temporal correlations of velocity and vorticity, as measured by both novel and standard applications of particle imaging velocimetry. The appearance of turbulent dynamics in a system which is nominally in the regime of Stokes flow can be understood by accounting for the local energy input by the swimmers, with a new dimensionless ratio analogous to the Reynolds number. The interaction between organisms and boundaries, and with one another, is modeled by application of the methods of regularized Stokeslets.

1 Introduction

The fluid dynamics of fast, large self-propelled objects, ranging from krill to whales, mosquitoes to eagles, is extensively studied and intuitively understood (Childress 1981). In these cases the Reynolds number Re ranges from somewhat >1 to enormous. At the other end of the spectrum are microscopic swimmers: bacteria, uni- and multi-cellular algae, and protists: which, although capable of swimming many body lengths per second, live in the regime Re ≪ 1. While the essential features of the swimming of individual organisms of this type are known (Lighthill 1975; Berg 2003), the manner in which the flows associated with locomotion couple many such swimmers to each other and to nearby surfaces are only now being fully explored. Flows generated cooperatively by flagella of unicellular organisms and by those of multicellular organisms can also drive significant advective transport of molecular solutes associated with life-processes (Solari et al. 2006, 2007; Short et al. 2006).

In this paper we provide experimental and theoretical insights into the remarkable collective dynamics of a particular bacterial system, expanding on our original reports (Dombrowski et al. 2004; Tuval et al. 2005). Much micro-bio-hydrodynamical research has focused on the morphologically similar swimming bacteria Escherichia coli, Salmonella typhymurium and Bacillus subtilis. The chief results described in this paper are derived from our investigations of fluid dynamical phenomena driven by individual and collective swimming of B. subtilis.

Individual cells of these generally non-pathogenic soil bacteria are rod-shaped (Fig. 1). Their length ranges from 2 to 8 μm, depending on nutrition and growth stage. In typical experiments they are approximately 4 μm long and somewhat less than 1 μm in diameter. They are peritrichously flagellated: the helical flagella, their means of propulsion, are distributed randomly over the cell body, emerging from motors that are fixed within the cell membrane. The shafts are able to rotate at various rates, typically on the order of 100 Hz. The flagella themselves are complex polymeric structures approximately 20 nm in diameter, with a length of 10–15 μm, considerably greater than a cell’s body, and a helical pitch of ∼2–4 μm. They are attached to the motors by a flexible hook which acts as a universal joint. When a bacterial cell swims smoothly forward, hydrodynamic interactions between the many helical flagella cause the formation of a propulsive bundle within which they co-rotate. The swimming speed of an individual is approximately 11% of the helix wave speed (Magariyama et al. 1995, 2001). The motors are fueled by proton gradients; their direction of rotation is reversible. Spontaneous reversals may occur as a function of the surrounding concentration of chemicals and of other factors and can play a major role in chemotaxis (Berg 1993, 2003). The cell bodies are not polar. The flagellar bundle can form at either end of a cell, whether E. coli (Turner and Berg 1995) or B. subtilis (Cisneros et al. 2006), an important aspect of group locomotion discussed later.

Fig. 1

Two Bacillus subtilis cells about to separate after cell division. Flagella can be seen emerging from the body. Many of them have been broken during sample preparation for this transmission electron micrograph. Scale bar is 1 μm

A single swimming bacterium has associated with it an extensive flow field which is produced entirely by drag forces on the fluid, exerted forward by the cell body and backward by the flagella. No wake remains behind moving cells or cell groups. When a cell stops rotating its flagella, all motion of the fluid and of the cell ceases. Motor boats are not analogs. The viscous forces are described by Slender Body Theory and extensions of Faxén’s and Stokes’ laws (Pozrikidis 1997). A key feature of these dynamics is that for an isolated swimmer the net propulsive force of the flagella must equal the opposing drag force of the body connected to the flagella, taking into account the effect of nearby surfaces or other organisms. While the creeping flow equations are linear and time reversible, in real world situations these features are only approximate or worse. Deviations from the ideal occur when flows affect boundary conditions such as location and orientation of nearby cells, the speed and directionality of flagella beating and the deformation of nearby interfaces. Some of these situations apply to the phenomena discussed in this paper, e.g., the effect of flows generated by the bacteria on their own spatial distribution and motional dynamics, which then modify the flows. A full accounting for these effects is necessary for a complete theory of the collective dynamics, but this is not yet at hand. The basic phenomenology of this collective behavior and its quantification by particle imaging velocimetry (PIV) are described in Sects. 2 and 3.

The swimming trajectories of living organisms can be modified by local shear and vorticity. For example, we describe in Sect. 4, that B. subtilis tend to swim upstream in a shear flow. Should we ascribe this to hydrodynamic interactions that passively orient cells which simply continue to rotate their flagella? Or perhaps might we infer that, when bacteria experience shear stress, they “want” to swim upstream? In Sect. 4 we show one example of this phenomenon, adequate for the purpose of demonstrating its importance for recruiting individuals into groups of co-directionally swimming cells. However, the specific recorded trajectories of more than 60 cells show wide variations in detail. There may be many microscopic origins for the recruitment of cells into correlated groups leading eventually to the collective behavior, but inferences concerning fundamentals of micro-bio-hydrodynamics require experiments designed to disentangle the physics from the biology.

Microorganisms use, exude, and respond to the presence of biologically significant molecules. Chemical interactions provide an avenue for change of the collective dynamic. Emission of molecules involved in signaling, and exudates of biopolymers that may radically change the viscosity of the embedding fluid, are both involved in quorum sensing (Miller and Bassler 2001) and the formation of biofilms (Kolter and Greenberg 2006). Before occurrence of these radical events, subtle chemical interactions can influence the biology and modify the behavior of individual cells. Even at low concentrations, polymer exudates modify the properties of the suspension. For instance, we observe that in slightly aged cultures of still normally motile bacteria, passive marker particles, as well as the bacteria themselves, can be coupled by polymer strands of cellular origin. We have observed (unpublished) that the water/air interface can accumulate bacterially-synthesized polymer surfactants that trap and immobilize bacteria arriving there. A nominally free surface becomes a stiff, no-slip boundary. We infer that the bacteria are immobilized because the flagellar motors are too weak to overcome the implied yield stress. Vigorously shaking a culture bounded by such an interface frees the bacteria. After shaking stops, the newly unoccupied surface soon becomes again populated by bacteria stuck in the inferred interfacial layer of polymer, while in the bulk fluid many cells swim normally, some attached to each other by polymers, forming immobile multicellular clumps. In biofluid mechanics, before reaching definitive conclusions about mechanisms involving free surfaces: caveat emptor.

On a larger scale, response to chemical gradients can initiate behavior that creates striking hydrodynamic flows (Figs. 2 and 3). For instance, respiration of B. subtilis depletes dissolved oxygen in the fluid medium. Transport from an interface between the aqueous suspension of these cells and the surrounding air replenishes it. Bacteria swim up the resultant gradient of oxygen concentration. In a shallow suspension the cells swim upward, toward the air. Accumulation at the interface results in an unstable gradient of mean fluid density, since the bacteria are approximately 10% denser than water. Such convective dynamics also occur with swimming cells of algae (Pedley and Kessler 1992; Hill and Pedley 2005), plants that swim upward, toward light, and/or because of orientation of the cells in the earth’s gravitational field. The initial volume fraction is typically fairly low in these situations, ≈10⁻³ or less. Theoretical approaches can therefore use Navier–Stokes equations that include a smoothed gravitational body force proportional to the local concentration of organisms and their mass density. An additional equation models transport of organisms due to swimming and advection by the flow (Hillesdon et al. 1995; Hillesdon and Pedley 1996; Tuval et al. 2005).

Fig. 2

Bacillus subtilis cells concentrated at a sloping water/air interface. This meniscus is produced by an air bubble in contact with the glass bottom of a bacterial culture 3 mm deep. Near the top of the image bacteria have accumulated, forming a monolayer of cells perpendicular to the air/water/glass contact line. Their lateral proximity and the adjacent surfaces immobilize them. Toward the bottom of the image the fluid becomes progressively deeper; the swimming cells exhibit collective dynamics. The accumulation occurs because bacteria swim up the gradient of oxygen produced by their consumption and by diffusion from the air bubble. The black specs are spherical latex particles 2 μm in diameter

Fig. 3

One randomly chosen instant of the bacterial swimming vector field estimated by PIV analysis. The arrow in the extreme lower left corner represents a magnitude of 50 μm/s. The turbulent appearance of the flow is evident here

These unstable stratifications evolve in the usual manner by a Rayleigh–Taylor instability which, in turn, can lead to highly concentrated populations (Dombrowski et al. 2004, Tuval et al. 2005) (Fig. 2). These concentrated accumulations of cells support the collective dynamics discussed here, which were first reported in a more qualitative manner some time ago (Kessler and Wojciechowski 1997; Kessler and Hill 1997). Closely related phenomena, jets and whirls, that occur near the edges of bacterial cultures that grow and expand on wet agar surfaces have been reported (Mendelson et al. 1999). Likewise, such phenomena can be seen in concentrated bacterial populations trapped in suspended thin aqueous films (Wu and Libchaber 2000; Sokolov et al. 2007). Models of various types have been proposed to address these phenomena, from very simple discrete-particle dynamics not involving hydrodynamics (Vicsek et al. 1995) to continuum models based on ideas from liquid crystal physics (Toner and Tu 1995; Simha and Ramaswamy 2002a), two-fluid models (Lega and Mendelson 1999; Lega and Passot 2003), numerical studies of idealized swimmers (Hernandez-Ortiz et al. 2005) and hydrodynamic models (Aranson et al. 2007). The emerging consensus is that hydrodynamic interactions between the bacteria are sufficient to account for the observed collective behavior, although some models suggest that steric interactions alone in a collection of self-propelled objects will produce the collective dynamics (Sambelashvili et al. 2007).

In Sects. 5 and 6 we describe some further mathematical aspects of modeling individual swimming dynamics and collective motions in bacterial systems. These results give insight into the details of flows and forces in the neighborhood of surfaces, and between nearby groups of cells. In particular, the great reduction in flow between closely-spaced organisms is argued to play an important role in the observed dynamics of the collective state, and forms the basis for a heuristic model for the locomotion of coherent groups of swimming cells. Section 7 outlines scaling arguments for turbulent-like behavior at low Re through the introduction of a new dimensionless quantity reflecting the power input from swimming organisms. The discussion in Sec. 8 highlights a number of important open questions for future work.

2 Collective phenomena: the Zooming BioNematic (ZBN)

The ZBN collective phase, occurs when the bacterial cells are very concentrated, i.e., nearly close-packed. They form codirectionally swimming domains that move chaotically, giving the appearance of turbulence. As is shown in Sect. 7, these regions may move at speeds larger than the average speed of single organisms. Maintenance of a sustaining environment is required when working with suspensions of living organisms. Bacillus subtilis require oxygen for swimming. The dynamics of the ZBN phase, driven by swimming, continue unabated for hours, suggesting that an adequate supply of oxygen and nutrients is available to the bacteria. Molecular transport into the bacterial suspension from the adjacent air involves molecular diffusion and also advection by collectively generated streaming. Bacteria consume ∼10⁶ molecules of O₂ per second per cell. As the solubility of oxygen is ∼10¹⁷ molecules/cm³, and the concentration of cells is ∼10¹¹ cm⁻³, in absence of transport into the suspension the oxygen would be gone in about one second. During experiments on the ZBN, the typical depth of the suspension is L ∼5 × 10⁻³ cm. With the diffusion coefficient of O₂ in water D = 2 × 10⁻⁵ cm²/s, the diffusion time, L ²/D is also of order 1 s. A scale for collective velocity is V ∼ 4 × 10⁻³ cm/s (Fig. 17 below), so that the advection time is again approximately 1 s. This fortuitous combination of characteristic times implies “just in time” oxygen delivery. The Péclet number, P _e  = VL/D, which measures the relative importance of advection and diffusion, is therefore of order unity for a small molecule such as oxygen; it can be considerably greater for larger molecules. The complex and quite fascinating details of the transport processes of food, waste products, and of molecular signals need extensive investigation, another example of the convolution of biology and fluid dynamics. The biochemistry of metabolism and sensory processes also plays a major role. Recent work (Solari et al. 2006; Short et al. 2006) describe investigations on diffusive transport necessarily augmented by advection due to the motion of flagella. There, the context is an aspect of the origin of multicellularity in a family of algae. In a sense, the collective behavior of a bacterial population converts it too into a type of multicellular “individual” (Shapiro and Dworkin 1997).

The volume of a single B. subtilis is ∼1.5 × 10⁻¹² cm³. Since the bodies are rod-shaped, concentrated populations, e.g., n – 10¹¹ cm⁻³, tend to form domains within which the self-stacked cell bodies are approximately parallel. The entire high concentration region consists of such domains separated by regions of disalignment (Figs. 2, 3). All the cells in one domain swim in the same direction, so that, unlike the analogous liquid crystals, the domains move and are dynamically polar. The cell bodies have no intrinsic polarity; on any one cell, the propelling flagella can flip to either end of the rod-shaped body. This appears to be one mechanism for quorum polarity: individual organisms joining the swimming direction of the majority. A domain is thus characterized by coherence of body alignment and polarity, hence coherence of swimming direction. The domains zoom about; they spontaneously form and disintegrate, giving the appearance of internally maintained turbulence. The next section describes PIV measurements of spatial and temporal correlations of velocity, vorticity and polar alignment.

The dynamical system of cells and water is driven by rotation of the helical flagella that emerge from the bodies of the bacteria. The flagella propel (force) the fluid phase backward; they exert an equal and opposite force on the bodies from which they emerge. Since the flagella are typically three times longer than the cell bodies, the flow generated by the flagella of a particular cell exerts a backward drag on the bodies of several cells located behind that particular one. Flows in the interior of domains are therefore rather small; propulsion arises mostly at the periphery. Further discussion and relevant calculations follow in Sects. 5 and 6, which also present results on cohesive hydrodynamic interactions.

3 Coherence of polar and angular order: a novel use of PIV

Our experiments were conducted with B. subtilis strain 1085B suspended in terrific broth (TB) (Ezmix Terrific Broth, Sigma; 47.6 g of broth mix and 8 ml of glycerin in 1 l of distilled water). Samples were prepared by adding 1 ml of −20°C stock to 50 ml of TB and incubating for 18 hours in a shaker bath at 37°C and 100 rpm. Then, 1 ml of bacteria suspension (concentration of around 10⁹cells/cm³) was mixed with 50 ml of fresh TB and incubated for another 5 h.

A single drop of suspension was placed on a glass-bottomed petri dish to be observed with an inverted microscope using a 20× bright field objective. This magnification is sufficient to observe individual cells and produce a reasonably wide field of view. Additional water reservoirs were placed in the closed chamber to induce high humidity and avoid evaporative flows at the edge of the drop. The sessile drop is imaged from below through the bottom of the petri dish and near the contact line, where dimensions of the medium are close to a thin layer and self-concentration mechanisms provide very high accumulations of cells (Dombrowski et al. 2004). Videos were obtained using a high-speed digital camera (Phantom V5) at a rate of 100 frames per second and with a resolution of 512 × 512 pixels. Sets of 1,000 frames were subsequently obtained from each of those videos and processed with a commercial particle-imaging-velocimetry system (DANTEC Flow Manager) in the cinemagraphic mode. The PIV system can estimate the most probable displacement of small rectangular regions in the image by implementing a simple pattern matching algorithm between two consecutive images (Willert et al. 1991; Keane et al. 1992). A sampling grid of 42 × 42 windows, each 16 pixels wide with 25% overlap, was chosen. Each window represents 2.7 μm. Given the displacement of these small evaluation regions at a given frame rate, a discrete velocity field is returned for each time step. The observed system is a layer with a sloping upper surface, varying in thickness from “zero” to ∼200 μm. These measurements are projections of a three-dimensional field into the plane defined by the area of view and the optical depth of field.

Measurement of the coherence lengths and times that characterize the dynamics of the ZBN can be done by the implementation of a PIV analysis either on the recorded motion of passive tracer particles or on the suspended bacteria themselves. The data presented here uses the latter technique. Passive tracer data is too sparse when the concentration of tracer particles is sufficiently low so as not to affect the basic phenomena. On the other hand, optical problems arise in the highly concentrated ZBN phase. The close-packed cells scatter light, producing distortion and diffraction effects that reduce the quality of the image. Individual cells are difficult to resolve in this setup. Though more work is needed to increase precision of velocity measures, analysing these diffuse images with PIV captures well the overall dynamics of the system in a quantitative way. A snapshot of the velocity field is shown in Fig. 3; the corresponding vorticity is in Fig. 4.

Fig. 4

Vorticity of the swimming velocity vector field shown in Fig. 3. Color bar indicates vorticity in seconds⁻¹. The graphing method discretizes vorticity levels

The motion of the suspension appears turbulent. Coherent regions, surges, plumes and jets occur intermittently. These domains of aligned motility are hundreds of times larger than bacterial dimensions, remaining coherent for a second or longer. Observed cinemagraphically, the leading segments of such plumes often roll-up into spirals, then disperse, either spontaneously or due to interactions with neighboring coherent regions. These observations relate to the trajectories, the paths of groups consisting of hundreds or thousands of bacteria. PIV provides only a quasi-instantaneous snapshot of streamlines associated with a derived velocity field.

Correlation functions were estimated from the quantitative data. The temporal correlation function of velocity is defined as the following statistic over the vector field v(x,t):

$$ J_v({{\mathbf{x}}}, t) = \frac{{\langle{{\mathbf{v}}}}({{\mathbf{x}}},s+t) \cdot{{\mathbf{v}}}({\mathbf {x}},s) \rangle_s - \langle{{\mathbf{v}}}({{\mathbf{x}}},s)\rangle^2_s} {\langle{\mathbf {v}}^2({{\mathbf{x}}},s)\rangle_s - \langle{{\mathbf{v}}}({{\mathbf{x}}},s)\rangle^2_s}. $$

(1)

The space correlation function is defined as

$$ I_v(r,t) = \frac{{\langle{{\mathbf{v}}}}({{\mathbf{x}}} + {{\mathbf{r}}},t)\cdot{{\mathbf{v}}}({\mathbf {x}},t) \rangle_{{{\mathbf{x}}},\theta} - \langle{{\mathbf{v}}}({{\mathbf{x}}},t)\rangle^2_{\mathbf {x}}}{\langle{{\mathbf{v}}}^2({{\mathbf{x}}},t)\rangle_{{\mathbf{x}}} - \langle{{\mathbf{v}}}({\mathbf {x}},t)\rangle^2_{{\mathbf{x}}}}, $$

(2)

where 〈·〉 _s is the average over time frames and 〈·〉 _x indicates the average over space coordinates x = (x, y). The first term in (2) is also averaged over all angles θ of r. Then I _v (r) depends only on the magnitude r ≡ |r|.

Similar definitions are used for the correlation of the vorticity scalar field Ω(x, t),

$$ J_\Omega({{\mathbf{x}}},t) = \frac{{\langle\Omega({{\mathbf{x}}},}s+t) \Omega({\mathbf {x}},s) \rangle_s - \langle\Omega({{\mathbf{x}}},s)\rangle^2_s} {\langle\Omega^2({{\mathbf{x}}},s)\rangle_s - \langle\Omega({\mathbf {x}},s)\rangle^2_s} $$

(3)

and

$$ I_\Omega(r,t) = \frac{{\langle\Omega({\bf x}} + {{\mathbf{r}}},t)\Omega({\mathbf {x}},t) \rangle_{{{\mathbf{x}}},\theta} - \langle\Omega({{\mathbf{x}}},t)\rangle^2_{\mathbf {x}}}{\langle\Omega^2({{\mathbf{x}}},t)\rangle_{{\mathbf{x}}} - \langle\Omega({\mathbf {x}},t)\rangle^2_{{\mathbf{x}}}}. $$

(4)

Using these measures on the PIV data, we obtain 1,000 different curves for I _v and I _Ω, one for each time realization, and 42 × 42 = 1,764 curves for J _v and J _Ω, one for each possible discrete coordinate in the PIV sampling grid. We further calculate averages of these sets to show the overall mean behavior of the correlation functions. Graphs are shown in Fig. 5. Comparison of the average plots with plots of individual cases show that, in light of the prevalence of positive and negative correlations, averaging does not provide good insights into dynamic events. The oscillations of correlation are somewhat reminiscent of vortex streets at high Re.

Fig. 5

Correlation functions from PIV analysis. (a) Spatial correlation function of velocity I _v (r). Four examples, corresponding to four different times, are shown in colors; the black trace is the average over 1000 time realizations. (b) Temporal correlation function of velocity J _v (t). Four examples corresponding to four particular locations in the field of view are shown in colors. Black is the average over space. Plots of the vorticity spatial correlation I _Ω(r). (c) and temporal correlation J _Ω(t). (d) are shown for four examples and, again in black, for the average. The oscillations in c correspond to alternation in the handedness of vorticity, as shown in Fig. 4. Error bars in a and b indicate typical statistical uncertainties

These analyses reveal correlation lengths of velocity on the order of 10 μm, which is about a typical vortex radius in Fig. 4. We also observe anticorrelation extending for more than 70 μm and coherence in time that persists for at least a second, suggestively close to the advection time mentioned at the end of Sect. 1. While these measures define some characteristic length and time scales of the system, these curves do not provide information on the continuity and dominance of extensive coherence of alignment and collective polar motion. A novel method of analysis of the velocity field, using the streamlines derived from PIV (Dombrowski et al. 2004) was employed to provide that insight.

The local velocity of domains of concentrated bacteria correlates with the direction of the axis of the cell bodies. In this way, the direction of the associated streamlines averaged over suitably chosen areas can provide a measure of the orientation of a local director vector, traditionally used to characterize liquid crystalline phases. In this context, the swimming co-direction defines the polarity of coherent behavior absent from standard liquid crystalline order (de Gennes and Prost 1993). Spatially rapid deviations of streamline directions from the local average provide a quantitative measure of the end of coherence within the projected plane. They may signal the occurrence of orientational singularities, such as excursions into the orthogonal dimension or the presence of boundaries that define unrelated regions of coherence that collide or fold into each other. Relatively low angle deviations of the director provide data on the splay and bend parameters that occur in the analysis of the liquid crystal free energy.

We now introduce a new method of analysis which consists of defining a scalar field to measure the level of coherent directional motion in the velocity field. The obvious choice is a local average Φ _R  = 〈cos θ〉 _R of the cosine of the angle between adjacent unit vectors of velocity, averaged over a small region defined by R. This average over the measured velocity field v _ij (t) is

$$ \Phi_R(i,j,t) = \frac{1}{N_R}\sum_{(l,m)\in B_R(i,j)} \frac{{{\mathbf{v}}} _{ij}(t) \cdot {{\mathbf{v}}}_{lm}(t)}{|{{\mathbf{v}}}_{ij}(t)||{{\mathbf{v}}}_{lm}(t)|}, $$

(5)

where B _R (i,j) is a quasi-circular region of radius R, centered at (i,j), containing N _R elements. When Φ _R  ∼ 1 the vectors inside the region B _R are nearly parallel. Values close to zero indicate strong misalignment. Negative values imply locally opposing streamlines. Resolution and noise level are determined by the choice of R.

Standard correlation functions based on the velocity field, as in Fig. 5, hide information on the contiguousness of correlations. Analyzing the streamline field in this novel way exhibits the global continuity of angular and polar correlations. The extent of the resultant sinuous domains depends on the choice of the averaging area ∼R ². Large values of R produce a strong smoothing of the local data, which may hide the details of the chaotic nature of flow by means of statistical cancellations. Hence, small values of R should be preferred. But on the other hand, too small values of R produce results that are more sensitive to noise in the raw data or that are biased by the specific shape of the averaging region, and the particular geometry of the grid chosen for the PIV analysis. Figure 6 shows the extent of continuous domains, derived from one data set, using different values of R. The regions colored dark red corresponds to 0.8 < Φ _R  < 1, which selects regions of high coherence. Inside these domains all velocities are parallel within an angle slightly lower than 37°.

Fig. 6

Instantaneous coherence measure Φ _R (Eq. 5) for R = 1 (a), R = 2 (b), R = 3 (c) and R = 4 (d). Axes and R are in PIV grid units (≃2 μm each). Grey boxes in the lower left corner indicate, in each case, the size and shape of the local averaging region used to estimate the measure. The color bar on the right indicates scale levels for values of Φ _R . The plotting method discretizes the countour levels. Note the near absence of dark blue regions, which would indicate counterstreaming

For liquid crystals, the conventional order parameter involves 〈cos²θ〉, thereby avoiding polarity. For the domains of coherent directional motion considered here, we can define an order parameter as

$$ P_R(t) = \langle\Phi_R(t)\rangle, $$

(6)

where this average extends over the entire area, i.e., all elements of the PIV image at time t. This quantity can be treated as a time series. We find that P _R (t) displays a stationary value with random fluctuations. Figure 7 shows histograms of these order parameters. This method of analysis will be used to determine the onset of the ZBN phase as a function of cell concentration n.

Fig. 7

Histograms of the order parameter P _R (t) for different values of R, the radius of the sampling area. Each one is generated with 1,000 time steps. The skewing of the distributions becoming two-peaked at low R (high resolution) may indicate bimodality in the coherent phase, or an approximately aligned transient phase

What is the distribution of values of Φ _R in the whole field of view for each time step? What fraction of the total area in the level map of Φ _R do they span? This approach asks for the probability of finding any given level of coherence in the flow, or the portion of the total that is spanned by each contour level in Fig. 6. These area fraction distributions are shown in Fig. 8 for four values of R. The data set in [−1, 1] is partitioned in bins of size 0.2. We see an obvious shift of the center of the distribution when R is changed. It is interesting that each distribution is basically constant, concluded by seeing that fluctuations (error bars) are typically small, meaning that the fraction of the system with a particular coherence level stays more or less the same over time. Given the three-dimensional volume-filling nature of the bacterial population, this average temporal stability of projected coherent area implies zero net divergence of swimmers. The up/down rate of departure is matched by incomers.

Fig. 8

Area fraction of coherent regions distributed over the whole range of Φ _R , averaged over 1,000 time frames. Error bars indicate standard deviation in each case

Another possibility is that the whole dynamics is limited to a very narrow layer and is therefore quasi-two-dimensional. But this is not the case, for we have observed that cells and clumps of cells or passive tracers tumble and move in and out of the focal plane, clearly proving that the dynamics is three-dimensional. Dynamics of recruiting and dropping of individuals into and out of phalanxes could be related to the topological details, with clear implications for mixing and transport phenomena. We expect that this observation will eventually provide a significant link to a more complete analysis.

4 Recruiting into ZBN domains

The recruiting of swimmers into a co-directionally swimming domain of cells, a phalanx, depends on several mechanisms. We have discovered, as discussed below, that individual cells of B. subtilis have a strong tendency to swim upstream in a shear flow. Similar observations have been made recently (Hill et al. 2007), in which upstream swimming of E. coli was found immediately adjacent to a surface. In contrast, our finding is not restricted to motion on the surface bounding a fluid, but simply in close enough proximity to be in a region of shear. In the context of the ZBN, shear flows can emerge from groups of co-directionally swimming cells, for a tightly knit group of propagating cells generates a backwash flow field, a lateral influx, and a flow forward, in the swimming direction. These flows, which are due to incompressibility, are shown in Sect. 5 (Figs. 12 and 13 below). They provide a mechanism for recruiting more individuals into a phalanx. Another organizing/recruiting mechanism occurs when one of these bacteria encounters an obstacle. It can flip the propelling flagella from “back” to “front”, resulting in reversal of locomotion, without turning the bacterial cell body (Cisneros et al. 2006). This action may be a behavioral manifestation of flagellar dynamics and orientational instability. Paradoxically, it can aid polar alignment in groups, just because the individual cells are not themselves polar. Individual mis-oriented cells can react by joining a colliding “obstacle”, a moving phalanx of others.

Swimming bacteria were suspended in Poiseuille flows within flat microslides (Vitrodynamics) with a 0.1 mm lumen. A fine motion linear actuator (Newport 850G) was used to depress a non-sticking syringe (Hamilton Gastight #1702) to produce a continuous and smooth fluid flow. This flow was coupled through a micropipette (∼50 μm) which is inserted into one side of the flat microslide. The velocity profile was determined by tracking 2 μm fluorescent particles (Bangs Labs) near the focal plane. By comparing the out-of-focus beads with their images at known distances from the focal plane, the depth and velocity of the tracer particles can be used to determine the 3D velocity field and the shear. Cell trajectories in these experiments were visualized by tracking the position of both ends of cells through a sequence of images in the plane of focus. The vector orientation of a cell was determined from the distance between the ends of the cell and the angle of the connecting line segment. The angle and length give the projection of the cell body in the plane of focus. Velocity of the cells is calculated from the change in position of the cell from one frame to the next. This velocity represents the speed and direction that the cell is moving in the lab reference frame. Due to the external shear stress experienced by the cell the velocity vector does not necessarily point in the same direction as its orientation. Data were obtained on 65 individual tracks that exhibit these characteristics, each modified by idiosyncratic details.

Figure 9 shows one representative trajectory. Reading from right to left, the trajectory consists of a downstream segment with the cell oriented across the flow, an upstream segment, and then again downstream. This behavior may be entirely hydrodynamic or it may be a behavioral response to differential shear stress. Orientation of the cell transverse to the swimming direction occurs in many cases, but not all. When it does, it implies the dissolution of the flagellar bundle, with individual flagella emerging approximately perpendicular to the body axis, as if driven by the fluid “wind” in which they operate. Our optical resolution is insufficient to ascertain whether the cell bodies and flagella are at different levels in the shear field, a possible explanation of the phenomenon. The interactions of cells with shear, the deconvolution of cell path lines and fluid stream lines and analysis of cell body orientation in relation to swimming direction are current endeavors covering many such observations.

Fig. 9

Upswimming of bacteria in a shear flow. a Trajectory and orientation of a particular bacterial cell swimming in a flow, with velocity in the +y direction, and shear dV _y /dz ∼ 1.0 s⁻¹. The small arrows show the apparent swimming direction and the projection of the body size on the plane of observation. b Trajectory of the velocity vectors in the laboratory reference frame. Vector on right indicates fluid flow direction. The velocity of the bacterium can be transverse to its orientation

5 Modeling self-propelled microorganisms

There is a long history of models for the swimming of individual microorganisms, dating back to classical works on flagellated eukaryotes (Taylor 1952), ciliates (Blake 1971a), and bacteria (Ramia et al. 1993). Very recent work has addressed the complex circular swimming of individual E. coli near surfaces (Lauga et al. 2006), where the specific interactions between helical flagella and a boundary are crucial. In this section we wish to return to the very simplest of models to examine the nature of flows in concentrated populations. In the creeping flow regime where Re ≪ 1, featuring linearity, superposition and time independence, a simple model of a self-propelled organism consists of two parts, a “body” B and an attached extendable “thruster” T that emerges from B. When forces within B provide an incremental backward push to T, the resulting increment of motion generates a surrounding field of fluid velocity. The motion of B is “forward” with velocity V _B relative to the surrounding stationary fluid; the motion of T is backward with velocity V _T . The velocity with which T emerges from B is v _r . Hence, since T is attached to B,

$$ {\mathbf {V}}_T = {{\mathbf{v}}}_r -{{\mathbf{V}}}_B. $$

When the respective drag coefficients are R _B and R _T , force balance is achieved when

$$ F_B = R_B|{{\mathbf{V}}}_B| = R_T|{{\mathbf{v}}}_r-{{\mathbf{V}}}_B| = R_T|{{\mathbf{V}}}_T| = F_T, $$

(7)

where F _B and F _T are the forward and backward force magnitudes on the fluid. A schematic diagram of swimmers and velocities is shown in Fig. 10, where the sphere and the ellipsoid indicate, respectively, B and T. The rotation rate of the flagella helix, times the helix pitch, times an efficiency factor, is represented by v _r .

Fig. 10

Diagram of a model swimmer showing V _B and V _T relative to the fluid, and the velocity v _r of T out of B

For bacteria, T represents the rotating bundle of helical flagella. An increment of motion consists of a slight turn of the bundle during an increment of time. For the simplified case presented here, we ignore rotation. This model generates the salient features of the fluid flow field that surrounds a self-propelled organism or, by superposition, a group of organisms. This model does not intend to elucidate the development over time of the locomotion of one or more swimmers, as in the models of Hernandez-Ortiz, et al. (2005), Saintillan and Shelley (2007), and the asymmetric stresslet of model of Cortez et al. (2005). Rather, it produces an instantaneous field of flow over the entire available space, as required by the time independence of Stokes flow. We re-emphasize that since the increment of linear displacement between B and T models an incremental turn of the propelling bundle of flagellar helices, it is inappropriate to consider an actual finite elongation of the organism followed by retraction of T to its original position. Calculation of the flow field of one or more organisms requires enforcement of no-slip conditions at bounding surfaces and at surfaces of the organisms. The computational model presented below considers B a sphere and T a rod of finite diameter. Forward and backward velocities, calculated by force balance, are used to specify V _B and V _T .

6 Flows and forces

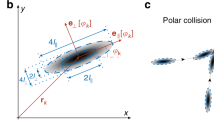
Each organism consists of one sphere (body B) of radius a _B and a cylinder (flagellum bundle T) of length ℓ, radius a _T along the z-axis, as depicted in Fig. 11. The figure also shows an infinite plane wall which will be included in some of our computations. When the wall is present, it is located at x _w = 0. The head has velocity (0,0,V _B ) and the tail has velocity (0,0,V _T ).

Fig. 11

Perspective view of the sphere-stick model and the wall

The approximate balance of forces is achieved as follows. The drag force on an isolated sphere moving at velocity (0, 0, V _B ) is

$$ {{\mathbf{F}}}_B = R_B{{\mathbf{V}}}_B=6\pi\mu a_B V_B (0,0,1), $$

(8)

where μ is the fluid viscosity and R _B represents the drag coefficient for the sphere. The force required to move a cylinder of length ℓ and radius a _T along its axis with velocity (0, 0, V _T ) is

$$ {{\mathbf{F}}}_T = R_T{{\mathbf{V}}}_T=\frac{4\pi\mu\ell}{\ln(\ell^2/a_T^2)-1} V_T (0,0,1), $$

(9)

where R _T is the drag coefficient of the cylinder. Force balance requires F _B  + F _T  = 0 which yields

$$ V_T = -\frac{3}{2}\frac{a_B}{\ell} \left[\ln(\ell^2/a_T^2)-1 \right] V_B. $$

(10)

Given the instantaneous velocities of the head and tail of the organism, our goal is to compute the surface forces that produce these velocities at all the surface points. For this we use the method of Regularized Stokeslets (Cortez 2001; Cortez et al. 2005). Briefly, the method assumes that each force is exerted not exclusively at a single point, but rather in a small sphere centered at a point x _k . The force distribution is given by

$$ {{\mathbf{F}}}({{\mathbf{x}}}) = {{\mathbf{F}}}_k\phi({{\mathbf{x}}}-{{\mathbf{x}}}_k), $$

(11)

where ϕ is a smooth narrow function (like a Gaussian) with total integral equal to 1. The limit of ϕ(x) as the width (given by a parameter ε) approaches zero is a Dirac delta δ(x). The role of the function ϕ is to de-singularize the velocity field that results from the application of a single force. For example, given a force F _k ϕ(x) centered at x _k and using the regularizing function

$$ \phi({{\mathbf{x}}}) = \frac{15 \varepsilon^4}{8\pi(|{\mathbf {x}}|^2+\varepsilon^2)^{7/2}}, $$

(12)

the resulting velocity is

$$ {{\mathbf{u}}}({{\mathbf{x}}}) = \left(\frac{1}{8\pi\mu}\right)\frac{{{\mathbf{g}}}_k} {(|{{\mathbf{x}}} - {{\mathbf{x}}}_k|^2 + \varepsilon^2)^{3/2}}, $$

(13)

where

$$ {{\mathbf{g}}}_k = [|{{\mathbf{x}}} - {{\mathbf{x}}}_k|^2 + 2\varepsilon^2]{{\mathbf{F}}}_k + [{\mathbf {F}}_k\cdot({{\mathbf{x}}}-{{\mathbf{x}}}_k)]({{\mathbf{x}}}-{{\mathbf{x}}}_k). $$

(14)

This is called a Regularized Stokeslet (Cortez 2001; Cortez et al. 2005). For a collection of N forces distributed on a discrete set of points covering the surfaces of the sphere and cylinder, the resulting velocity obtained by superposition is

$$ {{\mathbf{u}}}({{\mathbf{x}}}) = \left(\frac{1}{8\pi\mu}\right)\sum_{k=1}^{N} \frac{{{\mathbf{g}}}_k}{(|{\mathbf {x}} - {{\mathbf{x}}}_k|^2 + \varepsilon^2)^{3/2}}. $$

(15)

Equation (15) is the relationship between the forces exerted by the organisms on the fluid and the fluid velocity when there are no walls bounding the flow. This formula is used as follows: the surfaces (sphere and cylinder) of all organisms are discretized and an unknown force is placed at each point of the discretization. We assume that the velocities of all spheres and all cylinders are known to be V _B and V _T (they can be different for different organisms). Then Eq. 15 is used to set up and solve a linear system of equations for the surface forces of all organisms simultaneously. For N surface points per organism and M organisms, the size of the linear system is 3NM × 3NM. This ensures that the velocity on any one organism that results from the superposition of the Stokeslets on all organisms exactly equals the given boundary condition.

For the computations with flow near an infinite plane wall, the boundary conditions of zero flow at the wall are enforced using the method of images. The image system required to exactly cancel the flow due to a singular Stokeslet was developed by Blake (1971b). It requires the use of a Stokeslet, a dipole and a doublet outside the fluid domain, below the wall. This image system does not enforce zero flow at the wall when using the regularized Stokeslets in Eq. (15). However, the image system can be extended to the case of the regularized Stokeslet through the use of regularized dipoles and doublets. The details, discussed in Ainley et al. (2007), show that for any value of ε > 0, the system of images for the regularized Stokeslet exactly cancels the flow at the wall and reduces to the original system derived by Blake as ε → 0. The result of the images is a variation of Eq. (15) but the procedure to determine the forces is as before.

We consider first a single organism moving parallel to an infinite plane wall. The table below shows the dimensionless parameters used. Since the cylinder is simply a way of representing the effect of the flagellum bundle and the sphere is a simplification of the cell body, the specific dimensions of these elements do not exactly correspond to the organism. However, for a model motor rotating at 75 Hz and a helical flagellum with pitch 3 μm, the wave speed is 225 μm/s. The observed swimming speed of an organism is about 11% of the wave speed, or about 25 μm/s. Thus, the length scale used for the dimensionless parameters was L = 25 μm so that the dimensionless sphere speed is 1. A cell body of radius 2.5 μm has dimensionless radius 0.1, and so on. All parameters except for V _T were chosen as dimensionless values representative of the problem. The cylinder velocity V _T was computed using Eq. (10).

Parameter	Description
a B = 0.1	Radius of the sphere
a T = 0.02	Radius of the cylinder
ℓ  = 0.4	Length of the cylinder
V B = −1.0	Velocity of the sphere
V T = 1.8718	Velocity of the cylinder

In all simulations presented here, the discretizations resulted in 86 points per sphere and 88 points per cylinder. This give a maximum discretization size (longitudinal or latitudinal distance between neighboring particles) of h = 0.0524. The regularization parameter was set to ε = 0.0571 which is slightly larger than the discretization size. This is a typical choice based on accuracy considerations (Cortez et al. 2005).

Figure 12 shows the fluid velocity in a plane parallel to the wall and through the organism, and the flow in a plane through the organism and perpendicular to the wall. The contour lines are at 5, 10, 25, 50, 75 and 90% of the maximum speed. Those contours reveal the extent of the fluid disturbance created by an organism. Figure 13 shows the streamlines of the instantaneous velocity field, revealing circulation patterns.

Fig. 12

Plan and side views of velocity field around one organism near a wall. The numbers indicate contours where the fluid speed is 5, 10, 25, 50, 75 and 90% of the maximum speed. The infinite plane wall is located at x = 0

Fig. 13

Streamlines of the velocity field around one organism near a wall. Plan and side views

Consider now two organisms next to each other prescribed to move parallel to an infinite plane wall and to each other. The parameters are the same as those used in the previous example. Just as in the case of a single organism, the flow pattern suggests that the flow tends to “push” the organisms toward the wall and toward each other. This can be quantified by computing the total forces exerted by the organisms on the fluid in order to move parallel to the wall and to each other. Figure 14 shows the velocity field and the resulting forces exerted on the fluid by each of the two organisms. It is apparent that there is a component of the force pointing away from the wall, indicating that this component is needed to counteract the attraction effect of the wall in order to keep the organisms moving parallel to it. Similarly, the component of the force pointing away from the neighboring organism is required to counteract the attraction induced by the flow field, as noted in earlier work (Nasseri and Phan-Thien 1997). These results agree with experiments (Sokolov et al. 2007) showing that two bacteria swimming near each other, co-directionally, continue for long distances in these parallel paths.

Fig. 14

Velocity field around two organisms near a wall and resultant forces exerted by each organism on the fluid in order to move parallel to the wall and to each other. The forces are (2.72, −1.71, −0.22) |F _B | (left organism) and (2.72, 1.71, −0.22) |F _B | (right organism), where F _B is the drag on the sphere given by Eq. 8

We next compute the flow around several organisms placed in a common plane above the wall. The velocity is determined in that plane in order to visualize the effect of the prescribed motion of the group. Figure 15 shows the velocity around the organisms and a close-up view of the flow between some of them, while Fig. 16 shows the streamlines for the same configuration. The computed geometries and magnitudes of the flows generated by the locomotion provide some understanding of the forces between swimming organisms and between organisms and adjacent no-slip surfaces. The forces on each swimmer (Fig. 14) show the attraction of the cells to each other and to the nearby plane.

Fig. 15

Velocity field around several organisms above a wall (top) and a closer view of the velocity between them (bottom)

Fig. 16

Streamlines of the velocity field around several organisms near and above a wall. The flow is the same as that in Fig. 15

Additional computations show that in the absence of the plane, the vertical components vanish (by symmetry), and the horizontal attractive components diminish. The attractive force is due to transverse flow toward the organism axis (Fig. 12), required by conservation of volume: the body propels water forward, the tail pushes water backward, leaving a central region of inflow due to lowered pressure. In the absence of the nearby plane, the influx is weaker because of cylindrical symmetry. The same influx can be seen toward the centers (between body and tail) of organisms which are members of a multi-organism phalanx (Fig. 15). Transverse flows between the body of a follower and the tail of a preceder are also seen in the upper image of Fig. 15. Whether a sum over transverse flows in a 3D domain consisting of many close-packed organisms provides net radial cohesion remains to be seen.

Figures 15 and 16 also show the flows that penetrate or surround a group. It is evident that there is very little front-to-back penetration of fluid. The exchange is mostly lateral. The leading heads push water forward, the tail-end cells push water backward, generating much of the collective forward propulsion. The low velocities of flow in the interior (lower panels of Figs. 15 and 16) imply compensating forces and relatively little advective communication between cells, as discussed in the introduction. Similar calculations performed on groups of ten cells, and on staggered pairs show that the associated interior flows are weak, but vortical regions, as in Fig. 16, or even more spectacular, can significantly enhance transport of suspended particles or molecules.

7 Turbulence at Re ≪ 1?

To the casual observer, the ZBN phase of a concentrated suspension of swimming B. subtilis appears turbulent. More quantitatively, the analysis of the collective dynamics, using PIV based on the motion of the bacteria can reveal not only the correlation functions discussed earlier, but the entire distribution of velocities. Such statistical information can form the basis of analysis of the energy flows in these systems, from the “injection” scale of individual bacteria up to the system size. In this section we briefly discuss that velocity distribution and offer some dimensional analysis regarding an effective Reynolds number for these flows.

One important feature of the ZBN is that the collective speeds of coherent subpopulations of bacteria can be greater than the swimming speeds of individual cells. The distribution of speeds of uncorrelated cells of B. subtilis was shown to be approximately Maxwellian over an entire population (Kessler and Hill 1997). The swimming speed of individual cells can vary greatly even over observation times as short as one second (Kessler et al. 2000). When these locomoting cells form a phalanx, they all have approximately the same velocity. The histogram of speeds from our PIV studies, over the entire data set, regardless of angles between streamlines, is again approximately Maxwellian (Fig. 17, black curve). Can the analysis be improved by selecting data over only those regions where the angles between streamlines are smaller than some specified value, i.e., for regions of directional coherence? Does greater co-directionality correlate with a lesser variation in speeds within a domain? Using three thresholds of Φ, 0.8, 0.9 and 0.95, we obtain histograms of the speeds found in progressively more co-linear regions (Fig. 17, red, blue, green curves). These distributions are not Maxwellian; there is a finite lower threshold. This threshold measures the minimum speed required for coherence, for the swimming organisms to form a phalanx. The tail of the distributions at maximum velocity does not change appreciably for different values of Φ, indicating an upper limit of speed for these particular bacteria, a limit likely associated with physical constraints on the mechanism of propulsion. It is significant that the most probable value of the speed, the peak of the distribution, increases with higher values of Φ, and that the width of the distributions does not decrease. Speeds are greater in regions of greater coherence. The spread of velocities occurs because the histograms include data for many coherent domains.

Fig. 17

Experimentally observed distribution of velocities as a function of their angular spread. Within localities where angular spread is defined by Φ (Eq. 5) with R = 2, velocity distributions are plotted as histograms for Φ ₂ > −1.0, black; Φ ₂ > 0.8, blue; Φ ₂ > 0.9, red and Φ ₂ > 0.95, green. These plots imply that improved collective co-directionality correlate with higher mean speeds and displacement of lower thresholds of probability to higher speeds. The black histogram includes measurements of the magnitudes of all velocities, codirectional or not; it is approximately Maxwellian. Its lower mean than the colored curves indicates that the collective codirectional locomotion of cells is associated with speeds that are on average higher than those for uncorrelated ones

Let us turn now to the question of how to understand the existence of a turbulent dynamic at a formally low Re. Considering the suspension as a simple fluid, the conventional Reynolds number, the ratio of inertial and viscous forces, is

$$ Re = \frac{UL}{\nu}, $$

where ν is the kinematic viscosity, the mean collective velocity U ∼ 5 × 10⁻³ cm/s, L ∼ 10⁻² cm is a typical correlation length (Fig. 5). Thus, Re ≪ 1 for the typical value ν ∼ 10⁻² cm²/s. An increase of ν due to suspension effects further decreases Re. How can the quasi-turbulence be sustained?

One can analyze the observed dynamics by considering the force or power densities produced by the swimming organisms. A suitable dimensionless ratio can be constructed from the Stokes force that a single bacterial cell must exert to move itself at velocity v,

$$ {{\mathbf{f}}} = c\mu a{{\mathbf{v}}}, $$

(16)

where a is a characteristic length scale for the cell, μ is the viscosity of the medium and c is a geometrical factor of order 10¹ (for a sphere in an infinite medium c = 6π). If there is a concentration of n cells per unit volume the force density is

$$ F_n = cn\mu av. $$

(17)

On the scale of the coherent structures, the viscous dissipation force density in the collective phase is estimated as

$$ F_\mu=\frac{\mu U}{L^2}, $$

(18)

where μ U/L is the collective shear stress. Then, based on these arguments, we define the dimensionless “Bacterial swimming number” Bs,

$$ Bs = \frac{F_n}{F_\mu}=cna^3 \left(\frac{L}{a}\right)^2 \left(\frac{v}{U}\right). $$

(19)

For the nearly close-packed ZBN phase, n ∼ 10¹¹ cm⁻³. Taking the velocity ratio of order unity, a of order 10⁻⁴ cm, and L ≈ 10⁻² cm, the observed correlation length, Bs ∼ 10⁴. This “alternative Reynolds number” explains the possibility of a turbulent dynamics when Re ≪ 1. The large magnitude of Bs sweeps away details on the assumptions of parameters values. Note that even though the fluid dynamics is produced by the motion of flagella, so energy is injected locally into the system, the perceived turbulence is associated with large scales when compared with the cell-flagella complex.

This result can also be obtained via the standard non-dimensionalization of the Navier–Stokes equation with an included force/volume exerted by the swimming organisms. This appears as the divergence of the deviatoric stress tensor ${\varvec{\Upsigma}},$ where a typical form of stress tensor would be ${\varvec{\Upsigma}}\;\sim\;cn\mu a^2 v{\sigma},$ where again a is a characteristic size of the swimmer, and where the dimensionless tensor ${\varvec{\upsigma}}$ encodes the internal orientations of the swimmers. Hence, the fluid flow u is described by

$$ \rho\frac{D{{\mathbf{u}}}}{Dt} = -{\varvec{\nabla}}p+\mu\nabla^2{{\mathbf{u}}} + cn\mu a\gamma{{\mathbf{v}}}, $$

(20)

where ρ is the mean density of the suspension, we have introduced the local velocity v, and γ is a function that models the propulsive force of one organism. γ accounts for the fact that a single organism exerts on the fluid equal and opposite forces, displaced by approximately one organism length. Eq. 20 applies only to the case of rather low concentrations of bacteria. Dividing this equation by the term μ U/L ² delivers a new dimensionless number Bs′, based on stresses, as the magnitude of the forcing term:

$$ Bs' = cn\mu a\gamma\frac{|{{\mathbf{v}}}|}{\mu U/L^2}\gamma = cn L^2 a\gamma\left(\frac{v}{U}\right). $$

(21)

This dimensionless ratio is similar in spirit to Bs, except that now U and L ought to arise out of (20) as parameters that give a particular scale to the system. Note that both Bs and Bs′ are essentially geometric factors, the viscosity having cancelled (Tuval et al. 2005). Avoiding vectorial aspects of these arguments, a power-based ratio Bsp can be defined as F _n v/F _μ U, yielding

$$ Bsp=cna^3 \left(\frac{L}{a}\right)^2\left(\frac{v}{U}\right)^2. $$

(22)

Observing that v/U ∼ 1, we note that Bs ≃ Bsp.

We now sketch the outline of a model that uses the results of experiments together with an extrapolation of the calculation results in the previous section, e.g., Figs. 15 and 16. To estimate the collective velocity U of a phalanx, we consider a cylinder of aligned co-directionally swimming bacteria each swimming with the mean velocity v (Fig. 18). The propulsion of the cylindrical domain is due to the forces exerted on the fluid by the flagella emerging from one or more layers of cells at the rear of the cylinder. The bodies of cells at the front push fluid forward. Transverse flows enter and leave the side of the cylinder, with presumably a net volume conserving, and perhaps temporarily stabilizing influx. The concentration of bacteria per area is n ^2/3, the area is π R ², and S layers of cells contribute the force f (Eq. 16). Assuming the drag of the cylinder is CμLU, we find

$$ U=\left(\frac{\pi c}{C}\right)\left(\frac{SR^2an^{2/3}} {L}\right)v. $$

(23)

This result is independent of the fluid viscosity. For R = 10⁻³cm, L = 10⁻² cm, a = 10⁻⁶ cm, n ^2/3 = 2 × 10⁷ cm⁻² and Sπ c/C = 10, we obtain a phalanx moving faster than an individual, U = 1.8v, indicating that a more formal version of this approach may prove useful.

Fig. 18

Schematic diagram of a phalanx, a coherent domain of cells swimming to the left with collective velocity U. Arrows indicate direction of transverse fluid flow as in Figs. 15 and 16 due to the collective motion inside the domain

8 Discussion

This paper has described how hydrodynamics and biological behavior of a concentrated population of swimming microorganisms can combine to produce a collective dynamic, the ZBN, with interacting nematic-like domains that exhibit quorum polarity of propagation with spatial and temporal correlation. Relevant experiments on individual cell motility, and a novel approach for understanding locomotion and for calculating the flows that surround swimmers, provide ingredients for a realistic theoretical model of this complex two-phase system. Dimensional analysis demonstrates that the observed speeds of the collective domains are plausible, and that the occurrence of “turbulent" dynamics at Re ≪ 1 can be understood by considering the input of (swimming) energy from the occupants of the fluid.

We demonstrate that the results of PIV, obtained from high frame rate video microscopy images of the swimming cells, i.e. under difficult circumstances, can provide useful data on velocity and vorticity distributions, the latter exhibiting a rather satisfying alternation of signs, somewhat like vortex streets. It should be remembered that the PIV data were obtained from the bacteria, the motile suspended phase, not from added tracers in the water. Moreover, we have developed a novel measure of angular alignment (and deviation), based on the velocity vector field. That analysis shows the remarkable spatial extent of continuous alignment, as well as singular regions of defects. Whereas averages over many quasi-instantaneous correlations of vorticity and velocity show decays of order one second, the alignment data exhibits remarkable stability.

Transport of biologically significant molecules, for cell-cell communication, supply of nutrients and elimination of wastes, and for respiration can be greatly enhanced by the chaotic advection that accompanies the intermittent collisions, reconstitution and decay of the zooming domains. We have proposed a heuristic model of the formation of propagating coherent regions whose ingredients are the transverse flows and inward forces that accompany swimming (Fig. 14), up-flow swimming in shear flows (Sect. 4), flipping of flagella at obstacles (Cisneros et al. 2006), and, of course, geometrically determined stacking (steric repulsion).

What determines the breakup of domains? Extrapolating from Fig. 15 and calculations, not shown here, for phalanxes comprising more swimmers, the flow inside a domain is quite weak. The supply of oxygen to the interior cells (note Fig. 16) would be insufficient to maintain average levels of concentration. The interior cells will therefore swim transversely, up the gradient of oxygen concentration, or swim ever more slowly; both scenarios imply breakup. The swimming velocity distribution of individual cells is approximately Maxwellian, and very oxygen dependent (Kessler and Wojciechowski 1997). The uniform speed of cells in phalanxes is therefore quite remarkable. The decay time of averaged correlations is about one second (Fig. 5) and oxygen supply times (Sect. 1) are about the same. This would seem to be more than a coincidence. There are other possible contributors to the decay of coherence. Interior cells may begin tumbling in search of a more favorable chemical environment; phalanxes that collide break up; the head end of elongated domains, as in Fig. 18, may buckle (we occasionally observe very explicit cases of roll-up); instability of nematics (Simha and Ramaswamy 2002b) may also be a factor. The problem of understanding this intermittency clearly demands further work.