Determination of complete velocity gradient tensor by using cinematographic stereoscopic PIV in a turbulent jet

Abstract

Cinematographic stereoscopic PIV measurements were performed in the far field of an axisymmetric co-flowing turbulent round jet (Re _T ≈ 150, where Re _T is the Reynolds number based on Taylor micro scale) to resolve small and intermediate scales of turbulence. The time-resolved three-component PIV measurements were performed in a plane normal to the axis of the jet and the data were converted to quasi-instantaneous three-dimensional (volumetric) data by using Taylor’s hypothesis. The availability of the quasi-three-dimensional data enabled the computation of all nine components of the velocity gradient tensor over a volume. The use of Taylor’s hypothesis was validated by performing a separate set of time-resolved two component “side-view” PIV measurements in a plane along the jet axis. Probability density distributions of the velocity gradients computed using Taylor’s hypothesis show good agreement with those computed directly with the spatially resolved data. The overall spatial structure of the gradients computed directly exhibits excellent similarity with that computed using Taylor’s hypothesis. The accuracy of the velocity gradients computed from the pseudo-volume was assessed by computing the divergence error in the flow field. The root mean square (rms) of the divergence error relative to the magnitude of the velocity gradient tensor was found to be 0.25, which is consistent with results based on other gradient measurement techniques. The velocity gradients, vorticity components and mean dissipation in the self-similar far field of the jet were found to satisfy the axisymmetric isotropy conditions. The divergence error present in the data is attributed to the intrinsic uncertainty associated with performing stereoscopic PIV measurements and not to the use of Taylor’s hypothesis. The divergence error in the data is found to affect areas of low gradient values and manifests as nonphysical values for quantities like the normalized eigenvalues of the strain-rate tensor. However, the high gradients are less affected by the divergence error and so it can be inferred that structural features of regions of intense vorticity and dissipation will be faithfully rendered.

1 Introduction

Understanding the dynamics of intermediate and fine scales of turbulent shear flows is important to turbulence theory and to the development and validation of sub-grid scale models used in large-eddy simulations of shear flows. Previous works have attempted to characterize the small-scale motions and to understand the relationship between dissipation, vorticity and strain-rate (for example, Ashurst et al. 1987; Lund and Rogers 1994) in turbulent flows. This work requires detailed simultaneous three-dimensional velocity and velocity gradient information which have been derived mainly from direct numerical simulations (DNS) of turbulence. The availability of the three-dimensional velocity gradient data enables the study of structure, higher order statistics and scaling of important parameters like kinetic energy dissipation, strain-rate and vorticity.

Although DNS data have been the main source for simultaneous three-dimensional velocity gradients, early studies in the literature utilized measurements obtained from a single hot-wire to compute one-dimensional estimates of dissipation rate in turbulent shear flows (Antonia et al. 1980b). Subsequently, Balint et al. (1991) and Tsinober et al. (1992), among others, used multiple hot-wire probes to measure multiple components of the velocity gradient tensor simultaneously. Similar velocity gradient measurements have also been made using laser Doppler anemometry (LDA) by Ötügeny et al. (1998). The availability of multiple gradient components improves the dissipation rate estimate. All the above mentioned techniques invoke Taylor’s hypothesis to compute gradients along the mean streamwise direction. Hot-wire and LDA based gradient measurements are typically limited to a single point in space and therefore cannot provide insight into the spatial structure of the finest scales.

Particle image velocimetry (PIV) provides two in-plane velocity components, which can be employed to obtain four in-plane components of the instantaneous velocity gradient tensor. Stereoscopic PIV and scanning PIV provide the out-of-plane velocity component, and hence two more components of the velocity gradient tensor. However, the single plane PIV technique can resolve only one component of vorticity. Some implementations of particle tracking velocimetry (PTV) can provide all three components of the velocity in a three-dimensional volume by using multiple cameras, however, the large particle separations required for particle tracking prohibits velocity gradient measurements in small-scale flows (see Maas et al. 1993a, b).

Dual-plane stereoscopic PIV (DSPIV) has been employed to measure the complete velocity gradient tensor over a plane. Variations of this technique have been employed by a limited number of research groups. Kähler (2004) investigated the correlation between adjacent planes in turbulent boundary layers, Ganapathisubramani et al. (2005) characterized the eddy structure in turbulent boundary layers, Hu et al. (2001) investigated large scale structures in a lobed jet and Mullin and Dahm (2006) studied the intermediate- and fine-scales in turbulent flows using the dual-plane PIV technique. Although the dual-plane PIV technique enables computation of the complete gradient tensor, planar measurements (PIV and DSPIV) cannot determine the three-dimensional spatial structure of the dissipation scales or vorticity.

Holographic particle image velocimetry (HPIV) technique can provide complete 3D velocity fields and can be utilized to compute the complete velocity gradient tensor over a volume (see Meng and Hussain 1995; Zhang et al. 1997; Scherer and Bernal 1997; Barnhart et al. 1994). However, the complexity of the setup has precluded its widespread use in fluid mechanics.

Su and Dahm (1996) performed indirect measurements of the velocity gradient tensor using scalar image velocimetry (SIV). The technique is based on imaging the three-dimensional conserved scalar field with laser-induced fluorescence and inverting the conserved scalar transport equation to obtain all three velocity components. However, this technique requires smoothness and continuity constraints in the inversion used to obtain velocity field data.

Recently, Elsinga et al. (2006) described the tomographic particle image velocimetry technique that is capable of measuring all three velocity components in a three-dimensional volume. The technique makes use of several simultaneous views of the illuminated particles and uses 3D reconstruction of light intensity distribution by means of optical tomography. The study also demonstrated the feasibility of the technique by applying it to a wake flow.

A few researchers have employed time-resolved stereoscopic particle image velocimetry together with Taylor’s “frozen flow-field" hypothesis to obtain pseudo three-dimensional velocity fields. For example, Matsuda and Sakakibara (2005) applied this technique to investigate the large-scale structures in the far field of an axisymmetric jet and van Doorne and Westerweel (2007) utilized the same technique to study the flow fields of laminar, transitional and turbulent pipe flows.

The present study uses a technique that is similar to that used by Matsuda and Sakakibara (2005) and van Doorne and Westerweel (2007), but unlike those studies we focus on the measurement of the fine-scale structure of turbulence. Cinematographic stereoscopic particle image velocimetry is utilized to measure three components of velocity in a plane and Taylor’s hypothesis is employed to reconstruct a pseudo-volume of velocity data. Experiments were performed in the far field of an axisymmetric co-flowing jet where the Kolmogorov scale is large enough so that the dissipation scales can be largely resolved. The pseudo three-dimensional data are used to compute the complete velocity gradient tensor along with the three components of vorticity and other derived quantities such as three-dimensional dissipation rates. The goal of this study is to examine the accuracy of derived velocity and velocity gradients and to establish the validity of the data to investigate the structure of fine-scale dissipation and vorticity.

2 Experimental facility

2.1 Turbulent jet facility

The flow setup used in this study was designed by Tsurikov (2003) to produce a turbulent jet that has a large enough Kolmogorov scale in its far-field region. The facility is 92 cm wide by 92 cm long by 117 cm high, and was constructed of aluminum structural members and aluminum sheet for the walls. The facility consists of an axisymmetric turbulent jet exhausting into a co-flow of air. The jet issues upwards from a circular pipe, 26 mm in diameter, located at the center of the co-flow facility. The jet fluid was air that was stored in a large high pressure reservoir. The flow rate was controlled by a manually-operated valve and monitored using an electronic mass flowmeter (McMillan 50D-15). The co-flow was supplied by an industrial blower (Grainger/Dayton model 5C508) which was operated at fixed speed. The co-flow entered the jet facility through a network of PVC pipes, and was conditioned by sections of honeycomb and fine-mesh screens prior to entering the test section. Table 1 lists the jet and the co-flow characteristics at the jet exit and at the measurement location.

Table 1 Flow characteristics

The degree to which the jet is pure or co-flowing can be characterized in terms of the momentum radius (θ), given by ${\theta =\sqrt{J_o/\pi\rho_\infty {U_\infty}^2}}$ where the source momentum flux J _o = 0.25π D ²ρ _o U ² _o . Dahm and Dibble (1988) proposed that a jet with co-flow approximates a pure jet if x ₁/θ ≤ 2 (x ₁ is the axial direction, x ₂ and x ₃ are the two orthogonal radial directions). In the current study, stereoscopic PIV measurements were performed at a downstream location of x ₁ = 32D, which corresponds to x ₁/θ = 3.8 indicating that the jet is mildly co-flowing.

2.2 Cinematographic stereoscopic PIV

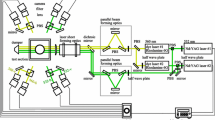
Cinematographic stereoscopic PIV measurements were obtained in the self-similar far-field region of the jet in a plane normal to its axis at a downstream location of x ₁/D = 32. The cinematographic PIV system (shown in Fig. 1) consists of a diode-pumped Nd:YLF laser (Coherent Evolution-90) with an output wavelength of 527 nm and a pair of high-framing rate CMOS cameras (Photron FASTCAM-Ultima APX). The laser was operated at 9 mJ per pulse at a repetition rate of 2 kHz. The two CMOS cameras had a resolution of 1,024 × 1,024 pixels and were synchronized with the laser at a framing rate of 2 kHz. Both cameras were fitted with a Nikon 105 mm lens with an aperture setting of f/5.6.

Fig. 1

Schematic of the time resolved stereoscopic particle image velocimetry system (inset shows a schematic representation of the jet)

The angular-displacement stereo PIV method, in which the cameras are rotated inwards such that their axes intersect at the mid-point of the domain to be recorded, was employed in this study. The stereo-cameras were oriented at an angle of 30° to the axis of the jet as shown in Fig. 1. To maintain focus over the entire field of view, the CMOS cameras and the lenses were oriented at the Scheimpflug condition. This arrangement introduced a strong perspective distortion and as a result the magnification varied across the image plane. This distortion was corrected by calibration using a fixed grid that contains marker points. The target was aligned with the laser sheet that illuminated the measurement plane and subsequently translated at intervals of 0.5 mm in both directions normal to the laser sheet. Digital images of the grid were captured by both cameras for various locations of the target. The acquired images of the grid were analyzed using TSI PivCalib software to compute the necessary magnification at different axial locations.

Glycerin-based droplets with a nominal size of 1-2 μm generated by a theatrical fog machine (Rosco Model 1600) were used as PIV seed particles. The response time (τ_R) of these seed particles is computed to be approximately 4 μs based on particle diameter of 1 μm (see Raffel et al. 1998 for details). The Stokes number, defined as St = τ_R/τ_F (with τ_F the characteristic flow time scale) must be much less than 1 for the particles to faithfully track the fluid motion (Raffel et al. 1998). Given that the goal of this study is to track small-scale motions, the characteristic flow time is the Kolmogorov time scale ${\tau_\eta = \sqrt{\nu/\epsilon}}$ which is approximately 15 ms (where ν is the kinematic viscosity of air and ε is the kinetic energy dissipation). This gives a Stokes number of 2.5 × 10⁻⁴ and hence indicates that the particles easily track the velocity fluctuations in the flow.

The particles were seeded into the co-flow and subsequently entrained by the spreading jet. The seed particles were illuminated by a laser sheet. The sheet thickness, which was not rigorously measured, is estimated to be 0.5–1 mm. The scattered light was captured by the two CMOS cameras in stereoscopic arrangement. Cinematographic images were acquired for duration of 1 s, corresponding to a total of 2,000 frames and 2 GB of data for each run. Images from the cameras were then transferred to a hard disk and were processed to compute vector fields. Successive particle images in the movie sequence were separated in time by 500 μs and were cross-correlated to compute PIV vector fields.

Vector fields were computed with the images from both cameras using an adaptive central-difference technique proposed by Wereley and Meinhart (2001). The final interrogation region was 16 × 16 pixels in size with 50% overlap. TSI Insight 6.1 software that employs the above mentioned technique was used for vector computation. A maximum pixel displacement with a magnitude of approximately seven pixels was observed for each camera. The vector fields were validated using a standard 3 × 3 local median filter and the missing vectors were interpolated using a 3 × 3 local mean technique. The number of spurious vectors was close to 3% in the entire dataset. The vectors from each camera were then combined using the magnification factors, which were found using the calibration procedure described earlier, to compute all three velocity components. The resolution of the resulting stereoscopic vector fields, as given by the interrogation window size, was about 3η × 3η (1.35 × 1.35 mm²) and successive vectors were separated by 1.5η (owing to 50% overlap). The total field size is 76 × 76 mm² (160 η × 160 η).

3 Quasi-instantaneous volume reconstruction

Figure 2 shows a time-sequence of four velocity vector fields in the “end-view” x ₂–x ₃ plane. The contours in the figures show the jet axial velocity component (u ₁) and the vectors reveal the in-plane velocity components (u ₂ and u ₃). The sequence of vector fields exhibit strong similarity to one another indicating that there is minimal change in the velocity fields in the time between PIV frames. The excellent temporal resolution suggests that Taylor’s “frozen flow-field” hypothesis can be applied to reconstruct a quasi-instantaneous three-dimensional velocity field with the cinematographic stereo PIV data.

Fig. 2

A sequence of four velocity vector fields in x ₂–x ₃ plane. The vectors show u ₂ and u ₃ velocity components. The color contours show u ₁ velocity component in m/s. The fields are separated in time by 1 ms

Mean and root mean square (rms) fields of all the three velocity components were computed based on the 2,000 (two runs) stereoscopic vector fields. Figure 3a shows the contours of ${\overline{u_1}}$ in an “end-view” plane (x ₂–x ₃ plane) at the measurement location (x ₁ = 32D). The figure shows ${\overline{u_1}}$ contours that are not completely round suggesting that the data have not converged sufficiently. The large-eddy time scale of the flow, τ = δ_1/2/(U _c−U _∞) is approximately 0.21 and 1 s of time-resolved data correspond to about 5τ. The mean and rms quantities that were computed from the data, therefore, includes only ten large eddies (two datasets) and hence may not be sufficiently converged. However, as will be shown in Sect. 4, the lack of convergence in the velocity data does not seem to significantly affect the accuracy of the axial velocity gradients computed using Taylor’s hypothesis.

Fig. 3

Taylor’s hypothesis used to compute axial coordinates. a Contours of ${\overline{u_1}}$ (m/s) and b volume computed using the convection velocity ${U_{\rm c}=\overline{u_1}}$

A convection velocity equal to the mean velocity at a given location was utilized to compute the axial coordinates ${(U_{\rm c}(x_2,x_3) =\overline{u_1}).}$ Since, the convection velocity varies over the x ₂–x ₃ plane the axial coordinates were different for different regions of the jet. The axial coordinate was computed as follows: all points in the first vector field of a sequence were assigned x ₁(x ₂,x ₃) = 0. The axial coordinates for any other vector field separated by KΔt were computed based on,

$${x_1(K\Delta t,x_2,x_3) = -K U_{\rm c}(x_2,x_3)\Delta t}$$

(1)

where K is an integer that defines the time gap between a given vector field and the first vector field in the sequence and Δt = 1 ms is the time separation between successive vector fields. It must be noted that Δt is not the time separation between successive particle images, which is 500 μs.

Figure 3b shows a sample grid computed using the technique described above. A total of 200 successive vector fields were used for the computation of this grid. The figure clearly shows a distorted grid conforming to the variations in the local convection velocity. The axial coordinates near the jet center are stretched while the coordinates in the shear layer are compressed since the mean jet axial velocity ${(\overline{u_1})}$ is higher near the center and lower at the peripheral locations.

The resolution of the pseudo three-dimensional field along the axial direction varies between η and 2η depending on the convection velocity and therefore the three-dimensional resolution of the raw data is 2η × 3η × 3η.

Figure 4a shows the energy spectrum of axial velocity E ₁₁ along κ₁, κ₂ and κ₃ directions, where κ₁, κ₂, κ₃ are the wave numbers in the axial and the two cross-plane directions (the wave number is defined as κ = 2π/Λ with units of radians/length, where Λ is the wavelength). The energy spectrum along κ₁ extends to a smaller wavenumber compared to κ₂ and κ₃ because the time-resolved data is available over a duration 1 s, which translates to a largest wavelength Λ _r (x ₁) ≈ 600 mm (based on mean axial velocity and the duration over which the time resolved data is available). However, the largest wavelength and consequently the smallest wavenumber in κ₂ and κ₃ directions is limited by the field of view of the vector field to Λ _r (x ₂) = Λ _r (x ₃) = 76 mm. Note that the variation in convection velocity over the “end-view” plane is ignored while computing the axial wavenumbers to simplify the process. A constant convection velocity ${\overline{u_1} = 0.66\,\hbox{m/s}}$ (this is the mean axial velocity over the plane) is used to convert frequency to wavenumber in the axial direction.

Fig. 4

Spectra of axial velocity in all three directions computed from raw data a E ₁₁ and b D ₁₁. Spectra of axial velocity in all three directions computed from filtered data c E ₁₁ and d D ₁₁

Figure 4a shows that E ₁₁ tends to become flat for high wave numbers in all three directions. This is the effect of measurement noise on the velocity data. The effect of noise on data at high wavenumbers is clearly apparent in the spectra of the velocity gradients shown in Fig. 4b. The velocity gradient energy spectrum is derived from the energy spectrum using the following relation,

$${D_{11}(k_i) = {\kappa_i}^2 E_{11}(\kappa_i),}$$

(2)

where κ _i is the wavenumber with i = 1, 2 or 3. The velocity gradient energy spectra shown in Fig. 4b are consistent with gradient energy spectra (i.e., dissipation spectra) computed from point measurement techniques in the low wavenumber regions where the noise effects are relatively weak, however, the effect of noise on the data is clearly apparent in the high wavenumber region as a rapid increase in energy above κη > 0.5. The flat region in the high wavenumber regime of E ₁₁ manifests as large values in D ₁₁. The mean kinetic energy dissipation computed by integrating the area under the curve of D ₁₁, would therefore include a large contribution from the noise affected high wavenumber region. This indicates that the data must be filtered to reduce the effect of noise on velocity gradients as is always done with single-point time-series measurements; therefore, a Gaussian smoothing filter with a filter width of λ _f = 3 η (i.e., full width of the Gaussian smoothing function at 1/e ² = 3η) was used to filter the data along all the three directions. This filter width was chosen to match the PIV interrogation window size of 3η to minimize loss of resolution in the cross-stream directions. The resulting spectra of E ₁₁ and D ₁₁ computed based on the filtered velocity field are shown in Fig. 4c, d. The spectra in comparison with the spectra from unfiltered data show that smoothing does indeed reduce the effect of noise on E ₁₁ and D ₁₁. The general shape and features of the filtered velocity gradient energy spectra in Fig. 4d including the peak around κη ≈ 0.1 is consistent with spectra in various other studies in the literature (see Antonia et al. 1982; Saddoughi and Veeravalli 1994; Mi and Nathan 2003). The cross-stream velocity components were also filtered using the same Gaussian filter and their respective spectra also reveal similar improvement at high wave numbers.

It must be noted that most point measurement techniques use the “Kolmogorov frequency” as the filter frequency to filter the data (for example, see Wyngaard and Tennekes 1970; Antonia et al. 1980a; Saddoughi and Veeravalli 1994). Kolmogorov frequency is given by,

$${f_\eta = {\frac{\overline{u_1}}{2\pi\eta}}}$$

(3)

Antonia et al. (1982) stated that it would be desirable to set the filter frequency at a larger value than f _η and found that the optimum setting for the filter frequency was about 1.75f _η on the basis of statistics of velocity gradients measured using hot-wires in circular and plane jets. However, they found that the variations in the statistics of gradients were relatively small once the filter frequency was greater than f _η. Mi and Nathan (2003) studied the effect of filter frequency on scalar dissipation and found that filtering the data at the Batchelor frequency (equivalent to Kolmogorov frequency for scalar dissipation) captured 99% of all dissipative structures and accurately represented the mean dissipation. This Kolmogorov frequency (f _η) corresponds to filtering the data at wavelength λ _f = 2πη (i.e., ≈6η). Therefore, the use of Gaussian filter with width of 3η is consistent with filtering the data at approximately 1.75f _η and should therefore capture the velocity gradients accurately.

The total size of the reconstructed quasi-instantaneous volume x ₁ × x ₂ × x ₃ = 1,300η × 160η × 160η (5δ_1/2 × 0.6δ_1/2 × 0.6δ_1/2). Figure 5a shows three-dimensional velocity vectors from a sample part of the total volume. The field of view of the volume in Fig. 5 is 250η × 160η × 160η (0.8δ_1/2 × 0.6δ_1/2 × 0.6δ_1/2). The mean velocity along the jet axial direction has been subtracted from each vector (only alternate vectors are shown in all three directions for clarity). The velocities are filtered using the Gaussian filter as discussed previously in this section. This filtered pseudo-volume of data was used to compute all nine components of the velocity gradient tensor. A second order central difference technique was employed to compute all gradients. Figure 5b shows contours of enstrophy (magnitude of the complete vorticity vector) in the same volume. Enstrophy was computed from the velocity gradients determined from the space–time volume.

Fig. 5

a Three-dimensional vector map of the flow field with axes normalized by local jet width. The mean velocity is subtracted along the jet axial direction. Only alternate vectors are shown in all three directions for clarity. b Contours of enstrophy with axes normalized by Kolmogorov length scale

4 Assessment of Taylor’s hypothesis: side-view PIV measurements

The use of Taylor’s hypothesis to compute the axial coordinates and the velocity gradients was validated by performing a separate set of experiments in a “side-view” x ₁–x ₂ plane. Time-resolved single camera two-component PIV measurements were made in side-view plane near the jet centerline and at outward radial locations at a downstream location of x ₁ = 32 D. The field of view was approximately 160 η × 160 η and comparable to the field of view of the “end-view” stereoscopic measurements. The experimental setup used for making these two-component PIV measurements was similar to the stereoscopic PIV setup except for the use of a single CMOS camera. All the other parameters such as the repetition rate of the laser, framing rate of the camera, the aperture setting of the 105 mm lens and the frame resolution of the camera were the same as that of the other experiment. The seeding of the jet and the processing of the images for velocity vectors were performed in a manner as explained in the previous section (see Sect. 2.2). The final resolution of the vector fields was identical to that of the stereoscopic measurements.

The time-resolved two-component PIV data were used to compute both time derivatives and direct spatial gradients for both measured velocity components (u ₁ and u ₂). The mean of the axial velocity component was computed and was used together with the time derivative to derive the spatial gradient as shown below:

$${U_{\rm c} = \overline{u_1}(x_1,x_2)}$$

(4)

$${{\frac{\partial u^d_1 (x_1,x_2)}{\partial x_1}} =\frac{-1}{U_{\rm c}}\frac{\partial u_1(x_1,x_2)}{\partial t}}$$

(5)

$${\frac{\partial u^d_2 (x_1,x_2)} {\partial x_1} =\frac{-1}{U_{\rm c}}\frac{\partial u_2(x_1,x_2)}{\partial t}}$$

(6)

The derived spatial gradients (noted with superscript d) were compared with the direct spatial gradients to assess the validity of Taylor’s hypothesis in these measurements. Sample instantaneous velocity gradient fields of ∂u ₁/∂x ₁ and ∂u ₂/∂x ₁, computed directly and with Taylor’s hypothesis are shown in Fig. 6. Note that all the gradients are plotted to the same scale. It can be seen that the basic spatial structure of the gradients is captured reasonably accurately by the use of Taylor’s hypothesis, but there are clearly differences in the magnitudes of the gradients in some regions. Similar results were obtained by Dahm and Southerland (1997) for the conserved scalar field in a turbulent flow since they observed that the qualitative structure of the gradients was similar.

Fig. 6

Comparison of direct and derived instantaneous spatial gradients of velocity obtained using planar-PIV along the jet-axis. a ∂u ₁/∂x ₁, b ∂u ^d ₁/∂x ₁, c ∂u ₂/∂x ₁ and d ∂u ^d ₂/∂x ₁

Further analysis on the similarity between direct and derived spatial gradients was performed by computing the correlation coefficients between the direct and derived spatial gradients as a function of radial location (x ₂ location). Figure 7a shows the radial profile of the mean axial velocity component (along x ₂ direction) that is consistent with the stereoscopic PIV measurements and other studies in the literature (for example, Wygnanski and Fiedler 1969). Figure 7b shows the radial profile of the correlation coefficient between ∂u ₁/∂x ₁ and ∂u ^d ₁/∂x ₁. The maximum correlation between the two quantities is along the centerline where a correlation of 0.79 was obtained. The general trend of the correlation profile follows the mean velocity profile of the jet shown in Fig. 7a. The correlation coefficient falls to 20% of the centerline value in the shear layer (x ₂ ≈ 0.4 δ_1/2). Figure 7b also shows the correlation between ∂u ₂/∂x ₁ and ∂u ^d ₂/∂x ₁. This correlation attains a maximum value of 0.86 at the jet centerline and appears to decay slower than the correlation for ∂u ₁/∂x ₁. The trend in the correlations is consistent with the correlation between direct and derived temperature gradients observed by Mi and Antonia (1994) in an axisymmetric turbulent jet where the correlation coefficient decreased from 0.92 on the axis of the jet to 0.78 at x ₂/δ_1/2 = 0.5.

Fig. 7

a Radial profile (along x ₂ direction) of mean axial velocity component ${(\overline{u_1}).}$ b Radial profiles of the correlation coefficient between ∂u ₁/∂x ₁ and ∂u ^d ₁/∂x ₁ (circles) and ∂u ₂/∂x ₁ and ∂u ^d ₂/∂x ₁ (squares)

The overall correlation coefficient between the derived and direct spatial gradients (across the entire field of view) was found to be 0.85 and 0.72 for ∂u ₁/∂x ₁ and ∂u ₂/∂x ₁, respectively. This is consistent with the correlation coefficient of 0.74 found by Dahm and Southerland (1997) in the case of scalar gradients.

Pope (2000; Fig. 5.8) gives a curve fit for the local turbulence intensity ${(\overline{{u^\prime_1}^2}/{\overline{u_1}}^2)}$ as a function of radial location (data for the curve fit taken from Hussein et al. 1994) which indicates that the local turbulence intensity remains close to a value of 0.1 for radial locations within 0.5δ_1/2 (i.e., x ₂ < 0.5δ_1/2). However, the local turbulence intensity exhibits rapid increase to values greater than unity for radial locations beyond δ_1/2. Taylor’s hypothesis is expected to breakdown in regions with large values of local turbulence intensity (Antonia et al. 1980a; Mi and Antonia 1994) and therefore the correlation between the direct and derived spatial gradients would be decrease dramatically beyond a radial location of x ₂ = δ_1/2. Consequently, the “end-view” cinematographic PIV technique used to obtain quasi-instantaneous volume of data should be greatly diminished in accuracy in the outer regions of the jet (e.g., x ₂ > δ_1/2).

It should be noted that the lack of correlation between the direct and derived gradients is not all due to the breakdown of Taylor’s hypothesis. It could also arise from velocity magnitude errors that are intrinsic to the stereo PIV technique. The gradients are computed from the velocity data using finite differencing schemes. Differentiation is a noise enhancing process and amplifies the errors present in the velocity data. Therefore, the inherent noise present in the velocity gradients also contributes to the differences between direct and derived spatial gradients. Raffel et al. (1998) explained that the uncertainty in the velocity gradients depends on the uncertainty in the velocity component, the spatial resolution of the sampling and the algorithm used to compute the gradients. They performed a simple error propagation analysis and indicated that a velocity gradient can be computed using a central difference scheme with an uncertainty of 0.7δU/Δ (where, δU is the uncertainty in the velocity component and Δ is the spacing between successive vectors). In the current study, the uncertainty in the rms values of the velocity gradients based on the above mentioned analysis is approximately 15% (given an uncertainty of approximately 1% in the velocity data. The uncertainty in velocity data is discussed in detail in Sect. 6). This is consistent with the results from previous studies by Ganapathisubramani et al. (2005) where the authors found similar uncertainties in velocity gradients. This is also consistent with the conclusions of Westerweel (1994) who computed the uncertainty in vorticity in a one-dimensional shear layer using synthetic PIV images and found that the value of vorticity could be computed with 10 to 20% accuracy at best (depending on the measurement noise), provided the velocity data are within 1 to 2% accuracy.

The use of Taylor’s hypothesis can be further tested by comparing the probability density functions (pdfs) of the derived and direct gradients calculated from the side-view PIV measurements. Figure 8a, b show the probability distributions of derived and direct gradients of ∂u ₁/∂x ₁ in two different scales (linear and semi-log). The distributions of ∂u ₁/∂x ₁ and ∂u ^d ₁/∂x ₁ are identical and do not possess any noticeable difference. Additionally, the rms values of ∂u ₁/∂x ₁ and ∂u ^d ₁/∂x ₁ were 22.09 and 19.65 s⁻¹, respectively, further indicating that the differences between the two gradients are minimal. Figure 8c, d show pdfs of ∂u ₂/∂x ₁ in linear and semi-logarithmic scales, respectively. It is seen that the derived and direct gradients of ∂u ₂/∂x ₁ for the side-view PIV data also exhibit excellent similarity over the entire range of gradient values.

Fig. 8

Probability distributions of velocity gradients. ∂u ₁/∂x ₁ compared to ∂u ^d ₁/∂x ₁ a linear scale, b semi-logarithmic scale, ∂u ₂/∂x ₁ compared to ∂u ^d ₂/∂x ₁, c linear scale and d semi-logarithmic scale

The qualitative similarity of the structure between direct and derived velocity gradients and the consistency between the probability distributions of direct and derived axial gradients validates the use of Taylor’s hypothesis to compute the axial gradients.

5 Accuracy assessment of stereoscopic measurements: axisymmetric isotropy

5.1 Velocity gradients

Quantification of the accuracy of velocity gradients can be carried out by comparing the moments of different velocity gradients with isotropic conditions. Mullin and Dahm (2006) compared the mean-square values of all components of the velocity gradient tensor to local isotropy conditions and found a reasonable agreement. However, as will be shown later, the velocity gradients in the current study do not satisfy local isotropy conditions, especially along the mean flow direction. Previous studies in the literature have also reported the failure of experimental data to satisfy local isotropy conditions. George and Hussein (1991) reported that the homogeneous isotropic conditions do not describe experimentally obtained derivative moments in the far field of circular jets and plane jets. They found that the data conformed to axisymmetric isotropy conditions and also noted that axisymmetric isotropy is necessary for total local isotropy. Antonia et al. (1991) identified the same issue in a DNS dataset of a turbulent boundary layer. Local axisymmetric isotropy requires that the following ratios are all equal to 1.

$${M_1 = \overline{\left(\frac{\partial u_1}{\partial x_2}\right)^{2}}/\overline{\left(\frac{\partial u_1}{\partial x_3}\right)^{2}}}$$

(7)

$${M_2 = \overline{\left({\frac{\partial u_2}{\partial x_1}}\right)^{2}}/\overline{\left({\frac{\partial u_3}{\partial x_1}}\right)^{2}}}$$

(8)

$${M_3 = \overline{\left({\frac{\partial u_2}{\partial x_2}}\right)^{2}}/\overline{\left({\frac{\partial u_3}{\partial x_3}}\right)^{2}}}$$

(9)

$${M_4 = \overline{\left({\frac{\partial u_2}{\partial x_3}}\right)^{2}}/\overline{\left({\frac{\partial u_3}{\partial x_2}}\right)^{2}}}$$

(10)

where, x ₁ is the preferred flow axis (mean flow direction).

Table 2 lists the mean-square values of all the nine velocity gradients. The above mentioned axisymmetric isotropy ratios are computed from the mean-square values listed in Table 2. The values of M ₁, M ₂, M ₃ and M ₄ are approximately equal to 0.89, 0.97, 1.01 and 1.09, respectively. It is clear from these values that the velocity derivatives are at worst within 10% of the axisymmetric isotropy conditions. This agreement is consistent with the results of George and Hussein (1991) where the velocity gradients were found to satisfy the axisymmetric isotropy conditions to within 10%.

Table 2 Root mean square statistics of all nine components of the velocity gradient tensor

5.2 Vorticity and dissipation

The axisymmetric isotropy relations also have implications on vorticity components and dissipation. The conditions require that,

$${\overline{{\omega_2}^2} = \overline{{\left({\frac{\partial u_1}{\partial x_3}}\right)}^2} + 2\overline{{\left({\frac{\partial u_1}{\partial x_1}}\right)}^2}}$$

(11)

$${\overline{{\omega_3}^2} = \overline{{\left({\frac{\partial u_1}{\partial x_2}}\right)}^2} + 2\overline{{\left({\frac{\partial u_1}{\partial x_1}}\right)}^2}}$$

(12)

$${\overline{{\omega_1}^2} = \overline{{\left({\frac{\partial u_3}{\partial x_2}}\right)}^2} +{\frac{5}{3}}\overline{{\left({\frac{\partial u_2}{\partial x_3}}\right)}^2} - {\frac{1} {3}}\overline{{\left({\frac{\partial u_1}{\partial x_1}}\right)}^2}}$$

(13)

where, ${\overline{{\omega_1}^2}, \overline{{\omega_2}^2}\,\hbox{and}\,\overline{{\omega_3}^2}}$ are the mean square values of the three components of vorticity.

Table 3 lists the actual mean square values of the vorticity computed from the time-resolved stereoscopic data and the axisymmetric isotropy estimates. The values in the table indicate that the data satisfy the axisymmetric conditions to within 5% and this is consistent with results from the previous studies by George and Hussein (1991) and Antonia et al. (1991).

Table 3 Root mean square statistics of all nine components of the velocity gradient tensor

Mean kinetic energy dissipation rate ${(\overline{\epsilon_{3D}})}$ was computed using all nine components of the gradients and was found to be 0.069 m²/s ³. This value of dissipation is comparable, but is approximately 25% higher than the dissipation estimate listed in Table 1. It must be noted that the dissipation estimate in Table 1 was derived based on homogeneous isotropy assumptions applied to a pure jet. Dissipation estimates can be calculated employing the axisymmetric form of mean dissipation from George and Hussein (1991) and Antonia et al. (1991),

$${\overline{\epsilon_a} = \nu\left[{\frac{5}{3}}\overline{{\left({\frac{\partial u_1}{\partial x_1}}\right)}^2} +2\overline{{\left({\frac{\partial u_1}{\partial x_3}}\right)}^2} +2\overline{{\left({\frac{\partial u_2}{\partial x_1}}\right)}^2} +{\frac{8}{3}}\overline{{\left({\frac{\partial u_2}{\partial x_3}}\right)}^2}\right]}$$

(14)

The mean dissipation estimate computed based on axisymmetric conditions is ${\overline{\epsilon_a} = 0.066\,\hbox{m}^2/\hbox{s}^3,}$ which is within 5% of mean dissipation ${(\overline{\epsilon_{3D}})}$ computed from the dataset.

6 Accuracy assessment of stereoscopic measurements: dilatation

A stringent test for the accuracy of the velocity gradients computed from time-resolved stereoscopic measurements is to use the data to compute the divergence error. The divergence error, i.e., the extent to which the data deviates from the zero divergence condition for incompressible flows ${(\nabla\cdot{u} = 0)}$ was determined. Figure 9a shows contours of the joint probability distribution of ∂u ₁/∂x ₁ and −(∂u ₂/∂x ₂ + ∂u ₃/∂x ₃). Divergence free data should fall along a 45° straight line (i.e. diagonal) and the deviation from this diagonal indicates the extent of divergence error in the data. Figure 9a reveals a scatter around the diagonal suggesting the presence of divergence error in the data. The correlation coefficient between the two quantities was computed to assess the extent of divergence error. The value of correlation coefficient was approximately 0.82 and this value is consistent with the correlation coefficient for the same parameters computed by Tsinober et al. (1992), who performed multi-probe hot-wire based studies.

Fig. 9

a Joint pdf between ∂u ₁/∂x ₁ and −(∂u ₂/∂x ₂ + ∂u ₃/∂x ₃), contours from 0.0001 to 0.001 are shown with a spacing of 0.0001. The divergence free line is marked for reference. b pdf of ξ, c pdf of ${\nabla\cdot {u}/|\nabla{u}|}$ and d joint pdf between ${\nabla\cdot {u}/|\nabla {u}|}$ and ${|\nabla{u}|.}$ Contours range from 0.0025 to 0.025 in increments of 0.0025

Zhang et al. (1997) performed holographic PIV experiments and provided a quantitative estimate of the local divergence error by computing the following ratio:

$${\xi = {\frac{(\partial u_1/\partial x_1+\partial u_2/\partial x_2 + \partial u_3/\partial x_3)^2}{(\partial u_1/\partial x_1)^2+(\partial u_2/\partial x_2)^2+(\partial u_3/\partial x_3)^2}}}$$

(15)

This ratio (ξ), for experimental data embedded with errors, lies between zero and unity. The smaller the value of ξ, the lesser the divergence error. Zhang et al. (1997) found that the mean value of ξ started at 0.74 at full measurement resolution (Δ ≈ 0.93 mm, where Δ is the measurement resolution) and decreased sharply with increasing control volume. The authors found that at a control-volume of (4Δ)³, the mean value of ξ reduced to 0.12. Zhang et al. (1997) also found that the mean value of ξ decreased when the data were smoothed using spatial filters. They used a Gaussian filter similar to the one utilized in the current study and found that ${\overline{\xi}}$ for a control volume of (2Δ)³ (this resolution is similar to the one used in this study) decreased to a value of 0.2. Figure 9b shows the distribution of ξ computed from the quasi-instantaneous space-time volume of data derived from the cinematographic stereoscopic measurements. The distribution has a maximum at ξ = 0 and a tail that extends to ξ = 1. The mean value of ξ is found to be 0.18 and this is comparable to the mean value of ξ computed from holographic PIV data with comparable control volume by Zhang et al. (1997).

Mullin and Dahm (2006) performed dual-plane stereoscopic PIV measurements and quantified the divergence error in their measurement by computing the local divergence value ${\nabla \cdot{u}}$ relative to the local norm of the velocity gradient tensor ${(\nabla {u}:\nabla {u})^{1/2}.}$ They found that the local divergence error followed a normal distribution with zero mean and the rms value of the relative divergence error was 0.35. Mullin and Dahm (2006) also performed simultaneous stereoscopic PIV measurements in two coincident planes and found that the “in-plane” velocity components possessed approximately 9% uncertainty and the “out-of-plane” velocity component has an uncertainty of about 16%. The authors stated that the divergence error was consistent with the uncertainty observed in the coincident-plane measurements. Figure 9c shows the distribution of the local divergence error relative to the local norm of the velocity gradient tensor for the current study. The mean value of this distribution is zero and its rms value is 0.25, which is consistent with the rms value of the divergence error from dual-plane stereoscopic PIV measurements of Mullin and Dahm (2006).

Since PIV errors tend not to vary with velocity magnitude, it is expected that high magnitude gradients will be more accurate than small gradients. This can be investigated by correlating the divergence error to the magnitude of the velocity gradient tensor. Figure 9d shows a joint probability distribution between the relative divergence value ${(\hbox{i.e.}, \nabla\cdot {u}/(\nabla {u}:\nabla {u})^{1/2})}$ and the norm of the velocity gradient tensor ${((\nabla {u}:\nabla {u})^{1/2}).}$ This was computed to study the extent of divergence error for various magnitudes of the velocity gradients. The figure shows that the divergence error is higher for lower magnitudes of ${(\nabla {u}:\nabla {u})^{1/2}}$ and the extent of divergence error decreases for higher values of ${(\nabla {u}:\nabla {u})^{1/2}.}$ Therefore, as expected, regions with large magnitudes of velocity gradients possess lower relative uncertainty. This suggests that regions of intense gradients such as vortex tubes or dissipation sheets, will be more accurately rendered than regions of low gradients.

Based on the results in Sect. 4, it can be concluded that error associated with the use of Taylor’s hypothesis poses minimal impact on divergence compared to the intrinsic PIV error. Therefore, the divergence error in the data can be attributed to the intrinsic uncertainty associated with stereoscopic PIV as implemented in the current study. Note that intrinsic stereoscopic PIV uncertainty includes error arising due to the misalignment of laser sheet with the calibration target, error due to geometric distortion, error associated with the PIV peak detection (peak detection includes uncertainty due to presence of flow gradients) and the least square error present in the recombination process utilized to compute stereoscopic vectors. This broad classification of “PIV error” is utilized to distinguish between the uncertainties in the experimental technique as opposed to those due to the use of Taylor’s hypothesis.

In addition to the intrinsic stereoscopic PIV errors and the error due to Taylor’s hypothesis, the divergence error also has a contribution from the noise resulting from computation of velocity gradients using finite differencing schemes. The uncertainty due to computation of velocity gradients can only be reduced by improving the quality of the velocity data. Analysis and reduction of uncertainties in velocity measurements obtained using PIV/stereoscopic PIV have been exhaustively explored by various researchers.

Piirto et al. (2005) compared five different interrogation techniques and showed that the rms of the bias error associated with discrete window shifting cross correlation algorithm was approximately 0.05 pixels. Wereley and Meinhart (2001) indicated that application of central differencing adaptive technique improves the accuracy of the velocity data. Their results based on Monte-Carlo simulations revealed that the velocity data are accurate to within 0.1% in about 4–5 iterations. In this study, the adaptive central iterative technique (four iterations) was employed together with the discrete window shifting algorithm. The interrogation windows were discretely shifted for every interrogation region at every iteration to compute the pixel displacements. Therefore for a displacement of five pixels (as in the current study) the uncertainty in the pixel displacements is less than 1%.

Lawson and Wu (1997) and Prasad (2000) indicated that the error in the out-of-plane component relative to the in-plane components is equal to 1/tanΘ (where Θ is half the included angle between the cameras in stereoscopic arrangement). In the current study, this angle was approximately 30°, suggesting that the error ratio is approximately 1.7. Therefore the uncertainty in the out-of-plane velocity component is marginally higher than the uncertainty in the in-plane velocity components.

The uncertainty present in the individual velocity components measured in the current work was estimated based on the above mentioned previous results in the literature. The uncertainty in the in-plane velocity component(s) is about 0.7% and the uncertainty in the out-of-plane velocity component is approximately 1.2% (1/tanΘ times the in-plane estimate). These estimates are consistent with previous uniform translation tests performed on stereoscopic PIV systems by Zang and Prasad (1997) and Bjorquist (2001) (among others). Those studies indicated that rms errors in the measured displacements were between 0.2 and 0.5% for the in-plane components and 0.8–1.2% in the out-of-plane component.

Following a simple error propagation analysis in liaison with the above mentioned velocity uncertainty estimates, the uncertainty corresponding to the rms values of different velocity gradients is approximately 15%, consistent with previous studies in the literature. Note that the relative uncertainty present in the higher magnitude velocity gradients (which are the values of interest in the current study) is much less than this estimate.

The use of the self-calibration technique illustrated by Wieneke (2005) could further reduce some of the other systematic errors associated with stereoscopic PIV and reduce the error in the velocity gradients noted in the current study. Implementation of this self-calibration technique to compute the PIV vector fields is a goal for our future work. Additionally, individual contributions from various PIV related uncertainties to the divergence error also merit further exploration.

Figure 10a, b shows instantaneous contours of magnitude of vorticity and relative divergence error, respectively. Figure 10a shows that vorticity (and consequently enstrophy, which is defined as the square of magnitude of vorticity) possesses a much larger scale compared to the Kolmogorov scale. Figure 10b shows contours of ${\nabla\cdot {u}/(\nabla {u}:\nabla {u})^{1/2}}$ in x ₂–x ₃ plane at the same instant, indicates that the structures in the divergence error field are much smaller in scale compared to the structures in the enstrophy field. Additionally, time-resolved movies of divergence error fields indicate that small-scale spatial structures in divergence error are also much shorter lived in time than the enstrophy structures.

Fig. 10

Instantaneous contours in x ₂–x ₃ plane for the following variables a Magnitude of vorticity vector (also, the square root of enstrophy) and b ${\nabla \cdot {u}/(\nabla {u}:\nabla {u})^{1/2}}$

The apparent small-scale and short lived nature of the divergence error can be further studied by computing correlations of enstrophy and divergence along all three directions. Figure 11a, b shows the auto-correlation functions of enstrophy and divergence along the x ₁ and x ₂ directions, respectively. It must be noted that the correlation along the x ₁ direction is a temporal correlation converted to spatial scale using Taylor’s hypothesis (one constant convection velocity was used to compute the axial extent and the variation of convection velocity over the x ₂–x ₃ plane was neglected for simplicity). The auto-correlations of enstrophy and divergence along all three directions (x ₃ is not shown, but is qualitatively similar to the correlation in the x ₂ direction) suggests that structure of divergence is indeed short-lived in time and compact in space, consistent with observations from the instantaneous data.

Fig. 11

Auto-correlation functions of enstrophy and divergence along a x ₁ and b x ₂ directions

The observed small spatial and temporal scale of the divergence error is consistent with the proposition that the source for the divergence error is the random noise in the velocity measurements and not due to Taylor’s hypothesis since convection velocity errors should exhibit large-scale features as do the u ₁ fluctuations (as seen in Fig. 2).

7 Accuracy assessment: eigenvalues of strain-rate tensor

The time-resolved stereoscopic data was used to compute the principal strain-rates or eigenvalues α, β and γ of the strain rate tensor. Since the trace of the strain rate tensor is invariant under rotation and is equal to the dilatation, the sum α + β + γ should be equal to zero. The deviation from zero can be attributed to the divergence error present in the data due to the errors in measurement of velocity from the stereoscopic arrangement and the error due to the application of Taylor’s hypothesis. The distribution of α + β + γ is identical to the distribution of divergence error in Fig. 9c and the rms value of the distribution is 0.25, which is consistent with the values computed from holographic PIV by Zhang et al. (1997) and dual-plane stereoscopic PIV by Mullin and Dahm (2006).

The eigenvalues of the strain-rate tensor can be used to determine the preferred modes of straining. Ashurst et al. (1987) proposed the use of the following parameter to study the preferred modes.

$${\beta^* = \frac{\sqrt{6}\beta}{\sqrt{\alpha^2 + \beta^2 + \gamma^2}}}$$

(16)

The value of β^* has one to one correspondence with a particular type of strain field and its value is supposed to yield the distribution of various strain states in the flow. The extreme values of β^* = ±1 correspond to axisymmetric expansion and contraction, respectively. Figure 12a shows the probability distribution of β^* computed from the pseudo-volume data, which is consistent with the distribution of β^* in other studies (e.g. Ashurst et al. 1987; Lund and Rogers 1994). Figure 12a also shows a plot of β^* from Lund and Rogers (1994) where the eigenvalues of the strain tensor were computed from a computational dataset of isotopic turbulence. Lund and Rogers investigated the impact of experimental errors on the strain-rate tensor by adding random noise to the DNS velocity gradient data. They superimposed Gaussian noise with a variance to the data such that the correlation coefficient between ∂u ₁/∂x ₁ and −(∂u ₂/∂x ₂ + ∂u ₃/∂x ₃) was 0.7. This value of the correlation is similar to the correlation between those quantities observed in the current study. Figure 12a also shows a plot of β^* from Lund and Rogers (1994) where the eigenvalues of the strain tensor were computed from DNS of isotopic turbulence with and without random noise. The pdf of β^* from the isotropic DNS data indicates that the distribution goes to zero for β^* = ±1. This characteristic led Ashurst et al. (1987) to conclude that “the two extreme cases of axisymmetric contraction/expansion do not occur in turbulent flows”. The pdf formed from the contaminated DNS data is seen to be broader and the peak in the distribution shifts to the left. The pdf of β^* computed from the stereoscopic data falls between the distributions of the original DNS data and the contaminated DNS data. The range of the pdf extends to ±1.8. It should be noted that magnitudes of β^* greater than unity are nonphysical and are solely due to measurement error. The range of |β^*| seen in the current measurements is consistent with results of multi-probe hot-wire based point measurements obtained by Tsinober et al. (1992). The experimental data seem to reproduce the general features of the β^* distribution.

Fig. 12

Eigen-value normalization. Probability distributions of a β^* and b s ^*. Joint probability distributions between the norm of velocity gradient tensor and c β^* and d s ^*. The contour levels range from 0.001 to 0.01 in increments of 0.001

Lund and Rogers (1994) argued that the normalization of β in Eq. 16 does not capture the entire range of strain orientations uniquely and proposed a new normalization,

$${s^* = {\frac{-3\sqrt{6}\alpha\beta\gamma}{{(\alpha^2 + \beta^2 +\gamma^2)}^{3/2}}}}$$

(17)

This new parameter is also bound by s ^* = ±1. Figure 12b shows the distribution of s ^* computed from the stereoscopic measurements and the plots for s ^* computed from the original DNS data and contaminated DNS data from Lund and Rogers (1994) are included for comparison. The pdf of s ^* computed in the current study is similar to the pdf of s ^* computed using the contaminated DNS data by Lund and Rogers (1994) and is dramatically different from the distribution of s ^* computed from the original DNS data. The value of s ^* in both the contaminated DNS data and the current study extends to ±1.5. The value of s ^* is found to be extremely sensitive to the divergence error present in the data. It must be noted that Lund and Rogers (1994) computed s ^* from isotropic turbulence data and the jet flow used in the current experimental work is not locally isotropic, but locally axisymmetric (as seen in Sect. 5). Nevertheless, the distribution of s ^* found in this study is consistent with the distribution of s ^* computed from holographic PIV measurements by Tao et al. (1999).

The pdfs of β^* and s ^* in Fig. 12a, b includes contributions from regions of low gradient values where the relative uncertainty in the gradients is larger. Since the relative divergence error decreases with increasing velocity gradients (as seen in Fig. 9d), the distribution of β^* and s ^* should be studied as a function of the magnitude of velocity gradient tensor. This can be achieved by evaluating the joint pdfs between the norm of the velocity gradient tensor and both β^* and s ^*. Figure 12c, d shows joint probability distributions between ${(\nabla {u}:\nabla {u})^{1/2}}$ and β^* and s ^*, respectively. The figures indicate that for larger values of velocity gradients, the values of both β^* and s ^* do not exceed unity. This observation suggests that normalized eigenvalues are reliable in regions of large velocity gradients and therefore these derived quantities can be used to analyze the flow structure in areas of intense gradients like vortex tubes, sheets, dissipative areas and regions of strong strain.

8 Conclusions

Cinematographic (2 kHz) stereoscopic PIV experiments were performed to resolve small- and intermediate-scales (scale ≈3η−160η) in the far field of an axisymmetric co-flowing jet. Measurements were performed in a plane normal to the axis of the jet. The time-resolved measurement was then converted to quasi-instantaneous three-dimensional flow field of the jet. Taylor’s hypothesis was applied to the data along the jet axial direction to reconstruct the axial spatial extent.

The quasi-three-dimensional data enabled the computation of all nine components of the velocity gradient tensor at each point in a volume. The use of Taylor’s hypothesis along the axial direction was assessed by performing a separate set time-resolved two-component PIV experiments in a “side-view” plane along the jet axis. This “side-view” plane enabled a comparison of streamwise gradients computed directly and by using Taylor’s hypothesis. Probability distributions of the direct spatial velocity gradients and velocity gradients computed using Taylor’s hypothesis were almost identical and validates the use of Taylor’s hypothesis. The instantaneous structure of the direct spatial gradients and the derived spatial gradients were found to be qualitatively similar.

The rms of the velocity gradients and the three components of vorticity were all found to satisfy the axisymmetric isotropy conditions proposed by George and Hussein (1991) to within 10%. The mean dissipation value ${(\overline{\epsilon_{3D}})}$ was found to be consistent with the dissipation estimate computed following the axisymmetric isotropy assumptions. The accuracy of the velocity gradients computed from the pseudo-volume data was investigated by computing the dilatation/divergence error in the flow field. The rms of the dilatation error relative to the norm of the velocity gradient tensor was found to be 0.25 and this value is consistent with results in other studies such as Zhang et al. (1997) and Mullin and Dahm (2006). Instantaneous maps and auto-correlation functions of divergence error reveals that its structure is relatively small-scale in all three directions compared to the vortical structures in the flow indicating that the source of divergence error could be the small-scale random-noise present in PIV measurements.

The “side-view” two component velocity data validates the use of Taylor’s hypothesis and indicates that the divergence error present in the data is primarily due to the intrinsic uncertainty associated with stereoscopic PIV. The dilatation error is found to affect areas of low velocity gradients that manifests as nonphysical results in quantities like normalized eigenvalues of the strain-rate tensor. However, closer examination indicates the effect of divergence error is minimal in areas of intense gradients where the overall spatial structure and statistics of the vorticity, dissipation and other derived quantities remain moderately unaffected.

Overall, the cinematographic stereoscopic PIV technique has here been shown as a viable alternative to dual-, multiple-plane or holographic PIV techniques to measure the complete velocity gradient tensor in low-speed flows. The technique allows direct measurement of quasi-instantaneous volume of data that could be utilized to study the structure of vorticity field, strain-rate field and kinetic energy dissipation in turbulent shear flows.