Analysis methodology for 3C-PIV data of rotary wing vortices

Abstract

3C-PIV data from tip vortices of either fixed-wing or rotating wing experiments are challenging from an analysis point of view. Model motion, vortex wander, spurious vectors, periodic and aperiodic effects, turbulence, and other disturbing effects are all present in the data. In most cases the vortices are not measured perpendicular to their axis as well. Engineers need time-averaged properties from the vortex in the vortex axis system for a proper modelization within simulation codes. This article describes the methods needed to deal with all the mentioned problem areas, including the conditional averaging and rotation into the vortex axis system. The methods are validated by using numerically generated vortex vector fields, and finally applied to experimental data from a hover condition of a model rotor.

1 Introduction

Flow measurement techniques of today are non-intrusive using either the Doppler effect in laser doppler velocimetry (LDV) or the shift of particle images in two successive exposures with very small time interval between them [particle image velocimetry (PIV)]. LDV typically has a very small probe volume, and for field measurements the volume must scan the area to be observed. PIV provides a large area with the instantaneous velocity field.

Often the flow structures to be observed are subject to random variations, either caused by model motion, natural air turbulence, or flow field instabilities. As an example, dynamic stall measurements are repeating the phenomenon cycle by cycle in general, but each cycle has strong individual time history in the post-stall regime. In helicopter rotor wakes, the model is subject to small motions that are non-harmonic in terms of rotor frequency, and thus blade tip vortex creation locations and the local blade aerodynamics are slightly different in each revolution. Since PIV provides an instantaneous measurement of the complete area, this technique is thought of as superior to LDV. A stereo arrangement allows to resolve the third flow component (3C).

1.1 Rotor blade tip vortex measurements using PIV

In Table 1, various rotor tests with application of PIV are listed with their operational conditions and resolutions obtained. Small scale rotors [9, 13, 19] are often operated at half or one third of the tip Mach number of large scale models [6, 15, 16, 23, 27, 29], which have the same tip Mach number as full scale rotors [22].

Table 1 Comparison of PIV measurement resolution, r _c =0.05c

The 3C-PIV technique was applied to a lightly loaded, two-bladed, untwisted hovering rotor [6], where the necessity of conditional averaging was emphasized. A comparison of 3C-LDV and 3C-PIV on a single-bladed small-scale model rotor was given [13]. Therein, the importance of the length of the measurement volume L _m , related to the core radius r _c to be measured, is shown. In case of PIV or other camera based techniques, the advantage of the instantaneous measurement of an entire area is associated with a smaller spatial resolution, which is defined by the size of the cross-correlation windows. The conclusion was that the results of (ensemble averaged) PIV data are not at all sufficient to resolve tip vortex core properties. In 1998, PIV was applied to a small scale tilt rotor model (TRAM) in DNW operated in descending forward flight [29]. The vortices were investigated right before interacting with a blade, and core radii of about r _c =0.25c were measured.

A 2C-PIV measurement was also compared to 3C-LDV measurements [19], where blade tip vortices of a four-bladed rectangular small scale model rotor were measured in forward flight. These data indicate the superiority of PIV compared to LDV due to both sufficient spatial resolution as well as the completeness of the instantaneous area measurement with all turbulent structures included. A 2C-PIV test on a large scale model rotor with swept back tapered blade tips was performed during the ERATO program [23]. For the vortices found, six vectors were within the core diameter, which is not enough to analyse the vortex properties. It was concluded that for good vortex core measurements the resolution had to be increased by a factor of about four. Following this result, a 2C-PIV measurement was performed with a higher resolution at a full-scale Bo105 helicopter while standing on ground but generating a thrust of 2000 kg to match the thrust condition planned for the HART II test [22]. Vortex core radii of r _c =0.045c and peak swirl velocities of V _s,max =0.42Ω R were measured which corresponds well with the model rotor hover measurements using LDV, for example [13].

3C-PIV measurements of tip vortices on a model rotor in forward flight were performed successfully in the NAL wind tunnel with comparable resolution [9]. The mesurement plane was parallel to the wind tunnel flow such that the vortex axis was inclined significantly at an angle of approximately 50° and the results needed a correction accounting for this. The vortices were traced downstream at y=0.76R and core radii of r _c =0.04c with peak swirl velocities of V _s,max =0.15Ω R were found. Another test called ATIC was performed twice at DNW using 2C-PIV in 1998 [16] and 2000 [15], using five-bladed sets of a Bo105 model rotor and an advanced design. In both tests, the vortex was traced downstream at y=0.67R at a view angle upstream selected in a way to cut the vortex axis orthogonal. Several advance ratios were investigated, including higher harmonic control (HHC) conditions. Young vortices were measured with core radii of r _c =0.05c and less, with peak swirl velocities of V _s,max =0.04−0.08Ω R.

A recent application to a two-bladed medium scale model rotor at low tip Mach numbers in low vertical climb was presented in Ref. [14]. Core radii of r _c =0.05c and maximum swirl velocities of up to V _s,max =0.44Ω R were found, and a void in the vortex centre that hindered an analysis of the flow field therein. Vortices were found to be elliptical to some extent.

1.2 PIV application in HART II

In 2001, the higher harmonic control aeroacoustic rotor test II (HART II), commonly performed by DLR, ONERA, NASA Langley, US Army AFDD in the large low-speed facility of the DNW [27, 30] was extensively using 3C-PIV for rotor wake measurements. The rotor is a 40% Mach scaled and dynamically scaled model of the B0105 main rotor with four blades, rectangular planform, −8°/R linear twist, a radius of 2 m, chord of 0.121 m, and a solidity of σ=0.077. The operational condition was at an advance ratio of μ=0.151, tip Mach number of 0.641, and a thrust coefficient of C _T =0.0044 representing a lightly loaded rotor (C _T /σ=0.0571, this is representative for a 2 ton Bo105 helicopter). Measurements were performed in a 6° descending flight condition with strongest BVI noise radiation throughout the rotor disk, and in hover. With no HHC applied, this defines the baseline case, referred to as BL in the following. The conditions are described in detail in Ref. [25].

One important parameter to characterize the quality of a measurement with respect to vortex core analysis is the ratio of the measurement length with respect to the core radius (L _m /r _c ), which will be addressed in Sect. 2.1. Another important parameter is the time delay between two successive images, see Sect. 2.2. In Table 1, the measurement resolution L _m /r _c , the time delay Δt, and the associated range of blade motion Δψ during the measurement is given for various tests. The HART II measurements are among the smallest values in both time delay and relative blade motion, and also for the spatial resolution, based on 5% chord.

The test set-up of HART II, measurement techniques applied, and some representative results were reported in detail in Ref. [27]. Details about PIV data acquisition and PIV processing from raw data images to vector maps were presented in Ref. [21]. General information about PIV and vector field analysis can be found in Ref. [20].

Major emphasis was placed on 3C-PIV measurements of rotor blade tip vortices in conditions with strong BVI, i.e., at a typical descent angle of 6° and an advance ratio of μ=0.151. Two 3C-PIV systems were applied simultaneously. DNW operated a system with a field of view of 0.46 m by 0.37 m size while the DLR system had different lenses, resulting in a field of view of 0.15 m by 0.13 m. The large field of view was intended for an overview of the area while the small field of view was intended for vortex analysis, i.e., the identification of vortex parameters like core radius, maximum swirl velocity, swirl velocity profile, axial flow, circulation etc.

The HHC conditions showed locally negative loading at the blade tips at some range of azimuth. At any location with negative loading at the blade tip area, the tip vortex has opposite sense of rotation. Inboard, the loading turns to lift and distributed vorticity is shed into the wake along the span, which later on rolls up into a vortex. In these cases pairs of counter-rotating vortices were present in the flow and both of these were measured by PIV systems.

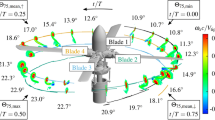
About 330 measurements were made at 70 locations distributed in the rotor disk, see Fig. 1 for 52 of them. The remaining locations were devoted to the measurement of multiple vortex systems which occurred in HHC cases. The measurement plane is vertical and rotated by ±30° in order to have the majority of vortices almost orthogonal to the measurement plane, at least from the top view. Each of these measurements were made with both PIV systems and with 100 repeats such that about 66,000 vector maps are available for analysis. Since this cannot be performed by hand, automated procedures had to be developed. Several topics have to be addressed for the analysis:

• Window size and overlap, Sect. 2.1

• Spurious vectors, Sect. 2.2

• Field operators and gradients, Sects. 2.3, 2.4

• Vortex centre detection, Sect. 2.5

• Model and camera support movement, vortex wander, Sect. 2.6

• Time averaging, Sect. 2.6

• Mean velocities, Sect. 2.7

• Rotation, Sect. 2.8

• Disturbing structures, Sect. 2.9

• Identification of parameters, Sect. 2.10

Fig. 1

PIV measurement locations in the rotor disk, μ=0.151

Some analysis has been made in the past with the identification of some of the parameters [2, 3]. The importance of rotation into the vortex axis system was shown in Ref. [25].

2 Analysis methodology

In all the figures of this paper with the in-plane velocity vectors, only every fifth vector is shown in both directions for the sake of visibility.

2.1 Cross-correlation: overlap and window size

The main parameter which defines the spatial resolution of the measurements beside the interrogation window size is the overlap of the windows. Both parameters affect the result obtained and thus the information which can be extracted like the vortex radii and the maximum swirl velocity. Most of the measurements of Table 1 do use an overlap of 50%, but nowhere the effect of overlap on the data to be extracted, like core radius or maximum swirl, was questioned. A numerical study using Vatistas model [24] has shown that the combination of a measurement resolution of L _m /r _c <0.5 with 50% overlap leads to errors up to 5% in the analysis of the core radius and maximum swirl velocity [26]. The larger the L _m /r _c , the higher the overlap must be to obtain the same accuracy and vice versa.

A massive oversampling can be used in order to reduce the scatter of the extracted parameters even if the bias caused by the limitations of larger interrogation windows cannot be avoided. The latter can only be obtained by a higher resolution during the test, for example by an increased optical resolution. As a consequence, in order to remain in a certain error regime, not only the cross-correlation window size is of importance, rather than the combination of this with the proper selection of overlap.

A comparison of the ratio L _m /r _c using the assumption of a core radius of r _c =0.05c for equivalence of comparison is given in Table 1. As pointed out in Ref. [13], the ratio L _m /r _c should be less than 0.2 for flows without streamline curvature, and even less when such curvature is present, like near the vortex core. From Table 1 it can be seen that the PIV system used in HART II performs well compared to the others, and can even be improved by using 16×16 pixel cross-correlation windows instead of the 24×24 size used in this paper, which would result in L _m =0.33r _c . Modern cameras with double resolution would result in half of the value, and very dense seeding allows for further reduction of the size of the cross-correlation windows. Thus, the requirements of L _m <0.2r _c for PIV systems are well at hand today.

2.2 Spurious vector elimination

Spurious vectors can be generated by rigid surfaces that reflect the laser light, low seeding density (very few particles are within the cross-correlation windows), or due to a too large time delay, which can result in particle movement out of the cross-correlation window or out of the light sheet. Other measurement errors can cause spurious vectors as well, as there are the recording conditions, particle density, laser intensity, and background light. Such erraneous vectors must be eliminated before an analysis of the vector field can start. As long as these vectors are not clustered they can be identified by statistical methods, comparing the vector of interest with its surroundings [28]. Vectors identified to be spurious then are replaced by the mean value of their surroundings. Only a small amount of spurious vectors was observed in the HART II data and most of them were removed using this method.

2.3 Operators indicating a vortex

For identification of a vortex centre flow field operators are used, which have large values in the vortex core where large gradients in the flow components are present. The most common operators are the vorticity ω _y , the Eigenvalues of the velocity gradient tensor λ₂, and the discriminant of the characteristic equation Q (also called as swirling strength) [7, 8]. A comparison of different operators for vortex detection is given in Ref. [1].

Typical vortical features of spiral and closed stream lines are observed at special singular points, i.e., the spiral and centre points, where often, but not necessarily, a pressure minimum is found as well. In a mathematical way these points are described by complex Eigenvalues of the velocity gradient tensor A=S+Ω which is composed of a strain tensor S and the vorticity tensor Ω [11]. This leads to the discriminant operator Q derived hereafter. Another definition starts from the gradient operator applied to the Navier-Stokes equation and leads to the Eigenvalues of the tensor S ²+Ω², which must be negative [8].

Based on the 2D measurement plane with x–z coordinates and the in-plane velocities u and w, the velocity gradient tensor is grad V=d V/d r=A.

$$\begin{aligned} \frac{{d{\mathbf{V}}}}{{d{\mathbf{r}}}} & = \left[ {\begin{array}{*{20}c} {\frac{{\partial u}}{{\partial x}}} & {{{\left({\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)} \mathord{\left/ {\vphantom {{\left({\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}} \\ {{{\left({\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)} \mathord{\left/ {\vphantom {{\left({\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}} & {\frac{{\partial w}}{{\partial z}}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & {{{\left({\frac{{\partial w}}{{\partial x}} - \frac{{\partial u}}{{\partial z}}} \right)} \mathord{\left/ {\vphantom {{\left({\frac{{\partial w}}{{\partial x}} - \frac{{\partial u}}{{\partial z}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}} \\ {{{\left({\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right)} \mathord{\left/ {\vphantom {{\left({\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}} & 0 \\ \end{array} } \right] \\ & = \left[ {\begin{array}{*{20}c} {\varepsilon _{xx} } & {\varepsilon _{xz} } \\ {\varepsilon _{zx} } & {\varepsilon _{zz} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & { - \omega _y } \\ {\omega _y } & 0 \\ \end{array} } \right] = S + \Omega = A \\ \end{aligned} $$

The first matrix represents the strain tensor S with elongational strain in the diagonal and the shear strains in the off-diagonal elements. Vorticity is in the second antisymmetric matrix Ω. Determinant and trace are defined as

$$\begin{aligned} \det A & = \frac{{\partial u}}{{\partial x}}\frac{{\partial w}}{{\partial z}} - \frac{{\partial u}}{{\partial z}}\frac{{\partial w}}{{\partial x}} \\ {\text{tr}}\,A & = \frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}} \\ \end{aligned} $$

A vortex is characterised by the invariance of the velocity gradient tensor A. This requires the determinant to be greater than zero and the Eigenvalue λ of the characteristic equation to be complex, i.e., the discriminant Q must be below zero.

$$\begin{aligned} 0 & = \lambda ^2 - \lambda {\text{tr}}\,A + \det A \\ \lambda _{1,2} & = {\text{tr}}\,A/2 \pm \sqrt Q \\ Q & = ({\text{tr}}\,A)^2 /4 - \det A < 0 \\ \end{aligned} $$

Following the definition that the second and third Eigenvalue of S ²+Ω² must be below zero, it follows that either

$$\lambda _2 = \left({\frac{{\partial u}}{{\partial x}}} \right)^2 + \frac{{\partial u}}{{\partial z}}\frac{{\partial w}}{{\partial x}} < 0\quad {\text{or}}\quad \lambda _{\text{2}} = \left({\frac{{\partial w}}{{\partial z}}} \right)^2 + \frac{{\partial u}}{{\partial z}}\frac{{\partial w}}{{\partial x}} < 0$$

The mean value of both is used in this paper. The vorticity ω _y , the discriminant Q, and the Eigenvalue λ₂ of the tensor S ²+Ω² are thus defined by

$$\begin{aligned} \omega _y & = {{\left({\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right)} \mathord{\left/ {\vphantom {{\left({\frac{{\partial u}}{{\partial z}} - \frac{{\partial w}}{{\partial x}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2} \\ Q & = \frac{{\left({\frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}}} \right)^2 }}{4} + \frac{{\partial w}}{{\partial x}}\frac{{\partial u}}{{\partial z}} - \frac{{\partial u}}{{\partial x}}\frac{{\partial w}}{{\partial z}} \\ \lambda _2 & = \frac{{\left({\frac{{\partial u}}{{\partial x}}} \right)^2 + \left({\frac{{\partial w}}{{\partial z}}} \right)^2 }}{2} + \frac{{\partial w}}{{\partial x}}\frac{{\partial u}}{{\partial z}} \\ \end{aligned} $$

In the vortex centre of a numerical vortex like Vatistas [26] or [5, 10, 18], ω ² _y =|Q|=|λ₂| (see [27]), these values can be directly compared in terms of magnitude.

2.4 Velocity gradients

The flow field derivatives (or velocity gradients) are a pre-requisite needed for the computation of the criteria of a vortex. A first suggestion is to apply the centre difference approach, which is one-dimensional. For the 50% overlap used in HART II data, the vectors separated by two in their indices are independent from each other.

$$\left. {\frac{{\partial u}}{{\partial x}}} \right|_{i,j} = \frac{{u_{i + 1,j} - u_{i - 1,j} }}{{x_{i + 1,j} - x_{i - 1,j} }}$$

In a sheared grid the derivatives at i, j require velocity components along the x coordinate direction. Then, they have to be interpolated from the grid which complicates the procedure.

However, as pointed out in Ref. [20], the data are two-dimensional and thus the local gradient in any direction should also depend on the surrounding flow. Based on the line integral for the circulation of the area around the point of interest in discretized form, the flow gradients at i, j can be expressed in terms of the surrounding flow components, i.e., by the centre differences at j−1, j and j+1. For equidistant grid spacing,

$$\left. {\frac{{\partial u}}{{\partial x}}} \right|_{i,j} = \frac{{\left. {\frac{{\partial u}}{{\partial x}}} \right|_{i,j - 1} + 2\left. {\frac{{\partial u}}{{\partial x}}} \right|_{i,j} + \left. {\frac{{\partial u}}{{\partial x}}} \right|_{i,j + 1} }}{4}$$

The same expression is obtained by a vertical smoothing over j using a Gaussian filter of (1 2 1). The derivative in the other direction is obtained by exchanging the x to z, i to j, and j to i. In general, the centre difference approach tends to increase noise while the circulation based approach tends to reduce noise since the usage of six velocities instead of two has an effectively smoothing effect.

2.5 Vortex centre identification

Blade tip vortices of hovering rotors are very well defined and have a single peak of vorticity, λ₂ or Q in their centre, as shown in Refs. [6, 13]. In contrast, the tip vortices of lightly loaded rotors in forward flight, especially those created on the advancing side, are often very weak and hard to detect. In HHC cases, inboard vortices are present that are generated in the form of a radially distributed vorticity without a designated centre. In these cases the flow field operators show a wide spread cloud of individual peak values of comparable intensity that do not allow the decision for a discrete vortex centre. In addition, these individual peaks are at different locations in each of the images.

To circumvent this problem, the area centre of a flow field operator can be used to define the centre of the vortical structure. This is the centre of gravity for all those data which are above a threshold in terms of a fraction of the maximum value of the operator used for vortex centre detection.

Even better results are obtained when computing new scalars based on the convolution integral of the flow field operators with a specially shaped norm function. This norm function shall represent the expected distribution of the operator. The best fit of the data with this norm function results in largest scalar values of the convolution integral. As an example, the norm shape function applied to the vorticity, λ₂ or Q operator, is shown in Fig. 2a. It represents the peak value distribution expected of the operator in the centre of a vortex, expressed in terms of the index range covered by the norm function, here an array of 13×13 indices is used.

Fig. 2

Norm shape functions used for convolution with flow field data, index space

In any case, the vortex centre must be expected anywhere between the grid points such that a maximum value of an operator or scalar on the grid cannot be used for the centre point, rather than area centre of this operator or scalar.

Another possibility to identify a vortex centre, that does not need the computation of flow field derivatives, is to identify the centre of swirl. This can be done by a convolution of the in-plane velocities with a discrete swirl mask as explained in Ref. [4]. Here, the swirl mask is created using a Vatistas type vortex [26] with a core radius of 2Δx and n=1. The swirl mask is decomposed into its horizontal and vertical vector components. The first mask is multiplied with the u component of the flow field and shown in Fig. 2b, the second mask has the same distribution as in Fig. 2b but rotated by 90° and is multiplied with the w component of the flow field.

The sum of both provides a qualitative scalar value of the rotational character of the flow and also indicates the sense of rotation, as is the case when using vorticity. In general, this swirl mask can be interpreted as a special areal wavelet, such that this convolution can also be named a wavelet analysis. The λ₂ and Q operators are insensitive to the sense of rotation and always negative in the centres of vorticity.

Results for the different methods are shown in Fig. 3. The data is from HART II with no HHC applied, pos. 17d of Fig. 1b (vortex age of 20°), first image. The vortex age is defined as the azimuthal range of blade revolution between its azimuth of vortex release and its azimuth at the time of vortex measurement. The vortex centre locations are computed by the area centre of the various scalars, which does not necessarily coincide with a local peak value when multiple peaks are present. The centre is marked by a “+” sign, and the core radius, identified by a best fit to a Vatistas swirl model, is marked as a circle around the centre. In this case the blade tip was almost unloaded and essentially the shear layer is present, with some vortical components. In any case the extremum value (positive and negative for ω _y and convolution of u, w; negative only for λ₂ and Q operators) of the various scalars computed for the image is searched first, then the area centre is computed in the vicinity of this extremum.

Fig. 3

Vortex centre identification by area centre of different scalars. Pos. 17d of Fig. 1b, vortex age: 20°, first image. Vortex centre at “+”, the core radius is indicated as circle

Since the distribution of vorticity is very noisy the identification of the centre of vorticity is difficult, Fig. 3a. In this case several minima are present. The convolution of vorticity with a bell-shaped norm function results in the scalar field of Fig. 3b. This plot is almost identically to the convolution of the swirl mask with the in-plane velocity field, but with a different scale. Due to the convolution, the noise is widely suppressed, and essentially three negative peaks and one positive peak can be found, the latter indicates a small vortex of opposite sense of rotation.

The λ₂ operator indicates vortical structures by negative values, Fig. 3c; the Q operator has an almost identical result with slightly more noise (not shown); both are in the same scalar range. Three peaks are clearly marked for local centres of vorticity, the pair in the middle of the image is of stronger nature than the single peak in the left half. The convolution of λ₂ with a bell-shaped norm function results in the scalar field of Fig. 3d, which is very similar to the convolution of Q not shown here. Now the central point is focused and identified as the strongest event in the image. Therefore, the methods in Fig. 3d and b are found to be best suited to identify the centre of vortical structures where no clear vortex can be detected.

As can be seen from Fig. 3, the core radii identified are strongly depending on the location of the vortex centre. However, the noise in individual data is affecting the identification of the core radius to some extent, but this will be alleviated using proper averaging of the data.

2.6 Conditional averaging

Due to elasticity of the support, the model was vibrating with low frequencies that were not rotor harmonics. Although these were of small nature (few mm) they were transferred to the blade tips and resulted in different vortex creation positions, each revolution of the rotor. A second source of vortex motion in the images was the elasticity of the camera support structure. When shaking, the field of view was slightly different at each individual measurement. This resulted in an apparent vortex motion in the field of view. The first source of motion was independent of the measurement location, while the second source depended on the proximity of the camera tower to the shear layer of the free-stream jet. A third source of vortex centre position changes was the vortex wander itself, depending on its age. For older vortices this can be much larger than the core radius of these vortices [26].

Thus, care must be taken for averaging the data. A simple (ensemble) average results in artificially large core radii and low value of vorticity and is not representative for any of the individuals [6]. The simple average was used in Ref. [13], where the comparison to LDV data led to the conclusion that PIV is not suitable for vortex core measurements. The simple average can only be used for the average location of the vortex centre and the total circulation of the vortex, which is obtained for radii far outside the core. A proper (conditional) averaging must retain the individual characteristics like peak swirl velocity and core radius but eliminate the random fluctuations.

In each of the individual images the centre is first identified, then all centres are shifted to coincide with each other. A new grid is generated with its centre in the centre of all the individual vortices. Then, all data are interpolated and averaged in the new grid. Before this, a statistical analysis of the vortex centre positions can be made, eliminating all positions that are a certain threshold away from the mean centre position, for example, two standard deviations. This ensures that outliers are not taken into account. Additionally, the peak vorticity at the vortex centre can be compared in the same way, eliminating all data that are either a certain threshold below the average, or above.

As an example for the differences of the averaging methods, the swirl velocity profile of the BL case at pos. 23 (at the rear of the disk where the vortex age is almost 1.5 revolutions) is shown in Fig. 4. The simple average leads to five times larger apparent core radii (r _c /R≈0.0175) than the conditional average, which is also very close to the individual shown (both r _c /R≈0.0035). Also, the peak velocities at the core radius found in the simple average are only about half the value found for the conditional average or for the individual. Outside the core, the different averaging methods approach each other.

Fig. 4

Effect of averaging method on swirl velocity profile, BL, pos. 23 of Fig. 1a, vortex age: 510°. Vortex centre at “+” computed by the area centre of λ₂-convolution, the core radius is identified by best fit to Vatistas swirl model and indicated as circle

The importance of conditional averaging can also be illustrated by the standard deviation of the flow components at each node of the grid. This is shown exemplarily for the u-component in Fig. 5a of the simple averaging method, and in (b) for the conditional averaging. Again, pos. 23 of Fig. 1 is taken here. The simple average has a much wider range of scatter compared to the conditional average, which is due to the scatter of vortex centre positions in the individual images. Once the centres are aligned, the fluctuation of flow components is significantly smaller. The vortex core radius is also much smaller as indicated by the circles in the graphs, which represent the result already shown in Fig. 4. In any case the maximum scatter is obtained in the vortex centre itself, with the largest deviations for the cross-flow component v. This is expected since this component contains the largest measurement errors.

Fig. 5

Effect of averaging method on standard deviation of flow components, BL, pos. 23 of Fig. 1a, vortex age: 510°. Vortex centre computed by the area centre of λ₂-convolution at "+", the core radius is computed by a best fit to Vatistas swirl model and indicated as a circle

2.7 Background velocity elimination

The flow field can be assumed as a superposition of a background flow field $\bar{\mathbf{V}}$ and a vortex flow field v _v , as suggested in [1].

$${\mathbf{V}} = \bar{\mathbf{V}} + {\mathbf{v}}_{v}$$

The background velocity components are to be identified for all the three components and subtracted from the flow field for analysis of vortex properties. It must be differentiated between the average and background velocity. The average of a flow component of a PIV image is defined as the sum of this component at all grid points, divided by the number of grid points, while the background flow velocity is defined by the undisturbed flow. Without a vortex in the flow average the background velocity is identical.

In cases where a vortex is not perfectly centred in an image (which is mostly the case) the swirl velocity field of this vortex biases the computation of the background in-plane velocities. This is most obvious when the vortex centre is located at one of the image borders and the swirl velocity field of only one side of the vortex dominates the figure. In any case, the axial velocity field of a vortex complicates the computation of the mean cross-flow velocity. The problem is even more complex when the vortex axis is inclined with respect to the measurement plane and part of the swirl velocities are contained in the cross-flow, as well as part of the axial velocity of the vortex becomes part of the in-plane velocity field.

Based on the assumption that the vortex convects with the background velocity, the in-plane components $\bar{u}$ and $\bar{w}$ can be computed from the velocities found in the vortex centre. This is not the case for the out-of-plane component $\bar{v}$ since an axial flow is expected in the vortex core with its maximum in the vortex centre, and asymptotically approaching zero outside the core radius. Therefore, $\bar{v}$ must be computed from the flow field sufficiently far outside the vortex core radius.

An example for the identification and elimination of the background in-plane velocities is given in Fig. 6 for the simple average of the BL case, pos. 17 of Fig. 1 (here the vortex age is about 27°). After removal of the background in-plane velocities, the vortex core in the centre of the figure (indicated by the circle) and the shear layer in the lower left quarter of the figure exhibit the largest in-plane velocities, but in the centre of the vortex (marked by the “+” sign) the velocity is zero.

Fig. 6

Identification and elimination of the background in-plane velocities, pos. 17 of Fig. 1

In cases where the shear layer of the blade creating the vortex (or another blade that just passed the field of view) is present, it contributes a significant out-of-plane or cross-flow velocity and biases the computation of$\bar{v}.$ To identify these areas, again the method of convolution can be used with the same norm function as used for the flow field operators and applied to the out-of-plane velocity component, since the thickness of these shear layers is usually small. Any locations where the scalar value of this convolution is exceeding a certain threshold indicate areas not to be used for the computation of $\bar{v}.$ A result of this method is given in Fig. 7 for the same case as used in Fig. 6. Therein the shear layer contributes even more to the cross-flow velocities than the centre of the tip vortex itself. However, the mean cross-flow component is identified from all flows outside the shear layer and outside the vortex core such that the outer areas are close to zero cross-flow after subtraction of the background components.

Fig. 7

Cross-flow velocities after elimination of the background component $(\bar{v}=-0.08\Omega R),$ pos. 17 of Fig. 1

Note that$-\bar{u}\cos 30^{\circ}-\bar{v}\sin 30^{\circ}=0.155\Omega R,$ which is essentially the wind speed (μ=0.151) plus the horizontal velocity induced by the rotor at this location. The difference of 0.004Ω R=0.87 m/s is little more than the accuracy of the wind tunnel jet velocity of ±0.4 m/s. The component lateral to the wind tunnel flow results in $-\bar{v}\cos 30^{\circ}+\bar{u}\sin 30^{\circ}=0.003\Omega R$ and is small compared to the other directions.

2.8 Rotation into the vortex axis system

Due to a fixed angle of view of the PIV systems into the three-dimensional vortex system of the rotor, the measurement plane was never orthogonal to the vortex axis. A correct analysis of the vortex parameters can only be made in the vortex axis system. Thus, the inclination angles between the measurement plane and the vortex axis have to be identified.

The assumption is made that the vector field does not change in a small volume along the vortex axis. In this case the measurement window can be shifted along the vortex axis without change of the velocity vectors therein. The rotation scheme is illustrated in Fig. 8. Two rotation angles are identified, the angle about the x-axis and the angle about the z-axis. First the rotation about z is performed, then the rotation about x. The final grid in a plane normal to the vortex axis is a sheared grid.

Fig. 8

Rotation from the measurement plane into the vortex axis system

Based on the assumption that in the vortex axis system the out-of-plane velocity distribution is rotationally symmetric, different methods were developed to identify these rotation angles. First, the out-of-plane and swirl velocity components at the core radius, identified from a horizontal cut through the vortex centre, are used. Let v _Vi+ and v _Vi- be the cross-flow velocity of the vortex found at the core radius to the right and left of the vortex centre, and w _Vi+ and w _Vi- be the in-plane vertical velocity component at the same locations. Then an inclination angle about the x-axis can be estimated as

$$\beta_{x} = \arctan\frac{v_{Vi+}-v_{Vi-}}{w_{Vi+}-w_{Vi-}}$$

The angle for rotation about the vertical axis is found from the vertical cut through the vortex centre, with usage of u instead of w. The second approach makes use of the global out-of-plane velocity gradients ∂v/∂x and ∂v/∂z. These are identified by means of regression analysis of the flow outside two times the core radii of the vortex centre. Related to the ratio of maximum swirl and the core radius, V _s,max /r _c , these can be used for a guess of rotational angles.

$$\beta_{x} = \arctan\frac{\partial v/\partial x}{V_{s,max}/r_{c}}$$

The angle about the vertical axis is found using ∂v/∂z instead. Using these angles the coordinates and velocity vectors are rotated into the assumed vortex axis system, usually leading to a sheared grid as depicted in Fig. 8. The resulting flow field is again analysed for the cross-flow distribution using any one of the methods to identify a vortex centre, and the procedure is repeated until the remaining rotation angles are below a certain threshold, for example 1°. Then, the analysis of vortex properties can be made. Usually the vortices appear elliptical in the original unrotated data, while they appear circular in the rotated data.

An example for the effect of rotation into the vortex axis system is shown in Fig. 9 for the simple average of the BL case, pos. 29, where the vortex is cut by the PIV measurement plane at an angle of β _z ≈45° when considering Fig. 1. The unrotated data in (a) show some ellipticity of the in-plane velocities (vector field) and also in the cross-flow, where global gradients exist in the areas outside the vortex core. The identification of rotation angles based on the cross-flow in the core radius and the swirl leads to angles of β _z =−45° about the vertical axis and β _x =3° about the horizontal axis.

Fig. 9

Effect of rotation into the vortex axis system on the velocity field, case BL, pos. 29

The resulting velocity field after rotation is also shown in Fig. 9b. Due to the sequence of rotation the grid is sheared, but the distribution of the in-plane velocity vectors is very round compared to the unrotated data. Also, the cross-flow is zero in the field outside the vortex, and in the vortex centre a peak is present as expected. A strong shear layer to the left of the tip vortex is clearly visible now.

After rotation into the vortex system the effective measurement area is smaller than the raw data area, and the grid effective spacing is smaller. In these cases the angle of the measurement plane relative to the vortex axis is effectively increasing the spatial resolution of the measurement.

2.9 Elimination of secondary structures

Based on the superposition principle, vortices and vortical shear layers from blades passing the measurement window are identified and numerically removed from the image such that the vortex of interest remains almost unaffected. Thereafter, its parameters can be identified without being biased by disturbing structures. Currently, this is performed manually in the measurement plane, and only for the in-plane velocities. The disturbing vortex is identified by a best fit to a Vatistas swirl model and its contribution is then subtracted from the entire velocity field. This can also be done iteratively until no fragments of the disturbing structure remain. In general, both (or more) structures could be identified simultaneously, but this is complicated by different orientation of their vortex axis with respect to the measurement plane and not implemented yet.

An example is given in Fig. 10a where two vortices of opposite sense of rotation are close to each other, and both are affecting the other vortex flow field adversely. In (a) the vortex centre was manually set to the centre of the disturbing structure, using the scalar field of λ₂-convolution. After elimination of this structure using a best fit to Vatistas swirl model the remaining vortex is clearly unaffected by other structures (b) and its parameters can be identified. To do even more, the shear layer at the lower left of the image could be eliminated by the same procedure.

Fig. 10

Elimination of disturbing structures. BL, pos. 47 of Fig. 1, simple average

2.10 Identification of vortex parameters

The identification of the swirl and the axial velocity profiles, the core radius and the circulation is often hindered by other flow structures in close proximity of the vortex of interest. These are shear layers with vorticity and additional vortices shed by other blades just passing the measurement window, especially where BVI takes place.

Using a best fit of a Vatistas vortex swirl model [26], the parameters describing the vortex are identified. This model is written in terms of the maximum swirl velocity V _s,max at the core radius r _c , the shape parameter n that describes the distribution of vorticity (and therewith the distribution of λ₂ and Q), and the radial distance from the vortex centre. The development of vortex circulation, and thus the fraction of total circulation at the core radius, is connected to the swirl velocity profile as well. All relations for the Vatistas vortex are given [27]. Note that all variables are made non-dimensional, i.e., the velocities are divided by Ω R, circulation and kinematic viscosity by Ω R ², vorticity by Ω, coordinates by the core radius r _c , the core radius by R, and the flow field operators by Ω².

$$\begin{aligned} V_{s} &= V_{s0}\frac{r}{(1+r^{2n})^{1/n}} \\ V_{s0} &= V_{s,max}2^{1/n} = \frac{\Gamma_v}{2\pi r_c}\\ \end{aligned}$$

Alternatively, the Lamb–Oseen [10, 18] or Newman [17] vortex can be fitted to the data. These are also written in terms of V _s,max and r _c , but the radial distribution function is different and a factor α of an exponential function defines the shape. Expanding the parameter α to the inclusion of the vortex age ψ _v the Hamel–Oseen [5] model can be used as well.

$$\begin{aligned} V_{s} &= V_{s0} \frac{1-e^{-\alpha r^2}}{r} \\ V_{s0}&= \frac{V_{s,max}}{1-e^{-\alpha}} = \frac{\Gamma_v}{2\pi r_c}\\ \end{aligned}$$

Vatistas model is used here, since with the shape parameter n a wide range of swirl shapes can be defined, covering the Scully vortex (n=1), the Lamb–Oseen vortex (n≈2), or the Rankine vortex (n=∞). When the data are cleaned from spurious vectors, mean values of the flow subtracted and rotated into the vortex axis system, the distribution of swirl velocities of all vectors is fitted with the Vatistas model using a least squares error method. The best fit is performed at a radial extension of 2–3 core radii.

3 Application to HART II data in hover

Since most of the experimental work done so far was applied to the hover case this is first used for application of the methods described. The vortex was measured at pos. 17h of Fig. 11, or pos. 17 of Fig. 1b, where in this case the blade position was at ψ=180° and the measurement location at ψ=136°, such that the vortex age is ψ _v =44°. This case is presented here in terms of raw data, processed data of an instantaneous image, simple and conditional averaged data, vortex wander, rotation into the vortex axis system, and identification of vortex parameters using a best fit to a Vatistas type vortex.

Fig. 11

Location of tip vortex measurement in hover

3.1 Individual data

First, the set of 100 individual images is processed separately and the results analysed statistically. Images with a vortex centre found more than two standard deviations away from the mean centre position are removed from the analysis, these are 14 of 100. In Fig. 12, the statistics for the remaining 86 images are given. In (a) the position of vortex centres is shown. They have an average standard deviation of 0.0013R=0.022c=2.7 mm in x-direction and almost twice as much in vertical direction, which is the range of the vertical positions of the blade tip.

Fig. 12

Analysis of individual data, hover, ψ _v =44°

The angles about the z-axis needed to rotate the vector field into the vortex axis are given in Fig. 12b, those about the x-axis are in the same range of scatter, but with different mean value. In both angles the standard deviation is ±4° about the AV, which appears reasonable. The core radii found are shown in (c) with a standard deviation of 9% of the AV. In (d) the maximum swirl velocities are shown, the standard deviation is 6% of the AV. The peak of cross-flow velocity is shown in (e). Here the variation is larger, which is due to four individual images where the peak is negative while in all other images it is positive. These four cases represent outliers which were not removed from the data set.

Figure 12f shows the horizontal velocity profile in a vertical cut through the individual vortex centre. The profiles coincide very well and represent the repeatability of the measurements and the appropriateness of vortex centre identification.

3.2 Conditional averaged data

Almost no rotation about the x-axis of the measurement plane is needed for rotation into the vortex axis system (β _x =0.3°), which means the vortex axis orientation is about parallel to the rotor disk at this early stage of the wake. A rotation of β _z =−25° about the vertical axis is found. 14° of this angle accounts for the angle between the PIV plane orientation (150°) and the azimuth of the measurement (136°), Fig. 11. The remaining angle of 11° represents the effect of radial contraction of the tip vortex right after its creation.

Results for both the data in the measurement plane and after rotation into the vortex axis system are shown in Fig. 13. The peak vorticity is found about 20% higher in the vortex axis system, and the effect of rotation is mainly a slight compression of the x-axis, while the vector field looks comparable in both diagrams (a) and (b). More differences are found in the cross-flow distribution shown in Fig. 13c for the measurement plane and (d) for the vortex axis system. Due to the vortex axis inclination with respect to the measurement plane the large swirl velocity becomes part of the cross-flow, with components at the core radius toward the observer in the lower region and away from the observer at the upper region. After rotation into the vortex axis system, only the axial velocity of the vortex is retained, which is directed toward the blade that created the vortex, Fig. 13d. All the area outside the vortex has almost no cross-flow component.

Fig. 13

PIV data of a hover case in the measurement plane and rotated into the vortex axis system, pos. 17h of Fig. 11, ψ _v =44°

In Table 2, the results are given for the parameter identification in the unrotated measurement plane (PIV), the individual average (IA), the conditional average (CA), and the simple average (SA), the latter three rotated into the vortex axis system using the first method of Sect. 2.8. At this age the vortex has a maximum swirl velocity of almost 25% of the tip speed and a core radius of little more than 5% chord, which is in good agreement with LDV data presented in Refs. [12, 13]. Both are also in perfect agreement with the average of the individual data shown in Fig. 12. At this early stage of the vortex age the peak axial velocity in the vortex centre is found to be 18% of the tip speed directed toward the generating blade. It can be seen from the results in Table 2 that the conditional average performs as well as the individual average since the different individual core sizes, swirl velocities, and rotation angles are averaged by both methods to the same resulting values. Thus, the conditional average is thought to be superior to the other methods, since it is significantly less computational intensive.

Table 2 Rotation angles and tip vortex parameters in hover, ψ _v =44°

3.3 Simple averaged data

The analysis results of the SA data, also rotated into the vortex axis system, are given in Table 2 as well. They have to be compared with the data from the CA. Both rotation angles agree within an accuracy of 1°, which indicates the independence of the methodology on the method of averaging. The angles also agree well with the average of the individual data given in Fig. 12c and d.

The maximum vorticity of the simple averaged data is only half of the value of the conditional average, which represents the effect of not accounting for the individual centre locations. This enlarges the core radius as well, and also reduces the peak value of axial velocity to 70% of the individual or the conditional average data. Again, the swirl shape parameter n is less sensitive to the method of averaging.

4 Conclusions

The 3C-PIV vector field processing for proper analysis of vortex parameters requires several methodologies to be applied. Especially the rotation into the vortex axis system allows a more consistent and reliable analysis of vortex core parameters.

• 1. The effect of cross-correlation window overlap is shown to be as important as the size of the cross-correlation window itself for converged estimates of the core radius and the maximum swirl velocity. Since the minimum cross-correlation window size is limited, the overlap must be adjusted following the core radii found in the data. This was not emphazied before, and an overlap of 50% was used virtually in all the literatures without questioning.

• 2. Various methodologies exist to compute velocity gradients, but care must be taken in application since some of them tend to increase noise artificially, and others tend to smooth the data too much. This depends on parameters of the pre-processing, like oversampling.

• 3. The identification of vortex centres is best performed using the area centre of the distribution of a representative scalar value. This can be vorticity (but this has a bad signal-to-noise ratio), or flow field operators like λ₂ or Q that additionally suppress apparent vorticity of shear layers from the wake of the blade. Further improvements are obtained using a convolution of normalized functions representing the expected distribution with the scalar fields.

• 4. The identification of the background velocity is complicated by the presence of the vortex flow field, and by shear layers from the blades. The background in-plane velocities can be analysed from the vortex centre under the assumption that the vortex convects with the background flow. The background out-of-plane or cross-flow velocity must be analysed from the flow outside the vortex proximity since the vortex itself has an axial velocity that is not part of the background, and that has a maximum in the vicinity of the vortex centre itself.

• 5. In most measurements the vortex axis is not normal to the measurement plane. When the inclination angles exceed about 10° the measurement plane must be re-oriented into the vortex axis system. This can be performed in the post-processing by identification of the rotation angles from the cross-flow and swirl velocities.

• 6. The vortex characteristics like core radius, maximum swirl, and shape of the swirl profile can only be analysed in the vortex axis system, using some of the usual mathematical models.

• 7. Results from conditional averaging are found to be very close to the average of individual results in terms of rotation angles, core radius, and maximum swirl.

The methodologies developed can be successfully applied to real world data like those obtained in the HART II test. Future work will put together the results for the creation of generalized vortex models to be used in rotor simulation environments, like prescribed or free-wake codes, for noise, vibration and performance prediction of rotors.