The effect of rotation on conical wave beams in a stratified fluid

Abstract

Experiments are conducted to test extant theory on the effect of uniform rotation Ω on the angle θ of conical beam wave propagation excited by a sphere vertically oscillating at frequency ω in a density stratified fluid. The near-constant Brunt–Väisälä frequency stratification N produced in situ in a rotating cylindrical tank exhibits no effect of residual motion for the range of Froude numbers investigated. Good agreement between experiment and theory is found over the range of angles 15°<θ<65° using the “synthetic schlieren” visualization technique. In particular, the cut-off for wave propagation at ω=2Ω, below which waves do not propagate, is clearly observed.

1 Introduction

Internal wave propagation in stationary stratified fluids has been the subject of considerable research since the pioneering experimental and theoretical study by Mowbray and Rarity (1967). In that study, two-dimensional wave beams appearing in the form of “St. Andrew’s Cross” were observed in a linearly stratified fluid disturbed by a cylinder oscillating vertically at small amplitude over a range of frequencies. The authors demonstrated that, for a linear periodic disturbance of frequency ω, the angle θ of the wave beam propagation with respect to the horizontal satisfies the dispersion relation:

$$ \theta = \sin ^{{ - 1}} {\left( {\omega \mathord{\left/ {\vphantom {\omega N}} \right. \kern-\nulldelimiterspace} N} \right)}, $$

(1)

where $N = {\sqrt { - {\left( {g \mathord{\left/ {\vphantom {g {\rho _{0} }}} \right. \kern-\nulldelimiterspace} {\rho _{0} }} \right)}{{\text{d}}\ifmmode\expandafter\bar\else\expandafter\=\fi{\rho }} \mathord{\left/ {\vphantom {{{\text{d}}\ifmmode\expandafter\bar\else\expandafter\=\fi{\rho }} {{\text{d}}z}}} \right. \kern-\nulldelimiterspace} {{\text{d}}z}} }$ is the Brunt–Väisälä (BV) frequency in the Boussinesq approximation, $\ifmmode\expandafter\bar\else\expandafter\=\fi{\rho }{\left( z \right)}$ is the stratification, ρ₀ is the characteristic density, and z is the vertical coordinate aligned antiparallel to gravity g. An important feature of the dispersion relation is the existence of an upper cut-off frequency ω=N, above which disturbances cannot propagate. This result also applies to axisymmetric disturbances from a localized source, in which case the wave beams are of conical form (Hendershott 1969).

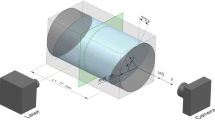
Following the seminal work of Mowbray and Rarity (1967), a number of original studies have appeared. Here, we mention just a few: the generation of conical wave beams produced by an oscillating axisymmetric body (Krishna and Sarma 1969), the effect of viscosity on beam propagation (Il’nykh et al. 1999; Sutherland et al. 1999), and a study on the reflection and interaction of wave beams (Tabaei et al. 2005). The scenario of particular relevance to this paper, the conical wave beam profile generated by an oscillating sphere, is shown in Fig. 1. A related arrangement, in which a spherical source in a rotating stratified fluid breathes fluid in and out periodically, was investigated by Hendershott (1969). The arrangement of an oscillating sphere, considered here, was first studied by Appleby and Crighton (1987). Subsequently, Voisin (1991) obtained an identical result for a pulsating sphere using a Green’s function approach. Most recently, Flynn et al. (2003) adopted the boundary layer approximation of Thomas and Stevenson (1972) to consider the effects of viscous attenuation for wave cones generated by an oscillating sphere. As is the case for wave beams generated by an oscillating cylinder, Flynn et al. (2003) found that, in the vicinity of an oscillating sphere, there is a transition from bimodal to unimodal wave beam structure; their analytical results were supported by experimental measurements.

Fig. 1

Schematic of conical wave propagation produced by a vertically oscillating sphere in a rotating stratified fluid of constant Brunt–Väisälä (BV) frequency

Of prime importance for internal wave propagation in atmospheres and oceans is the effect of rotation. The theory for linear disturbances in a fluid with constant BV frequency, with rotation and gravity vectors arbitrarily inclined, is well known; see, for example, LeBlond and Mysak (1978). For the case in which the background angular velocity Ω is antiparallel to gravity, the dispersion relation reduces to a simple form; the angle of conical wave propagation with respect to the horizontal is given by:

$$ \theta= \sin ^{- 1} \sqrt {\frac{{\omega ^2- 4\Omega ^2}} {{N^2- 4\Omega ^2}}} . $$

(2)

Assuming N>2Ω, the dispersion relation in Eq. 2 shows that propagating waves only exist for excitation frequencies in the range 2Ω<ω<N. Thus, in contrast to a stationary system, a rotating system has both an upper and a lower cut-off frequency, beyond which disturbances cannot propagate. The presence of rotation also affects the group velocity of conical wave propagation (LeBlond and Mysak 1978). Continued theoretical work on the effect of rotation may be found in Cushman-Roisin (1996).

A fundamental concern for experimental investigations of internal wave propagation in a rotating stratified fluid is the equilibrium state of the system. As pointed out by Barcilon and Pedlosky (1967), when a stratified fluid rotates with its container in rigid body motion, the isolines of constant density and pressure are the equilibrium paraboloids:

$$ z - \frac{{\Omega ^2 r^2}} {{2g}} = C, $$

(3)

where C is a constant and r and z are coordinates perpendicular and parallel to the rotation axis, respectively. The coincidence of the geopotential surfaces with the isopycnals means that the isopycnals have non-zero curvature; the steady diffusion equation, therefore, requires vertical motion, violating the assumption of rigid body motion (Greenspan 1969). Should the centrifugal force be sufficiently small compared to the gravitational force, however, the equilibrium paraboloids can be approximated by level surfaces. The parameter measuring the deviation of the gravitational potential from a level surface is the rotational Froude number (Barcilon and Pedlosky 1967):

$$ F = \frac{{\Omega ^2 a}} {g}, $$

(4)

where a is a characteristic radial scale of the container rotating about its vertical axis. For many laboratory experiments involving rotating stratified fluids, F is much smaller than unity and the residual motion due to curvature of the isopycnals is negligible.

Though the theory of internal wave propagation in a rotating stratified fluid has long been established, there has been no direct comparison with measurement; this is the goal of the present investigation. Of particular interest is the reduced regime of wave propagation compared to that for a fluid at rest; for a rotating fluid, there is an additional lower cut-off frequency, below which wave propagation is inhibited. We proceed with a description of the experimental apparatus in Sect. 2. The results of our experiments are presented in Sect. 3, and our conclusions are presented in Sect. 4.

2 Experimental setup and data acquisition

Experiments were conducted using the rotating-air-bearing platform built by Malkus some four decades ago. A cross-sectional sketch of the apparatus is given in Fig. 2. The fluid basin, centrally mounted on the platform, consists of a cylindrical Plexiglas tank, 50 cm deep and 68 cm in diameter, that fits snugly inside a slightly taller square tank, also made of Plexiglas. The inner tank contains stably-stratified saline fluid and the outer tank is filled with fresh water to minimize refraction effects for our optical visualization system.

Fig. 2

Schematic of the experimental setup

The inner tank was stratified from above (as opposed to from below; see, for example, Whitehead 1980) using the Oster (1965) method, with the platform rotating at a predetermined angular velocity in the range 0<Ω<0.5 rad/s. Diminishingly saline fluid from the double bucket system was fed through a polystyrene boat with a sponge base, floating on the surface of the rising water level. The flow rate into the boat was carefully controlled using flow meters to ensure a constant filling rate. During both filling and the ensuing experiment, the angular velocity varied by no more than ±3% and typically by less than ±2%. This variation was attributed to the motion control and to elements of the visualization system mounted asymmetrically on the rotating table. Prior to this investigation, the base plate was removed, machined flat, remounted, and leveled to within 1 mm/m. The data acquisition equipment placed around the perimeter of the platform was balanced with counterweights to minimize the effect of the uneven load. The estimated level of the fully loaded table was still 1 mm/m. The large overall load on the table required increased gas pressure to float the base plate. High pressure nitrogen supply tanks were used, which restricted the run time of an experiment to 4 h.

The density stratification in the rotating tank was measured using a PME salinity probe, calibrated with an Anton-Parr densitometer, accurate to ±0.0002 g/cm³. The probe was lowered slowly into the tank using a computer-controlled linear traverse driven by a micro-stepping motor, and the profile was recorded using a 16-bit DAQ system. The traverse was mounted so that the descent of the probe was vertical to within ±0.5°, as determined by a spirit level. We were fortunate that the constant density surfaces in the tank did not deform significantly at the low rotation rates used in this study. The paraboloids followed by the pycnoclines were most extreme at the highest rotation rate Ω=0.484 rad/s. In this worst case scenario, a simple calculation using Eq. 3 shows the slope of the pycnoclines varied from zero at the axis of rotation to their maximum inclination of 0.47° at the cylindrical wall (more information concerning the maximum pycnocline slopes is detailed later in Table 1). Furthermore, the maximum value of F in our experiments, calculated using Eq. 4, was 0.009. We therefore conclude that residual motion in our rotating stratified experiment was negligible.

Table 1 Experimental conditions showing the angular velocity Ω, fitted density gradients ${\left\langle {{{\text{d}}\ifmmode\expandafter\bar\else\expandafter\=\fi{\rho }} \mathord{\left/ {\vphantom {{{\text{d}}\ifmmode\expandafter\bar\else\expandafter\=\fi{\rho }} {{\text{d}}z}}} \right. \kern-\nulldelimiterspace} {{\text{d}}z}} \right\rangle },$ mid-depth densities ρ₀, BV frequencies N, and maximum free surface angles ϕ_m

After the density profile was recorded, the salinity probe was removed from the linear traverse and replaced by a metal rod 0.635 cm in diameter and 60 cm long, with a 5.08-cm-diameter sphere attached to the lower end. The sphere was immersed slowly through the free surface and then driven down to mid-depth of the stratified fluid, after which the system was left to settle for several minutes. Pre- and post-experiment density profiles showed no apparent permanent modification of the salinity profile due to insertion and retraction of the sphere. Internal wave cones were generated by vertical sinusoidal motion of the sphere about its resting position. The amplitude of oscillation was 1.5 cm, with oscillation periods in the range 7<τ<30 s. The amplitude was accurate to ±0.001 cm and the period to ±0.01 s.

The axisymmetric internal wave beams were visualized using the digital schlieren method (Sutherland et al. 1999). A pattern comprised of evenly spaced dots 0.19 cm in diameter, with 0.38 cm center-to-center horizontal and vertical spacings, was printed on a transparent sheet placed on one side of the filled tank. Uniform backlighting of the pattern was obtained using an electroluminescent sheet. The pattern was viewed through the tank, via a 45° mirror, using a CCD camera; see Fig. 2. The signal from the CCD camera was passed through a set of electrical slip rings, which allowed us to analyze data during an experimental run. To test for parallax in our system, we viewed a calibrated line oriented at 45° to the horizontal using the image acquisition system; on the level of accuracy of our system (0.5 mm), no discernible parallax was detected.

The distortion of the dot pattern due to internal wave motion was recorded and analyzed using Digiflow (Dalziel 2004). Although the wave beam structure was three dimensional in the form of upward and downward wave cones axisymmetric about the vertical, the images were analyzed using two-dimensional processing options in Digiflow. The method by which axisymmetric data can be retrieved from such planar data is described by Onu et al. (2003). However, our goal to measure the cone angle θ as a function of N, Ω, and ω was readily carried out using just the planar data, without the need for detailed axisymmetric analysis.

A gray-scale image from the experiment is shown in Fig. 3. The image shows the upper and lower halves of the wave cones generated for the parameters $\overline{N} = 1.06\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}},$ Ω=0.205 rad/s and ω=0.794 rad/s. The pixel intensity corresponds to the measured displacement of the dot pattern due to internal wave propagation, which can, in principle, be related to the perturbation of the local buoyancy field. The cone angle was measured objectively from images such as this one by using the radon transform function in MATLAB. Specifically, the angle at which the radon transform of an image achieved maximum intensity was defined to be the beam angle. From each image, up to four angle measurements could be taken. The first two measurements were obtained for the bright aspect of the beams, which generated maxima in the radon transform. The pixel intensities were then inverted and the process repeated for the dark aspect of the beams. These four measurements were averaged to determine the cone angle.

Fig. 3

Gray-scale image of the density–gradient perturbation field at $\overline{N} = 1.06\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}},$ Ω=0.205 rad/s formed by the sphere oscillating at frequency ω=0.794 rad/s

3 Presentation of results

Two sets of experiments were performed, in which the goal was to attain near equal BV frequencies for each of three different rotation rates. The resulting density profiles for Ω=0.0, 0.205, and 0.383 rad/s are shown in Fig. 4 and those for Ω=0.0, 0.285, and 0.484 rad/s are displayed in Fig. 5. The profiles have been shifted in the z direction to avoid overlap. For the experiments at the average BV frequency $\overline{N} = 1.06\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}},$ new batches of salt water were prepared prior to each run. For the experiments at $\overline{N} = 1.43\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}},$ the stratification was prepared using saline water from previous runs. We attribute the spikes in the density profiles in Fig. 5 to an improper electrical ground, although it is also conceivable that the probe’s encounter with particulates in the recycled salt water during its traverse played a role. This notwithstanding, the nearly linear density profiles are clear.

Fig. 4

Density profiles for nominal BV frequency $\overline{N} = 1.06\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}$ measured in situ at three rotation rates Ω₁=0.0 rad/s, Ω₂=0.205 rad/s, and Ω₃=0.383 rad/s. The solid line is the experimental data from the salinity probe and the dashed line is a linear fit

Fig. 5

Density profiles for nominal BV frequency $\overline{N} = 1.43\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}$ measured in situ at three rotation rates Ω₁=0.0 rad/s, Ω₂=0.285 rad/s, and Ω₃=0.484 rad/s. The solid line is the experimental data from the salinity probe and the dashed line is a linear fit

Linear least-square fits through the data show remarkably similar mean profiles obtained using the Oster filling method. Values of the average density gradients ${\left\langle {{{\text{d}}\ifmmode\expandafter\bar\else\expandafter\=\fi{\rho }} \mathord{\left/ {\vphantom {{{\text{d}}\ifmmode\expandafter\bar\else\expandafter\=\fi{\rho }} {{\text{d}}z}}} \right. \kern-\nulldelimiterspace} {{\text{d}}z}} \right\rangle },$ densities at the position of the sphere ρ₀, and buoyancy frequencies N determined using g=981 cm/s² are listed in Table 1. Also included in the table are the maximum slopes of the free surface, which mimic the internal isopycnal slopes, calculated using Eq. 3.

The results for nominal BV frequency $\overline{N} = 1.06\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}$ are presented in Fig. 6, in which the experimentally determined cone angle θ is plotted as a function of the nondimensional forcing frequency $\omega \mathord{\left/ {\vphantom {\omega {\overline{N} }}} \right. \kern-\nulldelimiterspace} {\overline{N} }$ for three different background rotation rates, Ω=0.0, 0.205, and 0.383 rad/s. In Fig. 7, the results for nominal BV frequency $\overline{N} = 1.43\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}$ are plotted for background rotation rates Ω=0.0, 0.285, and 0.484 rad/s. In each figure, the solid lines superimposed on the data are the corresponding theoretical solutions calculated using Eq. 2. The error bars are the experimental uncertainty in the beam angle arising from the radon transformation measurements.

Fig. 6

Conical beam angles θ for nominal BV frequency $\overline{N} = 1.06\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}$ measured at three rotation rates Ω₁=0.0 rad/s, Ω₂=0.205 rad/s, and Ω₃=0.383 rad/s. The solid line is the dispersion relation (Eq. 2)

Fig. 7

Conical beam angles θ for nominal BV frequency $\overline{N} = 1.43\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}$ measured at three rotation rates Ω₁=0.0 rad/s, Ω₂=0.285 rad/s, and Ω₃=0.484 rad/s. The solid line is the dispersion relation (Eq. 2)

Data was obtained only in the range 15°<θ<65°. Outside of this range, it was not possible to determine a clear measure of the beam angle for a variety of reasons. Below 15°, it became difficult to obtain a clear beam image, as the vertical oscillations of the sphere generated only very weak disturbances propagating in the near-horizontal direction; although evidence of a wave beam could be seen, a definitive measurement of the beam angle could not be made. Above 65°, the beam pattern became noticeably distorted, as the emanating beams interacted with the support rod and with waves reflected from the upper and lower boundaries.

For the nominal BV frequency $\overline{N} = 1.06\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}},$ no evidence of wave propagation was observed below the lower theoretical cut-off frequencies $\omega \mathord{\left/ {\vphantom {\omega {\overline{N} }}} \right. \kern-\nulldelimiterspace} {\overline{N} } = 0.387$ for Ω₂=0.205 rad/s and $\omega \mathord{\left/ {\vphantom {\omega {\overline{N} }}} \right. \kern-\nulldelimiterspace} {\overline{N} } = 0.723$ for Ω₃=0.383 rad/s. This was also the case for nominal BV frequency $\overline{N} = 1.43\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}},$ rad/s, below the lower cut-off frequencies of $\omega \mathord{\left/ {\vphantom {\omega {\overline{N} }}} \right. \kern-\nulldelimiterspace} {\overline{N} } = 0.399$ for Ω₂=0.285 rad/s and $\omega \mathord{\left/ {\vphantom {\omega {\overline{N} }}} \right. \kern-\nulldelimiterspace} {\overline{N} } = 0.677$ for Ω₃=0.484 rad/s. These observations below the lower cut-off frequencies have been marked as a zero beam angle in Figs. 6 and 7. As a point of note, in a number of cases, there was evidence of second harmonic beams being generated by the oscillating sphere below the theoretical cut-off frequency for the first harmonic. These observations suggest that nonlinear effects in the vicinity of the sphere were capable of generating second-harmonic wave beam propagation; this effect has been previously reported for a vertically oscillating elliptical cylinder by Sutherland and Linden (2002) and for reflecting wave beams by Tabaei et al. (2005).

Another feature of the experiments was the effect of rotation on group velocity. Theory predicts that, for a given beam angle, rotation reduces the magnitude of the group velocity according to the relation:

$$ \left| {\frac{{\left( {c_{\text{g}}^2 - \overline c _{\text{g}}^2 } \right)}} {{c_{\text{g}}^2 }}} \right| = \frac{{f^2 }} {{N^2 }}\left[ {\frac{{\left( {1 - {{f^2 } \mathord{\left/ {\vphantom {{f^2 } {N^2 }}} \right. \kern-\nulldelimiterspace} {N^2 }}} \right)\sin ^2 \theta + 1}} {{\left( {1 - {{f^2 } \mathord{\left/ {\vphantom {{f^2 } {N^2 }}} \right. \kern-\nulldelimiterspace} {N^2 }}} \right)\sin ^2 \theta + {{f^2 } \mathord{\left/ {\vphantom {{f^2 } {N^2 }}} \right. \kern-\nulldelimiterspace} {N^2 }}}}} \right], $$

(5)

where f=2Ω, and c_g and $\bar c_{\text{g}}$ are the magnitude of the group velocities of the waves, respectively, without and with rotation. As an example, for N=1.43 rad/s, Ω=0.484, and θ=20°, the group velocity in the along-beam direction of any given wave number satisfying the dispersion relation (Eq. 2) is approximately one quarter that for the non-rotating system. The implication is that it takes four times longer to establish a conical wave beam with θ=20° in a rotating system than in a non-rotating system. Whilst it was not possible to make rigorous quantitative measurements in this timescale, as visualization of the beam evolution was hampered by a combination of noise in the optical arrangement and the small variation in the rotation rate of the table, it was clear that it took considerably longer for the wave beams to become identifiable in the rotating experiments than in the non-rotating experiments, which is consistent with theoretical predictions.

In the accessible range of measurements, there is very good agreement between experiment and theory. This corroboration is emphasized in Fig. 8, which collapses all the data presented in Figs. 6 and 7 onto a single 45° line.

Fig. 8

Collapsed data for conical beam angle for all stratifications N and rotation rates Ω. The open triangles are for $\overline{N} = 1.06\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}$ and the filled circles are for $\overline{N} = 1.43\;{{\text{rad}}} \mathord{\left/ {\vphantom {{{\text{rad}}} {\text{s}}}} \right. \kern-\nulldelimiterspace} {\text{s}}.$  rad/s. The solid line is the dispersion relation (Eq. 2)

4 Conclusion

The dispersion relation (Eq. 2) governing the propagation of linear internal wave beams in a rotating, stratified, Boussinesq fluid is often utilized, but has never previously been compared with real experimental data. Using the “synthetic schlieren” method, we have visualized the axisymmetric wave cones generated by a vertically oscillating sphere in a rotating tank of salt-stratified water. The observed cone angle as a function of forcing frequency, stratification, and background rotation rate is found to be in good agreement with theory. Notably, the presence of rotation generates a lower frequency bound, below which periodic disturbances cannot propagate—a phenomenon of prime importance in geophysical processes, such as tidal conversion in the oceans.