Comment on the Clauser chart method for determining the friction velocity

Abstract

A known difficulty with using the Clauser chart method to determine the friction velocity in wall bounded flows is that it assumes, a priori, a logarithmic law for the mean velocity profile. Using both experimental and DNS data in the literature, this note explicitly shows how friction velocities obtained using the Clauser chart method can potentially mask subtle Reynolds-number-dependent behavior.

1 Introduction

In the experimental study of turbulent boundary layers, the determination of the friction velocity u _τ , defined as ${\sqrt {{\tau _{w} } \mathord{\left/ {\vphantom {{\tau _{w} } \rho }} \right. \kern-\nulldelimiterspace} \rho } },$ is critical, since most of the scaling laws for the turbulent boundary layer involve u _τ . Unfortunately, data that come from direct measurement of the wall shear stress are not always available, requiring the use of indirect methods to deduce the wall shear stress. Although a number of indirect techniques are available for determining u _τ , none are universally accepted. Boundary layer experimentalists commonly use the Clauser chart method (Fernholz and Finley 1996), which assumes a logarithmic law for the mean velocity profile¹. Problems with using the Clauser chart approach to determine the friction velocity are recognized by many researchers. George and Castillo (1997), for example, showed clear discrepancies between mean velocity profiles scaled using direct measurements of u _τ and approximations using the Clauser method. However, a clear explicit discussion of its shortcomings and the implications for masking Reynolds number dependencies is not found in the literature. The purpose of this note is to explicitly illustrate, using manufactured data, DNS data, and experimental data, how data scaled using u _τ obtained from the Clauser chart method can contaminate the data in such a way as to mask subtle Reynolds-number-dependent behavior in the near-wall region.

2 The Clauser chart method

In the Clauser chart method (Clauser 1956), the friction velocity is extrapolated from direct measurements of the free stream velocity U_∞ and the mean velocity profile U(y), where y is the normal distance from the wall. The method is based on the assumption that the velocity profile follows a universal logarithmic form in the overlap region of the boundary layer:

$$ \frac{{U{\left( y \right)}}} {{u_{\tau } }} = \frac{1} {\kappa }\ln {\left( {\frac{{yu_{\tau } }} {\nu }} \right)} + B $$

(1)

and that the constants κ and B are independent of the Reynolds number. If we multiply both sides of Eq. 1 by u _τ /U_∞, we obtain:

$$ \frac{{U{\left( y \right)}}} {{U_{\infty } }} = {\left[ {\frac{1} {\kappa }\frac{{u_{{^{\tau } }} }} {{U_{\infty } }}} \right]}\ln {\left( {\frac{{yU_{\infty } }} {\nu }} \right)} + {\left[ {\frac{1} {\kappa }\frac{{u_{\tau } }} {{U_{\infty } }}\ln {\left( {\frac{{u_{\tau } }} {{U_{\infty } }}} \right)} + B\frac{{u_{\tau } }} {{U_{\infty } }}} \right]} $$

(2)

Noting that the coefficient of friction C_f is defined as 2(u _τ /U_∞)², the Clauser chart equation can be written in the following form:

$$ \frac{{U{\left( y \right)}}} {{U_{\infty } }} = {\left[ {\frac{1} {\kappa }{\sqrt {\frac{{C_{{\text{f}}} }} {2}} }} \right]}\ln {\left( {\frac{{yU_{\infty } }} {\nu }} \right)} + {\left[ {\frac{1} {\kappa }{\sqrt {\frac{{C_{{\text{f}}} }} {2}} }\ln {\left( {{\sqrt {\frac{{C_{{\text{f}}} }} {2}} }} \right)} + B{\sqrt {\frac{{C_{{\text{f}}} }} {2}} }} \right]} $$

(3)

Since U(y) and U_∞ can be measured directly from experiments, and assuming that κ and B are constants, the only undetermined term in Eq. 3 is the coefficient of friction C_f. This equation defines a family of lines from which C_f can be determined by plotting the experimental data in this same form and selecting the line that most closely approximates the data between the region y⁺>50 and η<0.2. It is common to find different κ and B in the literature, e.g., κ variations of 0.38<κ<0.45 and B variations of 3.5<B<6.1 (Zanoun et al. 2003). The uncertainty of the experimental data can be obscured by the change of these constants.

3 Potential for data contamination

3.1 Hypothetical illustrations

Various aspects of the logarithmic law for the mean velocity profile have recently been questioned by some authors (Bradshaw and Huang 1995). In particular, there is debate as to whether κ and B are truly independent of the Reynolds number (Zanoun et al. 2003). Here, without taking either side on this debate, we highlight the problems with using the Clauser chart method to compute the friction velocity if, in fact, κ and B are not true universal constants.

To clearly illustrate this problem, consider the following hypothetical situation. Consider an experiment conducted to determine velocity profiles of turbulent boundary layer flow with measurements taken at a set of different downstream locations (with the same free stream velocity) corresponding to increasingly higher Reynolds numbers. Assume that the Clauser method described above is used to calculate the friction velocity at each of these locations, and that the data is subsequently normalized and plotted using the friction velocities so obtained. The friction velocities determined in this manner are denoted as u_τ|c. Next, assume that the “true” friction velocity, denoted here as u_τ|t, varies from the Clauser-chart-based experimentally determined friction velocities in the following manner:

$$ u_{{\tau |c}} = f{\left( {Re} \right)}u_{{\tau |t}} $$

(4)

By substitution of Eq. 4 into Eq. 1, one can show that the “true” velocity profiles associated with this situation can be written as:

$$ \frac{{U{\left( y \right)}}} {{u_{{\tau |t}} }} = f{\left( {Re} \right)}\frac{1} {\kappa }\log {\left( {\frac{{yu_{{\tau |t}} }} {\nu }} \right)} + f{\left( {Re} \right)}{\left( {B + \frac{1} {\kappa }\log {\left( {f{\left( {Re} \right)}} \right)}} \right)} $$

(5)

which should now be compared with Eq. 1. Note that the κ and additive constant B of the inner normalized velocity profiles are both Reynolds-number-dependent in this illustration. As a simple example, assume that the values of f(Re) at five different locations are f(Re)=0.8, 0.9, 1.0, 1.1, and 1.2, respectively. The difference between the “true” friction velocity u_τ|t and the Clauser-chart-based friction velocity u_τ|c can be defined quantitatively as:

$$ \frac{{u_{{\tau |t}} - u_{{\tau |c}} }} {{u_{{\tau |t}} }} = 1 - f{\left( {Re} \right)} $$

where this difference is approximately 20%, 10%, 0%, −10%, and −20%, respectively, for this hypothetical situation. Figure 1 shows the five mean velocity profiles plotted for this hypothetical case when normalized by the true friction velocity, clearly illustrating the different slopes for these five cases.

Fig. 1

Hypothetical velocity profiles generated in the form of $\frac{{{\left\langle U \right\rangle }}} {{u_{{\tau |t}} }} = \frac{n} {\kappa }\ln {\left( {\frac{{yu_{{\tau |t}} }} {\nu }} \right)} + n{\left( {B + \frac{1} {\kappa }\ln {\left( n \right)}} \right)}.$ Five profiles are shown corresponding to n=0.8, 0.9, 1.0, 1.1, and 1.2. Note that the “universal log law” corresponds to n=1

When plotting these same velocity profile data in nondimensional form using a computed set of Clauser-chart-based friction velocities, u_τ|c, the results shown in Fig. 2 are obtained. As can be seen, all of the profiles that were so clearly distinct in Fig. 1 have been artificially collapsed onto a single line in Fig. 2 as a result of the assumptions inherent in the Clauser chart method. Use of the Clauser chart method in this case would lead to erroneous conclusions concerning how the mean velocity profiles scale with Reynolds number.

Fig. 2

The velocity profiles of Fig. 1 normalized by friction velocities obtained using the Clauser chart method

As another example, consider a very weak Reynolds number dependence, f(Re)=Re ^0.02 _τ . The results for this hypothetical situation are illustrated in Figs. 3 and 4. (The values for κ and B for the Clauser chart are chosen to be 0.41 and 5.0, respectively.) Figure 3 shows the clear Reynolds-number-dependence of the hypothetical cases. The real κ (inverse of the slope) and additive constant of the log-region of the hypothetical velocity profiles are (0.357, 6.12), (0.346, 6.42), and (0.341, 6.55) for Re _τ =1,000, 5,000, and 10,000, respectively. The Clauser-chart-method-determined friction velocity collapses the Reynolds-number-dependent κ and intercept “log-region” onto a single line, as in Fig. 4, masking any Reynolds number dependence.

Fig. 3

Hypothetical velocity profiles generated in the form of $\frac{{{\left\langle U \right\rangle }}} {{u_{\tau } }} = \frac{{Re^{{0.02}}_{\tau } }} {\kappa }\ln {\left( {\frac{{yu_{\tau } }} {\nu }} \right)} + {\left( {Re^{{0.02}}_{\tau } } \right)}{\left( {B + \frac{1} {\kappa }\ln {\left( {Re^{{0.02}}_{\tau } } \right)}} \right)}.$ The ”universal log law” is also shown as a solid line

Fig. 4

The velocity profiles of Fig. 3 normalized by friction velocities obtained using the Clauser chart method

These manufactured examples are intended to clearly demonstrate how the Clauser chart method can contaminate data. In the next three subsections, similar comparisons are presented using real experimental and DNS data for pipe flow, channel flow, and zero-pressure-gradient boundary layer flow.

3.2 Example contamination using experimental pipe flow data

In pipe or channel flow, the wall shear stress (and thus, the friction velocity) can be deduced directly from measurements of the pressure gradient, so other approaches, such as using the Clauser chart, are not required. However, for the purpose of illustrating the degree to which the Clauser chart method can bias the data, we examine the data of Patel and Head (1969). Figure 5 shows mean velocity profiles measured at three different low Reynolds numbers (Re=U _c R/ν=4,430, 7,260, and 9,200). These three cases correspond to an Re _τ (Reynolds number based on friction velocity) of 150, 230, and 290, respectively. Since the pressure gradient is accurately known, the wall shear stress is known and the nondimensionalized data presented by Patel and Head is free from data reduction artifacts. The top set of curves in Fig. 5 show their data normalized by the “true” friction velocity. However, if a friction-velocity-based Clauser chart method were used, the data artificially collapses to a logarithmic profile, as shown by the bottom set of curves in Fig. 5. As the Reynolds number increases, the difference in the real friction velocity, u _τ , and that determined from the Clauser method decreases. For the cases discussed above, the differences are, from lowest to highest Reynolds number, 8%, 2%, and 0.2%. This suggests that, as the Reynolds number increases, the friction velocity obtained from Clauser chart method approaches the real friction velocity.

Fig. 5

The mean experimental velocity data of Patel and Head (1969) normalized by the “true” friction velocity (upper set of curves) and the friction velocities obtained by using the Clauser chart method (lower set of curves). The two sets of data are vertically offset here for clarity. The Reynolds number is defined by the pipe diameter and mean velocity

3.3 Example contamination using DNS data for channel flow

The turbulent channel flow DNS data of Moser et al. (1999) have been examined to illustrate the potential effect of using the Clauser chart method on channel flow. In Fig. 6, the velocity profiles normalized with the true friction velocities (upper set) and with the Clauser-chart-obtained friction velocities are provided. Note that the real κ and additive constant B for Moser et al.’s data (1999) are (0.375, 4.9), (0.41, 5.3), and (0.41, 5.3) for Re _τ = 180, 395, and 590, respectively, while the κ and B obtained by the Clauser chart method are 0.41 and 5.2, respectively. Although not as dramatic as the experimental pipe flow data of Patel and Head (1969), use of the Clauser chart method clearly results in obscuring the low Reynolds number dependency. Differences between the true friction velocity and the friction velocity obtained from the Clauser chart are 4.3%, 2.6%, and 2.5% for the cases shown. It is clear from Fig. 6 that the difference between the true friction velocity and that obtained from the Clauser chart method becomes smaller with increasing Reynolds number.

Fig. 6

The mean DNS velocity data of Moser et al. (1999) normalized by the “true” friction velocity (upper set of curves) and the friction velocities obtained by using the Clauser chart method (lower set of curves). The two sets of data are vertically offset here for clarity

3.4 Example contamination using experimental turbulent boundary layer flow data

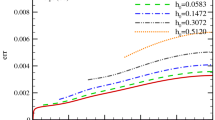
The low Reynolds number flat plate boundary layer data of Purtell et al. (1981) was selected to reveal the effects of using the Clauser chart method to obtain the friction velocity. Velocity profiles with Reynolds number values of Re _θ =465, 500, 1,340, 1,840, 3,480, and 5,100 are reported. Purtell et al. (1981) obtained measurements of the wall shear stress through two approaches: (1) direct measurements of the wall velocity gradients using hot-wire anemometer; and (2) an indirect approach that used computed values of dθ/dx and the Karman integral relation. They reported the differences between the two approaches to be within 5% and showed no systematic trends. In Fig. 7, the mean velocity profiles are plotted using their computed values of the wall shear stress and the value obtained from the Clauser chart method. The subtle low Reynolds number effect evident in the Purtell et al. (1981) data (upper set of Fig. 7) is masked by use of the Clauser chart method, as shown in the lower set of Fig. 7.

Fig. 7

Turbulent boundary layer data of Purtell et al. (1981) normalized by the “true” friction velocity (upper set of curves) and the friction velocities obtained by using the Clauser chart method (lower set of curves). The two sets of data are vertically offset here for clarity

4 Conclusion

The Clauser chart method assumes the existence of the universal logarithmic law. As a result, the use of this method to compute u _τ can result in an artificial collapse of the data onto the universal log-law. In this paper, it has been explicitly shown how possible low Reynolds number dependencies can be masked by use of the Clauser chart method. The difference between the true friction velocity and that obtained from the Clauser chart method diminishes with increasing Reynolds number.